On the Bias of the Maximum Likelihood Estimators of Parameters of the Weibull Distribution
Abstract
:1. Introduction
2. Maximum Likelihood Estimators and Different Bias-Corrected Maximum Likelihood Estimators
2.1. Maximum Likelihood Estimators
2.2. Analytic Bias-Corrected Maximum Likelihood Estimators
2.3. Bootstrap Bias-Corrected Estimators
3. Percentile Estimators
4. Least Squares Estimators
5. Simulation Study
5.1. Procedures
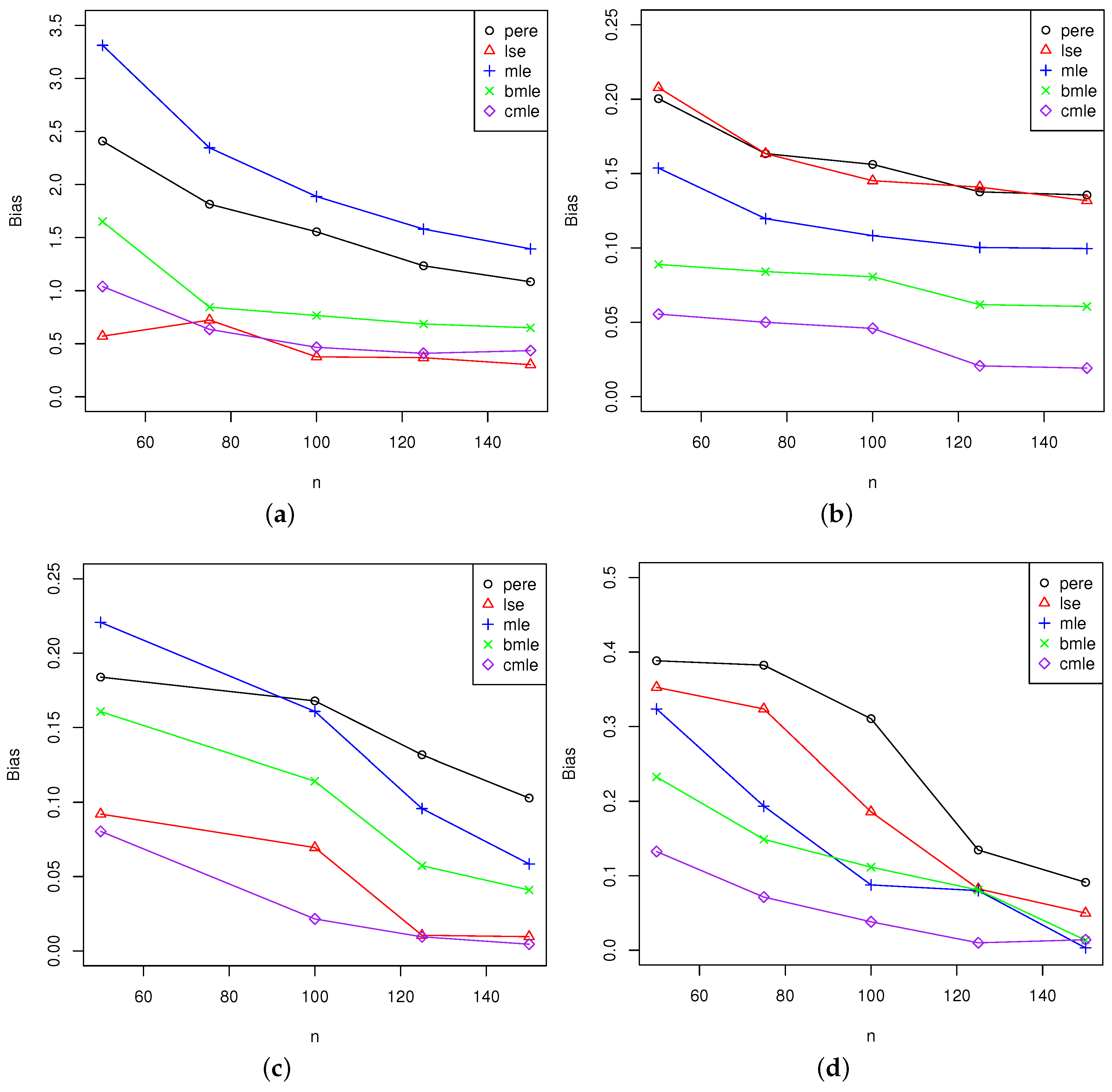
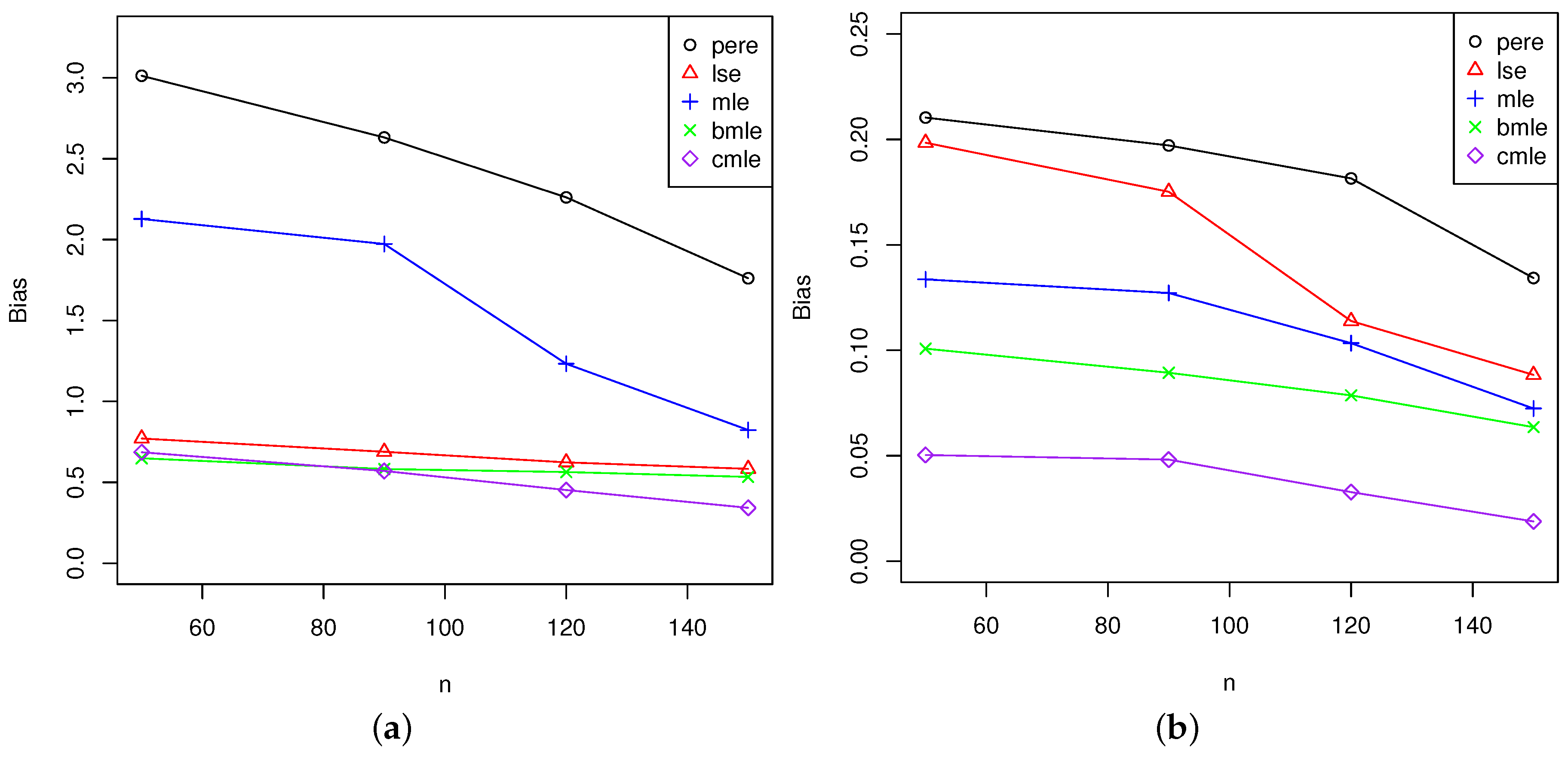
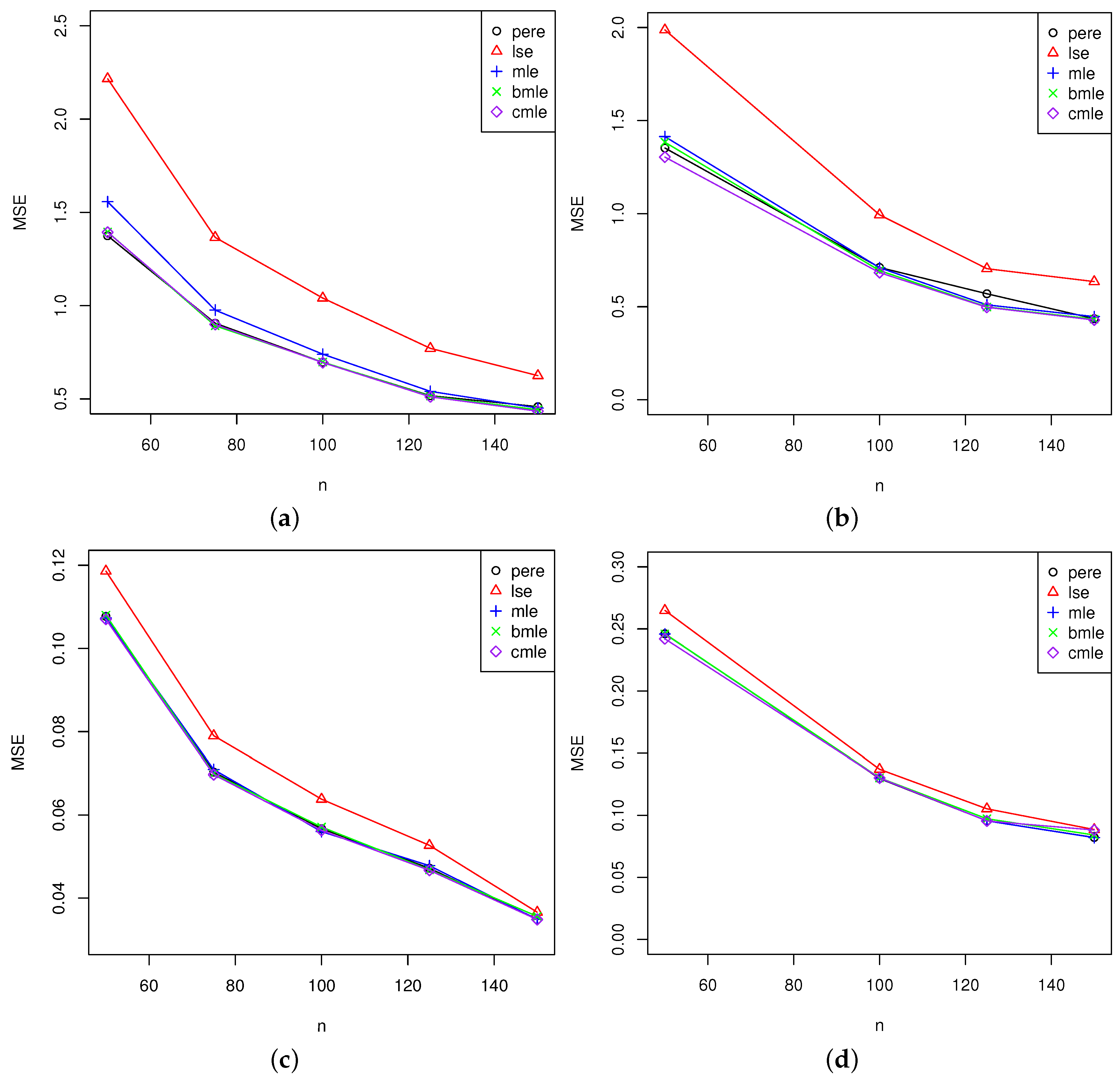
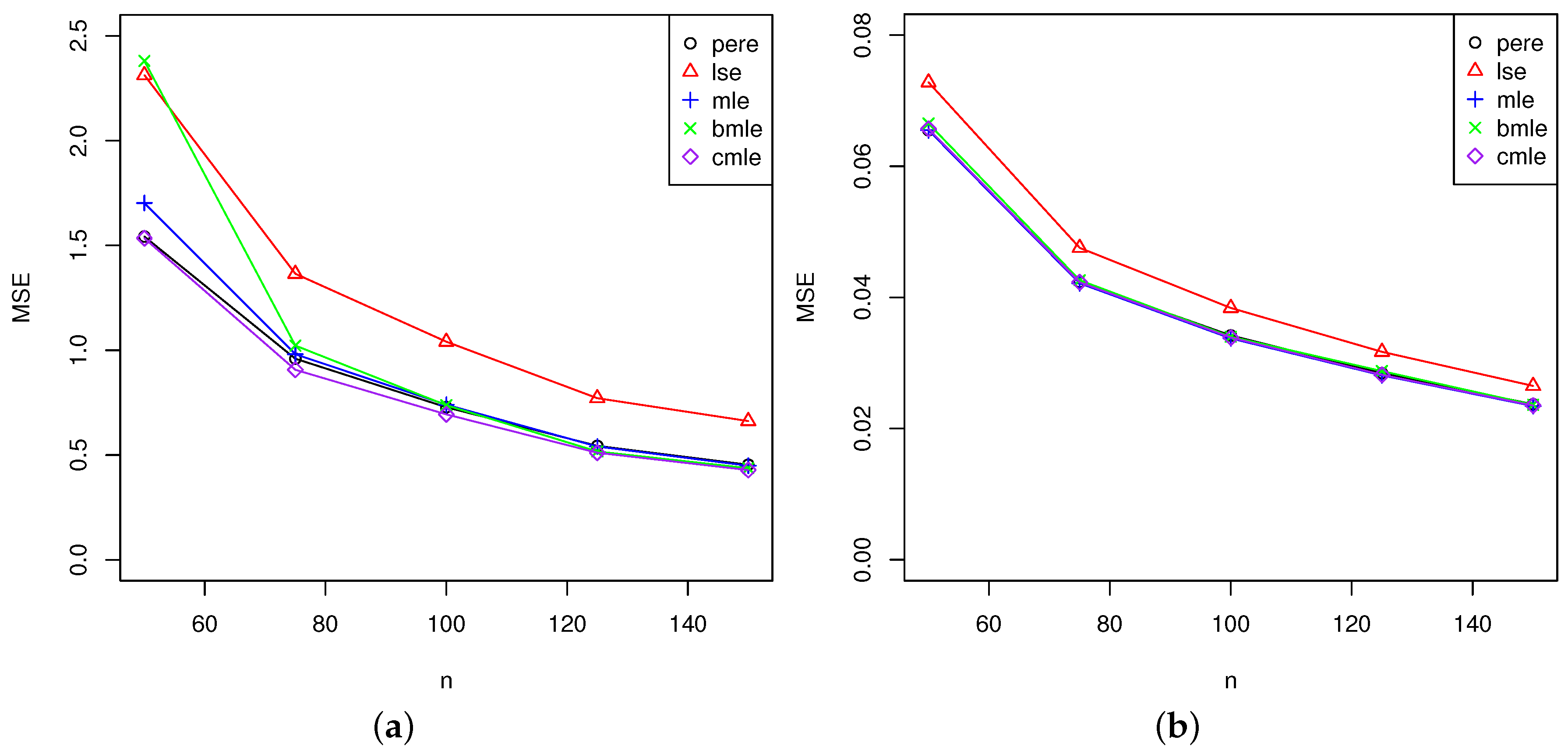
5.2. Analysis of the Results
5.2.1. Comparison of Maximum Likelihood Estimators and Bias-Corrected Maximum Likelihood Estimators
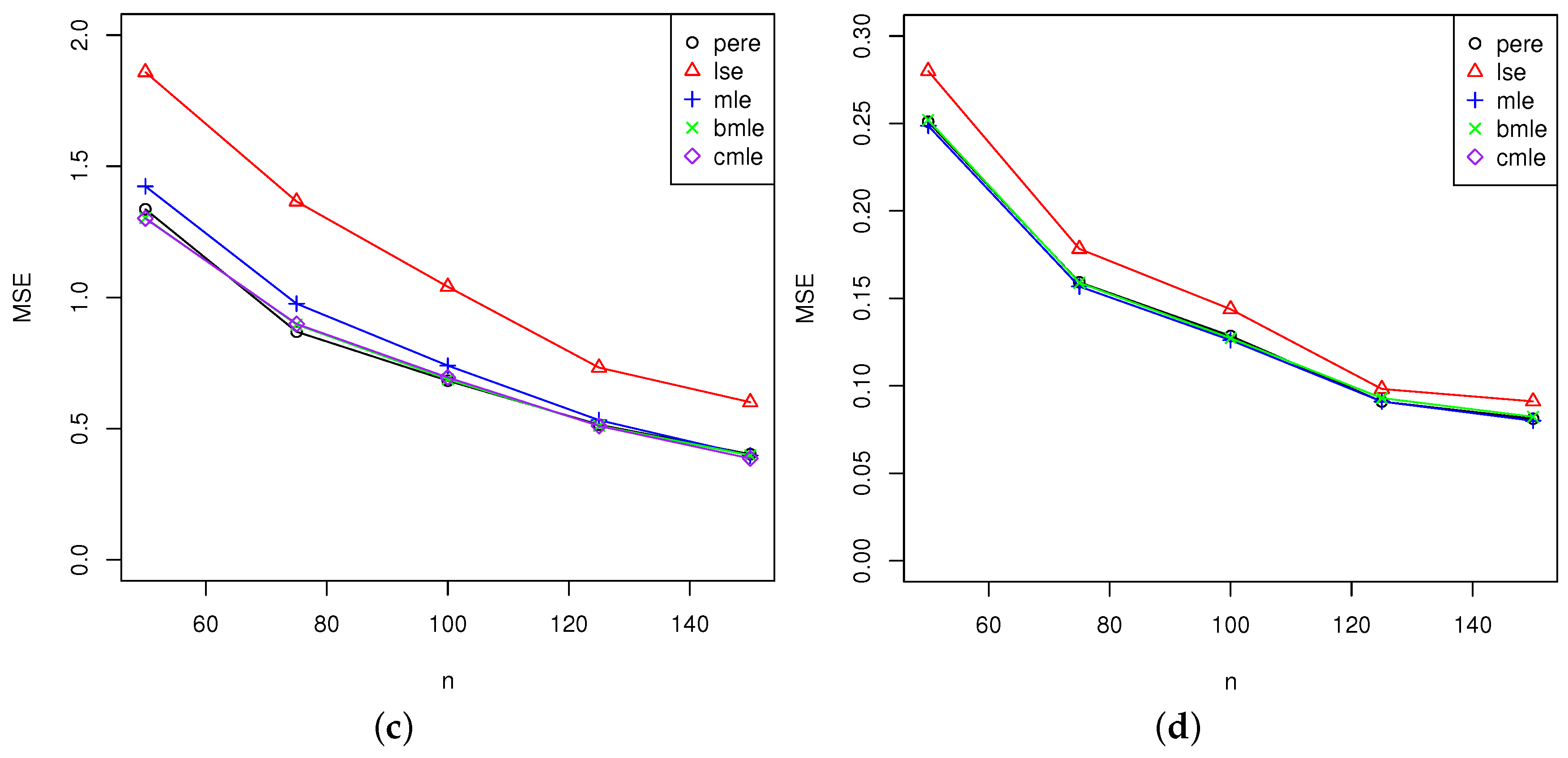
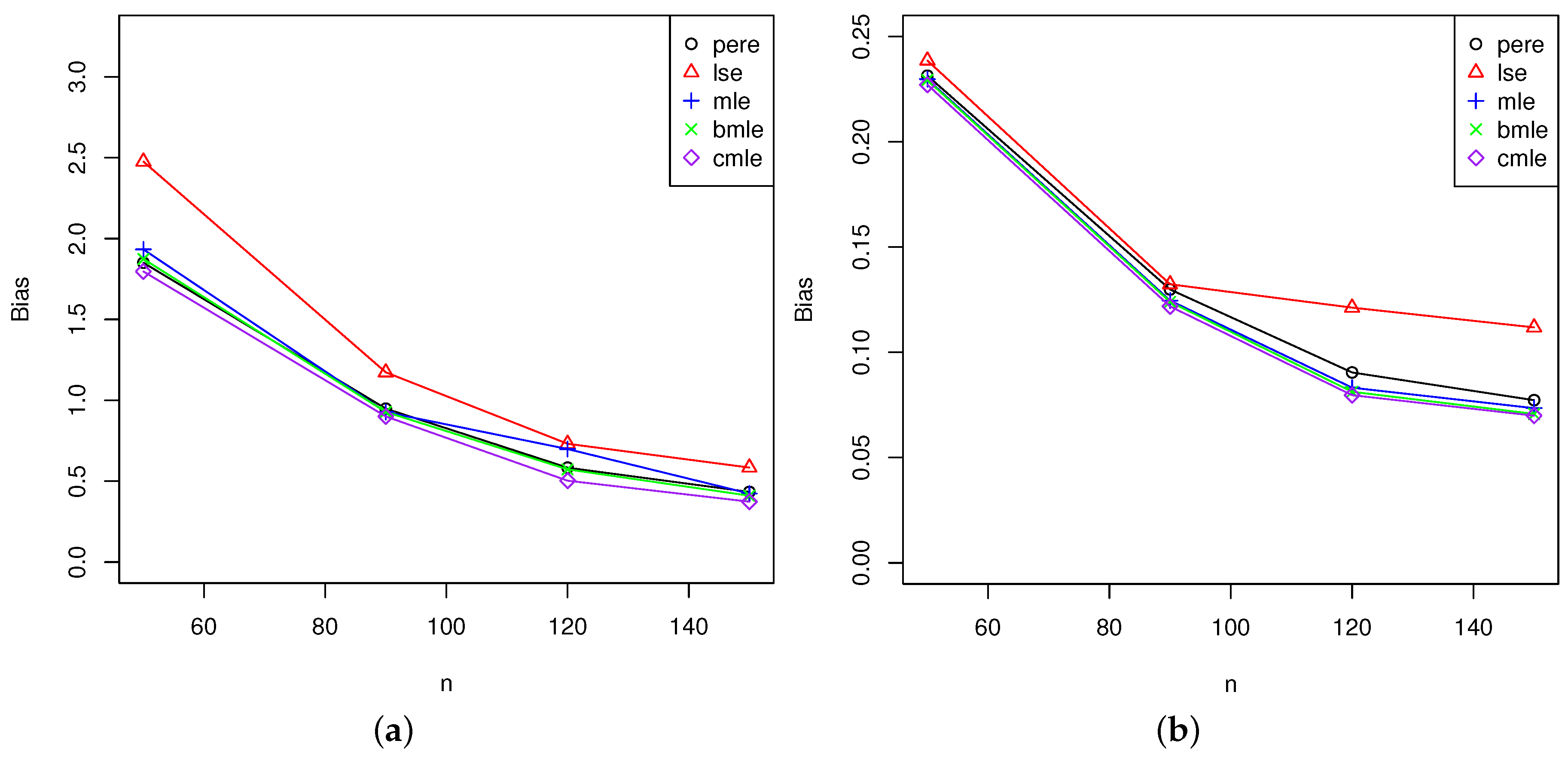
5.2.2. Analysis for All Estimators
6. Real Illustrative Example
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Specific Calculation
References
- Rosin, P.O.; Rammler, E.J. The Laws Governing the Fineness of Powdered Coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Ling, X.; Giles, D.E. Bias Reduction for the Maximum Likelihood Estimator of the Parameters of the Generalized Rayleigh Family of Distributions. Commun. Stat. Theory Methods 2009, 43, 1778–1792. [Google Scholar] [CrossRef]
- Fréchet, M. Sur la loi de Probabilité de Lécart Maximum. Ann. Soc. Pol. Math. 1927, 6, 93–116. [Google Scholar]
- Kaltschmidt, E.; Dzionara, M.; Donner, D.; Wittmann, H.G. Application of the Weibull Distribution on the Evaluation of the Aircraft System Operational Reliability. Mol. Gen. Genet. MGG 1967, 100, 364–373. [Google Scholar] [CrossRef] [PubMed]
- Mikolaj, P.G. Environmental applications of the weibull distribution function: Oil pollution. Science 1972, 176, 1019–1021. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.P. On application of the Weibull distribution in hydrology. Water Resour. Manag. 1987, 1, 33–43. [Google Scholar] [CrossRef]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, R-36, 106–108. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A Modified Weibull Distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Hirose, H. Maximum likelihood parameter estimation in the extended Weibull distribution and its applications to breakdown voltage estimation. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 524–536. [Google Scholar] [CrossRef]
- Fabiani, D.; Simoni, L. Discussion on application of the Weibull distribution to electrical breakdown of insulating materials. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 11–16. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Jarallah, A.H.R.A. Marshall-Olkin extended Weibull distribution and its application to censored data. J. Appl. Stat. 2005, 32, 1025–1034. [Google Scholar] [CrossRef]
- Akdaǧ, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Stat. Soc. 1968, 30, 248–275. [Google Scholar]
- Cordeiro, G.M.; Klein, R. Bias correction in ARMA models. Stat. Probab. Lett. 1994, 19, 169–176. [Google Scholar] [CrossRef]
- Giles, D.E. Bias-corrected maximum likelihood estimation of the parameters of the generalized Pareto distribution. Commun. Stat. Theory Methods 2012, 45, 2465–2483. [Google Scholar] [CrossRef]
- Wang, M.; Wang, W. Bias-corrected Maximum Likelihood Estimation of the Parameters of the Weighted Lindley Distribution. Commun. Stat. Simul. Comput. 2017, 46, 530–545. [Google Scholar] [CrossRef]
- Mackinnon, J.G.; Smith, A.A. Approximate bias corrections in econometrics. J. Econom. 1998, 85, 205–230. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. On bootstrap and analytical bias corrections. Econ. Lett. 1998, 58, 7–15. [Google Scholar] [CrossRef]
- Ho, L.L.; da Silva, A.F. Bias Correction for Mean Time to Failure and p-Quantiles in a Weibull Distribution by Bootstrap Procedure. Commun. Stat. Simul. Comput. 2005, 34, 617–629. [Google Scholar] [CrossRef]
- Focarelli, D. Bootstrap bias-corrected estimators to investigate the long-run properties of money demand in the euro area. Econ. Model. 2002, 22, 305–325. [Google Scholar] [CrossRef]
- Kao, J.H.K. Computer Methods for Estimating Weibull Parameters in Reliability Studies. IRE Trans. Reliab. Qual. Control 1958, 13, 15–22. [Google Scholar] [CrossRef]
- Kao, J.H.K. A Graphical Estimation of Mixed Weibull Parameters in Life-Testing of Electron Tubes. Technometrics 1959, 1, 389–407. [Google Scholar] [CrossRef]
- Mann, N.R.; Schafer, R.E.; Singpurwalla, N.D. Methods for statistical analysis of reliability and life data. J. R. Stat. Soc. 1974, 139, 1974. [Google Scholar]
- Gupta, R.D.; Kundu, D. Generalized exponential distribution: Different method of estimations. J. Stat. Comput. Simul. 2001, 69, 315–337. [Google Scholar] [CrossRef]
- Swain, J.; Venkatraman, S.; Wilson, J.R. Least-squares estimation of distribution function in Johnson’s translation system. J. Stat. Comput. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Murdoch, D. R-3.2.2 for Windows. Available online: https://cran.r-project.org/bin/windows/base/old/3.2.2/ (accessed on 27 August 2015).


| n | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 |
| n | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 | ||||||
| , | 10 | |||||
| 20 | ||||||
| 50 | ||||||
| 90 | ||||||
| 120 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 0.100 | 7.00 | 36.00 | 67.00 | 84.00 | 0.200 | 11.00 | 40.00 | 67.00 | 84.00 | 1.00 | 12.00 | 45.00 | |
| No. | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 67.00 | 84.00 | 1.00 | 18.00 | 46.00 | 67.00 | 85.00 | 1.00 | 18.00 | 47.00 | 72.00 | 85.00 | 1.00 | |
| No. | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 18.00 | 50.00 | 75.00 | 85.00 | 1.00 | 18.00 | 55.00 | 79.00 | 85.00 | 2.00 | 18.00 | 60.00 | 82.00 | |
| No. | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | ||
| 85.00 | 3.00 | 21.00 | 63.00 | 82.00 | 86.00 | 6.00 | 32.00 | 63.00 | 83.00 | 86.00 |
| 16.52175 | 16.63145 | 16.22125 | 16.60235 | 16.15814 |
| 83.64601 | 83.48114 | 83.655114 | 83.58114 | 83.669204 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Zhang, Z.; Cui, C. On the Bias of the Maximum Likelihood Estimators of Parameters of the Weibull Distribution. Math. Comput. Appl. 2017, 22, 19. https://doi.org/10.3390/mca22010019
Chen M, Zhang Z, Cui C. On the Bias of the Maximum Likelihood Estimators of Parameters of the Weibull Distribution. Mathematical and Computational Applications. 2017; 22(1):19. https://doi.org/10.3390/mca22010019
Chicago/Turabian StyleChen, Man, Zheng Zhang, and Cen Cui. 2017. "On the Bias of the Maximum Likelihood Estimators of Parameters of the Weibull Distribution" Mathematical and Computational Applications 22, no. 1: 19. https://doi.org/10.3390/mca22010019
APA StyleChen, M., Zhang, Z., & Cui, C. (2017). On the Bias of the Maximum Likelihood Estimators of Parameters of the Weibull Distribution. Mathematical and Computational Applications, 22(1), 19. https://doi.org/10.3390/mca22010019




