Abstract
This paper proposes a reliable network interdiction model with multiple unit costs, which maximizes the minimum arrival cost of the invader to the sink by setting obstacles on some arcs with limited resources in the given network. In other words, given a graph with a source and a sink, several arcs will be selected with limited resources such that each path contains as many weights as possible. This model needs to be transferred into a bilevel program because its constraints can hardly be listed explicitly even for a graph with a moderate size, because the number of paths between any two given points increases exponentially according to the size of the graph. This bilevel model is equivalent to an integer model with a low degree number of constraints by converting the inner programming to a shortest path problem. We first prove that this problem is non-deterministic polynomial-time (NP)-hard. Secondly, we reduce the number of constraints to the first power from the exponential degree by using the dual technique. Lastly, the national railway network is used to show the feasibility of our method.
1. Introduction
The network interdiction problem has been a classical problem in combinatorial optimization since the 1960s [1,2]. Recently, due to several malevolent intentional attacks such as terrorist attacks in Paris, the issue has acquired more attention. It can be seen as a special case of a static Stackelberg game [3,4]. Commonly, two players are involved in this problem: the interdictor and the invader. This problem concerns how the interdictor prevents the invader from getting through some arcs with sensors. The interdictor’s aim is to minimize the maximum flow of potential threats produced by invaders. Steinrauf et al. [5] and Ajay et al. [6] considered how to set sensors on some arcs to restrain the flow of drugs between big cities. However, an efficient optimal algorithm is not the emphasis of this study because this problem is proved to be non-deterministic polynomial-time (NP)-complete [7]. Practically, heuristic algorithms are often used for solving NP-complete problems rather than approximation algorithms. CPLEX (IBM ILOG CPLEX Optimization Studio, Ibm Corporation, Armonk, New York, USA), popular optimization software which we have been using, is usually used to solve mixed integer programs and can also help us figure out the interdiction problem. The probability of sensor failure, however, was hardly considered in earlier studies. Then, some more stochastic interdiction models were proposed after statistics become popular. Cormican et al. [8] presented a stochastic interdiction model and designed an approximation algorithm. Berry et al. [9] applied the interdiction model to a municipal water system. In that paper, the invader was toxic water which can be detected by water monitors. The interdiction problems used in many applications include military operations, such as critical infrastructure and key resources (CIKR) [10], homeland security [11], and border control [12,13]. The stochastic interdiction model is applied to thwart nuclear smuggling from the perspective of homeland security [14]; radiation sensors were installed to minimize the probability of evasion. With the application of CIKR, Scaparra et al. [15] proposed a bilevel program based on the network flow interdiction problem and provided an implicit enumeration (IE) algorithm. Essentially, most interdiction models are equivalent to bilevel mixed integer programs [15,16], whereas there cannot be a substantive breakthrough for these problems unless P = NP. The key point of the model is the inner program; this bilevel program can be transferred to a mixed integer program using dual techniques if the inner-level program is a linear one. Some other interdiction models have also been studied recently, such as the shortest path problem [17], matching problems [18], Program Evaluation and Review Technique (PERT) networks [19], and median problems [20].
Even with these studies, the interdiction models are not practical, especially for those situations including the invader’s multiple strikes. It is necessary to propose reliable models because the invader’s damage could be devastating. The idea of reliability is the basis of our previous work [21], and in this paper, we extend the model from the perspective of complexity, theory and practice. We extend the previous model [21] with multiple unit costs for both the interdictor and the invader. This model is transferred into a bilevel program because its constraints can hardly be listed explicitly, even for a graph with a moderate size. Besides proving the computational complexity of this problem, a practical case is given to illustrate the feasibility of our method.
This paper has two main contributions. Practically, the proposed model combined with the idea of reliability is more appropriate than the classic interdiction network models for applications in many fields, such as CIKR, border control and so on. Theoretically, this paper gives an approach to present a very complex integer program using the dual technique, even though it is still intrinsically difficult to solve this model from the perspective of computational complexity and we know it is impossible to solve this efficiently unless P = NP.
The remainder of this paper is organized as follows. Section 2 proposes an intuitive program as well as an equivalent bilevel program formulation. Section 3 proves that the proposed model is a NP-hard problem. The solution of this model is presented in Section 4. Section 5 illustrates the operability of our methods using the example of the national railway network. Finally, this study concludes the paper in Section 6.
2. Models
Let denote a directed network with node set N and arc set . Two special nodes are identified: the source node s and the sink node t. Each arc has an interdiction cost , an invader cost with a sensor on this arc and an invader cost without a sensor on this arc, and R is the limit on total interdiction cost. Our aim is to maximize the minimum cost of the invader spent from the source node s to the sink node t by setting some sensors in arcs within limited resources, i.e., to maximize the minimum cost within all paths from the source to the sink.
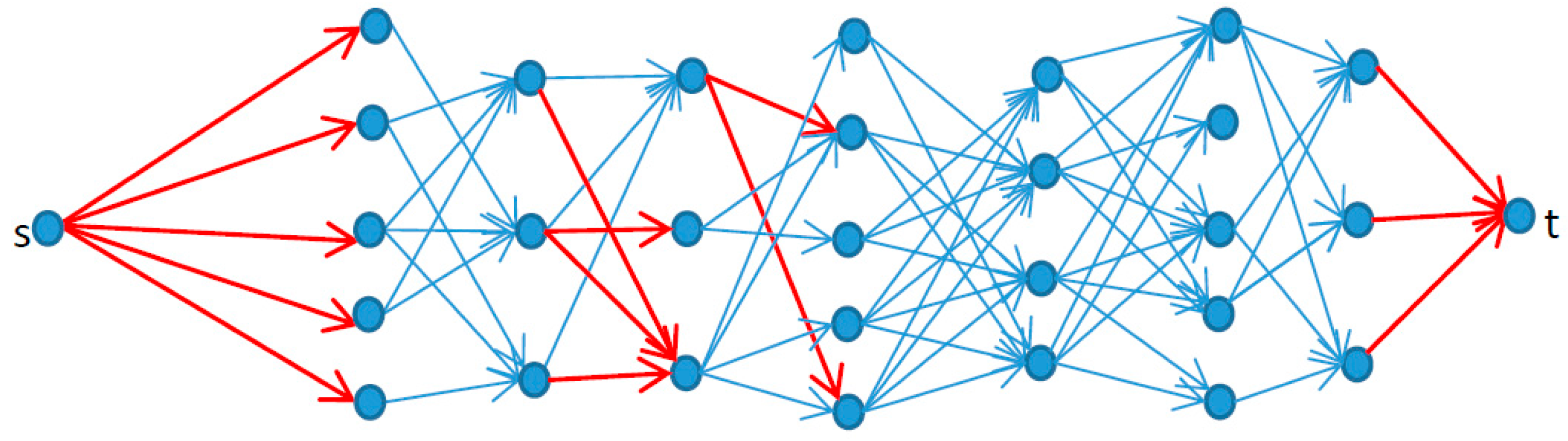
Figure 1 shows a simple example of this model by setting and for all arcs; the interdictor’s strategy is choosing some arcs to make the costs of the invader getting to t from s as high as possible.
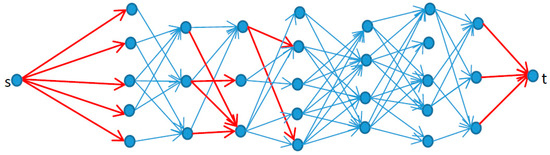
Figure 1.
An example of a reliable network interdiction model. The red lines indicate the paths chosen by the interdictor.
We can formulate for this problem:
where P* denotes all paths from s to t, RI represents the cost of the invader getting to t from s and decision variables are : if the interdictor sets up sensors on , otherwise .
It is generally impossible to present all the constraints in this model even though the network is a moderate size; thus, we show the following equivalent model. Let for each arc and have a similar meaning as in . Then we have the following equivalent bilevel program:
where is the shortest path from the source to the sink in the directed network with a given , and has the same meaning within the model . It is easy to confirm that the model is equivalent to the model and we will list this conclusion without proof.
Proposition 1.
Let be a feasible solution of and P. Then is an optimal solution of if and only if it is also an optimal solution of P.
We need to present formally as follows:
where is the incident matrix of , and is the n-dimensional vector. The first constraint is on the vertex s, the second one is on the vertex t and the other is on the other vertexes among the first n constraints in this model. Further, denotes the arc chosen by the invader, which is on the shortest path, and otherwise .
We will discuss the existence of an efficient algorithm for first before solving this model.
3. Computational Complexity
A decision form of is needed before discussing the computational complexity.
(decision). For any given network and , does there exist an such that and for each path from s to t?
Knapsack problem (decision): Given a set of items with each item having a positive integer profit and a positive integer weight and two positive integers and , there exists a subset such that and .
Theorem 1.
(decision) is NP-complete.
Proof of Theorem 1.
Consider a knapsack problem as defined above, which is well-known to be NP-complete [22]. Now we create a directed network with vertexes named as . For each item in the knapsack problem, create an arc directed from to with the cost of the interdictor and the cost of the invader and . Furthermore, define and . This completes the construction.
Suppose there exists a subset such that and . Let for and for the other arcs. Then it follows that
and
Conversely, suppose there exists an subject to and . Recap the construction of the arc set , let correspond to the arcs which , and then it follows:
and
Together with the fact that is clearly in NP, this implies that is NP-complete. □
From Theorem 1, is a NP-hard problem without a polynomial time algorithm unless P = NP, in other words, we need to turn to focus on the non-polynomial algorithm.
4. Model Solution
For the following linear programming relaxation of SP (RSP), we have:
Theorem 2.
for any given feasible solution of .
Proof of Theorem 2.
We only need to prove .
Firstly, we extend the constraint for each arc in to the constraint . That is
can be seen as a minimum cost flow problem where the flow value is 1 and the capacity of each arc is 1, whereas can be also seen as a minimum cost flow problem where the flow value is 1 but the capacity of each arc can be arbitrarily large. Both have the same optimal value because for each arc , i.e., .
is true because the coefficient matrix of is a unimodular matrix. □
The dual form of RSP (DRSP) is as follows:
Combined with the constraints of the upper-level program, we have the following program which has the same optimal value as .
The Mixed Integer Program (MIP) in Equation (11) can be solved by software (e.g., CPLEX); thus, we transfer with the exponential number of constraints to with the polynomial number of constraints. In fact, we have this conclusion.
Theorem 3.
For any given graph having the same parameter as :
where denotes the number of constraints in , while the number of constraints in is exponential to .
5. Numerical Results
5.1. Data Sources and Pre-Processing
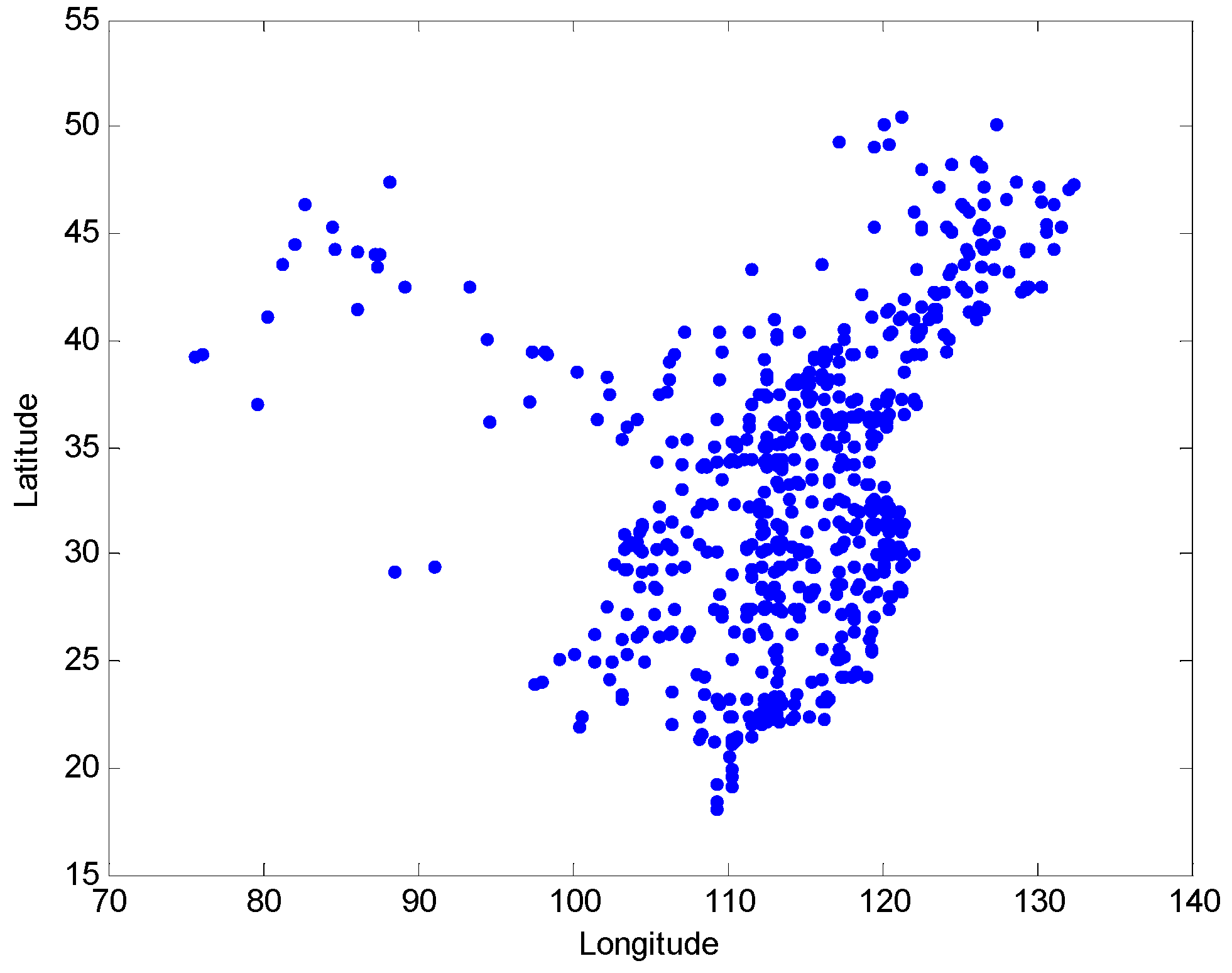
We downloaded the train lines data [23], which includes 3849 trains across China. Then we obtained the longitudes and latitudes of 616 major cities in China and plotted these cities according to their latitude and longitude in Figure 2.
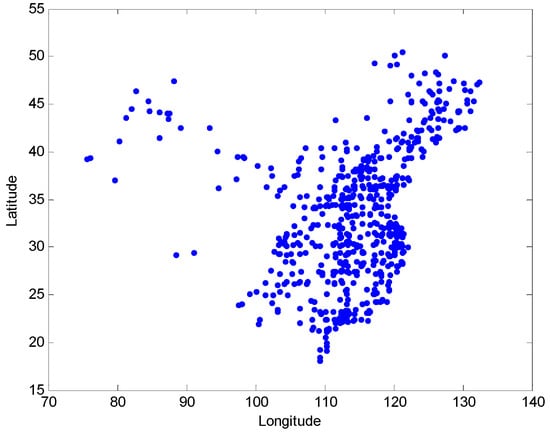
Figure 2.
The scatter plot of the 616 major cities in China.
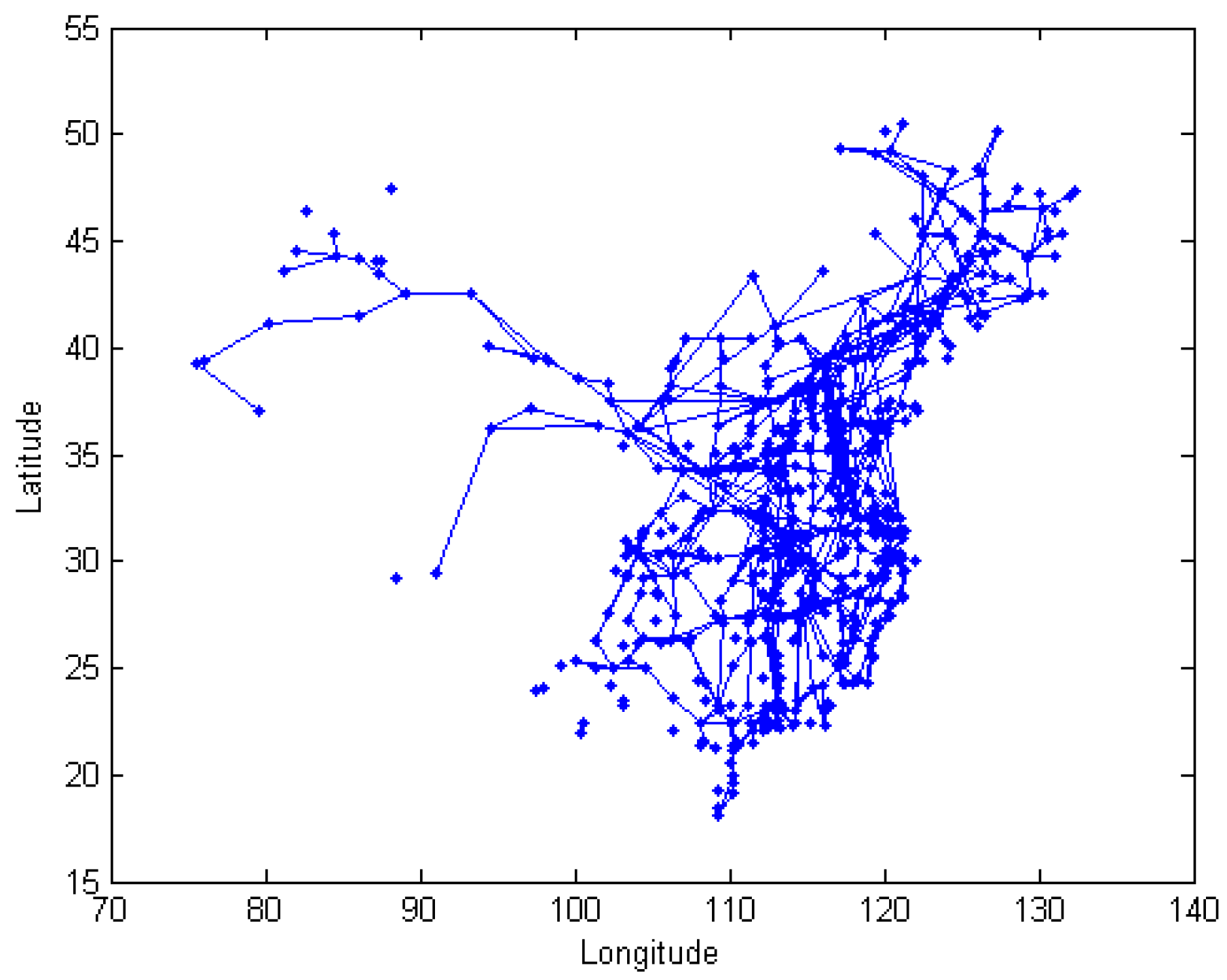
We got rid of some small cities in the data from the above website and obtained the railway information between the major cities, and plotted the railway map in Figure 3, combining it with Figure 2.
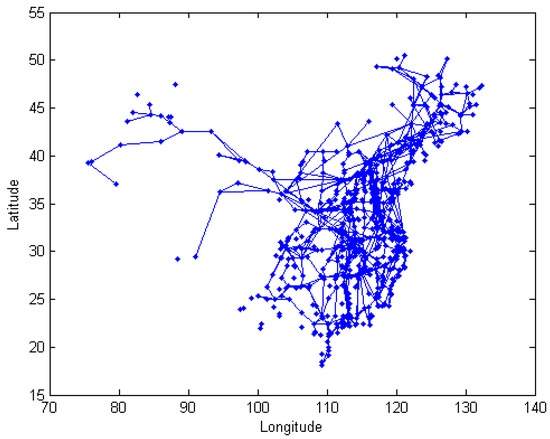
Figure 3.
The railway map between major cities.
5.2. Software and Parameter Setting
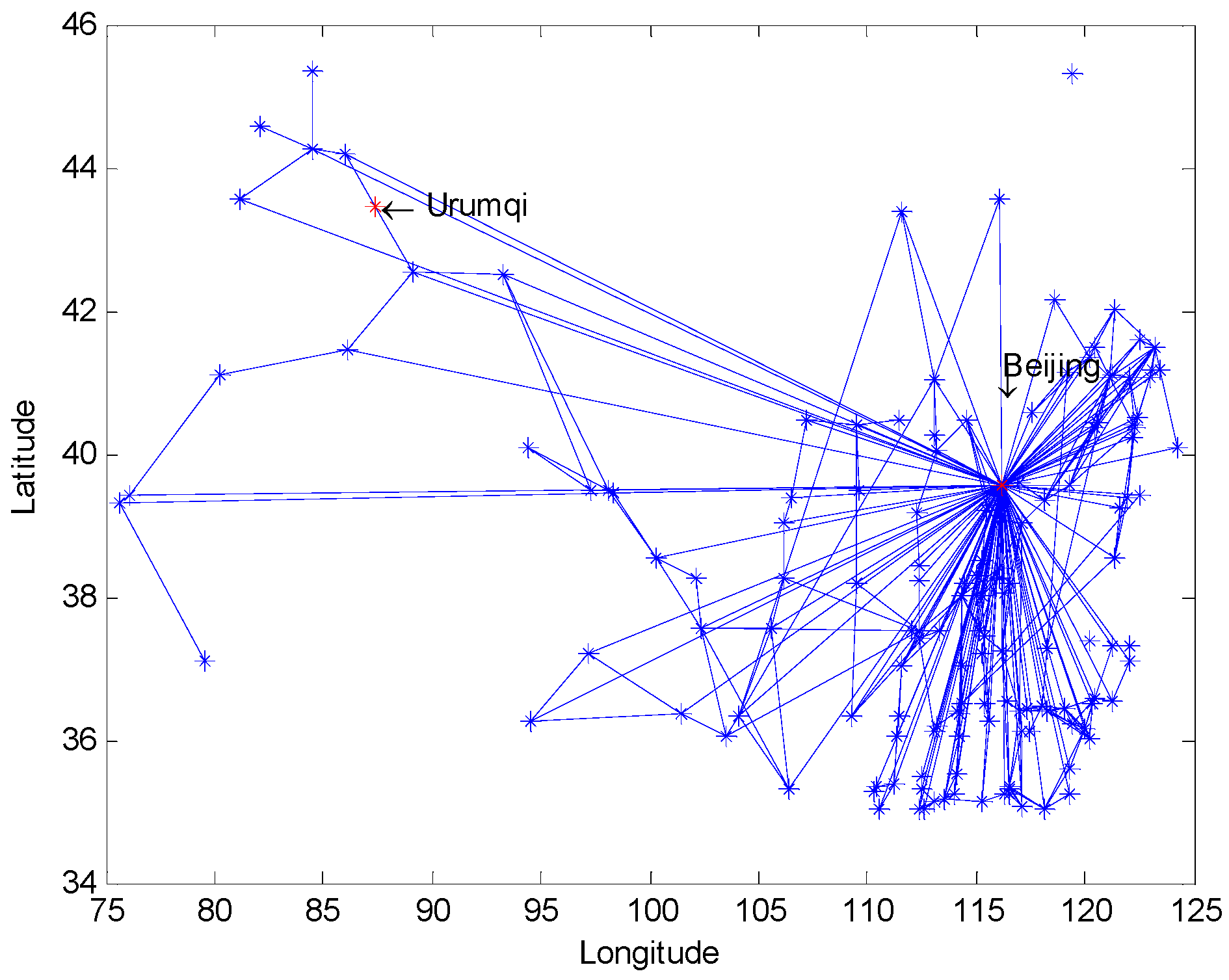
We used CPLEX to solve this model. The CPLEX program we used was an academic version 12.4 and was only able to solve limited sizes of models, so we simplified the number of nodes in the model which had no effect on presenting the conclusion from our experimental results. For example, when we set Urumqi as a source and Beijing as a sink, several southern and northeast cities will be deleted and the left network was shown in Figure 4.
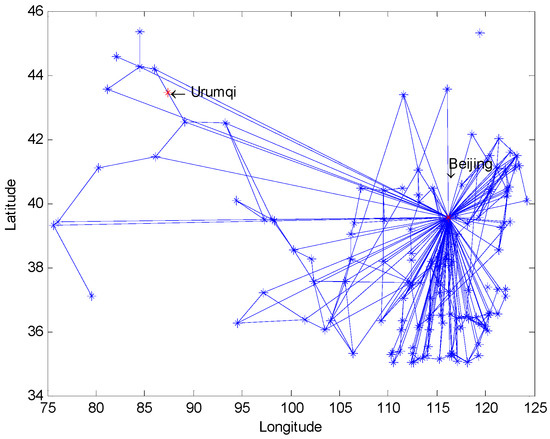
Figure 4.
The railway map without several southern and northeast cities; two red nodes denote Urumqi and Beijing, respectively.
Besides, we set (these numbers are scalar, and the following are the same) and for cities near Beijing, and and for cities far away from Beijing, and R = 30.
5.3. Solutions
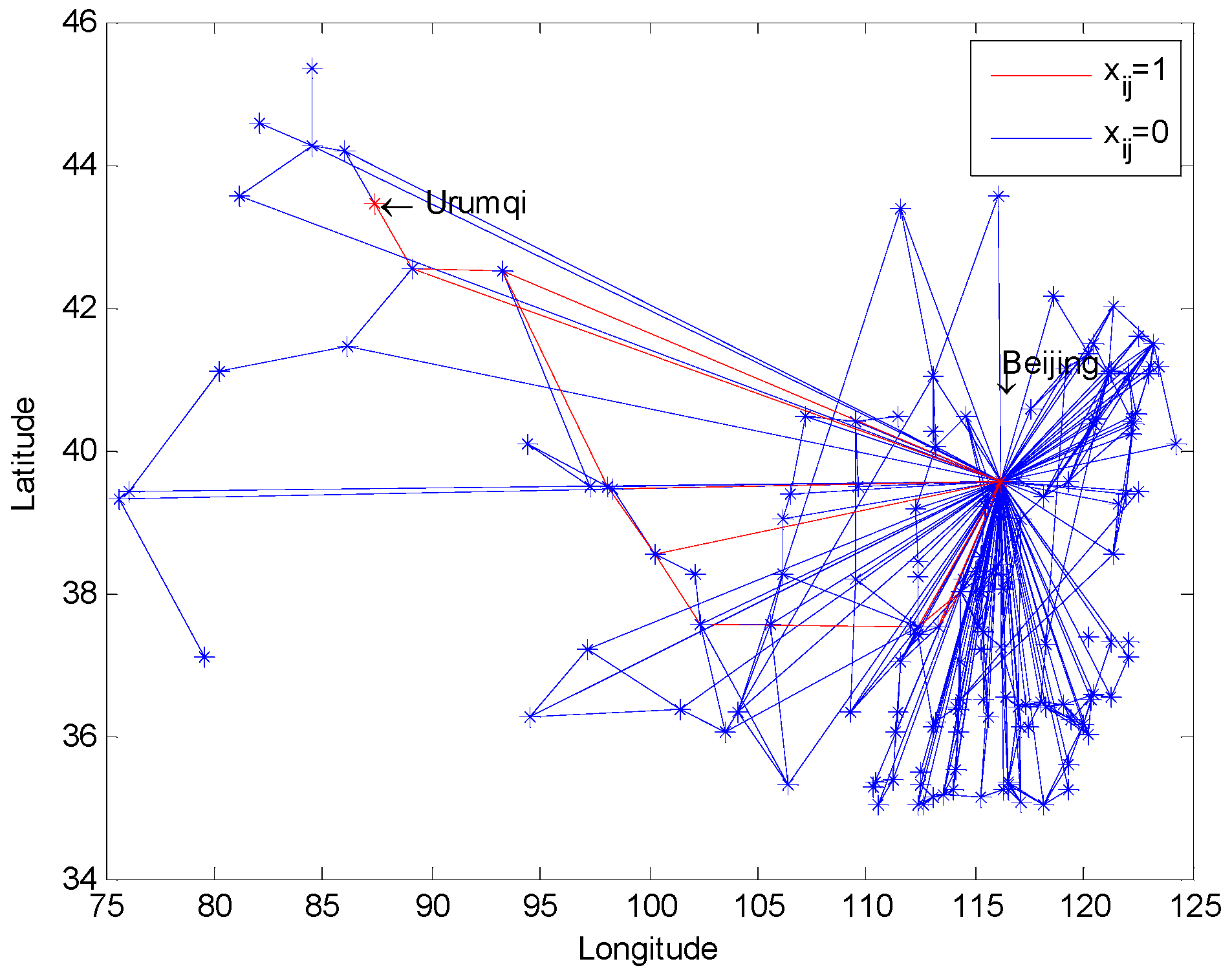
An optimal value is 11 with respect to the above example and is indicated in the red lines in Figure 5.
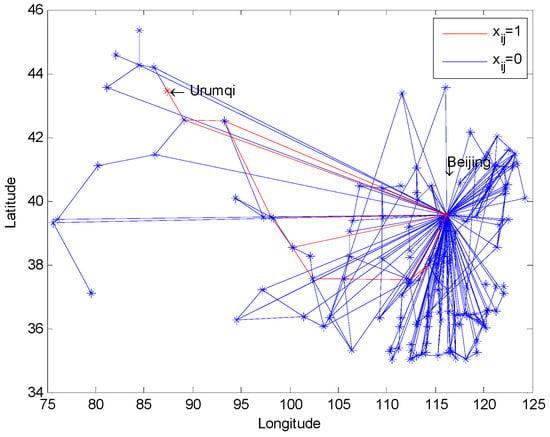
Figure 5.
Arcs choosing strategy () with the source node Urumqi and the sink node Beijing.
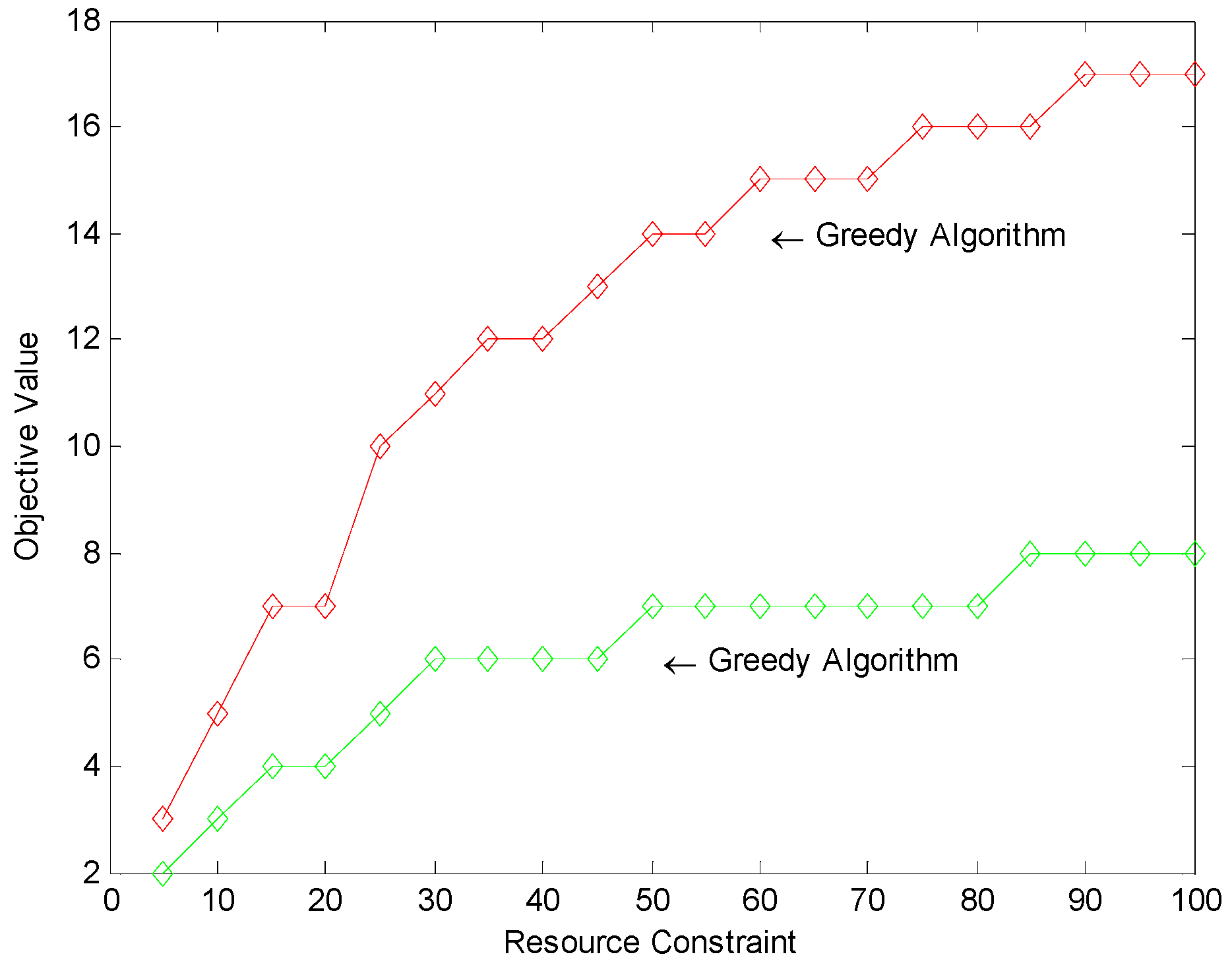
An intuitive thought may be choosing the minimum cut gradually. Two objective values are compared in Figure 6 and Table 1 with respect to the resource constraint . It proves that the greedy algorithm [24], which chooses the arcs of the least cost greedily unless exceeding the resource constraint R, is not a good one.
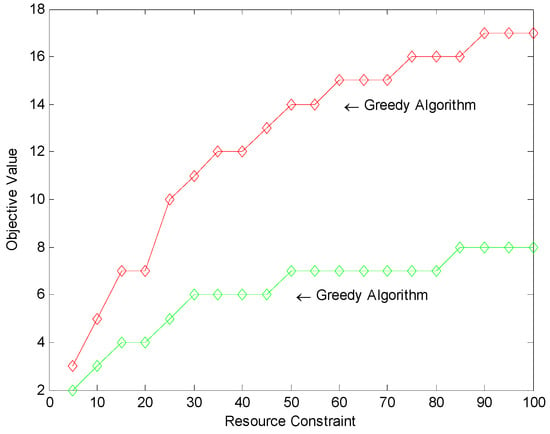
Figure 6.
Comparing the objective value of the proposed model (red) with the greedy algorithm (green).

Table 1.
Comparing the objective value of the proposed model with the greedy algorithm.
6. Conclusions
We simplified the model PATH in Equation (1) using the linear programming theory. This paper proposes a method to deal with bilevel integer programs theoretically and this model can be also directly used in the fields of border control, land defense and water resource monitoring.
Acknowledgments
This work is supported by the Fuyang Normal University Doctoral Research Foundation (Grant No. FSB201501001) and the Natural Science Foundation Anhui Provincial Education Department (Grant No. KJ2016A549, KJ2015A278, KJ2015A295, 2015KJ014).
Author Contributions
Jia Zhao conceived the idea, solved the models and wrote this paper; Gang Sun processed the data from the website and designed the experiments.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this article.
References
- Wollmer, R. Removing arcs from a network. Oper. Res. 1964, 12, 934–940. [Google Scholar] [CrossRef]
- Durbin, E. An Interdiction Model of Highway Transportation; Rand Corporation: Santa Monica, CA, USA, 1966. [Google Scholar]
- Simaan, M.; Cruz, J.B., Jr. On the Stackelberg strategy in nonzero-sum games. J. Optim. Theory Appl. 1973, 11, 533–555. [Google Scholar] [CrossRef]
- Sreekumaran, H.; Liu, A.L.; Uhan, N.A. Multi-agent decentralized network interdiction games. 2015. Available online: https://arxiv.org/abs/1503.01100 (accessed on 2 August 2016).
- Steinrauf, R.L. Network Interdiction Models; Naval Postgraduate School Monterey: Monterey, CA, USA, 1991. [Google Scholar]
- Malaviya, A.; Rainwater, C.; Sharkey, T. Multi-period network interdiction problems with applications to city-level drug enforcement. Iie Trans. 2011, 44, 368–380. [Google Scholar] [CrossRef]
- Wood, R.K. Deterministic network interdiction. Math. Comput. Model. 1993, 17, 1–18. [Google Scholar] [CrossRef]
- Cormican, K.; Morton, D.; Wood, K. Stochastic network interdiction. Oper. Res. 1998, 46, 184–197. [Google Scholar] [CrossRef]
- Watson, J.P.; Phillips, C.A.; Hart, W.E.; Phillips, C.A.; Watson, J.-P. Sensor placement in municipal water networks. J. Water Resour. Plan. Manag. 2003, 131, 237–243. [Google Scholar]
- Glick, S.J. Virtual Checkpoints and Cyber-Terry Stops: Digital Scans to Protect the Nation’s Critical Infrastructure and Key Resources. J. Nat’l Sec. L. & Pol’y. 2011, 6. [Google Scholar]
- Reiter, M.; Rohatgi, P. Homeland Security. Internet Comput. IEEE 2004, 8, 16–17. [Google Scholar] [CrossRef]
- Champion, P.D.; Hofstra, D.E.; Clayton, J.S. Border Control for Potential Aquatic Weeds. Stage 3. Weed Risk Assessment; Science for Conservation 271; Department of Conservation: New Plymouth, New Zealand, 2007; p. 41.
- Alden, E. Immigration and border control. Cato J. 2012, 32, 107–124. [Google Scholar]
- Morton, D.P.; Pan, F.; Saeger, K.J. Models for nuclear smuggling interdiction. IIE Trans. 2007, 39, 3–14. [Google Scholar] [CrossRef]
- Scaparra, M.P.; Church, R.L. A bilevel mixed-integer program for critical infrastructure planning. Comput. Oper. Res. 2008, 35, 1905–1923. [Google Scholar] [CrossRef]
- Royset, J.; Wood, R. Solving the bi-objective maximum-flow network-interdiction problem. INFORMS J. Comput. 2007, 19, 175–184. [Google Scholar] [CrossRef]
- Claudio, M.R.S.; Ramirez-Marquez, J.E. A bi-objective approach for shortest-path network interdiction. Comput. Ind. Eng. 2010, 59, 232–240. [Google Scholar]
- Zenklusen, R. Matching interdiction. Discret. Appl. Math. 2010, 158, 1676–1690. [Google Scholar] [CrossRef]
- Gutin, E.; Kuhn, D.; Wiesemann, W. Interdiction games on Markovian PERT networks. Manag. Sci. 2014, 61, 999–1017. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, Z.; Zhang, X.; Cai, X. The r-interdiction median problem with probabilistic protection and its solution algorithm. Comput. Oper. Res. 2013, 40, 451–462. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, J.; Yu, H. A minimum cost k-reliable network interdiction model. In Proceedings of the International Symposium on Operations Research and ITS Applications in Engineering, Technology and Management, Luoyang, China, 21–24 August 2013; pp. 105–109.
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman & Company: New York, NY, USA, 1979. [Google Scholar]
- List of All Trains in China; 59178.com. Available online: http://www. 59178. com/checi/ (accessed on 10 November 2012).
- Edmonds, J. Matroids and the greedy algorithm. Math Program. 1971, 1, 127–136. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).