Rational Spline Image Upscaling with Constraint Parameters
Abstract
:1. Introduction
2. A Bivariate Rational Interpolation
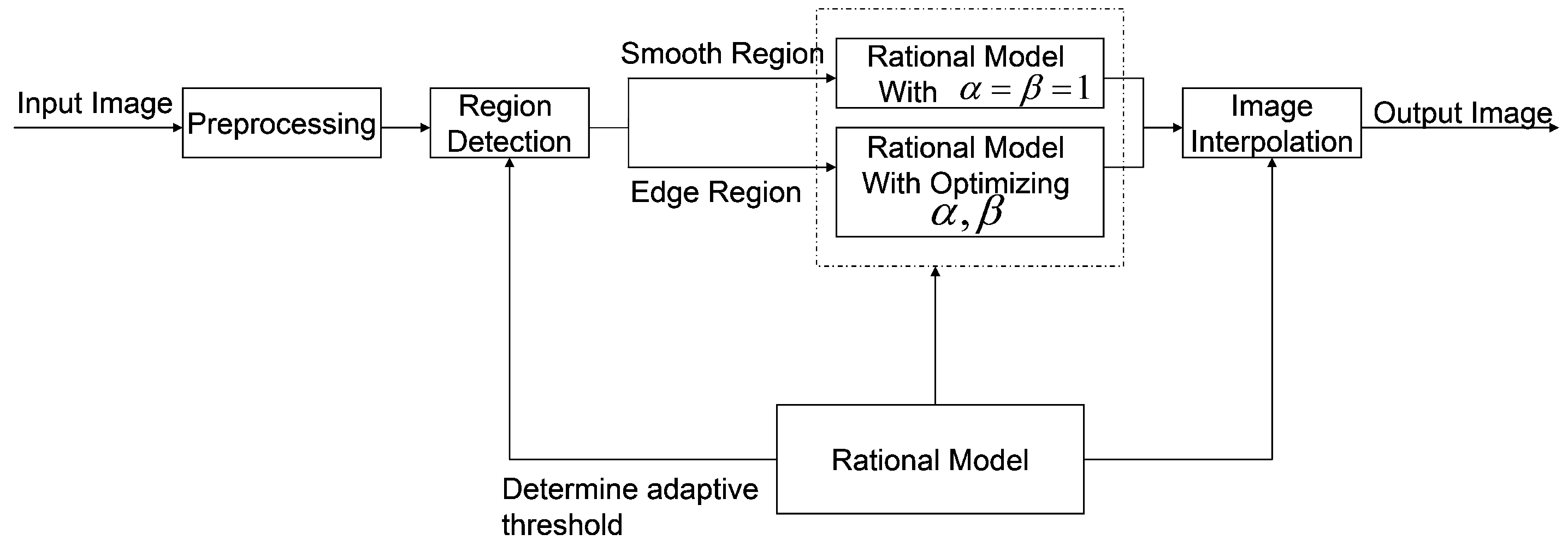
3. Basic Algorithms
3.1. Image Non-Smooth Areas Detection
3.2. Image Interpolation
3.3. Parameters Optimization
4. Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, J.; Anisetti, M.; Wu, W.; Damiani, E.; Jeon, G. Bayer demosaicking with polynomial interpolation. J. IEEE Trans. Image Process. 2016, 25, 5369–5382. [Google Scholar] [CrossRef]
- Pan, H.; Zou, Z.; Zhang, G.; Zhu, X. A penalized spline-based attitude model for high-resolution satellite imagery. J. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1849–1959. [Google Scholar] [CrossRef]
- Su, D.; Willis, P. Image interpolation by pixel-level data-dependent triangulation. Comput. Graph. Forum 2004, 23, 189–201. [Google Scholar] [CrossRef]
- Keys, R.G. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Hou, H.; Andrews, H. Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 508–517. [Google Scholar]
- Li, X.; Orchard, M.T. New edge-directed interpolation. IEEE Trans. Image Process. 2001, 15, 1521–1527. [Google Scholar]
- Zhang, L.; Wu, X. Image interpolation via directional filtering and data fusion. IEEE Trans. Image Process. 2001, 10, 1521–1527. [Google Scholar]
- Battiato, S.; Stanco, F. Alz: Adaptive learning for zooming digital images. In Proceedings of the International Conference on Consumer Electronics (ICCE 2007), Las Vegas, NV, USA, 10–14 January 2007.
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef] [PubMed]
- Battiato, S.; Giuffrida, E.U.; Rundo, F. A cellular neural network for zooming digital colour images. In Proceedings of the International Conference on Consumer Electronics (ICCE 2008), Las Vegas, NV, USA, 9–13 January 2008.
- Giachetti, A.; Asuni, N. Fast artifacts-free image interpolation. In Proceedings of the 2008 British Machine Vision Conference, Leeds, UK, 4–9 September 2008.
- Asuni, N.; Giachetti, A. Accuracy improvements and artifacts removal in edge based image interpolation. In Proceedings of the 3rd International Conference on Computer Vision Theory and Applications, Funchal, Portugal, 1 July 2008.
- Zhang, X.; Wu, X. Image interpolation by adaptive 2-d autoregressive modeling and soft-decision estimation. IEEE Trans. Image Process. 2008, 17, 887–896. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhao, D.; Xiong, R.; Ma, S.; Gao, W.; Sun, H. Image interpolation via regularized local linear regression. IEEE Trans. Image Process. 2011, 20, 3455–3469. [Google Scholar] [PubMed]
- Jeong, S.; Yoon, I.; Jeon, J.; Paik, J. Multi-frame example-based super-resolution using locally directional self-similarity. In Proceedings of the IEEE International Conference on Consumer Electronics, Las Vegas, NV, USA, 9–12 January 2015; pp. 353–358.
- Jha, A.K.; Kumar, A.; Schaefer, G.; Ahad, M.A.R. An adaptive distance-based edge preserving interpolation algorithm for natural images. In Proceedings of the 2015 IEEE International Conference on Informatics, Electronics and Vision, Fukuoka, Japan, 15–18 June 2015.
- Jensen, K.; Anastassiou, D. Subpixel edge localization and the interpolation of still images. IEEE Trans. Image Process. 1995, 4, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Carrato, S.; Tenze, L. A high quality 2 x image interpolator. IEEE Signal Process. Lett. 2000, 7, 132–135. [Google Scholar] [CrossRef]
- Woods, J.W. Two-dimensional discrete markovian fields. IEEE Trans. Inf. Theory 1972, 18, 232–240. [Google Scholar] [CrossRef]
- Said, A.; Pearlman, W.A. A new, fast and efficient image codec based on set partitioning of hierarchical trees. IEEE Trans. Circuits Syst. Video Technol. 1996, 6, 243–250. [Google Scholar] [CrossRef]
- Nyiri, E.; Gibaru, O.; Auquiert, P. Fast L1-ck polynomial spline interpolation algorithm with shape-preserving properties. Comput. Aided Geom. Des. 2011, 28, 65–74. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, R.; Shi, X.; Liu, F. Functional splines with different degrees of smoothness and their applications. Comput. Aided Des. 2008, 40, 616–624. [Google Scholar] [CrossRef]
- Wang, R.; Lang, F. Special multivariate quadratic spline space. Math. Comput. Model. 2009, 49, 760–769. [Google Scholar] [CrossRef]
- Duan, Q.; Zhang, Y.; Twizell, E. A bivariate rational interpolation and the properties. Appl. Math. Comput. 2006, 179, 190–199. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, Q.; Twizell, E. Convexity control of a bivariate rational interpolating spline surfaces. Comput. Graph. 2007, 31, 679–687. [Google Scholar] [CrossRef]
- Duan, Q.; Bao, F.; Zhang, Y. Shape control of a bivariate interpolating spline surface. Int. J. Comput. Math. 2008, 85, 813–825. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, F.; Zhang, C.; Qi, D. A weighted bivariate blending rational interpolation function and visualization control. J. Comput. Anal. Appl. 2012, 14, 1303–1321. [Google Scholar]
- Zhang, Y.; Bao, F.; Zhang, C.; Duan, Q. Local shape control of a bivariate rational interpolating surface with mixing conditions. In Proceedings of the 2011 Eighth International Symposium on Voronoi Diagrams in Science and Engineering (ISVD), Qing Dao, China, 28–30 June 2011; pp. 200–205.
- Sun, Q.; Bao, F.; Zhang, Y.; Duan, Q. A bivariate rational interpolation based on scattered data on parallel lines. J. Vis. Commun. Image Represent. 2013, 24, 75–80. [Google Scholar] [CrossRef]







| NEDI | DFDF | SAI | Our Method | |||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Light-tower | 22.78 | 0.7937 | 23.25 | 0.7971 | 22.86 | 0.8005 | 23.37 | 0.8009 |
| Dollar | 19.10 | 0.8084 | 19.21 | 0.8066 | 19.24 | 0.8055 | 19.36 | 0.8118 |
| Cliff | 25.08 | 0.7115 | 25.05 | 0.7184 | 25.16 | 0.7233 | 25.22 | 0.7268 |
| Barbara | 22.35 | 0.8513 | 23.64 | 0.8766 | 23.54 | 0.8635 | 24.12 | 0.8801 |
| Milkdrop | 30.97 | 0.9156 | 34.36 | 0.9196 | 32.39 | 0.9176 | 34.48 | 0.9216 |
| Couple | 28.65 | 0.9391 | 29.06 | 0.9413 | 29.32 | 0.9443 | 29.14 | 0.9420 |
| Goldhill | 26.60 | 0.7645 | 26.69 | 0.7678 | 26.92 | 0.7772 | 26.92 | 0.7750 |
| Door | 33.12 | 0.9446 | 33.08 | 0.9447 | 31.16 | 0.9467 | 33.20 | 0.9478 |
| Sky | 28.41 | 0.9154 | 28.95 | 0.8608 | 29.05 | 0.9364 | 28.96 | 0.9378 |
| Boat | 25.82 | 0.8941 | 25.54 | 0.8378 | 25.43 | 0.9120 | 25.61 | 0.8973 |
| Average | 25.22 | 0.8207 | 25.74 | 0.8225 | 25.58 | 0.8326 | 25.98 | 0.8384 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Zhang, Y.; Bao, F.; Zhang, C. Rational Spline Image Upscaling with Constraint Parameters. Math. Comput. Appl. 2016, 21, 48. https://doi.org/10.3390/mca21040048
Yao X, Zhang Y, Bao F, Zhang C. Rational Spline Image Upscaling with Constraint Parameters. Mathematical and Computational Applications. 2016; 21(4):48. https://doi.org/10.3390/mca21040048
Chicago/Turabian StyleYao, Xunxiang, Yunfeng Zhang, Fangxun Bao, and Caiming Zhang. 2016. "Rational Spline Image Upscaling with Constraint Parameters" Mathematical and Computational Applications 21, no. 4: 48. https://doi.org/10.3390/mca21040048
APA StyleYao, X., Zhang, Y., Bao, F., & Zhang, C. (2016). Rational Spline Image Upscaling with Constraint Parameters. Mathematical and Computational Applications, 21(4), 48. https://doi.org/10.3390/mca21040048





