Multi-Objective Optimization of a Spring Diaphragm Clutch on an Automobile Based on the Non-Dominated Sorting Genetic Algorithm (NSGA-II)
Abstract
:1. Introduction
2. Diaphragm Spring Multi-Objective Mathematical Model
2.1. Multiple Objective Functions
2.2. Design Variables
2.3. Constraints
- (1)
- (2)
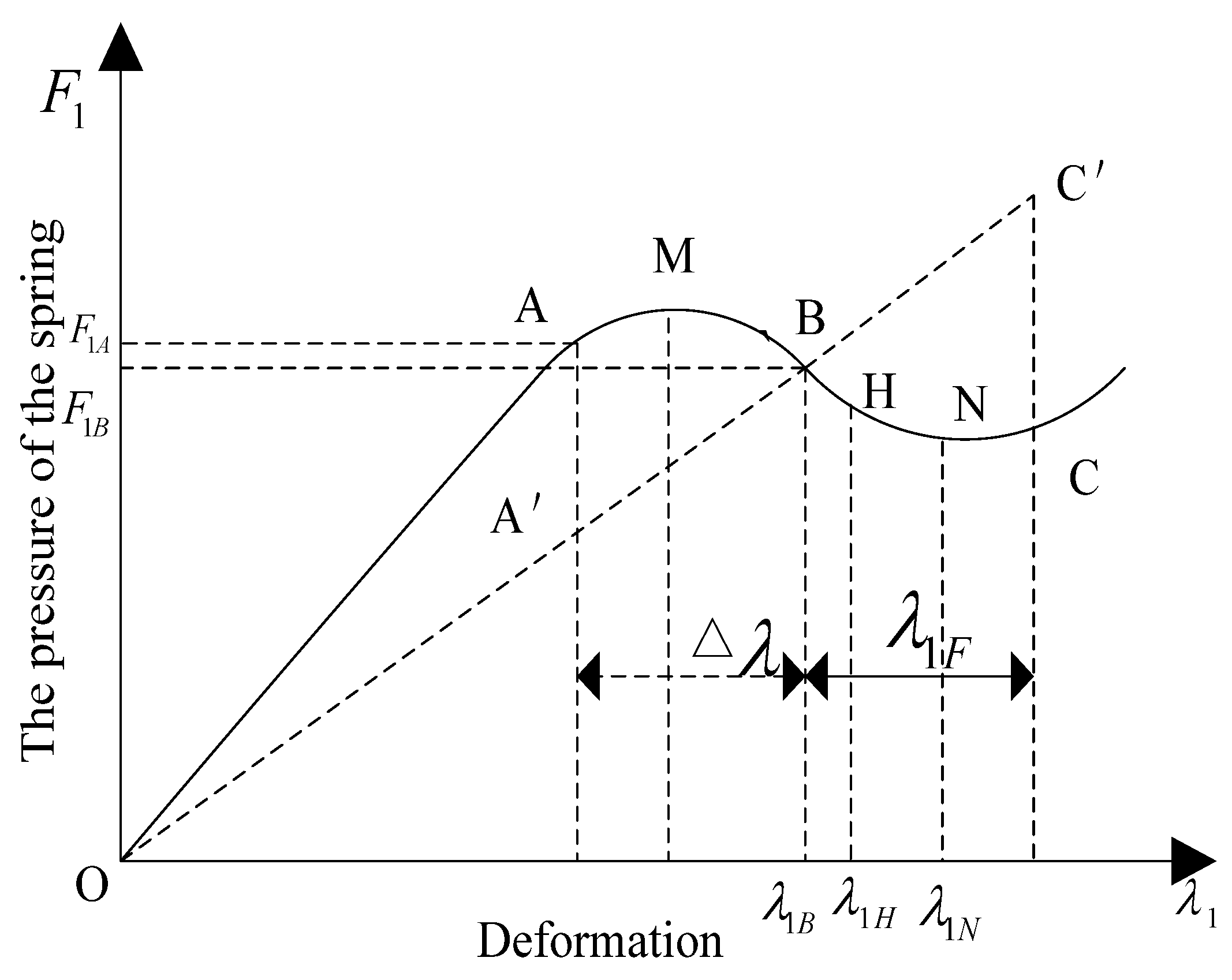
- To ensure the stable operation after the friction plate, the pressing force of the spring work after the damaged F1A should not be less than the new corresponding parameters F1B [3]:
- (3)
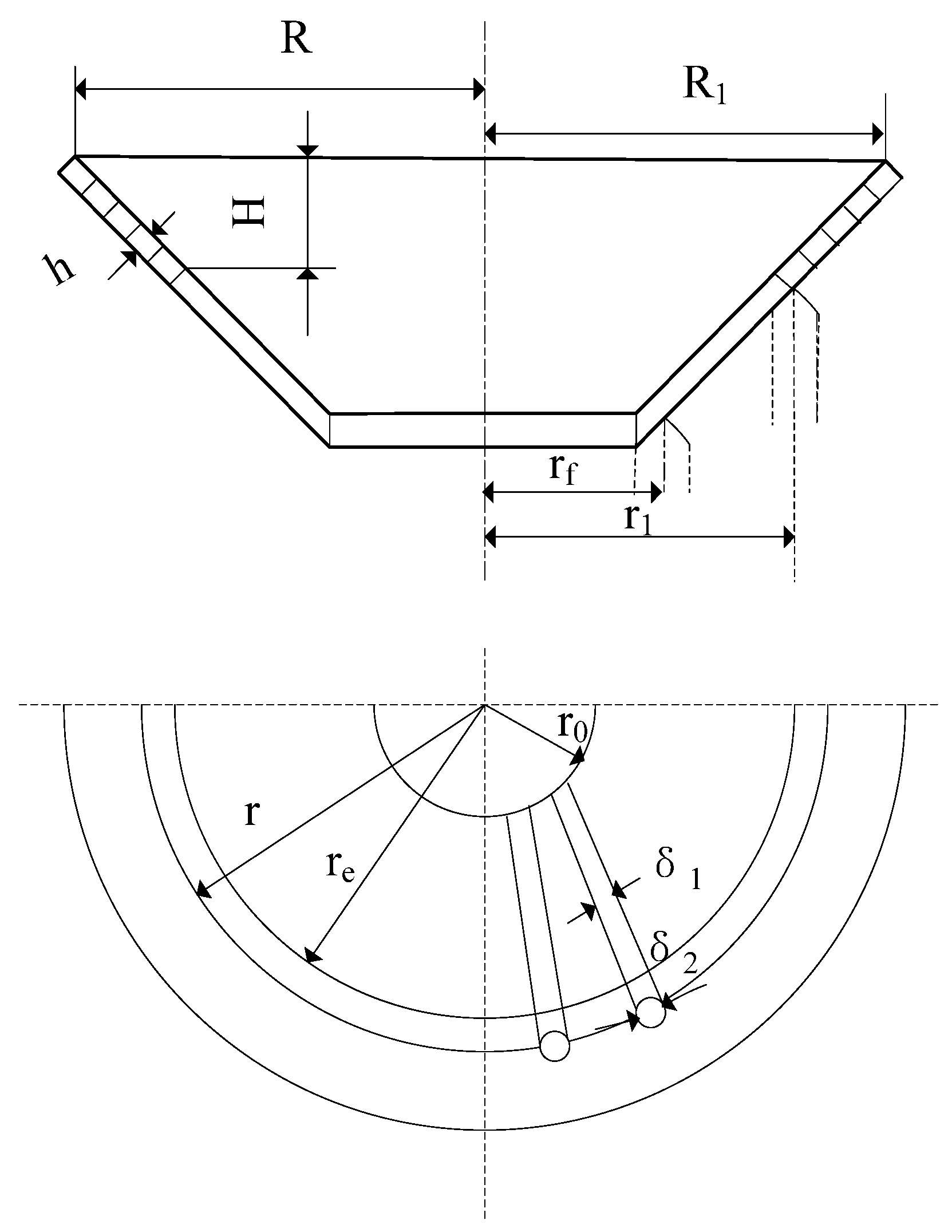
- Considering the depth-thickness ratio H/h has impactions on the load-deformation curve of the diaphragm, it should be met within a certain range. At the same time, the diaphragm spring initial cone angle α0 should be controlled within a certain range [8]. That is:
- (4)
- For the friction plate on the pressing force distribution, the radius of the big end of the friction plate R1 should be taken between the mean radius and the outside diameter of the friction plate, according to engineering experience [9]:
- (5)
- In order to meet the structural arrangement of the diaphragm spring actual situation, the big end of the radius R, the support ring radius R1, load radius r1 and inner diameter r should be in a certain range [9]:
- (6)
- To ensure the working point, the wear point and separation point should be distributed relatively reasonabley the new location λ1B should meet the following conditions [8]:
- (7)
- The work pressing force of the new designed diaphragm FB should be not less than the force FC in the separation process [9]:
- (8)
- In order to make diaphragm spring satisfy a certain leverage ratio during the separation, the ratio of the outer diameter to inner diameter should be met [3]:
- (9)
- To take advantage of spring material, part size should meet certain requirements, according to engineering experience [8]:
- (10)
- The highest point of the tensile stress σAmax(σCmax) in the bottom of the A (or C) dangerous parts of the diaphragm spring separating finger holes should meet a strength condition [9]:
- (11)
- During the diaphragm spring manufacturing process, there are some major dimensions machining errors, the error during assembly process should meet certain requirements [9]:
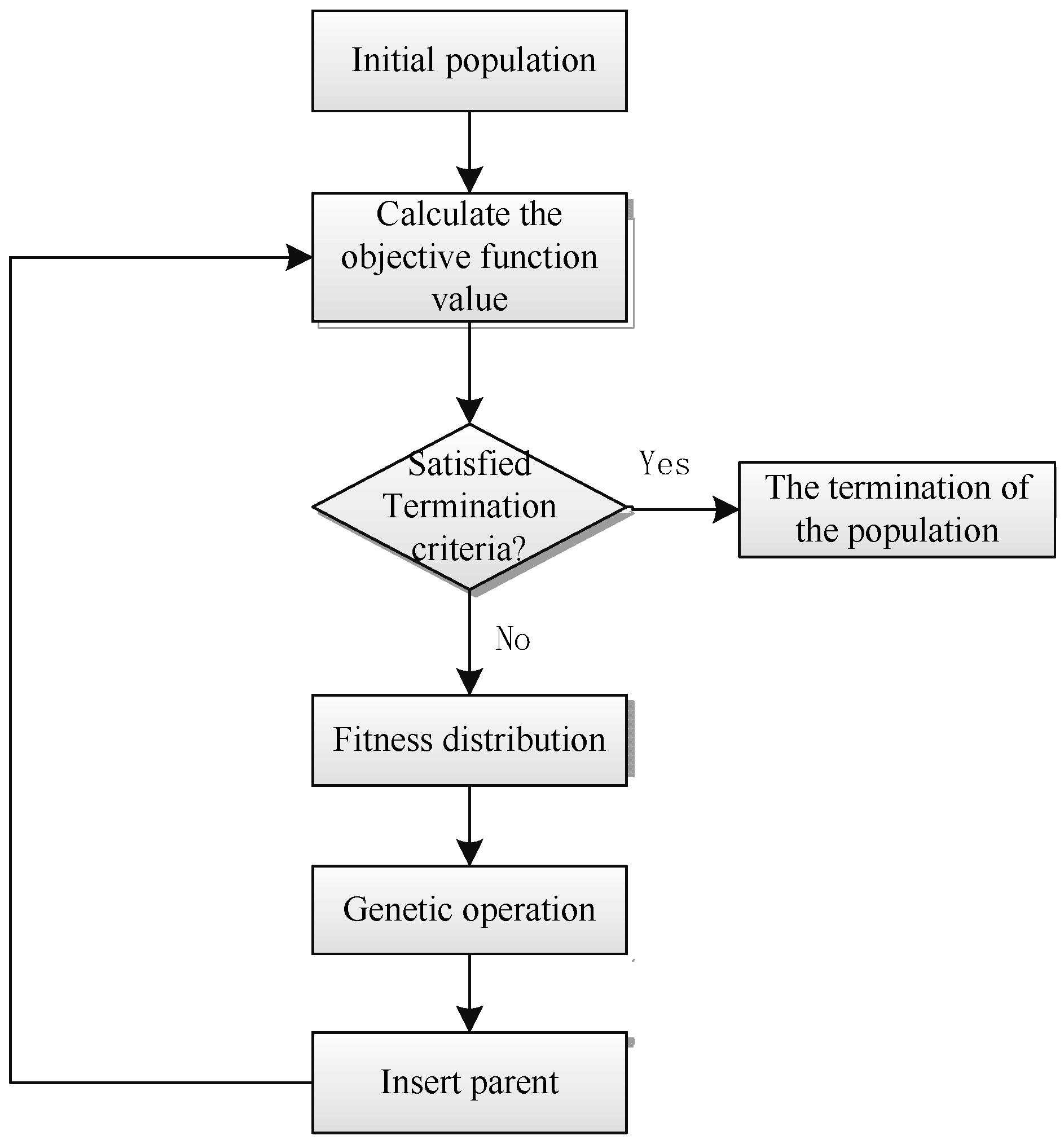
3. NSGA-II Algorithm and Multi-Objective Solution
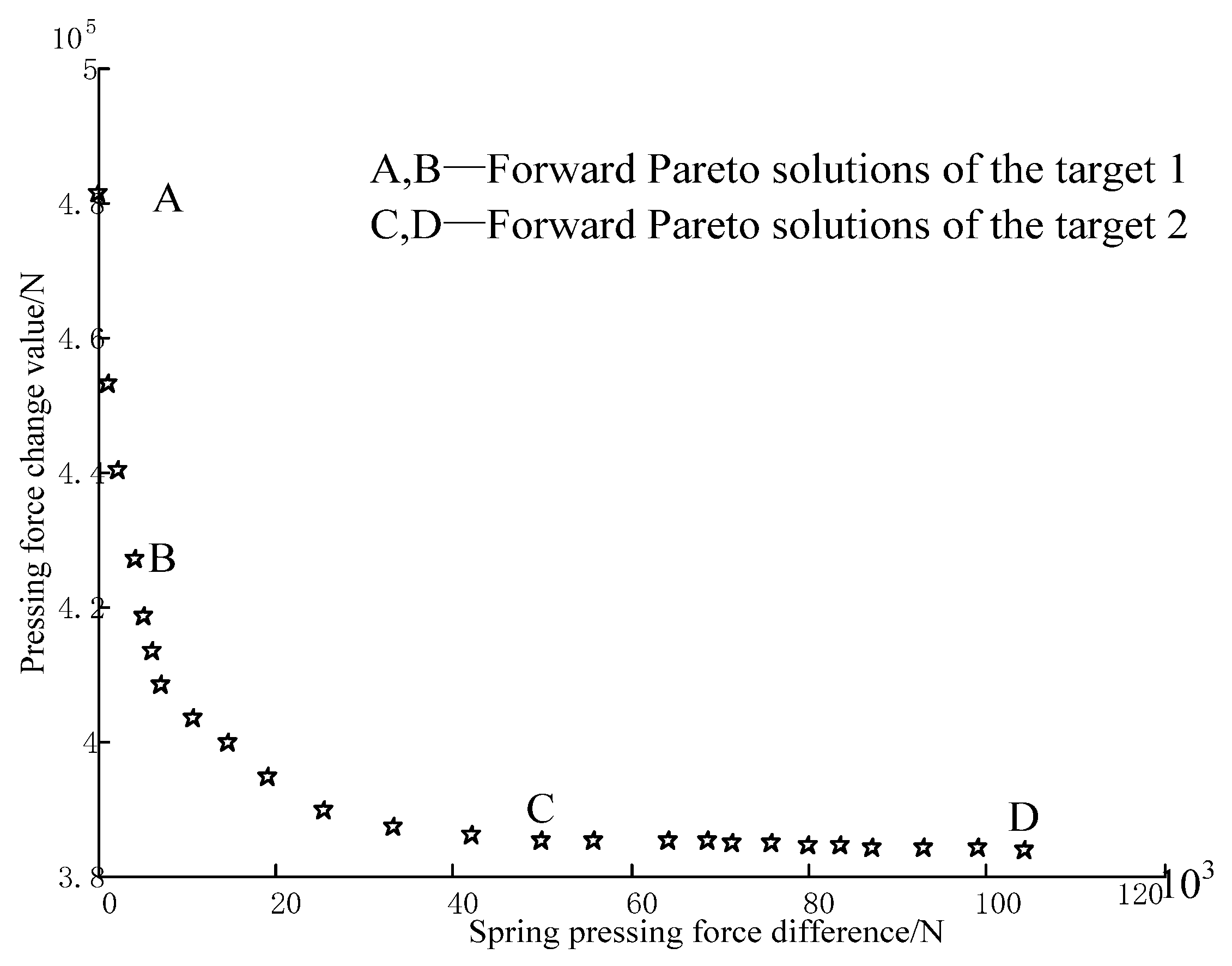
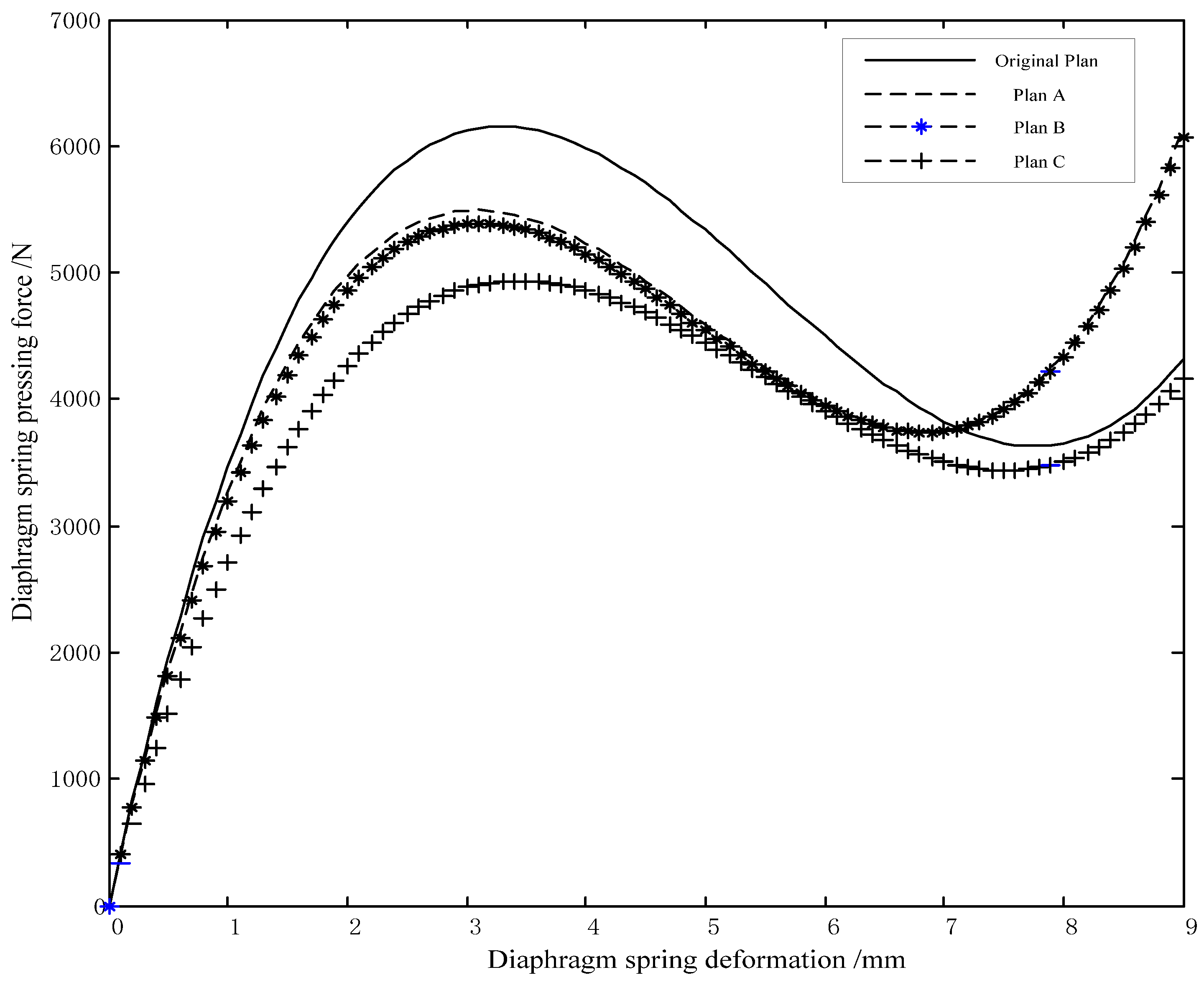
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xia, C.; Zhu, P.; Zhang, M.; Gao, X.; Lu, L. Dispersion of the mechanical parts performance indicators based on the concept of random vector. Chin. J. Mech. Eng. 2012, 25, 153–159. [Google Scholar] [CrossRef]
- Haugen, E.B. Probabilistic Mechanical Design; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Wu, Y.-H. Multi-objective optimization design of vehicle clutch diaphragm spring. In Proceedings of the International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; pp. 193–197.
- Tripathi, K. Some Design-Objectives and Design-Guidelines for Automotive Friction Clutch Based on Clutch Engagement Dynamics. J. Inst. Eng. 2014, 95, 51–61. [Google Scholar] [CrossRef]
- Amisano, F.; Ercole, G.; Mattiazzo, G.; Mauro, S.; Serra, G.; Velardocchia, M. The influence of the push plate mechanical characteristic on torque transmissibility in diaphragm spring. In Proceedings of the 3rd International AIMETA Tribology Conference, Vietri sul Mar, Italy, 18–20 September 2002; Volume 24, pp. 98–108.
- Xi, J.-Q.; Lu, J.; Pan, C. Modeling and simulation of the static characteristics of diaphragm spring clutches. J. Beijing Inst. Technol. 2015, 24, 188–193. [Google Scholar]
- Kaya, N. Optimal design of an automotive diaphragm spring with high fatigue resistance. Int. J. Veh. Des. 2006, 40, 126–143. [Google Scholar] [CrossRef]
- Zhao, L.-J.; Liu, T.; Song, B.-Y. Optimum design of automobile diaphragm spring clutch. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1421–1427.
- Ran, Z.Y.; Zhao, S.E.; Yu, L.I. Optimum Design for the Diaphragm Spring Clutch on Automobile with Genetic Algorithms. J. Chongqing Univ. 2003, 26, 77–81. [Google Scholar]
- Mohamad, N.; Iovenitti, P.; Vinay, T. Modelling and Optimisation of a Spring-Supported Diaphragm Capacitive MEMS Microphone. Engineering 2010, 2, 762–770. [Google Scholar] [CrossRef]
- Ye, Z.; Kaiyuan, Y. A Study of Belleville Spring and Diaphragm Spring in Engineering. J. Appl. Mech. 1990, 57, 1026–1031. [Google Scholar]
- Chan, C.-K.; Lai, W.-C.; Wu, M.; Wang, M.-Y.; Fang, W. Design and Implementation of a Capacitive-Type Microphone with Rigid Diaphragm and Flexible Spring Using the Two Poly Silicon Micromachining Processes. IEEE Sens. J. 2011, 11, 2365–2371. [Google Scholar] [CrossRef]
- Pasandideh, S.H.R.; Niaki, S.T.A.; Asadi, K. Bi-objective optimization of a multiproduct multi-period three-echelon supply chain problem under uncertain environments NSGA-II and NRGA. Inf. Sci. 2015, 292, 57–74. [Google Scholar] [CrossRef]
- Brownlee, A.E.I.; Wright, J.A. Constrained, mixed-integer and multi-objective optimization of building designs by NSGA-II with fitness approximation. Appl. Soft Comput. 2015, 35, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liao, S.; Liu, G. Thermo-economic muti-objective optimization for a solar-dish Brayton system using NSGA-II and decision making. Electr. Power Energy Syst. 2015, 64, 167–175. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Bhattacharya, R. Solving multi-objective parallel machine scheduling problem by modified NSGA-II. Appl. Math. Model. 2013, 37, 6718–6729. [Google Scholar] [CrossRef]
- Nourbakhsh, A.; Safikhaniand, H.; Derakhshan, S. The comparison of multi-objective particle swarm optimization and NSGA II algorithm: Applications in centrifugal pumps. Eng. Optim. 2011, 43, 1096–1113. [Google Scholar] [CrossRef]
- Murugan, P.; Kannan, S.; Baskar, S. Application of NSGA-II Algorithm to Single-Objective Transmission Constrained Generation Expansion Planning. IEEE Trans. Power Syst. 2009, 24, 1790–1797. [Google Scholar] [CrossRef]
| Plan | Objective Function | Algorithm |
|---|---|---|
| A | Penalty function method | |
| B | genetic algorithm | |
| C | NSGA-II |
| Population Size | Stop Algebra | Fitness Function Value Deviation | Optimal Front End Individual Coefficient | Maximum Iterative Algebra |
|---|---|---|---|---|
| 100 | 200 | 1 × 10−100 | 0.3 | 200 |
| Plan | H (mm) | h (mm) | R (mm) | r (mm) | R1 (mm) | r1 (mm) | |
|---|---|---|---|---|---|---|---|
| Original | 5.8 | 2.93 | 145.7 | 116.8 | 143.66 | 116.1 | 4.80 |
| A | 5.24 | 2.80 | 140.00 | 115.00 | 138.68 | 115.00 | 4.21 |
| B | 5.20 | 2.80 | 140.04 | 115.18 | 138.80 | 114.00 | 4.02 |
| C | 5.21 | 2.81 | 140.35 | 115.48 | 140.66 | 114.50 | 4.01 |
| Plan | Fb (N) | Fa (N) | Fc (N) | |Fb − Fa| (N) | |Fb − Fa|/|Fb| (%) |
|---|---|---|---|---|---|
| Original | 5226 | 5925 | 3817 | 699 | 13.37 |
| A | 4834 | 5185 | 3709 | 351 | 7.23 |
| B | 4757 | 5016 | 3715 | 259 | 5.44 |
| C | 4422 | 4603 | 3567 | 181 | 4.09 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Wang, C.; Zhu, J. Multi-Objective Optimization of a Spring Diaphragm Clutch on an Automobile Based on the Non-Dominated Sorting Genetic Algorithm (NSGA-II). Math. Comput. Appl. 2016, 21, 47. https://doi.org/10.3390/mca21040047
Zhou J, Wang C, Zhu J. Multi-Objective Optimization of a Spring Diaphragm Clutch on an Automobile Based on the Non-Dominated Sorting Genetic Algorithm (NSGA-II). Mathematical and Computational Applications. 2016; 21(4):47. https://doi.org/10.3390/mca21040047
Chicago/Turabian StyleZhou, Junchao, Chun Wang, and Junjun Zhu. 2016. "Multi-Objective Optimization of a Spring Diaphragm Clutch on an Automobile Based on the Non-Dominated Sorting Genetic Algorithm (NSGA-II)" Mathematical and Computational Applications 21, no. 4: 47. https://doi.org/10.3390/mca21040047
APA StyleZhou, J., Wang, C., & Zhu, J. (2016). Multi-Objective Optimization of a Spring Diaphragm Clutch on an Automobile Based on the Non-Dominated Sorting Genetic Algorithm (NSGA-II). Mathematical and Computational Applications, 21(4), 47. https://doi.org/10.3390/mca21040047






