On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem
Abstract
:1. Introduction
2. The Convergence Analysis of APP
3. The Convergence Rate Analysis of APP
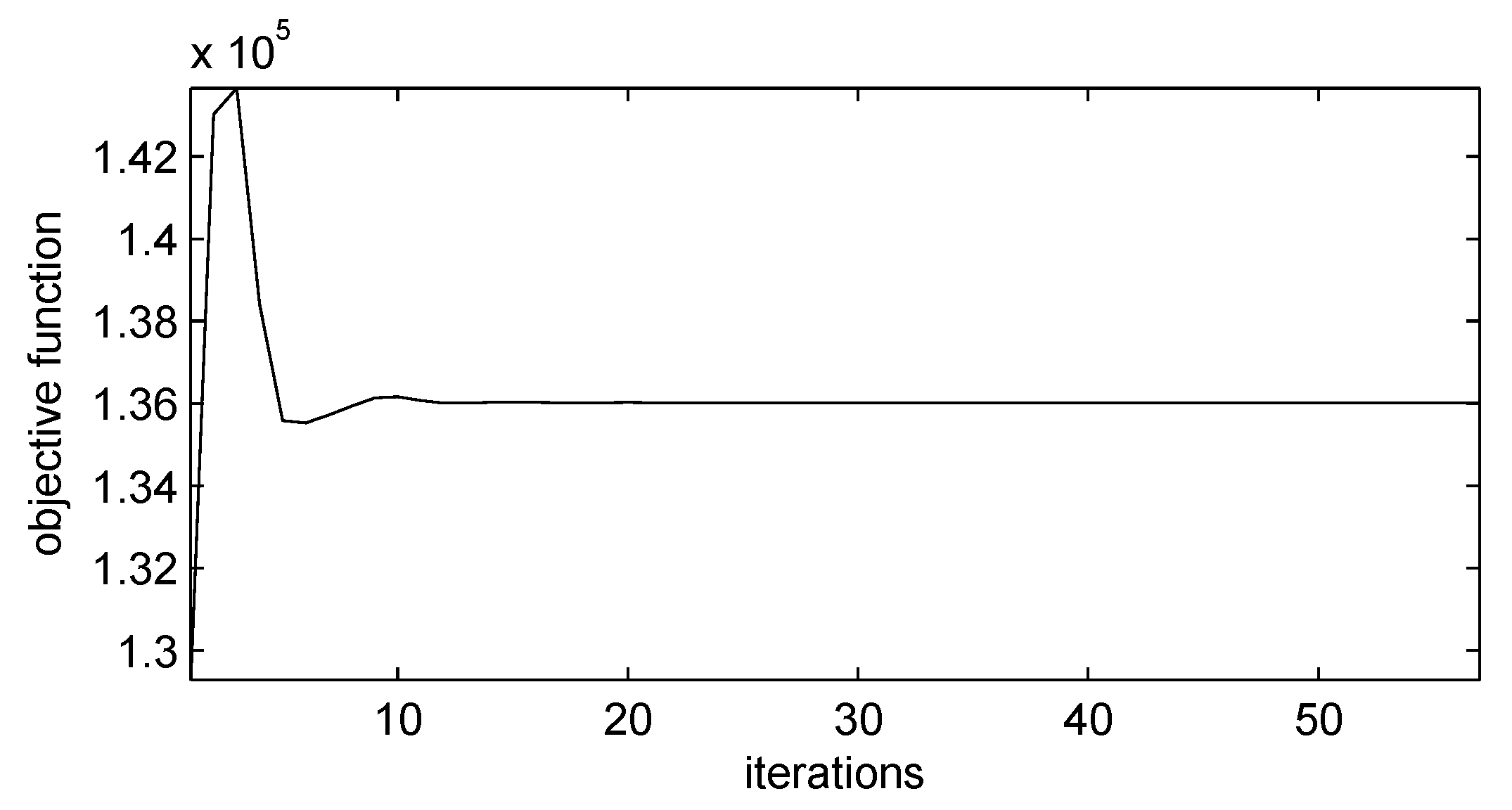
4. Numerical Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cohen, G.; Zhu., D.L. Decomposition coordination methods in large scale optimization problems: The non-differentiable case and the use of augmented lagrangians. Adv. Large Scale Syst. 1984, 1, 203–266. [Google Scholar]
- Cohen, G. Auxiliary problem principle and decomposition of optimization problems. J. Optim. Theory Appl. 1980, 32, 277–305. [Google Scholar] [CrossRef]
- Jiang, Q.Y.; Zhou, B.R.; Zhang, M.Z. Parallel augment lagrangian relaxation method for transient stability constrained unit commitment. IEEE Trans. Power Syst. 2013, 28, 1140–1148. [Google Scholar] [CrossRef]
- Chung, K.H.; Kim, B.H.; Hur, D. Distributed implementation of generation scheduling algorithm on interconnected power systems. Energy Convers. Manag. 2011, 52, 3457–3464. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Sheng, W. The decomposition and computation method for distributed optimal power flow based on message passing interface (MPI). Int. J. Electr. Power Energy Syst. 2011, 33, 1185–1193. [Google Scholar] [CrossRef]
- Kim, B.H.; Baldick, R. A comparison of distributed optimal power flow algorithms. IEEE Trans. Power Syst. 2000, 15, 599–604. [Google Scholar] [CrossRef]
- Kim, B.H.; Baldick, R. Coarse-grained distributed optimal power flow. IEEE Trans. Power Syst. 1997, 12, 932–939. [Google Scholar] [CrossRef]
- Batut, J.; Renaud, A. Daily generation scheduling optimization with transmission constraints: A new class of algorithms. IEEE Trans. Power Syst. 1992, 7, 982–989. [Google Scholar] [CrossRef]
- Beltran, C.; Heredia, F.J. Unit commitment by augmented lagrangian relaxation: Testing two decomposition approaches. J. Optim. Theory Appl. 2002, 112, 295–314. [Google Scholar] [CrossRef]
- Nemirovski, A. Prox-method with rate of convergence O(1/t) for variational inequalities with Lipschitz continuous monotone operators and smooth convex-concave saddle point problems. SIAM J. Optim. 2004, 15, 229–251. [Google Scholar] [CrossRef]
- Cai, X.J.; Gu, G.Y.; He, B.S. On the O(1/t) convergence rate of the projection and contraction methods for variational inequalities with Lipschitz continuous monotone operators. Comput. Optim. Appl. 2014, 57, 339–363. [Google Scholar] [CrossRef]
- He, B.; Yuan, X. On the O(1/n) convergence rate of the douglas-rachford alternating direction method. SIAM J. Numer. Anal. 2012, 50, 700–709. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, M.H. On the O(1/t) convergence rate of Ye-Yuan’s modified alternating direction method of multipliers. Appl. Math. Comput. 2014, 226, 367–373. [Google Scholar]
- He, B.S.; Yang, H.; Wang, S.L. Alternating direction method with self-adaptive penalty parameters for monotone variational inequalities. J. Optim. Theory Appl. 2000, 106, 337–356. [Google Scholar] [CrossRef]
- Chen, P.H.; Chang, H.C. Large-scale economic-dispatch by genetic algorithm. IEEE Trans. Power Syst. 1995, 10, 1919–1926. [Google Scholar] [CrossRef]

| i | |||||
|---|---|---|---|---|---|
| 1 | 40 | 80 | 0.03073 | 8.336 | 170.44 |
| 2 | 60 | 120 | 0.02028 | 7.0706 | 309.54 |
| 3 | 80 | 190 | 0.00942 | 8.1817 | 369.03 |
| 4 | 24 | 42 | 0.08482 | 6.9467 | 135.48 |
| 5 | 26 | 42 | 0.09693 | 6.5595 | 135.19 |
| 6 | 68 | 140 | 0.01142 | 8.0543 | 222.33 |
| 7 | 110 | 300 | 0.00357 | 8.0323 | 287.71 |
| 8 | 135 | 300 | 0.00492 | 6.999 | 391.98 |
| 9 | 135 | 300 | 0.00573 | 6.602 | 455.76 |
| 10 | 130 | 300 | 0.00605 | 12.908 | 722.82 |
| 11 | 94 | 375 | 0.00515 | 12.986 | 635.2 |
| 12 | 94 | 375 | 0.00569 | 12.796 | 654.69 |
| 13 | 125 | 500 | 0.00421 | 12.501 | 913.4 |
| 14 | 125 | 500 | 0.00752 | 8.8412 | 1760.4 |
| 15 | 125 | 500 | 0.00708 | 9.1575 | 1728.3 |
| 16 | 125 | 500 | 0.00708 | 9.1575 | 1728.3 |
| 17 | 125 | 500 | 0.00708 | 9.1575 | 1728.3 |
| 18 | 220 | 500 | 0.00313 | 7.9691 | 647.85 |
| 19 | 220 | 500 | 0.00313 | 7.955 | 649.69 |
| 20 | 242 | 550 | 0.00313 | 7.9691 | 647.83 |
| 21 | 242 | 550 | 0.00313 | 7.9691 | 647.81 |
| 22 | 254 | 550 | 0.00298 | 6.6313 | 785.96 |
| 23 | 254 | 550 | 0.00298 | 6.6313 | 785.96 |
| 24 | 254 | 550 | 0.00298 | 6.6313 | 785.53 |
| 25 | 254 | 550 | 0.00298 | 6.6313 | 785.53 |
| 26 | 254 | 550 | 0.00277 | 7.1032 | 801.32 |
| 27 | 254 | 550 | 0.00277 | 7.1032 | 801.32 |
| 28 | 10 | 150 | 0.52124 | 3.3353 | 1055.1 |
| 29 | 10 | 150 | 0.52124 | 3.3353 | 1055.1 |
| 30 | 10 | 150 | 0.52124 | 3.3353 | 1055.1 |
| 31 | 20 | 70 | 0.25098 | 13.052 | 1207.8 |
| 32 | 20 | 70 | 0.16766 | 21.887 | 810.79 |
| 33 | 20 | 70 | 0.2635 | 10.244 | 1247.7 |
| 34 | 20 | 70 | 0.30575 | 8.3707 | 1219.2 |
| 35 | 18 | 60 | 0.18362 | 26.258 | 641.43 |
| 36 | 18 | 60 | 0.32563 | 9.6956 | 1112.8 |
| 37 | 20 | 60 | 0.33722 | 7.1633 | 1044.4 |
| 38 | 25 | 60 | 0.23915 | 16.339 | 832.24 |
| 39 | 25 | 60 | 0.23915 | 16.339 | 834.24 |
| 40 | 25 | 60 | 0.23915 | 16.339 | 1035.2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Chen, Z. On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem. Math. Comput. Appl. 2016, 21, 35. https://doi.org/10.3390/mca21030035
Ren Y, Chen Z. On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem. Mathematical and Computational Applications. 2016; 21(3):35. https://doi.org/10.3390/mca21030035
Chicago/Turabian StyleRen, Yaming, and Zhongxian Chen. 2016. "On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem" Mathematical and Computational Applications 21, no. 3: 35. https://doi.org/10.3390/mca21030035
APA StyleRen, Y., & Chen, Z. (2016). On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem. Mathematical and Computational Applications, 21(3), 35. https://doi.org/10.3390/mca21030035






