New Exact Solutions of the System of Equations for the Ion Sound and Langmuir Waves by ETEM
Abstract
:1. Introduction
2. Basic Facts of the ETEM
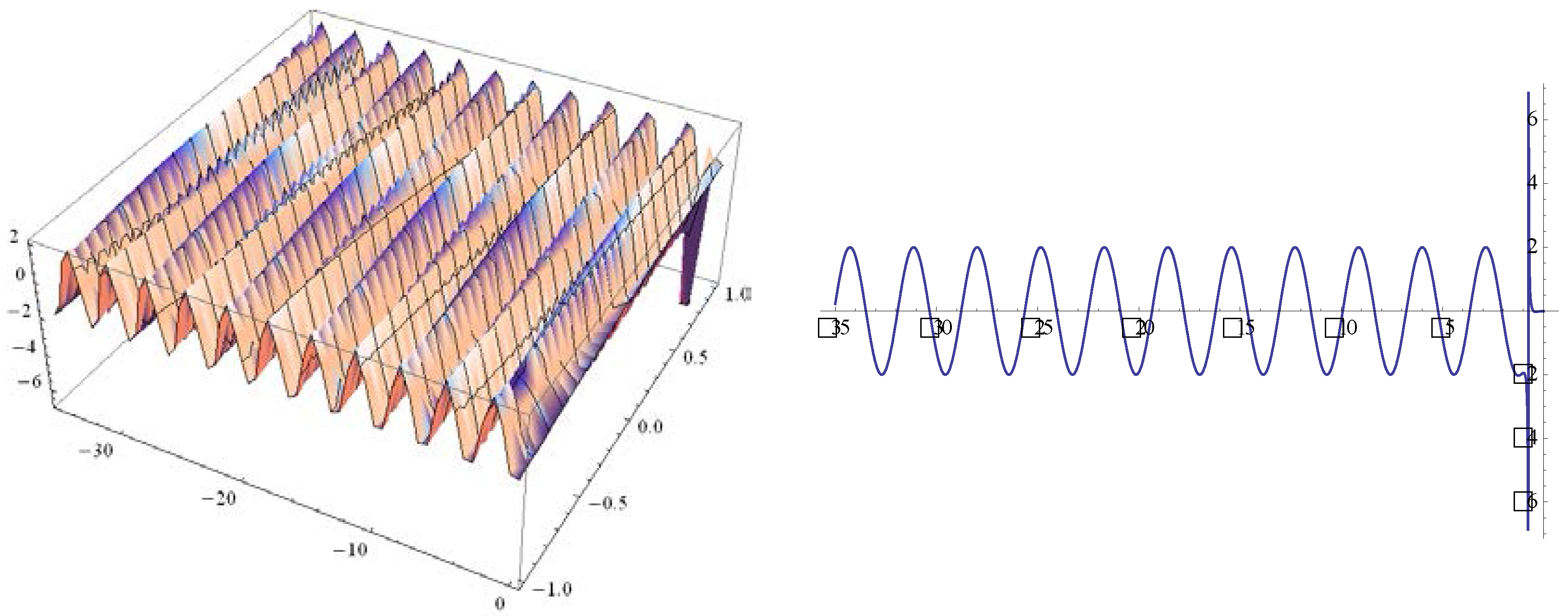
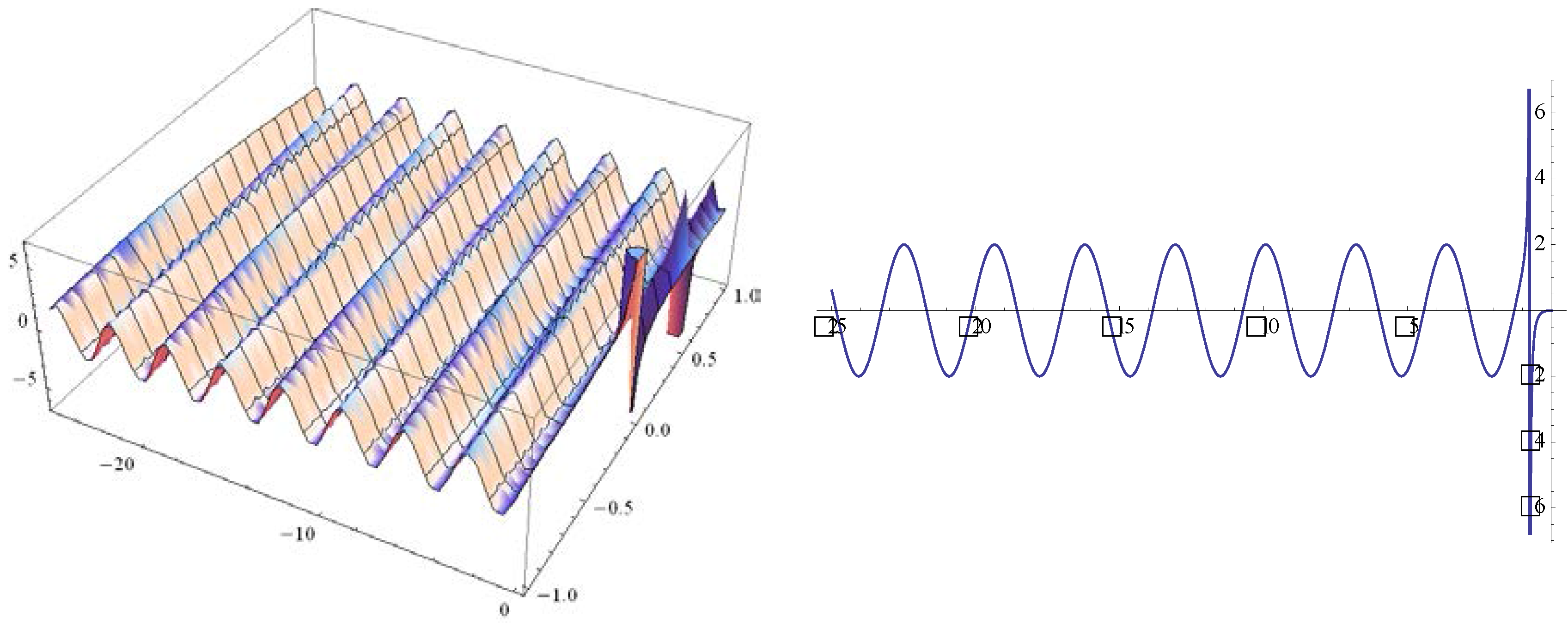
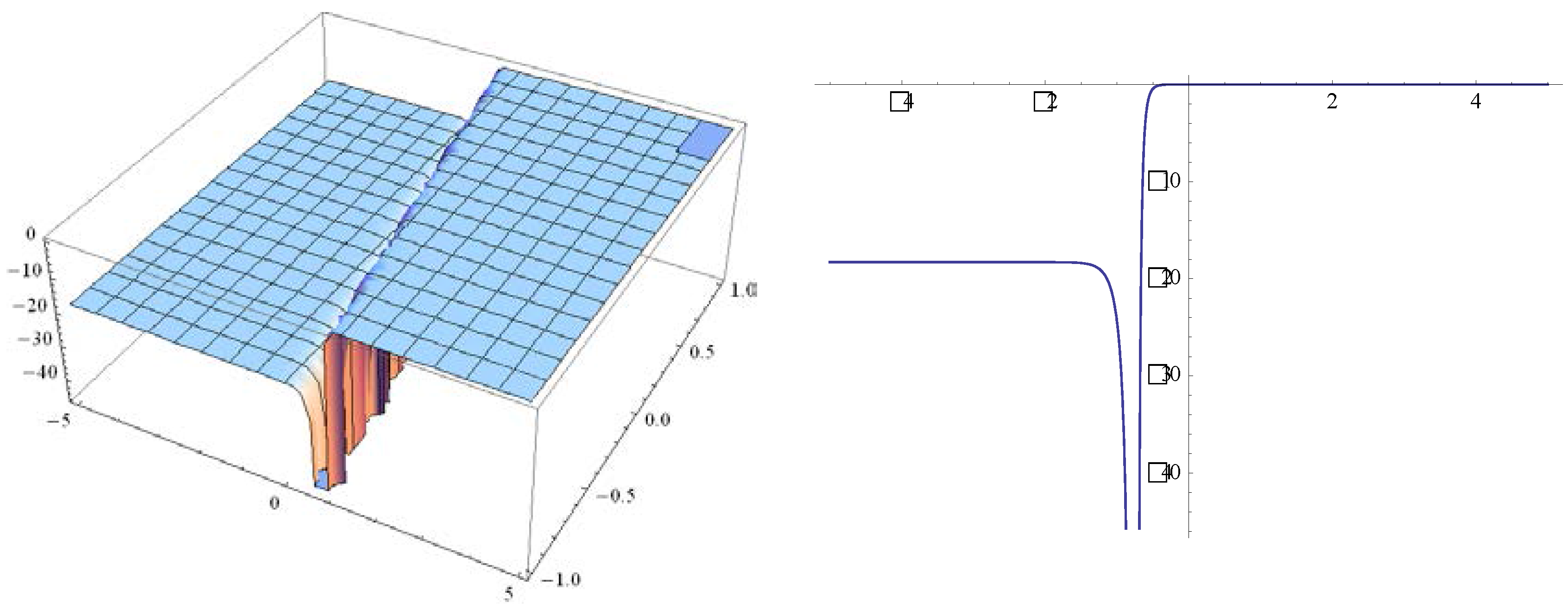
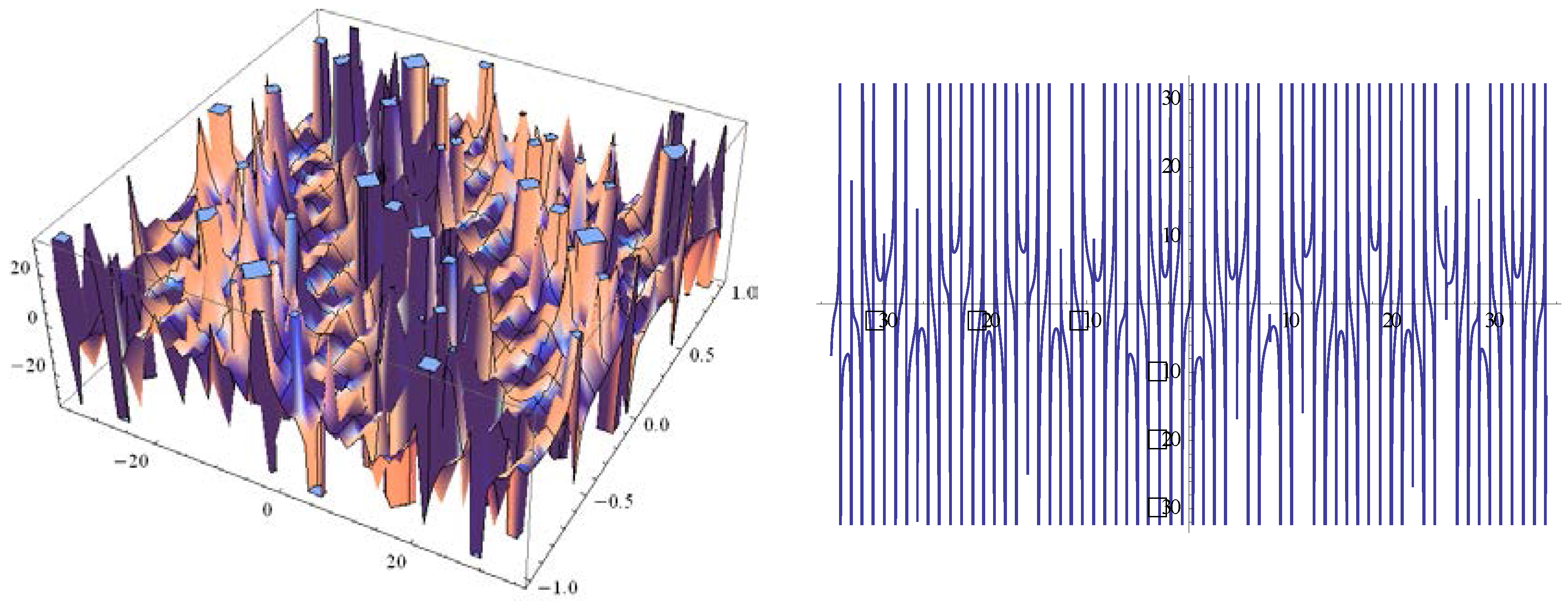
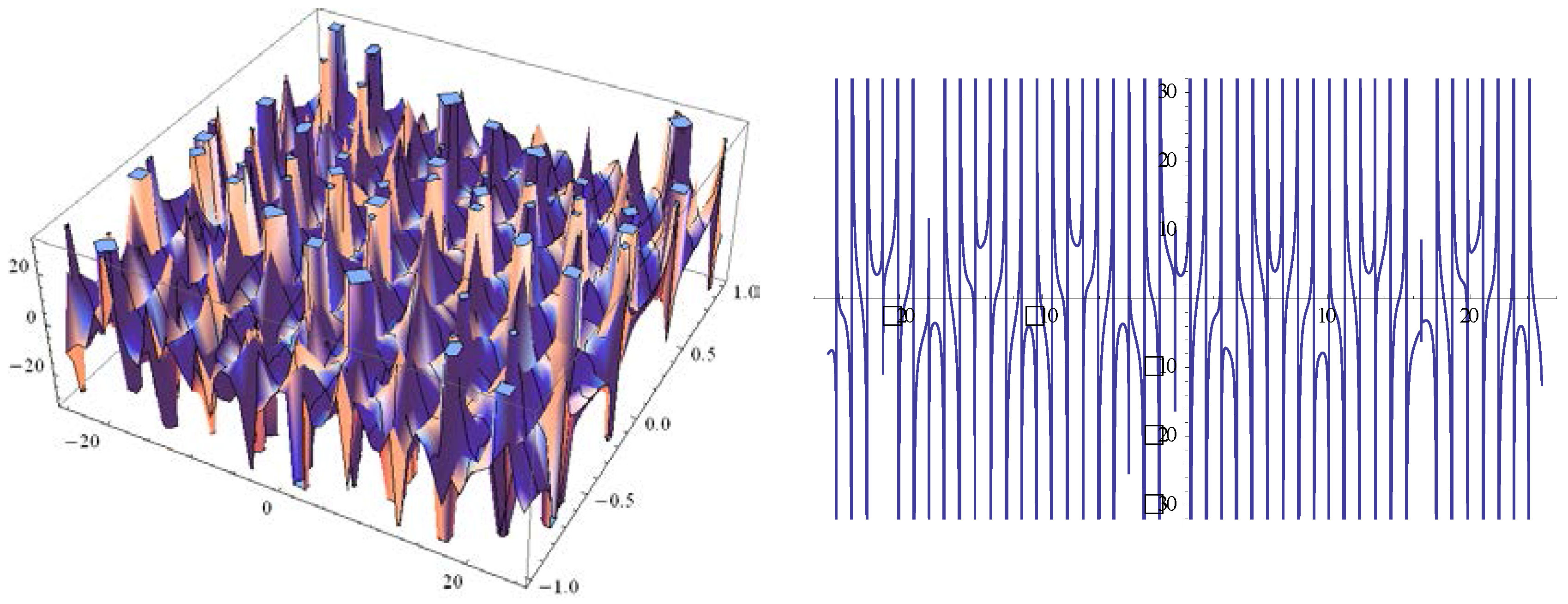
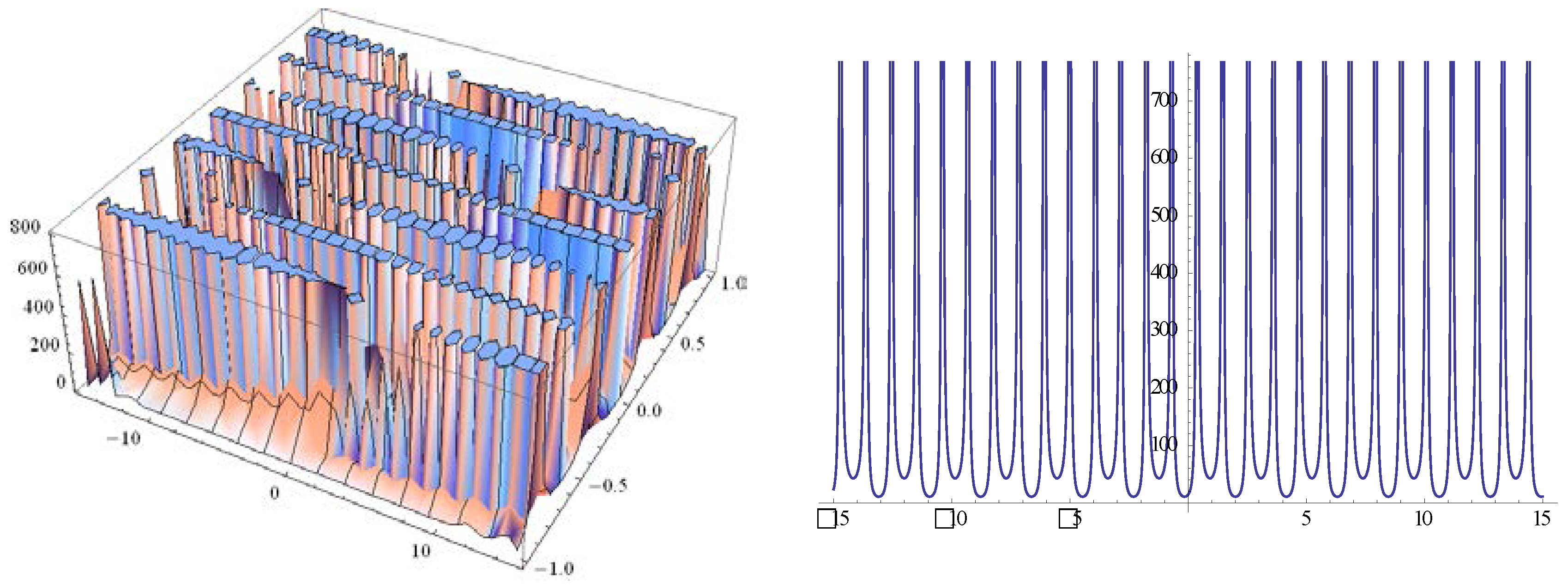
3. ETEM for the System of Equations for the Ion Sound and Langmuir Waves
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Degtyarev, L.M.; Nakhan’kov, V.G.; Rudakov, L.I. Dynamics of the formation and interaction of Langmuir solitons and strong turbulence. Zhurnal Eksp. Teor. Fiz. 1974, 67, 533–542. [Google Scholar]
- Degtyarev, L.M.; Zakharov, V.E.; Sagdeev, R.Z.; Solov’ev, G.I.; Shapiro, V.D.; Shevchenko, I.V. Langmuir collapse under pumping and wave energy dissipation. Zhurnal Eksp. Teor. Fiz. 1983, 85, 1221–1231. [Google Scholar]
- Anisimov, S.I.; Berezovskii, M.A.; Ivanov, M.F.; Petrov, I.V.; Rubenchick, A.M.; Zakharov, V.E. Computer simulation of the Langmuir collapse. Phys. Lett. A 1982, 92, 32–34. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Berezovskii, M.A.; Zakharov, V.E.; Petrov, I.V.; Rubenchik, A.M. Numerical simulation of a Langmuir collapse. Zhurnal Eksp. Teor. Fiz. 1983, 84, 2046–2054. [Google Scholar]
- D’yachenko, A.I.; Zakharov, V.E.; Rubenchik, A.M.; Sagdeev, R.Z.; Shvets, V.F. Numerical simulation of two-dimensional Langmuir collapse. Zhurnal Eksp. Teor. Fiz. 1988, 94, 144–155. [Google Scholar]
- Zakharov, V.E.; Pushkarev, A.N.; Rubenchik, A.M.; Sagdeev, R.Z.; Shvets, V.F. Numerical simulation of three-dimensional Langmuir collapse in plasma. Zhurnal Eksp. Teor. Fiz. 1988, 47, 287–290. [Google Scholar]
- Benilov, E.S. Stability of plasma solitons. Zhurnal Eksp. Theor. Fiz. 1985, 88, 120–128. [Google Scholar]
- Zakharov, V.E.; Pushkarev, A.N.; Sagdeev, R.Z.; Soloviev, S.I.; Shapiro, V.D.; Shvets, V.F.; Shevchenko, V.I. “Throughout” modelling of the one-dimensional Langmuir turbulence. Sov. Phys. Dokl. 1989, 34, 248–251. [Google Scholar]
- Dyachenko, A.I.; Pushkarev, A.N.; Rubenchik, A.M.; Sagdeev, R.Z.; Shvets, V.F.; Zakharov, V.E. Computer simulation of Langmuir collapse. Phys. D 1991, 52, 78–102. [Google Scholar] [CrossRef]
- Rubenchik, A.M.; Zakharov, V.E. Strong Langmuir Turbulence in Laser Plasma; Handbook of Plasma Physics; Elsevier Science Publishers: Amsterdam, The Netherlands, 1991; Volume 3, pp. 335–360. [Google Scholar]
- Musher, S.L.; Rubenchik, A.M.; Zakharov, V.E. Weak Langmuir turbulence. Phys. Rep. 1995, 252, 178–274. [Google Scholar] [CrossRef]
- Robinson, P.A.; Willes, A.J.; Cairns, I.H. Dynamics of Langmuir and ion-sound waves in type III solar radio sources. Astrophys. J. 1993, 408, 720–734. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Lu, W.; Wang, W.-H. The Nonlinear Langmuir Waves in a Multi-ion-Component Plasma. Commun. Theor. Phys. 2001, 35, 223–228. [Google Scholar]
- Soucek, J.; Krasnoselskikh, V.; de Wit, T.D.; Pickett, J.; Kletzing, C. Nonlinear decay of foreshock Langmuir waves in the presence of plasma inhomogeneities: Theory and Cluster observations. J. Geophys. Res. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Dodin, I.Y.; Geyko, V.I.; Fisch, N.J. Langmuir wave linear evolution in inhomogeneous nonstationary anisotropic plasma. Phys. Plasmas 2009, 16, 1–9. [Google Scholar] [CrossRef]
- Zaslavsky, A.; Volokitin, A.S.; Krasnoselskikh, V.V.; Maksimovic, M.; Bale, S.D. Spatial localization of Langmuir waves generated from an electron beam propagating in an inhomogeneous plasma: Applications to the solar wind. J. Geophys. Res. 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Ratcliffe, H.; Brady, C.S.; Rozenan, M.B.C.; Nakariakov, V.M. A comparison of weak-turbulence and particle-in-cell simulations of weak electron-beam plasma interaction. AIP Phys. Plasmas 2014, 21, 1–9. [Google Scholar] [CrossRef]
- Ajima, N.Y.; Wa, M.O. Formation and Interaction of Sonic-Langmuir Solitons. Prog. Theor. Phys. 1976, 56, 1719–1739. [Google Scholar] [CrossRef]
- Zakharov, V.E. Collapse of Langmuir Waves. Zhurnal Eksp. Teor. Fiz. 1972, 62, 1745–1759. [Google Scholar]
- Zhen, H.-L.; Tian, B.; Wang, Y.-F.; Liu, D.-Y. Soliton solutions and chaotic motions of the Zakharov equations for the Langmuir wave in the plasma. AIP Phys. Plasmas 2015, 22. [Google Scholar] [CrossRef]
- Dubinov, A.E.; Kitayev, I.N. New solutions of the Zakharov’s equation system for quantum plasmas in form of nonlinear bursts lattice. AIP Phys. Plasmas 2014, 21. [Google Scholar] [CrossRef]
- Khan, Y.; Faraz, N.; Yildirim, A. New soliton solutions of the generalized Zakharov equations using He’s variational approach. Appl. Math. Lett. 2011, 24, 965–968. [Google Scholar] [CrossRef]
- Yang, X.-L.; Tang, J.-S. Explicit exact solutions for the generalized Zakharov equations with nonlinear terms of any order. Comput. Math. Appl. 2009, 57, 1622–1629. [Google Scholar]
- Javidi, M.; Golbabai, A. Exact and numerical solitary wave solutions of generalized Zakharov equation by the variational iteration method. Chaos Solitons Fractals 2008, 36, 309–313. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Dai, C.-Q.; Wu, L.; Zhang, J.-F. Exact and numerical solitary wave solutions of generalized Zakharov equation by the Adomian decomposition method. Chaos Solitons Fractals 2007, 32, 1208–1214. [Google Scholar] [CrossRef]
- De Oliveira, G.I.; Rizzato, F.B. Scaling laws for breathing frequencies of solitary modes in the Zakharov equations. Phys. Rev. E 2001, 65. [Google Scholar] [CrossRef] [PubMed]
- Bulut, H.; Pandir, Y.; Demiray, S.T. Exact Solution of Nonlinear Schrödinger’s Equation with Dual Power-Law Nonlinearity by Extended Trial Equation Method. Waves Random Complex Media 2014, 24, 439–451. [Google Scholar] [CrossRef]
- Demiray, S.T.; Pandir, Y.; Bulut, H. New Soliton Solutions for Sasa-Satsuma Equation. Waves Random Complex Media 2015, 25, 417–428. [Google Scholar] [CrossRef]
- Demiray, S.T.; Pandir, Y.; Bulut, H. New Solitary Wave Solutions of Maccari System. Ocean Eng. 2015, 103, 153–159. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. New Exact Solutions of the New Hamiltonian Amplitude Equation and Fokas Lenells Equation. Entropy 2015, 17, 6025–6043. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. Some Exact Solutions of Generalized Zakharov System. Waves Random Complex Media 2015, 25, 75–90. [Google Scholar] [CrossRef]
- Demiray, S.T.; Pandir, Y.; Bulut, H. All Exact Travelling Wave Solutions of Hirota Equation and Hirota-Maccari System. Optik 2016, 127, 1848–1859. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Kadak, U.; Misirli, E. Classification of exact solutions for some nonlinear partial differential equations with generalized evolution. Abstr. Appl. Anal. 2012, 2012. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuluce Demiray, S.; Bulut, H. New Exact Solutions of the System of Equations for the Ion Sound and Langmuir Waves by ETEM. Math. Comput. Appl. 2016, 21, 11. https://doi.org/10.3390/mca21020011
Tuluce Demiray S, Bulut H. New Exact Solutions of the System of Equations for the Ion Sound and Langmuir Waves by ETEM. Mathematical and Computational Applications. 2016; 21(2):11. https://doi.org/10.3390/mca21020011
Chicago/Turabian StyleTuluce Demiray, Seyma, and Hasan Bulut. 2016. "New Exact Solutions of the System of Equations for the Ion Sound and Langmuir Waves by ETEM" Mathematical and Computational Applications 21, no. 2: 11. https://doi.org/10.3390/mca21020011
APA StyleTuluce Demiray, S., & Bulut, H. (2016). New Exact Solutions of the System of Equations for the Ion Sound and Langmuir Waves by ETEM. Mathematical and Computational Applications, 21(2), 11. https://doi.org/10.3390/mca21020011




