Abstract
In this study, the non-local Euler-Bernoulli beam theory was employed in the nonlinear free and forced vibration analysis of a nanobeam resting on an elastic foundation of the Pasternak type. The analysis considered the effects of the small-scale of the nanobeam on the frequency. By utilizing Hamilton’s principle, the nonlinear equations of motion, including stretching of the neutral axis, are derived. Forcing and damping effects are considered in the analysis. The linear part of the problem is solved by using the first equation of the perturbation series to obtain the natural frequencies. The multiple scale method, a perturbation technique, is applied in order to obtain the approximate closed solution of the nonlinear governing equation. The effects of the various non-local parameters, Winkler and Pasternak parameters, as well as effects of the simple-simple and clamped-clamped boundary conditions on the vibrations, are determined and presented numerically and graphically. The non-local parameter alters the frequency of the nanobeam. Frequency-response curves are drawn.
1. Introduction
Nanotechnology is the manipulation of matter on a supramolecular, molecular, and atomic scale. Many new devices and materials used in consumer products, electronics, biomaterials, medicine, energy production, etc., may be created with the help of nanotechnology. The exclusive properties of nanoscale materials are due to their very small size. The size effect of nano structures has an important role in their static and dynamic analysis. The classical continuum mechanics is not able to take into account the size effect in modeling of the material behavior at the nanoscale. Therefore, various size-dependent continuum theories, which are the non-local elasticity theory, strain gradient theory, the modified couple stress theory, the micropolar theory, and the surface elasticity theory, have been developed to include the small-scale effect. Among these theories, Eringen’s non-local elasticity theory [1,2] is a major subject among scientists. Peddison, et al. [3] were the first pioneers applying the non-local elasticity theory to nanostructures.
Vibration analysis of nanostructures is necessary for the ideal design of nanoelectromechanical systems (NEMS) and new nanodevices. The Winkler model is studied as a one-parameter model, namely Winkler-type elastic foundation, consists of a series of closely-spaced elastic springs, where as the Pasternak model studied as a two-parameter model, namely Pasternak-type elastic foundation, consists of a Winkler-type elastic spring and transverse shear deformation. In contrast, the nonlinear elastic foundation model studied as a three-parameter model, in which the layer is indicated by linear elastic springs, shear deformation, and cubic nonlinearity elastic springs. The work of Niknam and Aghdam [4] deals with the Eringen’s non-local elasticity theory for the evaluation of a closed-form solution of the buckling load and natural frequency of non-local functionally-graded (FG) beams on a nonlinear-type elastic foundation. Fallah and Aghdam [5] carried out post buckling and free vibration analysis of FG beams resting on an elastic foundation and subjecting axial force. Additionally, this author and its coauthors [6] investigated nonlinear free vibration and thermo-mechanical buckling analysis of a FG beam resting on a nonlinear type elastic foundation. Kanani, et al. [7] investigated the free and force vibration of a FG beam in the presence of large amplitude resting on a nonlinear elastic type foundation including shearing layer and cubic nonlinearity. Şimşek [8] developed a non-classical beam theory for the static and nonlinear vibration analysis of microbeams resting on a nonlinear elastic foundation on the base of the modified couple stress theory and Euler-Bernoulli beam theory.
Mustapha and Zhong [9] presented a mathematical model associated with single-walled carbon nanotube (SWCNT) vibration analysis. The SWCNT taken as a non-local Rayleigh beam is assumed to be axially loaded and embedded in a two parameter elastic medium. Mehdipour, et al. [10] employed continuum mechanics and elastic beam model. Their study aims to analyze the transverse vibration of a SWCNT having curved shape and embedded in a Pasternak elastic foundation. Work of Shen and Zhang [11] deals with the post-buckling nonlinear vibration and nonlinear bending of a SWCNT. The SWCNT modeled as a non-local beam including small-scale effect and resting on a two parameter elastic foundation in thermal environments. Arani, et al. [12] carried out a study related with the vibration behavior of single-walled boron nitride nanotubes in the presence of von Kármán geometric nonlinearity effects modeled with non-local piezoelasticity. Its nanotube surrounded by an elastic medium was assumed to be Winkler and Pasternak foundation model. Murmu and Pradhan [13] applied an existing method to a well-known Eringen non-local elasticity theory to analyze the stability response of SWCNT surrounded by Winkler- and Pasternak-type foundation models. Yas and Samadi [14] were presented buckling and free vibration analysis of nanocomposite Timeshenko beams reinforced by SWCNT resting on the two parameter medium.
Kazemi-Lari, et al. [15] considered the influence of viscoelastic foundation in the presence of interaction between surrounding viscoelastic medium and carbon nanotubes (CNTs) considering the action of a concentrated follower force. Surrounded medium is taken as the Kelvin–Voight, Maxwell, and standard linear solid types of viscoelastic foundation. Ghanvanloo, et al. [16] applied an existing method to a well-known classical Euler-Bernoulli beam model considering the instability and vibration response of CNT resting on a linear viscoelastic Winkler foundation. Refiei, et al. [17] applied an existing method to a well-known non-local Euler-Bernoulli beam theory to analyze the vibration characteristics of non-uniform SWCNT conveying fluid and also embedded in viscoelastic medium. It was concluded from their study that the nonlocal parameter, small-scale effect, may influence extremely the natural frequency and mode shape of the system. The main motivation for Arani and Amir’s [18] work is to develop an analytic model for the electro-thermal vibration of boron nitride nanotubes by using strain gradient theory, in which nanotubes coupled by visco-Pasternak medium. Wang and Li [19] carried out the study of the nonlinear free vibration of a nanotube in the presence of small-scale effect embedded in viscous matrix modeled with non-local elasticity theory and Hamilton principle. The work of Mahdawi, et al. [20] deals with the nonlinear free vibrational behavior of a double walled carbon nanotube (DWCNT) in the presence of compressive axial load. DWCNT was surrounded by a polymer matrix. The results of their study indicate that the surrounding medium may influence profoundly the vibrational behavior of the embedded CNT.
Most existing studies in the literature examine the vibrational behavior of nanostructures surrounded by an elastic medium. The natural frequency of a SWCNT conveying a viscous fluid and are also embedded in an elastic medium [21], free transverse vibration of an elastically-supported DWCNT embedded in an elastic matrix in the presence of initial axial force [22], axial vibration of SWCNT embedded in an elastic medium [23], vibration of nanotubes embedded in an elastic matrix [24], nonlinear free vibration of embedded DWCNT including the von Kármán geometric nonlinearity [25], nonlinear free vibration of clamped-clamped DWCNT surrounded by an elastic medium with consideration of the von Kármán geometric nonlinearity and the nonlinear van der Waals forces [26], forced vibration of an elastically-connected DWCNT carrying a moving nanoparticle [27], nonlinear vibration of embedded multiwalled carbon nanotubes (MWCNT) in thermal environments [28], vibration analysis of embedded MWCNT at an elevated temperature with considering the small-scale effect on the large amplitude [29], free transverse vibration of SWCNT embedded in elastic matrix under various boundary conditions [30], thermal vibration of SWCNT embedded in an elastic medium [31], thermal-mechanical vibration and buckling instability of a SWCNT conveying fluid and resting on an elastic medium [32], electro-thermo-mechanical vibration analysis of non-uniform and non-homogeneous boron nitride nanorod embedded in elastic medium [33], buckling behavior of SWCNT on a Winkler foundation under various boundary conditions [34], critical buckling temperature of SWCNT embedded in a one parameter elastic medium [35], and buckling analysis of SWCNT including the effect of temperature change and surrounding elastic medium [36] were studied with the aid of nonlocal elasticity theory. The surrounding elastic medium related with the above studies was described as the Winkler model with spring constant k.
Another class of size-dependent continuum theories that deal with the electro-thermal transverse vibration behavior of double-walled boron nitride nanotubes which are surrounded by an elastic medium was presented with the aid of non-local piezoelasticity cylindirical shell theory [37]. Free vibrations of SWCNT embedded in non-homogenous elastic matrix were studied with the aid of the non-local continuum shell theory [38]. The nonlinear free vibration of embedded MWCNT was investigated by using the multiple elastic beam models and continuum mechanics [39]. Nonlinear thermal stability and vibration of pre/post buckled temperature and microstructure-dependent FG beams resting on an elastic medium was investigated on the base of the modified couple stress theory [40]. The method of multiple scales (a perturbation method) is an efficient technique to solve the nonlinear differential equations. Free vibration analysis of beams resting on elastic foundation [41,42] and nonlinear free vibration behavior of simply supported DWCNT with considering the geometric nonlinearity were presented by using multiple scale method [43]. Nonlinear vibration of tensioned nanobeam and nanobeam with different boundary condition was studied by using non-local elasticity theory [44,45].
Lots of the work presented in the literature includes the vibration behavior of a nanobeam embedded in an elastic medium, whereas investigations on the two-parameter medium are rather limited. We examine the literature presented in the above, and it can be seen clearly that an elastic medium surrounded by a Pasternak-type model is limited in literature. Most of the above work is mainly related with the amplitude–frequency response of the nanotube. However, damping and forcing effect included studies on the nonlinear vibration properties of nanosystems are also rather limited. In the present study, the non-linear free vibration of the nanobeam resting on a two-parameter medium is studied by the non-local continuum theory. The small scale and damping effects are taken into account and nonlinear vibration behaviors of the nanobeam are illustrated.
2. Governing Equations
2.1. Non-Local Effects
In the classical (local) continuum theory, the stress at a point Χ depends only on the strain at the same point, while the non-local elasticity theory proposed by Eringen [1,2], regards the stress at a point as a function of strains at all points in the continuum. Therefore, the nonlocal stress tensor σ at point Χ can be written as:
where is the classical macroscopic stress tensor at point , is the non-local modulus, is the Euclidian distance and τ is a material constant, is the fourth order elasticity tensor, and and are the second order tensors representing stress and strain fields, respectively. A simplified equation of differential form is used as a non-local constitutive relation, the reason being is that solving of the integral constitutive Equation (2) is complicated.
where is the Laplacian operator. Here, the non-dimensional non-local nanoscale parameter τ is defined as , in which is constant appropriate to each material and is internal characteristic length and is external characteristic length. The constitutive equation of nonlocal elasticity for a beam takes the following form:
where E is the elasticity modulus.
2.2. Nonlocal Euler-Bernoulli Beam
This study is carried out on the basis of the non-local Euler-Bernoulli beam model. Two types of boundary conditions, which are simple-simple and clamped-clamped, are considered in this work and shown in Figure 1. The nanobeam is resting on a two parameter elastic foundation with the spring constants kL and kp of the Winkler elastic medium and Pasternak elastic medium, respectively. The equation of motion is obtained by using Hamilton’s principle. For the Euler-Bernoulli beam model, the displacement field is given as:
where are the axial and transverse displacements, respectively. The axial force and resultant bending moment for the beam model are:
where A is the area of the cross-section for the nanobeam. Taking into account the large amplitude nonlinear vibration, the von Kármán nonlinear strain (i.e., ) should be considered and strain-displacement relationship is given by:
where is the nonlinear extensional strain and is the bending strain. Then the von Kármán nonlinear strain (i.e., ) can be expressed as:
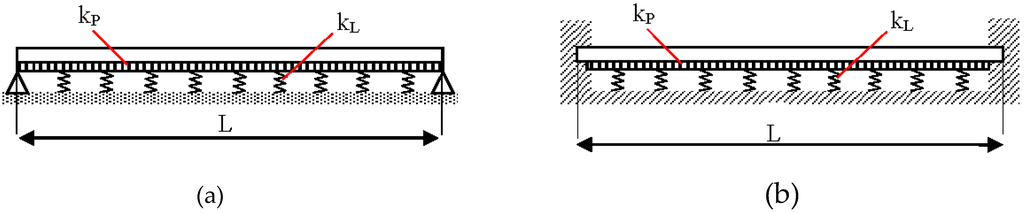
Figure 1.
Boundary conditions for different beam supports. (a) Simple-Simple case and (b) Clamped-Clamped case.
The force–strain and the moment–strain relations of the nonlocal beam theory can be obtained from Equations (4)–(8):
where I is the moment of inertia. The kinetic energy T can be written as:
where ρA is the mass per unit length. The strain energy U can be written as:
In addition, the virtual work by the external load from the elastic medium of the Pasternak type is given by:
where is the load exerted by the Pasternak-type elastic medium. The stiffness and the shear modulus parameters of the deformable medium are represented by and . Hamilton’s principle can be represented analytically by the following formula:
Inserting Equations (11)–(13) into Equation (14) and integrating by parts, and collecting the coefficients of and , the following equation of motion are obtained:
Substituting Equation (16) into Equation (10), one obtains the expressions of the non-local force N and non-local moment M as follows:
The longitudinal inertia can be neglected based on the discussion about the nonlinear vibration of continuous systems [46,47], then the axial normal force N can be represented as:
The nonlinear vibration equation of motion for the nanobeam resting on the Pasternak-type elastic foundation can be obtained by substituting Equations (17)–(19) into Equations (15) and (16) as follows:
The following non-dimensional quantities aims to study problem under general form are considered:
In the non-dimensional form considering the Equations (20) and (21) can be expressed as:
The non-dimensional form of boundary conditions can be expressed as;
The multiple scale method will be able to employ to the partial differential equations and boundary conditions to obtain the approximate solution for the problem [46,47]. Then, the introduction of the forcing and damping term in Equation (22) can also be seen as the nonlinear exact solution:
In order to include stretching and damping effects at order ε, deflection is transformed to obtain a weak nonlinear system. The following transformation is performed for the damping and forcing terms based on the multiple scale method:
Substituting Equations (25) and (26) into Equation (24) and performing some necessary simplifications, the simplified equations takes the following form:
The non-dimensional form of boundary conditions can be expressed as:
A straight forward asymptotic expansion can be introduced, which is why there is no quadratic non-linearity:
where ε is a small parameter to denote the deflections. Hence, a weakly non-linear system can be investigated by this procedure. New independent variables are introduced and the fast and slow time scales are written as:
Denoting the ordinary time derivatives can be transformed into partial derivatives as:
Inserting Equations (29) and (31) into Equation (27), we can get the following relation for the equation of motion and boundary conditions at different orders:
Order (ε0)
Order (ε ):
Fundamental frequencies are obtained by solving the first order of expansions, whereas the solvability condition is obtained by solving the second order of expansion. The first order of perturbation is linear, as given in Equation (12); the solution may be represented by:
where cc represents the complex conjugate of the preceding terms. Substituting Equation (34) into Equation (32), one obtains:
The following shape function for any beam segment can be considered for the solution of the equations:
The boundary conditions are applied and the frequency equations can be obtained. Using the functions in Equation (36) will give the dispersion relation shown below:
and substituting Equation (38) into Equation (33), we eliminate the terms producing secularities. Here stands for the solution related with non-secular terms. One obtains:
where cc represents the complex conjugate of preceding terms and NST represents the non-secular terms. Excitation frequency is assumed to close to one of the natural frequencies of the system; that is:
where σ is a detuning parameter of order 1, the solvability condition for Equations (39) and (40) is obtained as follows:
where .
Taking into account the real amplitude a and phase θ, the complex amplitude A in Equation (41) can be written as the following form:
Then amplitude and phase modulation equations are:
where . In the steady-state case, Equation (43) will be solved in the following section and variation of nonlinear amplitude will be discussed.
3. Numerical Results
Numerical examples for the simple-simple and clamped-clamped end condition beam frequencies are presented in this section. The linear fundamental frequencies for both types of boundary conditions will be evaluated, and the nonlinear frequencies for free, undamped vibrations will also be evaluated. In the case of the μ = f = σ = 0, one obtains:
from Equation (44). The steady-state real amplitude is represented by . The frequency of non-linear is:
where is the nonlinear correction terms.
At the steady state, become zero. The detuning parameter of frequency is as follows:
The linear frequencies and nonlinear correction terms with different small scale effect (nonlocal parameter) γ, the Winkler parameter (KL) and the Pasternak parameter (Kp) are given in Table 1 and Table 2 for the first five frequencies for simple-simple (S-S) and clamped-clamped (C-C) supported case, respectively. The similar conclusions are derived from these tables for the effect of non-local parameter and the stiffness coefficients of the Winkler and Pasternak foundation on the natural frequencies. It can be seen in Table 1 and Table 2 that non-dimensional natural non-local frequency of the nanobeam is smaller than the classical (local) natural frequency. Note that the non-local parameter γ = 0 corresponds to the classical nanobeams without the non-local effect. This is attributed to the effect of small scale effect. It is evident that an increase in the nonlocal parameter leads to the decrease in the natural frequency although correction term increases with nonlocal parameter. This situation can be interpreted that the non-local effect reduces the stiffness of the material and, hence, the comparative lower natural frequencies. The effect of the coefficients of the two parameter foundation on the frequency value of nanobeam is also seen in Table 1 and Table 2 that show the linear frequency with the Winkler parameter and the Pasternak parameter (Kp). In these tables, the dimensionless parameter of Winkler KL = 10, 100, 200 and of Pasternak Kp = 0, 5, 25, 50 are taken. It can be deduced from Table 1 and Table 2 that the linear frequencies increase when the Winkler and the Pasternak parameters increase with regardless of the type of boundary condition. Furthermore, for the considered values of the foundation parameters, the effect of both foundation parameters on the linear frequency is more prominent for C-C end condition.

Table 1.
The first five frequencies and correction term due to nonlinear terms for different γ, KL, and Kp values for simple-simple support conditions.

Table 2.
The first five frequencies and correction term due to nonlinear terms for different γ, KL, and Kp values for clamped-clamped support conditions.
Studies related to the nonlocal beams resting on the Pasternak type elastic foundation in the existing literature are rather limited for the analysis of fundamental and nonlinear frequency. However, the study of Yokoyama [48] includes the first few values of the classical EB beam resting on a Pasternak-type foundation. Also, the study of Mustapha and Zhong [9] includes the non-uniform SWCNT depended on a non-local Rayleigh beam resting on Pasternak-type foundation. A comparison study is performed to check the reliability of the present method. For this purposes, linear frequency of a local EB beam embedded Pasternak foundation for the S-S case are compared with those of the work of Mustapha and Zhong [9] and the work of Yokoyama [48]. It can be seen from the Table 3 that they only studied the first second values of the non-dimensional natural frequencies of a local EB beam embedded on a Pasternak foundation, which takes the value of 25 and 36. However, in this paper extensive natural frequency analyses were performed for the first five frequencies. It is obvious from Table 3 that there is good harmony between the three results.

Table 3.
Non-dimensional natural frequencies of a local EB beam embedded on a Pasternak foundation (γ = 0) for the simple-simple support conditions.
The effect of the non-local parameter on the natural frequency is examined and scrutinized in Figure 2 that plots the variation of the natural frequency (ω) with the non-local parameter (γ) for the S-S and CC nanobeam, respectively. It can be deduced from Figure 2 that the natural frequency decreases when the non-local parameter increases. Regardless of the type of boundary condition, it is observed that the non-local parameter has an influence on the natural frequency.
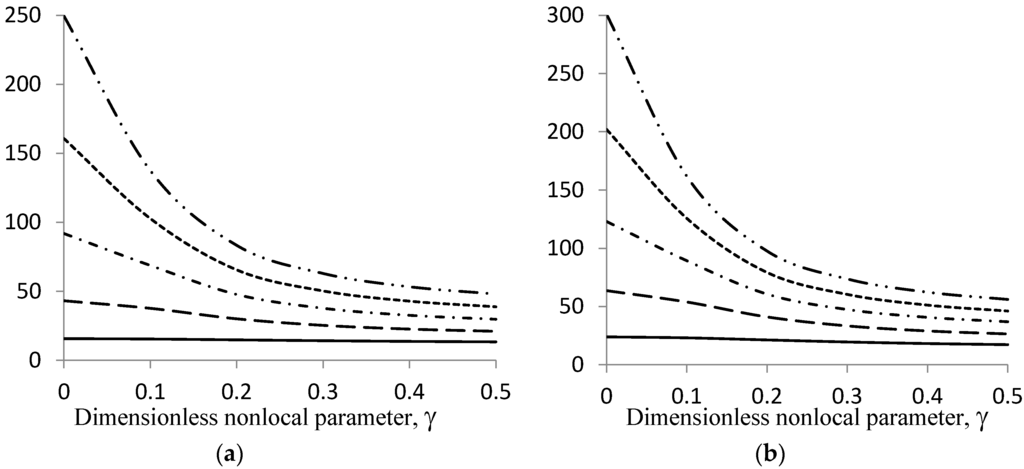
Figure 2.
Variation of the natural frequency with the dimensionless nonlocal parameter for KL = 10, Kp = 5. (a) S-S nanobeam and (b) C-C nanobeam (___ω1, _ _ω2, _._ ω3, - - ω4, _ . .ω5).
Variation of the nonlinear frequency with amplitude is shown for the first five modes of vibration in Figure 3, the frequencies are calculated taking into account the non-local parameter (γ = 0.3). It can be seen from Figure 3 that the nonlinear frequencies increase with an increase in the mode number.
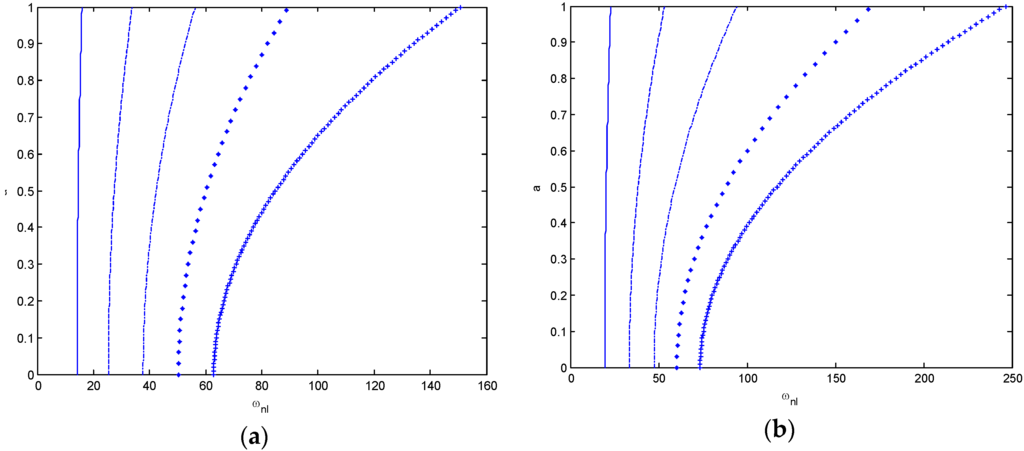
Figure 3.
Nonlinear frequency versus amplitude curves of nanobeam for different modes for the KL = 100, Kp = 5 and γ = 0.3. (a) simple-simple; (b) clamped-clamped (___ω1, _ _ω2, _._ ω3, ●●● ω4, +++ω5).
In Figure 4, Figure 5 and Figure 6, the nonlinear frequency versus amplitude curves of nanobeam are shown for the first mode and S-S and C-C boundary condition. One can observe a hardening behavior. The frequency response bending to the left side is called the softening nonlinearity, but to the right side is called the hardening nonlinearity. So, the behaviors in Figure 4, Figure 5 and Figure 6 are of hardening type, i.e., the nonlinear frequency increases as the vibration amplitude increases. Figure 4 shows the effect of the Winkler parameter KL on the nonlinear frequency versus amplitude curves with γ = 0.3 and Kp = 5. It can be seen in Figure 4 that the nonlinear frequency of nanobeam increases with the increment of the KL values. The Winkler parameter KL has a significant effect on the nonlinear frequency value. In Figure 5 and Figure 6, γ = 0.3 is fixed and Kp is increased. The nonlinear frequencies increase in both figures. From Figure 5 and Figure 6, it is noted that the Pasternak parameter Kp has a pronounced effect on the nonlinear frequency amplitude curves of nanobeam. It can be readily observed that the value of nonlinear natural frequency have a direct relation with the Winkler and Pasternak parameter value. The C-C nanobeam has the highest natural frequency and nonlinear frequencies since the end condition is the strongest for the C-C nanobeam.
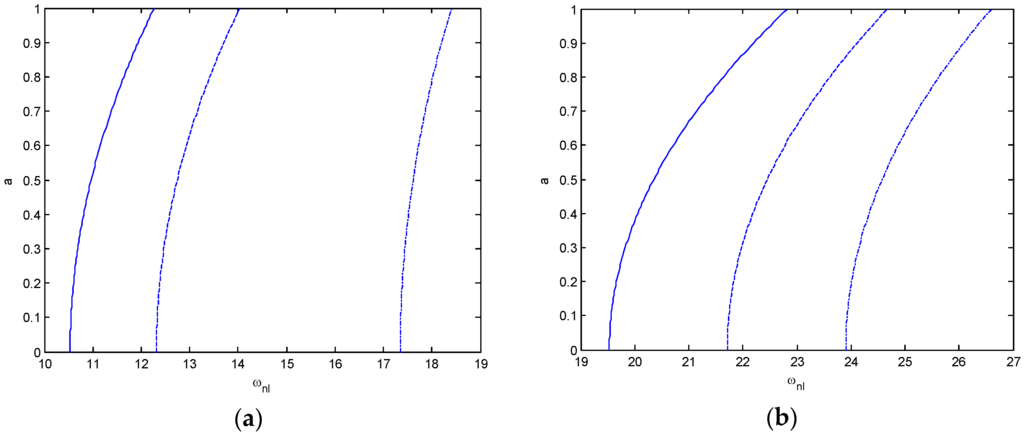
Figure 4.
Nonlinear frequency versus amplitude curves of nanobeam for the first mode and γ = 0.3. (a) simple-simple; (b) clamped-clamped (Kp = 5, ___ KL = 10, _ _ KL = 100, _._ KL = 200).
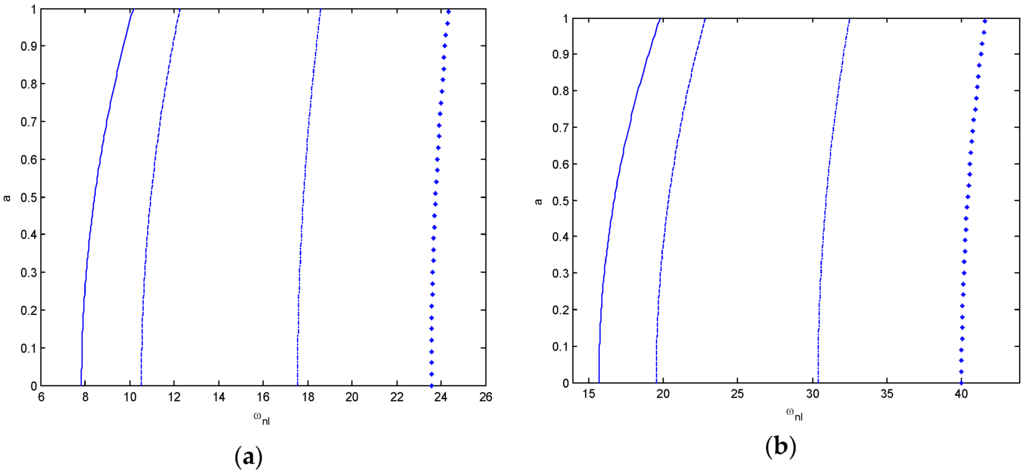
Figure 5.
Nonlinear frequency versus amplitude curves of nanobeam for the first mode KL = 10 and γ = 0.3. (a) simple-simple; (b) clamped-clamped (___ Kp = 0, _ _ Kp = 5, _._ Kp = 25, ●●● Kp = 50).
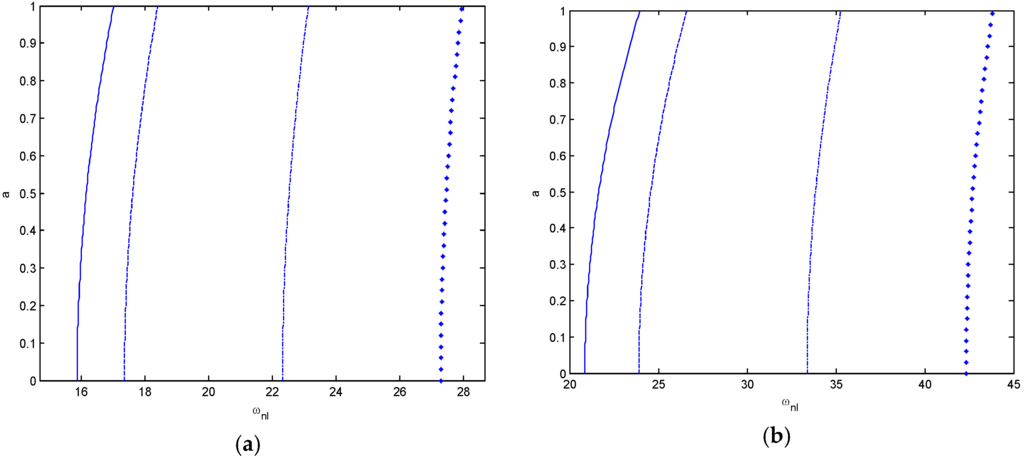
Figure 6.
Nonlinear frequency versus amplitude curves of nanobeam for the first mode KL = 200 and γ = 0.3. (a) simple-simple; (b) clamped-clamped (___ Kp = 0, _ _ Kp = 5, _._ Kp = 25, ●●● Kp = 50).
Frequency response curves are presented in Figure 7, Figure 8, Figure 9 and Figure 10. The detuning parameter σ shows the nearness of the external excitation frequency to the natural frequency of system. Several figures are drawn using Equation (46) assuming f = 1 and damping coefficient μ = 0.1. Increasing the forcing term increase amplitudes when σ < 0 and decreases the amplitudes when σ > 0 at different values. The maximum amplitudes happen when σ > 0. In Figure 7, the influence of the mode number on the hardening nonlinear properties is shown both types of boundary condition. Five different mode numbers are considered and compared. It can be seen that for the first mode or fundamental mode, the resonant amplitude is larger and the corresponding width is broader. Figure 8 presents the frequency response curves of S-S and C-C case for the first mode in order to discuss the influence of the Winkler parameter KL. It can be observed that, for S-S and C-C end condition, the amplitude decreases with the Winkler parameter increasing. Figure 9 and Figure 10 present the frequency response curves of S-S and C-C case for the first mode in order to discuss the influence of the Pasternak parameter Kp. It can be seen that for the fundamental mode, the amplitude decreases with the Pasternak parameter increasing. Both observations denote that the Winkler and Pasternak parameter has significant influences on the primary resonance of the nanobeam.
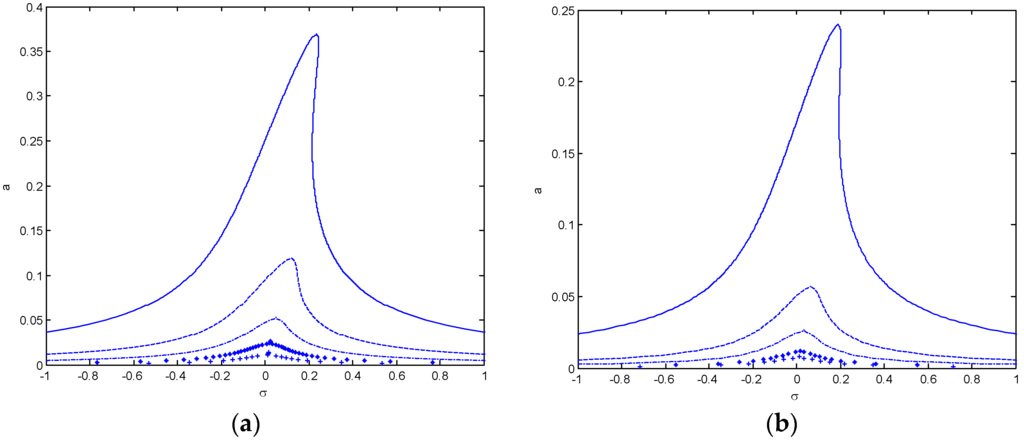
Figure 7.
Frequency-response curves for nanobeam with different modes for KL = 100, Kp = 5 and γ = 0.3. (a) simple-simple; and (b) clamped-clamped (___ω1, _ _ω2, _._ ω3, ●●● ω4, +++ω5).
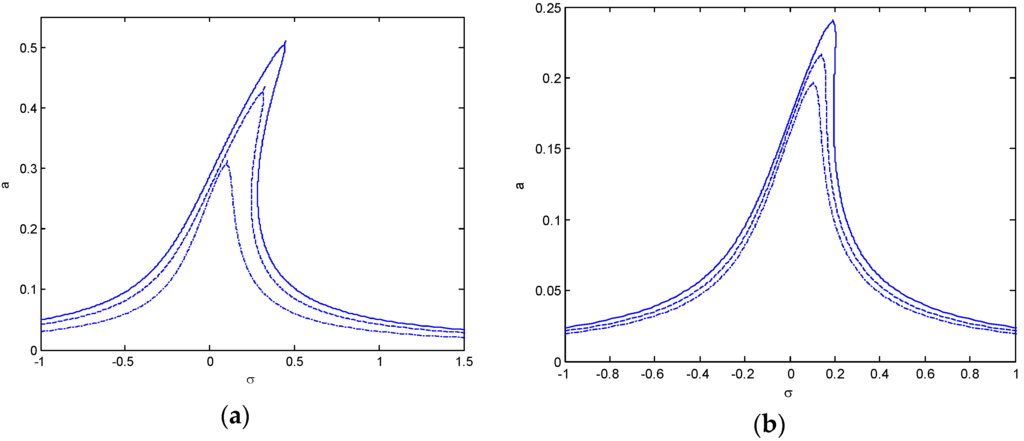
Figure 8.
Effects of Winkler parameter on frequency-response curves for the first mode and γ = 0.3. (a) simple-simple; (b) clamped-clamped (Kp = 5: ___ KL = 10, _ _ KL = 100, _._ KL = 200).
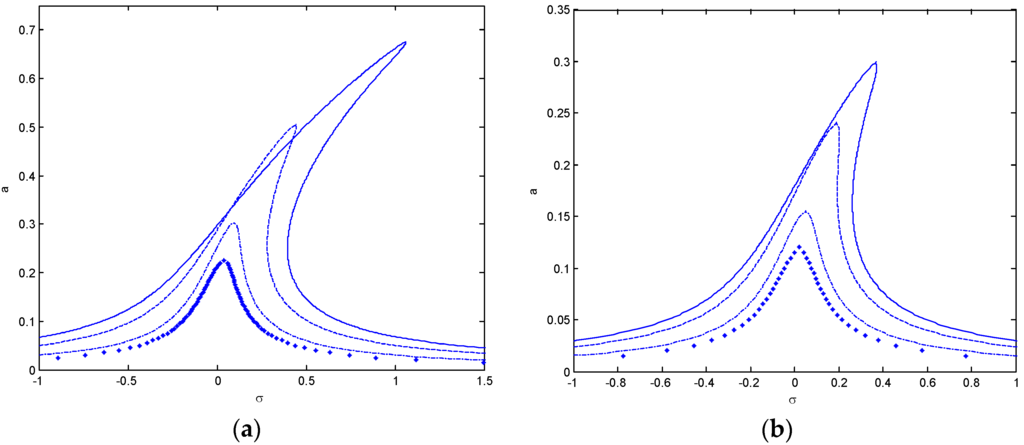
Figure 9.
Effects of the Pasternak parameter on frequency-response curves for the first mode and γ = 0.3. (a) simple-simple; (b) clamped-clamped (KL = 10: ___ Kp = 0, _ _ Kp = 5, _._ Kp = 25, ●●● Kp = 50).
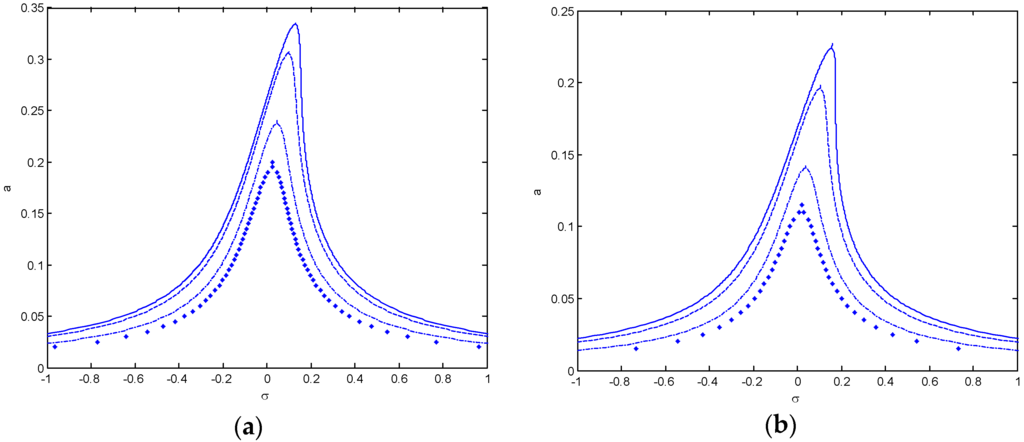
Figure 10.
Effects of the Pasternak parameter on frequency-response curves for the first mode, KL = 200 and γ = 0.3. (a) simple-simple; (b) clamped-clamped (___ Kp = 0, _ _ Kp = 5, _._ Kp = 25, ●●● Kp = 50).
4. Conclusions
In the present study, the free and force vibration of a nanobeam resting on an elastic foundation of the Pasternak type is investigated based on the non-local Euler Bernoulli beam theory. The non-linear equations of motion, including stretching of the neutral axis, are derived. The governing equations and boundary conditions are derived by using Hamilton’s principle. The multiple scale method is used to solve the governing differential equation of the nanobeam. The effect of different parameters, such as Winkler modulus, Pasternak shear modulus, and the non-local factor on frequencies is investigated for the nanobeam with simple-simple and clamped-clamped boundary conditions. The extensive numerical data is given in tabular form for various values of the parameters so that these results can be used as a reference for future studies. Results revealed that increasing the non-local parameters lead to decreasing the linear and nonlinear frequencies and to increasing the correction terms. Furthermore, increasing the Winkler and Pasternak parameters increase the values of both linear and nonlinear frequencies. Observed non-linearity is of the hardening type because of the stretching of the neutral axis.
Author Contributions
All authors contributed extensively to the work presented in this paper. N.T and S.M.B obtained the equations, drawn the figures and wrote the main paper. All authors discussed the results and implications and commented on the manuscript at all stages.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNT | Carbon Nanotube |
| SWCNT | Single walled carbon nanotube |
| DWCNT | Double walled carbon nanotube |
| MWCNT | Multi walled carbon nanotube |
References
- Eringen, A.C. On differential-equations of nonlocal elasticity and solutions of screw dislocation and surface-waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Niknam, H.; Aghdam, M.M. A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 2015, 119, 452–462. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. Eur. J. Mech. A Solids 2011, 30, 571–583. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Compos. B Eng. 2012, 43, 1523–1530. [Google Scholar] [CrossRef]
- Kanani, A.S.; Niknam, H.; Ohadi, A.R.; Aghdam, M.M. Effect of nonlinear elastic foundation on large amplitude free and forced vibration of functionally graded beam. Compos. Struct. 2014, 115, 60–68. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlinear static and free vibration analysis of microbeams based based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method. Compos. Struct. 2014, 112, 264–272. [Google Scholar] [CrossRef]
- Mustapha, K.B.; Zhong, Z.W. Free transverse vibration of an axially loaded non-prismatic single-walled carbon nanotube embedded in a two-parameter elastic medium. Comput. Mater. Sci. 2010, 50, 742–751. [Google Scholar] [CrossRef]
- Mehdipour, I.; Barari, A.; Kimiaeifar, A.; Domairry, G. Vibrational analysis of curved single-walled carbon nanotube on a Pasternak elastic foundation. Adv. Eng. Softw. 2012, 48, 1–5. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Nonlocal beam model for nonlinear analysis of carbon nanotubes on elastomeric substrates. Comput. Mater. Sci. 2011, 50, 1022–1029. [Google Scholar] [CrossRef]
- Arani, A.G.; Atabakhshian, V.; Loghman, A.; Shajari, A.R.; Amir, S. Nonlinear vibration of embedded SWBNNTs based on nonlocal Timoshenko beam theory using DQ method. Physica B 2012, 407, 2549–2555. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physica E 2009, 41, 1232–1239. [Google Scholar] [CrossRef]
- Yas, M.H.; Samadi, N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int. J. Press. Vessels Pip. 2012, 98, 119–128. [Google Scholar] [CrossRef]
- Kazemi-Lari, M.A.; Fazelzadeh, S.A.; Ghavanloo, E. Non-conservative instability of cantilever carbon nanotubes resting on viscoelastic foundation. Physica E 2012, 44, 1623–1630. [Google Scholar] [CrossRef]
- Ghanvanloo, E.; Daneshmand, F.; Rafiei, M. Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation. Physica E 2010, 42, 2218–2224. [Google Scholar] [CrossRef]
- Rafiei, M.; Mohebpour, S.R.; Daneshmand, F. Small-scale effect on the vibration of non-uniform carbon nanotubes conveying fluid and embedded in viscoelastic medium. Physica E 2012, 44, 1372–1379. [Google Scholar] [CrossRef]
- Arani, A.G.; Amir, S. Electro-thermal vibration of visco-elastically coupled BNNT systems conveying fluid embedded on elastic foundation via strain gradient theory. Physica B 2013, 419, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M. Nonlinear free vibration of nanotube with small scale effects embedded in viscous matrix. Mech. Res. Commun. 2014, 60, 45–51. [Google Scholar] [CrossRef]
- Mahdavi, M.H.; Jiang, L.Y.; Sun, X. Nonlinear vibration of a double-walled carbon nanotube embedded in a polymer matrix. Physica E 2011, 43, 1813–1819. [Google Scholar] [CrossRef]
- Lee, H.L.; Chang, W.J. Vibration analysis of a viscous-fluid-conveying single-walled carbon nanotube embedded in an elastic medium. Physica E 2009, 41, 529–532. [Google Scholar] [CrossRef]
- Kiani, K. Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subject to axial load using nonlocal shear deformable beam theories. Int. J. Mech. Sci. 2013, 68, 16–34. [Google Scholar] [CrossRef]
- Aydogdu, M. Axial vibration analysis of nanorods (carbon nanotubes) embedded in an elastic medium using nonlocal elasticity. Mech. Res. Commun. 2012, 43, 34–40. [Google Scholar] [CrossRef]
- Wang, B.L.; Wang, K.F. Vibration analysis of embedded nanotubes using nonlocal continuum theory. Compos. B Eng. 2013, 47, 96–101. [Google Scholar] [CrossRef]
- Ke, L.L.; Xiang, Y.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput. Mater. Sci. 2009, 47, 409–417. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.X.; Zhang, C.P.; Tang, Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Appl. Math. Model. 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlocal effects in the forced vibration of an elastically connected double-carbon nanotube system under a moving nanoparticle. Comput. Mater. Sci. 2011, 50, 2112–2123. [Google Scholar] [CrossRef]
- Ansari, R.; Ramezannezhad, H. Nonlocal Timoshenko beam model for the large-amplitude vibrations of embedded multiwalled carbon nanotubes including thermal effects. Physica E 2011, 43, 1171–1178. [Google Scholar] [CrossRef]
- Ansari, R.; Ramezannezhad, H.; Gholami, R. Nonlocal beam theory for nonlinear vibrations of embedded multiwalled carbon nanotubes in thermal environment. Nonlinear Dyn. 2012, 67, 2241–2254. [Google Scholar] [CrossRef]
- Kiani, K. A meshless approach for free transverse vibration of embedded single walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect. Int. J. Mech. Sci. 2010, 52, 1343–1356. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Thermo-mechanical vibration of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Comput. Mater. Sci. 2009, 46, 854–859. [Google Scholar] [CrossRef]
- Chang, T.P. Thermal–mechanical vibration and instability of a fluid-conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Appl. Math. Model. 2012, 36, 1964–1973. [Google Scholar] [CrossRef]
- Rahmati, A.H.; Mohammadimehr, M. Vibration analysis of non-uniform and non-homogeneous boron nitride nanorods embedded in elastic medium under combined loadings using DQM. Physica B 2014, 440, 88–98. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Reddy, G.K. Buckling analysis of single walled carbon nanotube on Winkler foundation using on nonlocal elasticity theory and DTM. Comput. Mater. Sci. 2011, 50, 1052–1056. [Google Scholar] [CrossRef]
- Narender, S.; Gopalakrishnan, S. Critical buckling temperature of single walled carbon nanotubes embedded in a one-parameter elastic medium based on nonlocal continuum mechanics. Physica E 2011, 43, 1185–1191. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Thermal effects on the stability of embedded carbon nanotubes. Comput. Mater. Sci. 2010, 47, 721–726. [Google Scholar] [CrossRef]
- Arani, A.G.; Amir, S.; Shajari, A.R.; Mozdianfard, M.R.; Maraghi, Z.K.; Mohammadimehr, M. Electro-thermal nonlocal vibration analysis of embedded DWBNNTs. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2011, 224, 745–756. [Google Scholar] [CrossRef]
- Mikhasev, G. On localized modes of free vibrations of single walled carbon nanotubes embedded in nonhomogeneous elastic medium. ZAMM 2014, 94, 130–141. [Google Scholar] [CrossRef]
- Fu, Y.M.; Hong, J.W.; Wang, X.Q. Analysis of nonlinear vibration for embedded carbon nanotubes. J. Sound Vib. 2006, 296, 746–756. [Google Scholar] [CrossRef]
- Komijani, M.; Esfahani, S.E.; Reddy, J.N.; Liu, Y.P.; Eslami, M.R. Nonlinear thermal stability and vibration of pre/post-buckled temperature and microstructure dependent functionally graded beams resting on elastic foundation. Compos. Struct. 2014, 112, 292–307. [Google Scholar] [CrossRef]
- Ozturk, B.; Coskun, S.B.; Koc, M.Z.; Atay, M.T. Homotopy perturbation method for free vibration analysis of beams on elastic foundation. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10, 012158. [Google Scholar] [CrossRef]
- Öz, H.R.; Pakdemirli, M.; Özkaya, E.; Yılmaz, M. Nonlinear vibrations of a slightly curved beam resting on a nonlinear elastic foundation. J. Sound Vib. 1998, 212, 295–309. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, W.; Zhang, L. Applied multiscale method to analysis of nonlinear vibration for double walled carbon nanotubes. Appl. Math. Model. 2011, 35, 2279–2289. [Google Scholar] [CrossRef]
- Bağdatlı, S.M. Non-linear vibration of nanobeams with various boundary condition based on nonlocal elasticity theory. Compos. B Eng. 2015, 80, 43–52. [Google Scholar] [CrossRef]
- Bağdatlı, S.M. Non-linear transverse vibrations of tensioned nanobeams using nonlocal beam theory. Struct. Eng. Mech. 2015, 55, 281–298. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley: New York, NY, USA, 1981. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Yokoyama, T. Vibrations and transient responses of Timoshenko beams resting on elastic foundations. Arch. Appl. Mech. 1987, 57, 81–90. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).