Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution
Abstract
1. Introduction
2. Background
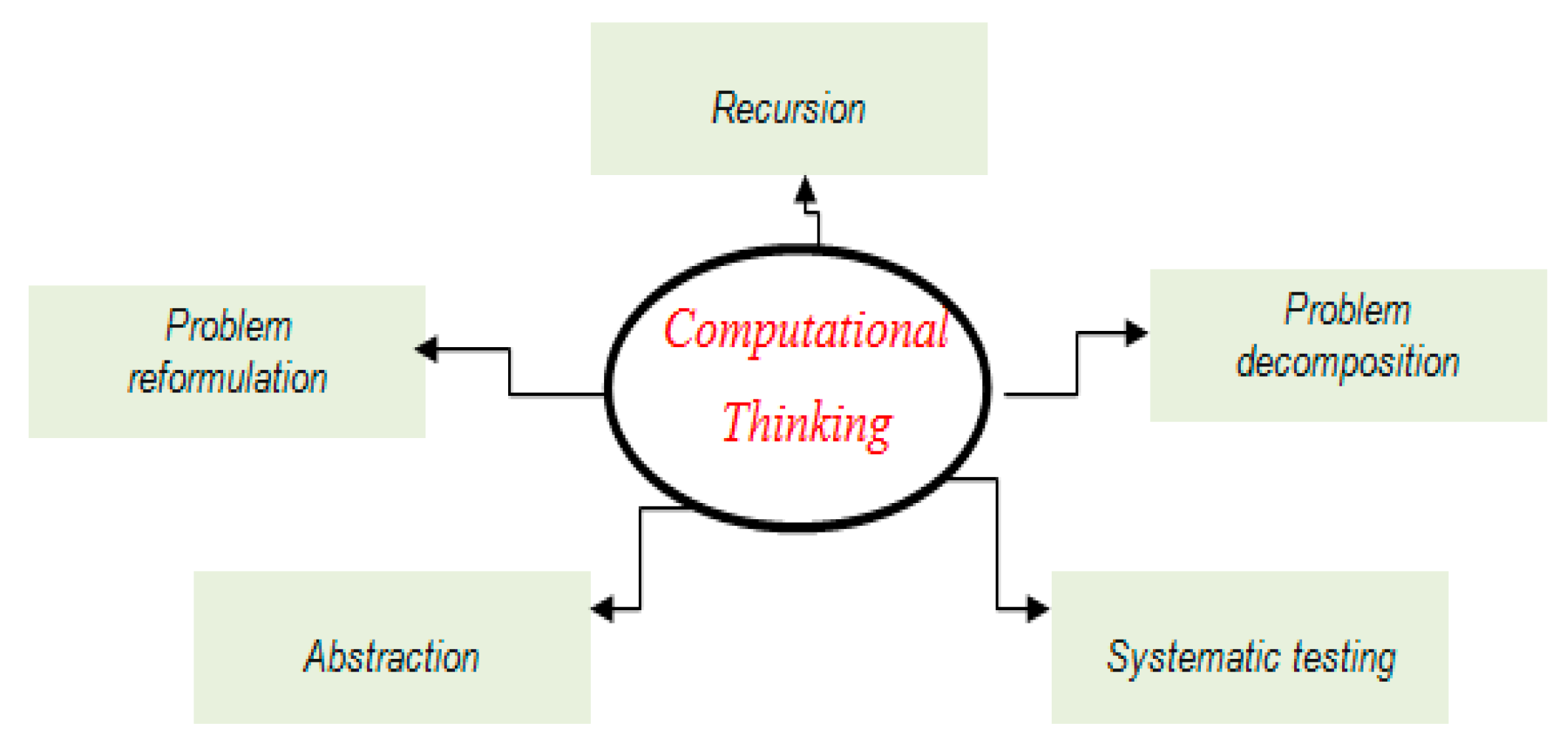
2.1. Computational Thinking (CT)
- Problem reformulation—reframe a problem into a solvable and familiar one.
- Recursion—construct a system incrementally based on preceding information.
- Problem decomposition—break the problem down into manageable units.
- Abstraction—model the core aspects of complex problems or systems.
- Systematic testing—take purposeful actions to derive solutions.
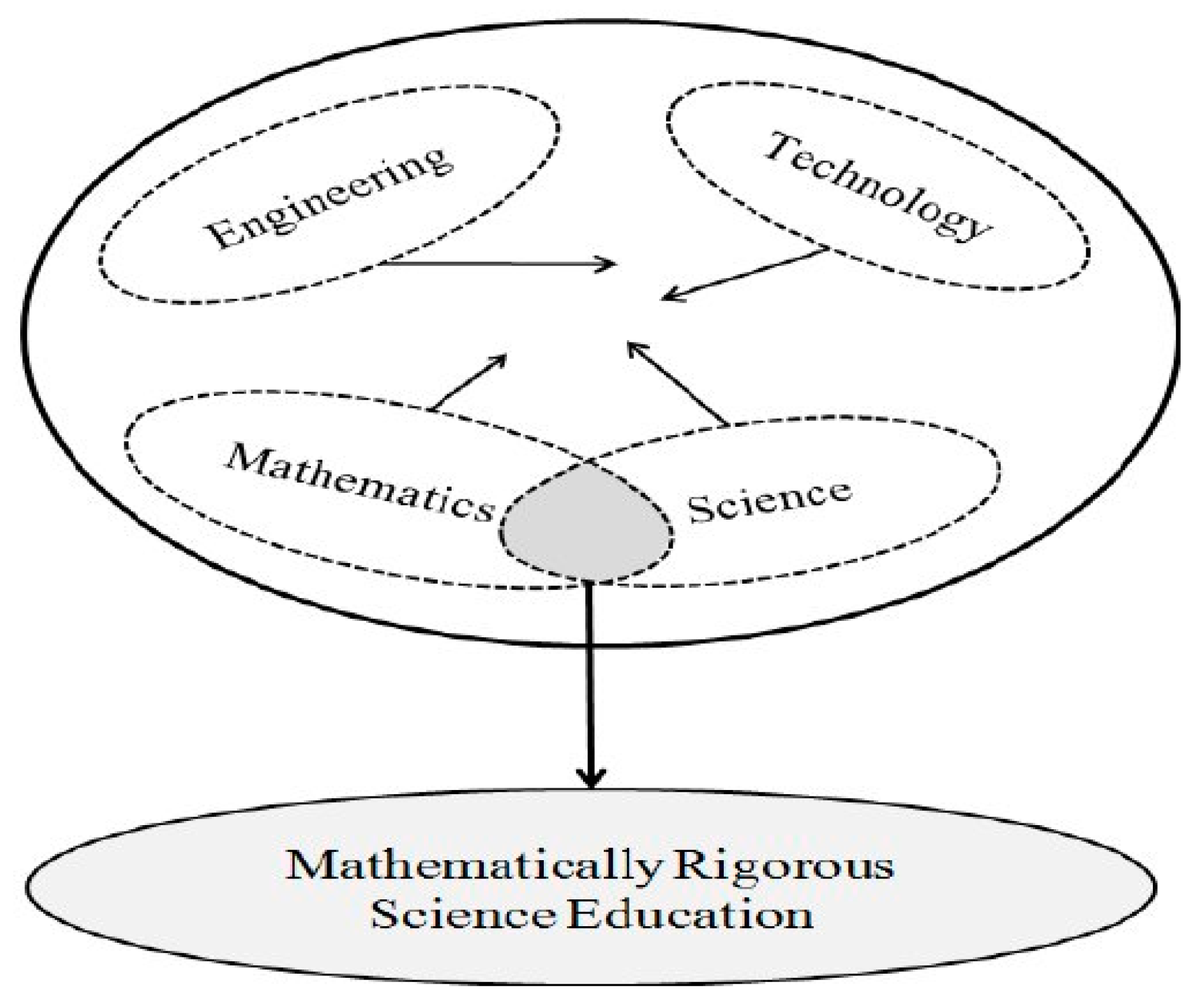
2.2. Science, Technology, Engineering and Mathematics (STEM) Education
2.3. Agriculture Education and Training (AET)
- – School-based agricultural education.
- – Vocational training in agricultural professions.
- – Education in rural household issues.
- – Education in environmental protection issues.
- – Education in agro-tourism issues.
- – Education in new technologies (Agriculture 4.0).
2.4. AET, CT and STEM
3. Research Methodology
3.1. Method
3.2. Framework and Research Questions
- -
- 1st axis: this involves the opinion of CT, opinion of STEM philosophy, educator’s training and evaluation of Greek agriculture education and training (GAET).
- -
- 2nd axis: this involves opinion of school environment, satisfaction of school environment and evaluation of GAET.
- -
- RQ1: Is there relation between opinion of STEM philosophy and opinion for CT?
- -
- RQ2: Is there relation between educators’ training and opinion for CT?
- -
- RQ3: Is there relation between opinion of STEM philosophy and Educators’ training?
- -
- RQ4: Is there relation between opinion for school environment and Satisfaction of School Environment?
- -
- RQ5: IS there relation between GAET (educators’ side) and GAET (students’ side)?
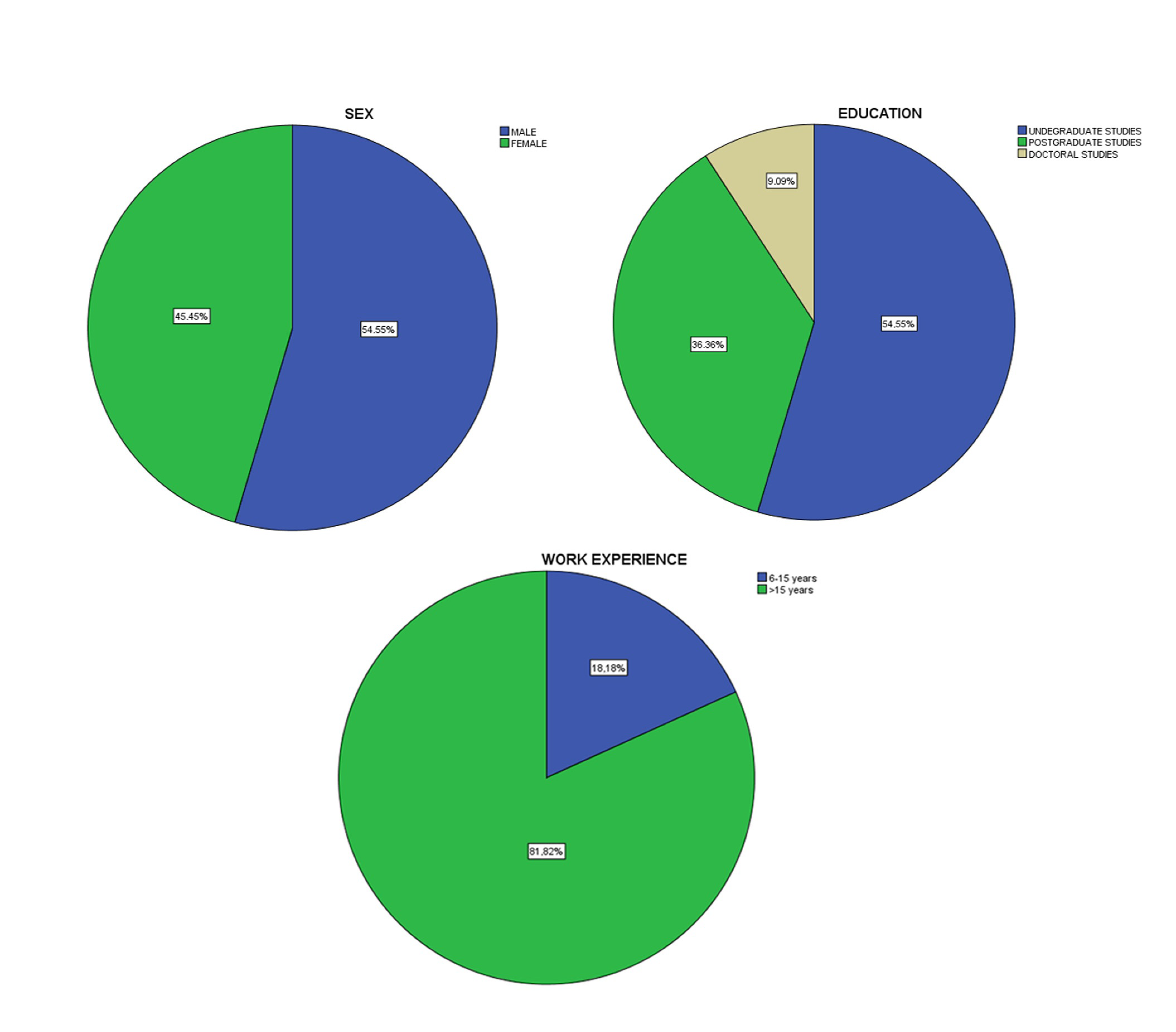
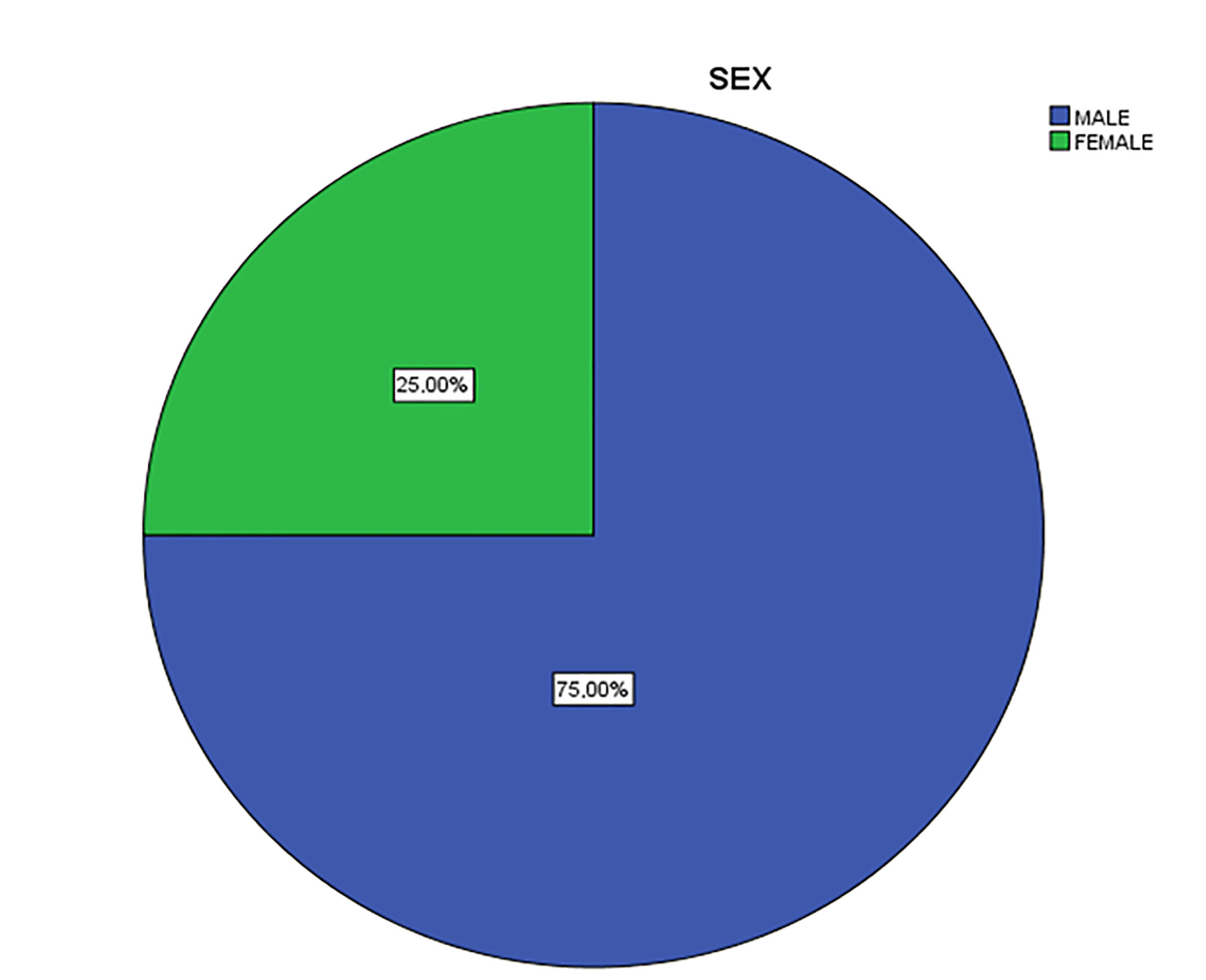
3.3. Participants
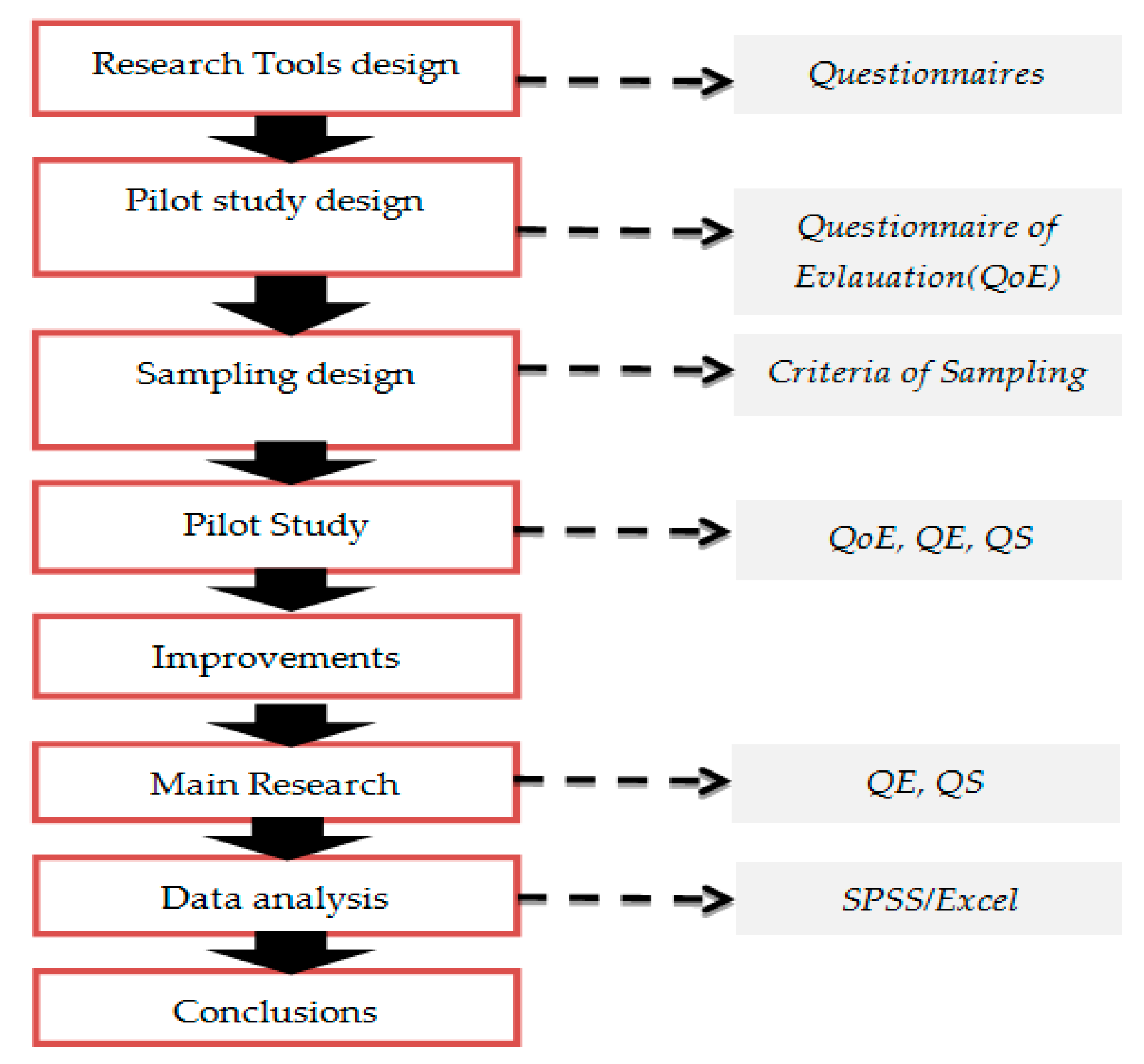
3.4. Research Procedure
- Research tools design (questionnaire of educators, QE, questionnaire of students, QS) based research framework;
- Pilot study design;
- Sampling design;
- Pilot study;
- Improvements to research tools;
- Main research;
- Data analysis (statistical analysis);
- Conclusions.
- Finding respondents (e-mail);
- Informing participants about the pilot research;
- Issuance of a survey questionnaire and main assessment questionnaire (pilot research);
- Collection of questionnaires;
- Data processing/conclusions and improvements.
- The main research includes the following steps:
- Finding respondents (e-mail);
- Informing participants about the main research;
- Issuance of the main research questionnaire;
- Collection of questionnaires;
- Data processing/conclusions and improvements.
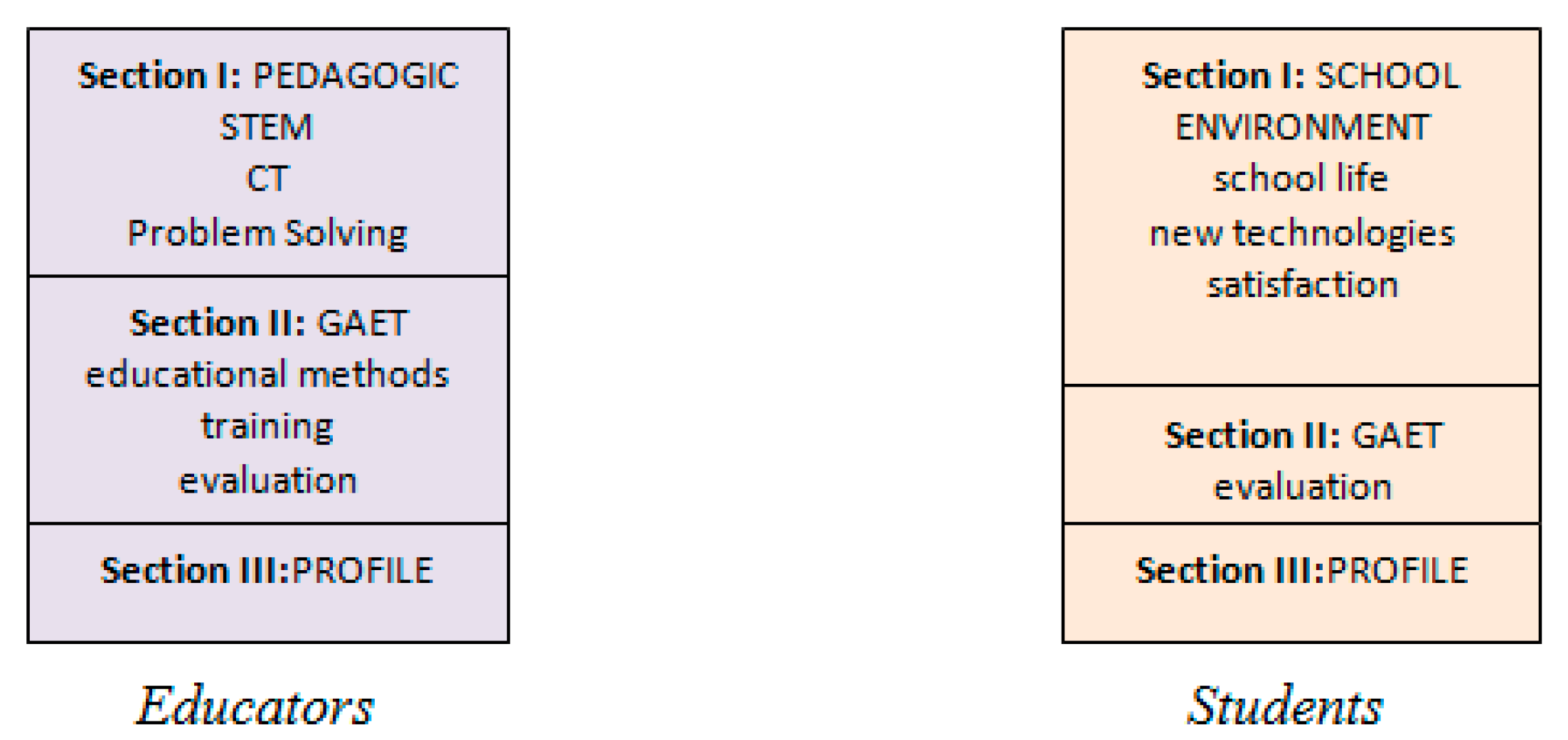
3.5. Tools
- Questionnaire of Educators (QE)
- -
- Section 1 (Pedagogic). It includes three basic questions with 12 items (totally) about STEM philosophy, CT and problem-solving methodology.
- -
- Section 2 (GAET). It includes three basic questions with 9 items (totally) relative to the usage of CT, STEM and problem-solving methodology in GAET, educators’ training and overall evaluation of GAET.
- -
- Section 3 (Profile). It includes socio-demographic characteristics (gender, education, work experience, employment situation).
- Questionnaire of Students (QS)
- -
- Section 1 (School environment). It includes three basic questions with 12 items (totally) about school life, using of new technologies and overall satisfaction of school environment (IEK).
- -
- Section 2 (GAET). It includes questions about overall evaluation of GAET.
- -
- Section 3 (Profile). It includes socio-demographic characteristics (gender, age).
- the format of the research questionnaire (legible letters, font, color, easy-to-use format, etc.);
- the structure of the research questionnaire (series of questions, thematic units);
- the content of the research questionnaire (questions, explanations);
- the satisfaction of the research goal (main research goal);
- the overall satisfaction by the research tools.
3.6. Sampling
- K1: teacher or student of the ΙΕΚΜC specialty “Viticulture and Oenology Technician”.
- K2: the ease of accessing the respondent,
- K3: free choice of answering the questionnaire or not.
3.7. Pilot Study
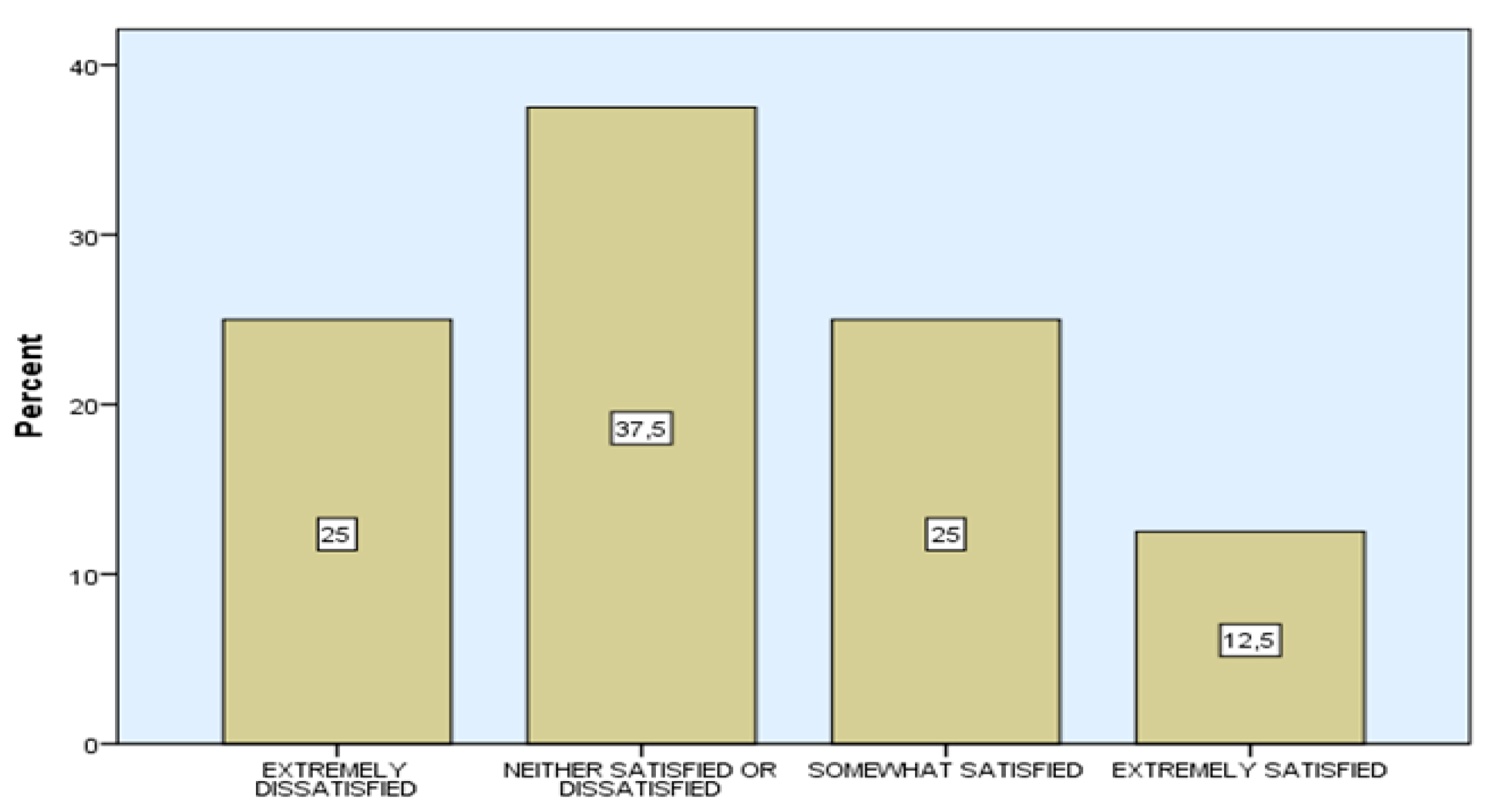
- Questionnaire format (QE, QS): significant satisfaction (75%—very satisfied) was found from the questionnaire format (QS) for students and, respectively, significant satisfaction (75%—sufficient satisfaction) from the questionnaire format (QE) for teachers.
- Questionnaire structure (QE, QS): very significant satisfaction (100%—very satisfied and sufficient satisfaction) was found from the structure of the questionnaire (series of questions, topics) for students (QS) and respectively, significant satisfaction (75%—sufficient satisfaction) in the form of a questionnaire (QE) for teachers.
- Questionnaire content (QE, QS): significant satisfaction (75%—very satisfied and sufficient satisfaction) was found from the content (questions, explanations) for the students (QS) and respectively, significant satisfaction (75%—very satisfied) from the format of the questionnaire (QE) for teachers.
- Satisfaction of the research goal (main research goal): it was observed from the results of the pilot research, that there is significant satisfaction (75%—very satisfied and sufficient satisfaction) of the content (questions, explanations) for the students (QS) and respectively, significant satisfaction (100%—very satisfied) from the form of the questionnaire (QE) for teachers.
- Overall questionnaire satisfaction: observed from the results of the pilot survey, very significant satisfaction (100%—very satisfied and sufficient satisfaction) from the structure of the questionnaire (series of questions, topics) for students (QS) and respectively, significant satisfaction (75%—very satisfied and sufficient satisfaction) from the form of the questionnaire (QE) for teachers.
- Verbal performance problems: there were few observations for verbal performance of the questions (grammar-syntax errors), 1 and 2 of the QE questionnaire and questions 3 and 4 of the QE questionnaire respectively.
3.8. Validation
- content validity: a research questionnaire should fully cover the dimensions of the main research objective [68] so it was considered appropriate, the design of QS and QE was based on the research framework developed in the context of this research, and it examined in detail two key research factors (CT, STEM).
- criterion validity: this became impossible because the use of a criterion, i.e., an existing reliable and valid questionnaire (weighted), which concerns the investigation of the main research purpose for GAET, was not found. Here, perhaps, there was a gap in terms of researching CT and STEM views on AET.
3.9. Data Analysis
4. Results
4.1. Educator Survey
- -
- The most important opinions expressed were the following: (a) it helps in the problem solution (average 3.55) and (b) it is useful for the utilization of Information Technology and Science (average 3.55).
- -
- the least important opinion was linked to STEM education (average 2.09).
- -
- The most important opinions were the following: through the classical experiment (average 3.91).
- -
- The least important opinions were the following: simulation (average 3.09) and theoretical analysis (average 3.09).
4.2. Student Survey
- -
- The most significant t opinions were those regarding: (a) the application of knowledge to real world problems (average 4.75) and (b) the use of models or prototypes in problem solving at school or life (average 3.75).
- -
- The least important opinions were the following: using algorithms for problem solving (average 0.88) and I can solve problems more easily (average 1.13).
4.3. Evaluation Comparison of Greek Agriculture Education and Training (GAET) between Educators and Students
5. Discussion
6. Conclusions
- There is a strong relationship between STEM philosophy and CT for teachers.
- There is a significant relationship between satisfaction with the school environment (IEKMC) and students’ opinion of the school environment.
- Educators consider STEM and STEM philosophy equally important for education.
- Students rate GAET higher than instructors.
- -
- the sample is expanded nationwide;
- -
- mixed research methods with a combination of quantitative and qualitative approaches are adopted for better analysis of the findings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Psycharis, S.; Kotzampasaki, E. A didactic Scenario for Implementation of Computational Thinking using Inquiry Game Learning. In Proceedings of the International Conference of Education and E-Learning ICEEL 2017, Bangkok, Thailand, 2–4 November 2017. [Google Scholar]
- Psycharis, S. STEAM in Education: A Literature review on the role of Computational Thinking, Engineering Epistemology and Computational Science. Computational STEAM Pedagogy (CSP). Sci. Cult. 2018, 4, 51–72. [Google Scholar]
- Psycharis, S.; Kallia, M. The effects of computer programming on high school students’ reasoning skills and mathematical self-efficacy and problem solving. Instr. Sci. 2017, 45, 583–602. [Google Scholar] [CrossRef]
- National Academy of Engineering (NAE); National Research Council (NRC). STEM Integration in K-12 Education: Status, Prospects, and an Agenda for Research; The National Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- National Research Council (NRC). A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas. 2012. Available online: www.nap.edu/catalog.php?record_id=13165 (accessed on 22 December 2020).
- Demartini, C.; Benussi, L. Do Web 4.0 and Industry 4.0 Imply Education X. 0? IT Prof. 2017, 19, 4–7. [Google Scholar] [CrossRef]
- Kamble, S.S.; Gunasekaran, A.; Gawankar, S.A. Sustainable Industry 4.0 framework: A systematic literature review identifying the current trends and future perspectives. Process Saf. Environ. Prot. 2018, 117, 408–425. [Google Scholar] [CrossRef]
- Tekinerdogan, B. Strategies for Technological Innovation in Agriculture 4.0 Reports; Wageningen University: Wageningen, The Netherlands, 2018. [Google Scholar]
- European Commission. Shaping Europe’s digital future. Policy: Digital Learning & ICT in Education. Available online: https://ec.europa.eu/digital-single-market/en/digital-learning-ict-education (accessed on 22 December 2020).
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef]
- Psycharis, S.; Kalovrektis, K.; Xenakis, A. A Conceptual Framework for Computational Pedagogy in STEAM education: Determinants and perspectives. Hell. J. Stem Educ. 2020, 1, 17–32. [Google Scholar]
- Papert, S. Mindstorms: Children, Computers and Powerful Ideas; Basic Books: New York, NY, USA, 1980. [Google Scholar]
- Papert, S. Situating constructionism. In Constructionism; Papert, S., Harel, I., Eds.; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Denning, P.J. The profession of it: Beyond computational thinking. Commun. ACM 2009, 52, 28–30. [Google Scholar] [CrossRef]
- Cuny, J.; Snyder, L.; Wing, J.M. Demystifying Computational Thinking for Non-Computer Scientists. Unpublished Manuscript in Progress. 2010. Available online: http://www.cs.cmu.edu/CompThink/resources/TheLinkWing.pdf (accessed on 22 December 2020).
- Tang, X.; Yin, Y.; Lin, Q.; Hadad, R.; Zhai, X. Assessing computational thinking: A systematic review of empirical studies. Comput. Educ. 2020, 103798. [Google Scholar] [CrossRef]
- Wing, J.M. Computational thinking and thinking about computing. Philos. Trans. R. Soc. Lond.-A Math. Phys. Eng. Sci. 2008, 366, 3717–3725. [Google Scholar]
- Henderson, P.B.; Cortina, T.J.; Wing, J.M. Computational thinking. ACM Sigcse Bull. 2007, 39, 195–196. [Google Scholar] [CrossRef]
- Grover, S.; Pea, R.; Cooper, S. Designing for deeper learning in a blended computer science course for middle school students. Comput. Sci. Educ. 2015, 25, 199–237. [Google Scholar] [CrossRef]
- Fessakis, G.; Komis, V.; Mavroudi, E.; Prantsoudi, S. Exploring the scope and the conceptualization of Computational Thinking at the K-12 classroom level curriculum. In Computational Thinking in the STEM Disciplines: Foundations and Research Highlights; Khine, M.S., Ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Fessakis, G.; Prantsoudi, S. Computer science teachers’ perceptions, beliefs and attitudes on computational thinking in greece. Inform. Educ. 2019, 18, 227–258. [Google Scholar] [CrossRef]
- CSTA; ISTE. Operational Definition of Computational Thinking for K–12 Education. 2011. Available online: http://csta.acm.org/Curriculum/sub/CurrFiles/CompThinkingFlyer.pdf (accessed on 22 December 2020).
- Malyn-Smith, J.; Lee, I. Application of the occupational analysis of computational thinking-enabled STEM professionals as a program assessment tool. J. Comput. Sci. Educ. 2012, 3, 2–10. [Google Scholar] [CrossRef]
- Otterborn, A.; Schönborn, K.J.; Hultén, M. Investigating preschool educators’ implementation of computer programming in their teaching practice. Early Child. Educ. J. 2020, 48, 253–262. [Google Scholar] [CrossRef]
- Kong, S.; Lai, M.; Sun, D. Teacher development in computational thinking: Design and learning outcomes of programming concepts, practices and pedagogy. Comput. Educ. 2020, 151, 103872. [Google Scholar] [CrossRef]
- Jocius, R.; Joshi, D.; Dong, Y.; Robinson, R.; Catete, V.; Barnes, T.; Albert, J.; Andrews, A.; Lytl, N. Code, connect, create: The 3c professional development model to support computational thinking infusion. In Proceedings of the Annual Conference on Innovation and Technology in Computer Science Education, ITiCSE, Trondheim, Norway, 17–19 June 2020; pp. 971–977. [Google Scholar]
- Mills, K.; Angevine, C.; Weisgrau, J. Resources for computational thinking: Co-designing with teachers. In Proceedings of the Annual Conference on Innovation and Technology in Computer Science Education, ITiCSE, Trondheim, Norway, 17–19 June 2020; p. 1343. [Google Scholar]
- Caeli, E.N.; Bundsgaard, J. Computational thinking in compulsory education: A survey study on initiatives and conceptions. Educ. Technol. Res. Dev. 2020, 68, 551–573. [Google Scholar] [CrossRef]
- Adler, R.F.; Kim, H. Enhancing future K-8 teachers’ computational thinking skills through modeling and simulations. Educ. Inf. Technol. 2018, 23, 1501–1514. [Google Scholar] [CrossRef]
- Yadav, A.; Stephenson, C.; Hong, H. Computational thinking for teacher education. Commun. ACM 2017, 60, 55–62. [Google Scholar] [CrossRef]
- Weese, J.L. Bringing Computational Thinking to K-12 and Higher Education. Ph.D. Thesis, Kansas State University, Manhattan, KS, USA, 2017. [Google Scholar]
- Kovács, G.; Harangus, K. Translator trainees’ reading literacy, problem solving, and translation skills A comparative estudy. Acta Univ. Sapientiae Philol. 2020, 11, 141–157. [Google Scholar] [CrossRef]
- Scherer, R.; Siddiq, F.; Sánchez Viveros, B. A meta-analysis of teaching and learning computer programming: Effective instructional approaches and conditions. Comput. Hum. Behav. 2020, 109, 106349. [Google Scholar] [CrossRef]
- Wong, G.K.W.; Cheung, H.Y. Exploring children’ s perceptions of developing twenty-first century skills through computational thinking and programming. Interact. Learn. Environ. 2020, 28, 438–450. [Google Scholar] [CrossRef]
- Moon, J.; Do, J.; Lee, D.; Choi, G.W. A conceptual framework for teaching computational thinking in personalized OERs. Smart Learn. Environ. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Ho, M.T.; La, V.P.; Nguyen, M.H.; Pham, T.H.; Vuong, T.T.; Vuong, H.M.; Pham, H.H.; Hoang, A.D.; Vuong, Q.H. An analytical view on STEM education and outcomes: Examples of the social gap and gender disparity in Vietnam. Child. Youth Serv. Rev. 2020, 119, 105650. [Google Scholar] [CrossRef]
- Moomaw, S. Teaching STEM in the Early Years: Activities for Integrating Science, Technology, Engineering, and Mathematics; Redleaf Press: St. Paul, MN, USA, 2013. [Google Scholar]
- Talley, T. The STEM Coaching Handbook: Working with Teachers to Improve Instruction; Routledge: New York, NY, USA, 2016. [Google Scholar]
- Corlu, M.; Capraro, R.M. Capraro Introducing STEM Education: Implications for Educating Our Teachers for the Age of Innovation. Educ. Sci. 2014, 39, 74–85. [Google Scholar]
- Corlu, M.S. FeTeMM eğitimi araştırmaları: Alanda merak edilenler, fırsatlar ve beklentiler [STEM education research: Latest trends, opportunities, and expectations]. Turk. J. Educ. Res. 2014, 3, 4–10. [Google Scholar]
- Williams, J. STEM education: Proceed with caution. Des. Technol. Educ. Int. J. 2011, 1, 26–35. [Google Scholar]
- Akman, B. Mathematics in preschool. Hacet. Univ. J. Educ. 2002, 23, 244–248. [Google Scholar]
- Başkan, Z.; Alev, N.; Karal, I.S. Physics and mathematics teachers’ ideas about topics that could be related or integrated. Procedia Soc. Behav. Sci. 2010, 2, 1558–1562. [Google Scholar] [CrossRef][Green Version]
- Ogilve, J.F.; Monagan, M.B. Teaching mathematics to chemistry students with symbolic computation. J. Chem. Educ. 2007, 84, 889–896. [Google Scholar] [CrossRef]
- Pratt, D.L. Mathematics usage in secondary science courses and textbooks. Sch. Sci. Math. 1985, 85, 394–406. [Google Scholar] [CrossRef]
- Fensham, P.J. Science Education Policy-Making: Eleven Emerging Issues; ED-2007/WS/51–CLD 2855.7; UNESCO: Paris, France, 2008. [Google Scholar]
- Patrinopoulos, M.; Iatrou, P. Implementation of STEM Tinkering Approaches in Primary School Education in Greece. Sino-Us Engl. Teach. 2019, 16, 510–516. [Google Scholar] [CrossRef]
- Hellenic Institute of Educational Policy (HIEP). Open Schools for Open Societes (OSOS). 2017. Available online: http://www.iep.edu.gr/images/IEP/PROKIRIKSEIS-ERGA/Erga/2017/2017-09-25_Prosklisi_OSOS.pdf (accessed on 22 December 2020).
- Smyrnaiou, Z.; Petropoulou, E.; Sotiriou, M. Applying argumentation approach in STEM education: A case study of the European student parliaments project in Greece. Am. J. Educ. Res. 2015, 3, 1618–1628. [Google Scholar]
- Kotsifakos, D.; Kostis, B.; Douligeris, C. Science, technology, engineering and mathematics (STEM) for vocational education in Greece. In Proceedings of the 2017 IEEE Global Engineering Education Conference (EDUCON), Athens, Greece, 25–28 April 2017. [Google Scholar]
- Psycharis, S.; Kotzampasaki, E. The impact of a STEM inquiry game learning scenario on computational thinking andcomputer self-confidence. Eurasia J. Math. Sci. Technol. Educ. 2019, 15, 1–18. [Google Scholar] [CrossRef]
- OECD. Science, Technology and Industry Scoreboard. 2015. Available online: www.oecd.com (accessed on 22 December 2020).
- Ruamchimplee, T.; Poungsuk, P.; Hongmaneerat, K.; Sachiyo, M. Development strategies for increasing agricultural teacher competency in rural Thai secondary schools. Rev. Escpacios 2020, 41, 7–19. [Google Scholar]
- Williams, D.L.; Dollisso, A.D.D. Rationale for research on including sustainable agriculture in the high school agricultural education curriculum. J. Agric. Educ. 1998, 39, 51–56. [Google Scholar] [CrossRef]
- Cribb, J. The Coming Famine: The Global Food Crisis and What We Can Do to Avoid It; CSIRO Publishing: Collingwood, Australia, 2010. [Google Scholar]
- Reeve, E.M. 21st-century skills needed by students in technical and vocational education and training (TVET). Asian Int. J. Soc. Sci. 2016, 16, 65–82. [Google Scholar] [CrossRef]
- Phadung, M.; Namburi1, S.; Dermrach, P.; Latekeh, I. Effects of Enhancing Computational Thinking Skills using Educational Robotics Activities for Secondary Students. In 5th ICRIEMS Proceedings; Faculty of Mathematics and Natural Sciences, Yogyakarta State University: Yogyakarta, Indonesia, 2018; ISBN 978-602-74529-3-0. [Google Scholar]
- Roehrig, G.H.; Moore, T.J.; Wang, H.H.; Park, M.S. Is adding the E enough? Investigating the impact of K-12 engineering standards on the implementation of STEM integration. Sch. Sci. Math. 2012, 112, 31–44. [Google Scholar] [CrossRef]
- Association of Public and Land-Grant Universities. Human Capacity Development; APLU: Washington, DC, USA, 2009. [Google Scholar]
- National Research Council. Transforming Agricultural Education for a Changing World; The National Academies Press: Washington, DC, USA, 2009. [Google Scholar]
- Balschweid, M.A. Teaching biology using agriculture as the context: Perceptions of high school students. J. Agric. Educ. 2002, 43, 56–67. [Google Scholar] [CrossRef]
- Balschweid, M.A. Science can be fun? A look at student attitudes towards science after completing a year–long biology course taught using agriculture as the context. In Proceedings of the 30th Annual National Agriculture Education Research Conference, Orlando, FL, USA, 10 December 2003; pp. 277–288. Available online: http://aaaeonline.org/allconferences.php (accessed on 22 December 2020).
- Stubbs, E.A.; Myers, B.E. Multiple Case Study of STEM in School-based Agricultural Education. J. Agric. Educ. 2015, 56, 188–203. [Google Scholar] [CrossRef]
- Ejiwale, J.A. Facilitating teaching and learning across STEM fields. J. Stem Educ. 2012, 13, 87–94. [Google Scholar]
- Phipps, L.J.; Osborne, E.W. Handbook on Agricultural Education in Public Schools; The Interstate Printers & Publishers: Danville, IL, USA, 1988. [Google Scholar]
- EURYDICE. Hellenic Qualification Framework. Available online: https://eacea.ec.europa.eu/national-policies/eurydice/content/national-qualifications-framework-33_el (accessed on 22 December 2020).
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education; Routledge Falmer, Taylor & Francis Group: London, UK, 2008. [Google Scholar]
- Robson, C.; McCartan, K. Real World Research, 4th ed.; Wiley Edition: Hoboken, NJ, USA, 2016. [Google Scholar]
- Welch, S. Sampling by referral in a dispersed population. Public Opin. Q. 1975, 39, 237–245. [Google Scholar] [CrossRef]
- Klerkx, L.; Jakku, E.; Labarthe, P. A review of social science on digital agriculture, smart farming and agriculture 4.0: New contributions and a future research agenda. NJAS-Wagening. J. Life Sci. 2019, 90, 100315. [Google Scholar] [CrossRef]
- Czerkawski, C.; Lyman, E.W., III. Exploring Issues about Computational Thinking in Higher Education. TechTrends 2015, 59, 57–65. [Google Scholar] [CrossRef]


| IEK (Total) | Viticulture & Oenology Technician | |
|---|---|---|
| Staff | 84 | 29 |
| Students | 310 | 51 |
| Opinion of STEM | Aver. |
|---|---|
| Emphasis on applying knowledge to real-world problems | 4.55 |
| Support of critical thinking | 4.55 |
| Assistance in problem-solving | 4.55 |
| Creativity amplifying | 4.55 |
| It is important for National Economic Development | 4.55 |
| Opinion of CT | Aver. |
|---|---|
| Assistance in problem-solving | 3.55 |
| Useful for the utilization of Information Technology and Science | 3.55 |
| Linked to STEM training | 2.09 |
| It is distinguished for its interdisciplinary application | 3.18 |
| Opinion of CT | Aver. |
|---|---|
| Simulation | 3.09 |
| Typical experiments | 3.91 |
| Through theoretical analysis (and solving exercises on paper) | 3.09 |
| Spearman’s Rho | Opinion of STEM (Totally) | Opinion of CT (Totally) | Training Personnel |
|---|---|---|---|
| Opinion of STEM (totally) | 0.7280 ** 0.000 | −0.184 0.412 | |
| Opinion of CT (totally) | 0.728 ** 0.000 | −0.153 0.498 | |
| Training Personnel | −0.184 0.412 | −0.153 0.498 |
| Opinion of CT | Aver. |
|---|---|
| I apply knowledge to real world problems | 4.75 |
| I can solve problems more easily | 1.13 |
| I am learning to use algorithms to solve problems | 0.88 |
| I can analyze a problem, break it down into parts to solve it | 3.63 |
| I can use templates or models to solve a problem at school or in everyday life | 3.75 |
| I can identify patterns or models in a lesson or in everyday life | 3.00 |
| I can evaluate a model or model that appears to me in a course (e.g., physics) or in everyday life | 1.25 |
| Factors | Score (max = 5.0) |
|---|---|
| Infrastructure | 1.63 |
| Curriculum | 1.0 |
| Educators | 0.75 |
| Didactic techniques | 1.00 |
| Spearman’s Rho | Opinion of School Environment (IEKMC) (Totally) [SE] | Overall Satisfaction of School Environment (IEKMC) (Totally) [SAT] |
|---|---|---|
| Opinion of School Environment (IEKMC)(totally) [SE] | 0.478 * 0.018 | |
| Overall Satisfaction of School Environment (IEKMC) (totally) [SAT] | 0.478 * 0.180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chondrogiannis, E.; Symeonaki, E.; Papachristos, D.; Loukatos, D.; Arvanitis, K.G. Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution. Eur. J. Investig. Health Psychol. Educ. 2021, 11, 230-250. https://doi.org/10.3390/ejihpe11010018
Chondrogiannis E, Symeonaki E, Papachristos D, Loukatos D, Arvanitis KG. Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution. European Journal of Investigation in Health, Psychology and Education. 2021; 11(1):230-250. https://doi.org/10.3390/ejihpe11010018
Chicago/Turabian StyleChondrogiannis, Eleftherios, Eleni Symeonaki, Dimitris Papachristos, Dimitrios Loukatos, and Konstantinos G. Arvanitis. 2021. "Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution" European Journal of Investigation in Health, Psychology and Education 11, no. 1: 230-250. https://doi.org/10.3390/ejihpe11010018
APA StyleChondrogiannis, E., Symeonaki, E., Papachristos, D., Loukatos, D., & Arvanitis, K. G. (2021). Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution. European Journal of Investigation in Health, Psychology and Education, 11(1), 230-250. https://doi.org/10.3390/ejihpe11010018







