Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis
Abstract
:1. Introduction
2. Multi-Criteria Decision Making
3. Material and Methods
3.1. Problem Statement
3.2. Criteria Weight Measurement Using Entropy Method
3.3. TOPSIS
3.4. EDAS Method
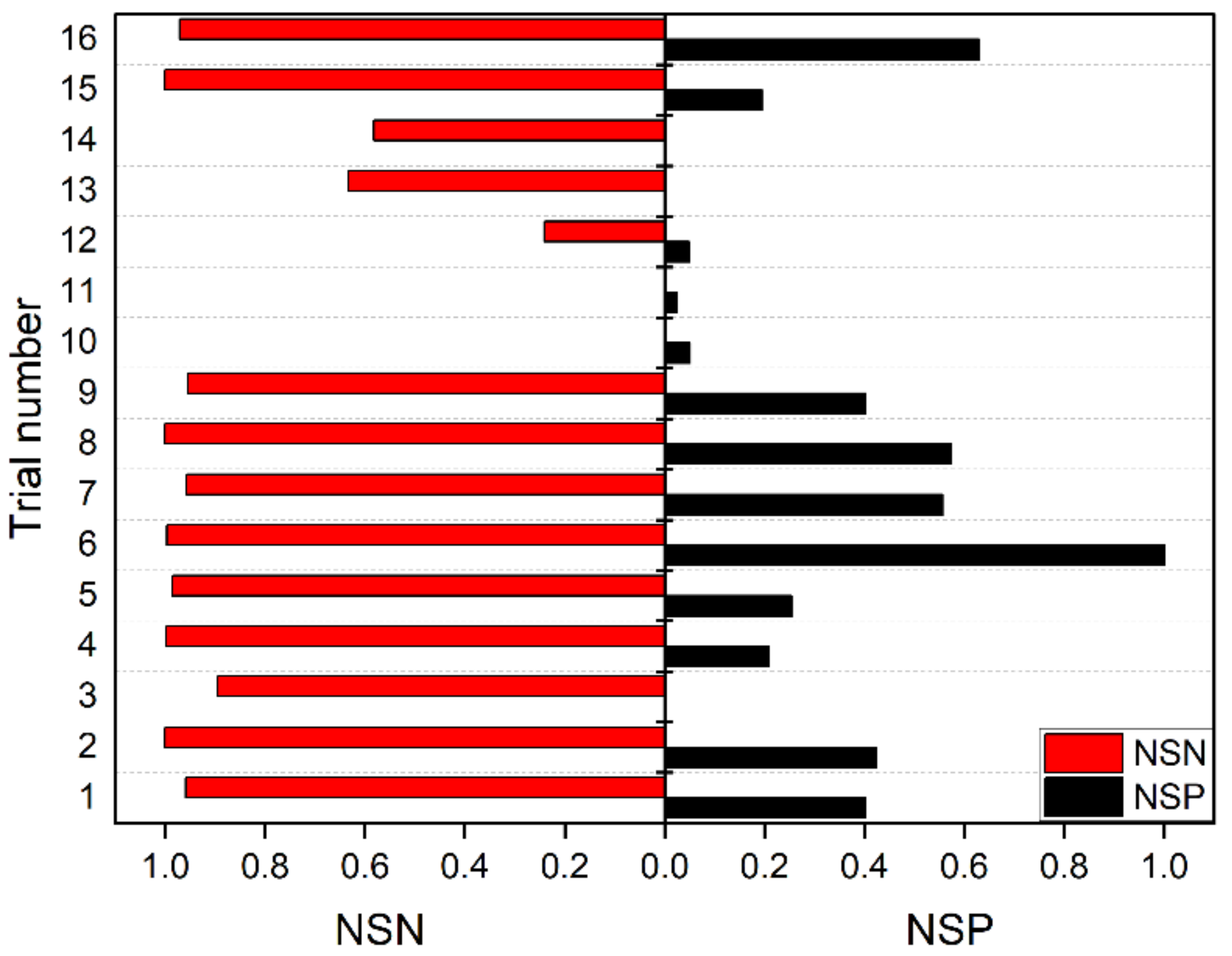
3.5. VIKOR Method
3.6. MOORA Method
4. Parametric Optimization for Friction Materials Using MCDM Techniques
4.1. Case Study 1
4.2. Case Study 2
5. Conclusions
- (a)
- All the considered MCDM techniques appear to be quite suitable for solving these types of multi-objective parametric optimization problems for friction materials having conflicting physical as well as tribological properties.
- (b)
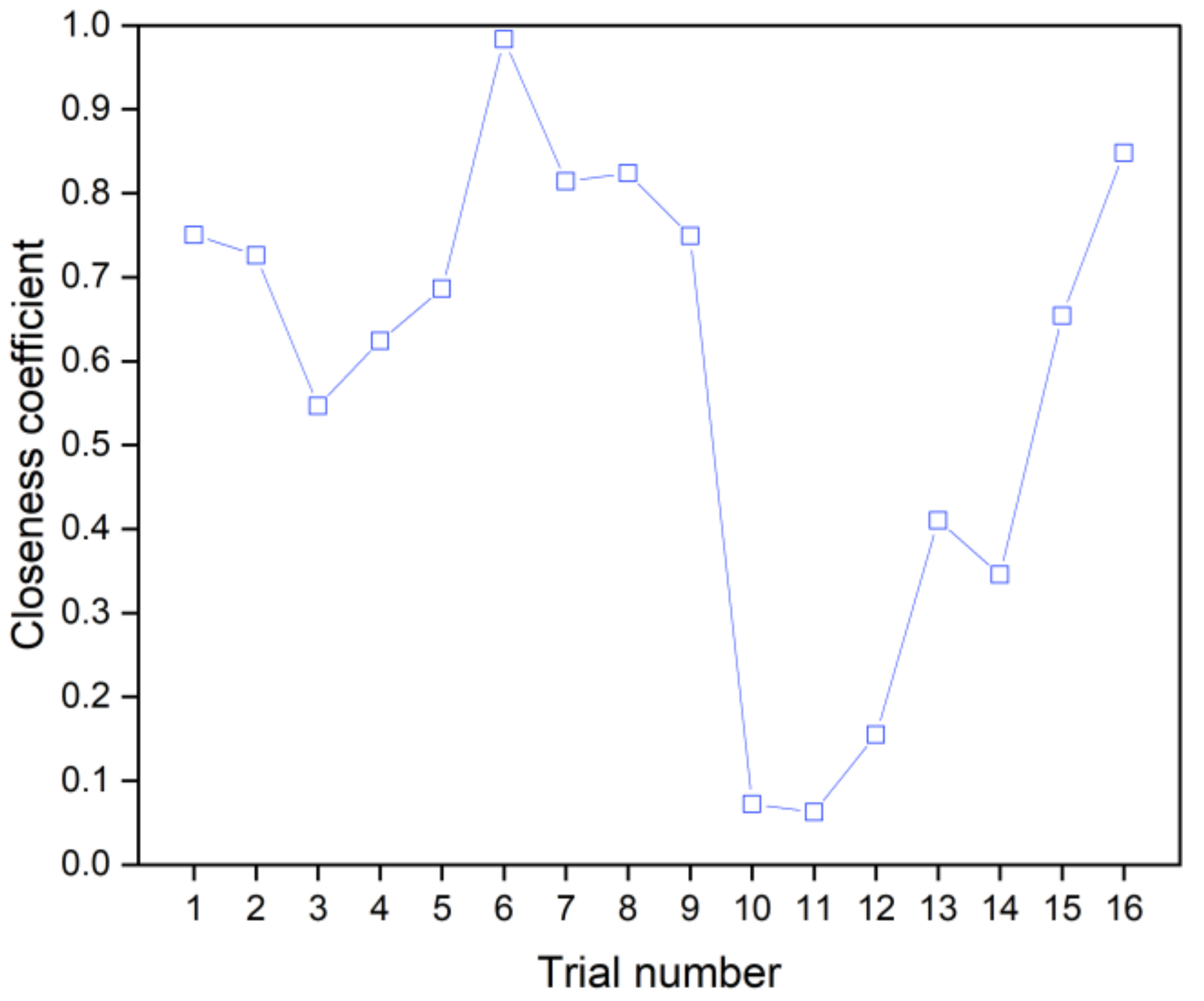
- For the first case study, all the MCDM techniques identify experimental trial number 6 with parametric intermix as molding time = 8 min, molding temperature = 175 °C, molding pressure = 27 MPa, sintering time = 10 h, and sintering temperature = 225 °C for attaining the favorable values of surface hardness, porosity and specific wear rate.
- (c)
- In the second case study, to achieve the most desired values of surface hardness, coefficient of friction, and wear/application, trial number 9 with the parametric setting as molding pressure = 27.90 MPa, molding temperature = 170 °C, curing time = 8 min and sintering time = 1 h is identified as the optimal combination by the considered MCDM techniques.
- (d)
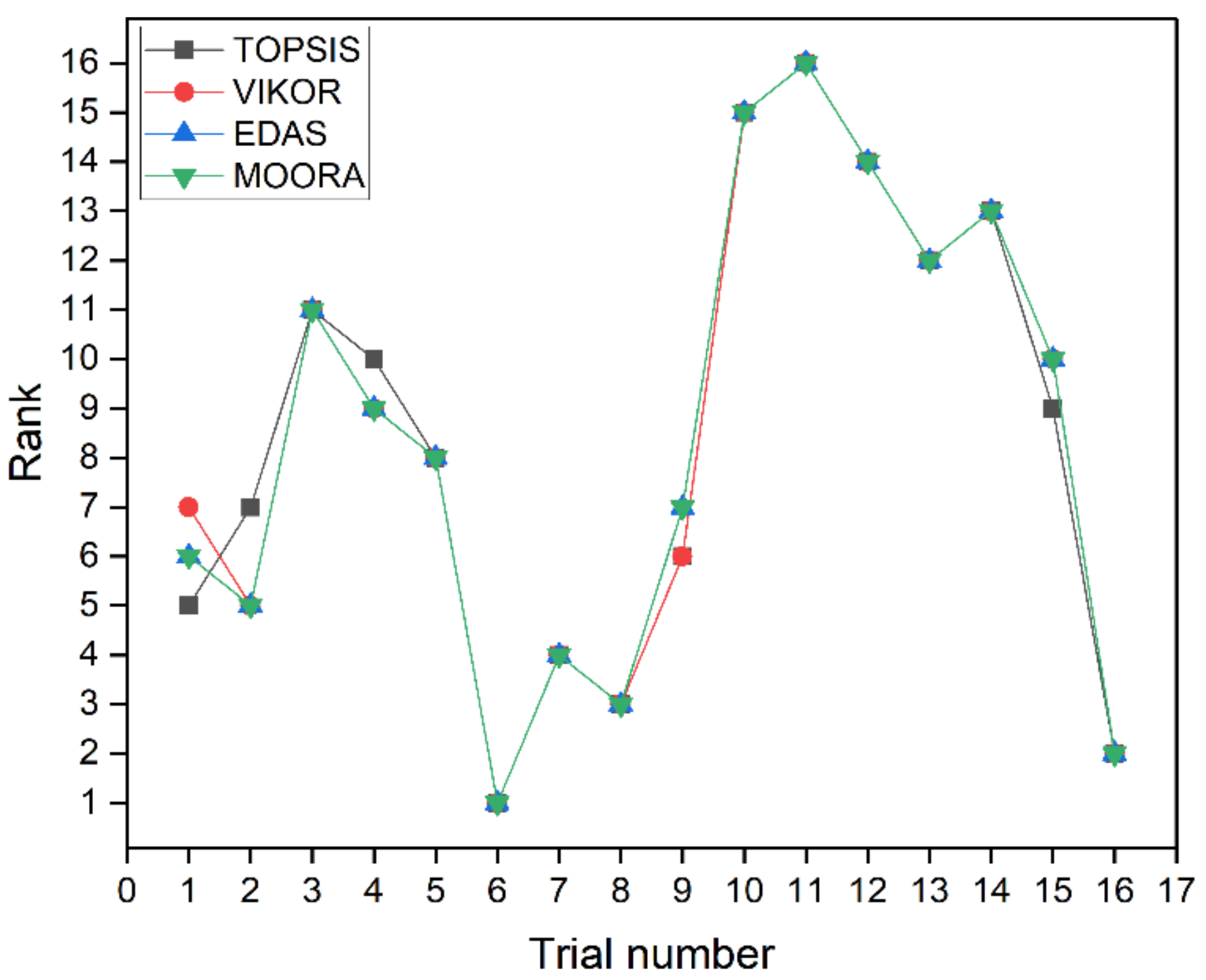
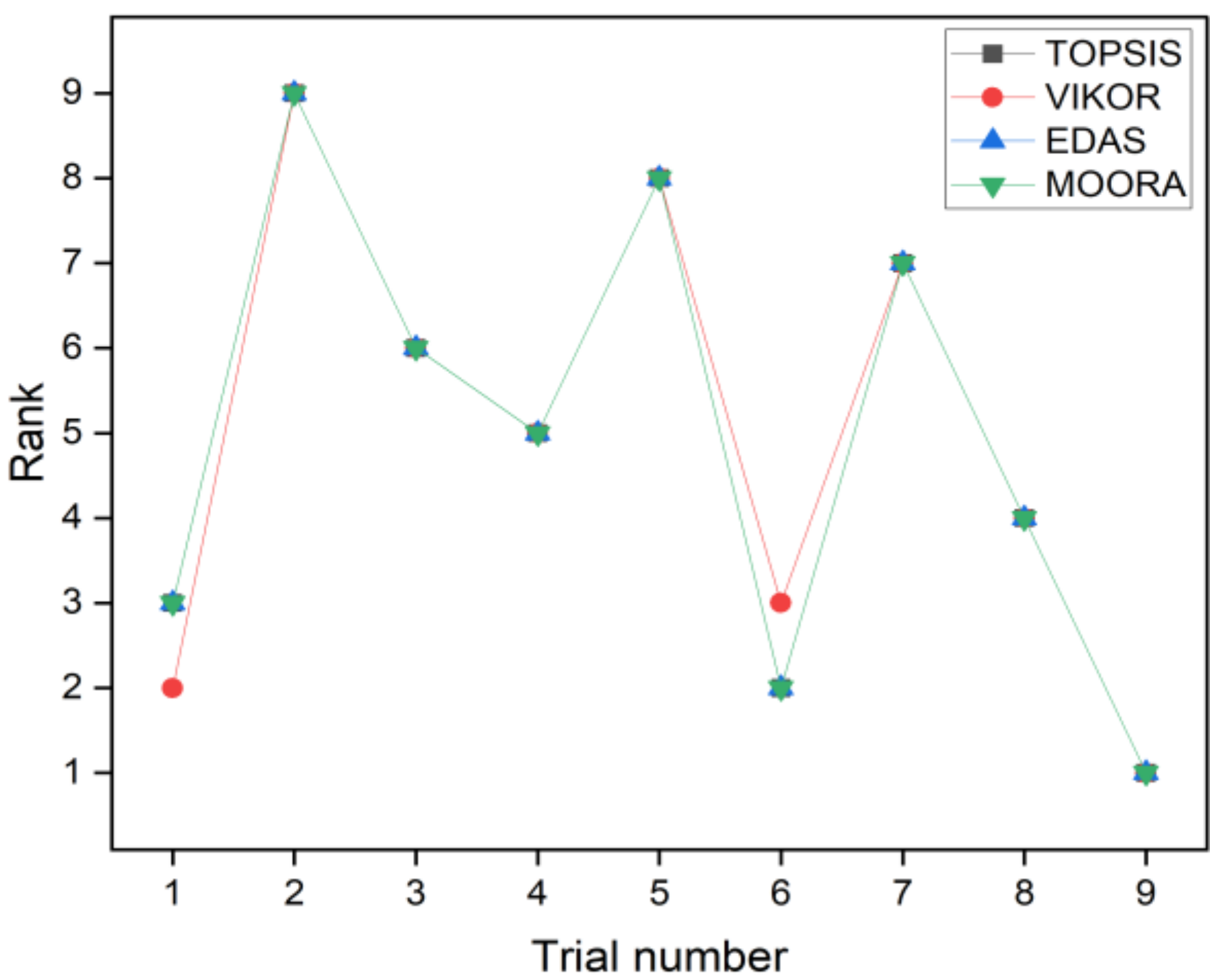
- Based on Spearman’s rank correlation coefficients, it is noticed that the ranking performance of TOPSIS, EDAS, and MOORA methods is quite comparable for both the case studies. There are minor variations in the rankings for the VIKOR method.
- (e)
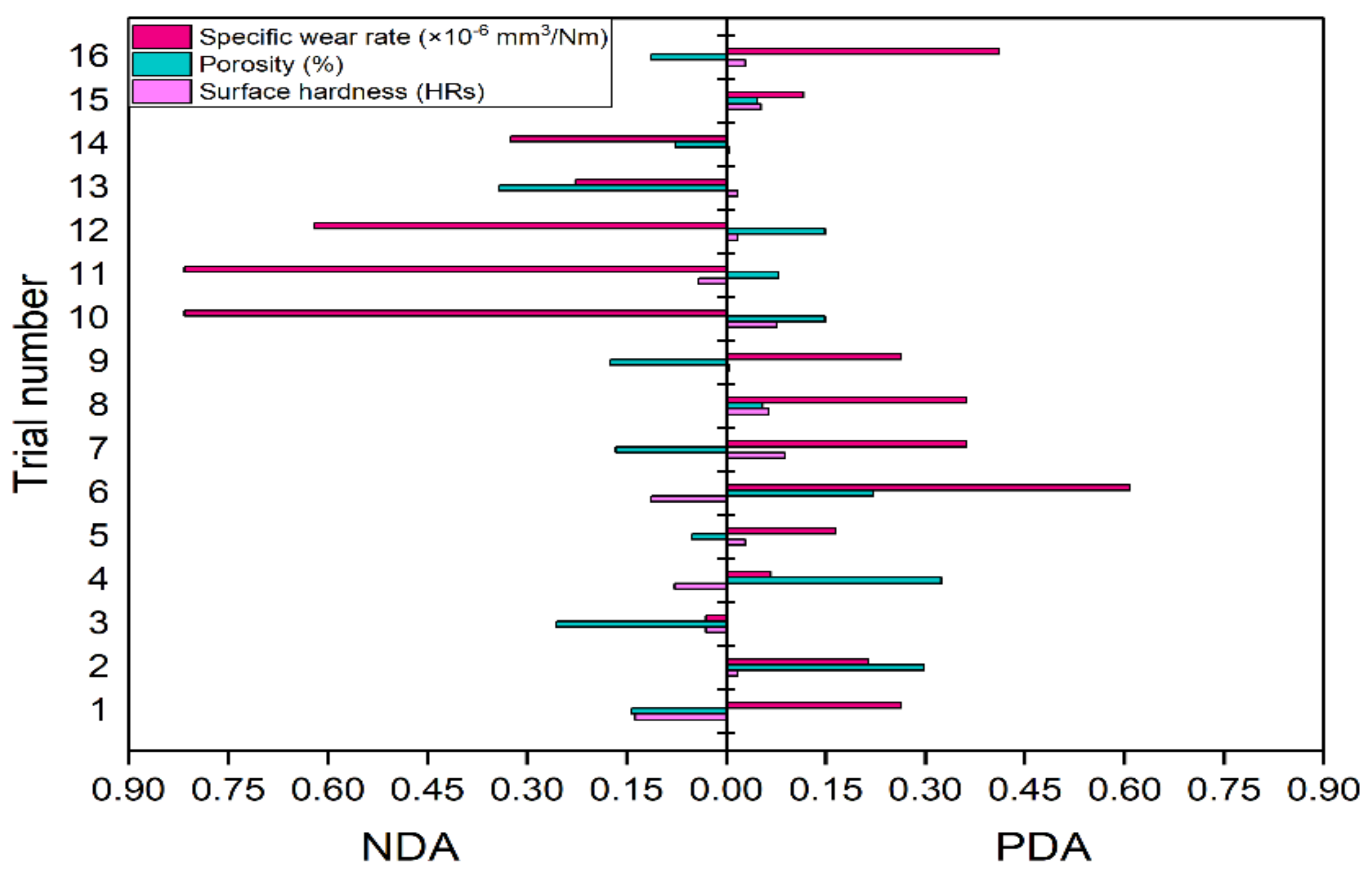
- For case study 1, the past researchers derived the best combination of the process parameters that did not at all exist among the considered experimental trials (outside the scope of the experimental plan). The response values at that combination are imputed by linear regression and mean of means approaches. Based on the linear regression approach, the present solutions for porosity and specific wear rate achieve 3% and 47% improvements, respectively, as compared to those obtained by the past researchers, whereas the improvements are 18% and 57%, respectively, based on the mean of means approach. There are 7% and 10% degradations in surface hardness with respect to the previous observations for linear regression and mean of means imputed solutions, respectively.
- (f)
- In case study 2, the past researchers identified trial number 2 as the best parametric combination. However, trial number 9, identified as the optimal parametric intermix by all the considered MCDM techniques, achieves 23.44%, 13.16%, and 90% improvements in the values of surface hardness, coefficient of friction, and wear/application, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, T.F. Relationship between Formulation and Noise of Phenolic Resin Matrix Friction Lining Tested in Acoustic Chamber on Automotive Brake Dynamometer. Ph.D. Thesis, Southern Illinois University, Carbondale, IL, USA, 2008. [Google Scholar]
- American National Standards Institute. Friction Coefficient Identification System for Brake Linings: SAE Recommended Practice; Society of Automotive Engineers: Warrendale, PA, USA, 1986. [Google Scholar]
- Krenkel, W.; Langhof, N. Ceramic matrix composites for high performance friction applications. In Proceedings of the IV Advanced Ceramics and Applications Conference, Belgrade, Serbia, 17 January 2017; pp. 13–28. [Google Scholar]
- Hee, K.W.; Filip, P. Performance of ceramic enhanced phenolic matrix brake lining materials for automotive brake linings. Wear 2005, 259, 1088–1096. [Google Scholar] [CrossRef]
- Han, Y.; Tian, X.; Yin, Y. Effects of ceramic fiber on the friction performance of automotive brake lining materials. Tribol. Trans. 2008, 51, 779–783. [Google Scholar] [CrossRef]
- Saffar, A.; Shojaei, A. Effect of rubber component on the performance of brake friction materials. Wear 2012, 274, 286–297. [Google Scholar] [CrossRef]
- Fan, Y.; Matějka, V.; Kratošová, G.; Lu, Y. Role of Al2O3 in semi-metallic friction materials and its effects on friction and wear performance. Tribol. Trans. 2008, 51, 771–778. [Google Scholar] [CrossRef]
- Verma, P.C.; Ciudin, R.; Bonfanti, A.; Aswath, P.; Straffelini, G.; Gialanella, S. Role of the friction layer in the high-temperature pin-on-disc study of a brake material. Wear 2016, 346, 56–65. [Google Scholar] [CrossRef]
- Langhof, N.; Rabenstein, M.; Rosenlöcher, J.; Hackenschmidt, R.; Krenkel, W.; Rieg, F. Full-ceramic brake systems for high performance friction applications. J. Eur. Ceram. Soc. 2016, 36, 3823–3832. [Google Scholar] [CrossRef]
- Kumar, M.; Bijwe, J. Studies on reduced scale tribometer to investigate the effects of metal additives on friction coefficient—Temperature sensitivity in brake materials. Wear 2010, 269, 838–846. [Google Scholar] [CrossRef]
- Öktem, H.; Uygur, İ.; Akıncıoğlu, G.; Kır, D.; Karakaş, H. Evaluation of non-asbestos high performance brake pads produced with organic dusts. In Proceedings of the 24th International Conference on Metallurgy and Materials, Brno, Czech Republic, 3–5 June 2015; pp. 3–5. [Google Scholar]
- Han, L.; Huang, L.; Zhang, J.; Lu, Y. Optimization of ceramic friction materials. Compos. Sci. Technol. 2006, 66, 2895–2906. [Google Scholar] [CrossRef]
- Cai, P.; Wang, T.; Wang, Q. Formulation optimization of friction material with golden section approach. Tribol. Trans. 2016, 59, 28–32. [Google Scholar] [CrossRef]
- Aleksendrić, D.; Senatore, A. Optimization of manufacturing process effects on brake friction material wear. J. Compos. Mater. 2012, 46, 2777–2791. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, K.S.; Jang, H. Optimization of manufacturing parameters for a brake lining using Taguchi method. J. Mater. Process. Technol. 2003, 136, 202–208. [Google Scholar] [CrossRef]
- Ibhadode, A.O.; Dagwa, I.M. Development of asbestos-free friction lining material from palm kernel shell. J. Braz. Soc. Mech. Sci. Eng. 2008, 30, 166–173. [Google Scholar] [CrossRef] [Green Version]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Keshavarz, G.M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Chatterjee, P.; Banerjee, A.; Mondal, S.; Boral, S.; Chakraborty, S. Development of a hybrid meta-model for material selection using design of experiments and EDAS method. Eng. Trans. 2018, 66, 187–207. [Google Scholar]
- Opricovic, S.; Tzeng, G.-H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Brauers, W.K.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Chakraborty, S. Applications of the MOORA method for decision making in manufacturing environment. Int. J. Adv. Manuf. Technol. 2011, 54, 1155–1166. [Google Scholar] [CrossRef]
- Mahale, V.; Bijwe, J.; Sinha, S. Application and comparative study of new optimization method for performance ranking of friction materials. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 143–154. [Google Scholar] [CrossRef]
- Satapathy, B.K.; Bijwe, J. Performance of friction materials based on variation in nature of organic fibres: Part II. Optimisation by balancing and ranking using multiple criteria decision model (MCDM). Wear 2004, 257, 585–589. [Google Scholar]
- Öktem, H.; Shinde, D. Tribological performance evaluation on brake friction material by using multi-objective optimization methods. Ind. Lubr. Tribol. 2021. [Google Scholar] [CrossRef]
- Raju, S.S.; Murali, G.B.; Patnaik, P.K. Ranking of Al-CSA composite by MCDM approach using AHP-TOPSIS and MOORA methods. J. Reinf. Plast. Compos. 2020, 39, 721–732. [Google Scholar] [CrossRef]
- Khan, M.M.; Dey, A. Selection of optimal processing condition during abrasive wear of in-situ ZA-37/TiCp composites using MCDM technique. Ceram. Int. 2021, 47, 20090–20107. [Google Scholar] [CrossRef]
- Jeganmohan, S.; Sugozu, B.; Kumar, M.; Selvam, D.R. Experimental investigation on the friction and wear characteristics of palm seed powder reinforced brake pad friction composites. J. Inst. Eng. India Ser. D 2020, 101, 61–69. [Google Scholar] [CrossRef]
- Singh, T.; Pattnaik, P.; Pruncu, C.I.; Tiwari, A.; Fekete, G. Selection of natural fibers based brake friction composites using hybrid ELECTRE-entropy optimization technique. Polym. Test. 2020, 89, 106614. [Google Scholar] [CrossRef]
- Singh, T. Optimum design based on fabricated natural fiber reinforced automotive brake friction composites using hybrid CRITIC-MEW approach. J. Mater. Res. Technol. 2021, 14, 81–92. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]






| Exp. No. | Manufacturing Process Parameter | Response | ||||||
|---|---|---|---|---|---|---|---|---|
| Molding Time (min) | Molding Temp. (°C) | Molding Pressure (MPa) | Heat Treatment Time (h) | Heat Treatment Temp. (°C) | Surface Hardness (HRs) | Porosity (%) | Specific Wear Rate (× 10−6 mm3/Nm) | |
| 1 | 6 | 150 | 27 | 4 | 175 | 73 | 14.22 | 7.706 |
| 2 | 6 | 175 | 29.5 | 6 | 200 | 86 | 21.53 | 8.219 |
| 3 | 6 | 200 | 32 | 8 | 225 | 82 | 12.34 | 10.788 |
| 4 | 6 | 225 | 34.5 | 10 | 250 | 78 | 21.97 | 9.761 |
| 5 | 8 | 150 | 29.5 | 8 | 250 | 87 | 15.73 | 8.733 |
| 6 | 8 | 175 | 27 | 10 | 225 | 75 | 20.26 | 4.110 |
| 7 | 8 | 200 | 34.5 | 4 | 200 | 92 | 13.84 | 6.678 |
| 8 | 8 | 225 | 32 | 6 | 175 | 90 | 17.50 | 6.678 |
| 9 | 10 | 150 | 32 | 10 | 200 | 85 | 13.69 | 7.706 |
| 10 | 10 | 175 | 34.5 | 8 | 175 | 91 | 19.06 | 19.007 |
| 11 | 10 | 200 | 27 | 6 | 250 | 81 | 17.90 | 19.007 |
| 12 | 10 | 225 | 29.5 | 4 | 225 | 86 | 19.06 | 16.953 |
| 13 | 12 | 150 | 34.5 | 6 | 225 | 86 | 10.92 | 12.843 |
| 14 | 12 | 175 | 32 | 4 | 250 | 85 | 15.32 | 13.870 |
| 15 | 12 | 200 | 29.5 | 10 | 175 | 89 | 17.38 | 9.247 |
| 16 | 12 | 225 | 27 | 8 | 200 | 87 | 14.72 | 6.165 |
| Exp. No. | Normalized Matrix | Weighted Normalized Matrix | ||||
|---|---|---|---|---|---|---|
| Surface Hardness | Porosity | Sp. Wear Rate | Surface Hardness | Porosity | Sp. Wear Rate | |
| 1 | 0.215392 | 0.210500 | 0.169328 | 0.004052 | 0.036067 | 0.137130 |
| 2 | 0.253749 | 0.318710 | 0.180601 | 0.004774 | 0.054607 | 0.146259 |
| 3 | 0.241947 | 0.182670 | 0.237051 | 0.004552 | 0.031298 | 0.191975 |
| 4 | 0.230145 | 0.325223 | 0.214484 | 0.004330 | 0.055723 | 0.173699 |
| 5 | 0.256700 | 0.232852 | 0.191895 | 0.004830 | 0.039896 | 0.155406 |
| 6 | 0.221293 | 0.299910 | 0.090311 | 0.004163 | 0.051386 | 0.073138 |
| 7 | 0.271453 | 0.204874 | 0.146739 | 0.005107 | 0.035103 | 0.118837 |
| 8 | 0.265551 | 0.259054 | 0.146739 | 0.004996 | 0.044386 | 0.118837 |
| 9 | 0.250799 | 0.202654 | 0.169328 | 0.004719 | 0.034722 | 0.137130 |
| 10 | 0.268502 | 0.282146 | 0.417651 | 0.005052 | 0.048342 | 0.338234 |
| 11 | 0.238996 | 0.264975 | 0.417651 | 0.004496 | 0.045400 | 0.338234 |
| 12 | 0.253749 | 0.282146 | 0.372518 | 0.004774 | 0.048342 | 0.301683 |
| 13 | 0.253749 | 0.161649 | 0.282206 | 0.004774 | 0.027697 | 0.228544 |
| 14 | 0.250799 | 0.226783 | 0.304773 | 0.004719 | 0.038857 | 0.246820 |
| 15 | 0.262601 | 0.257277 | 0.203189 | 0.004941 | 0.044081 | 0.164553 |
| 16 | 0.256700 | 0.217901 | 0.135467 | 0.004830 | 0.037335 | 0.109708 |
| MCDM | TOPSIS | EDAS | VIKOR | MOORA |
|---|---|---|---|---|
| TOPSIS | 1 | 0.9882 | 0.9853 | 0.9882 |
| EDAS | 0.9882 | 1 | 0.9971 | 1 |
| VIKOR | 0.9853 | 0.9971 | 1 | 0.9971 |
| MOORA | 0.9882 | 1 | 0.9971 | 1 |
| Exp. No. | Molding Pressure (MPa) | Molding Temperature (°C) | Curing Time (min) | Heat Treatment Time (h) | Surface Hardness (Scale B) | Coefficient of Friction | Wear/Application (g) |
|---|---|---|---|---|---|---|---|
| 1 | 16.74 | 150 | 6 | 1 | 84 | 0.44 | 0.023 |
| 2 | 16.74 | 160 | 8 | 2 | 64 | 0.38 | 0.170 |
| 3 | 16.74 | 170 | 10 | 3 | 81 | 0.39 | 0.037 |
| 4 | 23.32 | 150 | 8 | 3 | 79 | 0.41 | 0.027 |
| 5 | 22.32 | 160 | 10 | 1 | 80 | 0.35 | 0.043 |
| 6 | 22.32 | 170 | 6 | 2 | 89 | 0.42 | 0.023 |
| 7 | 27.90 | 150 | 10 | 2 | 81 | 0.35 | 0.037 |
| 8 | 27.90 | 160 | 6 | 3 | 82 | 0.41 | 0.023 |
| 9 | 27.90 | 170 | 8 | 1 | 79 | 0.43 | 0.017 |
| Exp. No. | Normalized Matrix | Weighted Normalized Matrix | ||||
|---|---|---|---|---|---|---|
| Surface Hardness | Coefficient of Friction | Wear/Application | Surface Hardness | Coefficient of Friction | Wear/Application | |
| 1 | 0.349391 | 0.367612 | 0.121066 | 0.003261 | 0.003184 | 0.118887 |
| 2 | 0.266203 | 0.317483 | 0.894836 | 0.002484 | 0.002750 | 0.878733 |
| 3 | 0.336913 | 0.325838 | 0.194758 | 0.003144 | 0.002822 | 0.191254 |
| 4 | 0.328594 | 0.342548 | 0.142121 | 0.003067 | 0.002967 | 0.139564 |
| 5 | 0.332753 | 0.292419 | 0.226341 | 0.003106 | 0.002533 | 0.222268 |
| 6 | 0.370188 | 0.350903 | 0.121066 | 0.003455 | 0.003040 | 0.118887 |
| 7 | 0.336913 | 0.292419 | 0.194758 | 0.003144 | 0.002533 | 0.191254 |
| 8 | 0.341072 | 0.342548 | 0.121066 | 0.003183 | 0.002967 | 0.118887 |
| 9 | 0.328594 | 0.359258 | 0.089484 | 0.003067 | 0.003112 | 0.087873 |
| MCDM | TOPSIS | EDAS | VIKOR | MOORA |
|---|---|---|---|---|
| TOPSIS | 1 | 1 | 0.98333 | 1 |
| EDAS | 1 | 1 | 0.98333 | 1 |
| VIKOR | 0.98333 | 0.98333 | 1 | 0.98333 |
| MOORA | 1 | 1 | 0.98333 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shinde, D.; Öktem, H.; Kalita, K.; Chakraborty, S.; Gao, X.-Z. Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis. Processes 2021, 9, 1570. https://doi.org/10.3390/pr9091570
Shinde D, Öktem H, Kalita K, Chakraborty S, Gao X-Z. Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis. Processes. 2021; 9(9):1570. https://doi.org/10.3390/pr9091570
Chicago/Turabian StyleShinde, Dinesh, Hasan Öktem, Kanak Kalita, Shankar Chakraborty, and Xiao-Zhi Gao. 2021. "Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis" Processes 9, no. 9: 1570. https://doi.org/10.3390/pr9091570
APA StyleShinde, D., Öktem, H., Kalita, K., Chakraborty, S., & Gao, X.-Z. (2021). Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis. Processes, 9(9), 1570. https://doi.org/10.3390/pr9091570








