Effect of Tip Clearance Size on Tubular Turbine Leakage Characteristics
Abstract
:1. Introduction
2. Numerical Model
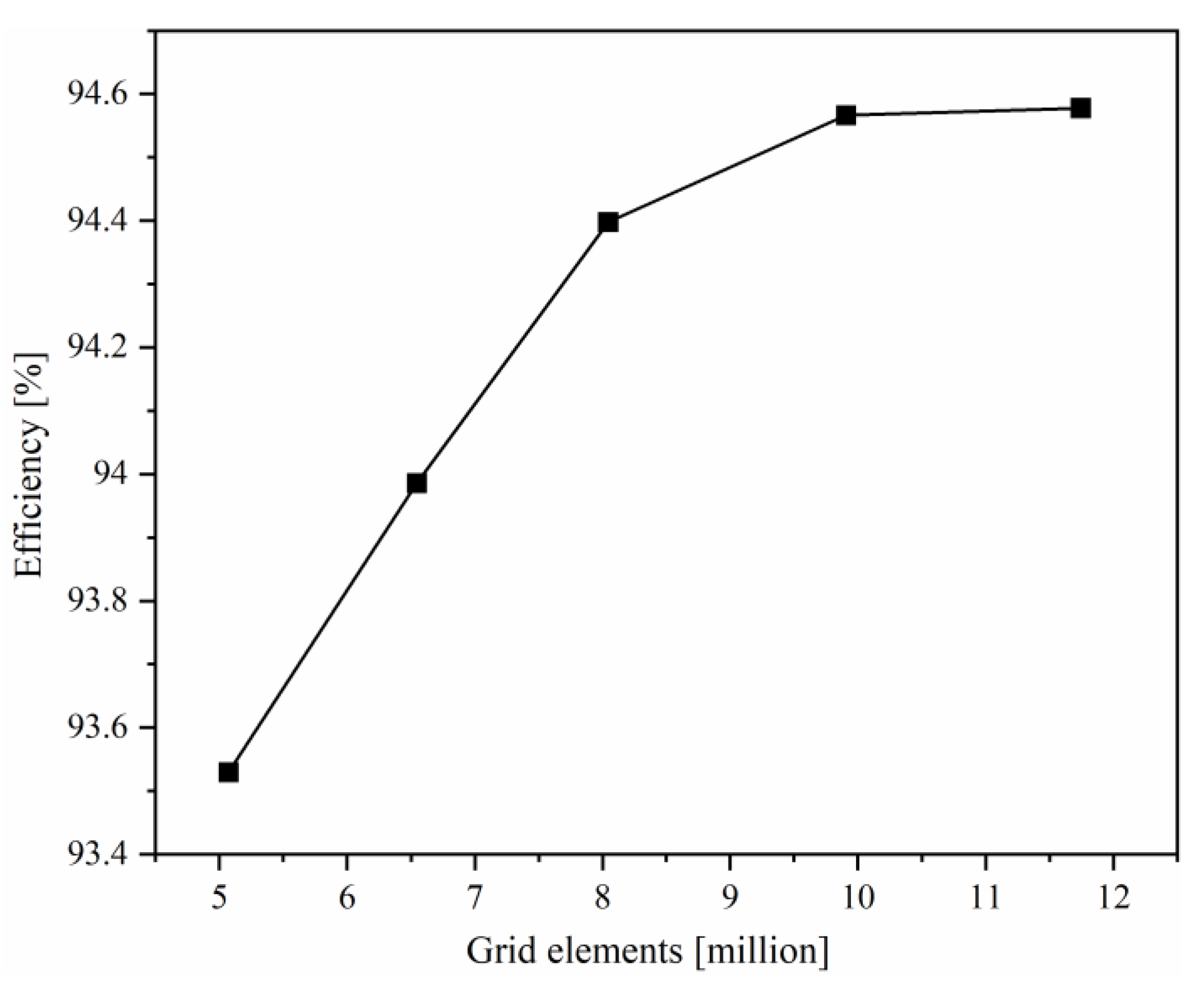
2.1. Computational Method
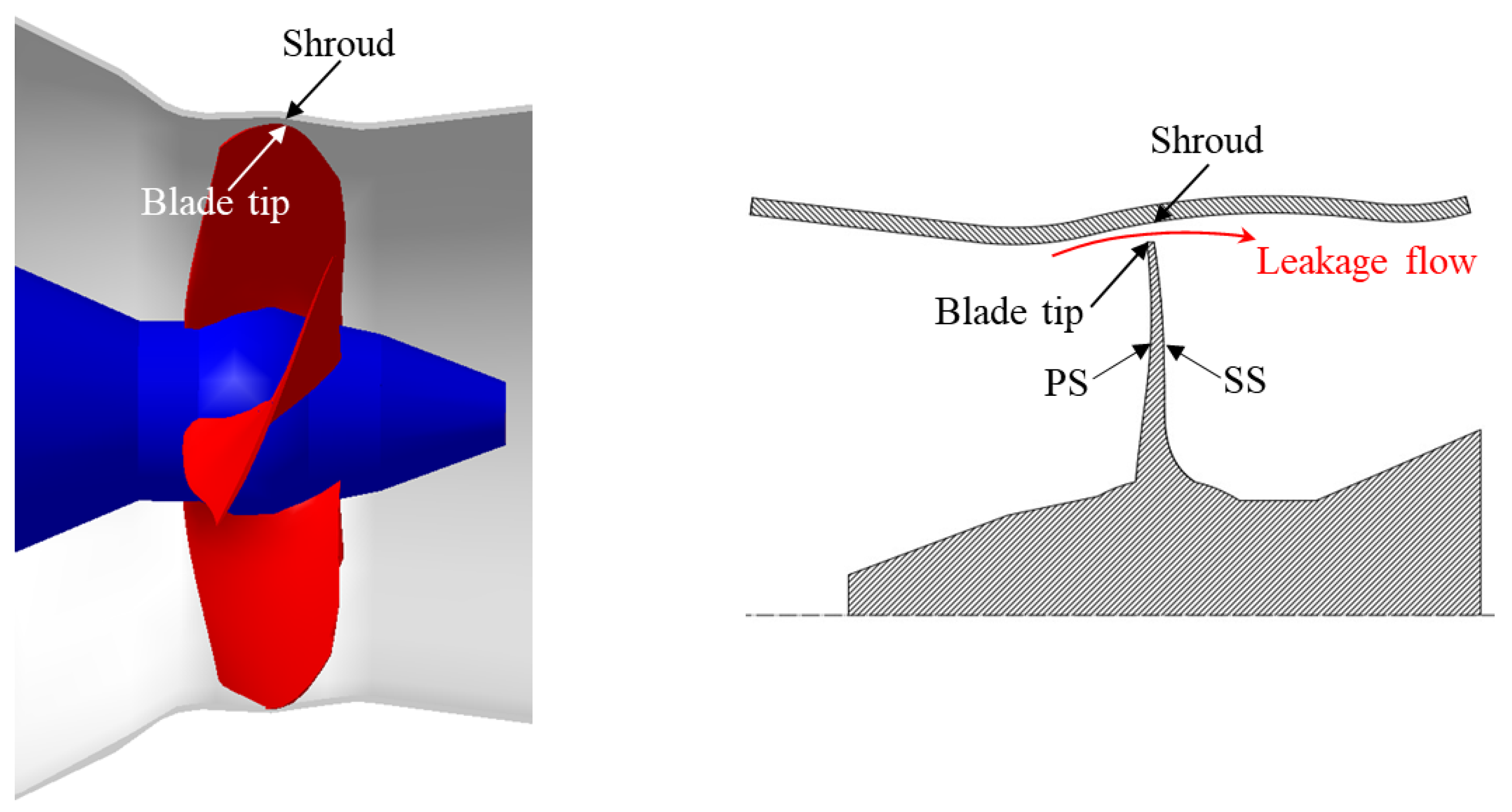
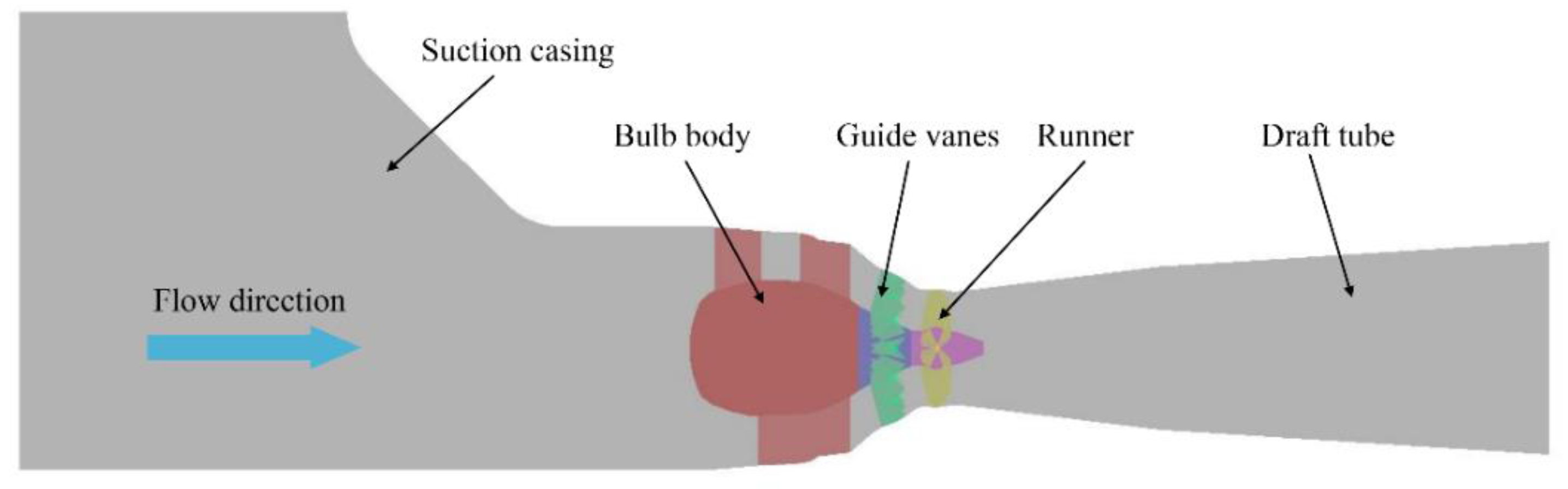
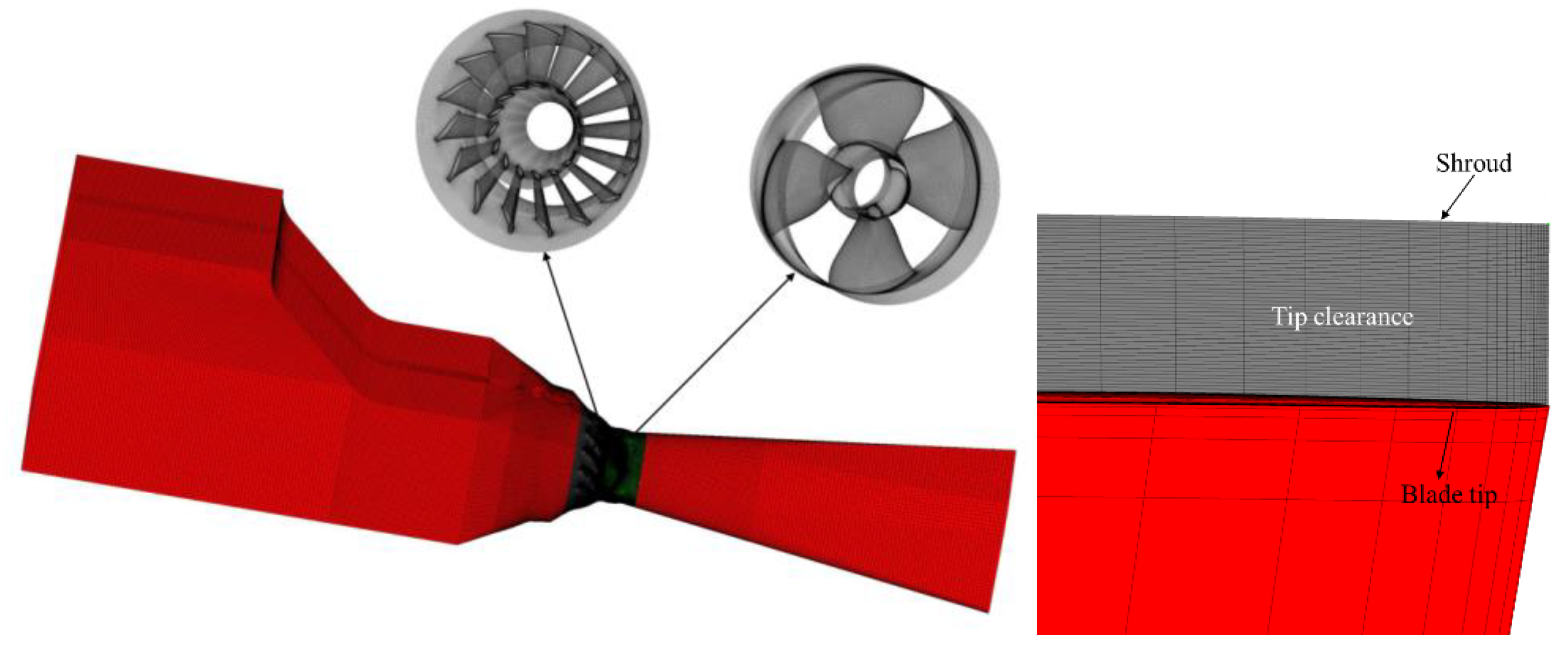
2.2. Computational Model
3. Numerical Results and Discussion
3.1. Tip Leakage Flow Characteristics
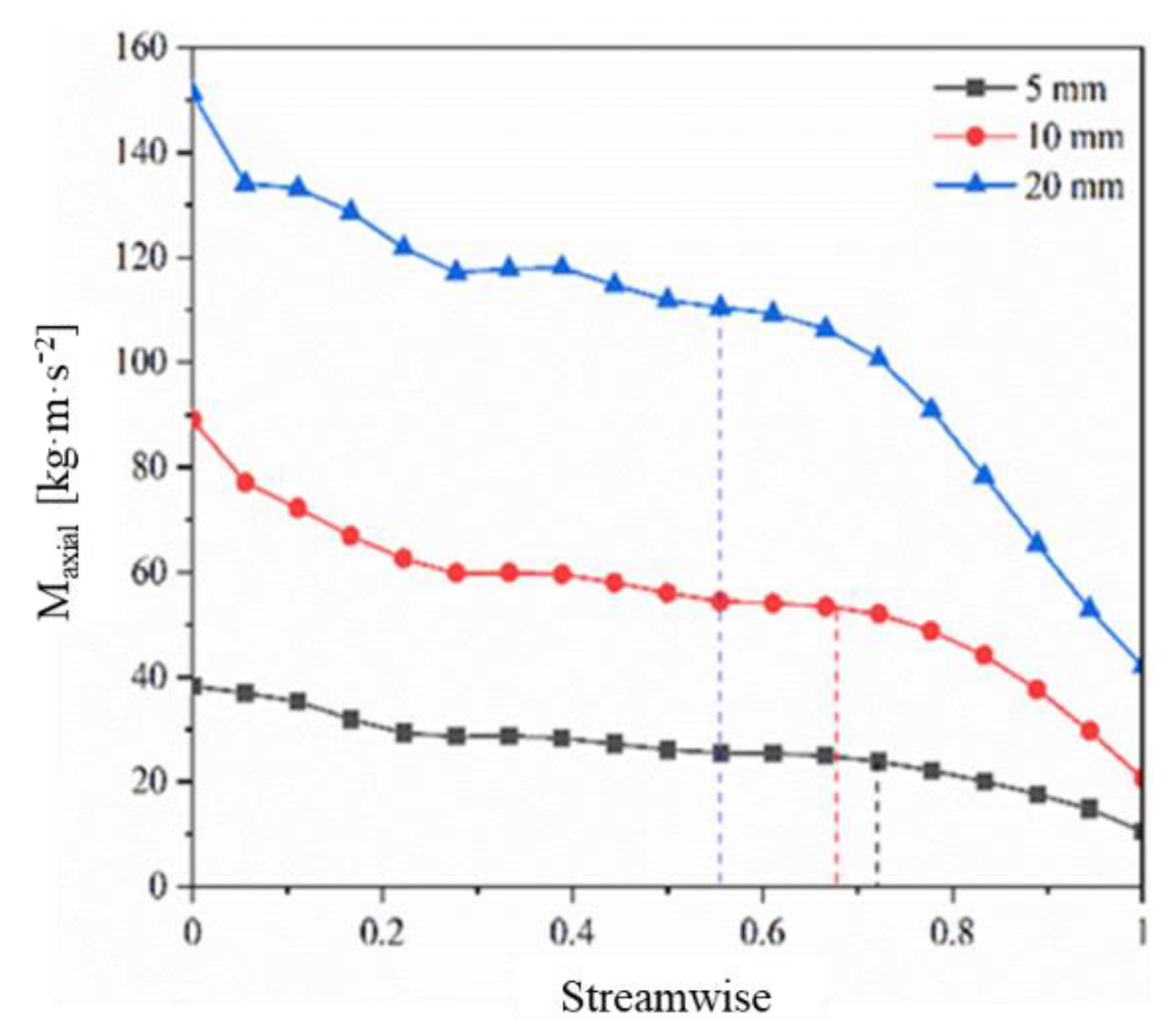
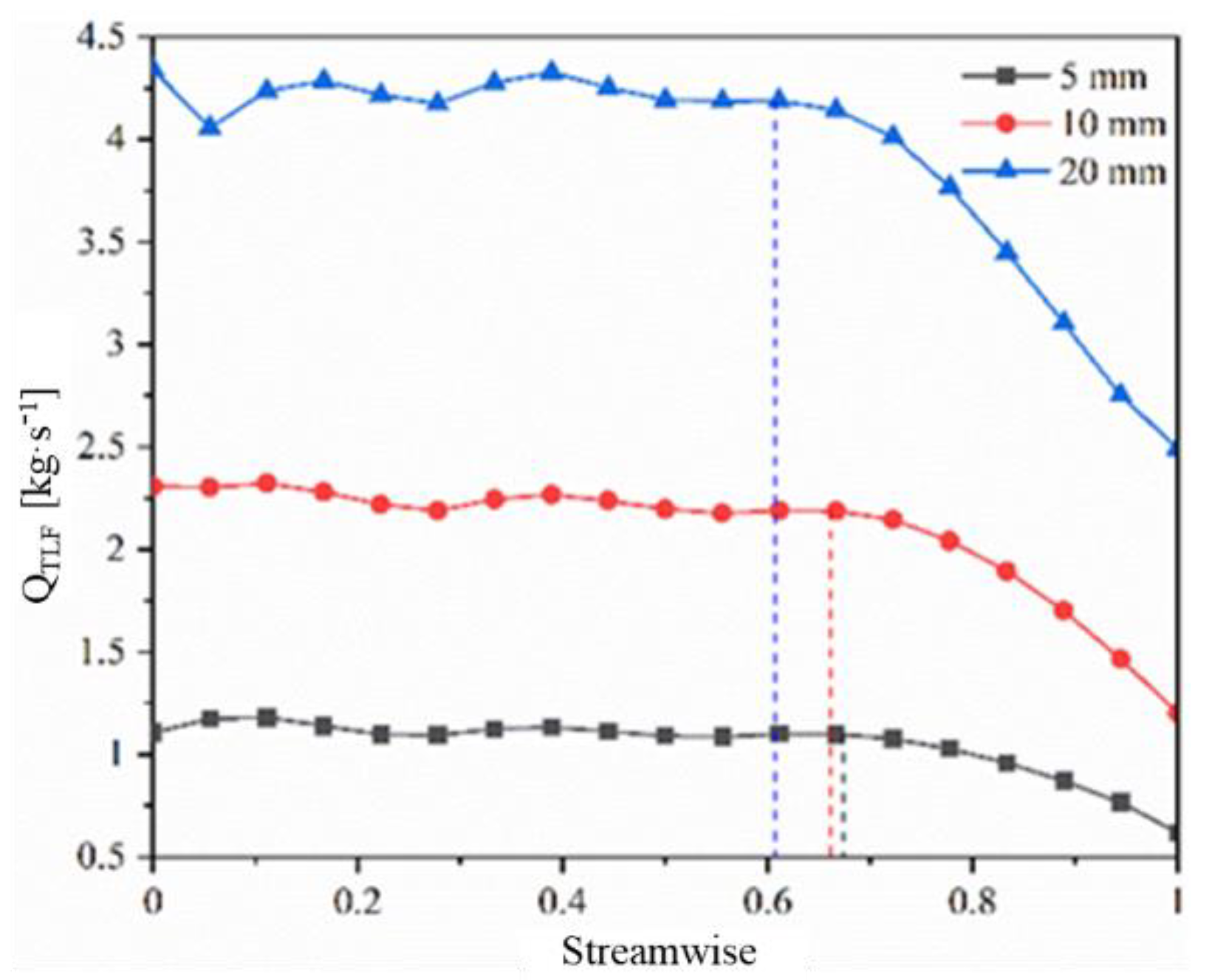
3.1.1. Axial Momentum and Flow
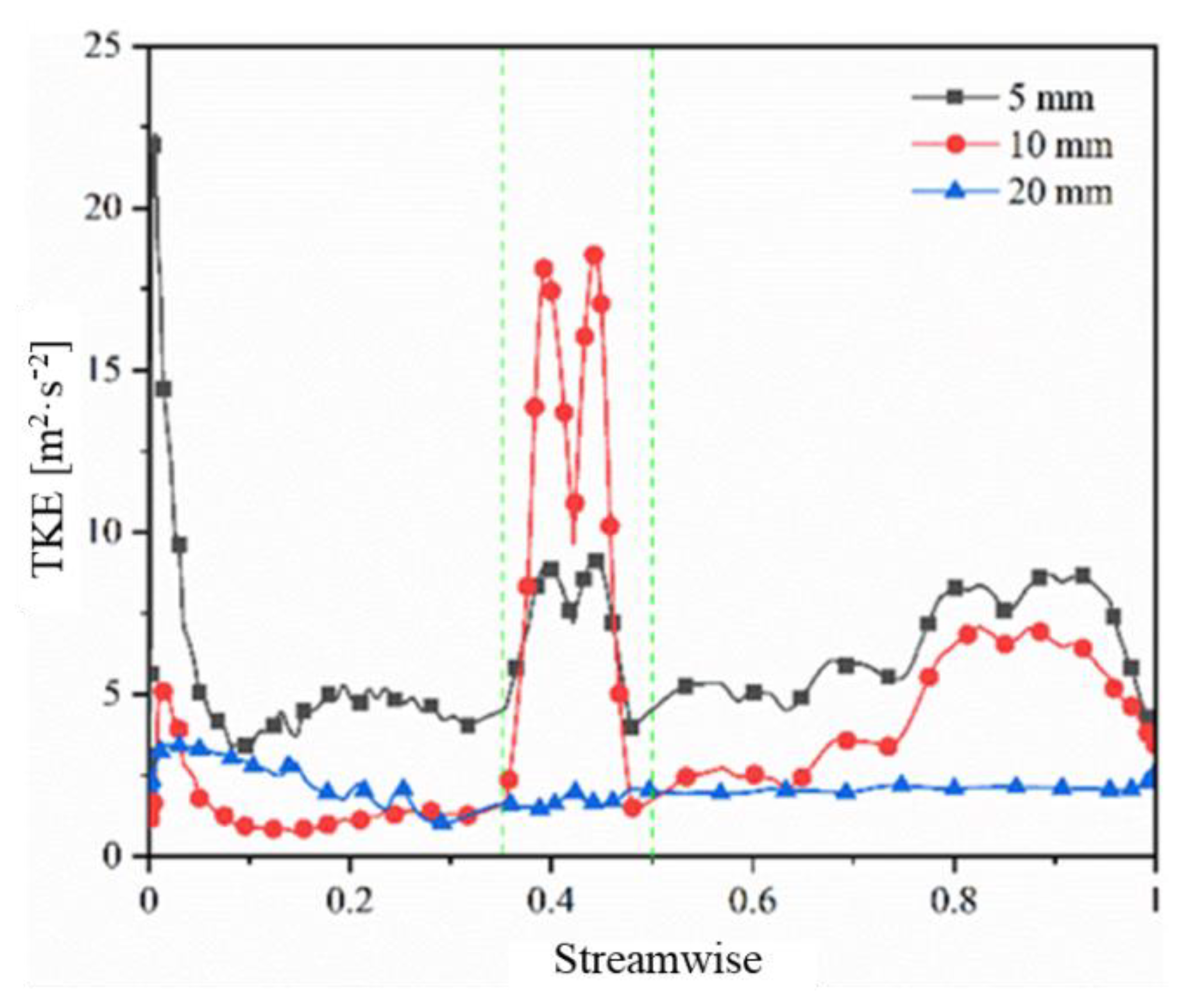
3.1.2. Leakage Velocity and Turbulent Kinetic Energy
3.2. Tip Leakage Vortex Characteristics
3.2.1. TLV Structure
3.2.2. TLV Strength under Different Gaps
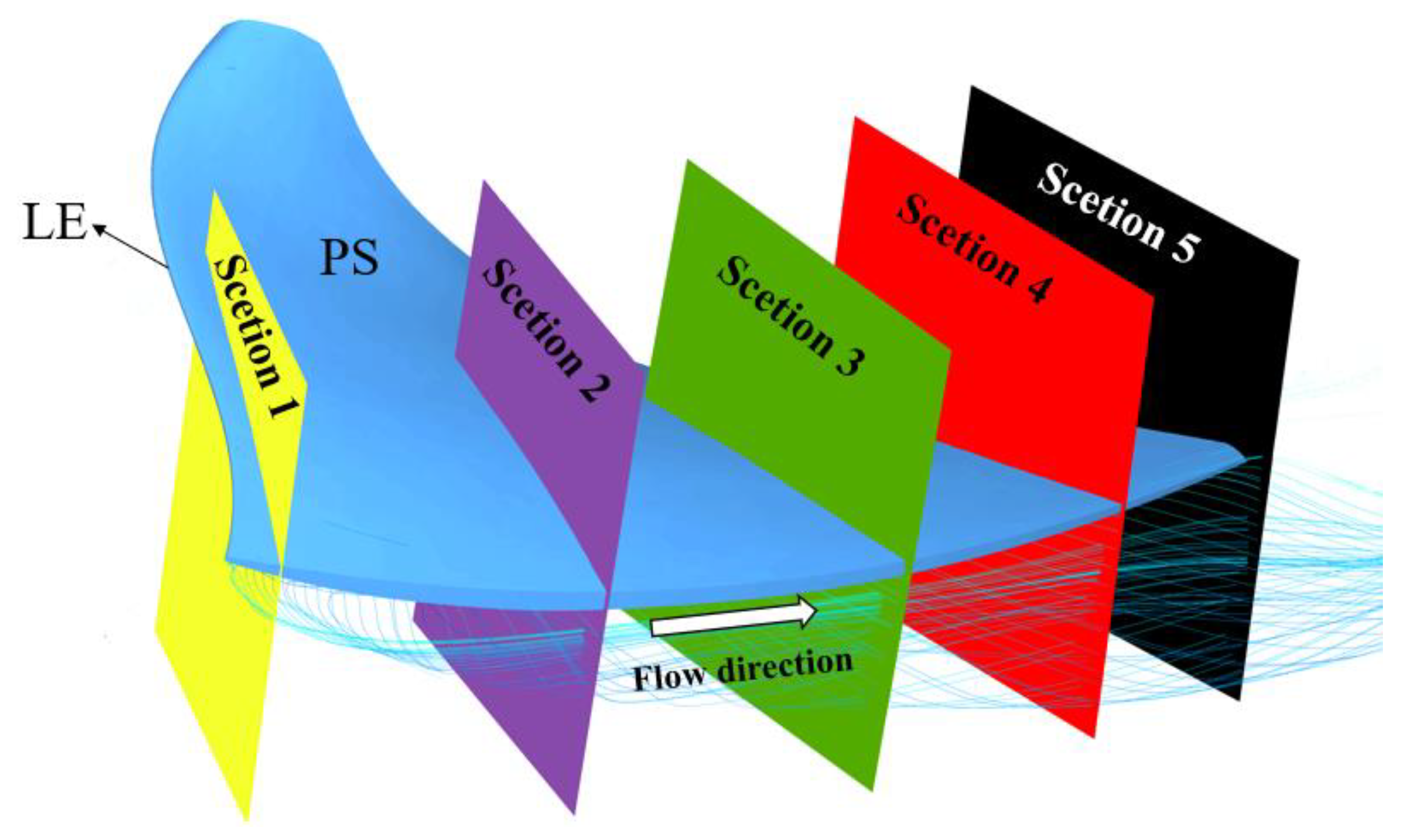
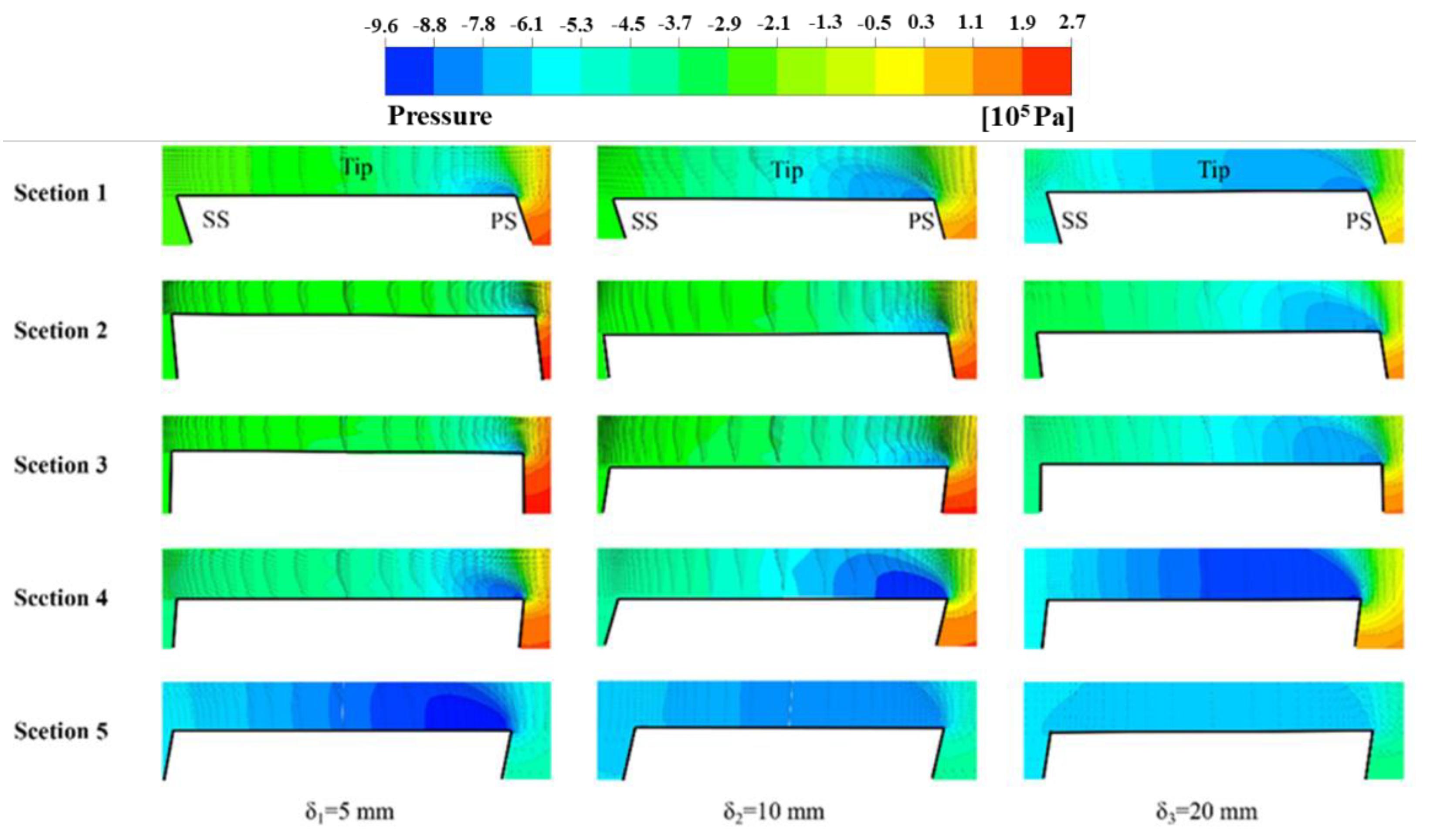
3.2.3. Flow Characteristics in Gaps
4. Conclusions
- (1)
- The gap size is proportional to the axial momentum and flow rate of the leakage flow. With an increase in the gap size, both the axial momentum and leakage amount increase. The gap size is proportional to the leakage flow velocity and inversely proportional to the turbulent kinetic energy. The variation of velocity and turbulent kinetic energy at 35–50% of the flow direction shows the law of trough and peak, respectively.
- (2)
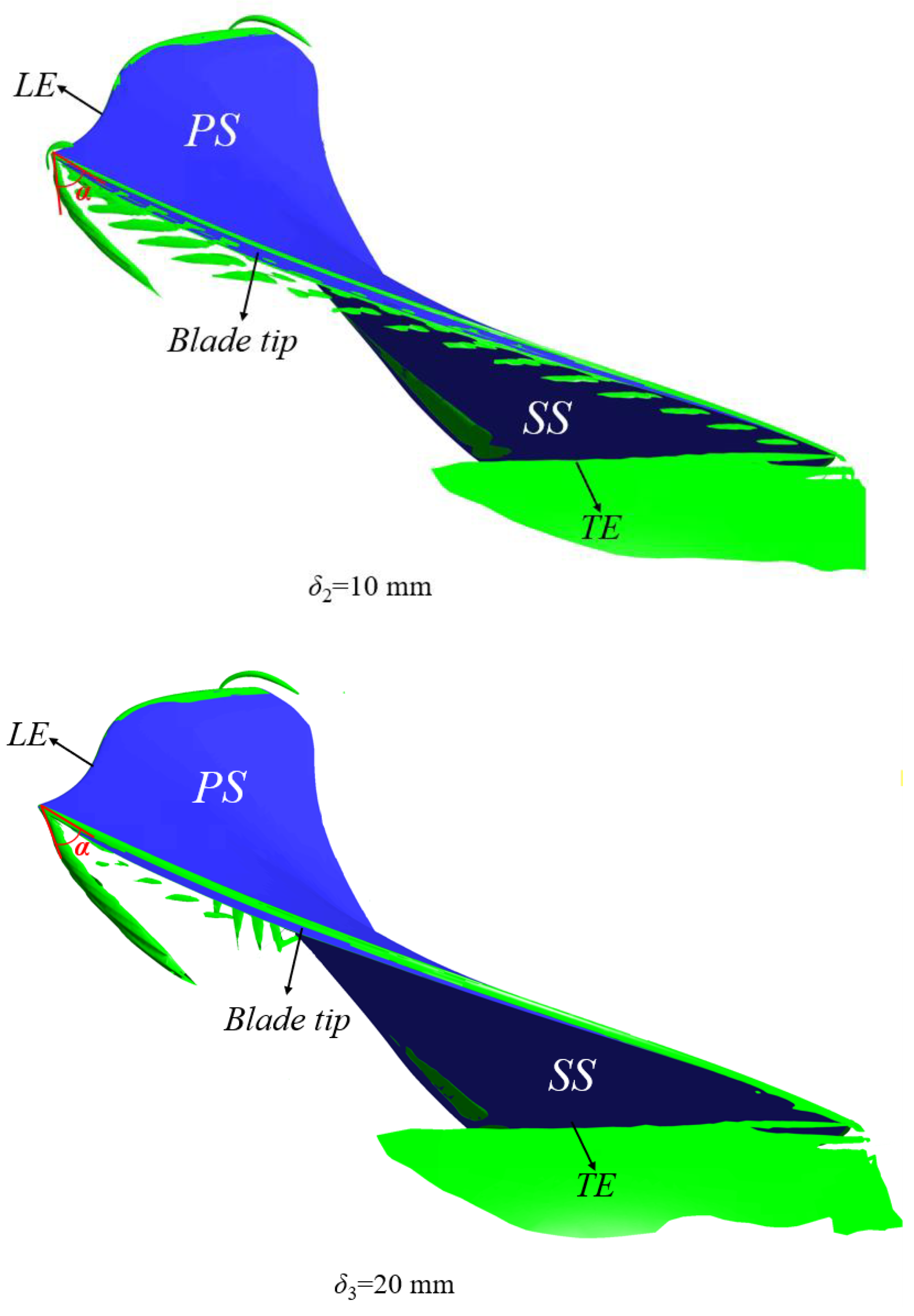
- The leakage vortex is divided into two parts: the PTLV and STLV. The vortex intensities of these two parts increase with an increase in clearance. However, for a large clearance structure (δ3 = 20 mm), the vortex core of the STLV overlaps with Core A of the PTLV, and Core B of the PTLV becomes the main part of the TLV.
- (3)
- The existence of the “right angle effect” of the blade tip causes the flow separation phenomenon near the pressure side of the blade tip, resulting in a local low-pressure zone, thus generating a local separation vortex at this position. With an increase in the clearance, the strength of the separation vortex also increased, which aggravated the flow instability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of renewable energy sources in future power systems: The role of storage. Renw. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Guney, M.S. Solar power and application methods. Renew. Sustain. Energy Rev. 2016, 57, 776–785. [Google Scholar] [CrossRef]
- Giannuzzi, A.; Diolaiti, E.; Lombini, M.; Rosa, A.; Marano, B. Enhancing the efficiency of solar concentrators by controlled optical aberrations: Method and photovoltaic application. Appl. Energy 2015, 145, 211–222. [Google Scholar] [CrossRef]
- Yang, C.X.; Lu, M.T.; Zheng, Y.; Tian, Q.X.; Zhang, Y.Q. Inlet passage’s development and optimization of new tidal unit-shaft tubular turbine. Appl. Mech. Mater. 2014, 607, 312–316. [Google Scholar] [CrossRef]
- Liu, Y.B.; Han, Y.D.; Tan, L.; Wang, Y.M. Blade rotation angle on energy performance and tip leakage vortex in a mixed flow pump as turbine at pump mode. Energy 2020, 206, 118084. [Google Scholar] [CrossRef]
- Chang, X.L.; Liu, X.H.; Zhou, W. Hydropower in China at present and its further development. Energy 2010, 35, 4400–4406. [Google Scholar] [CrossRef]
- Elbatran, A.H.; Yaakob, O.B.; Ahmed, Y.M.; Shabara, H.M. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Behrouzi, F.; Nakisa, M.; Maimun, A.; Ahmed, Y.M. Global renewable energy and its potential in Malaysia: A review of Hydrokinetic turbine technology. Renew. Sustain. Energy Rev. 2016, 62, 1270–1281. [Google Scholar] [CrossRef]
- Kramer, M.; Wieprecht, S.; Terheiden, K. Minimizing the air demand of micro-hydro impulse turbines in counter pressure operation. Energy 2017, 133, 1027–1034. [Google Scholar] [CrossRef]
- Denton, J.D. The 1993 IGTI scholar lecture: Loss mechanisms in turbomachines. Turbomach 1993, 115, 621–656. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion induced leakage flow from guide vane clearance gap in a low specific speed Francis turbine. Renew. Energy 2017, 107, 253–261. [Google Scholar] [CrossRef]
- You, D.H.; Wang, M.; Moin, P.; Mittal, R. Vortex dynamics and low-pressure fluctuations in the tip-clearance flow. Fluids Eng. 2007, 129, 1002–1014. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Bai, X.B.; Long, X.P.; Ji, B.; Peng, X.X.; Farhat, M. Large Eddy Simulation of the Tip-leakage Cavitating flow with an insight on how cavitation influences vorticity and turbulence. Appl. Math. Model. 2019, 77, 788–809. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, D.S.; Zhao, R.J.; Shi, W.D.; Jin, Y.X. Effect of blade tip geometry on tip leakage vortex dynamics and cavitation pattern in axial-flow pump. Sci. China Technol. Sci. 2017, 60, 1480–1493. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, L.; Wang, Z. Numerical evaluation of the clearance geometries effect on the flow field and performance of a hydrofoil. Renew. Energy 2016, 99, 390–397. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Influence of C groove on suppressing vortex and cavitation for a NACA0009 hydrofoil with tip clearance in tidal energy. Renew. Energy 2020, 148, 907–922. [Google Scholar] [CrossRef]
- Taha, Z.; Sugiyono; Tuan Ya, T.M.Y.S.; Sawada, T. Numerical investigation on the performance of Wells turbine with non-uniform tip clearance for wave energy conversion. Appl. Ocean Res. 2011, 33, 321–331. [Google Scholar] [CrossRef]
- Guénette, V.; Houde, S.; Ciocan, D.; Dumas, J.; Deschênes, C. Numerical prediction of a bulb turbine performance hill chart through RANS simulations. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 032007. [Google Scholar] [CrossRef]
- Zhang, D.S.; Shi, W.D.; Wu, S.Q.; Pan, D.Z. Numerical and experimental investigation of tip leakage vortex trajectory and dynamics in an axial flow pump. Comput. Fluids 2013, 112, 61–71. [Google Scholar] [CrossRef]
- Xiao, X.W.; McCarter, A.A.; Lakshminarayana, B. Tip Clearance Effects in a Turbine Rotor: Part I—Pressure Field and Loss. J. Turbomach. 2001, 123, 296–304. [Google Scholar] [CrossRef]
- Lemay, S.; Aeschlimann, V.; Fraser, R.; Ciocan, G.D.; Deschenes, C. Velocity field investigation inside a bulb turbine runner using endoscopic PIV measurements. Exp. Fluids 2015, 56, 120. [Google Scholar] [CrossRef]
- Shi, G.T.; Liu, Z.K.; Xiao, Y.X.; Yang, H.; Li, H.L.; Liu, X.B. Effect of the inlet gas void fraction on the tip leakage vortex in a multiphase pump. Renew. Energy 2020, 150, 46–57. [Google Scholar] [CrossRef]
- Menter, F.R.; Rumsey, C.L. Assessment of Two-Equation Turbulence Models for Transonic Flows. AIAA 1994, 94, 2343. [Google Scholar]
- Ding, A.; Ren, X.; Li, X.; Gu, C. Numerical investigation of turbulence models for a superlaminar journal bearing. Adv. Tribol. 2018, 2018, 2841303. [Google Scholar] [CrossRef] [Green Version]
- Erler, E.; Vo, H.D.; Yu, H. Desensitization of axial compressor performance and stability to tip clearance zize. J. Turbomach. 2015, 138, 031006. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Han, Y.D.; Tan, L. Influence of rotating speed on tip leakage vortex in a mixed flow pump as turbine at pump mode. Renew. Energy 2020, 162, 144–150. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. Stud. Turbul. Using Numer. Simul. Databases 1988, 1, 193–208. [Google Scholar]
- Laborde, R.; Chantrel, P.; Mory, M. Tip clearance and tip vortex cavitation in an axial flow pump. J. Fluids Eng. 1997, 119, 680–685. [Google Scholar] [CrossRef]
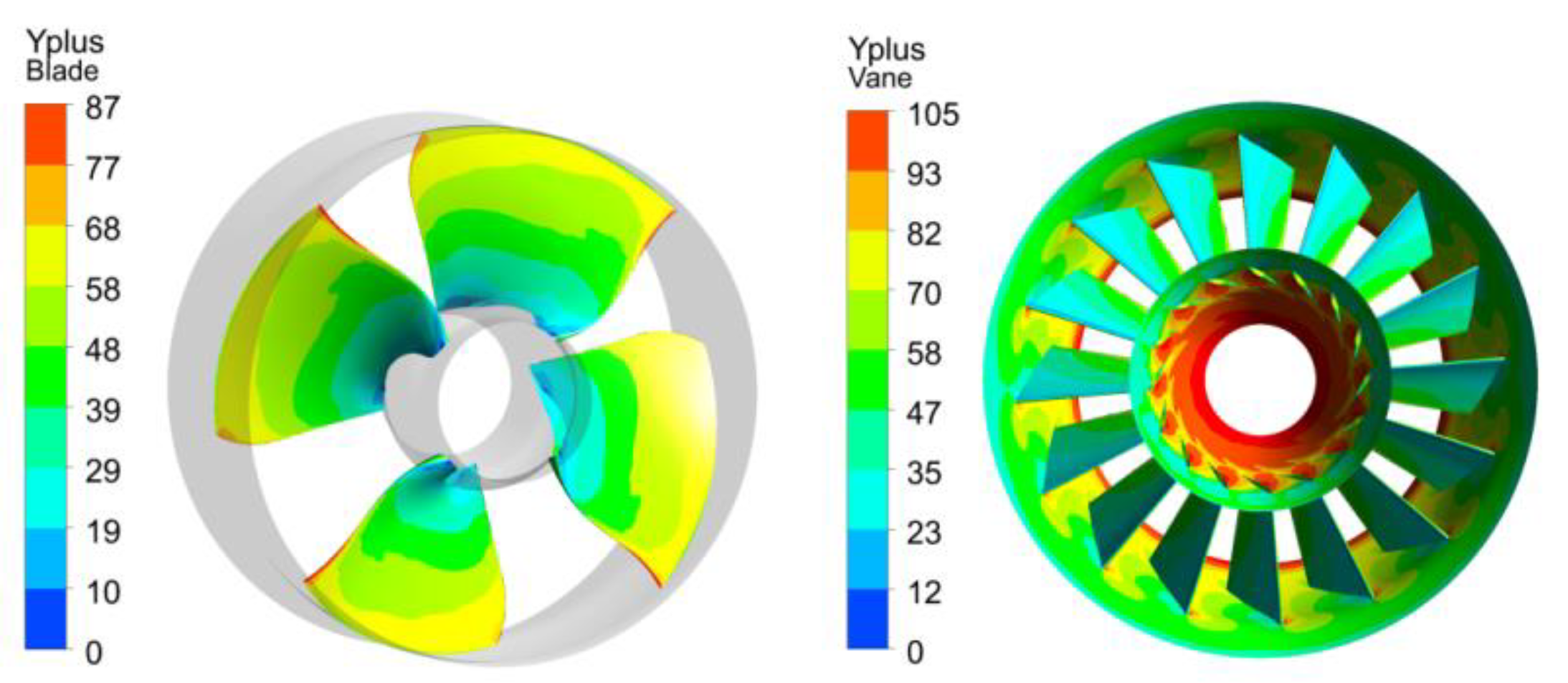
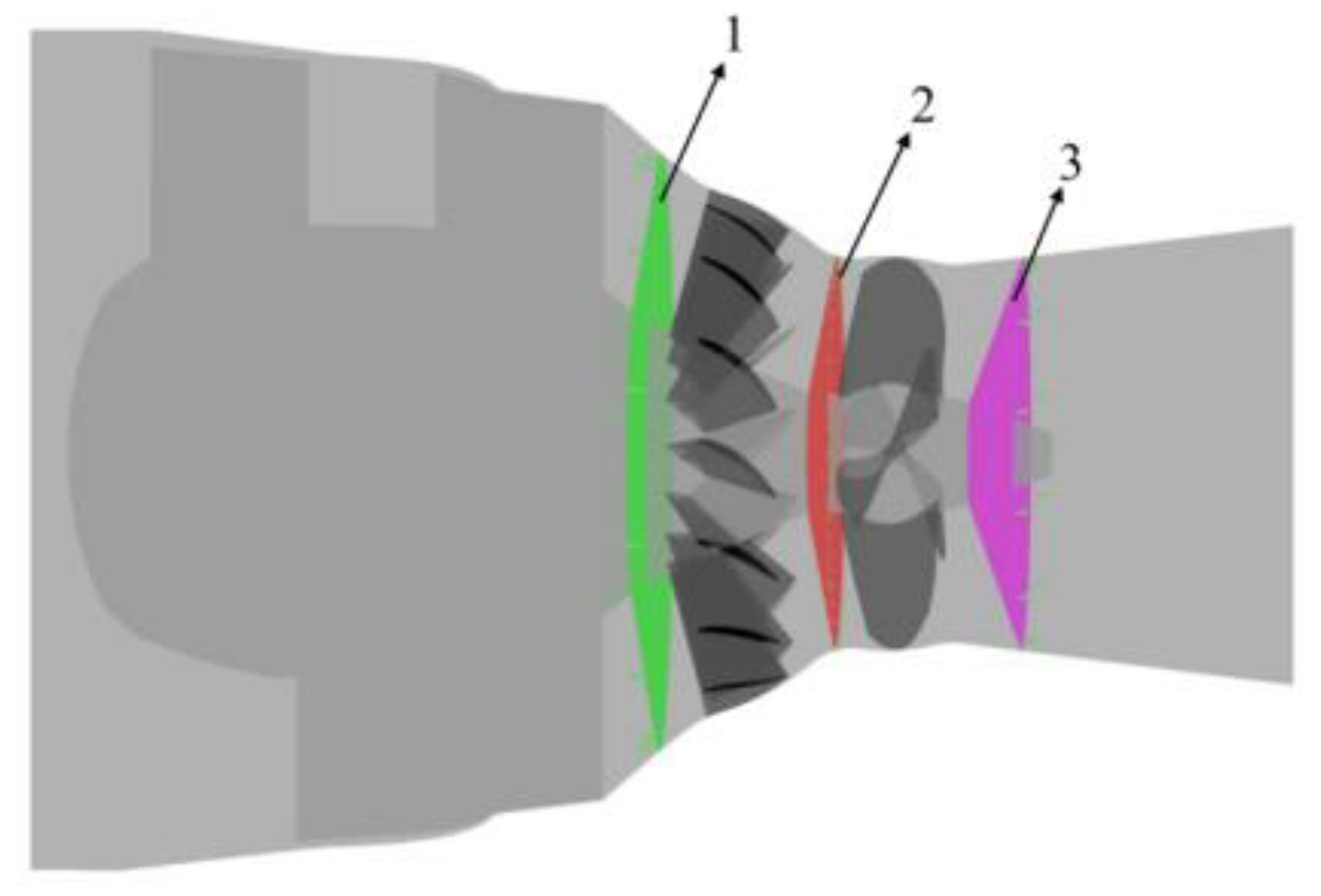




| Parameter | Unit | Value |
|---|---|---|
| Rated speed (Nr) | r/min | 68.18 |
| Rated flow (Qr) | m3/s | 375.2 |
| Maximum head (Hmax) | m | 11 |
| Minimum head (Hmin) | m | 2.6 |
| Rated head (Hr) | m | 7.8 |
| Runner diameter (D1) | m | 7.25 |
| Blade (Z) | — | 4 |
| Guide vane (Z0) | — | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, Z.; Zhu, B.; Wang, W. Effect of Tip Clearance Size on Tubular Turbine Leakage Characteristics. Processes 2021, 9, 1481. https://doi.org/10.3390/pr9091481
Li X, Li Z, Zhu B, Wang W. Effect of Tip Clearance Size on Tubular Turbine Leakage Characteristics. Processes. 2021; 9(9):1481. https://doi.org/10.3390/pr9091481
Chicago/Turabian StyleLi, Xinrui, Zhenggui Li, Baoshan Zhu, and Weijun Wang. 2021. "Effect of Tip Clearance Size on Tubular Turbine Leakage Characteristics" Processes 9, no. 9: 1481. https://doi.org/10.3390/pr9091481
APA StyleLi, X., Li, Z., Zhu, B., & Wang, W. (2021). Effect of Tip Clearance Size on Tubular Turbine Leakage Characteristics. Processes, 9(9), 1481. https://doi.org/10.3390/pr9091481






