Abstract
In cake filtration processes, where particles in a suspension are separated by forming a filter cake on the filter medium, the resistances of filter cake and filter medium cause a specific pressure drop which consequently defines the process energy effort. The micromechanics of the filter cake formation (interactions between particles, fluid, other particles and filter medium) must be considered to describe pore clogging, filter cake growth and consolidation correctly. A precise 3D modeling approach to describe these effects is the resolved coupling of the Computational Fluid Dynamics with the Discrete Element Method (CFD-DEM). This work focuses on the development and validation of a CFD-DEM model, which is capable to predict the filter cake formation during solid-liquid separation accurately. The model uses the Lattice-Boltzmann Method (LBM) to directly solve the flow equations in the CFD part of the coupling and the DEM for the calculation of particle interactions. The developed model enables the 4-way coupling to consider particle-fluid and particle-particle interactions. The results of this work are presented in two steps. First, the developed model is validated with an empirical model of the single particle settling velocity in the transition regime of the fluid-particle flow. The model is also enhanced with additional particles to determine the particle-particle influence. Second, the separation of silica glass particles from water in a pressurized housing at constant pressure is experimentally investigated. The measured filter cake, filter medium and interference resistances are in a good agreement with the results of the 3D simulations, demonstrating the applicability of the resolved CFD-DEM coupling for analyzing and optimizing cake filtration processes.
1. Introduction
Many industrial applications use cake filtration for the separation of solids from liquids [1], whereby a porous filter medium on which a filter cake is formed. The pressure drop of the separation defines the process energy effort. It is composed of the pressure drops of the filter cake and the pure filter medium as well as the transition pressure drop which is the result of the interactions between the first particle layer and the filter medium [2]. Therefore, a detailed investigation of the filter cake structure and interactions between filter medium and particles is necessary to determine and describe specific parameters like the resistances of the filter cake and the filter medium. For the description of these micro processes, the numerical multiphase flow simulation can be applied.
In general, the fluid flow is calculated first with subsequent determination of the particle movement in the fluid. The occurring interactions between particles and the fluid can be considered entirely or just in parts. The 1-way coupling methods focus on the fluid flow influencing the particles, while particle movement does not affect the fluid flow field. The 2-way coupling methods also include the impact of the moving particle on the fluid flow. At low particle concentrations in suspensions with non-deformable, very stiff, non-adhesive and ideal spherical particles, the filtration process can be simulated by the Computational Fluid Dynamics (CFD) using models of the porous structure (Euler), two—phase CFD models (Euler-Euler) and CFD with Lagrangian particle tracking. In our previous work, the filter cake formation at static filtration [3] and fractionation in cross-flow filtration [4] were studied with Lagrangian particle tracking. The same method was used for the study of particle deposition in the electret nonwovens [5,6]. Hosseini and Tafreshi [7] simulated the aerosol flow through nanofiber filter media.
However, the particle deformation and adhesion in the contacts between particles and fibers could not be considered within this method. It is assumed that in case of contact, the particle sticks to the fiber or other already deposited particles. This scenario is permissible for the particle deposition in gas phase filtration, however, for the particle separation from liquids the sticking probability with fibers must be taken into account. The deformations, the relative movement and the reorganization of the particles in the filter cake are important mechanisms of the cake formation, which cannot be predicted by either 1-way coupling or 2-way coupling.
Moreover, at high concentrations in suspensions with deformable and adhesive particles with irregular shape, the interaction between particles in the flow [8,9,10], as well as in the filter cake and with the filter medium cannot be neglected [10,11,12], also indicating the need for higher order resolved coupling methods. In this context, the Discrete Element Method (DEM) is a powerful method to simulate the motion and interactions of individual particles in particulate systems under the influence of different forces and moments [13,14,15,16,17]. The forces can include contact, adhesion, drag, buoyancy forces, gravity, etc. Thus, the kinematics and dynamics of each individual particle and the entire particle collective can be obtained, taking into account effects such as particle size distribution, irregular particle shape, deformation, sticking and breakage of particles.
The coupling of the described DEM with the CFD considers the interactions between particles, particles and filter medium as well as fluid-particle interactions in 4-ways (Figure 1). CFD-DEM coupled methods can then also be divided into two groups of volume-averaged and resolved simulations. In the volume-averaged simulations, the CFD-DEM coupling does not fully resolve the fluid flow around each individual particle. The flow is calculated on the basis of the volume-averaged Navier-Stokes equations. Since the majority of the numerical studies of fluid-particle flows in literature were performed with the unresolved coupling, the CFD-DEM is a commonly used term for the volume-averaged method [18,19,20,21]. Vångö et al. [22] gave an overview of unresolved coupling methods for the solid-liquid packed bed simulations. Zhao and Shan [23] used CFD-DEM coupling in unresolved simulations for the description of sand particles settling in water to form a sand pile. Our previous CFD-DEM studies cover the description of the micro-processes of filter pore clogging, formation and consolidation of the filter cake and the resulting pressure drop at the static solid-liquid surface separation with adhesive, spherical and non-spherical particles [2,3,24,25].
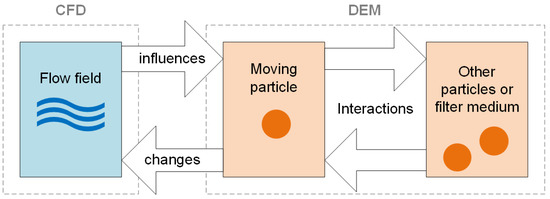
Figure 1.
Specification of the 4-way CFD-DEM coupling. Each interaction is illustrated by an arrow.
The unresolved coupling works well if the volume of the grid cells is much larger than the particle volume. If the volume of a grid cell approaches the particle volume, the cell might be fully occupied by a particle, which results in numerical problems. The collision behavior of the particles can also be affected by viscous forces [26]. The viscous forces can influence the cake formation [25] and separation process [27]. The numerical studies based on the unresolved CFD-DEM coupling cannot calculate these forces directly and need therefore an additional model, which considers the energy dissipation due to surrounding fluid.
The influence of a neighbor particle on the settling behavior is called the drafting kissing and tumbling (DKT) phenomenon [28,29]. It describes the drafting, kissing and tumbling process, when two particles settle at a specific distance from each other. The unresolved CFD-DEM models are not suitable for the direct prediction of the influence of particle concentration (swarm effect) and need specific correlations for the drag force [25,30,31].
However, these complex particle-fluid interactions which also have a strong influence on the particle contact interactions can be simulated by the resolved coupling of DEM with CFD. In this approach, the DEM calculates the kinetics and dynamics for each single particle depending on all relevant forces including the contact interactions between particles and with the filter medium surface, such as the deformation, adhesion and friction forces. The above-mentioned drag, buoyancy and viscous forces due to flow are obtained by CFD simulation of the flow and explicitly considered via a coupling in the momentum balance of the DEM [24,25,30].
One of the most accurate 3D modeling approaches to describe the flow is Direct Numerical Simulation (DNS). For this, the Lattice-Boltzmann Method (LBM) is used as an especially well-suited numerical scheme to approximate the transient Navier-Stokes equations with moving boundaries [29,32,33,34]. The oblique collisions between a single particle and a solid wall surface in liquid influencing by hydro dynamical forces in contact have been simulated with LBM-DEM by Zhang et al. [35] with particular attention on rolling and sliding effects. Other research articles present the usage of CFD-DEM with the LBM to simulate the spouted gas fluidized beds [36,37]. The solid-liquid separation was numerically investigated with a mixture of resolved and unresolved coupling by Kuruneru et al. [38]. Rettinger and Rüde [39] proposed a new algorithm for the 4-way coupling LBM of suspensions and compared their results with semi–empirical correlations and to simulate a hopper [40].
In this work, the numerical study of the micro processes between the polydisperse particles during the deposition at the beginning of the filter cake formation is achieved by the resolved coupling between CFD and DEM methods. The realized 4-way coupling allows a detailed view on the micromechanics of the cake formation and interparticulate interactions. Small deformations during particle contacts are also calculated with the soft-sphere model. The experimental investigations complement the simulation results and the numerically calculated filter resistances represent the experimentally obtained results of the filter cake formation processes.
2. Materials and Methods
2.1. Filtration Equation
In the separation process, the suspension flows through the filter medium to separate particles from fluid on the filter medium surface. The process is characterized by the filter resistances, which can be divided into the two pressure drops of the filter cake and the filter medium resistance . The filtration Equation (1) [1,41,42] describes the flow velocity of the filtrate depending on the total pressure difference and both resistances:
where μ is the dynamic viscosity of liquid.
The resistance of the filter medium can be divided into the pure filter medium resistance and the interference resistance , which describes the resistance of the filter medium under consideration of the first particle layer on the medium, that can block the medium pores [2]:
Experimentally obtained data are often restricted to the mass of the filtrate, whereby numerical simulations allow the direct calculation of the filtrate velocity depending on the structure of the filter medium and the formed filter cake. For the evaluation of filtration experiments and numerical results, the filter equation needs to be transformed to a linear relation according to Equation (3):
where t is the filtration time, is the filtrate volume, is the specific filter cake resistance, is the filtration constant and is the filter area.
Subsequently, the resistance of the filter medium can be calculated from the y-intercept and the specific filter cake resistance corresponds to the slope of this linear function [1,2].
2.2. Filtration Experiments
The resistances of filter cake and medium are measured in accordance with the VDI guideline 2762 [43]. The filtration experiments are performed with a laboratory scale pressurized housing at constant pressure, which is maintained by a constant liquid level above the filter medium. To achieve a hydrostatic pressure of the desired value = 1000 Pa, the pressurized housing is first filled with water and second the suspension is poured in while the liquid level is kept nearly constant. The aqueous suspension used in the filtration experiments contains spherical silica glass particles (Potters-Ballotini) with sizes in the range between 63 and 100 µm. The filter medium mounted in the pressurized housing is a twill weave woven wire cloth produced by Haver & Boecker (Figure 2). The parameters of filtration and properties of the filter medium are listed in Table 1.

Figure 2.
Photograph of the woven wire cloth.

Table 1.
Parameters of the experiment.
The mesh size of the filter medium describes the distance between two wires in the quadratic pores. The filtrate mass flow rate is measured in time that allows to calculate the filter resistances, which are then compared with the simulation results. Each filtration experiment performed in this work was repeated three times at the same conditions to increase the statistical significance.
2.3. Numerical Simulations
The calculated numerical model is based on resolved CFD-DEM coupling. DNS calculates the fluid flow directly by solving the Navier-Stokes equations (NSE). The Lattice-Boltzmann method is based on the physical principles of the kinetic theory of gases [44,45] that approaches a solution of the NSE. The use of LBM allows computation of the laminar fluid flow for low Reynolds numbers or even higher Reynolds numbers if the lattice dimensions are small enough to resolve the turbulent movement of the fluid. The first subsection outlines the principles of the CFD method. DEM is used to calculate the movement of the particles and will be explained in the second section. The third section describes the method for the coupling of the fluid flow with the particle movement and the calculation of interactions. The model will be implemented in the in-house developed software DNSlab [3].
2.3.1. Fluid Flow Calculation with CFD
The CFD calculations are carried out by the LBM, meaning that the equations for conservation of mass (4) and momentum (5) in the fluid phase corresponding to the transient Navier-Stokes equations are approximated using the D3Q15 discretization scheme and velocity boundary conditions applied at the particle boundaries [46,47]:
where is the velocity vector, describes the volume forces like gravitation force, and is the pressure gradient, represents the Navier term (inertial effects) and is the Stokes term (viscous effects). and depend on the position in the flow domain and the time .
2.3.2. Particle Movement Calculation with DEM
The movement of each single particle and its interactions with other particles and filter media are calculated with the DEM by solving Newton’s second law. The equation of translational motion is given as:
with particle mass , contact force between particle i and particle or filter medium , fluid-particle interaction force and gravitational force .
The forces acting between particles as well as particles and filter medium surface are computed with a contact model implemented in the DEM solver. In this study, the dominantly elastic spherical glass particles and the elastic steel filter medium are used. In the case of an elastic contact, the normal force in Equation (7) can be described according to the Hertzian model depending on the equivalent Young’s modulus , equivalent radius and normal overlap of contact partners (particles and filter media) [48,49]:
2.3.3. CFD-DEM Coupling
The coupling between the LBM for CFD and the DEM method is based on the transfer of momentum from the particles to the fluid and the fluid volume displacement due to particle motion. Figure 3a illustrates the particle moving in direction of the arrow in a time step. Then, in this rigid lattice structure, former fluid nodes (white) become particle nodes and former particle nodes become fluid nodes (blue). Pressure and velocity values are interpolated from surrounding fluid nodes when new fluid nodes arise from particle movement.
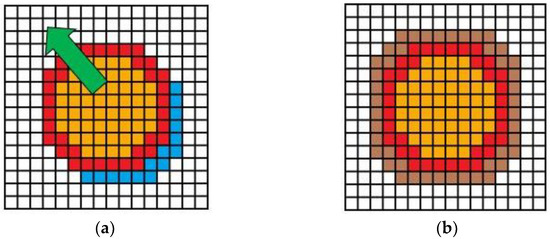
Figure 3.
LBM coupling scheme with particle (orange), particle boundary (red) and fluid (white) nodes. (a) New fluid nodes (blue) after particle movement, (b) surrounding layer of fluid nodes (brown) used to compute viscous and pressure forces which act on the particle.
The resistance force on the particles is described by an integration of shear and pressure forces over the particle surface illustrated by the brown fluid layer in Figure 3b. The fluid-particle interaction force considered in DEM in Equation (6) includes the buoyancy force (Equation (8)), the shear force (Equation (9)) and the pressure force (Equation (10)):
with the particle volume .
The following image (Figure 4) explains the calculation of . The particle moves with velocity through the flow region . denotes the solid-liquid interface, i.e., the particle surface. A fluid layer around the particle with thickness is needed for the evaluation of the local flow velocities and pressures. is a point on the particle surface and the unit vector in the normal direction in this point. The shear force acting from the fluid on the particle depends on the tangential part of the relative flow velocity .
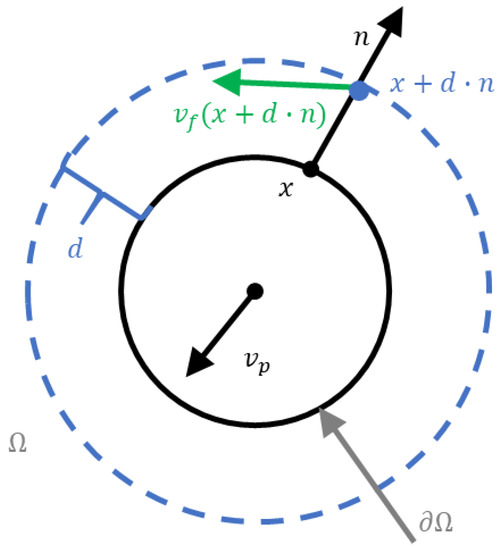
Figure 4.
Variables used for shear force calculation in CFD-DEM coupling.
2.4. Particle Sedimentation
The fluid-particle interactions as well as between particles in a liquid are studied with the validation case of the particle sedimentation in a small channel and validate the results with the analytical solution.
2.4.1. Theory
The numerical model considers particle-fluid, particle-particle and particle-filter medium interactions. For the validation of the numerical CFD-DEM simulations, the single particle sedimentation in a closed channel is investigated (Figure 5). The particle is generated and dropped at the top of the 3D model. After the acceleration by the gravitational force, it reaches the terminal velocity , which for an otherwise empty and infinitely sized fluid domain is given as:
where the particle diameter, fluid density, the drag coefficient and the gravitational acceleration [50].
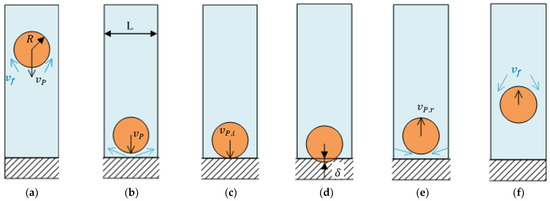
Figure 5.
Particle impact on a solid surface and rebound in a closed container with liquid: (a) particle sedimentation down to the bottom wall and counter flow of liquid, (b) particle approaches the wall and squeezes liquid from the gap, (c) first contact with wall, (d) particle-wall contact deformation δ, (e) rebound of particle, fluid streams back into gap, (f) rebound of particle, counter flow of fluid.
The drag coefficient depends on the particle Reynolds number :
where is the settling velocity, and the fluid viscosity.
This dimensionless number is also used to describe the flow regime around the particle, where the Stokes regime has < 0.25, the transition regime is between 0.25 and 103 and the turbulent regime has > 103 [50].
In the considered case of the closed container, the settling velocity can be significantly influenced by the side walls [8,51]. The decrease of the terminal velocity is described by the increase of the drag force, where the wall effect is considered as a correction of the drag coefficient [52]. The model of Ladenburg [50,53] in Equation (13) describes the wall effect on the settling particle in a finite cylindrical channel which is considered by the channel diameter . The model is valid in the Stokes regime ( < 0.25):
When the particle approaches the horizontal wall at the bottom (Figure 5a), it can decelerate by the counter flow of fluid because of the downwards movement of the solid volume. Before impact, the viscous forces (Figure 5b) occurring due to squeezing flow in the decreasing gap between the particle and surfaces can also reduce the particle velocity (Figure 5c). The kinetic impact energy of the particle can be further reduced by adhesion, inelastic deformation, such as viscoelastic or plastic, and friction in the contact with the wall surface (Figure 5d). During the rebound phase the fluid forces can also reduce the particle velocity (Figure 5e,f).
2.4.2. 3D Models
Four 3D models are implemented to examine the influence of the voxel length, boundary conditions and effects of the filter medium. The models A1, B1 and D1 have solid, non-porous walls on top and at the bottom and periodic boundary conditions on the sides. Model C1 is completely surrounded by walls like a closed box. Each model is realized as a voxel grid, which uses a cubic lattice for the computation. The particle settles down accelerated by gravity until it collides on the bottom wall or in case D1 on the filter medium. The wire cloth in D1 is also used in the numerical simulations of the filtration process, which is described in the next section. Table 2 summarizes the parameters for the performed simulations.

Table 2.
Model parameters of the simulated cases.
The numerical calculations are performed at the high-performance computer of TU Kaiserslautern. The four model cases A1, B1, C1 and D1 have the same geometrical dimensions (Figure 6). The higher voxel length of the model B1 results in a coarser grid used to study the influence of the grid refinement on the particles settling velocity.
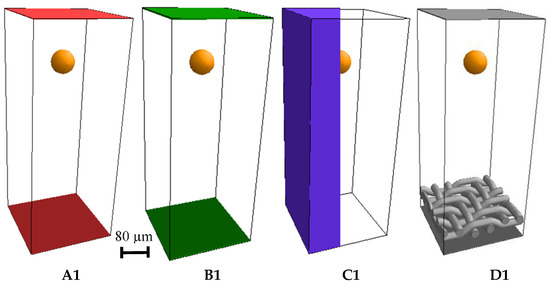
Figure 6.
Different model arrangements to investigate particle settling behavior. The particle is 80 µm in diameter for each case. (A1) Basic model with periodic boundaries, (B1) basic model with coarser grid, (C1) basic model with solid wall boundaries, (D1) basic model with filter medium.
In order to examine the influence of the boundary conditions and particle number additional models are created. Therefore, different sized containers were created with periodic boundaries (A2, A3,) and with solid wall boundaries (C2, C3) (Figure 7). Furthermore, models with two and three sedimenting particles are generated (A4, A5) (Figure 7). The simulation models are used to further verify the simulation method by comparing them to the empirical model of the particle settling velocity.
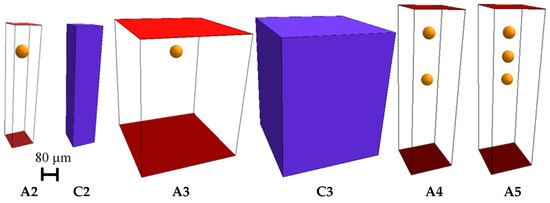
Figure 7.
(A2) from model A1 which is reduced in width, with periodic boundaries, (C2) from model C1 which is reduced in width, with solid wall boundaries, (A3) from model A1 which is enlarged in width, with periodic boundaries, (C3) from model C1 which enlarged in width, with solid wall boundaries, (A4) from model A1 which is enlarged in height and one added particle, with periodic boundaries, (A5) from model A1 which is enlarged in height and two added particles, with periodic boundaries.
The models A2 and C2 are generated by the reduction of the width of the corresponding models A1 and C1. Due to the increase in the width of models A1 and C1, models A3 and C3 are created, respectively. In the additional simulation cases A4 and A5, the effect of neighboring particles (two and three) on the settling behavior is observed (Figure 7).
2.5. Separation Process
For the CFD-DEM simulation of the separation process, a model of the experimentally investigated filter medium is mathematically generated and discretized as a voxel grid. It represents a twill weave wire cloth that is used in experiments (Section 2.2). It outlines a section of the filter area including 16 woven wires with periodic boundary conditions, representing the real weave structure completely. The image of the side view in Figure 8 reveals the voxel structure of the generated wires in the filter medium. The chosen voxel length of 2.5 µm leads to a coarsening of both pores and fibers. This coarser grid allows a simulation of the filter cake formulation in a reasonable computation time.
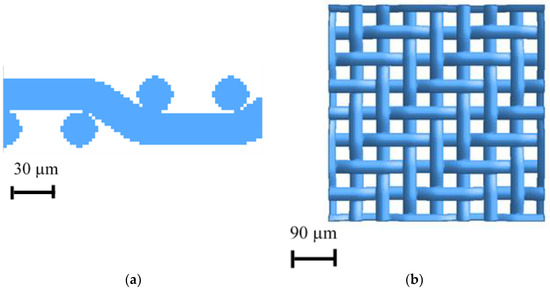
Figure 8.
Computed wire cloth, (a) side view in a sectional plane through a wire, (b) top view of the complete model wire cloth structure.
The formation of the filter cake is realized with an absolute number of 161 particles, which are separated from the inflowing suspension. Analogous to the experiment, the filtration simulation is performed at a constant pressure difference. The solid particles are generated randomly distributed in the inflow plane of the container at z = 0 at the top of the model. The generation rate of particles corresponds to the concentration of 1011 m−3. Table 3 summarizes the relevant parameters of the filtration simulation.

Table 3.
Model parameters of the woven wire cloth filter medium, particles and fluid.
The simulated particles are spherical and also represented by voxels. The particle size distribution of the generated particles (Figure 9) is based on the particle system of the filtration experiments. The volumetric particle size distribution (Q3) of the glass beads was measured in water with the Horiba Laser Diffraction Particle Size Analyzer (Retsch GmbH, Haan, Germany) in the experiments and then transformed into the number-based distribution (Q0) which can be used as input parameter in the simulations.
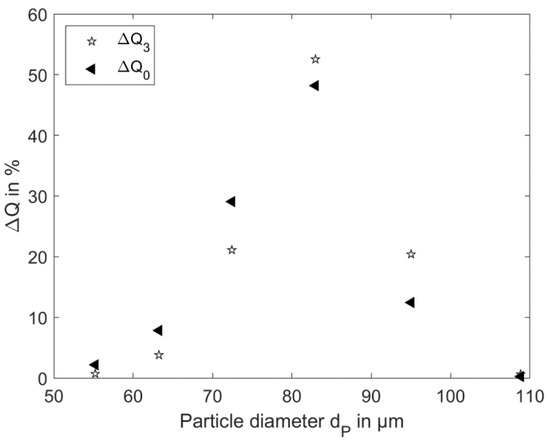
Figure 9.
Particle size distribution of the glass particles used in experiments and simulations.
The computation of the pressure force on the particles was switched off because of the occurring pressure fluctuations, which made the calculation of the pressure forces unstable. Similar pressure fluctuations were observed by Rettinger [54]. Because of creeping flow regime in the simulated filtration process, the pressure forces acting on the particles are negligible compared to viscous shear forces, and therefore can be neglected.
3. Results
3.1. Filtration Experiments
The filtration experiments were performed with the pressurized housing setup, as described in Section 2.2, and glass particles with the particle size distribution shown in Figure 9. The measured data are presented in Figure 10 and described by the filtration curve according to the filtration Equation (3). The filter resistances (filter medium and specific filter cake resistance) are evaluated by the slope and y-intercept of the filtration curve. In the experimental setup, a perforated plate was used as spacer to support the wire cloth. The pure filter medium resistance was achieved by subtracting the setup resistance from the obtained total resistances. This is necessary for a comparison between experimental and simulation results in Section 3.4 because the spacer was not simulated.
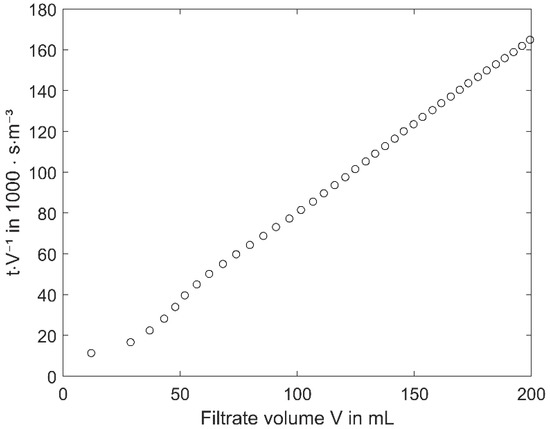
Figure 10.
Typical filtration diagram obtained in the pressurized housing experiments with the filter medium (no spacer) and the filter cake formed from glass particles.
The slope of the graph reveals the experimental specific filter cake resistance of = 7.7·1010 m−2, and the y-intercept of the graph yields the filter medium resistance with Equation (2) to = 6.3·107 m−1. Because of the slightly varying pressure difference in the experiments, the pure filter medium resistance is obtained in the range between 2.1·106 m−1 and 3.9·106 m−1.
3.2. Simulation of the Particle Sedimentation
For the evaluation of the settling velocity in water in a container with a geometry that corresponds to the model cases A1, B1, C1 and D1, the theoretical approach according to Ladenburg [53] (Equation (13)) is used. The selected single particle has a diameter of 80 µm. With that, a theoretical terminal particle velocity of = 4.2 mm·s−1 and the Reynolds number = 0.3324 are calculated. This indicates that the particle settles at the beginning of the transition regime between the laminar and turbulent flow. This analytical solution is compared to the results of the simulations concerning the single particle settling in models A1, B1, C1 and D1 in the next section.
The simulation results of the validation cases reveal the particle settling velocity in different model setups described in Section 2.4.2. Figure 11 gives a detailed view on the settling behavior of a single particle in the basic model A1. The images on the diagram illustrate the particle positions and fluid velocity magnitude around the particle at the five characteristic time points marked in the graph. In the beginning (image 1) the particle is accelerated by gravity until is reached (image 2). It settles keeping the terminal velocity constant until the fluid between the particle and the wall starts to get displaced and decelerates the particle (image 4). The particle approximates the wall (image 5) until the impact.
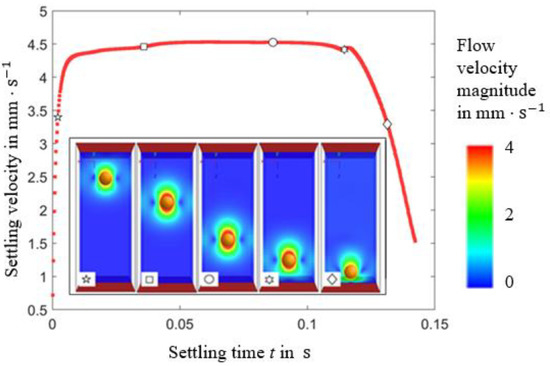
Figure 11.
Particle settling velocity with the corresponding images at characteristic time points of sedimentation obtained in the simulation case A1.
The following Figure 12 compares the simulation case A1 with cases B1, C1 and D1 showing the particle after two milliseconds of sedimentation. The comparison of A1 with B1 shows the influence of voxel size. The comparison A1 with C1 indicates the effect of boundary conditions. Case D1 describes the particle settling onto a filter medium. According to these four cases, Figure 13 compares the particle Reynolds numbers from the beginning of the acceleration until the particle reaches its terminal velocity. The numerical solution of the force balance on the sedimenting particle that included gravity, buoyancy and drag according to Ladenburg is also shown (Figure 13).
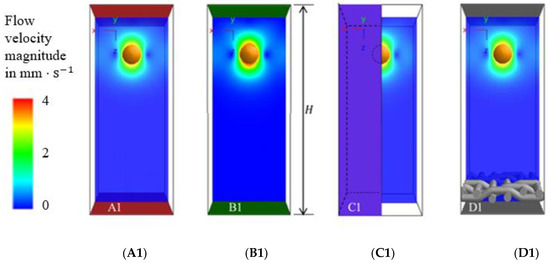
Figure 12.
Particle settling behavior at time 2 ms after it was dropped in different model arrangements, particle diameter = 80 µm, model height = 800 µm, voxel length: (A1) 2 µm, (B1) 4 µm, (C1) 2 µm, (D1) 2 µm.
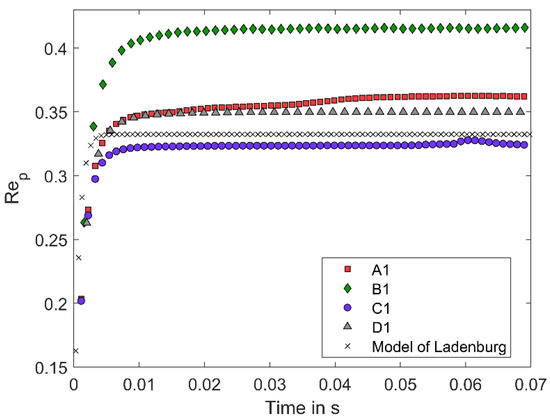
Figure 13.
Particle Reynolds number from simulations A1, B1, C1 and D1 compared to the theoretical sedimentation curve according to Ladenburg.
The particle terminal velocity obtained in the simulation C1 is closest to the terminal velocity calculated with the model of Ladenburg. This is because the model boundary conditions of the case C1 match the conditions of the analytical model of Ladenburg. Model C1 has solid walls on every boundary and represents an isolated single particle in a channel with a square area having an edge length that corresponds to the diameter of Ladenburg’s cylindrical channel. The other simulation cases had periodic boundary conditions and therefore cannot be compared with the model of Ladenburg. Model B1 significantly over predicts the terminal velocity of the particle. This can be explained by the larger voxel sizes in comparison to case A1, which has the same boundary conditions. These simulations showed that to predict the flow around the particle in the studied Reynolds number range, the ratio of the particle size to the voxel size has to be not smaller than 40. The models A1 and D1 only differ in the bottom conditions. Therefore, the velocities at a large distance from the bottom are identical. The particle falling on the solid wall exhibits a slightly larger terminal velocity than on the filter medium.
In suspensions, the mean distance between the particles can characterize the particle concentration. At volume fractions of the dispersed phase in the suspension higher than about 0.05 vol%, the movement of particles is strongly dependent on the concentration [9,10,47]. The settling velocity of two spheres in an infinite fluid depends on the distance between their centers as well as on the flow regime i.e., [9,48]. At higher numbers, especially in the transition regime, the experimental results showed a reduction of the terminal velocity for settling of two spheres with a decrease of their distance [9]. To reproduce this effect in the numerical simulations, the periodic boundary condition is applied in models A1, A2 and A3 and compared to a solid wall boundary in models C1, C2 and C3 respectively. The model width was varied to achieve three different distances from particle to lateral model boundaries. The width of models A1 and C1 was reduced two times (A2, C2) and doubled (A3, C3) respectively (e.g., for A in Figure 14). The periodic lateral boundary conditions in the model cases A allow to study the influence of neighboring particles on the settling behavior as shown in the grayscale images in Figure 14 (A2). The distance between centers of neighboring particles corresponds to the width of the computational domain .
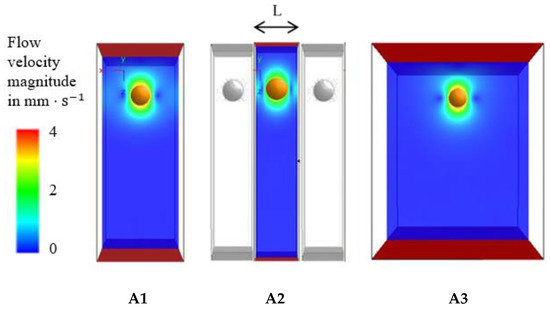
Figure 14.
Variation of the model width and influence of the periodic boundary conditions illustrated as neighboring particles in the grayscale images in A2: (A1) basic model, (A2) narrow channel (half the width of A1), (A3) wider channel (double width of A1), (t = 2 ms).
The resulting particle velocities in different cases are compared in Figure 15a by means of corresponding Reynolds numbers of the particles during the sedimentation process. The effect of the side walls can be explained by the upward flow of displaced fluid in the closed channel. With the decreasing distance of the particle to the walls in the sequence C1, C3 and C2 the Reynolds number or the terminal velocity (Figure 15a) decreases. In cases with the periodic boundary conditions, the presence of neighboring particles settling in parallel reduces also the settling terminal velocity. However, compared to the wall effect at the same distance, the hindrance of the motion because on the particles, the so-called swarm effect in the concentrated suspension, is weaker. Both effects become similar as the distance increases. Comparing the cases A3 and C3 having the same relative distance of 0.125, then both particles move at nearly the same velocity, almost undisturbed by the boundary condition. The effect of the horizontal wall, when the particle approaches the solid bottom can be observed in all cases (Figure 15b). However, this effect is stronger in presence of neighboring particles than in the case of the side walls. The increase of the distance to both these types of neighbors leads to a significant increase in the bottom wall effect. The reduction in settling velocity starts at the larger distances to the bottom wall with the increasing distance to the side neighbors or walls.
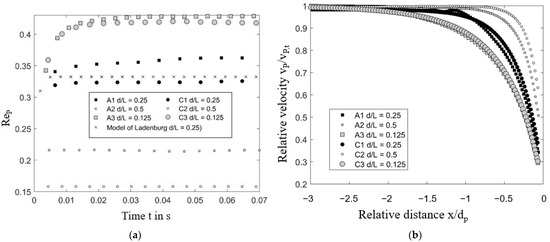
Figure 15.
(a) Influence of model width on the settling behavior for different models: with periodic boundaries (A1, A2, A3) and solid wall boundaries (C1, C2, C3), as well as theoretical approach according to Ladenburg. (b) Ratio of the particle velocity () to the maximum velocity (terminal velocity ) depending on the ratio of the distance to wall and particle diameter dp.
The studied case of the particles moving in parallel is complemented with another interaction that can occurs in settling suspensions when the particles follow one another settling in a row. For this, the case A1 that has periodic boundary conditions on the side walls was extended with two (in A4) and three (in A5) particles respectively (Figure 16). In case A4, particle 1 is generated at the same position as in the single particle simulation (A1), the upper particle 2 is created at an initial distance of (distance between the particle centers). In case A5 with three particles, particle 3 is located between particles 1 and 2, the particle centers have a distance of .
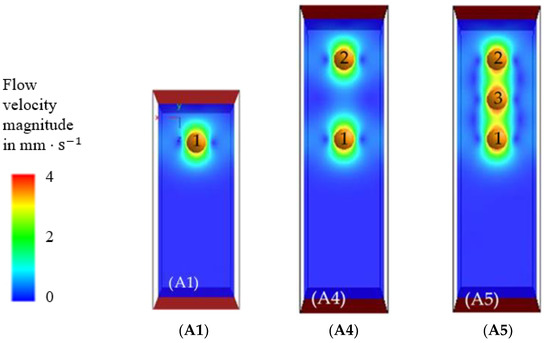
Figure 16.
Variation of number and distance between particles settling in a row. Particle 1 has the same initial position in all simulations. Particle 2 has the same position in A4 and A5. (A1) basic model, (A4) basic model enlarged in height with one additional particle, (A5) basic model enlarged in height with two additional particles, (t = 2 ms).
The change of the vertical position of each particle during settling time is compared in Figure 17a. When the position is zero, the particle would collide at the bottom wall. As seen in the curves, the second particle from the bottom wall (P2 in A4 and P3 in A5) collides on the first particle (P1 in A4 and A5), are decelerated and not rebounded because of the fluid influence, then the second particles roll over the first particle and then hit the bottom wall later. The single particle (A1) is moving with the lowest vertical velocity (Figure 17b). The more particles are sedimenting, the faster each one of them is moving. In simulation A4, the two particles with an initial distance of 4 reach nearly the same velocity. The particle P1(A4) hits the bottom wall, particle P2(A4) collides with the first particle and gets decelerated, then it gets accelerated on the way over the first particle until it hits the bottom wall. In the simulation case A5 with three particles, the particles reach the highest velocities. The particle P3(A5) moving in between P1(A5) and P2(A5) is the fastest particle. It collides onto P1(A5) and then is subjected to a collision by P2(A5) from above.
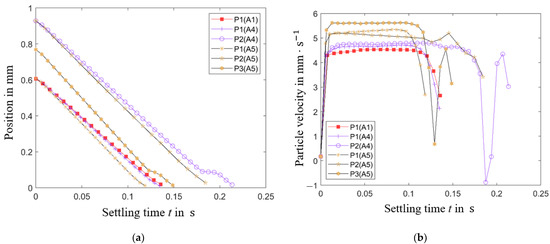
Figure 17.
Influence of the neighboring particles following one another on the settling behavior: (a) vertical distance of the particle to the bottom wall over settling time, (b) particle vertical velocity component (in z-direction) over time.
3.3. Simulation of the Filtration Process
The numerical 3D CFD-DEM simulation of the filtration process was performed with the parameters described in Section 2.5. The process time of 98 ms was simulated. Figure 18 illustrates the instantaneous fluid velocities and particle positions obtained by the numerical computations.
- In (a) the filter medium model is shown before the particle generation.
- In (b) the calculated flow velocities and the initial particle positions are shown at the beginning of the filtration when the first particles are reaching the filter medium and the fluid passes through the filter medium. The local flow velocity maxima in the area of the pores can be seen. Accordingly, the time-dependent filtrate velocity (Figure 19a) shows a maximum before this point of time because of the minimum pressure loss that is determined only by the filter medium.
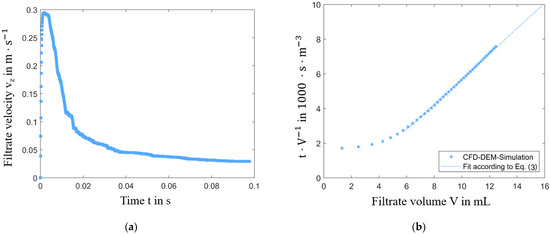 Figure 19. (a) Time-dependent filtrate velocity and (b) filter curve obtained with CFD-DEM simulation and described by filter equation in Equation (3).
Figure 19. (a) Time-dependent filtrate velocity and (b) filter curve obtained with CFD-DEM simulation and described by filter equation in Equation (3). - In (c) it can be seen that some particles are already clogging the pores of the filter medium, which leads to the increase of the pressure drop and the resulting decrease of the filtrate volume flow.
- In (d) the further filter cake formation process at the real time of 98 ms is shown. The filter cake height reaches 0.5 mm. It can be seen in Figure 20 that at this time point 145 particles have already been deposited in the filter cake and the other 16 generated particles are still settling. The particles in the filter cake do not remain fixed, some of them move slowly resulting in a reorganization and packing of the filter cake. These cake formation micro processes take place due to fluid flow, gravitation and contact forces between the particles.
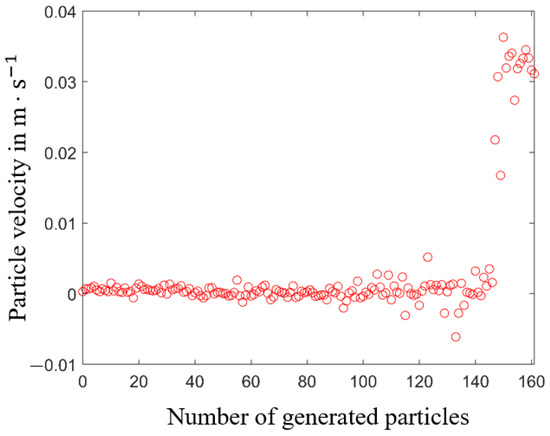 Figure 20. Particle velocities at the time point of 98 ms.
Figure 20. Particle velocities at the time point of 98 ms.

Figure 18.
CFD-DEM simulation of the filtration process with the woven wire cloth filter medium (a) filter medium model, before the process starts at = 0 ms, (b) inflowing suspension at = 3.9 ms, (c) particles are retained by the filter medium = 40 ms, (d) filter cake formation at = 98 ms.
The filtrate velocity drastically decreases, when the particles reach the filter medium and the pore clogging begins at 3.9 ms of filtration time (Figure 19a). After 98 ms of filtration, the filtrate velocity is nearly constant. Figure 19b represents the simulation results concerning the time-dependent filtrate volume V in the form of the linear filter Equation (3). The graph within the first 2 mL of filtrate volume represents the pure fluid running through the medium. The resulting pure filter media resistance is = 3.4·106 m−1. After the particle-free fluid flow through the filter, the slope of the curve increases and after 6 mL of filtrate volume becomes linear. When the linear section of the graph begins, the linear fit represents the specific filter cake resistance. The slope of it according to Equation (3) leads to the specific filter cake resistance of = 7.8·1010 m−2 (Figure 19b).
3.4. Comparison of Simulation and Experiment
The results of the simulation describe the beginning of the filtration and filter cake formation. In the simulations a filtration of 161 particles was performed. To compare with the experimental results (significant higher number of particles and higher filter cakes), the linear fit of the calculated filter curve was extended to the experimentally obtained filtrate volume. The experimentally obtained and calculated filter curves are compared in Figure 21.
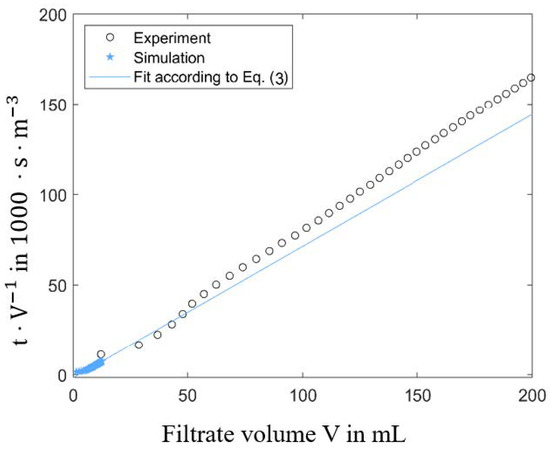
Figure 21.
Comparison of experimentally obtained and calculated filtration curves.
The fitted linear slope of the simulated filtration curve shows a good agreement with the experimental data. The specific filter cake resistance obtained with the simulation = 7.8·1010 m−2 matches the experimental value of = 7.7·1010 m−2. The experimentally obtained values of were in the range between 2.1·106 m−1 and 3.9·106 m−1, which is in good agreement with the simulation results of = 3.4·106 m−1.
4. Conclusions
In this work, a numerical model of the cake filtration process was developed based on the resolved coupling of CFD and DEM methods. This model describes the interactions between particles, particles with the filter medium, and particles with the flow due to the implementation of LBM for solving the Navier-Stokes equations in a fine voxel grid. The developed CFD-DEM coupling was investigated by means of the different particle sedimentation test cases, which can be described with empirical equations. The influence of the side walls in the closed container on the particle settling behavior could be predicted with the empirical model. The CFD-DEM resolved coupling can also reproduce the effect of the bottom wall. The simulation predicts the influence of the neighboring particles resulting in increasing settling velocity with the adding of particles in a row and reducing distances between the particles. As expected the prediction of the settling velocity can be improved by the choice of a smaller voxel length. It was found that at the ratio of particle diameter and voxel length of 40, the fluid-particle interactions can be predicted accurately.
The resulting filter medium and filter cake resistances from the cake filtration simulations are in good agreement with the results obtained by pressurized housing experiments. The simulation was performed only for the beginning of the filtration. This small period of time can hardly be obtained in experimental investigations, and the numerical investigations allow to resolve the micro processes between particles, medium and fluid during filter cake formation.
The performed comparison between 3D simulation and experimental investigation demonstrates a great potential of resolved CFD-DEM coupling for analyzing and optimizing cake filtration processes.
Author Contributions
V.P.: Conceptualization, methodology, data curation, visualization, validation, investigation, formal analysis, writing—original draft preparation writing—review and editing; K.S.: Methodology, formal analysis, writing—review and editing, software S.A.: Methodology, formal analysis, writing—review and editing resources, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a research scholarship for junior researcher donated by the Technische Universität Kaiserslautern (TUK) embedded in the emphasis of the Research Initiative “MathApp” of the Federal State of Rhineland-Palatinate.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ripperger, S.; Gösele, W.; Alt, C.; Loewe, T. Filtration, 1. Fundamentals. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2013; pp. 1–38. ISBN 1435-6007. [Google Scholar] [CrossRef]
- Hund, D.; Lösch, P.; Kerner, M.; Ripperger, S.; Antonyuk, A. CFD-DEM study of bridging mechanisms at the static solid-liquid surface filtration. Powder Technol. 2020, 600–609. [Google Scholar] [CrossRef]
- Hund, D.; Schmidt, K.; Ripperger, S.; Antonyuk, S. Direct numerical simulation of cake formation during filtration with woven fabrics. Chem. Eng. Res. Des. 2018, 139, 26–33. [Google Scholar] [CrossRef]
- Lösch, P.; Nikolaus, K.; Antonyuk, S. Fractionating of finest particles using cross-flow separation with superimposed electric field. Sep. Purif. Technol. 2021, 257, 117820. [Google Scholar] [CrossRef]
- Kerner, M.; Schmidt, K.; Hellmann, A.; Schumacher, S.; Pitz, M.; Asbach, C.; Ripperger, S.; Antonyuk, S. Numerical and experimental study of submicron aerosol deposition in electret microfiber nonwovens. J. Aerosol Sci. 2018, 122, 32–44. [Google Scholar] [CrossRef]
- Kerner, M.; Schmidt, K.; Schumacher, S.; Puderbach, V.; Asbach, C.; Antonyuk, S. Evaluation of electrostatic properties of electret filters for aerosol deposition. Sep. Purif. Technol. 2020, 239, 116548. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Tafreshi, H.V. 3-D simulation of particle filtration in electrospun nanofibrous filters. Powder Technol. 2010, 201, 153–160. [Google Scholar] [CrossRef]
- Brauer, H. Grundlagen der Einphasen- und Mehrphasenströmungen; Sauerländer: Aarau, Switzerland, 1971. [Google Scholar]
- Sommerfeld, M.; Horender, S. Fluid Mechanics. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Wakeman, R. The influence of particle properties on filtration. Sep. Purif. Technol. 2007, 58, 234–241. [Google Scholar] [CrossRef]
- Anlauf, H. Wet Cake Filtration: Fundamentals, Equipment, Strategies; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2020; ISBN 3527346066. [Google Scholar]
- Hieke, M.; Nirschl, H. Einfluss der Salzkonzentration auf das rheologische Verhalten wässriger anorganischer Suspensionen bei der Filtration. Chem. Ing. Tech. 2007, 79, 1939–1944. [Google Scholar] [CrossRef][Green Version]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Guo, Y.; Curtis, J.S. Discrete Element Method Simulations for Complex Granular Flows. Annu. Rev. Fluid Mech. 2015, 47, 21–46. [Google Scholar] [CrossRef]
- Pöschel, T.; Schwager, T. Computational Granular Dynamics: Models and Algorithms; Springer: Berlin, Germany, 2005; ISBN 9783540277200. [Google Scholar]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM Modelling of Non-spherical Particulate Systems: Theoretical Developments and Applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Antonyuk, S.; Khanal, M.; Tomas, J.; Heinrich, S.; Mörl, L. Impact breakage of spherical granules: Experimental study and DEM simulation. Chem. Eng. Process. Process Intensif. 2006, 45, 838–856. [Google Scholar] [CrossRef]
- Qian, F.; Huang, N.; Lu, J.; Han, Y. CFD–DEM simulation of the filtration performance for fibrous media based on the mimic structure. Comput. Chem. Eng. 2014, 71, 478–488. [Google Scholar] [CrossRef]
- Breuninger, P.; Weis, D.; Behrendt, I.; Grohn, P.; Krull, F.; Antonyuk, S. CFD–DEM simulation of fine particles in a spouted bed apparatus with a Wurster tube. Particuology 2019, 42, 114–125. [Google Scholar] [CrossRef]
- Riefler, N.; Ulrich, M.; Morshäuser, M.; Fritsching, U. Particle penetration in fiber filters. Particuology 2018, 40, 70–79. [Google Scholar] [CrossRef]
- Volk, A.; Ghia, U.; Stoltz, C. Effect of grid type and refinement method on CFD-DEM solution trend with grid size. Powder Technol. 2017, 311, 137–146. [Google Scholar] [CrossRef]
- Vångö, M.; Pirker, S.; Lichtenegger, T. Unresolved CFD–DEM modeling of multiphase flow in densely packed particle beds. Appl. Math. Model. 2018, 56, 501–516. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD–DEM simulation of fluid–particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Deshpande, R.; Antonyuk, S.; Iliev, O. Study of the filter cake formed due to the sedimentation of monodispersed and bidispersed particles using discrete element method-computational fluid dynamics simulations. AIChE J. 2019, 65, 1294–1303. [Google Scholar] [CrossRef]
- Deshpande, R. Investigation of the Filter Cake Formation Process using DEM-CFD Simulation with Experimentally Calibrated Parameters; Fraunhofer Verlag: Stuttgart, Germany, 2019; ISBN 3839615194. [Google Scholar]
- Joseph, G.G.; Zenit, R.; Hunt, M.L.; Rosenwinkel, A.M. Particle–wall collisions in a viscous fluid. J. Fluid Mech. 2001, 433, 329–346. [Google Scholar] [CrossRef]
- Heuzeroth, F.; Fritzsche, J.; Werzner, E.; Mendes, M.A.A.; Ray, S.; Trimis, D.; Peuker, U.A. Viscous force—An important parameter for the modeling of deep bed filtration in liquid media. Powder Technol. 2015, 283, 190–198. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Z.L.; Mi, J.C. Drafting, kissing and tumbling process of two particles with different sizes. Comput. Fluids 2014, 96, 20–34. [Google Scholar] [CrossRef]
- Krause, M.J.; Klemens, F.; Henn, T.; Trunk, R.; Nirschl, H. Particle flow simulations with homogenised lattice Boltzmann methods. Particuology 2017, 34, 1–13. [Google Scholar] [CrossRef]
- Deen, N.G.; van Sint Annaland, M.; van der Hoef, M.A.; Kuipers, J.A.M. Review of discrete particle modeling of fluidized beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Golshan, S.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N.; Blais, B.; Kuipers, J.A.M. Review and implementation of CFD-DEM applied to chemical process systems. Chem. Eng. Sci. 2020, 221, 115646. [Google Scholar] [CrossRef]
- Cook, B.K.; Noble, D.R.; Williams, J.R. A direct simulation method for particle-fluid systems. Eng. Comput. 2004, 21, 151–168. [Google Scholar] [CrossRef]
- Third, J.R.; Chen, Y.; Müller, C.R. Comparison between finite volume and lattice-Boltzmann method simulations of gas-fluidised beds: Bed expansion and particle–fluid interaction force. Comput. Part. Mech. 2016, 3, 373–381. [Google Scholar] [CrossRef]
- Brumby, P.E.; Sato, T.; Nagao, J.; Tenma, N.; Narita, H. Coupled LBM–DEM Micro-scale Simulations of Cohesive Particle Erosion Due to Shear Flows. Transp. Porous Media 2015, 109, 43–60. [Google Scholar] [CrossRef]
- Zhang, C.; Soga, K.; Kumar, K.; Sun, Q.; Jin, F. Numerical study of a sphere descending along an inclined slope in a liquid. Granul. Matter 2017, 19. [Google Scholar] [CrossRef]
- Li, B.; Zhang, S.-B.; Teng, Z.-Y.; Bian, Y.-M.; Zhang, J.; Ba, X.-Y. Mesoscale simulation and analysis of spouted bed with LBM-DEM four direction coupling. Jisuan Lixue Xuebao/Chin. J. Comput. Mech. 2018, 35, 527–532. [Google Scholar] [CrossRef]
- Xiong, Q.; Madadi-Kandjani, E.; Lorenzini, G. A LBM–DEM solver for fast discrete particle simulation of particle–fluid flows. Contin. Mech. Thermodyn. 2014, 26, 907–917. [Google Scholar] [CrossRef]
- Kuruneru, S.T.W.; Marechal, E.; Deligant, M.; Khelladi, S.; Ravelet, F.; Saha, S.C.; Sauret, E.; Gu, Y. A Comparative Study of Mixed Resolved–Unresolved CFD-DEM and Unresolved CFD-DEM Methods for the Solution of Particle-Laden Liquid Flows. Arch. Comput. Methods Eng. 2019, 26, 1239–1254. [Google Scholar] [CrossRef]
- Rettinger, C.; Rüde, U. A coupled lattice Boltzmann method and discrete element method for discrete particle simulations of particulate flows. Comput. Fluids 2018, 172, 706–719. [Google Scholar] [CrossRef]
- Rettinger, C.; Rüde, U. Dynamic Load Balancing Techniques for Particulate Flow Simulations. Computation 2019, 7, 9. [Google Scholar] [CrossRef]
- Stiess, M. Mechanische Verfahrenstechnik 2; Springer Berlin Heidelberg: Heidelberg, Germany, 1997; ISBN 978-3-662-08599-8. [Google Scholar]
- Tichy, J.W. Zum Einfluss des Filtermittels und der Auftretenden Interferenzen Zwischen Filterkuchen und Filtermittel bei der Kuchenfiltration. Ph.D. Dissertation, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2007. Available online: https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/1856 (accessed on 9 May 2021).
- Verein Deutscher Ingenieure e.V. VDI 2762: Filtrierbarkeit von Suspensionen Bestimmung des Filterkuchenwiderstands. VDI Richtline. In VDI-Handbuch Verfahrenstechnik und Chemieingenieurwesen, Band 5: Spezielle Verfahrenstechniken; Verein Deutscher Ingenieure e.V.: Düsseldorf, Germany, 2010. [Google Scholar]
- Junk, M.; Yong, W.-A. Rigorous Navier-Stokes Limit of the Lattice Boltzmann Equation; Berichte der Arbeitsgruppe Technomathematik (AGTM Report)—243. Available online: https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/1273 (accessed on 9 May 2021).
- Thömmes, G.; Becker, J.; Junk, M.; Vaikuntam, A.K.; Kehrwald, D.; Klar, A.; Steiner, K.; Wiegmann, A. A Lattice Boltzmann Method for Immiscible Multiphase Flow Simulations Using the Level Set Method; Berichte des Fraunhofer ITWM No. 134. 2008. Available online: https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/1989 (accessed on 9 May 2021).
- Gervais, P.-C.; Bémer, D.; Bourrous, S.; Ricciardi, L. Airflow and particle transport simulations for predicting permeability and aerosol filtration efficiency in fibrous media. Chemical Engineering Science 2017, 165, 154–164. [Google Scholar] [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer-Verlag: London, UK, 2019. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Die Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Langston, P.A.; Tüzün, U.; Heyes, D.M. Discrete element simulation of granular flow in 2D and 3D hoppers: Dependence of discharge rate and wall stress on particle interactions. Chem. Eng. Sci. 1995, 50, 967–987. [Google Scholar] [CrossRef]
- Stiess, M. Mechanische Verfahrenstechnik—Partikeltechnologie 1; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-32551-2. [Google Scholar]
- Fidleris, V.; Whitmore, R.L. Experimental Determination of Wall Effect for Spheres Falling Axially in Cylindrical Vessels. British J. Appl. Phys. 1961, 12, 490. [Google Scholar] [CrossRef]
- Brown, P.P.; Lawler, D.F. Sphere Drag and Settling Velocity Revisited. J. Environ. Eng. 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Ladenburg, R. Über den Einfluß von Wänden auf die Bewegung einer Kugel in einer reibenden Flüssigkeit. Ann. Phys. 1907, 328, 447–458. [Google Scholar] [CrossRef]
- Rettinger, C.; Rüde, U. An Efficient Four-Way Coupled Lattice Boltzmann—Discrete Element Method for Fully Resolved Simulations of Particle-Laden Flows. arXiv 2020, arXiv:2003.01490. Available online: https://arxiv.org/pdf/2003.01490 (accessed on 9 May 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).