Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells
Abstract
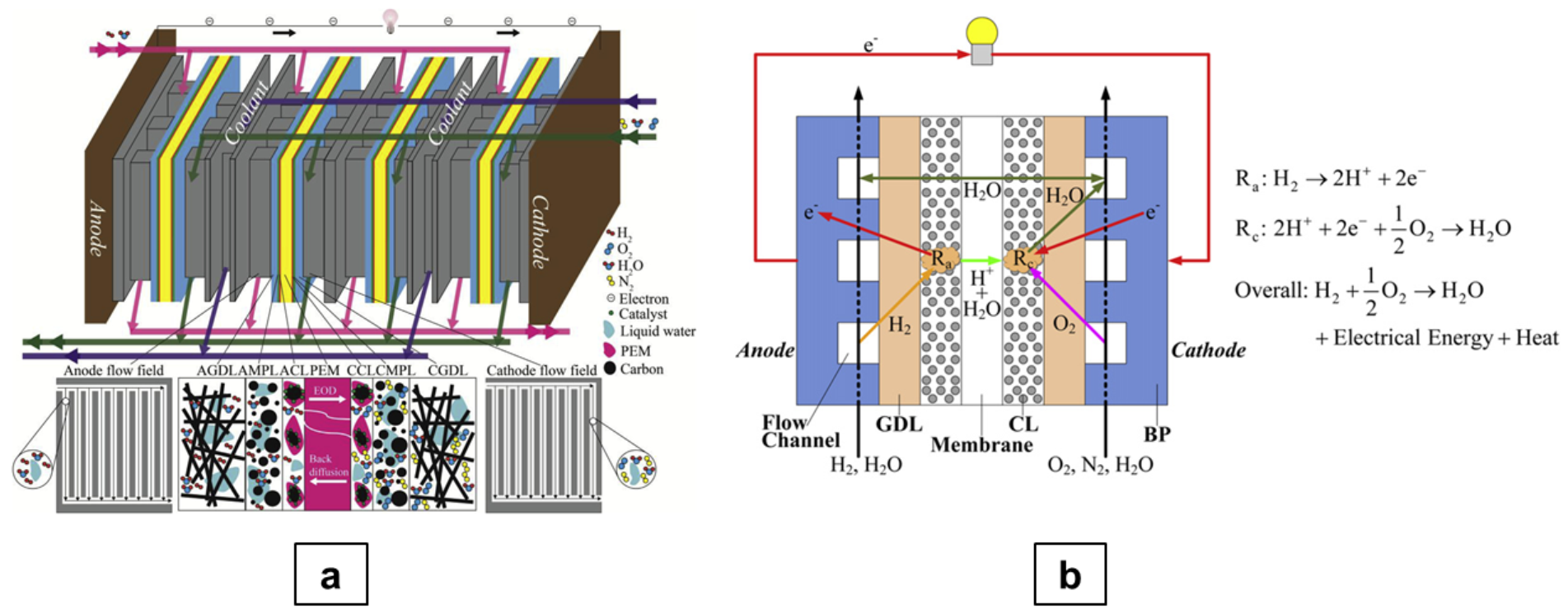
1. Introduction
2. Electrochemistry
3. Modelling Methods for CFD Simulation of PEM Fuel Cells
3.1. Governing Equations
- Laminar: A common assumption in the numerical modelling of PEMFC is the consideration of laminar flows. This hypothesis is well justified by the typical velocity ranges in the gas channels (GC), with Reynolds number , further reduced in porous materials due to flow resistance.
- Steady State: The typical time-scales for PEMFC testing are in the order of minutes, thus justifying the assumption. For this reason, the governing equations presented in this paper are in the steady-state form. However, PEMFC testing cycles [9] and related transient simulations [10] are seeing a growing interest, as well as physical phenomena developing on relatively long time-scales (e.g., finite sorption rates with 100–1000 s [11,12]).
- Multi-physics: All the models aiming at simulating processes in a PEMFC (or in a portion of it) include more than one component. Therefore, solid parts with different physics and macroscopic properties (e.g., GDL, CL and/or BPP) will be present alongside fluid continua, requiring dedicated modifications (source terms, material properties) to each equation.
- Multi-phase: Despite the fact that, in the following part of this section, a so-called single-phase approach will be presented, this is to be intended for fluid modelling in GC, GDL and CL. The dissolved water in the membrane (i.e., its presence in isolated clusters of molecules) is always accounted for, therefore introducing more than a single water phase in the simulation.
- Macro-homogeneous: All cell-scale models express the morphological/structural characteristics of solid parts via averaged (or effective) quantities, e.g., porosity, tortuosity, thermal/electrical conductivity, etc. With particular regard to porous parts (GDL and CL), the real fibrous structure is not directly modelled, and its effect is replaced by the use of calibrated integral properties. This allows great computational efficiency when simulating cell/stack domains.
3.1.1. Mixture Multi-Phase (MMP)
3.1.2. Eulerian Multi-Phase (EMP)
3.1.3. Volume of Fluid (VOF)
3.2. Boundary Conditions
3.3. Gas Diffusion Layers: Key Modelling Aspects
3.3.1. Porosity
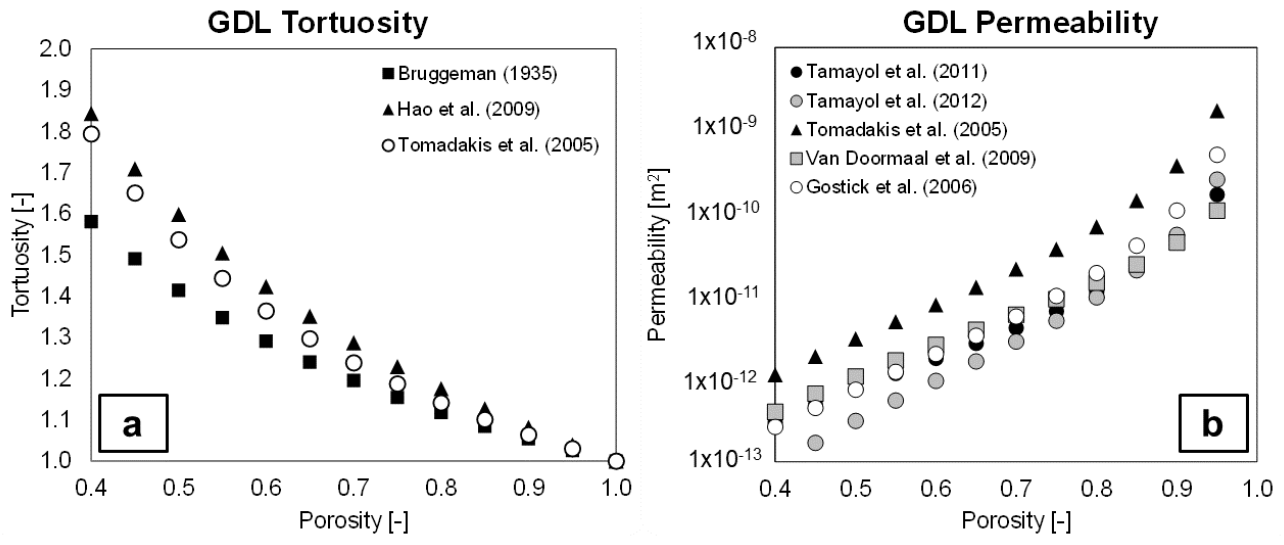
3.3.2. Tortuosity
3.3.3. Permeability
3.3.4. Thermal Conductivity and Thermal Contact Resistance
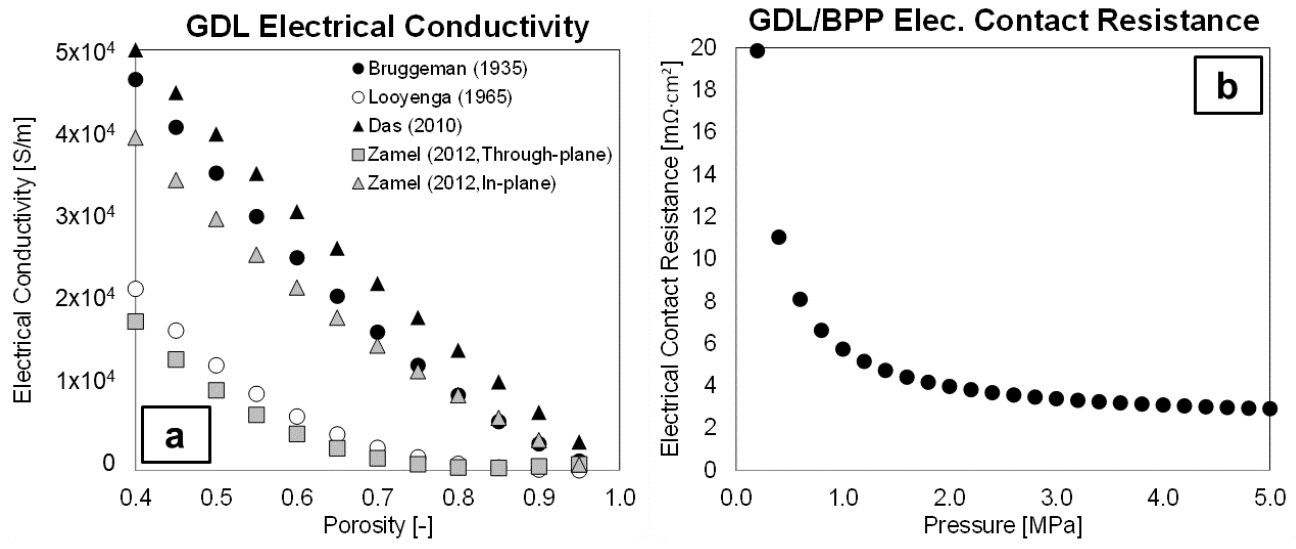
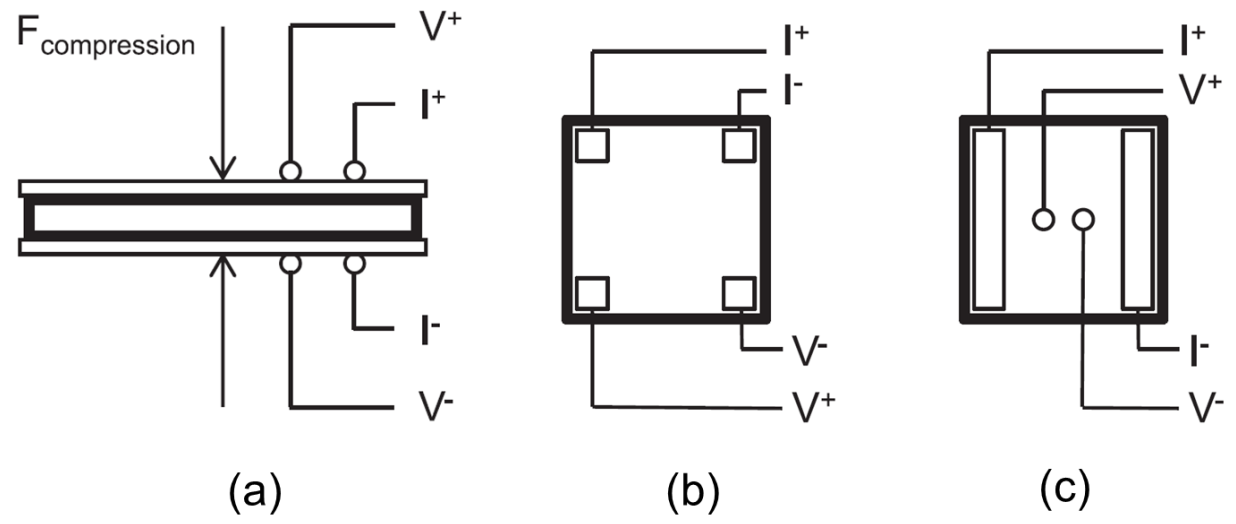
3.3.5. Electrical Conductivity and Electrical Contact Resistance
3.3.6. Compression Effect
3.4. Polymeric Membrane: Key Modelling Aspects
3.4.1. Diffusive Model
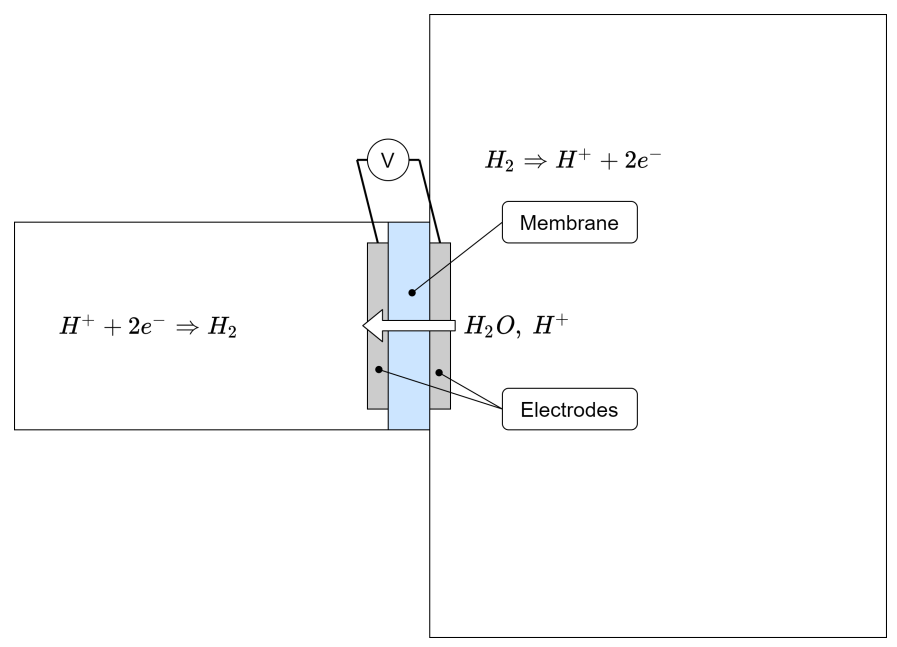
- H+ transport influences H2O transport via a mechanism called electro-osmotic drag. The entity of it depends on the membrane hydration itself. It is included in simulations via a dedicated coefficient, although a large uncertainty on it is a potential source of inaccuracy.
- HO influences H+ transport via increasing the protonic conductivity with its presence, thus facilitating the H+ migration through the polymer chain charged sites (SO3−) via multiple mechanisms (direct/vehicular/hopping mechanisms).
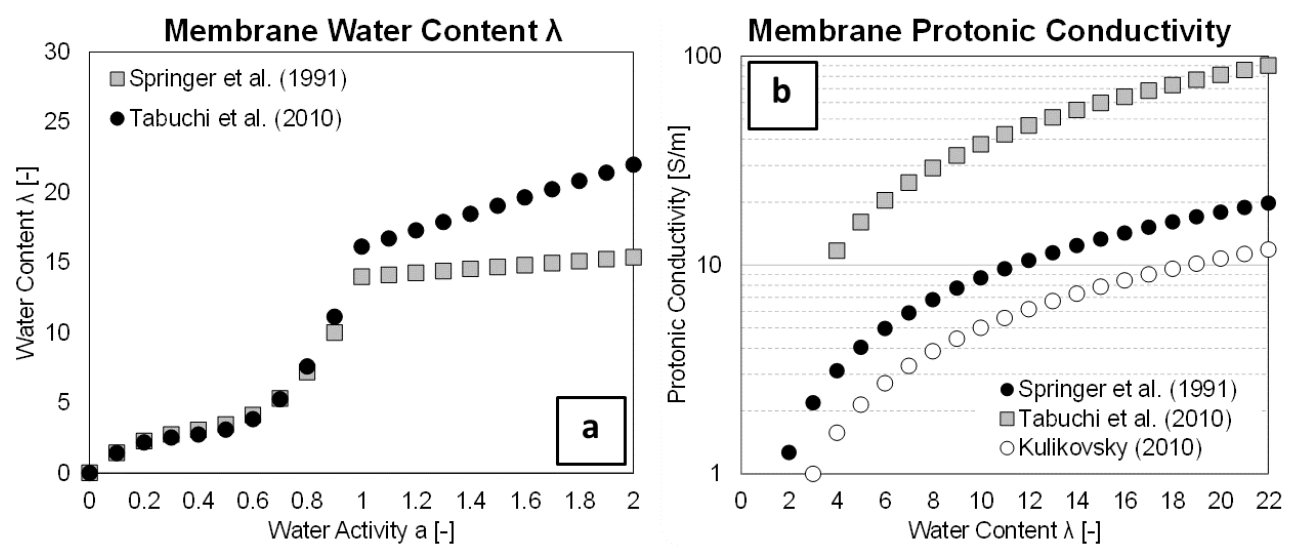
3.4.2. Membrane Water Content
3.4.3. Proton Transport in Membrane
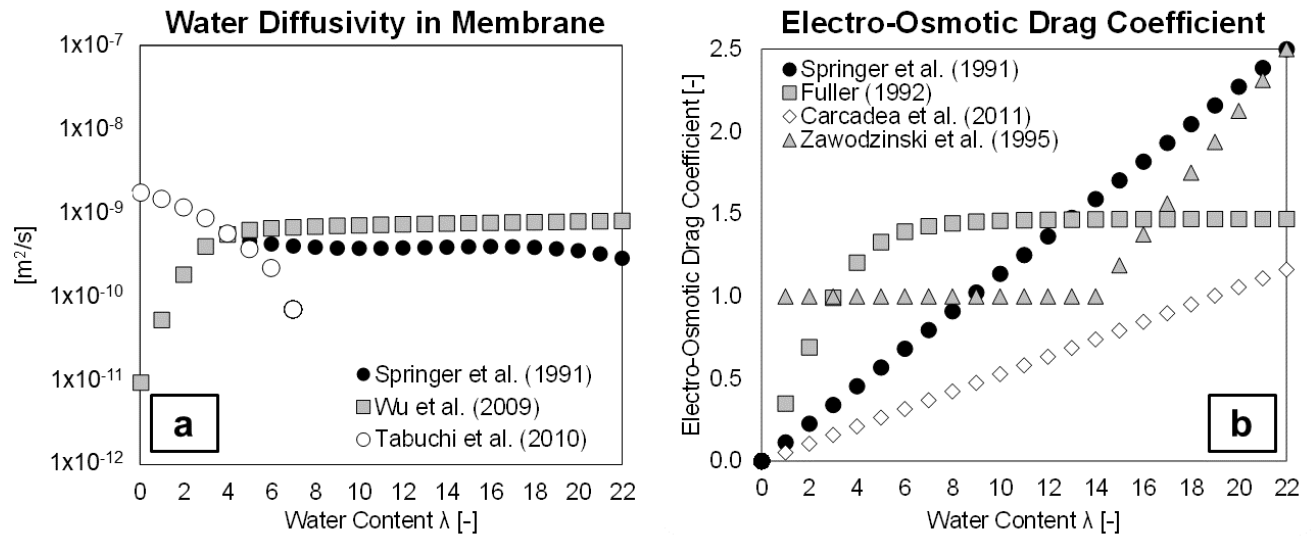
3.4.4. Water Transport in Membrane
3.5. Catalyst Layers: Key Modelling Aspects
3.5.1. Modelling Approaches for CL
- Ultra-thin layer model: It is the simplest approach, consisting of neglecting the CL thickness and representing it with an infinitely thin surface where reactions take place as interfacial processes at the contact between membrane and GDL. Clearly, this approach is computationally very efficient and consequently attractive for the simulation of an entire cell. On the other hand, it prevents the analysis of the phenomena occurring within the catalyst layer and the role of the microstructure on cell performance. Berning and Djilali [86] used this model to analyse the effects of different parameters (e.g., GDL porosity and thickness) on the cell performance. However, note that this way to model the CL lead to an overestimation of the current density.
- Macro-homogeneous model (also called pseudo-homogeneous model): Similar to the GDL macro-homogeneous approach previously presented, it is a more accurate approach for CL modelling as it considers the finite CL thickness, with averaged transport coefficients describing the effect of variations in compositional parameters describing platinum catalyst, carbon support, solid GDL matrix and electrolyte materials [87]. However, it cannot assess the complex multi-material structure of the CL.
- Agglomerate model: It is the most complex and sophisticated approach, including both the composition and the structural distribution of CL materials. Generally, in this type of approach the CL is composed by agglomerates, each of them presenting ionomer and Pt/C particles. Agglomerate models results agree with experimental observations showing that a CL is composed by the agglomeration of catalyst particles (Pt and C) and an ionomer [88]. There are two types of pores, primary and secondary: the former are the internal pores within the agglomerates, while the latter are between the different agglomerates. The primary pores inside the agglomerate could be filled by an ionomer phase, as in the model presented in [88]. In this case, within these pores the diffusion of the reactants is permitted only in the dissolved phase, whereas the secondary pores may be partially or fully filled with liquid water. Each agglomerate has a radius and may be covered with an ionomer film of uniform thickness. Another agglomerate model is the one presented by Xing [89], where the generated liquid water occupies the void spaces of both the primary and secondary pores, reducing the void space. The generated liquid water is initially formed inside the primary pores, partially occupying the space until it fills them completely. When the primary pores are fully filled, the liquid water fills the secondary pores as a thin film surrounding the carbon agglomerate. This means that the presence of liquid water in the secondary pores depends on the filling of the primary pores. The effective species diffusivity in the primary pores will therefore be composed of the diffusivity through (I) the ionomer phase, (II) the liquid phase and (III) the void space, whereas the effective species diffusivity in the secondary pores will depend on the volume fraction of liquid.
3.5.2. Electrochemistry Modelling in CL
3.5.3. Dissolved Water Treatment in CL
3.5.4. Heat Generation in CL
4. Validation Techniques for CFD Simulation of PEM Fuel Cells
4.1. Measurement Techniques for Fuel Cell Stacks
4.1.1. Gas Composition Anode/Cathode
Infrared Spectroscopy
Mass Spectrometer
Gas Chromatography
Colorimetric Tubes
4.1.2. Liquid Water Content
Transparent Cell
Neutron Imaging
X-ray Imaging
Magnetic Resonance Imaging
Raman Spectroscopy
4.1.3. Current Density Distribution
Printed Circuit Board (PCB)
Segmented Cells
Magnetic Resonance
Magnetotomography
4.1.4. Temperature Distribution
Infrared Thermography
Micro-Thermocouples
In-Fibre Bragg Grating (FBG) Sensors
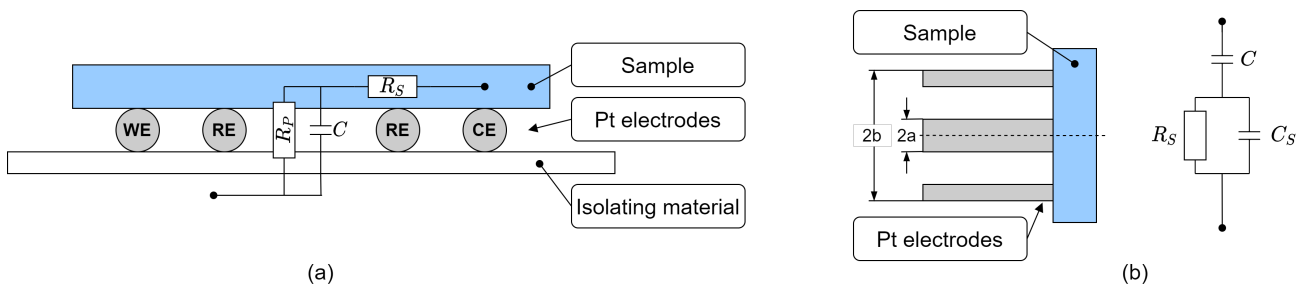
4.2. Measurement Techniques for Material Parameters
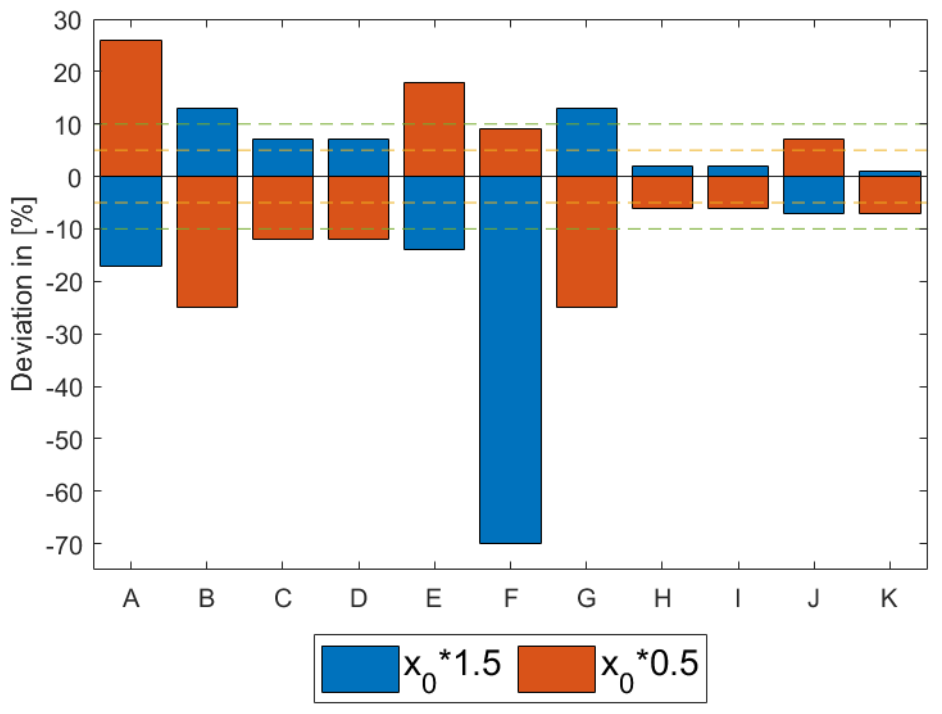
- high impact: current density deviates by more than 10% (absolute) or
- medium impact: current density deviates between 5% to 10% (absolute)
- (A)
- Membrane thickness
- (B)
- Membrane ionic conductivity
- (C)
- Cathode CL thickness
- (D)
- Cathode CL exchange current density
- (E)
- GDL thickness
- (F)
- GDL porosity
- (G)
- GDL electrical conductivity
- (H)
- Membrane sulfonic acid group concentration
- (I)
- Membrane water diffusion coefficient
- (J)
- Cathode CL transfer coefficient
- (K)
- GDL contact angle
4.2.1. Thickness Measurement
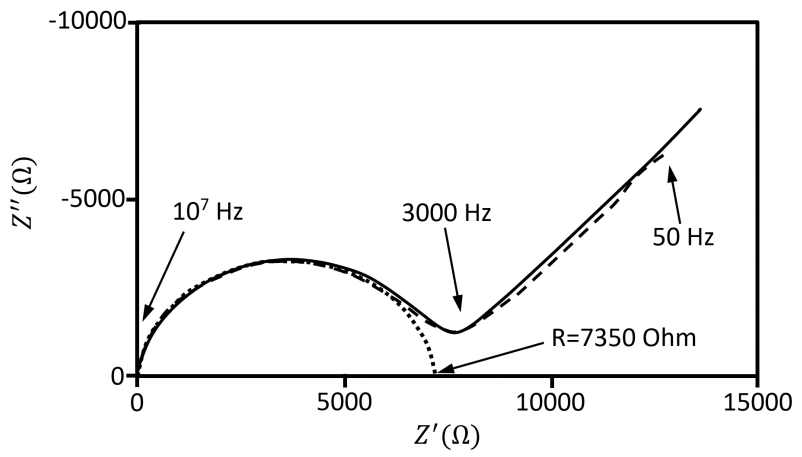
4.2.2. Ionic Conductivity
4.2.3. Water Diffusion Coefficient/Electro-Osmotic Drag Coefficient
4.2.4. Ion-Exchange Capacity
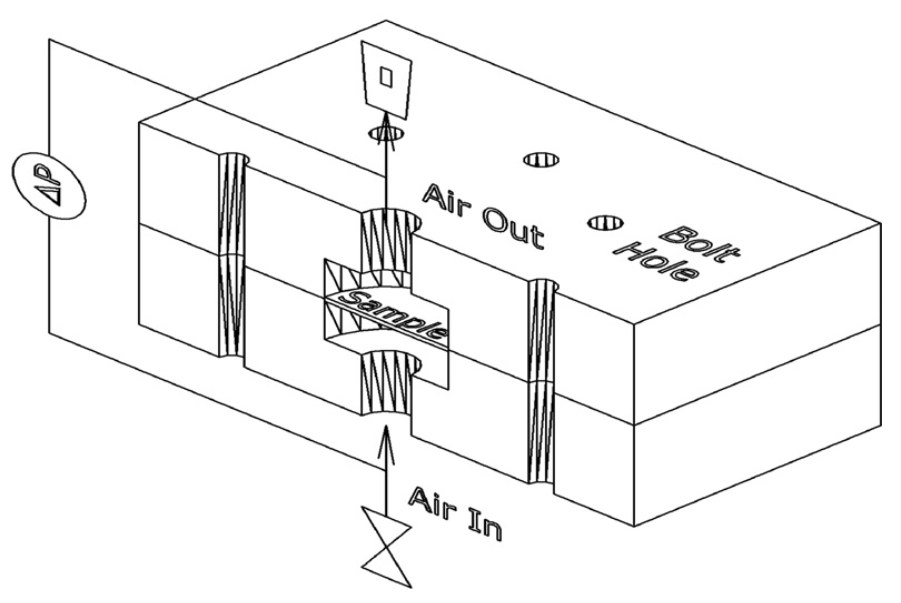
4.2.5. Porous Media Characterisation
Permeability/Porosity
- (1)
- (2)
- (3)
Electrical Conductivity
4.2.6. (Reference) Exchange Current Density
5. Conclusions
- In the first block, the most common modelling approaches for the simulation of fluid/heat/charge transport in PEMFC are presented, namely, the Mixture Multi-Phase (MMP), the Eulerian Multi-Phase (EMP) and the Volume of Fluid (VOF). The multi-part and multi-physics feature of PEMFC and the ubiquitous effect of water transport and phase-change on all the concurring phenomena are the pillars of all the mentioned methods, and their inclusion in model equations is elucidated. Then, a component-based analysis of key properties for multidimensional modelling of GDL, membrane and CL are provided, and the most common correlations from the literature are presented and discussed.
- In the second part, the most advanced measuring methods to measure fluid properties (e.g., gas composition and liquid water content), electrical variables (e.g., current distribution) and material characterisation (e.g., permeability and conductivity) are presented. The variety of the surveyed techniques renders the complexity of the problem and testifies how insufficient is PEMFC testing only based on cell polarisation curves.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACL | Anode Catalyst Layer |
| BPP | Bipolar Plate |
| CL | Catalyst Layer |
| CCL | Cathode Catalyst Layer |
| CCM | Catalyst-Coated Membrane |
| CFD | Computational Fluid Dynamics |
| CCM | Catalyst-Coated Membrane |
| ECR | Electrical Contact Resistance |
| EIS | Electrochemical Impedance Spectroscopy |
| EMP | Eulerian Multi-Phase |
| EW | Equivalent Weight |
| FC | Fuel Cell |
| FRA | Frequency Response Analyzer |
| FTIR | Fourier Transform Infrared Spectroscopy |
| GC | Gas Channels |
| GDL | Gas Diffusion Layer |
| HOR | Hydrogen Oxidation Reaction |
| HT-PEMFC | High-Temperature PEMFC |
| IEC | Ion Exchange Capacity |
| IP | In-Plane |
| LSC | Long Side Chain |
| MEA | Membrane Electrode Assembly |
| MMP | Mixture Multi-Phase |
| MPL | Micro-Porous Layer |
| NMR | Nuclear Magnetic Resonance |
| OCV | Open Circuit Voltage |
| ORR | Oxygen Reduction Reaction |
| PCB | Printed Circuit Board |
| PEM | Polymer Electrolyte Membrane |
| PFSA | Perfluoronated Sulfonic Acid |
| RH | Relative Humidity |
| SEM | Scanning Electron Microscopy |
| SSC | Short Side Chain |
| STM | Scanning Transmission X-ray Microscopy |
| TCR | Thermal Contact Resistance |
| TP | Through-Plane |
| TPB | Triple-Phase Boundary |
| VOF | Volume Of Fluid |
| XCT | X-ray Computed Tomography |
| a | Activity [-] |
| Volume Fraction [-] | |
| Anodic/Cathodic Transfer Coefficient [-] | |
| c | Species Concentration [kmol/m] |
| D | Diffusion Coefficient [m/s] |
| d | Fiber Diameter [m] |
| Porosity [-] | |
| F | Faraday Constant |
| h | Latent Heat of Evaporation [J/kg] |
| j | Volumetric Current Density [A/m] |
| k | Thermal Conductivity [W/m/K] |
| Electric Conductivity [S/m] | |
| K | Absolute Permeability [m] |
| Water Content [-] | |
| M | Molecular Weight [kg/mol] |
| Molecular Viscosity [Pa s] | |
| Electro-Osmotic Drag Coefficient [-] | |
| Electrical Potential [V] | |
| Solid Volume Fraction [-] | |
| Density [kg/m] | |
| S | Source Term |
| s | Liquid Water Volume Fraction [-] |
| Ionic Conductivity [S/m] | |
| Tortuosity [-] | |
| Mobility [m mol/s/J] | |
| Velocity Vector [m/s] | |
| x | Mole Fraction [-] |
| Y | Mass Fraction [-] |
| Specific Active Surface Area [1/m] |
| a | Anode |
| c | Cathode |
| e | Electrolyte |
| Effective | |
| g | Gas |
| l | Liquid |
| m | Membrane |
| Mixture | |
| Reversible | |
| s | Solid |
References
- European Commission. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions: The European Green Deal; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- European Parliament. Regulation (EU) 2019/631 of the European Parliament and of the Council: Setting CO2 Emission Performance Standards for New Passenger Cars and for New Light Commercial Vehicles, and Repealing Regulations (EC) No 443/2009 and (EU) No 510/2011; European Parliament: Bruxelles, Belgium, 2019. [Google Scholar]
- Bethoux, O. Hydrogen Fuel Cell Road Vehicles: State of the Art and Perspectives. Energies 2020, 13, 5843. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Multi-phase models for water and thermal management of proton exchange membrane fuel cell: A review. J. Power Sources 2018, 391, 120–133. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Bernardi, D.M. A Mathematical Model of the Solid-Polymer-Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477. [Google Scholar] [CrossRef]
- Berning, T.; Djilali, N. A 3D, Multiphase, Multicomponent Model of the Cathode and Anode of a PEM Fuel Cell. J. Electrochem. Soc. 2003, 150, A1589. [Google Scholar] [CrossRef]
- Höflinger, J.; Hofmann, P.; Geringer, B. Experimental PEM-Fuel Cell Range Extender System Operation and Parameter Influence Analysis; SAE Technical Paper Series; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.Y. Transient analysis of polymer electrolyte fuel cells. Electrochim. Acta 2005, 50, 1307–1315. [Google Scholar] [CrossRef]
- Opekar, F.; Svozil, D. Electric resistance in a Nafion membrane exposed to air after a step change in the relative humidity. J. Electroanal. Chem. 1995, 385, 269–271. [Google Scholar] [CrossRef]
- Satterfield, M.B.; Benziger, J.B. Non-Fickian water vapor sorption dynamics by Nafion membranes. J. Phys. Chem. B 2008, 112, 3693–3704. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure, 2nd ed.; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Kumbur, E.C.; Sharp, K.V.; Mench, M.M. Validated Leverett Approach for Multiphase Flow in PEFC Diffusion Media. J. Electrochem. Soc. 2007, 154, B1295. [Google Scholar] [CrossRef]
- Ye, Q.; van Nguyen, T. Three-Dimensional Simulation of Liquid Water Distribution in a PEMFC with Experimentally Measured Capillary Functions. J. Electrochem. Soc. 2007, 154, B1242. [Google Scholar] [CrossRef]
- Kumar, R.R.; Suresh, S.; Suthakar, T.; Singh, V.K. Experimental investigation on PEM fuel cell using serpentine with tapered flow channels. Int. J. Hydrog. Energy 2020, 45, 15642–15649. [Google Scholar] [CrossRef]
- Chadha, K.; Martemianov, S.; Thomas, A. Study of new flow field geometries to enhance water redistribution and pressure head losses reduction within PEM fuel cell. Int. J. Hydrog. Energy 2021, 46, 7489–7501. [Google Scholar] [CrossRef]
- Pan, W.; Wang, P.; Chen, X.; Wang, F.; Dai, G. Combined effects of flow channel configuration and operating conditions on PEM fuel cell performance. Energy Convers. Manag. 2020, 220, 113046. [Google Scholar] [CrossRef]
- Dhahad, H.A.; Alawee, W.H.; Hassan, A.K. Experimental study of the effect of flow field design to PEM fuel cells performance. Renew. Energy Focus 2019, 30, 71–77. [Google Scholar] [CrossRef]
- Taccani, R.; Zuliani, N. Effect of flow field design on performances of high temperature PEM fuel cells: Experimental analysis. Int. J. Hydrog. Energy 2011, 36, 10282–10287. [Google Scholar] [CrossRef]
- Chandan, A.; Hattenberger, M.; El-kharouf, A.; Du, S.; Dhir, A.; Self, V.; Pollet, B.G.; Ingram, A.; Bujalski, W. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)—A review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, J.; Tang, Y.; Song, C.; Navessin, T.; Shi, Z.; Song, D.; Wang, H.; Wilkinson, D.P.; et al. High temperature PEM fuel cells. J. Power Sources 2006, 160, 872–891. [Google Scholar] [CrossRef]
- Bose, S.; Kuila, T.; Nguyen, T.X.H.; Kim, N.H.; Lau, K.t.; Lee, J.H. Polymer membranes for high temperature proton exchange membrane fuel cell: Recent advances and challenges. Prog. Polym. Sci. 2011, 36, 813–843. [Google Scholar] [CrossRef]
- Wang, C.Y. Fundamental models for fuel cell engineering. Chem. Rev. 2004, 104, 4727–4765. [Google Scholar] [CrossRef]
- Fuller, T.F.; Newman, J. Water and Thermal Management in Solid–Polymer–Electrolyte Fuel Cells. J. Electrochem. Soc. 1993, 140, 1218–1225. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Berg, P. On the modeling of water transport in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6913–6927. [Google Scholar] [CrossRef]
- Wu, H.W. A review of recent development: Transport and performance modeling of PEM fuel cells. Appl. Energy 2016, 165, 81–106. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y. Three-dimensional analysis of transport and electrochemical reactions in polymer electrolyte fuel cells. J. Power Sources 2004, 125, 40–51. [Google Scholar] [CrossRef]
- D’Adamo, A.; Riccardi, M.; Locci, C.; Romagnoli, M.; Fontanesi, S. Numerical Simulation of a High Current Density PEM Fuel Cell; SAE Technical Paper Series; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Riccardi, M.; d’Adamo, A.; Vaini, A.; Romagnoli, M.; Borghi, M.; Fontanesi, S. Experimental Validation of a 3D-CFD Model of a PEM Fuel Cell. E3S Web Conf. 2020, 197, 05004. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Dutta, S.; Shimpalee, S.; van Zee, J.W. Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell. Int. J. Heat Mass Transf. 2001, 44, 2029–2042. [Google Scholar] [CrossRef]
- Berning, T.; Lu, D.M.; Djilali, N. Three-dimensional computational analysis of transport phenomena in a PEM fuel cell. J. Power Sources 2002, 106, 284–294. [Google Scholar] [CrossRef]
- Ferreira, R.B.; Falcão, D.S.; Oliveira, V.B.; Pinto, A. 1D + 3D two-phase flow numerical model of a proton exchange membrane fuel cell. Appl. Energy 2017, 203, 474–495. [Google Scholar] [CrossRef]
- Pharoah, J.G. On the permeability of gas diffusion media used in PEM fuel cells. J. Power Sources 2005, 144, 77–82. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Shiomi, T.; Aoki, O.; Kubo, N.; Shinohara, K. Effects of heat and water transport on the performance of polymer electrolyte membrane fuel cell under high current density operation. Electrochim. Acta 2010, 56, 352–360. [Google Scholar] [CrossRef]
- Tsukamoto, T.; Aoki, T.; Kanesaka, H.; Taniguchi, T.; Takayama, T.; Motegi, H.; Takayama, R.; Tanaka, S.; Komiyama, K.; Yoneda, M. Three-dimensional numerical simulation of full-scale proton exchange membrane fuel cells at high current densities. J. Power Sources 2021, 488, 229412. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X. Effective transport properties for polymer electrolyte membrane fuel cells—With a focus on the gas diffusion layer. Prog. Energy Combust. Sci. 2013, 39, 111–146. [Google Scholar] [CrossRef]
- Cindrella, L.; Kannan, A.M.; Lin, J.F.; Saminathan, K.; Ho, Y.; Lin, C.W.; Wertz, J. Gas diffusion layer for proton exchange membrane fuel cells—A review. J. Power Sources 2009, 194, 146–160. [Google Scholar] [CrossRef]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Tamayol, A.; Bahrami, M. In-plane gas permeability of proton exchange membrane fuel cell gas diffusion layers. J. Power Sources 2011, 196, 3559–3564. [Google Scholar] [CrossRef]
- Tamayol, A.; McGregor, F.; Bahrami, M. Single phase through-plane permeability of carbon paper gas diffusion layers. J. Power Sources 2012, 204, 94–99. [Google Scholar] [CrossRef]
- Froning, D.; Drakselová, M.; Tocháčková, A.; Kodým, R.; Reimer, U.; Lehnert, W.; Bouzek, K. Anisotropic properties of gas transport in non-woven gas diffusion layers of polymer electrolyte fuel cells. J. Power Sources 2020, 452, 227828. [Google Scholar] [CrossRef]
- Rashapov, R.R.; Unno, J.; Gostick, J.T. Characterization of PEMFC Gas Diffusion Layer Porosity. J. Electrochem. Soc. 2015, 162, F603–F612. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of anisotropic permeabilities in carbon paper gas diffusion layers. J. Power Sources 2009, 186, 104–114. [Google Scholar] [CrossRef]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Tamayol, A.; Bahrami, M. Analytical determination of viscous permeability of fibrous porous media. Int. J. Heat Mass Transf. 2009, 52, 2407–2414. [Google Scholar] [CrossRef]
- Tamayol, A.; Bahrami, M. Parallel Flow Through Ordered Fibers: An Analytical Approach. J. Fluids Eng. 2010, 132. [Google Scholar] [CrossRef]
- van Doormaal, M.A.; Pharoah, J.G. Determination of permeability in fibrous porous media using the lattice Boltzmann method with application to PEM fuel cells. Int. J. Numer. Methods Fluids 2009, 59, 75–89. [Google Scholar] [CrossRef]
- Gostick, J.T.; Fowler, M.W.; Pritzker, M.D.; Ioannidis, M.A.; Behra, L.M. In-plane and through-plane gas permeability of carbon fiber electrode backing layers. J. Power Sources 2006, 162, 228–238. [Google Scholar] [CrossRef]
- Gurau, V.; Bluemle, M.J.; de Castro, E.S.; Tsou, Y.M.; Zawodzinski, T.A.; Mann, J.A. Characterization of transport properties in gas diffusion layers for proton exchange membrane fuel cells. J. Power Sources 2007, 165, 793–802. [Google Scholar] [CrossRef]
- Feser, J.P.; Prasad, A.K.; Advani, S.G. Experimental characterization of in-plane permeability of gas diffusion layers. J. Power Sources 2006, 162, 1226–1231. [Google Scholar] [CrossRef]
- Taira, H.; Liu, H. In-situ measurements of GDL effective permeability and under-land cross-flow in a PEM fuel cell. Int. J. Hydrog. Energy 2012, 37, 13725–13730. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A Criterion for Non-Darcy Flow in Porous Media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Feser, J.P.; Prasad, A.K.; Advani, S.G. On the relative influence of convection in serpentine flow fields of PEM fuel cells. J. Power Sources 2006, 161, 404–412. [Google Scholar] [CrossRef]
- Sadeghi, E.; Bahrami, M.; Djilali, N. Analytic determination of the effective thermal conductivity of PEM fuel cell gas diffusion layers. J. Power Sources 2008, 179, 200–208. [Google Scholar] [CrossRef]
- Sadeghi, E.; Bahrami, M.; Djilali, N. A Compact Thermal Resistance Model for Determining Effective Thermal Conductivity in the Fibrous Gas Diffusion Layers of Fuel Cells. In Heat Transfer: Volume 1; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2008; pp. 439–447. [Google Scholar] [CrossRef]
- Sadeghifar, H.; Bahrami, M.; Djilali, N. A statistically-based thermal conductivity model for fuel cell Gas Diffusion Layers. J. Power Sources 2013, 233, 369–379. [Google Scholar] [CrossRef]
- Dagan, G. Flow and Transport in Porous Formations; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. Effective thermal conductivity and thermal contact resistance of gas diffusion layers in proton exchange membrane fuel cells. Part 1: Effect of compressive load. J. Power Sources 2011, 196, 246–254. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. Effect of Compression on the Effective Thermal Conductivity and Thermal Contact Resistance in PEM Fuel Cell Gas Diffusion Layers. In Volume 7: Fluid Flow, Heat Transfer and Thermal Systems, Parts A and B; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2010; pp. 385–393. [Google Scholar] [CrossRef]
- Khandelwal, M.; Mench, M.M. Direct measurement of through-plane thermal conductivity and contact resistance in fuel cell materials. J. Power Sources 2006, 161, 1106–1115. [Google Scholar] [CrossRef]
- Das, P.K.; Li, X.; Liu, Z.S. Effective transport coefficients in PEM fuel cell catalyst and gas diffusion layers: Beyond Bruggeman approximation. Appl. Energy 2010, 87, 2785–2796. [Google Scholar] [CrossRef]
- Looyenga, H. Dielectric constants of heterogeneous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X.; Shen, J. Numerical estimation of the effective electrical conductivity in carbon paper diffusion media. Appl. Energy 2012, 93, 39–44. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, G.; Shih, A.J.; Hu, S.J. A micro-scale model for predicting contact resistance between bipolar plate and gas diffusion layer in PEM fuel cells. J. Power Sources 2007, 163, 777–783. [Google Scholar] [CrossRef]
- Mishra, V.; Yang, F.; Pitchumani, R. Measurement and Prediction of Electrical Contact Resistance Between Gas Diffusion Layers and Bipolar Plate for Applications to PEM Fuel Cells. J. Fuel Cell Sci. Technol. 2004, 1, 2–9. [Google Scholar] [CrossRef]
- Laedre, S.; Kongstein, O.E.; Oedegaard, A.; Seland, F.; Karoliussen, H. Measuring In Situ Interfacial Contact Resistance in a Proton Exchange Membrane Fuel Cell. J. Electrochem. Soc. 2019, 166, F853–F859. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Song, H.; Wang, S.; Zhou, Y.; Hu, S.J. Estimation of contact resistance in proton exchange membrane fuel cells. J. Power Sources 2006, 162, 1165–1171. [Google Scholar] [CrossRef]
- Mortazavi, M.; Santamaria, A.D.; Chauhan, V.; Benner, J.Z.; Heidari, M.; Médici, E.F. Effect of PEM fuel cell porous media compression on in-plane transport phenomena. J. Power Sources Adv. 2020, 1, 100001. [Google Scholar] [CrossRef]
- Radhakrishnan, V.; Haridoss, P. Effect of GDL compression on pressure drop and pressure distribution in PEMFC flow field. Int. J. Hydrog. Energy 2011, 36, 14823–14828. [Google Scholar] [CrossRef]
- Nitta, I.; Himanen, O.; Mikkola, M. Thermal conductivity and contact resistance of compressed gas diffusion layer of PEM fuel cell. Hels. Univ. Technol. Adv. Energy Syst. 2008, 36, 1–21. [Google Scholar] [CrossRef]
- Nitta, I.; Hottinen, T.; Himanen, O.; Mikkola, M. Inhomogeneous compression of PEMFC gas diffusion layer: Part I. Experimental. J. Power Sources 2007, 171, 26–36. [Google Scholar] [CrossRef]
- Hottinen, T.; Himanen, O.; Karvonen, S.; Nitta, I. Inhomogeneous compression of PEMFC gas diffusion layer: Part II. Modeling the effect. J. Power Sources 2007, 171, 113–121. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, J.; Sundén, B. On electric resistance effects of non-homogeneous GDL deformation in a PEM fuel cell. Int. J. Hydrog. Energy 2017, 42, 28537–28548. [Google Scholar] [CrossRef]
- Ge, J.; Higier, A.; Liu, H. Effect of gas diffusion layer compression on PEM fuel cell performance. J. Power Sources 2006, 159, 922–927. [Google Scholar] [CrossRef]
- Carcadea, E.; Varlam, M.; Ingham, D.B.; Ismail, M.S.; Patularu, L.; Marinoiu, A.; Schitea, D. The effects of cathode flow channel size and operating conditions on PEM fuel performance: A CFD modelling study and experimental demonstration. Int. J. Energy Res. 2018, 42, 2789–2804. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Transport in Polymer-Electrolyte Membranes. J. Electrochem. Soc. 2003, 150, A1008. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Analytical Modeling of Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Fuller, P.T. Solid-Polymer-Electrolyte Fuel Cells; University of California: Berkeley, CA, USA, 1992. [Google Scholar]
- Carcadea, E.; Ingham, D.; Stefanescu, I.; Ionete, R.; Ene, H. The influence of permeability changes for a 7-serpentine channel pem fuel cell performance. Int. J. Hydrog. Energy 2011, 36, 10376–10383. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Davey, J.; Valerio, J.; Gottesfeld, S. The water content dependence of electro-osmotic drag in proton-conducting polymer electrolytes. Electrochim. Acta 1995, 40, 297–302. [Google Scholar] [CrossRef]
- Motupally, S.; Becker, A.J.; Weidner, J.W. Diffusion of Water in Nafion 115 Membranes. J. Electrochem. Soc. 2000, 147, 3171. [Google Scholar] [CrossRef]
- Nguyen, T.V.; White, R.E. A Water and Heat Management Model for Proton–Exchange–Membrane Fuel Cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Quasi-3D Modeling of Water Transport in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2003, 150, A1432. [Google Scholar] [CrossRef]
- Berning, T.; Djilali, N. Three-dimensional computational analysis of transport phenomena in a PEM fuel cell—A parametric study. J. Power Sources 2003, 124, 440–452. [Google Scholar] [CrossRef]
- Khajeh-Hosseini-Dalasm, N.; Kermani, M.J.; Moghaddam, D.G.; Stockie, J.M. A parametric study of cathode catalyst layer structural parameters on the performance of a PEM fuel cell. Int. J. Hydrog. Energy 2010, 35, 2417–2427. [Google Scholar] [CrossRef]
- Khajeh-Hosseini-Dalasm, N.; Fesanghary, M.; Fushinobu, K.; Okazaki, K. A study of the agglomerate catalyst layer for the cathode side of a proton exchange membrane fuel cell: Modeling and optimization. Electrochim. Acta 2012, 60, 55–65. [Google Scholar] [CrossRef]
- Xing, L. An agglomerate model for PEM fuel cells operated with non-precious carbon-based ORR catalysts. Chem. Eng. Sci. 2018, 179, 198–213. [Google Scholar] [CrossRef]
- Carcadea, E.; Varlam, M.; Marinoiu, A.; Raceanu, M.; Ismail, M.S.; Ingham, D.B. Influence of catalyst structure on PEM fuel cell performance—A numerical investigation. Int. J. Hydrog. Energy 2019, 44, 12829–12841. [Google Scholar] [CrossRef]
- Tao, W.Q.; Min, C.H.; Liu, X.L.; He, Y.L.; Yin, B.H.; Jiang, W. Parameter sensitivity examination and discussion of PEM fuel cell simulation model validation. J. Power Sources 2006, 160, 359–373. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, G.; Xuan, J.; Jiao, K. Three-dimensional multi-phase model of PEM fuel cell coupled with improved agglomerate sub-model of catalyst layer. Energy Convers. Manag. 2019, 199, 112051. [Google Scholar] [CrossRef]
- Xing, L.; Liu, X.; Alaje, T.; Kumar, R.; Mamlouk, M.; Scott, K. A two-phase flow and non-isothermal agglomerate model for a proton exchange membrane (PEM) fuel cell. Energy 2014, 73, 618–634. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Srinivasan, S.; Appleby, A.J.; Martin, C.R. Temperature Dependence of the Electrode Kinetics of Oxygen Reduction at the Platinum/Nafion Interface—A Microelectrode Investigation. J. Electrochem. Soc. 1992, 139, 2530–2537. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Song, C.; Xia, Z.; Li, H.; Wang, H.; Zhang, J. PEM fuel cell relative humidity (RH) and its effect on performance at high temperatures. Electrochim. Acta 2008, 53, 5315–5321. [Google Scholar] [CrossRef]
- Sun, W.; Peppley, B.A.; Karan, K. An improved two-dimensional agglomerate cathode model to study the influence of catalyst layer structural parameters. Electrochim. Acta 2005, 50, 3359–3374. [Google Scholar] [CrossRef]
- Song, C.; Tang, Y.; Zhang, J.L.; Zhang, J.; Wang, H.; Shen, J.; McDermid, S.; Li, J.; Kozak, P. PEM fuel cell reaction kinetics in the temperature range of 23–120 °C. Electrochim. Acta 2007, 52, 2552–2561. [Google Scholar] [CrossRef]
- Yuan, X.Z. Electrochemical Impedance Spectroscopy in PEM Fuel Cells: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- O’Hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Boston, MA, USA, 2013. [Google Scholar]
- Revankar, S.T.; Majumdar, P. Fuel Cells: Principles, Design, and Analysis; Mechanical and Aerospace Engineering Series; CRC Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Wang, H.H.; Yuan, X.Z.; Li, H. PEM Fuel Cell Durability Handbook; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Zhang, J.; Zhang, H.; Wu, J. PEM Fuel Cell Testing and Diagnosis; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Miyaoka, H.; Miyaoka, H.; Ichikawa, T.; Ichikawa, T.; Kojima, Y. Highly purified hydrogen production from ammonia for PEM fuel cell. Int. J. Hydrog. Energy 2018, 43, 14486–14492. [Google Scholar] [CrossRef]
- Maass, S.; Finsterwalder, F.; Frank, G.; Hartmann, R.; Merten, C. Carbon support oxidation in PEM fuel cell cathodes. J. Power Sources 2008, 176, 444–451. [Google Scholar] [CrossRef]
- Lim, K.H.; Lee, W.H.; Jeong, Y.; Kim, H. Analysis of Carbon Corrosion in Anode under Fuel Starvation Using On-Line Mass Spectrometry in Polymer Electrolyte Membrane Fuel Cells. J. Electrochem. Soc. 2017, 164, F1580–F1586. [Google Scholar] [CrossRef]
- Shao, Y.; Dodelet, J.P.; Wu, G.; Zelenay, P. PGM-Free Cathode Catalysts for PEM Fuel Cells: A Mini-Review on Stability Challenges. Adv. Mater. (Deerfield Beach Fla.) 2019, 31, e1807615. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Chen, J.; Liu, H.; Yan, C.; Hou, Y.; He, Q.; Zhang, J.; Hissel, D. Anode purge management for hydrogen utilization and stack durability improvement of PEM fuel cell systems. Appl. Energy 2020, 275, 115110. [Google Scholar] [CrossRef]
- David, N.; von Schilling, K.; Wild, P.M.; Djilali, N. In situ measurement of relative humidity in a PEM fuel cell using fibre Bragg grating sensors. Int. J. Hydrog. Energy 2014, 39, 17638–17644. [Google Scholar] [CrossRef]
- Zhao, J.; Jian, Q.; Huang, Z. Visualization study on enhancing water transport of proton exchange membrane fuel cells with a dead-ended anode by generating fluctuating flow at anode compartment. Energy Convers. Manag. 2020, 206, 112477. [Google Scholar] [CrossRef]
- Bozorgnezhad, A.; Shams, M.; Kanani, H.; Hasheminasab, M.; Ahmadi, G. Two-phase flow and droplet behavior in microchannels of PEM fuel cell. Int. J. Hydrog. Energy 2016, 41, 19164–19181. [Google Scholar] [CrossRef]
- Rahimi-Esbo, M.; Ramiar, A.; Ranjbar, A.A.; Alizadeh, E. Design, manufacturing, assembling and testing of a transparent PEM fuel cell for investigation of water management and contact resistance at dead-end mode. Int. J. Hydrog. Energy 2017, 42, 11673–11688. [Google Scholar] [CrossRef]
- Aslam, R.M.; Ingham, D.B.; Ismail, M.S.; Hughes, K.J.; Ma, L.; Pourkashanian, M. Simultaneous thermal and visual imaging of liquid water of the PEM fuel cell flow channels. J. Energy Inst. 2019, 92, 311–318. [Google Scholar] [CrossRef]
- Meyer, Q.; Ashton, S.; Boillat, P.; Cochet, M.; Engebretsen, E.; Finegan, D.P.; Lu, X.; Bailey, J.J.; Mansor, N.; Abdulaziz, R.; et al. Effect of gas diffusion layer properties on water distribution across air-cooled, open-cathode polymer electrolyte fuel cells: A combined ex-situ X-ray tomography and in-operando neutron imaging study. Electrochim. Acta 2016, 211, 478–487. [Google Scholar] [CrossRef]
- Boillat, P.; Lehmann, E.H.; Trtik, P.; Cochet, M. Neutron imaging of fuel cells—Recent trends and future prospects. Curr. Opin. Electrochem. 2017, 5, 3–10. [Google Scholar] [CrossRef]
- Salva, J.A.; Iranzo, A.; Rosa, F.; Tapia, E. Validation of cell voltage and water content in a PEM (polymer electrolyte membrane) fuel cell model using neutron imaging for different operating conditions. Energy 2016, 101, 100–112. [Google Scholar] [CrossRef]
- Coz, E.; Théry, J.; Boillat, P.; Faucheux, V.; Alincant, D.; Capron, P.; Gébel, G. Water management in a planar air-breathing fuel cell array using operando neutron imaging. J. Power Sources 2016, 331, 535–543. [Google Scholar] [CrossRef]
- Chevalier, S.; Ge, N.; George, M.G.; Lee, J.; Banerjee, R.; Liu, H.; Shrestha, P.; Muirhead, D.; Hinebaugh, J.; Tabuchi, Y.; et al. Synchrotron X-ray Radiography as a Highly Precise and Accurate Method for Measuring the Spatial Distribution of Liquid Water in Operating Polymer Electrolyte Membrane Fuel Cells. J. Electrochem. Soc. 2017, 164, F107–F114. [Google Scholar] [CrossRef]
- Patel, V.; Battrell, L.; Anderson, R.; Zhu, N.; Zhang, L. Investigating effect of different gas diffusion layers on water droplet characteristics for proton exchange membrane (PEM) fuel cells. Int. J. Hydrog. Energy 2019, 44, 18340–18350. [Google Scholar] [CrossRef]
- Rahimian, P.; Battrell, L.; Anderson, R.; Zhu, N.; Johnson, E.; Zhang, L. Investigation of time dependent water droplet dynamics on porous fuel cell material via synchrotron based X-ray imaging technique. Exp. Therm. Fluid Sci. 2018, 97, 237–245. [Google Scholar] [CrossRef]
- Banerjee, R.; Ge, N.; Han, C.; Lee, J.; George, M.G.; Liu, H.; Muirhead, D.; Shrestha, P.; Bazylak, A. Identifying in operando changes in membrane hydration in polymer electrolyte membrane fuel cells using synchrotron X-ray radiography. Int. J. Hydrog. Energy 2018, 43, 9757–9769. [Google Scholar] [CrossRef]
- Dunbar, Z.W.; Masel, R.I. Magnetic resonance imaging investigation of water accumulation and transport in graphite flow fields in a polymer electrolyte membrane fuel cell: Do defects control transport? J. Power Sources 2008, 182, 76–82. [Google Scholar] [CrossRef]
- Teranishi, K.; Tsushima, S.; Hirai, S. Analysis of Water Transport in PEFCs by Magnetic Resonance Imaging Measurement. J. Electrochem. Soc. 2006, 153, A664. [Google Scholar] [CrossRef]
- Tsushima, S.; Teranishi, K.; Hirai, S. Magnetic Resonance Imaging of the Water Distribution within a Polymer Electrolyte Membrane in Fuel Cells. Electrochem. Solid-State Lett. 2004, 7, A269. [Google Scholar] [CrossRef]
- Peng, Z.; Badets, V.; Huguet, P.; Morin, A.; Schott, P.; Tran, T.B.H.; Porozhnyy, M.; Nikonenko, V.; Deabate, S. Operando Micro-Raman study of the actual water content of perfluorosulfonic acid membranes in the fuel cell. J. Power Sources 2017, 356, 200–211. [Google Scholar] [CrossRef]
- Huguet, P.; Morin, A.; Gebel, G.; Deabate, S.; Sutor, A.K.; Peng, Z. In situ analysis of water management in operating fuel cells by confocal Raman spectroscopy. Electrochem. Commun. 2011, 13, 418–422. [Google Scholar] [CrossRef]
- Kendrick, I.; Fore, J.; Doan, J.; Loupe, N.; Vong, A.; Dimakis, N.; Diem, M.; Smotkin, E.S. Operando Raman Micro-Spectroscopy of Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2016, 163, H3152–H3159. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, J.; Wang, Y.; Yin, Y.; Jiao, K. Investigation of current density spatial distribution in PEM fuel cells using a comprehensively validated multi-phase non-isothermal model. Int. J. Heat Mass Transf. 2020, 150, 119294. [Google Scholar] [CrossRef]
- Rasha, L.; Cho, J.; Millichamp, J.; Neville, T.P.; Shearing, P.R.; Brett, D. Effect of reactant gas flow orientation on the current and temperature distribution in self-heating polymer electrolyte fuel cells. Int. J. Hydrog. Energy 2021, 46, 7502–7514. [Google Scholar] [CrossRef]
- Peng, L.; Shao, H.; Qiu, D.; Yi, P.; Lai, X. Investigation of the non-uniform distribution of current density in commercial-size proton exchange membrane fuel cells. J. Power Sources 2020, 453, 227836. [Google Scholar] [CrossRef]
- Reshetenko, T.; Kulikovsky, A. On the distribution of local current density along a PEM fuel cell cathode channel. Electrochem. Commun. 2019, 101, 35–38. [Google Scholar] [CrossRef]
- Chevalier, S.; Olivier, J.C.; Josset, C.; Auvity, B. Polymer Electrolyte Membrane Fuel Cell Characterisation Based on Current Distribution Measurements. ECS Trans. 2018, 86, 211–220. [Google Scholar] [CrossRef]
- Hwnag, J.; Chang, W.; Peng, R.; Chen, P.; Su, A. Experimental and numerical studies of local current mapping on a PEM fuel cell. Int. J. Hydrog. Energy 2008, 33, 5718–5727. [Google Scholar] [CrossRef]
- Ogawa, K.; Sasaki, T.; Yoneda, S.; Tsujinaka, K.; Asai, R. Two-dimensional spatial distributions of the water content of the membrane electrode assembly and the electric current generated in a polymer electrolyte fuel cell measured by 49 nuclear magnetic resonance surface coils: Dependence on gas flow rate and relative humidity of supplied gases. J. Power Sources 2019, 444, 227254. [Google Scholar] [CrossRef]
- Hauer, K.H.; Potthast, R.; Wüster, T.; Stolten, D. Magnetotomography—A new method for analysing fuel cell performance and quality. J. Power Sources 2005, 143, 67–74. [Google Scholar] [CrossRef]
- Plait, A.; Giurgea, S.; Hissel, D.; Espanet, C. New magnetic field analyzer device dedicated for polymer electrolyte fuel cells noninvasive diagnostic. Int. J. Hydrog. Energy 2020, 45, 14071–14082. [Google Scholar] [CrossRef]
- Wang, M.; Guo, H.; Ma, C. Temperature distribution on the MEA surface of a PEMFC with serpentine channel flow bed. J. Power Sources 2006, 157, 181–187. [Google Scholar] [CrossRef]
- Wilkinson, M.; Blanco, M.; Gu, E.; Martin, J.J.; Wilkinson, D.P.; Zhang, J.J.; WANG, H. In Situ Experimental Technique for Measurement of Temperature and Current Distribution in Proton Exchange Membrane Fuel Cells. Electrochem. Solid-State Lett. 2006, 9, A507. [Google Scholar] [CrossRef]
- David, N.A.; Wild, P.M.; Hu, J.; Djilali, N. In-fibre Bragg grating sensors for distributed temperature measurement in a polymer electrolyte membrane fuel cell. J. Power Sources 2009, 192, 376–380. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Sternig, C.; Fink, C.; Hacker, V.; Theiler, A.; Tatschl, R. Theoretical study of the influence of material parameters on the performance of a polymer electrolyte fuel cell. J. Power Sources 2015, 297, 329–343. [Google Scholar] [CrossRef]
- Al-Baghdadi, M.A.R.S.; Al-Janabi, H.A.K.S. Numerical analysis of a proton exchange membrane fuel cell. Part 2: Parametric study. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 931–939. [Google Scholar] [CrossRef]
- Baik, K.D.; Hong, B.K.; Kim, M.S. Effects of operating parameters on hydrogen crossover rate through Nafion membranes in polymer electrolyte membrane fuel cells. Renew. Energy 2013, 57, 234–239. [Google Scholar] [CrossRef]
- Büchi, F.N.; Scherer, G.G. Investigation of the Transversal Water Profile in Nafion Membranes in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2001, 148, A183. [Google Scholar] [CrossRef]
- Wilson, M.S.; Valerio, J.A.; Gottesfeld, S. Low platinum loading electrodes for polymer electrolyte fuel cells fabricated using thermoplastic ionomers. Electrochim. Acta 1995, 40, 355–363. [Google Scholar] [CrossRef]
- Ai, S.; Tatsuya, H.; Ryuji, M.; Hideyuki, T.; Nozomu, H.; Hiromitsu, T.; Williams, M.C.; Akira, M. Porosity and Pt content in the catalyst layer of PEMFC: Effects on diffusion and polarization characteristics. Int. J. Electrochem. Sci. 2010, 5, 1948–1961. [Google Scholar]
- Meyer, Q.; Hack, J.; Mansor, N.; Iacoviello, F.; Bailey, J.J.; Shearing, P.R.; Brett, D.J.L. Multi–Scale Imaging of Polymer Electrolyte Fuel Cells using X–ray Micro– and Nano–Computed Tomography, Transmission Electron Microscopy and Helium–Ion Microscopy. Fuel Cells 2019, 19, 35–42. [Google Scholar] [CrossRef]
- Pokhrel, A.; El Hannach, M.; Orfino, F.P.; Dutta, M.; Kjeang, E. Failure analysis of fuel cell electrodes using three-dimensional multi-length scale X-ray computed tomography. J. Power Sources 2016, 329, 330–338. [Google Scholar] [CrossRef]
- Wilson, M.S.; Gottesfeld, S. Thin-film catalyst layers for polymer electrolyte fuel cell electrodes. J. Appl. Electrochem. 1992, 22, 1–7. [Google Scholar] [CrossRef]
- Jhong, H.R.M.; Brushett, F.R.; Kenis, P.J.A. The Effects of Catalyst Layer Deposition Methodology on Electrode Performance. Adv. Energy Mater. 2013, 3, 589–599. [Google Scholar] [CrossRef]
- Haug, A.T.; White, R.E.; Weidner, J.W.; Huang, W.; Shi, S.; Stoner, T.; Rana, N. Increasing Proton Exchange Membrane Fuel Cell Catalyst Effectiveness Through Sputter Deposition. J. Electrochem. Soc. 2002, 149, A280. [Google Scholar] [CrossRef]
- Hitchcock, A.P.; Berejnov, V.; Lee, V.; West, M.; Colbow, V.; Dutta, M.; Wessel, S. Carbon corrosion of proton exchange membrane fuel cell catalyst layers studied by scanning transmission X-ray microscopy. J. Power Sources 2014, 266, 66–78. [Google Scholar] [CrossRef]
- Young, A.P.; Colbow, V.; Harvey, D.; Rogers, E.; Wessel, S. A Semi-Empirical Two Step Carbon Corrosion Reaction Model in PEM Fuel Cells. J. Electrochem. Soc. 2013, 160, F381–F388. [Google Scholar] [CrossRef]
- Keiser, H.; Beccu, K.D.; Gutjahr, M.A. Abschätzung der porenstruktur poröser elektroden aus impedanzmessungen. Electrochim. Acta 1976, 21, 539–543. [Google Scholar] [CrossRef]
- Kelly, P.M.; Jostsons, A.; Blake, R.G.; Napier, J.G. The determination of foil thickness by scanning transmission electron microscopy. Phys. Status Solidi (a) 1975, 31, 771–780. [Google Scholar] [CrossRef]
- Susac, D.; Berejnov, V.; Hitchcock, A.P.; Stumper, J. STXM Study of the Ionomer Distribution in the PEM Fuel Cell Catalyst Layers. ECS Trans. 2011, 41, 629–635. [Google Scholar] [CrossRef]
- Berejnov, V.; Susac, D.; Stumper, J.; Hitchcock, A.P. Nano to Micro Scale Characterization of Water Uptake in The Catalyst Coated Membrane Measured by Soft X-ray Scanning Transmission X-ray Microscopy. ECS Trans. 2011, 41, 395–402. [Google Scholar] [CrossRef]
- Croll, L.M.; Stöver, H.D.H.; Hitchcock, A.P. Composite Tectocapsules Containing Porous Polymer Microspheres as Release Gates. Macromolecules 2005, 38, 2903–2910. [Google Scholar] [CrossRef]
- White, R.T.; Wu, A.; Najm, M.; Orfino, F.P.; Dutta, M.; Kjeang, E. 4D in situ visualization of electrode morphology changes during accelerated degradation in fuel cells by X-ray computed tomography. J. Power Sources 2017, 350, 94–102. [Google Scholar] [CrossRef]
- Epting, W.K.; Gelb, J.; Litster, S. Resolving the Three-Dimensional Microstructure of Polymer Electrolyte Fuel Cell Electrodes using Nanometer-Scale X-ray Computed Tomography. Adv. Funct. Mater. 2012, 22, 555–560. [Google Scholar] [CrossRef]
- Griesser, S.; Buchinger, G.; Raab, T.; Claassen, D.P.; Meissner, D. Characterization of Fuel Cells and Fuel Cell Systems Using Three-Dimensional X-ray Tomography. J. Fuel Cell Sci. Technol. 2007, 4, 84–87. [Google Scholar] [CrossRef]
- Singh, Y.; White, R.T.; Najm, M.; Haddow, T.; Pan, V.; Orfino, F.P.; Dutta, M.; Kjeang, E. Tracking the evolution of mechanical degradation in fuel cell membranes using 4D in situ visualization. J. Power Sources 2019, 412, 224–237. [Google Scholar] [CrossRef]
- Lee, C.H.; Park, H.B.; Lee, Y.M.; Lee, R.D. Importance of Proton Conductivity Measurement in Polymer Electrolyte Membrane for Fuel Cell Application. Ind. Eng. Chem. Res. 2005, 44, 7617–7626. [Google Scholar] [CrossRef]
- Guo, X.; Fang, J.; Watari, T.; Tanaka, K.; Kita, H.; Okamoto, K.i. Novel Sulfonated Polyimides as Polyelectrolytes for Fuel Cell Application. 2. Synthesis and Proton Conductivity of Polyimides from 9,9-Bis(4-aminophenyl)fluorene-2,7-disulfonic Acid. Macromolecules 2002, 35, 6707–6713. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Springer, T.E.; Davey, J.; Jestel, R.; Lopez, C.; Valerio, J.; Gottesfeld, S. A Comparative Study of Water Uptake By and Transport Through Ionomeric Fuel Cell Membranes. J. Electrochem. Soc. 1993, 140, 1981–1985. [Google Scholar] [CrossRef]
- Kidena, K.; Ohkubo, T.; Takimoto, N.; Ohira, A. PFG-NMR approach to determining the water transport mechanism in polymer electrolyte membranes conditioned at different temperatures. Eur. Polym. J. 2010, 46, 450–455. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, H.; Colinsun, J.; Zhang, J. AC impedance technique in PEM fuel cell diagnosis—A review. Int. J. Hydrog. Energy 2007, 32, 4365–4380. [Google Scholar] [CrossRef]
- Rezaei Niya, S.M.; Hoorfar, M. Study of proton exchange membrane fuel cells using electrochemical impedance spectroscopy technique—A review. J. Power Sources 2013, 240, 281–293. [Google Scholar] [CrossRef]
- Baricci, A.; Bisello, A.; Serov, A.; Odgaard, M.; Atanassov, P.; Casalegno, A. Analysis of the effect of catalyst layer thickness on the performance and durability of platinum group metal-free catalysts for polymer electrolyte membrane fuel cells. Sustain. Energy Fuels 2019, 3, 3375–3386. [Google Scholar] [CrossRef]
- Brunetto, C.; Moschetto, A.; Tina, G. PEM fuel cell testing by electrochemical impedance spectroscopy. Electr. Power Syst. Res. 2009, 79, 17–26. [Google Scholar] [CrossRef]
- Beattie, P.D.; Orfino, F.P.; Basura, V.I.; Zychowska, K.; Ding, J.; Chuy, C.; Schmeisser, J.; Holdcroft, S. Ionic conductivity of proton exchange membranes. J. Electroanal. Chem. 2001, 503, 45–56. [Google Scholar] [CrossRef]
- Fitt, A.D.; Owen, J.R. Simultaneous measurements of conductivity and thickness for polymer electrolyte films: A simulation study. J. Electroanal. Chem. 2002, 538–539, 13–23. [Google Scholar] [CrossRef]
- Gardner, C.L.; Anantaraman, A.V. Measurement of membrane conductivities using an open-ended coaxial probe. J. Electroanal. Chem. 1995, 395, 67–73. [Google Scholar] [CrossRef]
- Karpenko, L.V.; Demina, O.A.; Dvorkina, G.A.; Parshikov, S.B.; Larchet, C.; Auclair, B.; Berezina, N.P. Comparative Study of Methods Used for the Determination of Electroconductivity of Ion-Exchange Membranes. Russ. J. Electrochem. 2001, 37, 287–293. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, K.H.; Chu, J.Y.; Kim, A.R.; Yoo, D.J. Enhanced Hydroxide Conductivity and Dimensional Stability with Blended Membranes Containing Hyperbranched PAES/Linear PPO as Anion Exchange Membranes. Polymers 2020, 12, 3011. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Gu, N.; Cheng, Z.; Yang, X.; Wang, E.; Dong, S. Methods to study the ionic conductivity of polymeric electrolytes using a.c. impedance spectroscopy. J. Solid State Electrochem. 2001, 6, 8–15. [Google Scholar] [CrossRef]
- Tsampas, M.N.; Pikos, A.; Brosda, S.; Katsaounis, A.; Vayenas, C.G. The effect of membrane thickness on the conductivity of Nafion. Electrochim. Acta 2006, 51, 2743–2755. [Google Scholar] [CrossRef]
- Lim, T.M.; Ulaganathan, M.; Yan, Q. Advances in membrane and stack design of redox flow batteries (RFBs) for medium- and large-scale energy storage. In Advances in Batteries for Medium and Large-Scale Energy Storage; Elsevier: Amsterdam, The Netherlands, 2015; pp. 477–507. [Google Scholar] [CrossRef]
- Mikhailenko, S.; Guiver, M.; Kaliaguine, S. Measurements of PEM conductivity by impedance spectroscopy. Solid State Ionics 2008, 179, 619–624. [Google Scholar] [CrossRef]
- Büchi, F.N.; Scherer, G.G. In-situ resistance measurements of Nafion 117 membranes in polymer electrolyte fuel cells. J. Electroanal. Chem. 1996, 404, 37–43. [Google Scholar] [CrossRef]
- Badessa, T.S.; Shaposhnik, V.A. Electrical Conductance Studies on Ion Exchange Membrane Using Contact-Difference Method. Electrochim. Acta 2017, 231, 453–459. [Google Scholar] [CrossRef]
- Luo, Z.; Chang, Z.; Zhang, Y.; Liu, Z.; Li, J. Electro-osmotic drag coefficient and proton conductivity in Nafion membrane for PEMFC. Int. J. Hydrog. Energy 2010, 35, 3120–3124. [Google Scholar] [CrossRef]
- Alakanandana, A.; Subrahmanyam, A.R.; Siva Kumar, J. Structural and Electrical Conductivity studies of pure PVA and PVA doped with Succinic acid polymer electrolyte system. Mater. Today Proc. 2016, 3, 3680–3688. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. Phys. Chem. 1889, 4. [Google Scholar] [CrossRef]
- Ge, S.; Yi, B.; Ming, P. Experimental Determination of Electro-Osmotic Drag Coefficient in Nafion Membrane for Fuel Cells. J. Electrochem. Soc. 2006, 153, A1443. [Google Scholar] [CrossRef]
- Sellin, R.C.; Mozet, K.; Ménage, A.; Dillet, J.; Didierjean, S.; Maranzana, G. Measuring electro-osmotic drag coefficients in PFSA membranes without any diffusion assumption. Int. J. Hydrog. Energy 2019, 44, 24905–24912. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Neeman, M.; Sillerud, L.O.; Gottesfeld, S. Determination of water diffusion coefficients in perfluorosulfonate ionomeric membranes. J. Phys. Chem. 1991, 95, 6040–6044. [Google Scholar] [CrossRef]
- Edmondson, C.A.; Fontanella, J.J.; Chung, S.H.; Greenbaum, S.G.; Wnek, G.E. Complex impedance studies of S-SEBS block polymer proton-conducting membranes. Electrochim. Acta 2001, 46, 1623–1628. [Google Scholar] [CrossRef]
- Tsushima, S.; Teranishi, K.; Hirai, S. Water diffusion measurement in fuel-cell SPE membrane by NMR. Energy 2005, 30, 235–245. [Google Scholar] [CrossRef]
- Gong, X.; Bandis, A.; Tao, A.; Meresi, G.; Wang, Y.; Inglefield, P.; Jones, A.; Wen, W.Y. Self-diffusion of water, ethanol and decafluropentane in perfluorosulfonate ionomer by pulse field gradient NMR. Polymer 2001, 42, 6485–6492. [Google Scholar] [CrossRef]
- Kreuer, K. On the development of proton conducting materials for technological applications. Solid State Ionics 1997, 97, 1–15. [Google Scholar] [CrossRef]
- Suresh, G.; Scindia, Y.; Pandey, A.; Goswami, A. Self-diffusion coefficient of water in Nafion-117 membrane with different monovalent counterions: A radiotracer study. J. Membr. Sci. 2005, 250, 39–45. [Google Scholar] [CrossRef]
- Schneider, E.W.; Verbrugge, M.W. Radiotracer method for simultaneous measurement of cation, anion and water transport through ion-exchange membranes. Appl. Radiat. Isot. 1993, 44, IN11-1408. [Google Scholar] [CrossRef]
- Sawada, S.i.; Yamaki, T.; Nishimura, H.; Asano, M.; Suzuki, A.; Terai, T.; Maekawa, Y. Water transport properties of crosslinked-PTFE based electrolyte membranes. Solid State Ionics 2008, 179, 1611–1614. [Google Scholar] [CrossRef]
- Sawada, S.; Yamaki, T.; Asano, M.; Suzuki, A.; Terai, T.; Maekawa, Y. Water diffusion in fluoropolymer-based fuel-cell electrolyte membranes investigated by radioactivated-tracer permeation technique. Proc. Radiochem. 2011, 1, 409–413. [Google Scholar] [CrossRef]
- Rivin, D.; Kendrick, C.E.; Gibson, P.W.; Schneider, N.S. Solubility and transport behavior of water and alcohols in Nafion™. Polymer 2001, 42, 623–635. [Google Scholar] [CrossRef]
- Pivovar, B.S. An overview of electro-osmosis in fuel cell polymer electrolytes. Polymer 2006, 47, 4194–4202. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Derouin, C.; Radzinski, S.; Sherman, R.J.; van Smith, T.; Springer, T.E.; Gottesfeld, S. Water Uptake by and Transport Through Nafion 117 Membranes. J. Electrochem. Soc. 1993, 140, 1041–1047. [Google Scholar] [CrossRef]
- Fuller, T.F.; Newman, J. Experimental Determination of the Transport Number of Water in Nafion 117 Membrane. J. Electrochem. Soc. 1992, 139, 1332–1337. [Google Scholar] [CrossRef]
- Weng, D.; Wainright, J.S.; Landau, U.; Savinell, R.F. Electro–osmotic Drag Coefficient of Water and Methanol in Polymer Electrolytes at Elevated Temperatures. J. Electrochem. Soc. 1996, 143, 1260–1263. [Google Scholar] [CrossRef]
- Ise, M.; Kreuer, K.; Maier, J. Electroosmotic drag in polymer electrolyte membranes: An electrophoretic NMR study. Solid State Ionics 1999, 125, 213–223. [Google Scholar] [CrossRef]
- Jeon, J.D.; Kwak, S.Y. Ionic cluster size distributions of swollen nafion/sulfated beta-cyclodextrin membranes characterized by nuclear magnetic resonance cryoporometry. J. Phys. Chem. B 2007, 111, 9437–9443. [Google Scholar] [CrossRef]
- Moukheiber, E.; de Moor, G.; Flandin, L.; Bas, C. Investigation of ionomer structure through its dependence on ion exchange capacity (IEC). J. Membr. Sci. 2012, 389, 294–304. [Google Scholar] [CrossRef]
- Dutta, K.; Kundu, P.P. (Eds.) Progress and Recent Trends in Microbial Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Karas, F.; Hnát, J.; Paidar, M.; Schauer, J.; Bouzek, K. Determination of the ion-exchange capacity of anion-selective membranes. Int. J. Hydrog. Energy 2014, 39, 5054–5062. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, A.D.; Kumar, V.; Kundu, P.P. Incorporation of nano-Al 2 O 3 within the blend of sulfonated-PVdF-co-HFP and Nafion for high temperature application in DMFCs. RSC Adv. 2015, 5, 63465–63472. [Google Scholar] [CrossRef]
- Kumar, P.; Dutta, K.; Das, S.; Kundu, P.P. Membrane prepared by incorporation of crosslinked sulfonated polystyrene in the blend of PVdF-co-HFP/Nafion: A preliminary evaluation for application in DMFC. Appl. Energy 2014, 123, 66–74. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, P.; Nandy, A.; Kundu, P.P. A nanocomposite membrane composed of incorporated nano-alumina within sulfonated PVDF-co-HFP/Nafion blend as separating barrier in a single chambered microbial fuel cell. RSC Adv. 2016, 6, 23571–23580. [Google Scholar] [CrossRef]
- Schauer, J.; Llanos, J.; Žitka, J.; Hnát, J.; Bouzek, K. Cation-exchange membranes: Comparison of homopolymer, block copolymer, and heterogeneous membranes. J. Appl. Polym. Sci. 2012, 124, E66–E72. [Google Scholar] [CrossRef]
- Higa, M.; Nishimura, M.; Kinoshita, K.; Jikihara, A. Characterization of cation-exchange membranes prepared from poly(vinyl alcohol) and poly(vinyl alcohol-b-styrene sulfonic acid). Int. J. Hydrog. Energy 2012, 37, 6161–6168. [Google Scholar] [CrossRef]
- Perusich, S.A. FTIR equivalent weight determination of perfluorosulfonate polymers. J. Appl. Polym. Sci. 2011, 120, 165–183. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.W.; Popov, B.N. A review of gas diffusion layer in PEM fuel cells: Materials and designs. Int. J. Hydrog. Energy 2012, 37, 5850–5865. [Google Scholar] [CrossRef]
- Jordan, L.; Shukla, A.; Behrsing, T.; Avery, N.; Muddle, B.; Forsyth, M. Diffusion layer parameters influencing optimal fuel cell performance. J. Power Sources 2000, 86, 250–254. [Google Scholar] [CrossRef]
- Williams, M.V.; Kunz, H.R.; Fenton, J.M. Influence of Convection Through Gas-Diffusion Layers on Limiting Current in PEM FCs Using a Serpentine Flow Field. J. Electrochem. Soc. 2004, 151, A1617. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, C.; Cho, C. Characterization of Effective In-Plane Electrical Resistivity of a Gas Diffusion Layer in Polymer Electrolyte Membrane Fuel Cells through Freeze–Thaw Thermal Cycles. Energies 2020, 13, 145. [Google Scholar] [CrossRef]
- Kim, H.; Lee, Y.J.; Lee, S.J.; Chung, Y.S.; Yoo, Y. Fabrication of carbon papers using polyacrylonitrile fibers as a binder. J. Mater. Sci. 2014, 49, 3831–3838. [Google Scholar] [CrossRef]
- Williams, M.V.; Begg, E.; Bonville, L.; Kunz, H.R.; Fenton, J.M. Characterization of Gas Diffusion Layers for PEMFC. J. Electrochem. Soc. 2004, 151, A1173. [Google Scholar] [CrossRef]
- Becker, J.; Flückiger, R.; Reum, M.; Büchi, F.N.; Marone, F.; Stampanoni, M. Determination of Material Properties of Gas Diffusion Layers: Experiments and Simulations Using Phase Contrast Tomographic Microscopy. J. Electrochem. Soc. 2009, 156, B1175. [Google Scholar] [CrossRef]
- Ismail, M.S.; Hughes, K.J.; Ingham, D.B.; Ma, L.; Pourkashanian, M. Effects of anisotropic permeability and electrical conductivity of gas diffusion layers on the performance of proton exchange membrane fuel cells. Appl. Energy 2012, 95, 50–63. [Google Scholar] [CrossRef]
- Sharma, S.; Siginer, D.A. Permeability Measurement Methods in Porous Media of Fiber Reinforced Composites. Appl. Mech. Rev. 2010, 63. [Google Scholar] [CrossRef]
- El-kharouf, A.; Mason, T.J.; Brett, D.J.; Pollet, B.G. Ex-situ characterisation of gas diffusion layers for proton exchange membrane fuel cells. J. Power Sources 2012, 218, 393–404. [Google Scholar] [CrossRef]
- Mangal, P.; Pant, L.M.; Carrigy, N.; Dumontier, M.; Zingan, V.; Mitra, S.; Secanell, M. Experimental study of mass transport in PEMFCs: Through plane permeability and molecular diffusivity in GDLs. Electrochim. Acta 2015, 167, 160–171. [Google Scholar] [CrossRef]
- Phillips, R.K.; Friess, B.R.; Hicks, A.D.; Bellerive, J.; Hoorfar, M. Ex-situ Measurement of Properties of Gas Diffusion Layers of PEM Fuel Cells. Energy Procedia 2012, 29, 486–495. [Google Scholar] [CrossRef][Green Version]
- Banerjee, R.; Kandlikar, S.G. Effect of Temperature on In-Plane Permeability of the Gas Diffusion Layer of PEM Fuel Cell. ECS Trans. 2011, 41, 489–497. [Google Scholar] [CrossRef]
- Ismail, M.S.; Damjanovic, T.; Hughes, K.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Rosli, M. Through-Plane Permeability for Untreated and PTFE-Treated Gas Diffusion Layers in Proton Exchange Membrane Fuel Cells. J. Fuel Cell Sci. Technol. 2010, 7. [Google Scholar] [CrossRef]
- Fink, C.; Karpenko-Jereb, L.; Ashton, S. Advanced CFD Analysis of an Air-cooled PEM Fuel Cell Stack Predicting the Loss of Performance with Time. Fuel Cells 2016, 16, 490–503. [Google Scholar] [CrossRef]
- Bednarek, T.; Tsotridis, G. Issues associated with modelling of proton exchange membrane fuel cell by computational fluid dynamics. J. Power Sources 2017, 343, 550–563. [Google Scholar] [CrossRef]
- Pant, L.M.; Mitra, S.K.; Secanell, M. Absolute permeability and Knudsen diffusivity measurements in PEMFC gas diffusion layers and micro porous layers. J. Power Sources 2012, 206, 153–160. [Google Scholar] [CrossRef]
- Joseph, J.; Siva Kumar Gunda, N.; Mitra, S.K. On-chip porous media: Porosity and permeability measurements. Chem. Eng. Sci. 2013, 99, 274–283. [Google Scholar] [CrossRef]
- Rigby, S.P.; Fletcher, R.S.; Raistrick, J.H.; Riley, S.N. Characterisation of porous solids using a synergistic combination of nitrogen sorption, mercury porosimetry, electron microscopy and micro-focus X-ray imaging techniques. Phys. Chem. Chem. Phys. 2002, 4, 3467–3481. [Google Scholar] [CrossRef]
- Bera, B.; Mitra, S.K.; Vick, D. Understanding the micro structure of Berea Sandstone by the simultaneous use of micro-computed tomography (micro-CT) and focused ion beam-scanning electron microscopy (FIB-SEM). Micron (Oxford Engl. 1993) 2011, 42, 412–418. [Google Scholar] [CrossRef]
- Gunde, A.C.; Bera, B.; Mitra, S.K. Investigation of water and CO2 (carbon dioxide) flooding using micro-CT (micro-computed tomography) images of Berea sandstone core using finite element simulations. Energy 2010, 35, 5209–5216. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 036307. [Google Scholar] [CrossRef]
- Clelland, W.D.; Fens, T.W. Automated Rock Characterization With SEM/Image-Analysis Techniques. SPE Form. Eval. 1991, 6, 437–443. [Google Scholar] [CrossRef]
- Gunda, N.S.K.; Choi, H.W.; Berson, A.; Kenney, B.; Karan, K.; Pharoah, J.G.; Mitra, S.K. Focused ion beam-scanning electron microscopy on solid-oxide fuel-cell electrode: Image analysis and computing effective transport properties. J. Power Sources 2011, 196, 3592–3603. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Nield, D.A. The limitations of the Brinkman-Forchheimer equation in modeling flow in a saturated porous medium and at an interface. Int. J. Heat Fluid Flow 1991, 12, 269–272. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int. J. Heat Mass Transf. 2001, 44, 1735–1749. [Google Scholar] [CrossRef]
- Pant, L.M.; Mitra, S.K.; Secanell, M. A generalized mathematical model to study gas transport in PEMFC porous media. Int. J. Heat Mass Transf. 2013, 58, 70–79. [Google Scholar] [CrossRef]
- Carnes, B.; Djilali, N. Analysis of coupled proton and water transport in a PEM fuel cell using the binary friction membrane model. Electrochim. Acta 2006, 52, 1038–1052. [Google Scholar] [CrossRef]
- Aydin, Ö.; Zedda, M.; Zamel, N. Challenges Associated with Measuring the Intrinsic Electrical Conductivity of Carbon Paper Diffusion Media. Fuel Cells 2015, 15, 537–544. [Google Scholar] [CrossRef]
- Sadeghifar, H. In-plane and through-plane electrical conductivities and contact resistances of a Mercedes-Benz catalyst-coated membrane, gas diffusion and micro-porous layers and a Ballard graphite bipolar plate: Impact of humidity, compressive load and polytetrafluoroethylene. Energy Convers. Manag. 2017, 154, 191–202. [Google Scholar] [CrossRef]
- Morris, D.R.; Gostick, J.T. Determination of the in-plane components of the electrical conductivity tensor in PEM fuel cell gas diffusion layers. Electrochim. Acta 2012, 85, 665–673. [Google Scholar] [CrossRef][Green Version]
- Ismail, M.S.; Damjanovic, T.; Ingham, D.B.; Pourkashanian, M.; Westwood, A. Effect of polytetrafluoroethylene-treatment and microporous layer-coating on the electrical conductivity of gas diffusion layers used in proton exchange membrane fuel cells. J. Power Sources 2010, 195, 2700–2708. [Google Scholar] [CrossRef]
- Tanaka, S.; Shudo, T. Experimental and numerical modeling study of the electrical resistance of gas diffusion layer-less polymer electrolyte membrane fuel cells. J. Power Sources 2015, 278, 382–395. [Google Scholar] [CrossRef]
- Todd, D.; Schwager, M.; Mérida, W. Three-Dimensional Anisotropic Electrical Resistivity of PEM Fuel Cell Transport Layers as Functions of Compressive Strain. J. Electrochem. Soc. 2015, 162, F265–F272. [Google Scholar] [CrossRef][Green Version]
- Bockris, J.O.; Reddy, A.K.N.; Gamboa-Aldeco, M. Modern Electrochemistry 2A: Fundamentals of Electrodics, 2nd ed.; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2012. [Google Scholar]
- Muthukrishnan, A.; Nabae, Y.; Hayakawa, T.; Okajima, T.; Ohsaka, T. Fe-containing polyimide-based high-performance ORR catalysts in acidic medium: A kinetic approach to study the durability of catalysts. Catal. Sci. Technol. 2015, 5, 475–483. [Google Scholar] [CrossRef]
- Woodroof, M.D.; Wittkopf, J.A.; Gu, S.; Yan, Y.S. Exchange current density of the hydrogen oxidation reaction on Pt/C in polymer solid base electrolyte. Electrochem. Commun. 2015, 61, 57–60. [Google Scholar] [CrossRef]
- Fink, C.; Fouquet, N. Three-dimensional simulation of polymer electrolyte membrane fuel cells with experimental validation. Electrochim. Acta 2011, 56, 10820–10831. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Innerwinkler, P.; Kelterer, A.M.; Sternig, C.; Fink, C.; Prenninger, P.; Tatschl, R. A novel membrane transport model for polymer electrolyte fuel cell simulations. Int. J. Hydrog. Energy 2014, 39, 7077–7088. [Google Scholar] [CrossRef]


| Equation | |
|---|---|
| Mass | |
| Momentum | |
| Species | |
| Energy | |
| Charge | |
| GC | GDL | CL | Solid Parts | |
|---|---|---|---|---|
| Mass | ||||
| Momentum | ||||
| Species | Anode H: | |||
| Anode HO: | ||||
| Cathode O: | ||||
| Cathode HO: | ||||
| Energy | Anode CL: | BPP: | ||
| Cathode CL: | Membrane: | |||
| Charge | Anode CL: | |||
| Cathode CL: |
| Equation | |
|---|---|
| Mass (gas) | |
| Momentum (gas) | |
| Species (gas) | |
| Water (liquid) | |
| Energy (gas) | |
| Energy (liquid) | ) |
| GC | GDL | CL | |
|---|---|---|---|
| Mass (gas) | |||
| Momentum (gas) | |||
| Species (gas) | Anode H: | ||
| Anode HO: | |||
| Cathode O: | |||
| Cathode HO: | |||
| Water (liquid) | Anode HO: | ||
| Cathode HO: | |||
| Energy (gas) | |||
| Energy (liquid) | |||
| Reference | Correlation | Notes |
|---|---|---|
| [31] | ||
| [45] | ||
| [46] | ||
| (2D parallel flow) | ||
| (2D normal flow) |
| Reference | Correlation | Notes |
|---|---|---|
| [41] | ||
| [42] | ||
| [46] | ||
| (2D parallel flow) | ||
| (2D normal flow) | ||
| [49] | ||
| [50] |
| Ref. | Correlation | Notes |
|---|---|---|
| [63] | Bulk conductivity: though-/in-plane directions not distinguished. | |
| [64] | Bulk conductivity: though-/in-plane directions not distinguished. | |
| [31] | Bulk conductivity: though-/in-plane directions not distinguished. | |
| [65] | Through-plane: | |
| , , | ||
| In-plane: | ||
| , , |
| Reference | Correlation | Notes |
|---|---|---|
| [69] | Overestimated ECR in the 2 range. |
| Ref. | Correlation | Notes |
|---|---|---|
| [6] | ||
| [78] | is the water content at saturation and is the value obtained when and . | |
| [36] |
| Reference | Correlation |
|---|---|
| [6] | |
| [80] | |
| [81] | |
| [82] |
| Ref. | Correlation | Notes |
|---|---|---|
| [6] | ||
| [83] | ||
| [84] | with | |
| [81] | ||
| [26,85] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
d’Adamo, A.; Haslinger, M.; Corda, G.; Höflinger, J.; Fontanesi, S.; Lauer, T. Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells. Processes 2021, 9, 688. https://doi.org/10.3390/pr9040688
d’Adamo A, Haslinger M, Corda G, Höflinger J, Fontanesi S, Lauer T. Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells. Processes. 2021; 9(4):688. https://doi.org/10.3390/pr9040688
Chicago/Turabian Styled’Adamo, Alessandro, Maximilian Haslinger, Giuseppe Corda, Johannes Höflinger, Stefano Fontanesi, and Thomas Lauer. 2021. "Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells" Processes 9, no. 4: 688. https://doi.org/10.3390/pr9040688
APA Styled’Adamo, A., Haslinger, M., Corda, G., Höflinger, J., Fontanesi, S., & Lauer, T. (2021). Modelling Methods and Validation Techniques for CFD Simulations of PEM Fuel Cells. Processes, 9(4), 688. https://doi.org/10.3390/pr9040688










