Modeling of the Refractive Index for the Systems MX+H2O, M2X+H2O, H3BO3+MX+H2O, and H3BO3+M2X+H2O. M = K+, Na+, or Li+ and X = Cl− or SO42−
Abstract
1. Introduction
2. Method
2.1. Molar Refraction and Refractive Index
- m is the number of data points.
2.2. Polarizability
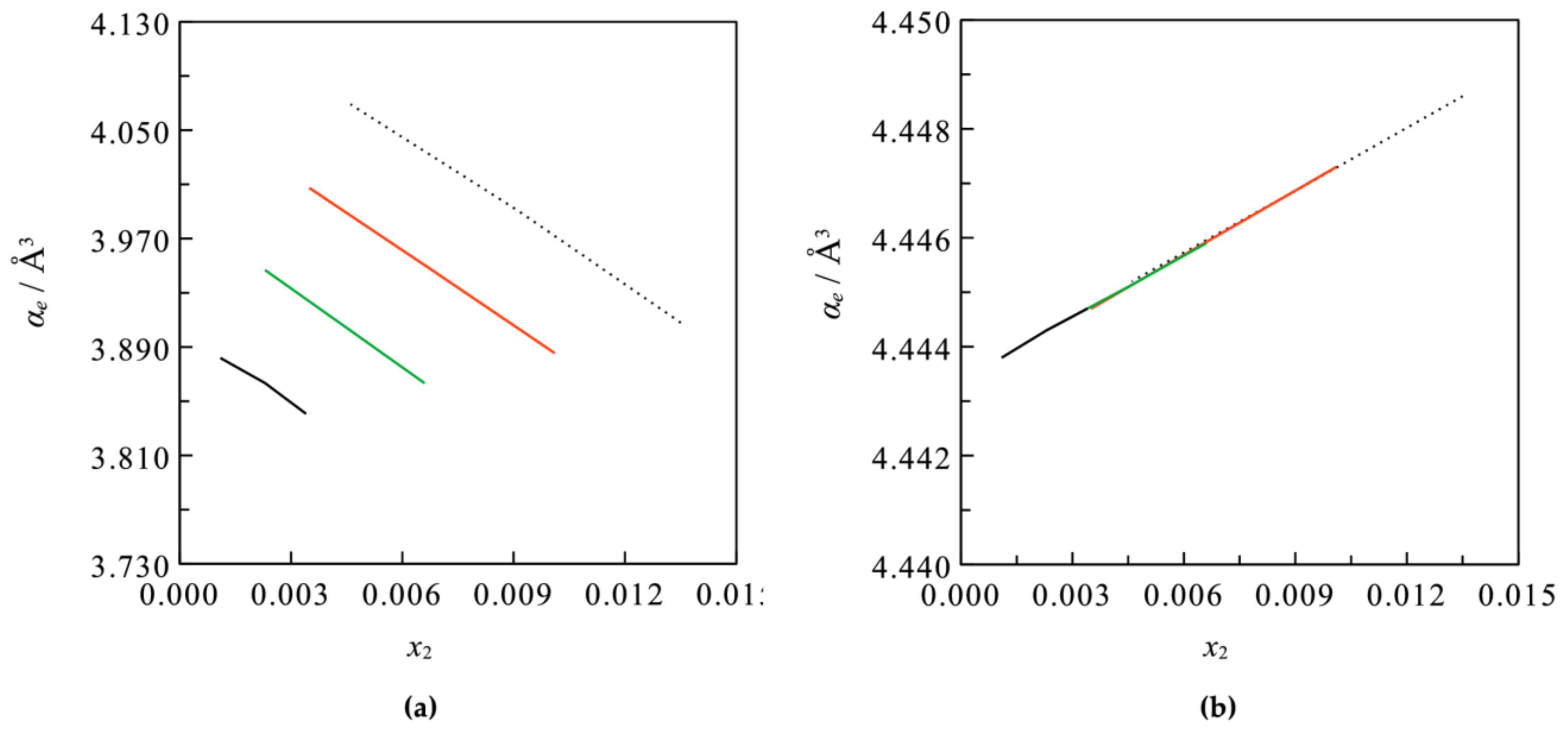
3. Results
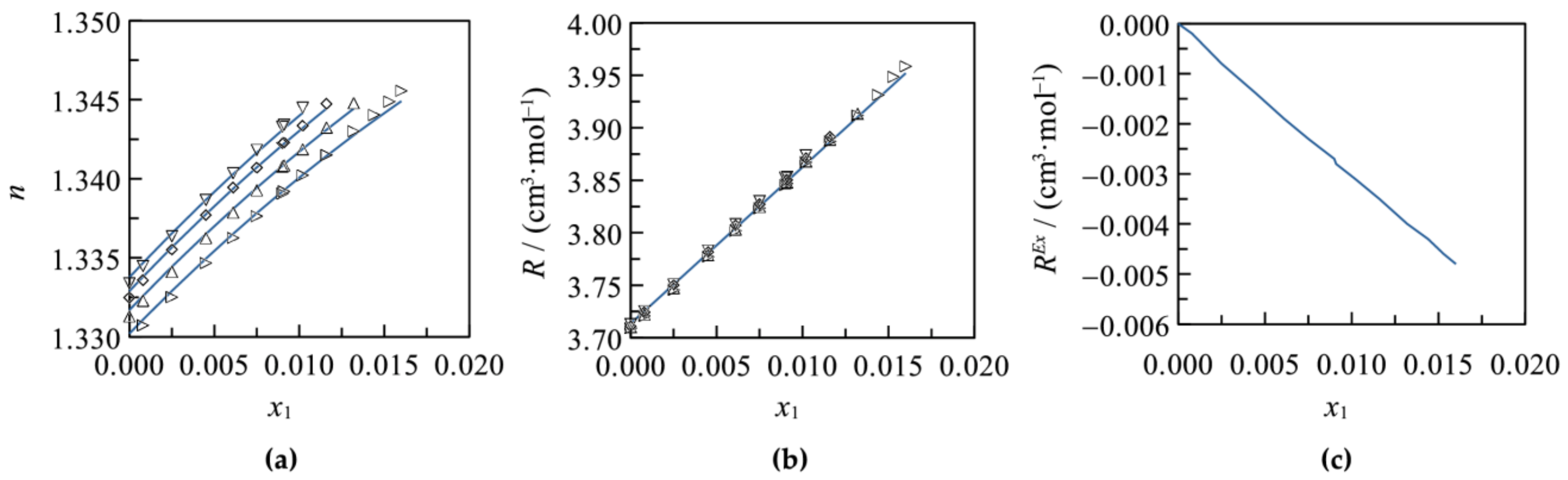
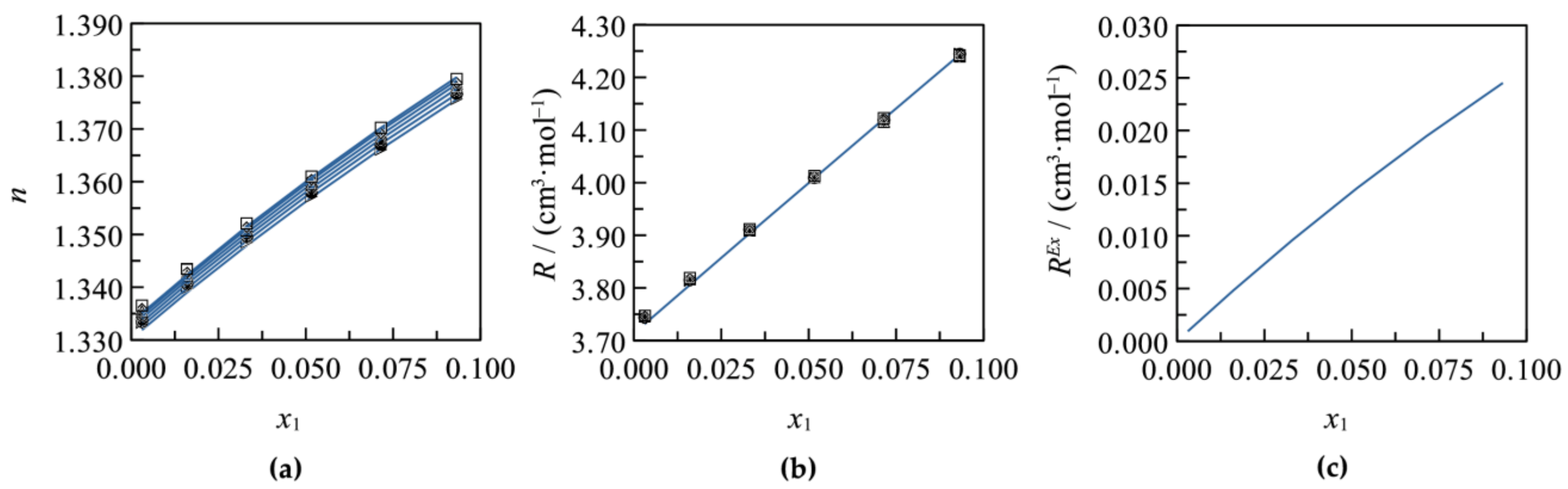
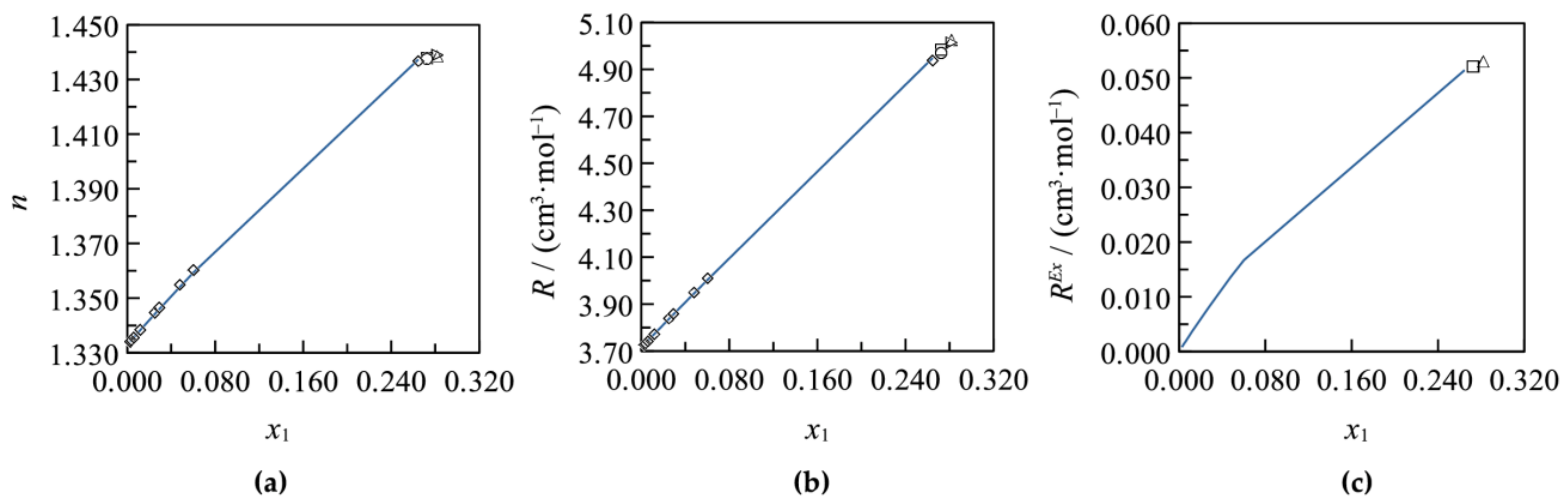
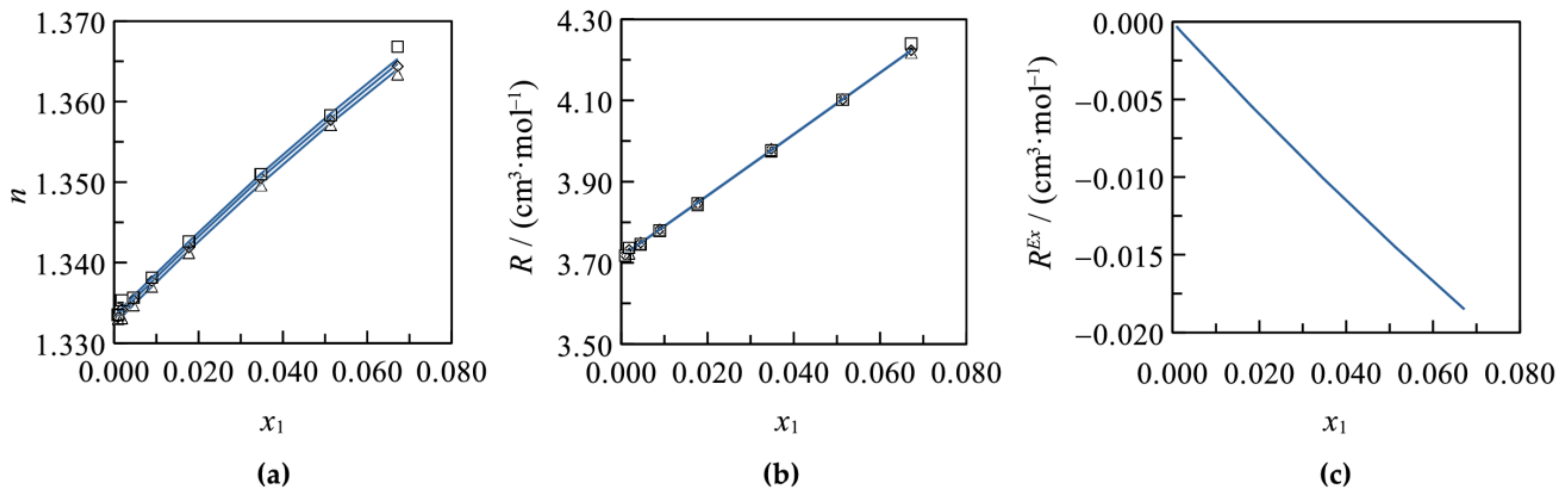
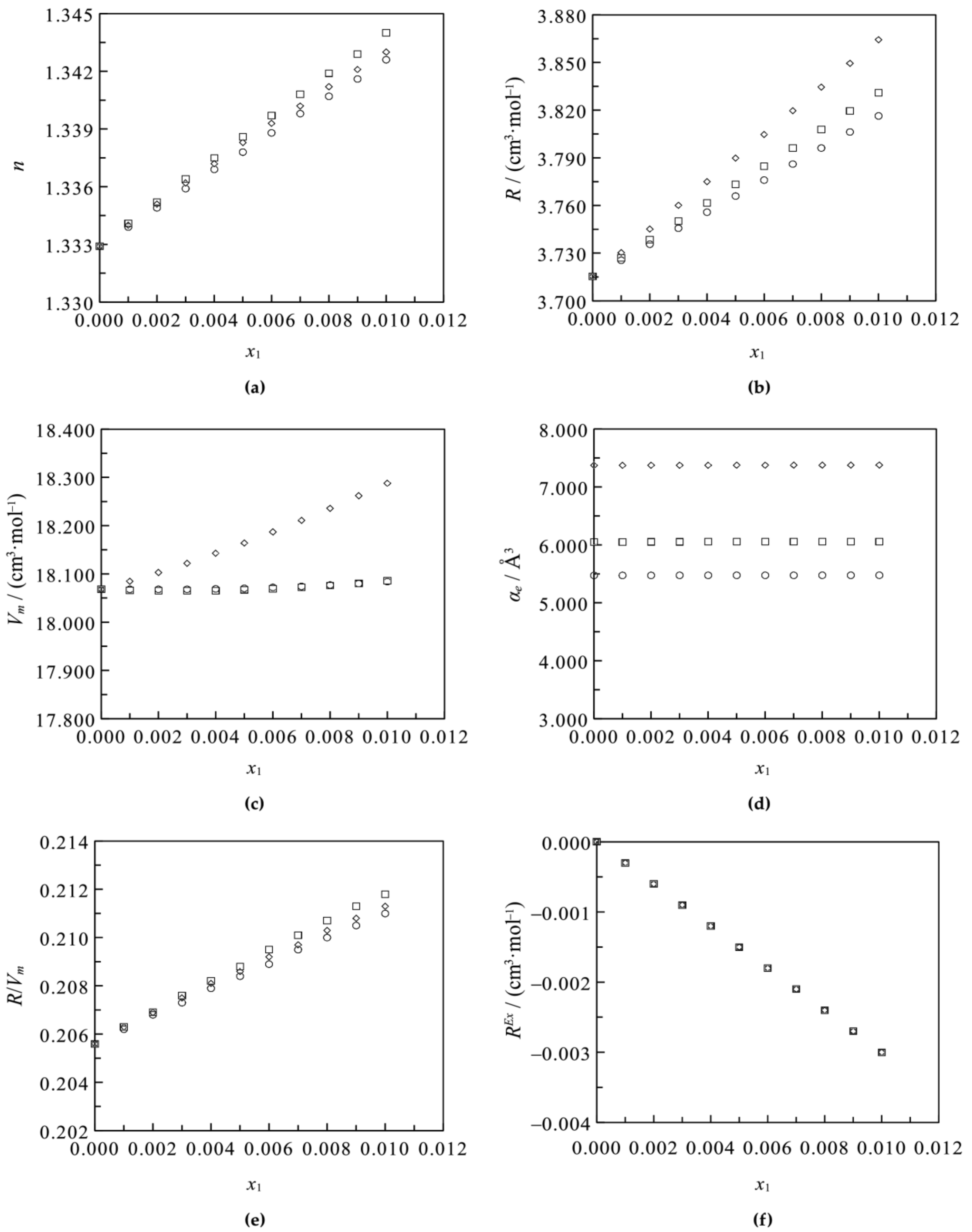
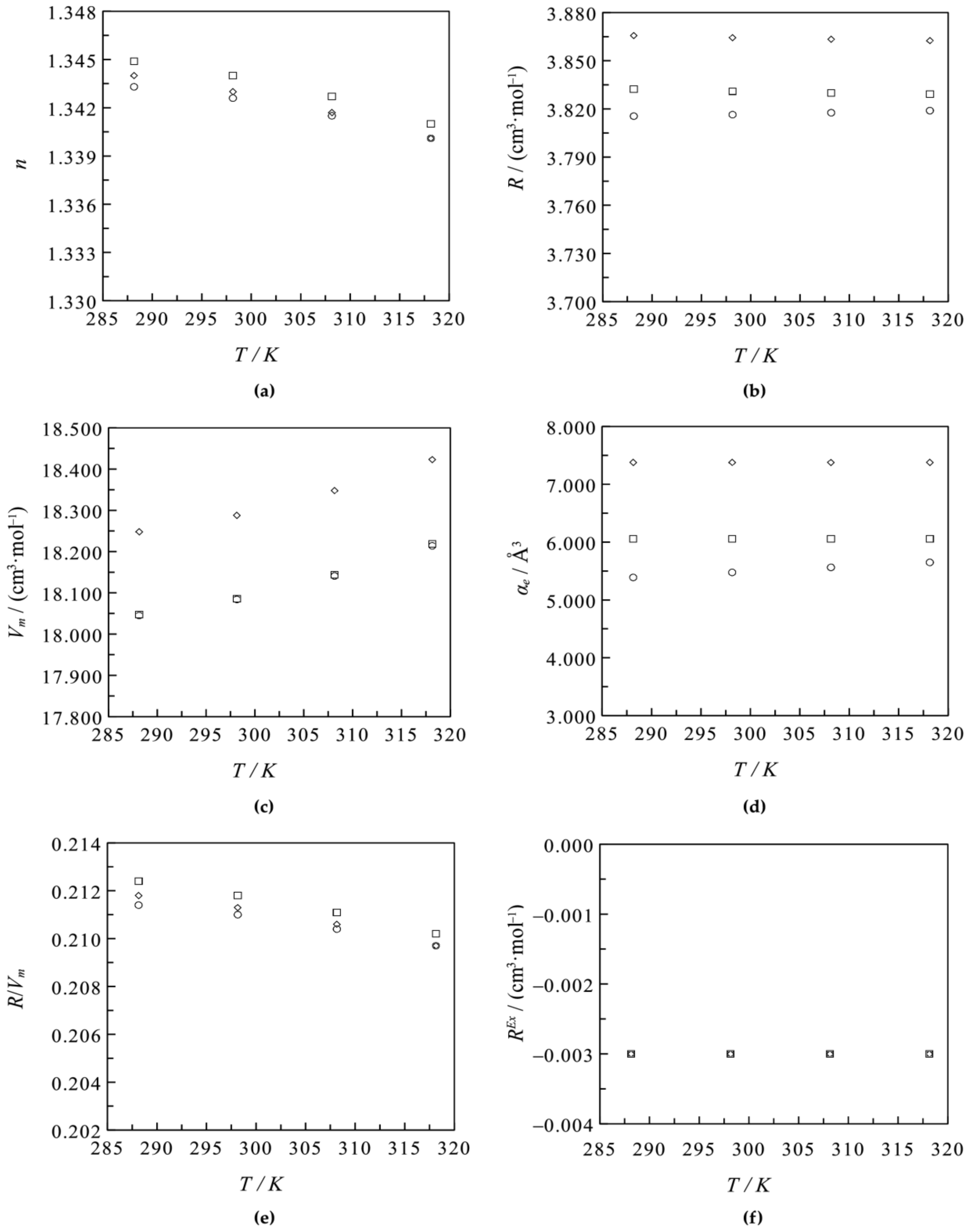
3.1. Binary Systems
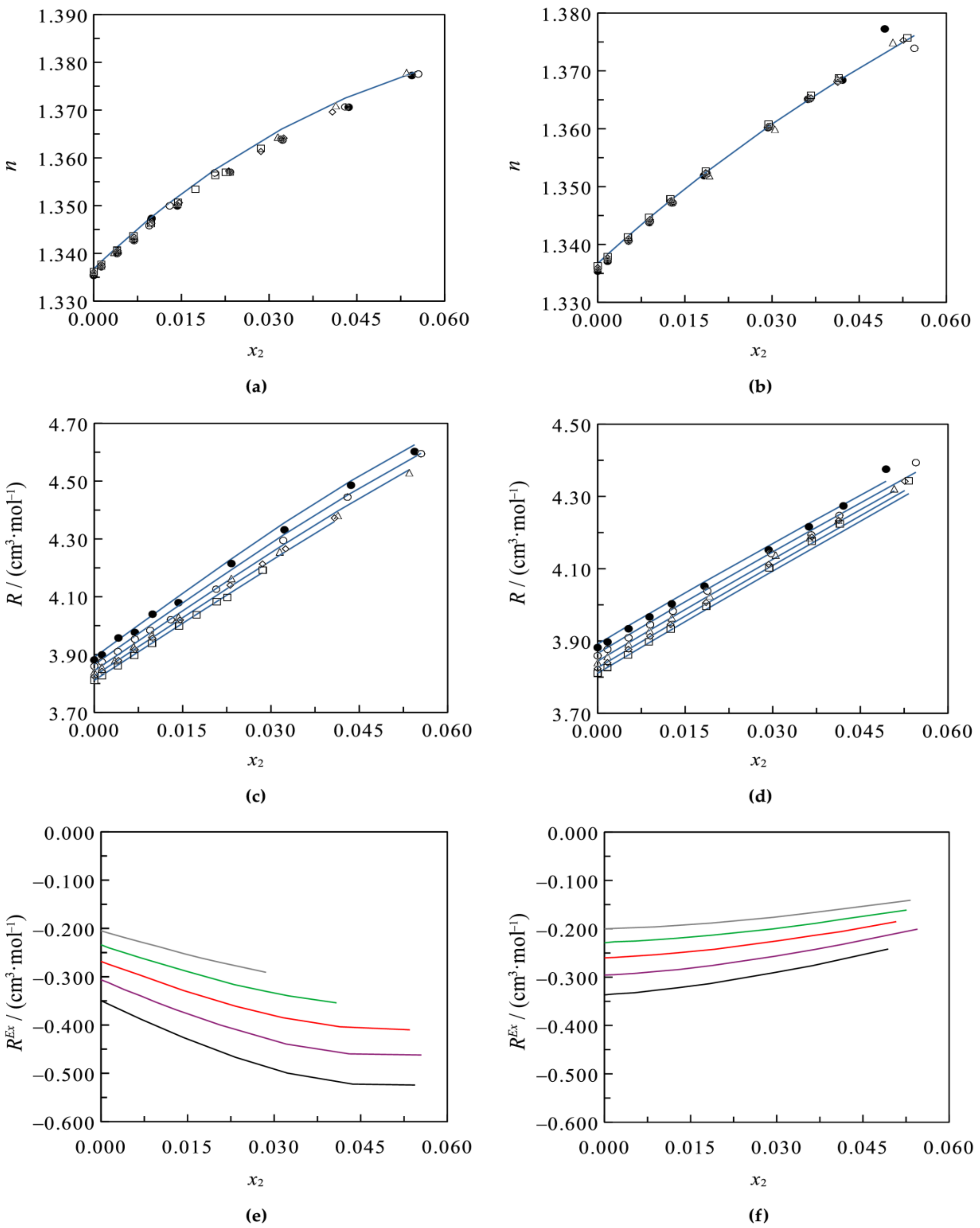
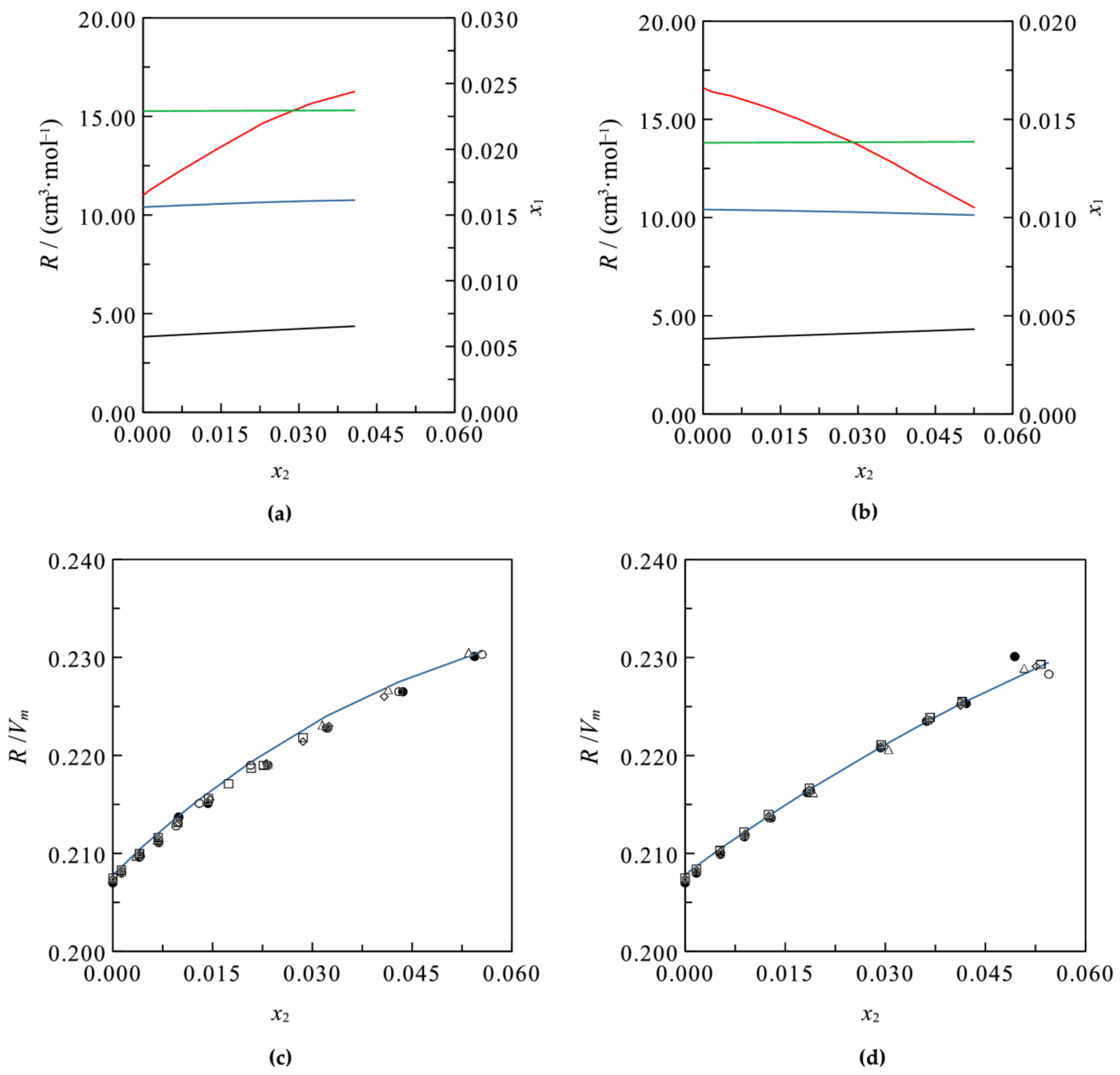
3.2. Ternary Systems
3.3. Models’ Estimation Applicability
4. Conclusions
- The proposed model represents appropriately the refractive index and molar refraction. It is robust and has interpolation and extrapolation capabilities.
- The method proposed to estimate the electronic polarizability coefficient of the solutes is simple and robust.
- The interactions of boric acid, sodium, potassium, lithium, chloride, and sulfate ions with water molecules are relevant to explain the behaviors of the molar refraction and the refractive index of the binary and ternary systems studied.
- For the binary aqueous solutions of lithium chloride and sodium chloride, the ion–ion interactions are also relevant.
- The solute concentration effect is greater than the temperature effect on the molar refraction and refractive index of the solutions studied.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- An, N.; Zhuang, B.; Li, M.; Lu, Y.; Wang, Z.-G. Combined Theoretical and Experimental Study of Refractive Indices of Water–Acetonitrile–Salt Systems. J. Phys. Chem. B 2015, 119, 10701–10709. [Google Scholar] [CrossRef]
- Biradar, U.V.; Dongarge, S.M. Refractive Index of Salt (NaCl) from Aquous Solution. Int. J. Comput. Inf. Sci. 2015, 4, 35–39. [Google Scholar]
- Wang, F.A.; Wang, J.Y.; Zhang, P.; Li, C.W.; Ren, B.Z. Measurement and Modeling of Refractive Indices for Multicomponent Chromium Compound Solutions. Chem. Eng. Technol. 2008, 31, 426–432. [Google Scholar] [CrossRef]
- Garces, I.; Reyes, J. Correlación Generalizada Para Predecir El Indice de Refracción En Soluciones Salinas Naturales. Modelo Predictivo Para El Sistema Na-Cl-SO4 a 1.0 Atm. Inf. Technol. 1997, 8, 189–194. [Google Scholar]
- Takubo, H. Refractive Index as a Measure for Saturation and Supersaturation in Crystal Growth of Water-Soluble Substances. J. Cryst. Growth 1990, 104, 239–244. [Google Scholar] [CrossRef]
- Galleguillos, H.R.; Flores, E.K.; Aguirre, C.E. Density and Refractive Index for Boric Acid + Potassium Chloride + Water and Disodium Tetraborate + Potassium Chloride + Water Systems at (20, 25, and 30) °C. J. Chem. Eng. Data 2001, 46, 1632–1634. [Google Scholar] [CrossRef]
- Tapia, J.; González, R.; Townley, B.; Oliveros, V.; Álvarez, F.; Aguilar, G.; Menzies, A.; Calderón, M. Geology and Geochemistry of the Atacama Desert. Antonie van Leeuwenhoek 2018, 111, 1273–1291. [Google Scholar] [CrossRef]
- Pavlovic-Zuvic, P. La industria del litio en Chile. Rev. Ing. 2014, 209, 24–29. [Google Scholar]
- Peiró, L.T.; Méndez, G.V.; Ayres, R.U. Lithium: Sources, Production, Uses, and Recovery Outlook. JOM 2013, 65, 986–996. [Google Scholar] [CrossRef]
- Alavia, W.; Lovera, J.A.; Cortez, B.A.; Graber, T.A. Solubility, Density, Refractive Index, Viscosity, and Electrical Conductivity of Boric Acid + Lithium Sulfate + Water System at (293.15, 298.15, 303.15, 308.15 and 313.15) K. J. Chem. Eng. Data 2013, 58, 1668–1674. [Google Scholar] [CrossRef]
- Kavanagh, L.; Keohane, J.; Garcia Cabellos, G.; Lloyd, A.; Cleary, J. Global Lithium Sources—Industrial Use and Future in the Electric Vehicle Industry: A Review. Resources 2018, 7, 57. [Google Scholar] [CrossRef]
- Pavlovic-Zuvic, P.; Parada-Frederick, N.; Vergara-Edwards, L. Recovery of potassium chloride, potassium sulfate and boric acid from the salar de atacama brines. In Proceedings of the 6th International Symposium on Salt, Toronto, ON, Canada, 24–28 May 1983; pp. 377–394. [Google Scholar]
- Ossandón, K.; Pinto, P.; Cisternas, L.A. Planning and Scheduling of Salt Harvest in Solar Evaporation Ponds. Comput. Chem. Eng. 2010, 34, 620–630. [Google Scholar] [CrossRef]
- Li, D.; Zeng, D.; Yin, X.; Gao, D.; Fan, Y. Phase Diagrams and Thermochemical Modeling of Salt Lake Brine Systems: IV. Thermodynamic Framework and Program Implementation for Multicomponent Systems. Calphad 2020, 71, 101806. [Google Scholar] [CrossRef]
- Guo, Y.; Song, J.; Zhao, K.; Yu, Y.; Deng, T. Solubilities, Densities and Refractive Indices of the Reciprocal Quaternary Systems (Na+, K+//Cl−, B5O8−-H2O) and (Li+, K+//Cl−, B5O8−-H2O) at 298.15 K and Atmospheric Pressure. Fluid Phase Equilibria 2020, 516, 112594. [Google Scholar] [CrossRef]
- Song, W.; Gang, H.; Ma, Y.; Yang, S.; Mu, B. Migration Behavior of Lithium during Brine Evaporation and KCl Production Plants in Qarhan Salt Lake. Minerals 2017, 7, 57. [Google Scholar] [CrossRef]
- Mohr, S.H.; Mudd, G.M.; Giurco, D. Lithium Resources and Production: Critical Assessment and Global Projections. Minerals 2012, 2, 65. [Google Scholar] [CrossRef]
- Guo, Y.; Li, L.; Cao, L.; Yu, X.; Wang, S.; Deng, T. Solubilities, Densities and Refractive Indices in the Aqueous Quaternary System of Lithium Sulfate, Lithium Metaborate, and Lithium Carbonate at 288.15, 298.15, 308.15 K and 0.1 MPa. J. Chem. Eng. Data 2017, 62, 508–515. [Google Scholar] [CrossRef]
- Alavia, W.; Lovera, J.A.; Graber, T.A.; Azúa, D.; Soto, I. Modeling of the Density, Viscosity and Electrical Conductivity of Aqueous Solutions Saturated in Boric Acid in Presence of Lithium Sulfate or Sodium Sulfate at 293.15 to 313.15 K. Fluid Phase Equilibria 2021, 532, 112864. [Google Scholar] [CrossRef]
- Pacak, P. Molar Refractivity and Interactions in Solutions. 1. Molar Refractivity of Some Monovalent Ions in Aqueous and Dimethyl Sulfoxide Solutions. Chem. Pap. 1989, 43, 489–500. [Google Scholar]
- Pacak, P. Molar Refractivity and Interactions in Solutions. 2. Molar Refractivity of Tetraalkylammonium Salts in Aqueous and Dimethyl Sulfoxide Solutions. Chem. Pap. 1989, 43, 501–505. [Google Scholar]
- Deosarkar, S.D.; Pandhare, V.V.; Kattekar, P.S. Densities and Refractive Indices of Potassium Salt Solutions in Binary Mixture of Different Compositions. J. Eng. 2012, 2013, 368576. [Google Scholar] [CrossRef]
- Li, M.; Zhuang, B.; Lu, Y.; Wang, Z.-G.; An, L. Accurate Determination of Ion Polarizabilities in Aqueous Solutions. J. Phys. Chem. B 2017, 121, 6416–6424. [Google Scholar] [CrossRef]
- Wang, C.C.; Tan, J.Y.; Liu, L.H. Wavelength and Concentration-Dependent Optical Constants of NaCl, KCl, MgCl2, CaCl2, and Na2SO4 Multi-Component Mixed-Salt Solutions. Appl. Opt. 2017, 56, 7662–7671. [Google Scholar] [CrossRef]
- Leyendekkers, J.V.; Hunter, R.J. The Tammann-Tait-Gibson Model for Aqueous Electrolyte Solutions: Application to the Refractive Index. J. Phys. Chem. 1977, 81, 1657–1663. [Google Scholar] [CrossRef]
- Leyendekkers, J.V.; Hunter, R.J. Refractive Index of Aqueous Electrolyte Solutions. Extrapolations to Other Temperatures, Pressures, and Wavelengths and to Multicomponent Systems. J. Chem. Eng. Data 1977, 22, 427–431. [Google Scholar] [CrossRef]
- Padova, J. Ion–solvent interaction in mixed solvents: Part III. The molar refraction of electrolytes. Can. J. Chem. 1965, 43, 458–462. [Google Scholar] [CrossRef]
- Li, M.; Lu, Y.; An, L. Ion Polarizabilities in Binary Liquid Mixtures of Water/Organic Solvents. J. Phys. Chem. B 2018, 122, 10023–10030. [Google Scholar] [CrossRef]
- Umaley, K.D.; Pethe, G.B.; Aswar, A.S. Volumetric, Viscometric, Acoustical, and Optical Studies of Glutamic Acid in Aqueous Zinc and Copper Chloride Solutions. Russ. J. Phys. Chem. B 2013, 7, 11–22. [Google Scholar] [CrossRef]
- Tan, C.-Y.; Huang, Y.-X. Dependence of Refractive Index on Concentration and Temperature in Electrolyte Solution, Polar Solution, Nonpolar Solution, and Protein Solution. J. Chem. Eng. Data 2015, 60, 2827–2833. [Google Scholar] [CrossRef]
- Baxter, G.P.; Boylston, A.C.; Mueller, E.; Black, N.H.; Goode, P.B. The refractive power of the halogen salts of lithium, sodium and potassium in aqueous solution. J. Am. Chem. Soc. 1911, 33, 901–922. [Google Scholar] [CrossRef][Green Version]
- Yu, X.; Wang, H.; Guo, Y.; Deng, T. Phase Equilibrium and Solvation Effect of the Ternary Mixture Solvent System (LiCl + CH3OH + H2O) at 298.15, 308.15 and 318.15 K. J. Solut. Chem. 2019, 48, 515–527. [Google Scholar] [CrossRef]
- Urréjola, S.; Sánchez, A.; Hervello, M.F. Refractive Indices of Sodium, Potassium, and Ammonium Sulfates in Ethanol–Water Solutions. J. Chem. Eng. Data 2010, 55, 2924–2929. [Google Scholar] [CrossRef]
- Silva, R.M.M.; Minim, L.A.; Coimbra, J.S.R.; Rojas, E.E.G.; da Silva, L.H.M.; Minim, V.P.R. Density, Electrical Conductivity, Kinematic Viscosity, and Refractive Index of Binary Mixtures Containing Poly(Ethylene Glycol) 4000, Lithium Sulfate, and Water at Different Temperatures. J. Chem. Eng. Data 2007, 52, 1567–1570. [Google Scholar] [CrossRef]
- Wang, F.A.; Chen, H.S.; Zhu, J.Q.; Song, J.C.; Wang, Z.C. Estimation of Excess Enthalpy for Binary Systems. Chem. Eng. J. 2002, 85, 235–243. [Google Scholar] [CrossRef]
- Stelson, A.W. Urban Aerosol Refractive Index Prediction by Partial Molar Refraction Approach. Environ. Sci. Technol. 1990, 24, 1676–1679. [Google Scholar] [CrossRef]
- Teodorescu, M.; Secuianu, C. Refractive Indices Measurement and Correlation for Selected Binary Systems of Various Polarities at 25 °C. J. Solut. Chem. 2013, 42, 1912–1934. [Google Scholar] [CrossRef]
- Krishna, T.S.; Nain, A.K.; Chentilnath, S.; Punyaseshudu, D.; Munibhadrayya, B. Densities, Ultrasonic Speeds, Refractive Indices, Excess and Partial Molar Properties of Binary Mixtures of Imidazolium Based Ionic Liquid with Pyrrolidin-2-One at Temperatures from 298.15L to 323.15K. J. Chem. Thermodyn. 2016, 101, 103–114. [Google Scholar] [CrossRef]
- Cai, C.; Miles, R.E.H.; Cotterell, M.I.; Marsh, A.; Rovelli, G.; Rickards, A.M.J.; Zhang, Y.; Reid, J.P. Comparison of Methods for Predicting the Compositional Dependence of the Density and Refractive Index of Organic–Aqueous Aerosols. J. Phys. Chem. A 2016, 120, 6604–6617. [Google Scholar] [CrossRef]
- Harvey, A.H.; Gallagher, J.S.; Sengers, J.M.H.L. Revised Formulation for the Refractive Index of Water and Steam as a Function of Wavelength, Temperature and Density. J. Phys. Chem. Ref. Data 1998, 27, 761–774. [Google Scholar] [CrossRef]
- Apelblat, A. A New Two-Parameter Equation for Correlation and Prediction of Densities as a Function of Concentration and Temperature in Binary Aqueous Solutions. J. Mol. Liq. 2016, 219, 313–331. [Google Scholar] [CrossRef]
- Patwardhan, V.S.; Kumar, A. A Unified Approach for Prediction of Thermodynamic Properties of Aqueous Mixed-Electrolyte Solutions: Part I: Vapor Pressure and Heat of Vaporization. AIChE J. 1986, 32, 1419–1428. [Google Scholar] [CrossRef]
- Patwardhan, V.S.; Kumar, A. A Unified Approach for Prediction of Thermodynamic Properties of Aqueous Mixed-Electrolyte Solutions: Part II: Volume, Thermal, and Other Properties. AIChE J. 1986, 32, 1429–1438. [Google Scholar] [CrossRef]
- Cottrel, A.; Lucchetti, R. Gretl: GNU Regression, Econometric and Time-Series Library. 2020. Available online: http://gretl.sourceforge.net/ (accessed on 2 March 2021).
- Tang, I.N.; Munkelwitz, H.R. Water Activities, Densities, and Refractive Indices of Aqueous Sulfates and Sodium Nitrate Droplets of Atmospheric Importance. J. Geophys. Res. Atmos. 1994, 99, 18801–18808. [Google Scholar] [CrossRef]
- Lühdemann, R. Über Die Konzentrationsabhängigkeit Der Äquivalentrefraktion Einiger Salze Und Säuren in Wässeriger Lösung. Zeitschrift für Physikalische Chemie 1935, 29B, 133–149. [Google Scholar] [CrossRef]
- Cheng, F.; Cao, Q.; Guan, Y.; Cheng, H.; Wang, X.; Miller, J.D. FTIR Analysis of Water Structure and Its Influence on the Flotation of Arcanite (K2SO4) and Epsomite (MgSO4·7H2O). Int. J. Miner. Process. 2013, 122, 36–42. [Google Scholar] [CrossRef]
- Pyper, N.C.; Pike, C.G.; Edwards, P.P. The Polarizabilities of Species Present in Ionic Solutions. Mol. Phys. 1992, 76, 353–372. [Google Scholar] [CrossRef]
- Conte, P. Effects of Ions on Water Structure: A Low-Field 1H T1 NMR Relaxometry Approach. Magn. Reson. Chem. 2015, 53, 711–718. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, A.A.; Simonson, J.M. Ion Association in Aqueous LiCl Solutions at High Concentration: Predicted Results via Molecular Simulation. J. Chem. Phys. 2006, 124, 154509. [Google Scholar] [CrossRef]
- Heydweiller, A. Optische Untersuchungen an Wasserigen Elektrolytlosungen. Physikalische Zeitschrift 1925, 26, 526–556. [Google Scholar]
- Pearson, R.G. Absolute Electronegativity and Hardness: Application to Inorganic Chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Ayers, P.W.; Melin, J. Further Links between the Maximum Hardness Principle and the Hard/Soft Acid/Base Principle: Insights from Hard/Soft Exchange Reactions. Phys. Chem. Chem. Phys. 2007, 9, 3853–3856. [Google Scholar] [CrossRef]
- Molina, J.J.; Lectez, S.; Tazi, S.; Salanne, M.; Dufrêche, J.-F.; Roques, J.; Simoni, E.; Madden, P.A.; Turq, P. Ions in Solutions: Determining Their Polarizabilities from First-Principles. J. Chem. Phys. 2011, 134, 014511. [Google Scholar] [CrossRef] [PubMed]
- Volkov, A.G.; Paula, S.; Deamer, D.W. Two Mechanisms of Permeation of Small Neutral Molecules and Hydrated Ions across Phospholipid Bilayers. Bioelectrochem. Bioenerg. 1997, 42, 153–160. [Google Scholar] [CrossRef]
- Tessman, J.R.; Kahn, A.H.; Shockley, W. Electronic Polarizabilities of Ions in Crystals. Phys. Rev. 1953, 92, 890–895. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and Soft Acids and Bases, HSAB, Part 1: Fundamental Principles. J. Chem. Educ. 1968, 45, 581. [Google Scholar] [CrossRef]
- Alavia, W.; Lovera, J.; Graber, T.A. Thermodynamic Modeling of the Solubility of Boric Acid in the Systems Boric Acid+lithium Sulfate + water, Boric Acid+sodium Sulfate + water and Boric Acid + potassium Sulfate + water at 293.15–313.15K. Fluid Phase Equilibria 2015, 398, 63–71. [Google Scholar] [CrossRef]









| System | Temperature Range (K) | Refractive Index | Density | ||
|---|---|---|---|---|---|
| Maximum Concentration (Mol·kg−1) | Reference | Maximum Concentration (Mol·kg−1) | Reference | ||
| H3BO3+H2O | 293.15, 298.15, 303.15 | 1.0000 | [6] | 1.0000 | [6] |
| Na2SO4+H2O | 288.15, 298.15, 308.15, 318.15 | 3.42297 | [33] | 2.2250 (273.15–372.15) K | [41] |
| Li2SO4+H2O | 278.15, 298.15, 308.15, 318.15 | 2.2740 | [34] | 2.2740 | [34] |
| K2SO4+H2O | 288.15, 298.15, 308.15, 318.15 | 0.90485 | [33] | 0.71 | [41] |
| NaCl+H2O | 293.15, 298.15, 303.15, 308.15, 313.18, 318.15 | 6.0190 | [30] | 6.0111 (273.15–368.15) K | [41] |
| LiCl+H2O | 298.15, 308.15, 318.15 | 3.5557 Saturation | [31] [32] | 3.315 | [31] [32] |
| KCl+H2O | 293.15, 298.15, 303.15 | 4.0000 | [6] | 4.0000 | [6] |
| H3BO3+Na2SO4+H2O | 293.15, 298.15, 303.15, 308.15, 313.15 | 3.3242 | [19] | 3.3242 | [19] |
| H3BO3+Li2SO4 +H2O | 293.15, 298.15, 303.15, 308.15, 313.15 | 3.14720 | [10] | 3.14720 | [10] |
| H3BO3+KCl+H2O | 293.15, 298.15, 303.15 | 1.0269 a | [6] | 1.0269 a | [6] |
| System | bj/ (cm3·mol−1) | R∞,0ja/ (cm3·Mol−1) | R∞,1j/ (cm3·Mol−1·K−1) | R∞j/ (cm3·Mol−1) | SE/ (cm3·Mol−1) | r2 |
|---|---|---|---|---|---|---|
| H3BO3+H2O | −47.4674 ± 10.7813 a | 9.6379 ± 0.1494 | 0 | 0.0002 | 0.9866 | |
| Na2SO4+H2O | −1.0000 | 15.2688 ± 0.0298 | 0 | 15.34 ± 0.09 c [36] 15.13 ± 0.04 d [45] | 0.00064 | 0.9981 |
| Li2SO4+H2O | −1.0000 | 13.8070 ± 0.1329 | 0.0218 ± 0.0089 b | 12.81 e | 0.00136 | 0.9825 |
| K2SO4+H2O | −1.0000 | 18.6035 ± 0.0851 | 0 | 19.55 ± 0.21 c [36] | 0.00046 | 0.9894 |
| NaCl+H2O | 1.0000 | 9.4808 ± 0.0221 | 0 | 9.20 ± 0.18 c [36] 9.26 [46] | 0.0007 | 0.9977 |
| LiCl+H2O | 1.0000 | 8.5582 ± 0.0098 | 0 | 8.74 [46] | 0.0005 | 0.9999 |
| KCl+H2O | −1.0000 | 11.2102 ± 0.0280 | 0 | 11.25 ± 0.06 [36] | 0.0005 | 0.9985 |
| Compound | αe (Å3) a | αe (Å3) b | αe (Å3) c | αe (Å3) d |
|---|---|---|---|---|
| H3BO3 | 3.820 | |||
| Na2SO4 | 5.988 | 4.907 ± 0.083 | 3.978 | 5.921 |
| Li2SO4 | 5.473 | 4.528 ± 0.052 | 3.734 | 5.544 |
| K2SO4 | 7.374 | 6.224 ± 0.128 | ||
| NaCl | 3.758 | 3.532 ± 0.034 | 2.391 | 3.65 |
| LiCl | 3.392 | 3.271 ± 0.033 | 2.262 | 3.462 |
| KCl | 4.443 | 4.126 ± 0.024 | 2.931 | 4.465 |
| Ion | rbare (Å) a | αe (Å3) | αe (Å3) b | αe (Å3) cryst c | η d | HSAB Classification e |
|---|---|---|---|---|---|---|
| Li+ | 0.94 | 0.03 | 0.03 | 0.03 | 35.12 | Hard acid |
| Na+ | 1.17 | 0.4 | 0.279 ± 0.001 | 0.41 | 21.08 | Hard acid |
| K+ | 1.49 | 1.08 | 0.873 ± 0.009 | 1.33 | 13.64 | Hard acid |
| Cl− | 1.64 | 3.36 | 3.253 ± 0.033 | 2.96 | 4.70 | Hard base |
| SO42− f | 5.28 | 4.432 ± 0.110 | Hard base |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alavia, W.; Soto, I.; Lovera, J.A. Modeling of the Refractive Index for the Systems MX+H2O, M2X+H2O, H3BO3+MX+H2O, and H3BO3+M2X+H2O. M = K+, Na+, or Li+ and X = Cl− or SO42−. Processes 2021, 9, 525. https://doi.org/10.3390/pr9030525
Alavia W, Soto I, Lovera JA. Modeling of the Refractive Index for the Systems MX+H2O, M2X+H2O, H3BO3+MX+H2O, and H3BO3+M2X+H2O. M = K+, Na+, or Li+ and X = Cl− or SO42−. Processes. 2021; 9(3):525. https://doi.org/10.3390/pr9030525
Chicago/Turabian StyleAlavia, Wilson, Ismael Soto, and Jorge A. Lovera. 2021. "Modeling of the Refractive Index for the Systems MX+H2O, M2X+H2O, H3BO3+MX+H2O, and H3BO3+M2X+H2O. M = K+, Na+, or Li+ and X = Cl− or SO42−" Processes 9, no. 3: 525. https://doi.org/10.3390/pr9030525
APA StyleAlavia, W., Soto, I., & Lovera, J. A. (2021). Modeling of the Refractive Index for the Systems MX+H2O, M2X+H2O, H3BO3+MX+H2O, and H3BO3+M2X+H2O. M = K+, Na+, or Li+ and X = Cl− or SO42−. Processes, 9(3), 525. https://doi.org/10.3390/pr9030525






