Abstract
A symmetrical NACA 0018 airfoil is often used in such applications as small-to-medium scale vertical-axis wind turbines and aerial vehicles. A review of the literature indicates a large gap in experimental studies of this airfoil at low and moderate Reynolds numbers in the previous century. This gap has limited the potential development of classical turbulence models, which in this range of Reynolds numbers predict the lift coefficients with insufficiently accurate results in comparison to contemporary experimental studies. Therefore, this paper validates the aerodynamic performance of the NACA 0018 airfoil and the characteristics of the laminar separation bubble formed on its suction side using the standard uncalibrated four-equation Transition SST turbulence model and the unsteady Reynolds-averaged Navier-Stokes (URANS) equations. A numerical study was conducted for the chord Reynolds number of 160,000, angles of attack between 0 and 11 degrees, as well as for the free-stream turbulence intensity of 0.05%. The calculated lift and drag coefficients, aerodynamic derivatives, as well as the location and length of the laminar bubble quite well agree with the results of experimental measurements taken from the literature for validation. A sensitivity study of the numerical model was performed in this paper to examine the effects of the time-step size, geometrical parameters and mesh distribution around the airfoil on the simulation results. The airfoil data sets obtained in this work using the Transition SST and the k-ω SST turbulence models were used in the improved double multiple streamtube (IDMS) to calculate aerodynamic blade loads of a vertical-axis wind turbine. The characteristics of the normal component of the aerodynamic blade load obtained by the Transition SST approach are much better suited to the experimental data compared to the k-ω SST turbulence model.
1. Introduction
The aerodynamic performance of almost all micro-air-aircraft, high-altitude unmanned-air-vehicles, compressor blades in turbomachines, and wind turbines is strongly influenced by laminar separation bubbles, which may form at low Reynolds numbers [1,2,3]. The presence of a laminar separation bubble in the boundary layer increases its thickness, which also increases the drag of the airfoil that can be several times larger in comparison with the drag of the airfoil without a bubble. The lift, moment and stall behavior of airfoils can also be affected by a laminar separation bubble [4,5]. The presence of bubbles, which are an attribute of low Reynolds numbers, can also cause problems during wind tunnel measurements due to undesirable scale effects [6,7]. Vertical-axis wind turbines have recently attracted a lot of interest in small structures installed in an urban environment [8,9,10,11], as well as in medium power structures [12] and offshore multi-MW turbines [13,14,15]. Simplified momentum methods and vortex models are still widely used engineering tools for analyzing the aerodynamic performance of vertical axis wind turbines [16]. The momentum-based models and vortex models are still popular because of their simplification and speed of computation, which is a very important advantage in the design process [11]. As shown in the literature, appropriate modifications of these models can significantly improve the accuracy of the obtained results [16,17,18]. However, simplified methods require external 2D airfoil data. The precision of the simplified methods depends on the quality of these data. As can be seen when comparing older experimental data with modern ones, there are considerable differences in polar data [4,19,20,21]. Quite significant differences in the results of polar data can also be seen in numerical analysis [19,22]. Differences in experimental data sets may result, inter alia, from different conditions of the undisturbed flow stream [21]. The problems that occur in the numerical data result from the fact that the phenomena of laminar-turbulent transition in the boundary layer are not taken into account [23]. Therefore, it is very important to understand the characteristics of the laminar separation bubble to improve airfoil design methods. Another possible approach would be to use other modern-day techniques, e.g., system identification, but unfortunately this would significantly increase the costs and evaluation time [24,25].
Depending on the flow class, the mechanism of the laminar-turbulent transition may be different. The natural transition process is due to flow instabilities in the laminar boundary layer known as Tollmien-Schlichting (T-S) waves. Viscosity destabilizes the T-S waves that start to grow, which leads to three-dimensional non-linear disturbances which eventually transform into turbulent spots [26,27,28]. In turbomachinery applications such as turbines or compressors, the bypass transition imposed on the boundary layer by high freestream turbulence is the main transition mechanism [23,29,30,31]. Separation-induced transition is also a very important transition mechanism. In this case, a laminar boundary layer separates due to the influence of a pressure gradient, whereas the transition process develops in the separated shear layer [32,33]. In the range of Reynolds numbers between 10,000 and the laminar boundary layer on the upper surface of the airfoil is prone to separation. The separated shear layer strongly modifies the flow. For Reynolds numbers below , the flow does not reattach, but a wide wake is visible behind the airfoil. In the case of higher Reynolds numbers, this separated flow may undergo laminar to turbulent transition. The turbulent flow can reattach to the airfoil surface creating the laminar separation bubble. This phenomenon is caused by a strong adverse pressure gradient that makes the laminar boundary layer to separate from the curved surface of the airfoil. An increase in pressure is associated with the decrease in velocity towards the trailing edge of the airfoil. When the laminar layer is separated from the airfoil surface, the result is a wedge-shaped recirculation area. The separated laminar flow eventually turns into turbulent flow. The transition region is not located on the surface of the airfoil, but is observed on the outer boundary of the separated flow away from the airfoil. The reattachment point is the point where the turbulent boundary layer again meets the airfoil surface. The volume of fluid limited by these two regions of separated laminar flow and turbulent flow is called a laminar separation bubble (Figure 1). Inside this volume, a circulating zone is formed in which there is almost no energy exchange with the outer flow, which makes the laminar bubble more stable [6,21]. A laminar separation bubble can be characterized by its size and location. These parameters depend on the airfoil profile, the angle of attack, the turbulence intensity, and freestream Reynolds number [2,34,35]. Bubbles are classified as short or long depending on what percentage of the chord length it occupies. The size of the bubble affects the pressure distribution characteristics. Short bubbles whose size does not exceed one percent of the chord length contribute much less to these distributions than long bubbles [34].
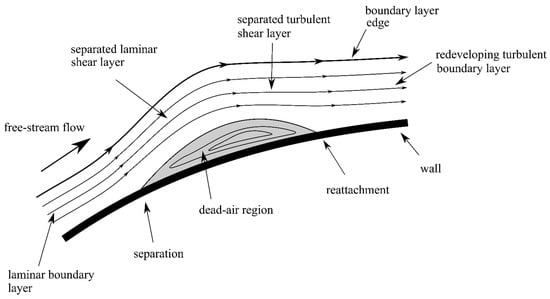
Figure 1.
Laminar separation bubble—reproduced from [2].
Despite the fact that the NACA airfoils of the four-digit series were developed many decades ago, they are still widely used in the design of Darrieus wind turbines [14,36]. Roh et al. [37] investigated, among other things, the shape of the blade profiles in the performance of a straight-bladed Darrieus wind turbine using the multiple stream tube (MST) method. His findings indicate that symmetrical airfoils have better performance in terms of maximum aerodynamic efficiency and minimal drag compared to cambered profiles. In addition, the thicker profiles provided higher aerodynamic efficiency at lower tip speed ratios compared to the thinner airfoils. Similar findings were also obtained by, among others, Mohamed [38] and Islam et al. [39]. As already mentioned in the previous two paragraphs of this section, transition phenomena occur on its surface during the flow around the profile in the range of low Reynolds numbers.
One of the first experimental results of the aerodynamic characteristics of NACA 0018 were performed by Jacobs and Sherman in 1937 [40]. However, the results obtained by these authors suffer from too high a level of turbulence in the variable density tunnel. Timmer [41] reported that an effective Reynolds number was much higher than the test Reynolds number in the experiment. The characteristics of the NACA 0018 airfoil at low Reynolds numbers were also measured by Laneville and Vittecoq in 1986 [22,42]. However, the measurements of the static airfoil characteristics were performed for only one Reynolds number, equal to 38,000. To the best of the authors’ knowledge, and according to Timmer [41], until 2008, no other experimental datasets of this airfoil had been published at low and medium Reynolds numbers. Sheldahl and Klimas published a comprehensive database of seven symmetric airfoils (NACA-0009, -0012, -0012H -0015, -0018, -0021, -0025) in 1981 over a very wide range of angles of attack and Reynolds numbers [43]. These data, however, differ significantly from other modern measurements [19,22]. This is probably due to the extrapolation procedure used by these authors to obtain the NACA 0018 airfoil characteristics for low Reynolds numbers. However, this database is very often used in simplified aerodynamic models for Darrieus wind turbines [20]. In more recent studies using more modern measurement techniques, the transition effects are more visible [4,19,21,41,44,45,46]. These are experimental studies in which the flow conditions are also the closest to those considered in this article. One of the main differences between these studies is the value of the turbulence intensity at the inlet of the wind tunnel: <0.07% [41], <0.1% [19,46], <0.2% [45], <0.3% [21]. The results of experimental studies are mostly aerodynamic forces, less often velocity profiles in the boundary layer, pressure distributions and characteristics of a laminar bubble.
Modern methods of computational fluid dynamics (CFD) allow for a much more accurate analysis of the flow structures around an airfoil. Before the transition turbulence models appeared on the market, the main tools in the hands of an engineer were turbulence models considering the entire boundary layer as turbulent. Interestingly, in the range of low Reynolds numbers, classical two-equation turbulence models, for example the k-ω or k-ε models, predict aerodynamic forces (mainly lift) similar to the experimental results obtained by Sheldahl and Klimas [22,47,48,49]. However, the analysis of transition phenomena requires an appropriate approach. The impact of laminar-turbulent transition effects is not considered in most of today’s CFD analysis. The reason for this is that transition models have been developed to simulate specific flow classes and not the entire flow spectrum as with industrial turbulence models. One of the reasons for this was that there are different transition mechanisms. The second reason is the lack of appropriate procedures to describe transition flows with linear and non-linear effects in a typical Reynolds-averaged Navier–Stokes (RANS) approach. One of the most recent approaches developed in recent years to model transition phenomena is the correlation-based model—the Transition SST turbulence model [50,51]. Compared to previous transition approaches, the Transition SST turbulence model finds the transition based on local flow conditions by using a transport equation that tracks these local conditions. Earlier transition models, such as, e.g., the eN model proposed by Smith and Gamberoni [52], proved difficult to implement in modern general-purpose CFD codes and were based on global flow parameters [51]. In the case of numerical analysis of the airfoil in a homogeneous flow, this approach does not have to give unreasonable results for the location of the transition [2]. A much greater challenge for a transition turbulence model is the correct determination of the transition characteristics in the boundary layer of the airfoil in a flow of variable turbulence intensity, e.g., in the case of a blade of the Darrieus wind turbine rotor [53]. This, however, requires the turbulence model to use local turbulence parameters to analyze the transition characteristics. Quite extensive research on the characteristics of the laminar separation bubble on the NACA 0021 airfoil and in the range of low Reynolds numbers was carried out by Choudhry et al. using the Transition SST and approaches [2]. Choudhry et al. reported that, due to the generation of additional turbulence, the Transition SST predicted earlier reattachment as compared to the experiments and the . Melani et al. [19] compiled many experimental and numerical aerodynamic characteristics of the NACA 0018 airfoil at low and moderate Reynolds numbers. The data sets collected in their work suggest that the lower the Reynolds number, the larger the differences in the results of the aerodynamic forces, especially for Reynolds numbers in the range from 40 k to 160 k. Melani at al. [19] also presented the lift force characteristic for the Reynolds number of 150 k obtained using the Transition SST approach, these data are also available in [54]. The results indicate a high agreement with the experiments in the range of angles of attack up to 6 degrees. To the best of the authors’ knowledge, [19] is the only work in which the NACA 0018 airfoil performance was analyzed in a similar range of Reynolds numbers using the Transition SST turbulence approach.
This article uses the original Transition SST approach implemented in ANSYS Fluent code. The numerical results of the aerodynamic forces obtained in this paper are very similar to those published by Melani at al. [19]. Additionally, this article presents the characteristics of a laminar separation bubble, which was not taken into account in the work of Melani et al. [19]. The results of the numerical tests presented in this article are the starting point for future research towards the calibration of the original Transition SST model. This article places particular emphasis on examining the sensitivity of the numerical model, providing the reader with the information needed for further research (Section 2). Furthermore, a test case of the application in practice of the obtained airfoil data in a simplified analytical method to predict the aerodynamic loads of the Darrieus rotor blade is presented here (Section 4).
2. Numerical Methods
The present numerical investigation uses the well-known NACA 0018 airfoil (Figure 2a) designed by the National Advisory Committee for Aeronautics (NACA). In this paper, a numerical analysis is carried out on a two-dimensional airfoil section with chord length c of 1 m at a Reynolds number of 160,000. The freestream flow is clean, and the turbulence intensity corresponds to wind tunnel experiments by Timmer [41]. In Timmer’s measurements, the turbulence intensity in the test section varies from 0.02% do 0.07%. In this paper, the turbulence intensity is assumed to be 0.05%. The effect of turbulence intensity on the aerodynamic characteristics of the airfoil was not investigated in these studies. The other flow parameters were as follows: the density of the air , the dynamic viscosity of the air .
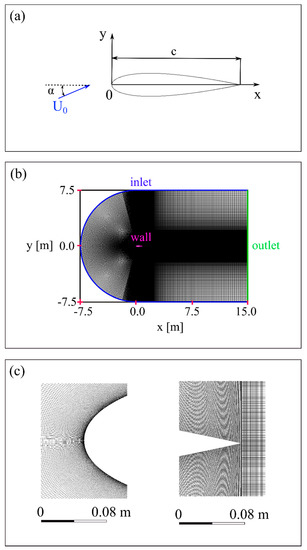
Figure 2.
The NACA 0018 airfoil and the definition of the angle of attack (a); C-type structured mesh around the airfoil and the boundary conditions (b); the mesh in the vicinity of the leading edge and the trailing edge of the NACA 0018 airfoil (c).
The incompressible, two-dimensional Unsteady Reynolds Averaged Navier–Stokes (URANS) equations were employed, with the SIMPLE pressure velocity coupling scheme and second-order discretization for all variables. The Green-Gauss Node-Based method was chosen in these simulations [55]. The flow around the NACA 0018 airfoil was numerically investigated using the commercial Computational Fluid Dynamics (CFD) code ANSYS Fluent 19.1 [56]. To investigate the aerodynamic characteristics of the NACA 0018 airfoil, the four-equations transition SST turbulence model was adopted [23]. This correlation-based approach using local flow variables was developed to simulate a wide range of engineering flows. It is based on the well-known two-equation k-ω Menter’s Shear Stress Transport (SST) turbulence model, which models the turbulent kinetic energy and the rate of its dissipation [57].
Simulations were performed using a C-mesh surrounding the NACA 0018 airfoil and extending 7.5c from the semicircular edge of the domain and 15c from the vertical edge of the domain. On the vertical edge of the domain, the “pressure outlet” boundary condition was assumed, and the “velocity inlet” boundary condition on the remaining edges of the domain was taken into account. Of course, there was a “wall” boundary condition at the airfoil edges, ensuring zero velocity on the airfoil surfaces. In this paper, the turbulence intensity was assumed to be 0.05%. The turbulent intensity near the leading edge of the airfoil was 0.005%. The second very important parameter determining the turbulence is its scale. In this work, the value of the turbulent length scale at the inlet was determined on the basis of earlier analysis by Rogowski [49] and the suggestion of ANSYS Fluent Theory Guide 19.0 [56]: the length scale, l, was calculated based on the boundary layer thickness, δ99, as l = 0.4 δ99. The thickness of the boundary layer was estimated based on velocity profile close to the airfoil surface for the angle of attack of 0 deg. For all simulations presented in this paper, the turbulence length scale was established to be 0.001 m. The intermittency at the inlet was equal to 1. The effect of turbulence intensity and intermittency on the aerodynamic characteristics of the airfoil was not investigated in these studies. The center of the first cell over the airfoil surface is located at a nondimensional height of . The mesh, presented in Figure 2b,c, consisted of 700,400 elements. The number of mesh points on the airfoil edges was 830. Originally, the NACA 0018 airfoil had a blunt trailing edge, but in these studies it was assumed that the trailing edge of the airfoil was sharp.
The independence study of the mesh presented in Figure 2 and described above is shown in Figure 3. These tests were carried out for an angle of attack equal to 6 degrees and for five grids with a different number of mesh points on the airfoil. The basic parameters of the grids used in this analysis are given in Table 1. As can be seen in Figure 3, as the total number of mesh elements increases, the lift coefficient increases. However, starting from Case 3, the increase in this coefficient is almost negligible. The increase in the lift coefficient for the last case (Case 5), in comparison with the penultimate case (Case 4), is around 0.05%. In the case of the drag coefficient, first a decrease is observed, and then a slight increase. However, starting from Case 3, an almost constant value of this aerodynamic force coefficient can be observed. The mesh independence study carried out proved that the aerodynamic characteristics of the airfoil did not depend on the mesh, starting from Case 3.
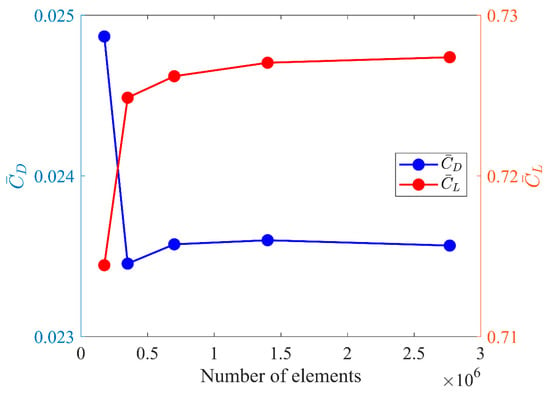
Figure 3.
Mesh independence study for NACA 0018.

Table 1.
Mesh parameters for mesh independence study.
Another very important aspect of CFD calculations is the size of the computing domain. The cases described in the literature are generally consistent in terms of domain size compared to the chord length of the airfoil. They indicate, however, that the influence of the domain size on the accuracy of the obtained CFD results depends on the type of mesh selected, its density, and the physical properties of the flow [58]. The simulations presented in this paper were carried out for an angle of attack of 6 degrees and for three mesh sizes. The domains differed by the value of the radius of the semi-circular front edge, . The radius was measured from the origin of the coordinate system placed at the leading edge of the airfoil to the half-circular boundary of the computational domain (please see Figure 2). These radii were 3.75c for the smallest domain, 7.5c, and 15c for the largest domain. The density of the mesh elements around the airfoil was identical for all investigated cases—that is, the number of mesh points at the edges of the airfoil was 830 and the growth rate of the grid elements in a direction normal to the airfoil edges was identical. The total number of elements in the smallest mesh was 432,600, and in the largest one the total number was 1,486,800. The averaged values of the lift and drag coefficients are presented in Table 2. The simulation time in these tests was 10 s. Of course, the simulation time is also important in CFD simulations; however, this aspect will be discussed in detail in the next paragraph. The results presented in Table 2 were averaged for the last 9th second. The largest differences in the aerodynamic force coefficients can be observed for the smallest investigated domain. The last two columns in Table 2 show the percent increase in the lift and drag coefficients. The lift coefficient for the medium domain differs by 0.18% compared to the large domain whereas the drag coefficient by 0.82%. When comparing the medium domain with the smallest domain, the difference in lift coefficient is 0.43%, and the difference in drag coefficient is 3.28%. Therefore, it can be concluded that the optimal results of the aerodynamic characteristics can be obtained using the medium computational domain. In the present study, the distance to the vertical computational domain outlet from the trailing edge of the airfoil was not investigated, and in all simulations this was equal to 14c, which has been confirmed to be sufficiently large for such simulations [59,60].

Table 2.
Effect of computing domain size.
As mentioned above, the length of the simulation time period is also a very important aspect in CFD simulations. Before starting the calculation process, the initial conditions must be specified. The easiest way is to assume uniform velocity and pressure throughout the zone. At the beginning of the transient calculations, however, significant oscillations of the aerodynamic force coefficients appeared—this is an effect of the initial conditions. Numerical simulations must run until this effect disappears. The characteristics of the aerodynamic force coefficients of the NACA 0018 airfoil as a function of the simulation time for all angles of attack analyzed in this work are presented in Figure 4. The time step size was assumed to be 0.0001 s. The effect of the time step size will be discussed in more detail below. As can be seen from Figure 4, depending on the angle of attack, after 4–7 s, the effects associated with homogeneous initial conditions disappeared. For an angle of attack of 0 degrees, both components of the aerodynamic force were the largest. This is typical behavior for transient flows. However, when increasing the angle of attack, these oscillations disappeared. It is possible that this effect was related to the appearance of a laminar-turbulent bubble. As shown in the results section of this paper, a bubble is present on both the pressure and suction side of the airfoil; however, the separation of the boundary layer and its reattachment was only visible up to an angle of attack of 2 degrees for the pressure side. On the other hand, the presence of a bubble on the suction side was visible throughout the investigated range of angles of attack. The presence of the laminar separation bubbles changes the flow conditions in such a way that an additional camber can be seen by the outer flow, making the flow more stable [41]. In this work, all of the results presented in Figure 4 were averaged for every one second. Standard deviation was also calculated for each averaged interval. Figure 5 shows the averaged values of the aerodynamic force coefficients and their standard deviation. The results shown in this figure are only for an angle of attack of 6 degrees. The results of the mean values of the aerodynamic forces, along with their standard deviation for the 9th second of simulation and for the entire investigated range of angles of attack, are presented in this paper in the results section and discussed in detail. When analyzing the characteristics of the standard deviation as a function of simulation time, it can be seen that this value is close to zero from 8 s of movement for the lift coefficient and from 7 s of movement for the drag coefficient.
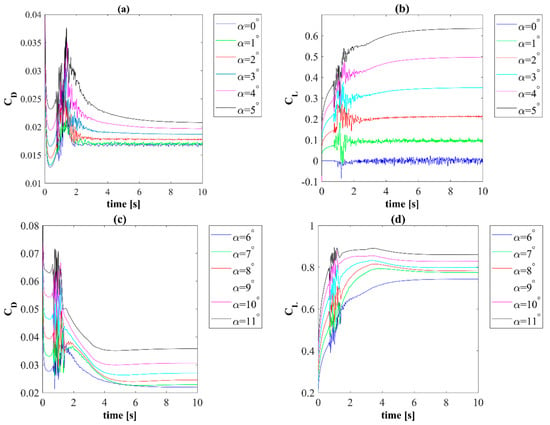
Figure 4.
Characteristics of the aerodynamic force coefficients of the NACA 0018 airfoil as a function of the simulation time: (a,c) Drag coefficients; (b,d) Lift coefficients.
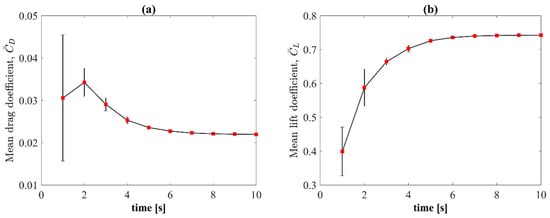
Figure 5.
Averaged values of the aerodynamic force coefficients and their standard deviation at 6. degrees. (a) Mean drag coefficient; (b) Mean lift coefficient.
In all of the results presented in this paper, the time step size was assumed to be 0.0001 s. In the URANS approach, the choice of an appropriate time step size is a crucial issue for correctly capturing flow behavior around the airfoil [48,61]. To investigate the effect of the time step size on the value of the aerodynamic force coefficients, we chose four time step lengths: 0.00001, 0.0001, 0.001, and 0.01. The same level of residuals of was set for all numerical analyses for all calculated variables. For the time-dependent solution using the implicit formulation, ANSYS Fluent requires multiple iterations to be specified at each time step. This value sets the maximum number of iterations per time step. If the convergence criterion is not met, this number of iterations will be calculated, and the solution will be carried out at the next step. In these studies, this value was assumed to be 20. For fully implicit formulation, there is no stability criterion that needs to be fulfilled in order to determine the time step size. However, in unsteady simulation, a good way to judge whether the assumed time step is sufficient is to observe whether the convergence criterion has been met at each time step after 5–10 iterations [56]. In all the cases analyzed in this work, the assumed convergence criterion was met, also for each investigated time step mentioned above. The convergence analysis for the aerodynamic force coefficients was performed for an angle of attack equal to 6 degrees, and the results are presented in Figure 6. To make the results readable, a linear scale is used for the Y-axis, whereas a logarithmic scale is used for the X-axis. As can be seen from Figure 6, for the two smallest time steps analyzed, there is practically no difference in the results of either the lift coefficient or the drag coefficient. Therefore, for the further research reported in this paper, we used a time step of 0.0001 s.
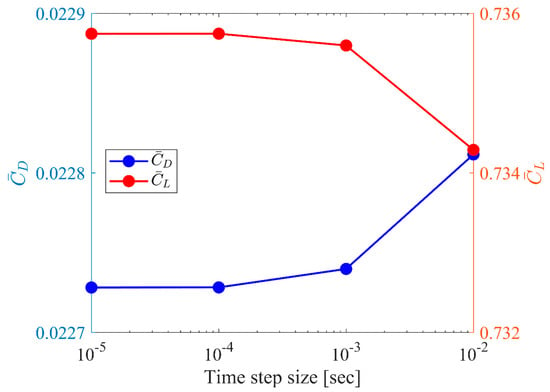
Figure 6.
Averaged lift and drag coefficients versus time step size.
3. Simulation Results and Validation
In the previous section, the numerical model was discussed in detail, along with the sensitivity analysis of the solution due to various model parameters. This section provides results ranging from “developer” results of the aerodynamic force coefficients to detailed flow field parameters. The validation of the obtained results was carried out using the experimental results available in the literature.
3.1. Lift and Drag Coefficients
This subsection presents the results of the aerodynamic force coefficients for a series of angles of attack from 0 to 11 degrees. The results for the Transition SST turbulence model are presented in graphs (Figure 7 and Figure 8) and in Table 3, so that they can be used effectively by every reader. All the experimental series used in this paper for comparison come from the available literature [4,21,41,46]. The results of numerical analysis used to compare our airfoil data set calculated using the Transition SST turbulence model come from both the literature [19] and the authors’ previous research [47]. Kątski and Rogowski [47] conducted numerical studies on the NACA 0018 airfoil using the k-ω SST approach and a hybrid mesh: structured in the vicinity of the airfoil edges, and non-structured in the remaining area. Additionally, in this work, two more series of calculations were performed: one using the k-ω SST model implemented in FLOWer solver [11], and the other using the XFOIL tool.
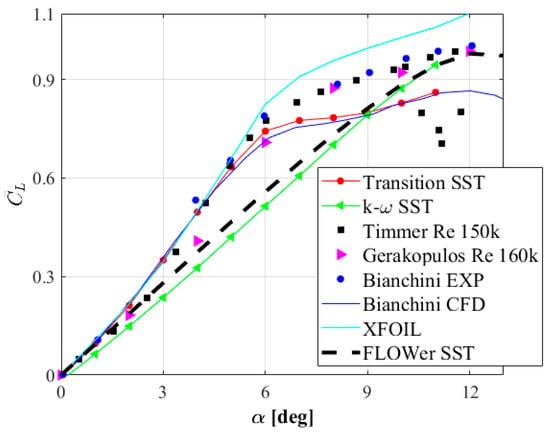
Figure 7.
Lift coefficient versus angle of attack. Validation of the CFD results with the experimental and numerical data [19,21,41,47].
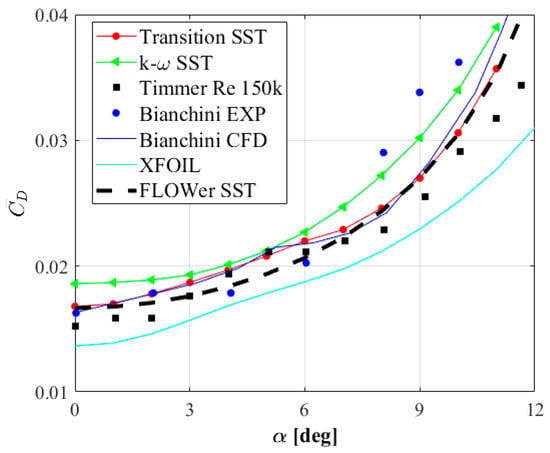
Figure 8.
Drag coefficient versus angle of attack. Validation of the CFD results with the experimental and numerical data [19,41,47].

Table 3.
Tabulated values of the lift and drag coefficients with standard deviation.
As can be seen from Figure 7, all numerical approaches except the k-ω SST turbulence models agree well with all experiments up to an angle of attack of 6 degrees, and differ slightly for the rest of the characteristics. In Figure 7, it can be seen that the lift coefficient curve has two slopes (two aerodynamic derivatives, ) ranging from zero to the critical angle of attack (stall angle). The range of angles of attack in the first region extends from 0 to 6 degrees, and the other from 6 to 11 degrees. The lift force coefficient curve is almost linear in each of these regions; however, the slope of the curve in the first region is steeper. All the experiments used in this work for comparison show a similar trend. The presence of two regions on the lift force coefficient characteristic is related to boundary layer and separated shear layer development. Gerakopoulos et al. [21] estimated the first region for the range of angles of attack to be from 0 to 8 degrees, and the second region for the range of angles of attack to be from 10 to 14 degrees. The 3D effects, which were not taken into account in the CFD analysis, are probably responsible for the underestimation of the first region. The aerodynamic derivative estimated by Gerakopulos et al. is 0.11 for the first region and 0.02 for the second. Based on CFD tests, these values were found to be 0.12 for the first region and 0.0197 for the second region, respectively. The results obtained with the XFOIL code were also correctly estimated up to an angle of attack of 6 degrees. For this approach, the first region was also limited to this angle of attack. Above an angle of 6 degrees, the results of were slightly overestimated compared to the experiment.
As can be seen from Figure 7, the lift coefficient characteristic obtained by the k-ω SST approach differs from the other characteristics. This is because the k-ω SST turbulence model takes into account the entire boundary layer on the airfoil as a turbulent layer. Therefore, for the lift coefficient characteristic, the laminar bubble is absent, and the actual values of the lift coefficient provided by this model are lower than the experimental values.
The drag coefficient results are shown in Figure 8. The minimum experimental values of this coefficient are 0.0152 in the case of Timmer’s studies [41] and 0.016 in the case of the measurements of Bianchini [19]. The minimum value obtained by the Transition SST model used in this work was equal to 0.0168, which is close to the value of 0.0163 obtained by Bianchini [19]. The FLOWer solver estimated a minimum drag coefficient of 0.01667. The numerical approach using ANSYS Fluent code, the hybrid mesh and the k-ω SST turbulence model most overestimated the minimum value of the drag coefficient, in this case, it was 0.0186, which is higher than Timmer’s measurements by 22.37% and 16.25% higher than the experimental data of Bianchini. The XFOIL code predicted a lowest minimum drag coefficient value of 0.01365. As the angle of attack increases, the numerical results of the drag force coefficient are close to the experimental data of Timmer. The drag coefficients measured by Bianchini are higher than the Timmer results at higher angles of attack, starting from 6 degrees. These differences between data sets at higher angles of attack may be due to differences in experimental conditions, which, in the case of such low Reynolds numbers, may significantly affect the aerodynamic characteristics of the forces [21,34,62,63].
Comparing the obtained characteristics quantitatively with the experiment of Timmer [41], the average relative error [47] for the range of angles of attack from 0 to 6 degrees is 3.9%, while in the range of angles of attack from 6 to 11 degrees, it is 9.8%. In the case of the drag coefficient , the mean relative error is 5.6% for the first range of angles of attack and 6.5% for the second range. The mean relative error in the entire tested range of angles of attack from to is 6.2% for the drag coefficient and 7% for the lift coefficient. Such a deviation of the numerical results of the lift coefficients in comparison to the experiments in the second area of angles of attack can also result from the use of the original Transition SST formulation, which was implemented as a general-purpose turbulence model, developed to cover most of the flow classes found in the industry, and it requires calibration for specific issues [2]. Such calibration was not performed in these studies, in order to give a benchmark for further research. As mentioned above, another possible reason for differences between the experimental and numerical results may be the 3D effects, which were not taken into account in the presented studies. Comparing the results obtained using the XFOIL code with Timmer’s measurements [41], the relative error was found to be approximately twice as high as the predictions of the Transition SST model in the range of angles of attack from 0 to 6 degrees (13.2% for drag and 6.4% for lift). In the range of angles of attack from 6 to 11 degrees, XFOIL gave an error of 11.8% for the drag coefficient and 8.7% for the lift. The largest relative error was found for the k-ω SST models, and was equal to approximately 20% in the case of the lift force coefficient in the whole range of investigated angles of attack. For both the k-ω SST model and the XFOIL approach, a similar value was obtained for the drag coefficient relative error, equal to approximately 12%. One of the reasons for this deviation in the case of the XFOIL model was documented by Melani et al. [19]. The problems resulting from the overestimation of the lift coefficients probably result from the model’s inability to correctly estimate the intensity of the laminar separation bubbles formed on the profile surface [64]. Problems have also been noted in the handling of large separation regions which also favor in excess lift overestimation [65].
Table 3 presents the averaged values of the aerodynamic force coefficients, along with the values of the standard deviation for each coefficient. The values of standard deviation are shown in parentheses next to the force coefficient values.
3.2. Pressure Distributions
The aerodynamic force coefficients presented in the previous subsection obviously depend on the pressure distribution around the NACA 0018 airfoil. This subsection presents the averaged static pressure distributions around the airfoil for the analyzed range of angles of attack. The obtained pressure distributions presented in Figure 9 were averaged for the last second of simulation (from 9 s to 10 s). As discussed in Section 2 of this paper, the simulations were performed using a time step of 0.0001 s. The averaging of the pressure distributions around the airfoil was performed using 10,000 samples (Figure 10). These distributions were compared with the experiments by Nakano [4] and by Gerakopulos [21]. The experimental data of Gerakopulos are only available for the suction side of the airfoil. For the comparison of the obtained pressure distributions, the results calculated using the XFOIL code were also added. As can be seen in Figure 9, the computed characteristics of the pressure distributions correspond quite well with the experimental data, in particular for lower angles of attack. It is worth paying attention to the fact that despite slight differences in the results for different methods, this characteristic inflection of the curves, indicating the occurrence of a laminar-turbulent transition, occurs everywhere in very similar locations on the suction side of the airfoil. From Figure 10, it can be seen that the laminar-turbulent transition moves towards the leading edge of the airfoil as the angle of attack increases. It can also be seen that the length of the laminar-turbulent bubble decreases with the increase of the angle of attack.
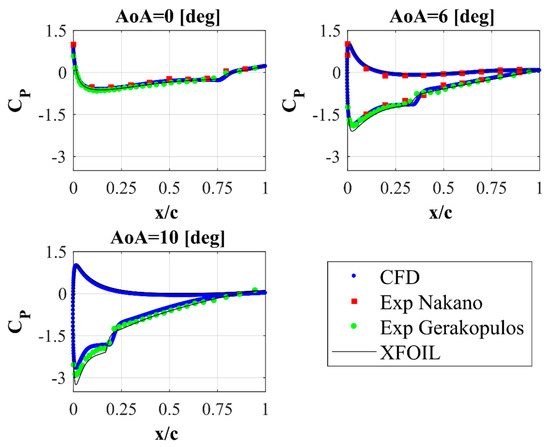
Figure 9.
Pressure coefficient distributions over NACA 0018 airfoil. Validation of the CFD results by the Transition SST; Nakano [4] (for the suction and pressure side of the airfoil) and Gerakopulos et al. [21] (for the suction side of the airfoil).
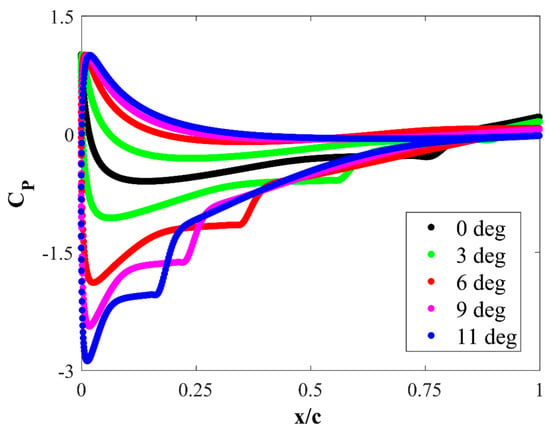
Figure 10.
Pressure coefficient distributions over NACA 0018 airfoil for five angles of attack.
3.3. Laminar Separation Bubble Characteristics and Mean Velocity Distributions in the Near-Wall Region
An undoubted advantage of the Transition SST turbulence model used in comparison with the classic k-ω or k-ε models is the possibility of analyzing phenomena occurring locally in the boundary layer. The pressure distribution characteristics shown above suggest the presence of a laminar-turbulent bubble in the boundary layer. In these studies, the skin friction coefficient distributions were used to analyze the size of the laminar separation bubble. An example of the distribution of this parameter is shown in Figure 11 for an angle of attack of 6 degrees. The suction and pressure sides of the airfoil are shown in different colors.
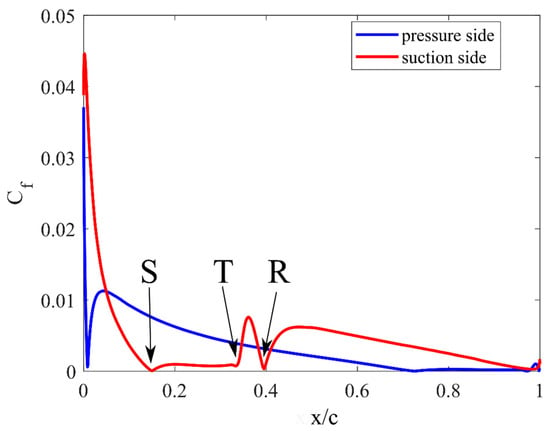
Figure 11.
Skin friction coefficient distributions over NACA 0018 airfoil at an angle of attack of 6 degrees. Location of separation (S), transition (T) and reattachment (R).
Following Choudhry et al. [2], the separation point of the laminar boundary layer and the location of its reattachment were determined at the two extremes of the function, as shown in Figure 11. The location of the laminar-turbulent transition was determined between the separation point of the laminar boundary layer and the reattachment location at the point at which the curve rises sharply. Because there is no unequivocal answer in the literature with respect to finding the location of the transition location, in this work, the criterion for determining the location of the transition was the place where the value increased by 20% compared to the minimum value. The characteristics of these three characteristic points are shown in Figure 12 and Figure 13. The separation point of the laminar layer is marked with the symbol S, the transition point with the symbol T, and the reattachment point with the symbol R. In addition, the results shown in these figures are given for the suction side (SS) of the airfoil and for the pressure side (PS). The obtained numerical results of the size of the laminar bubble were compared with two sets of experimental data, by Gerakopulos et al. [21] and by Nakano et al. [4]. From Figure 12, it is clear that the calculated characteristics of the laminar bubble are very consistent with the experimental results. In the case of the Gerakopulos experiment, the derivative in the range of angles of attack from 0 to 8 degrees (first region) is 0.05, and 0.01 in the range of angles of attack from 10 to 14 degrees (second region). In the analysis of these authors [21], the first region was estimated in the range of angles of attack from 0 to 6 degrees, and the second from 6 to 11 degrees. The derivative obtained in these studies was 0.05 for the first region and 0.02 for the second region. Gerakopulos estimated the derivative to be 0.07 in the first region and 0.02 in the second. CFD analysis showed values of 0.074 and 0.037, respectively. From Figure 12, it can be seen that the size of the laminar bubble decreases with increasing angle of attack. For an angle of attack of 0 degrees, it is 0.39c, while for an angle of 11 degrees, it is 0.15c, where c is the chord length. In the case of the pressure side of the airfoil, for an angle of attack larger than 2 degrees, the CFD analysis did not show the reattachment points.
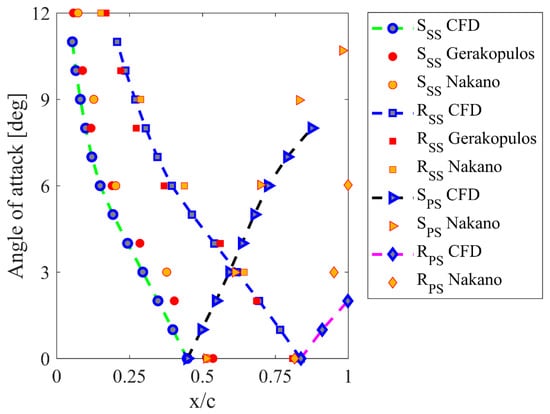
Figure 12.
Variation of separation and reattachment locations with the angle of attack. Validation of the CFD results using the Transition SST turbulence model with the experiments of Nakano et al. [4] and Gerakopulos et al. [21].
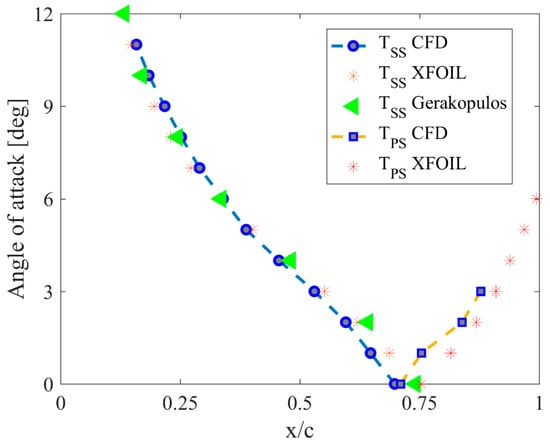
Figure 13.
Variation of transition location with the angle of attack. Validation of the CFD results using the Transition SST turbulence model using the experiment of Gerakopulos et al. [21].
To make the obtained results more readable, the distributions of the laminar-turbulent transition location are presented in a separate graph (Figure 13). In this case, the experimental data of Gerakopulos and values calculated using the XFOIL code were used for comparison. The consistency of all the results presented in this figure is very high. In the case of the Gerakopulos experiment, the derivative in the range of angles of attack from 0 to 8 degrees is 0.07, while for the range of angles of attack from 8 to 14, it is equal to 0.02. The CFD results of these derivatives are 0.06 for a range of rake angles from 0 to 6 degrees, and 0.035 for angles ranging from 6 to 11 degrees.
The aerodynamic performance of an airfoil is strongly influenced by laminar separation bubbles, which may form at low Reynolds numbers. The laminar separation bubble is essentially a recirculation zone. It has the shape of a wedge that forms on the surface of the airfoil when the laminar layer is separated. To show the flow behavior in the area of the laminar separation bubble and to check the effectiveness of the Transition SST turbulence model under these flow conditions, calculations of mean velocities across the boundary layer for an angle of attack equal to 6 degrees were performed. The obtained numerical results of velocity profiles in the near-wall region were compared with the experimental results obtained by Nakano et al. [4] using the high-resolution PIV technique. As can be seen from the graph shown in Figure 12, for an angle of attack of 6 degrees, the separation point is located at x/c = 0.1495, whereas the reattachment point is located at x/c = 0.395. In the Nakano experiment, the separation location was found at x/c of 0.2; therefore, the locations of the velocity profiles on the airfoil suction side cover almost the entire bubble size predicted by the Transition SST turbulence model. By analyzing the obtained averaged velocity profiles, both on the pressure and suction surface (Figure 14 and Figure 15), a high agreement with the experimental results can be stated. The shift of the separation point towards the leading edge in the CFD tests may be caused by a slightly different level of turbulence intensity in the undisturbed flow stream. In the experiments of Nakano et al. [4], the streamwise turbulence intensity was about 1%. In our research, the turbulence intensity more closely corresponded to the flow conditions in the Timmer measurements. Istvan and Yarusevych showed experimentally that in the laminar-turbulent transition process, a laminar separation bubble formed on the NACA0018 airfoil at moderate Reynolds numbers, and the separation point moved away from the leading edge of the airfoil with increasing free-stream turbulence intensity [66]. Another reason is, of course, the neglect of the third dimension of the numerical model, which can be very important in the case of such thick profiles. In the experimental studies by Istvan and Yarusevych, it was proved that at different levels of fee-stream turbulence intensity, spanwise-oriented shear layer vortex structures were observed near the location of the mean transition. Istvan and Yarusevych reported that despite the low level of turbulence intensity (0.06%) and the spanwise coherence of these structures, spanwise undulations were visible as they moved downstream, leading to localized vortex breakup [66]. These effects are neglected in the 2D numerical model. To visualize the laminar separation bubble, vorticity contour maps were prepared around the airfoil (Figure 16). This drawing was made for four angles of attack: 0 deg, 4 deg, 8 deg and 11 degrees. In addition, this picture shows the locations of the three points characterizing the laminar separation bubble.
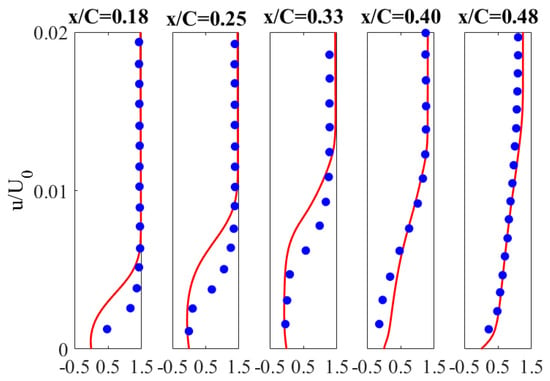
Figure 14.
Near-wall distributions of mean velocity on the airfoil suction side at the angle of attack of 6 degrees; comparison of the numerical results (blue dots) with the experiment (red line) [4].
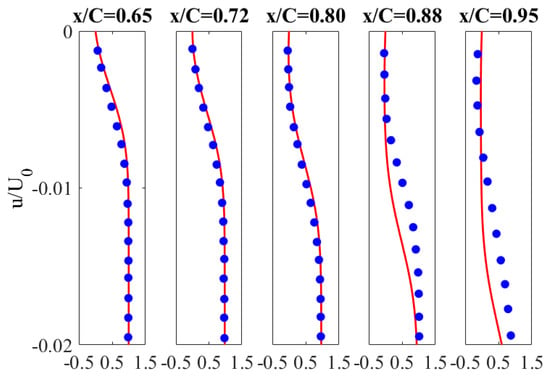
Figure 15.
Near-wall distributions of mean velocity on the airfoil pressure side at the angle of attack of 6 degrees; the comparison of the numerical results (blue dots) with the experiment (red line) [4].
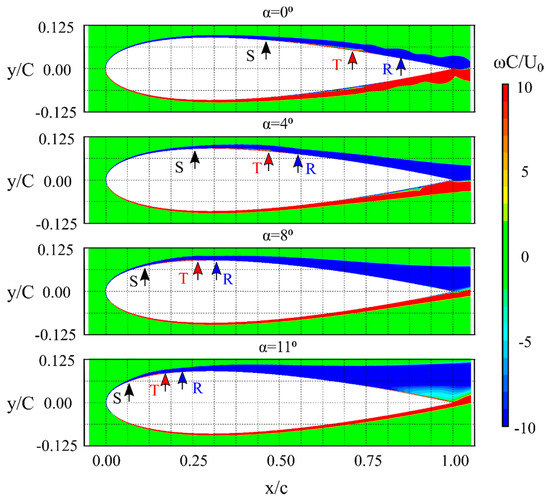
Figure 16.
Instantaneous non-dimensional vorticity contours for four angles of attack. Location of separation (S), transition (T) and reattachment (R).
4. Vertical Axis Wind Turbine Test Case
The aim of this chapter is to show that the aerodynamic characteristics of the NACA 0018 airfoil obtained in this work by means of the Transition SST turbulence model and discussed in Section 3 can be used to calculate the aerodynamic performance of a vertical axis wind turbine. For this purpose, an H-Darrieus wind turbine rotor was selected for analysis. The blade Reynolds number of this rotor corresponds to the Reynolds number of the airfoil presented in Section 3. The blade Reynolds number is defined as , where is the wind turbine rotational speed, is the rotor radius, is the blade chord and is the kinematic viscosity of the fluid. The numerical model of the rotor selected in this analysis does not take into account the rotating shaft or the blade struts, and it was derived from the rotor developed and investigated at the Delft University [67,68]. A sketch of this wind turbine rotor is shown in Figure 17a. The rotor has a diameter of 1 m, a blade height of 1 m and a chord length of 6 cm. The rotor runs at 800 rpm at a tip speed ratio speed of 4.5. Free stream velocity was chosen to be 9.3 m/s. The tip speed ratio is defined as the ratio of the velocity of the rotor blade to the free stream velocity. Typical low-solidity Darrieus wind turbines achieve their maximum aerodynamic efficiency in the tip speed ratio range from 4 to 5 [20]. During the operation of the rotor, aerodynamic loads arise on its blades (Figure 17a). The aerodynamic force of a single blade is usually projected in two directions: tangent and normal to the blade trajectory. Both of these components are dependent on the angle of the rotor relative to the wind direction (azimuthal angle, θ). As the azimuthal angle changes continuously, the components of the aerodynamic force are time dependent. The fluctuations of these forces are so large that they cannot be considered to be in a steady state. Therefore, it is necessary to conduct a CFD analysis, which brings with it several problems: it is time consuming, parallel computations are usually necessary, and it does not give satisfactory results in terms of low tip speed ratios due to the deep-stall phenomenon. Therefore, simplified methods are still used in engineering practice to analyze the aerodynamic blade loads. However, these methods are not deterministic and require aerodynamic airfoil characteristics from the outside. These characteristics can be derived both from experimental measurements as well as from numerical calculations [20].
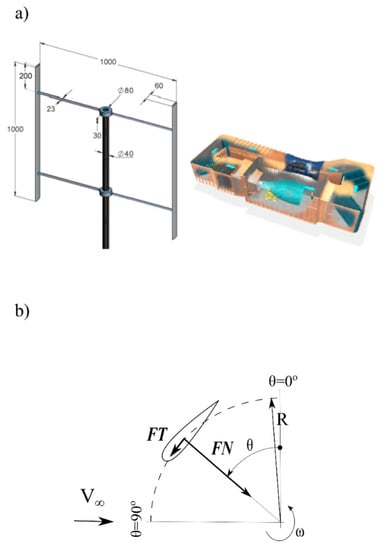
Figure 17.
(a) The VAWT model and the schematics of the Open Jet wind tunnel Facility of TU Delft [68]. (b) Aerodynamic blade loads: the normal and tangential forces, and [48].
The present work employs the improved double multiple streamtube (IDMS) approach [17]. The method revises the standard DMS approach [69] in terms of the wake expansion, decambering and dynamic stall effects. The method has been proven to be ac-curate for wind turbine simulations for various solidity levels when compared with experimental data and CFD solutions, not only in terms of global, but also for azimuthal loads [11]. Similar with DMS, the streamtube of the rotor is divided into two parts in IDMS; upwind and downwind regimes. Within the upwind regime, the flow angle is generally positive, and this is where most of the power of the turbine is generated. In contrast, the downwind regime usually generates little to no mechanical power. However, the standard DMS method often overestimates the driving moment within this area. This is especially true for the H-Darrieus turbine, which has relatively high solidity [11]. This issue is better treated using the IDMS approach. The IDMS method is embedded into a momentum code B-GO developed at the University of Stuttgart [70]. The calculations made use of the aerodynamic data presented in Chapter 3. The employed polar data were:
- CFD polar calculated using the SST model
- CFD polar calculated using the transitional SST model
- Polar obtained from the measurement of Timmer
- Polar data calculated using XFOIL with the critical amplification factor of N = 9.0.
The results of the numerical analysis of the rotor blade loads are presented in Figure 18 and Figure 19. The results are presented in the form of dimensionless coefficients calculated as:
where and are normal and tangential aerodynamic blade load components, is the rotor radius, and , where is the air density and is the free stream wind velocity of 9.3 m/s. These results are compared with the experimental data obtained by Castelein et al. [68] using the PIV technique. However, the experimental results of the aerodynamic forces were not measured directly on the rotor blades, but on the basis of an analysis of the velocity field distributions around the rotating rotor blade. In the case of a rotor operating at a tip speed ratio of 4.5, the results of the tangential force are subject to considerable error. This problem has been known for years, and it results from the size of both components of the aerodynamic blade load [71]. The tangent component is an order of magnitude lower than the normal component. Therefore, the authors of this experiment do not recommend using these values for validation [68].
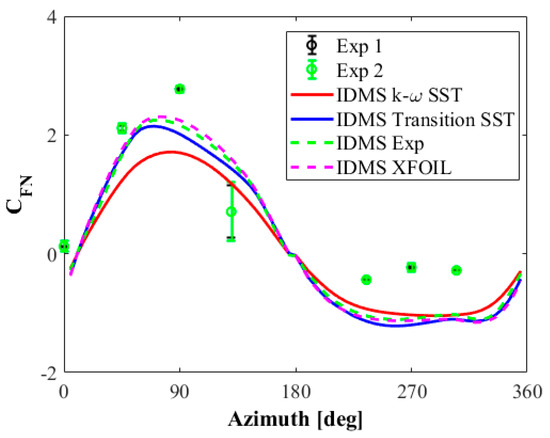
Figure 18.
Normal blade load as a function of azimuthal position; comparison with the experiment [67].
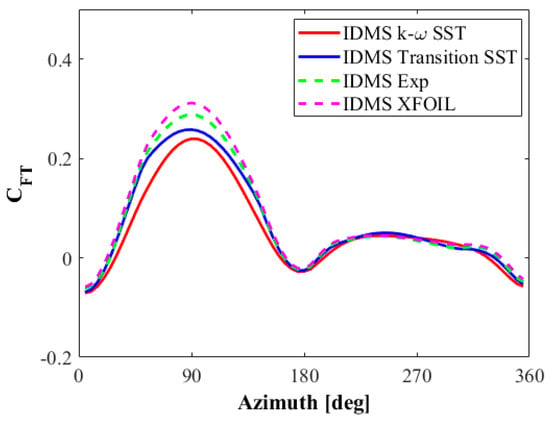
Figure 19.
Tangential blade load as a function of azimuthal position.
The numerical results of the normal component of the aerodynamic blade load shown in Figure 18 are in favor of the aerodynamic characteristics determined using the transition turbulence models. The results obtained using the k-ω SST turbulence model to predict the polars of the NACA 0018 are much worse. In this study, only polars calculated by the FLOWer solver were taken into account. This is due to the fact that for the same blade angles of attack, the values of the lift force predicted by the Transition SST model are higher than those calculated using the k-ω SST model. In this work, the aerodynamic characteristics of the airfoil were calculated for almost ideal flow conditions. However, it should be remembered that the turbulence intensity can change the aerodynamic characteristics of the airfoil and therefore also the shape of the normal force curve in the downwind part of the rotor.
5. Conclusions
The main purpose of this paper was to analyze the aerodynamic characteristics of a NACA 0018 airfoil with a Reynolds number of 160,000. This article uses the Transition SST four-equation turbulence model based on the two-equation k-ω SST model. Based on the numerical studies of the airfoil, the following conclusions were drawn:
- This paper continues the research carried out by Królak and presented in his thesis [72]. Królak used the same geometric model, the Reynolds-averaged Navier–Stokes (RANS) technique, and the Transition SST turbulence model. The results of the aerodynamic force coefficients and the pressure distributions were burdened with considerable numerical errors. In particular, there were considerable nonphysical oscillations around the transition location. This article shows that the numerical calculations of the NACA airfoil should be carried out in a transient mode. Langtry reported similarly in many of the analyzed test cases [51].
- The analysis of the aerodynamic properties of the NACA 0018 airfoil was possible only in the transient mode, which, however, significantly increased the computational effort and increased the simulation time of a single case.
- The use of the Transition SST model made it possible to find two regions on the characteristic that were characterized by two aerodynamic derivatives in the range up to the critical angle of attack, instead of one derivative, as predicted by the two-equation k-ω SST turbulence model. The first region was found up to an angle of attack of 6 degrees, and the second up to 11 degrees.
- The values of the aerodynamic derivatives corresponded quite well with the experimental data; however, above the angle of attack equal to 6 degrees, the results of the lift coefficient were underestimated compared to the experimental data. This is probably due to the 3D effects, which were not included in these numerical studies.
- The Transition SST approach predicted the minimum drag coefficient by far the most accurately in comparison to the experimental results.
- The Transition SST model relatively accurately estimated the location and size of the laminar separation bubble on the suction surface of the airfoil. The average relative error in the localization of the separation point for the entire range of the investigated angles of attack was 22% compared to the experiment of Gerakopulos [21]. The reattachment point was estimated much more precisely; the mean relative error was 5.5%. This gives there was a mean relative error of 22% in estimating the length of the laminar separation bubble. The underestimation of the separation point of the laminar boundary layer in the CFD analysis compared to the experiment may be the result of using a two-dimensional numerical model that neglected the evolution of vortex structures in the direction of the span [66]. Another likely reason is that the model was not calibrated for this particular issue. The original formulation of the Transition SST model was calibrated for the small separation bubbles visible in the machines [2].
- The use of the more expensive turbulence model, i.e., the Transition SST model, to calculate the airfoil characteristics of the NACA 0018, however, significantly improved the normal force distribution of the Darrieus wind turbine rotor calculated using simplified aerodynamic methods.
Author Contributions
Conceptualization, K.R.; methodology, K.R. and G.B.; software, K.R., G.K. and G.B.; validation K.R., G.K. and G.B.; numerical analysis, K.R., G.K. and G.B.; writing—Original draft preparation, K.R.; Writing—review and editing, K.R. and G.B.; visualization, K.R., supervision, K.R. and G.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
Calculations were carried out in the Warsaw Supercomputer Center (ICM) (GB83-33).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| chord length | |
| drag coefficient | |
| averaged drag coefficient | |
| skin friction coefficient | |
| normal force coefficient | |
| lift coefficient | |
| averaged lift coefficient | |
| tangential force coefficient | |
| static pressure coefficient | |
| normal force | |
| tangential force | |
| R | reattachment point; rotor radius of the Darrieus wind turbine rotor |
| the radius of the front edge of the domain size | |
| S | separation point |
| SD | standard deviation |
| T | transition point |
| free stream wind velocity (in NACA 0018 simulations) | |
| free stream wind velocity (in VAWT calculations) | |
| angle of attack | |
| dynamic viscosity | |
| kinematic viscosity | |
| air density | |
| wind turbine rotational speed; vorticity |
References
- Lin, J.M.; Pauley, L.L. Low-Reynolds-number separation on an airfoil. AIAA J. 1996, 34, 1570–1577. [Google Scholar] [CrossRef]
- Choudhry, A.; Arjomandi, M.; Kelso, R. A study of long separation bubble on thick airfoils and its consequent effects. Int. J. Heat Fluid Flow 2015, 52, 84–96. [Google Scholar] [CrossRef]
- Jimenez, P.; Lichota, P.; Agudelo, D.; Rogowski, K. Experimental validation of total energy control system for UAVs. Energies 2020, 13, 14. [Google Scholar] [CrossRef]
- Nakano, T.; Fujisawa, N.; Oguma, Y.; Takagi, Y.; Lee, S. Experimental study on flow and noise characteristics of NACA0018 airfoil. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 511–531. [Google Scholar] [CrossRef]
- Zhang, W.; Hain, R.; Kähler, C.J. Scanning PIV investigation of the laminar separation bubble on a SD7003 airfoil. Exp. Fluids 2008, 45, 725–743. [Google Scholar] [CrossRef]
- Lissaman, P. Low-Reynolds-number airfoils. Annu. Rev. Fluid Mech. 1983, 15, 223–239. [Google Scholar] [CrossRef]
- Ol, M.V.; McAuliffe, B.R.; Hanff, E.S.; Scholz, U.; Kähler, C. Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities. AIAA J. 2005, 5149. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Montazeri, H.; Blocken, B. Effect of the shaft on the aerodynamic performance of urban vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 616–630. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Müller, G.; Chavushoglu, M.; Kerri, M.; Tsuzaki, T. A resistance type vertical axis wind turbine for building integration. Renew. Energy 2017, 111, 803–814. [Google Scholar] [CrossRef]
- Bangga, G.; Dessoky, A.; Wu, Z.; Rogowski, K.; Hansen, M.O.L. Accuracy and consistency of CFD and engineering models for simulating vertical axis wind turbine loads. Energy 2020, 206, 118087. [Google Scholar] [CrossRef]
- Rogowski, K.; Hansen, M.O.L.; Bangga, G. Performance Analysis of a H-Darrieus Wind Turbine for a Series of 4-Digit NACA Airfoils. Energies 2020, 13, 3196. [Google Scholar] [CrossRef]
- Cheng, Z.; Madsen, H.A.; Gao, Z.; Moan, T. Effect of the number of blades on the dynamics of floating straight-bladed vertical axis wind turbines. Renew. Energy 2017, 101, 1285–1298. [Google Scholar] [CrossRef]
- Bedon, G.; Schmidt Paulsen, U.; Madsen, H.A.; Belloni, F.; Raciti Castelli, M.; Benini, E. Computational assessment of the DeepWind aerodynamic performance with different blade and airfoil configurations. Appl. Energy 2017, 185, 1100–1108. [Google Scholar] [CrossRef]
- Cheng, Z.; Madsen, H.A.; Gao, Z.; Moan, T. A fully coupled method for numerical modeling and dynamic analysis of floating vertical axis wind turbines. Renew. Energy 2017, 107, 604–619. [Google Scholar] [CrossRef]
- Goude, A.; Aġren, O. Numerical simulation of a farm of vertical axis marine current turbines. In Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 335–344. [Google Scholar] [CrossRef]
- Bangga, G.; Dessoky, A.; Lutz, T.; Krämer, E. Improved double-multiple-streamtube approach for H-Darrieus vertical axis wind turbine computations. Energy 2019, 182, 673–688. [Google Scholar] [CrossRef]
- Rainbird, J.M.; Bianchini, A.; Balduzzi, F.; Peiró, J.; Graham, J.M.R.; Ferrara, G.; Ferrari, L. On the influence of virtual camber effect on airfoil polars for use in simulations of Darrieus wind turbines. Energy Convers. Manag. 2015, 106, 373–384. [Google Scholar] [CrossRef]
- Melani, P.F.; Balduzzi, F.; Ferrara, G.; Bianchini, A. An Annotated Database of Low Reynolds Aerodynamic Coefficients for the NACA0018 Airfoil. AIP Conf. Proc. 2019, 2191, 020110. [Google Scholar] [CrossRef]
- Paraschivoiu, I. Wind Turbine Design with Emphasis on Darrieus Concept; Presses Internationales Polytechnique: Montréal, QC, Canada, 2009. [Google Scholar]
- Gerakopulos, R.; Boutilier, M.S.H.; Yarusevych, S. Aerodynamic Characterization of a NACA 0018 Airfoil at Low Reynolds Numbers. In Proceedings of the AIAA 2010-4629, 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef]
- Rogowski, K.; Maroński, R.; Hansen, M.O.L. Steady and unsteady analysis of NACA 0018 airfoil in vertical-axis wind turbine. J. Theor. Appl. Mech. 2018, 51, 203–212. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Lichota, P.; Szulczyk, J.; Noreña, D.A.; Vallejo Monsalve, F.A. Power spectrum optimization in the design of multisine manoeuvre for identification purposes. J. Theor. Appl. Mech. 2017, 55, 1193–1203. [Google Scholar] [CrossRef]
- Lichota, P. Multi-Axis Inputs for Identification of a Reconfigurable Fixed-Wing UAV. Aerospace 2020, 7, 113. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Genç, M.S.; Karasu, I.; Açıkel, H.H.; Akpolat, M.T. Low Reynolds Number Flows and Transition; Gençm, S., Ed.; InTech-Open Access: Rijeka, Croatia, 2012; pp. 1–28. [Google Scholar]
- Abu-Ghannam, B.J.; Shaw, R. Natural transition of boundary layers—the effects of turbulence, pressure gradient, and flow history. J. Mech. Eng. Sci. 1980, 22, 213–228. [Google Scholar] [CrossRef]
- Morkovin, M.V. On the Many Faces of Transition; Wells, C.S., Ed.; Viscous Drag Reduction; Plenum Press: New York, NY, USA, 1969; pp. 1–31. [Google Scholar]
- Kubacki, S.; Jonak, P.; Dick, E. Evaluation of an algebraic model for laminar-to-turbulent transition on secondary flow loss in a low-pressure turbine cascade with an end wall. Int. J. Heat Fluid Flow 2019, 77, 98–112. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. An algebraic model for bypass transition in turbomachinery boundary layer flows. Int. J. Heat Fluid Flow 2019, 58, 68–83. [Google Scholar] [CrossRef]
- Mayle, R.E. The Role of Laminar-Turbulent Transition in Gas Turbine Engines. J. Turbomach. 1991, 113, 509–537. [Google Scholar] [CrossRef]
- Mayle, R.E.; Schulz, A. The Path to Predicting Bypass Transition. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Turbomachinery, Birmingham, UK, 10–13 June 1996; Volume 1. V001T01A065. [Google Scholar] [CrossRef]
- Tani, I. Low Speed Flows Involving Bubble Separations. Prog. Aerosp. Sci. 1964, 5, 70–103. [Google Scholar] [CrossRef]
- Swift, K.M. An Experimental Analysis of the Laminar Separation Bubble at Low Reynolds Numbers. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2009. [Google Scholar]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Kawabata, T.; Shimizu, K.; Ogasawara, T.; Nakai, A.; Kasuya, T. Wind tunnel and numerical study of a straight-bladed vertical axis wind turbine in three-dimensional analysis (Part I: For predicting aerodynamic loads and performance). Energy 2016, 106, 443–452. [Google Scholar] [CrossRef]
- Roh, S.C.; Kang, S.H. Effects of a blade profile, the Reynolds number, and the solidity on the performance of a straight bladed vertical axis wind turbine. J. Mech. Sci. Technol. 2013, 27, 3299–32307. [Google Scholar] [CrossRef]
- Mohamed, M.H. Performance investigation of H-rotor Darrieus turbine with new airfoil shapes. Energy 2012, 47, 522–530. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Desirable airfoil features for smaller-capacity straight-bladed VAWT. Wind Eng. 2007, 31, 165–196. [Google Scholar] [CrossRef]
- Jacobs, E.N.; Sherman, A. Airfoil Section Characteristics as Affected by Variations of the Reynolds Number. NACA Rep. 1937, 586, 227–267. [Google Scholar]
- Timmer, W.A. Two-Dimensional Low-Reynolds Number Wind Tunnel Results for Airfoil NACA 0018. Wind. Eng. 2008, 32, 525–537. [Google Scholar] [CrossRef]
- Laneville, A.; Vittecoq, P. Dynamic stall: The case of the vertical axis wind turbine. J. Sol. Energy Eng. 1986, 108, 141–145. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report SAND80-2114; Sandia National Labs: Albuquerque, NM, USA, 1981.
- Boutilier, M.S.H.; Yarusevych, S. Parametric study of separation and transition characteristics over an airfoil at low Reynolds numbers. Exp. Fluids 2012, 52, 1491–1506. [Google Scholar] [CrossRef]
- Claessens, M.C. The Design and Testing of Airfoils in Small Vertical Axis Wind Turbines. Master’s Thesis, TU Delft, Delft, The Netherlands, 2006. [Google Scholar]
- Bianchini, A.; Balduzzi, F.; Rainbird, J.M.; Peiro, J.; Graham, J.M.R.; Ferrara, G.; Ferrari, L. An Experimental and Numerical Assessment of Airfoil Polars for Use in Darrieus Wind Turbines—Part II: Post-stall Data Extrapolation Methods. J. Eng. Gas. Turbine Power 2016, 138. [Google Scholar] [CrossRef]
- Kątski, B.; Rogowski, K. Analysis of the Aerodynamic Properties of the NACA 0018 Airfoil in the Range of Low Reynolds Numbers; Krzysztof, S., Ed.; Mechanics in Aviation ML-XIX 2020; ITWL and PTMTS: Warsaw, Poland, 2020; Volume 1, pp. 57–65. [Google Scholar]
- Rogowski, K. Numerical studies on two turbulence models and a laminar model for aerodynamics of a vertical-axis wind turbine. J. Mech. Sci. Technol. 2018, 32, 2079–2088. [Google Scholar] [CrossRef]
- Rogowski, K.; Hansen, M.O.L.; Lichota, P. 2-D CFD Computations of the Two-Bladed Darrieus-Type Wind Turbine. J. Appl. Fluid Mech. 2018, 11, 835–845. [Google Scholar] [CrossRef]
- Divakaran, U.; Ramesh, A.; Mohammad, A.; Velamati, R.K. Effect of Helix Angle on the Performance of Helical Vertical Axis Wind Turbine. Energies 2021, 14, 393. [Google Scholar] [CrossRef]
- Langtry, R.B. A Correlation-Based Transition Model using Local Variables for Unstructured Parallelized CFD Codes. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2006. [Google Scholar] [CrossRef]
- Smith, A.M.O.; Gamberoni, N. Transition, Pressure Gradient and Stability Theory; Douglas Aircraft Company, El Segundo Division: Los Angeles, CA, USA, 1956. [Google Scholar]
- Rogowski, K.; Hansen, M.O.L.; Maroński, R.; Lichota, P. Scale Adaptive Simulation Model for the Darrieus Wind Turbine. J. Phys. Conf. Ser. 2016, 753, 022050. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Rainbird, J.M.; Peiro, J.; Graham, J.M.R.; Ferrara, G.; Ferrari, L. An Experimental and Numerical Assessment of Airfoil Polars for Use in Darrieus Wind Turbines—Part I: Flow Curvature Effects. J. Eng. Gas Turbine Power 2016, 138, 032602. [Google Scholar] [CrossRef]
- Guo, Z.; Fletcher, D.F.; Haynes, B.S. Implementation of a height function method to alleviate spurious currents in CFD modelling of annular flow in microchannels. Appl. Math. Model. 2015, 39, 4665–4686. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent Theory Guide, Release 19.0.; ANSYS, Inc.: Canonsburg, PA, USA.
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Goetten, F.; Finger, D.F.; Marino, M.; Bil, C. A review of guidelines and best practices for subsonic aerodynamic simulations using RANS CFD. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology (APISAT), Gold Coast, Australia, 4–6 December 2019. [Google Scholar]
- Schlipf, M.; Tismer, A.; Riedelbauch, S. On the application of hybrid meshes in hydraulic machinery CFD simulations. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 062013. [Google Scholar] [CrossRef]
- Schmidt, S.; Thiele, F. Detached Eddy Simulation of Flow around A-Airfoil. Flow Turbul. Combust. 2003, 71, 261–278. [Google Scholar] [CrossRef]
- Bangga, G.; Lutz, T.; Dessoky, A.; Krämer, E. Unsteady Navier-Stokes studies on loads, wake and dynamic stall characteristics of a two-bladed vertical axis wind turbine. J. Renew. Sustain. Energy 2017, 9, 053303. [Google Scholar] [CrossRef]
- Marchman, J.F. Aerodynamic Testing at Low Reynolds Numbers. J. Aircr. 1987, 24, 107–114. [Google Scholar] [CrossRef]
- Laitone, E.V. Wind tunnel tests of wings at Reynolds numbers below 70,000. Exp. Fluids 1997, 23, 405–409. [Google Scholar] [CrossRef]
- Du, L. Numerical and Experimental Investigations of Darrieus Wind Turbine Start-up and Operation. Ph.D. Thesis, Durham University, Durham, UK, 2016. [Google Scholar]
- Yao, J.; Yuan, W.; Wang, J.; Xie, J.; Zhou, H.; Peng, M.; Sun, Y. Numerical simulation of aerodynamic performance for two dimensional wind turbine airfoils. Procedia Eng. 2012, 31, 80–86. [Google Scholar] [CrossRef]
- Istvan, M.S.; Yarusevych, S. Effects of free-stream turbulence intensity on transition in a laminar separation bubble formed over an airfoil. Exp. Fluids 2018, 59, 1–21. [Google Scholar] [CrossRef]
- Tescione, G.; Ragni, D.; He, C.; Ferreira, C.J.S.; van Bussel, G.J.W. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Castelein, D.; Ragni, D.; Tescione, G.; Ferreira, C.J.S.; Gaunaa, M. Creating a benchmark of Vertical Axis Wind Turbines in Dynamic Stall for validating numerical models. In Proceedings of the 33rd Wind Energy Symposium, AIAA SciTech, AIAA 2015-0723, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Paraschivoiu, I. Double-multiple streamtube model for studying vertical-axis wind turbines. J. Propul. Power 1988, 4, 370–377. [Google Scholar] [CrossRef]
- Bangga, G. Comparison of Blade Element Method and CFD Simulations of a 10 MW Wind Turbine. Fluids 2018, 3, 73. [Google Scholar] [CrossRef]
- Strickland, J.H.; Webster, B.T.; Nguyen, T.A. Vortex Model of the Darrieus Turbine: An Analytical and Experimental Study. J. Fluids Eng. 1979, 101, 500–505. [Google Scholar] [CrossRef]
- Królak, G. Numerical Analysis of Aerodynamic Characteristics of the NACA 0018 Airfoil Used in the Darrieus Wind Turbines. Master’s Thesis, Warsaw University of Technology, Warsaw, Poland, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).