Modular Feedback Control of Networked Systems by Clustering: A Drinking Water Network Case Study
Abstract
1. Introduction
2. Problem Formulation
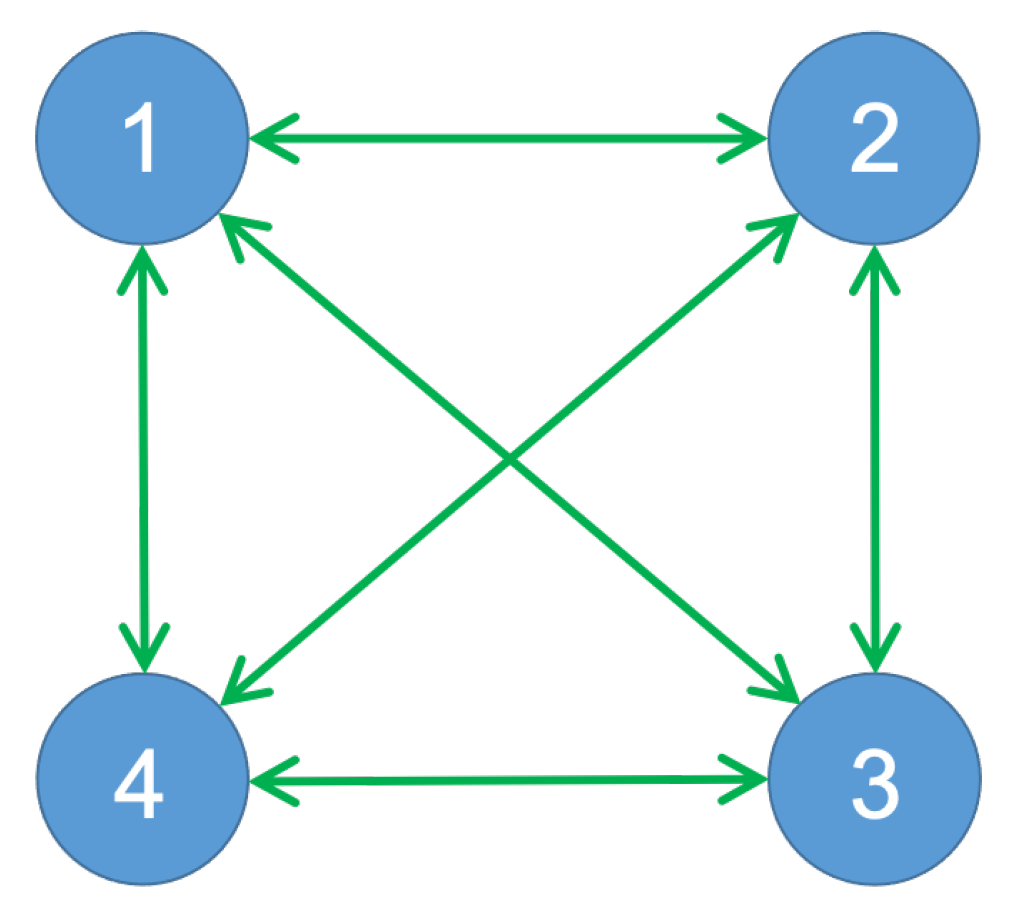
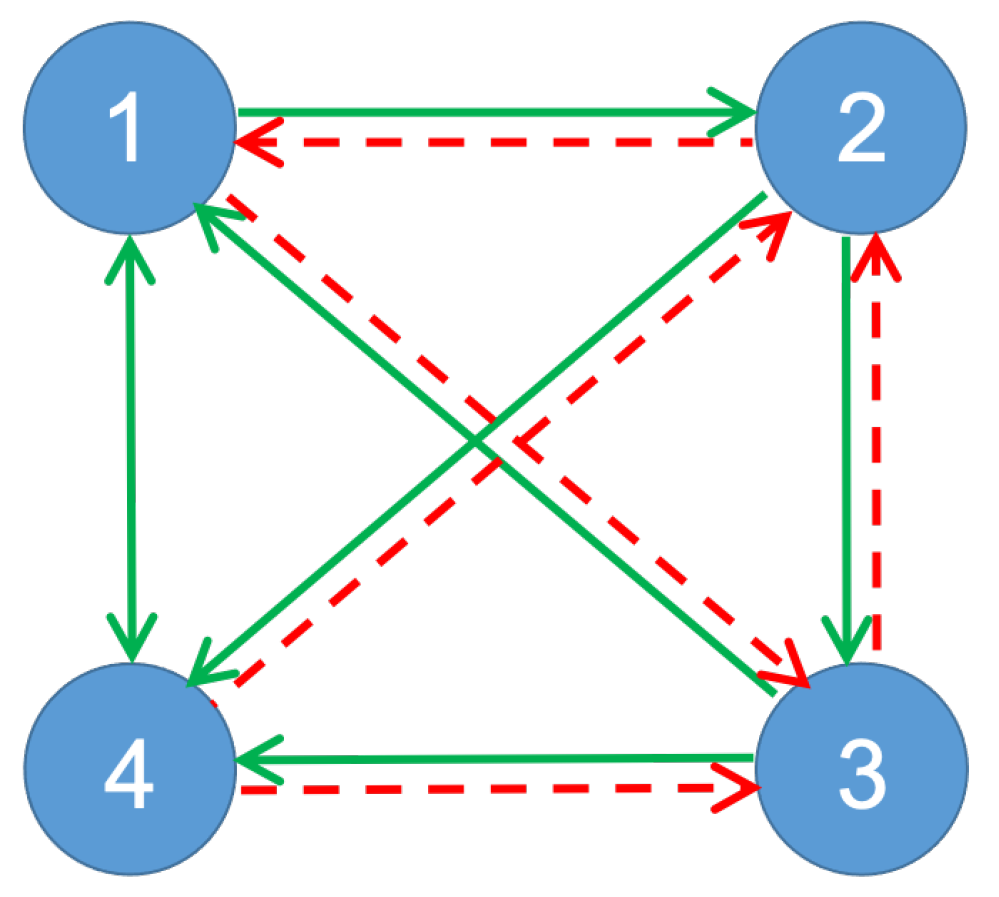
2.1. Modular Control Law and Communication Constraints
2.2. Stability
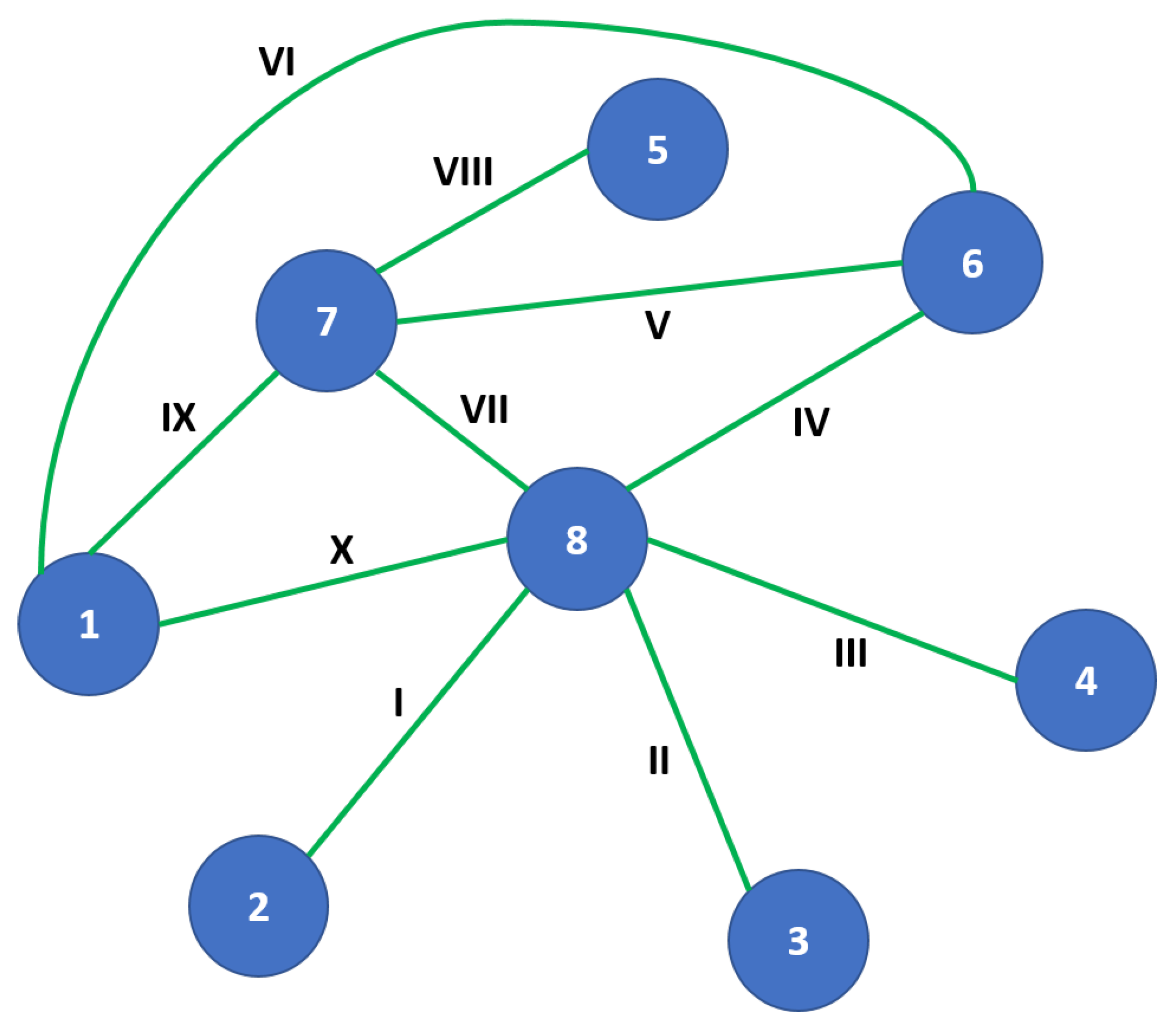
3. Modular Controller Design
Design Method
4. Dealing with Computational Burden
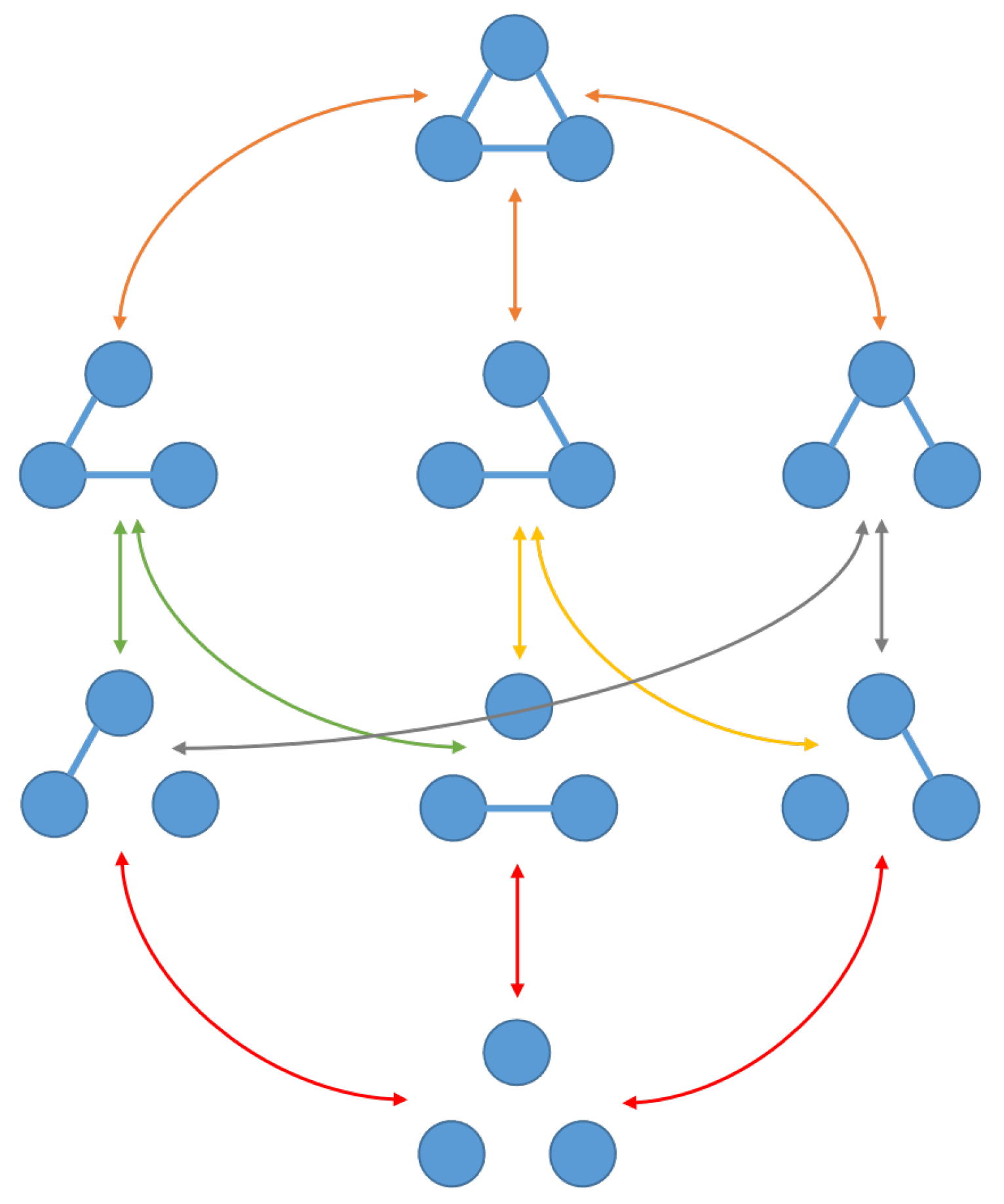
- Exploiting Convexity: Since constraint (11) is convex, any convex combination of solutions is also a solution. Given that W is common for all topologies, new solutions are generated by simply combining the results for matrices corresponding to different topologies. Likewise, it is straightforward to check that the same holds for .With this idea in mind, the problem can be simplified by solving only a subset of topologies that can be used to generate the rest of the topologies. For instance, it is possible to solve the decentralized topology, and then topologies with only one active link, i.e., instead solving LMIs the problem is reduced to the resolution of LMIs, thus avoiding the combinatorial explosion. Interestingly, the resulting feedback solution will preserve the values for the common elements in the feedback gains combined. Also, the values of the noncommon elements are easy to calculate due to the block structure of the modular controller (recall that blocks corresponding to a link become zero when the link is disabled).This strategy can be very convenient for hierarchical control, where an upper control layer can compute a convex combination of to generate a feedback gain for the desired topology, e.g., by searching for the combination that maximizes the trace of W (or minimizes the trace of P).
- Ascendants replaced by descendants: Any topology provides a feasible solution for all its ascendants (see Definition 1). Thus, it is possible to remove topologies from set and simply use one of its descendants (Definition 2) instead to reduce the number of constraints of the problem.
- Branch-and-bound-like approaches: Those topologies that degrade the most the performance of the controller are removed, e.g., those that decrease the most the trace of W. Please note that given a topology, its trace of W, i.e., when the LMI is solved for this specific topology, is a lower bound for all its descendants. This fact is used to compute a modular controller only for those topologies that provide the best performance according to the aforementioned criterion.
- Topology clustering: For large-scale systems, clustering the different agents/subsystems in super agents can be an interesting approach to handle the computational burden. For instance, the agents clustering could be achieved by different algorithms in the line of those described in [28,40,42,44], where the partitioning is performed by pre-selecting those sets of agents that are not highly interrelated with other agents and may separately work well offline prior to proceed with the control law implementation.
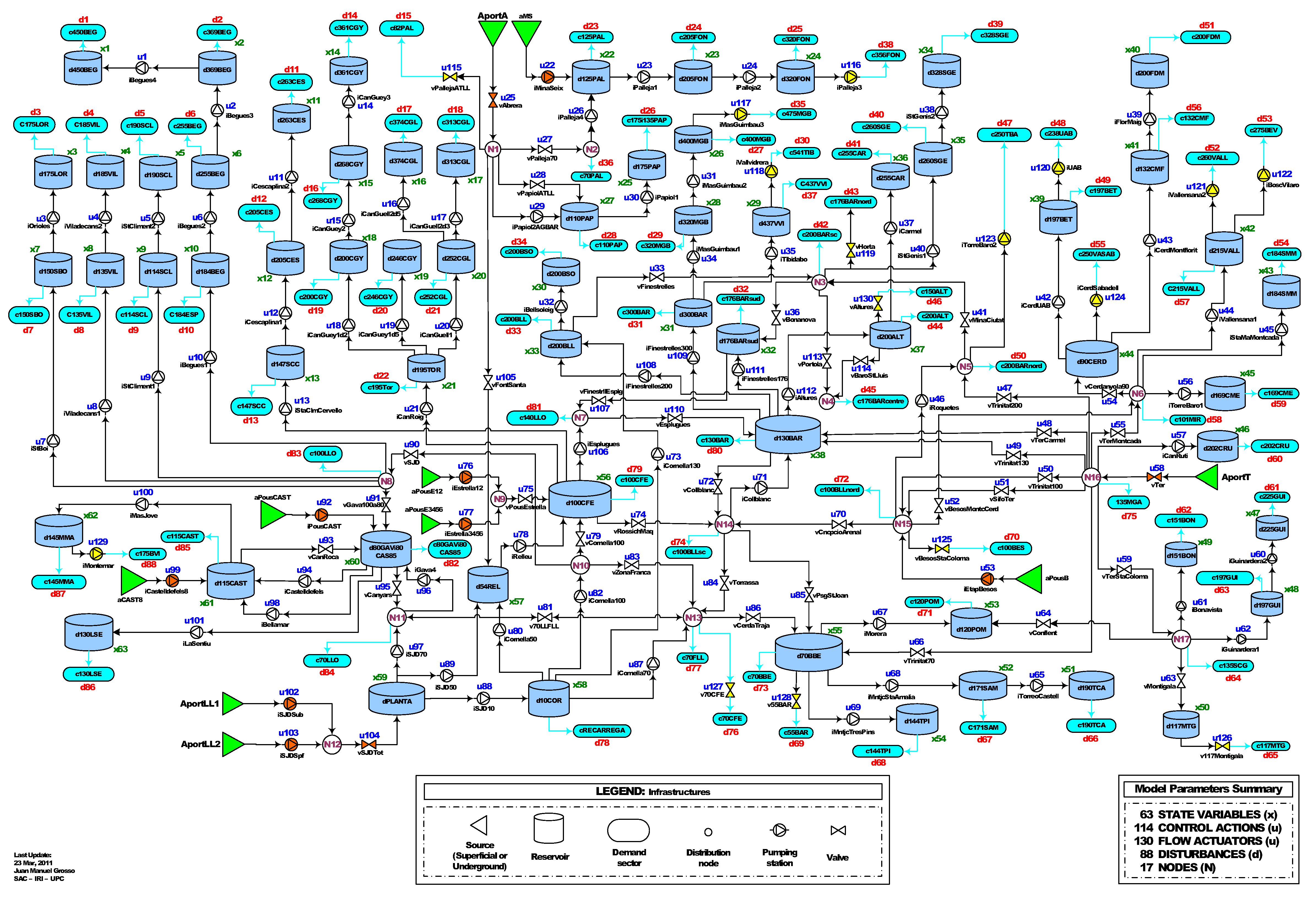
5. Case Study: Barcelona DWN
5.1. Barcelona DWN Description
- Water tanks differences equationswhere is the water level in tank i, and and are respectively the i-th and j-th inflows and outflows in m. The aggregation of all differences equations allows us to reformulate the problem aswith being the disturbances vector, , and where the rest of variables are defined as introduced in Section 2.
- Mass-balance constraints imposed by the nodeswith and defined as before. Equation (16) can be rewritten in matrix form and considering the known disturbances aswhere and respectively deal with the flows associated with the control variables and those corresponding to the water demands.
- Bounds on inputs, i.e.,where the values and are the upper and lower limits of the different actuators at the DWN, respectively.
- Bounds on states at tanks, i.e.,being and respectively the minimum and maximum levels at the water tanks.
5.2. Control Variables Parameterization
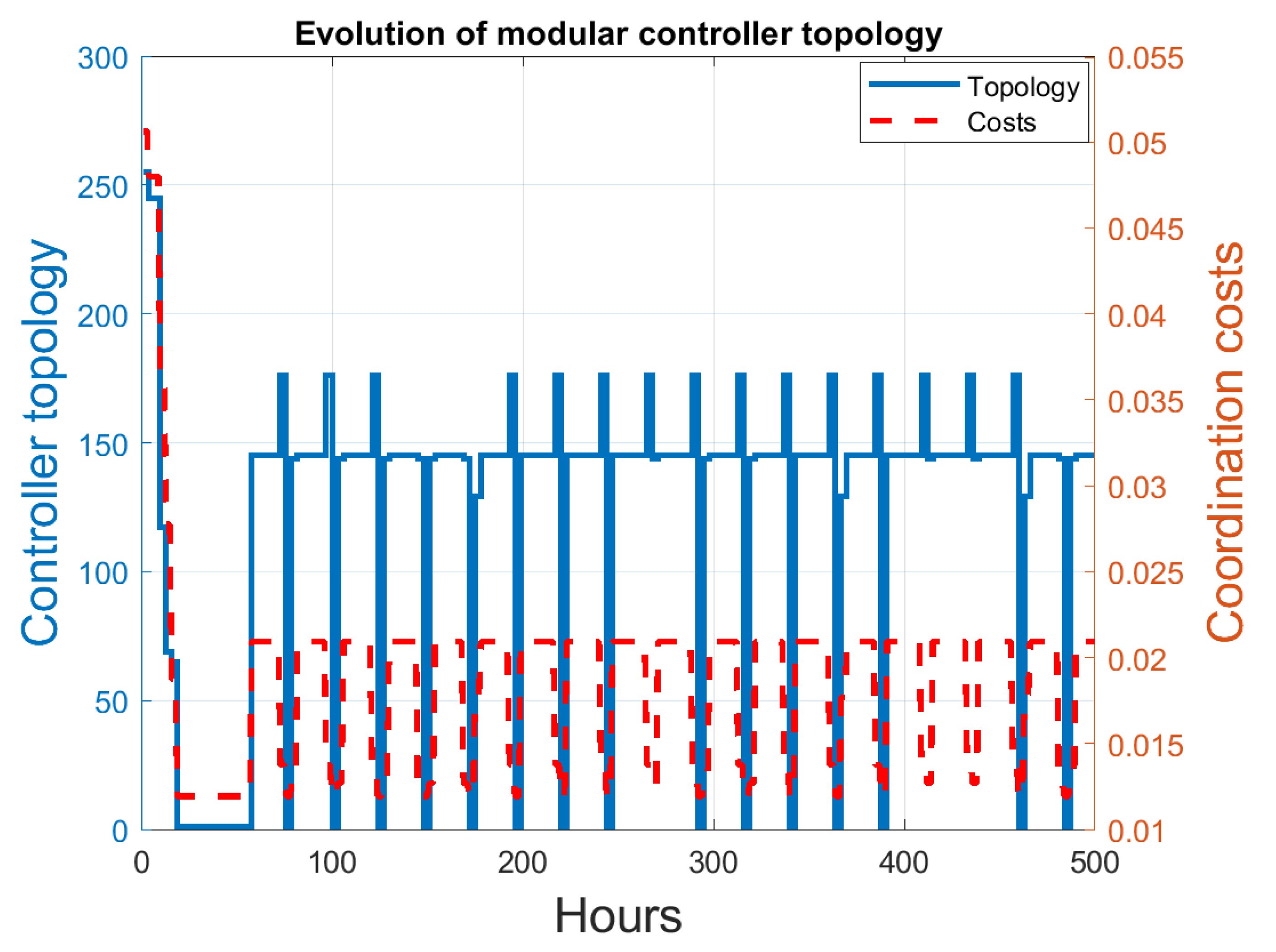
5.3. Modular Controller for the Barcelona DWN
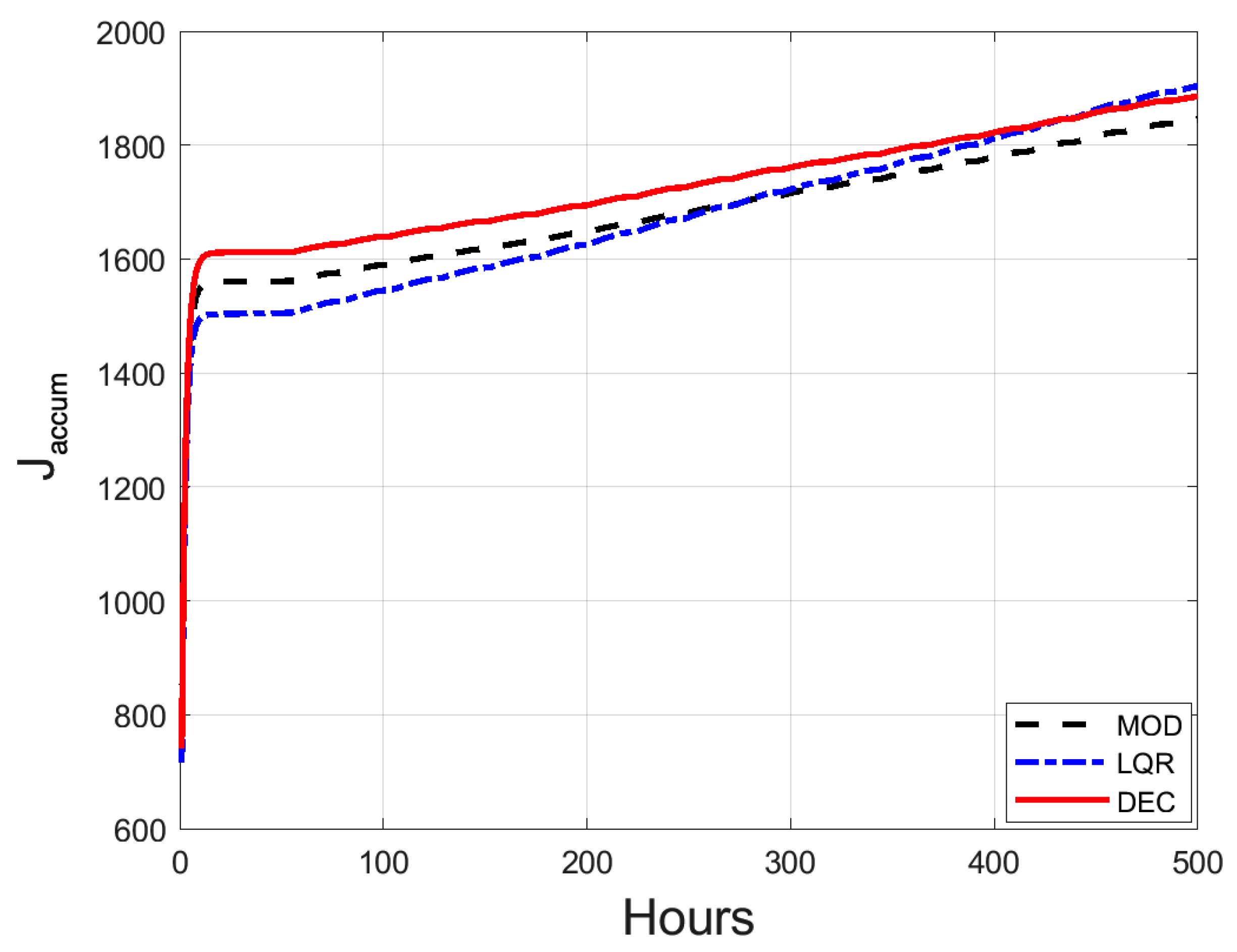
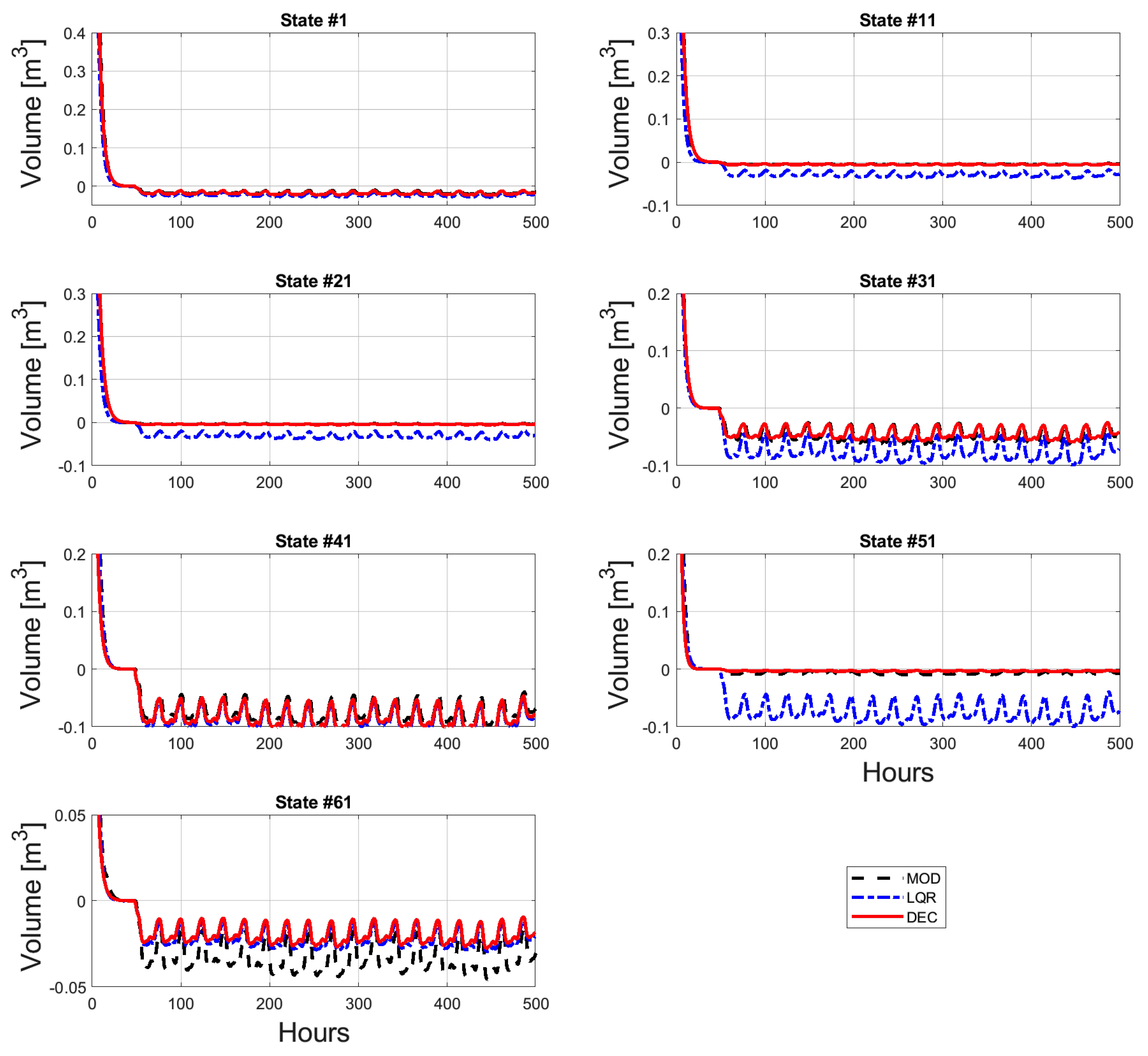
- Modular controller (MOD), obtained using the procedure described in Section 3. Here, the topologies are assessed every three time steps, so that the feedback controller providing the minimum expected cost before the next topology change instant is selected. Please note that system stability is guaranteed despite topology changes due to the existence of a common Lyapunov function.
- Linear-quadratic regulator (LQR), designed for the centralized system.
- Decentralized controller (DEC), which has been obtained following the coalitional approach of [8] for the decentralized communication topology.
- The former is related to the reliable modularity the control strategy confers since the overall system gains certain upper-level of robustness against fault events that might occur. Notice that the coordination and noncentralized features of the proposed approach make that, once a problem takes place, the system keeps working by isolating the affected part while the rest is self-adjusted to provide water to demand sectors.
- On the other hand, the latter factor, also operationally related to the former, relies on the fact that the approach acts as a fast decision-maker given its offline design and low online computational burden. This feature allows the system operator to promptly react facing possible problems (caused by a fault event), avoiding scenarios of water supply lacking.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hespanha, J.P.; Naghshtabrizi, P.; Xu, Y. A survey of recent results in networked control systems. Proc. IEEE 2007, 95, 138–162. [Google Scholar] [CrossRef]
- Negenborn, R.R.; Maestre, J.M. Distributed model predictive control: An overview and roadmap of future research opportunities. IEEE Control Syst. Mag. 2014, 34, 87–97. [Google Scholar] [CrossRef]
- Lian, F.; Chakrabortty, A.; Duel-Hallen, A. Game-theoretic multi-agent control and network cost allocation under communication constraints. IEEE J. Sel. Areas Commun. 2017, 35, 330–340. [Google Scholar] [CrossRef]
- Lin, F.; Fardad, M.; Jovanović, M.R. Design of optimal sparse feedback gains via the alternating direction method of multipliers. IEEE Trans. Autom. Control 2013, 58, 2426–2431. [Google Scholar] [CrossRef]
- Rotkowitz, M.; Lall, S. Decentralized control information structures preserved under feedback. In Proceedings of the 41st IEEE Conference on Decision and Control (CDC), Las Vegas, NV, USA, 10–13 December 2002; pp. 569–575. [Google Scholar]
- Furieri, L.; Kamgarpour, M. Robust distributed control beyond quadratic invariance. In Proceedings of the 57th IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 3728–3733. [Google Scholar]
- Maestre, J.M. Distributed model predictive control based on game theory. Ph.D. Thesis, University of Seville, Seville, Spain, 2010. [Google Scholar]
- Maestre, J.M.; Muñoz de la Peña, D.; Jimenez Losada, A.; Algaba, E.; Camacho, E.F. A coalitional control scheme with applications to cooperative game theory. Optim. Control Appl. Methods 2014, 35, 592–608. [Google Scholar] [CrossRef]
- Polyak, B.T.; Khlebnikov, M.V.; Shcherbakov, P. An LMI approach to structured sparse feedback design in linear control systems. In Proceedings of the 12th European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 833–838. [Google Scholar]
- Blanchini, F.; Franco, E.; Giordano, G. Structured-LMI conditions for stabilizing network-decentralized control. In Proceedings of the 52nd IEEE Conference on Decision and Control (CDC), Firenze, Italy, 10–13 December 2013; pp. 6880–6885. [Google Scholar]
- Blanchini, F.; Franco, E.; Giordano, G. Network-decentralized control strategies for stabilization. IEEE Trans. Autom. Control 2015, 60, 491–496. [Google Scholar] [CrossRef]
- Tanaka, T.; Langbort, C. The bounded real lemma for internally positive systems and H-infinity structured static state feedback. IEEE Trans. Autom. Control 2011, 56, 2218–2223. [Google Scholar] [CrossRef]
- Arauz, T.; Maestre, J.M.; Tian, X.; Guan, G. Design of PI controllers for irrigation canals based on linear matrix inequalities. Water 2020, 12, 855. [Google Scholar] [CrossRef]
- Lopez-Rodriguez, F.; Maestre, J.M.; Muros, F.J.; Camacho, E.F. A modular feedback approach for distributed control. In Proceedings of the 21st IFAC World Congress, Berlin, Germany, 12–17 July 2020; pp. 4086–4091. [Google Scholar]
- Fele, F.; Maestre, J.M.; Camacho, E.F. Coalitional control: Cooperative game theory and control. IEEE Control Syst. Mag. 2017, 37, 53–69. [Google Scholar] [CrossRef]
- Fele, F.; Debada, E.; Maestre, J.M.; Camacho, E.F. Coalitional control for self-organizing agents. IEEE Trans. Autom. Control 2018, 63, 2883–2897. [Google Scholar] [CrossRef]
- Marzband, M.; Ardeshiri, R.R.; Moafi, M.; Uppal, H. Distributed generation for economic benefit maximization through coalition formation–based game theory concept. Int. Trans. Electr. Energy Syst. 2017, 27, e2313. [Google Scholar] [CrossRef]
- Baldivieso-Monasterios, P.R.; Trodden, P.A. Coalitional predictive control: Consensus-based coalition forming with robust regulation. Automatica 2021, 125, 109380. [Google Scholar] [CrossRef]
- Muros, F.J. El control coalicional en el marco de la teoría de juegos cooperativos. Rev. Iberoam. Automática e Informática Ind. 2021, in press. [Google Scholar] [CrossRef]
- Chanfreut, P.; Maestre, J.M.; Camacho, E.F. Coalitional model predictive control on freeways traffic networks. IEEE Trans. Intell. Transp. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Fele, F.; Maestre, J.M.; Hashemy, S.M.; Muñoz de la Peña, D.; Camacho, E.F. Coalitional model predictive control of an irrigation canal. J. Process Control 2014, 24, 314–325. [Google Scholar] [CrossRef]
- Maestre, J.M.; Ishii, H. A PageRank based coalitional control scheme. Int. J. Control Autom. Syst. 2017, 15, 1983–1990. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; di Nardo, A.; Carravetta, A.; Ramos, H.M.; Adeyeye, K. Zero-net energy management for the monitoring and control of dynamically-partitioned smart water systems. J. Clean. Prod. 2020, 252, 119745. [Google Scholar] [CrossRef]
- Fletscher, L.A.; Maestre, J.M.; Peroni, C.V. Coalitional planning for energy efficiency of HetNets powered by hybrid energy sources. IEEE Trans. Veh. Technol. 2018, 67, 6573–6584. [Google Scholar] [CrossRef]
- Masero, E.; Fletscher, L.A.; Maestre, J.M. A coalitional model predictive control for the energy efficiency of next-generation cellular networks. Energies 2020, 13, 6546. [Google Scholar] [CrossRef]
- Ananduta, W.; Pippia, T.; Ocampo-Martinez, C.; Sijs, J.; De Schutter, B. Online partitioning method for decentralized control of linear switching large-scale systems. J. Frankl. Inst. 2019, 356, 3290–3313. [Google Scholar] [CrossRef]
- Masero, E.; Frejo, J.R.D.; Maestre, J.M.; Camacho, E.F. A light clustering model predictive control approach to maximize thermal power in solar parabolic-trough plants. Sol. Energy 2021, 214, 531–541. [Google Scholar] [CrossRef]
- Siniscalchi-Minna, S.; Bianchi, F.D.; Ocampo-Martinez, C.; Domínguez-García, J.L.; De Schutter, B. A non-centralized predictive control strategy for wind farm active power control: A wake-based partitioning approach. Renew. Energy 2020, 150, 656–669. [Google Scholar] [CrossRef]
- Muros, F.J.; Maestre, J.M.; Algaba, E.; Alamo, T.; Camacho, E.F. Networked control design for coalitional schemes using game-theoretic methods. Automatica 2017, 78, 320–332. [Google Scholar] [CrossRef]
- Muros, F.J.; Algaba, E.; Maestre, J.M.; Camacho, E.F. Harsanyi power solutions in coalitional control systems. IEEE Trans. Autom. Control 2017, 62, 3369–3381. [Google Scholar] [CrossRef]
- Muros, F.J.; Algaba, E.; Maestre, J.M.; Camacho, E.F. The Banzhaf value as a design tool in coalitional control. Syst. Control Lett. 2017, 104, 21–30. [Google Scholar] [CrossRef]
- Stoustrup, J. Plug & play control: Control technology towards new challenges. Eur. J. Control 2009, 15, 311–330. [Google Scholar] [CrossRef]
- Bendtsen, J.; Trangbaek, K.; Stoustrup, J. Plug-and-play control—Modifying control systems online. IEEE Trans. Control Syst. Technol. 2013, 21, 79–93. [Google Scholar] [CrossRef]
- Riverso, S.; Farina, M.; Ferrari-Trecate, G. Plug-and-play decentralized model predictive control for linear systems. IEEE Trans. Autom. Control 2013, 58, 2608–2614. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Networked control under random and malicious packet losses. IEEE Trans. Autom. Control 2017, 62, 2434–2449. [Google Scholar] [CrossRef]
- Azimi-Sadjadi, B. Stability of networked control systems in the presence of packet losses. In Proceedings of the 42nd IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 9–12 December 2003; pp. 676–681. [Google Scholar]
- Yu, M.; Wang, L.; Chu, T.; Xie, G. Stabilization of networked control systems with data packet dropout and network delays via switching system approach. In Proceeding of the 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; pp. 3539–3544. [Google Scholar]
- Zheng, Y.; Yongsong, W.; Shaoyuan, L. Coupling degree clustering-based distributed model predictive control network design. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1749–1758. [Google Scholar] [CrossRef]
- Jain, A.; Chakrabortty, A.; Biyik, E. Distributed wide-area control of power system oscillations under communication and actuation constraints. Control Eng. Pract. 2018, 74, 132–143. [Google Scholar] [CrossRef]
- Barreiro-Gomez, J.; Ocampo-Martinez, C.; Quijano, N. Time-varying partitioning for predictive control design: Density-games approach. J. Process Control 2019, 75, 1–14. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Creus, R.; Minoves, M. Improving water management efficiency by using optimization-based control strategies: The Barcelona case study. Water Supply 2009, 9, 565–575. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C.; Bovo, S.; Puig, V. Partitioning approach oriented to the decentralised predictive control of large-scale systems. J. Process Control 2011, 21, 775–786. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of predictive control strategies to the management of complex networks in the urban water cycle. IEEE Control Syst. Mag. 2013, 33, 15–41. [Google Scholar] [CrossRef]
- Muros, F.J.; Maestre, J.M.; Ocampo-Martinez, C.; Algaba, E.; Camacho, E.F. A game theoretical randomized method for large-scale systems partitioning. IEEE Access 2018, 6, 42245–42263. [Google Scholar] [CrossRef]
- Buluç, A.; Meyerhenke, H.; Safro, I.; Sanders, P.; Schulz, C. Recent advances in graph partitioning. In Algorithm Engineering. Selected Results and Surveys; Lecture Notes in Computer Science; Kliemann, L., Sanders, P., Eds.; Springer: Cham, Switzerland, 2016; Volume 9220, Chapter 25; pp. 117–158. [Google Scholar]
- Meyerhenke, H.; Sanders, P.; Schulz, C. Parallel graph partitioning for complex networks. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 2625–2638. [Google Scholar] [CrossRef]
- Guo, Y.; Hong, S.; Chafi, H.; Iosup, A.; Epema, D. Modeling, analysis, and experimental comparison of streaming graph-partitioning policies. J. Parallel Distrib. Comput. 2017, 108, 106–121. [Google Scholar] [CrossRef]
- Rahimian, F.; Payberah, A.H.; Girdzijauskas, S.; Jelasity, M.; Haridi, S. A distributed algorithm for large-scale graph partitioning. ACM Trans. Auton. Adapt. Syst. 2015, 10, 12:1–12:24. [Google Scholar] [CrossRef]
- Schneider, R. A solution for the partitioning problem in partition-based-moving-horizon estimation. IEEE Trans. Autom. Control 2017, 62, 3076–3082. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F.; Simone, A. Water distribution system clustering and partitioning based on social network algorithms. Procedia Eng. 2015, 119, 196–205. [Google Scholar] [CrossRef]
- Pizzuti, C. A multiobjective genetic algorithm to find communities in complex networks. IEEE Trans. Evol. Comput. 2012, 16, 418–430. [Google Scholar] [CrossRef]
- Tsumura, K.; Yamamoto, H. Optimal multiple controlling nodes problem for multi-agent systems via Alt-PageRank. In Proceedings of the 4th IFAC Workshop on Distributed Estimation and Control in Networked Systems (NECSYS), Koblenz, Germany, 25–26 September 2013; pp. 433–438. [Google Scholar]
- Barcelli, D.; Ocampo-Martinez, C.; Puig, V.; Bemporad, A. Decentralized model predictive control of drinking water networks using an automatic subsystem decomposition approach. In Proceedings of the 12th IFAC Symposium on Large Scale Systems: Theory and Applications (LSS), Villeneuve d’Ascq, France, 12–14 July 2010; pp. 572–577. [Google Scholar]
- Tedesco, F.; Ocampo-Martinez, C.; Casavola, A.; Puig, V. Centralized and Distributed Command Governor Approaches for Water Supply Systems Management. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 586–595. [Google Scholar] [CrossRef]
- Rahman, A.; Wu, Z.Y. Multistep Simulation-Optimization Modeling Approach for Partitioning Water Distribution System into District Meter Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018018. [Google Scholar] [CrossRef]
- Campisano, A.; Creaco, E.; Modica, C. RTC of valves for leakage reduction in water supply networks. J. Water Resour. Plan. Manag. 2010, 136, 138–141. [Google Scholar] [CrossRef]
- Page, P.R.; Abu-Mahfouz, A.M.; Mothetha, M.L. Pressure management of water distribution systems via the remote real-time control of variable speed pumps. J. Water Resour. Plan. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef]
- Salomons, E.; Housh, M. A practical optimization scheme for real-time operation of water distribution systems. J. Water Resour. Plan. Manag. 2020, 146, 04020016. [Google Scholar] [CrossRef]
- Zhang, F. The Schur Complement and Its Applications; Numerical Methods and Algorithm Series; Springer: New York, NY, USA, 2005; Volume 4. [Google Scholar]
- Vanderberghe, L.; Boyd, S. Semidefinite Programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef]
- Grosso, J.M.; Ocampo-Martinez, C.; Puig, V.; Joseph, B. Chance-constrained model predictive control for drinking water networks. J. Process Control 2014, 24, 504–516. [Google Scholar] [CrossRef]
- Kothare, M.V.; Balakrishnan, V.; Morari, M. Robust constrained model predictive control using linear matrix inequalities. Automatica 1996, 32, 1361–1379. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maestre, J.M.; Lopez-Rodriguez, F.; Muros, F.J.; Ocampo-Martinez, C. Modular Feedback Control of Networked Systems by Clustering: A Drinking Water Network Case Study. Processes 2021, 9, 389. https://doi.org/10.3390/pr9020389
Maestre JM, Lopez-Rodriguez F, Muros FJ, Ocampo-Martinez C. Modular Feedback Control of Networked Systems by Clustering: A Drinking Water Network Case Study. Processes. 2021; 9(2):389. https://doi.org/10.3390/pr9020389
Chicago/Turabian StyleMaestre, José María, Francisco Lopez-Rodriguez, Francisco Javier Muros, and Carlos Ocampo-Martinez. 2021. "Modular Feedback Control of Networked Systems by Clustering: A Drinking Water Network Case Study" Processes 9, no. 2: 389. https://doi.org/10.3390/pr9020389
APA StyleMaestre, J. M., Lopez-Rodriguez, F., Muros, F. J., & Ocampo-Martinez, C. (2021). Modular Feedback Control of Networked Systems by Clustering: A Drinking Water Network Case Study. Processes, 9(2), 389. https://doi.org/10.3390/pr9020389