Energy Management in Smart Building by a Multi-Objective Optimization Model and Pascoletti-Serafini Scalarization Approach
Abstract
1. Introduction
2. Multi-Objective Optimization Problem and Some Preliminaries
3. Problem Description and Mathematical Model
- Solar photovoltaic production is considered for self-consumption but with the possibility of selling the surplus to the power grid;
- It is considered that each EV leaves and arrives to the building once a day. All EVs are connected to the electric network as soon as they get home.
- The arrival and departure times are known and for each EV the initial SoC is known at the arrival time. The EV battery can be charged/discharged between arrival and departure.
Formulation of MOOP
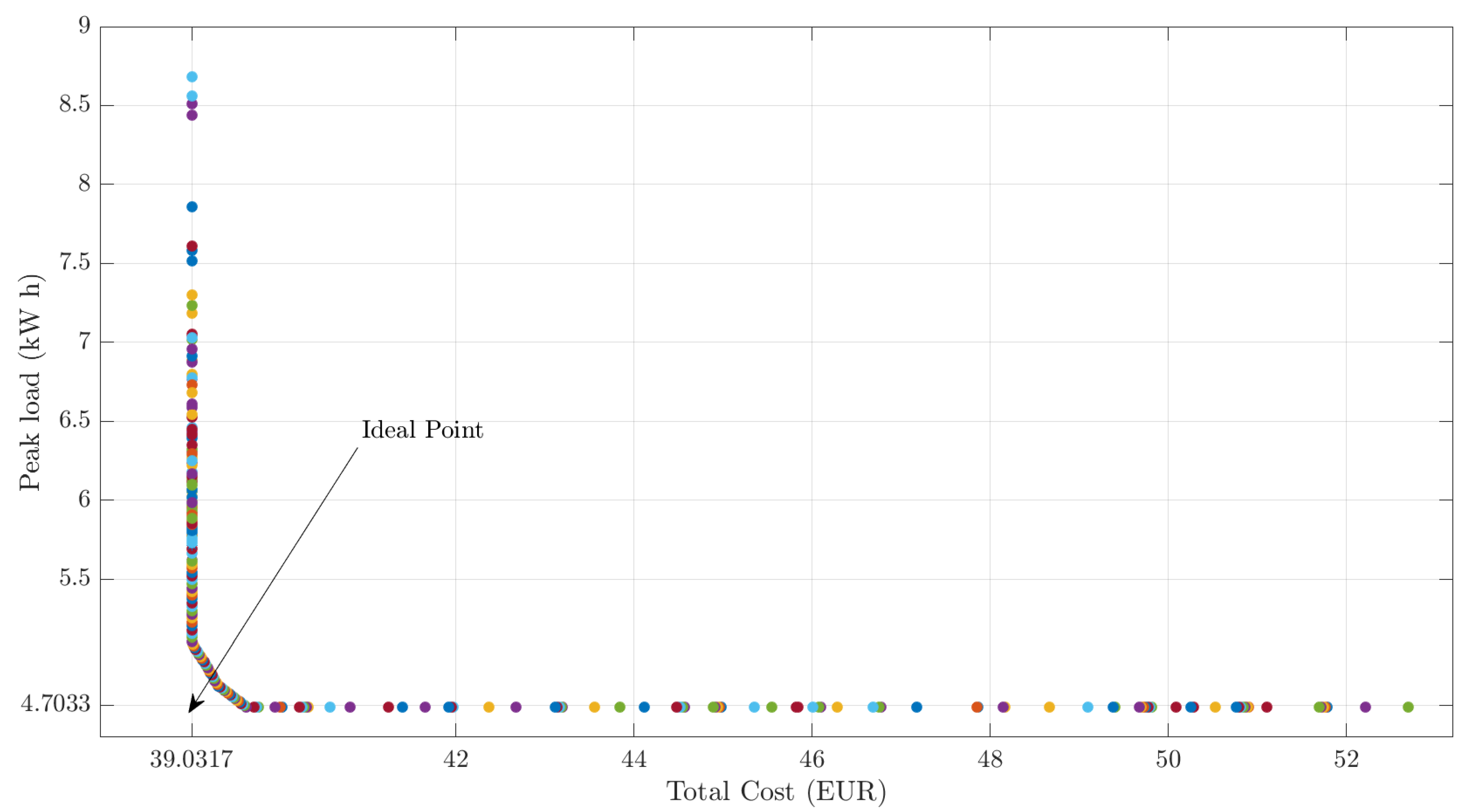
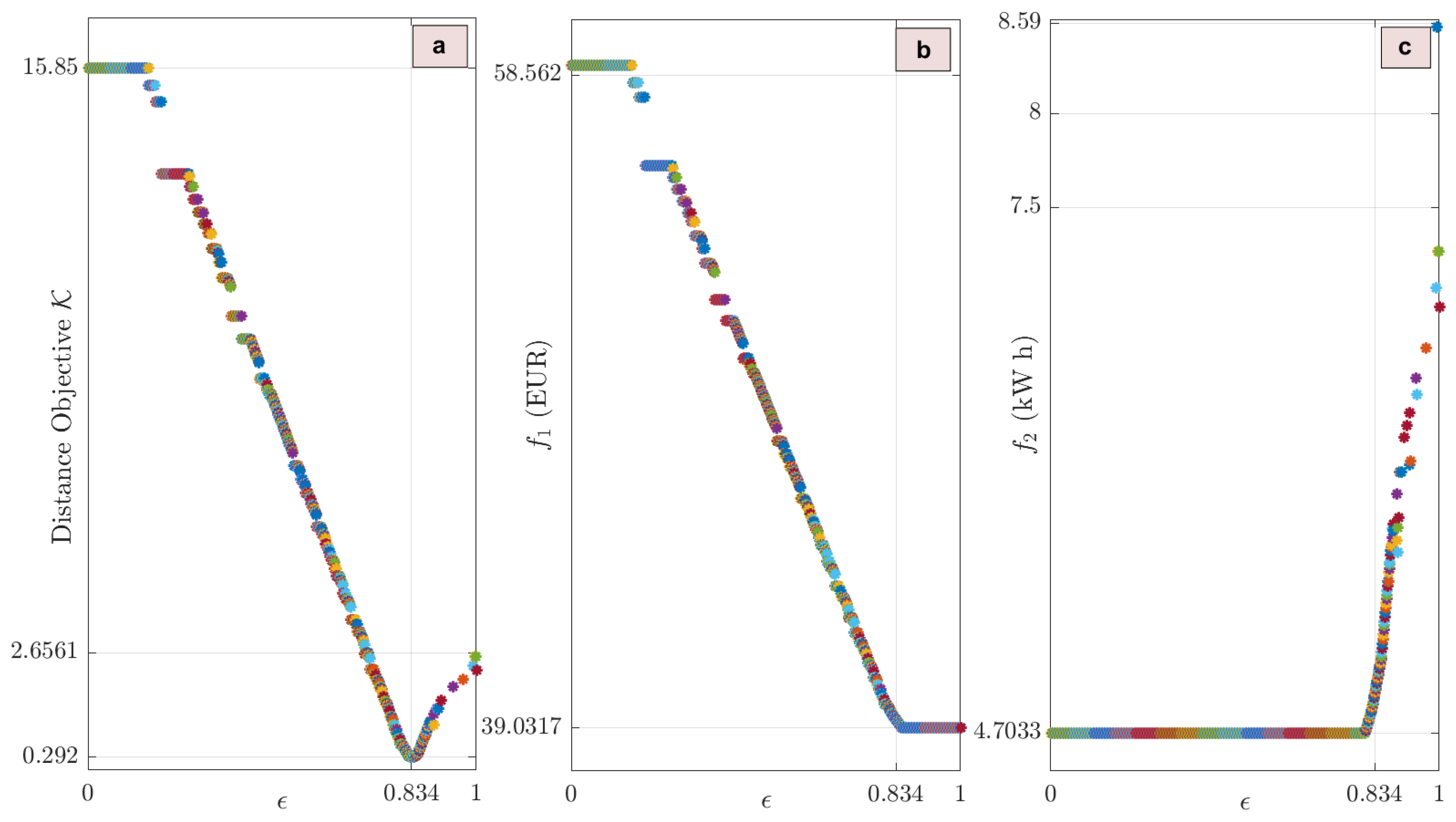
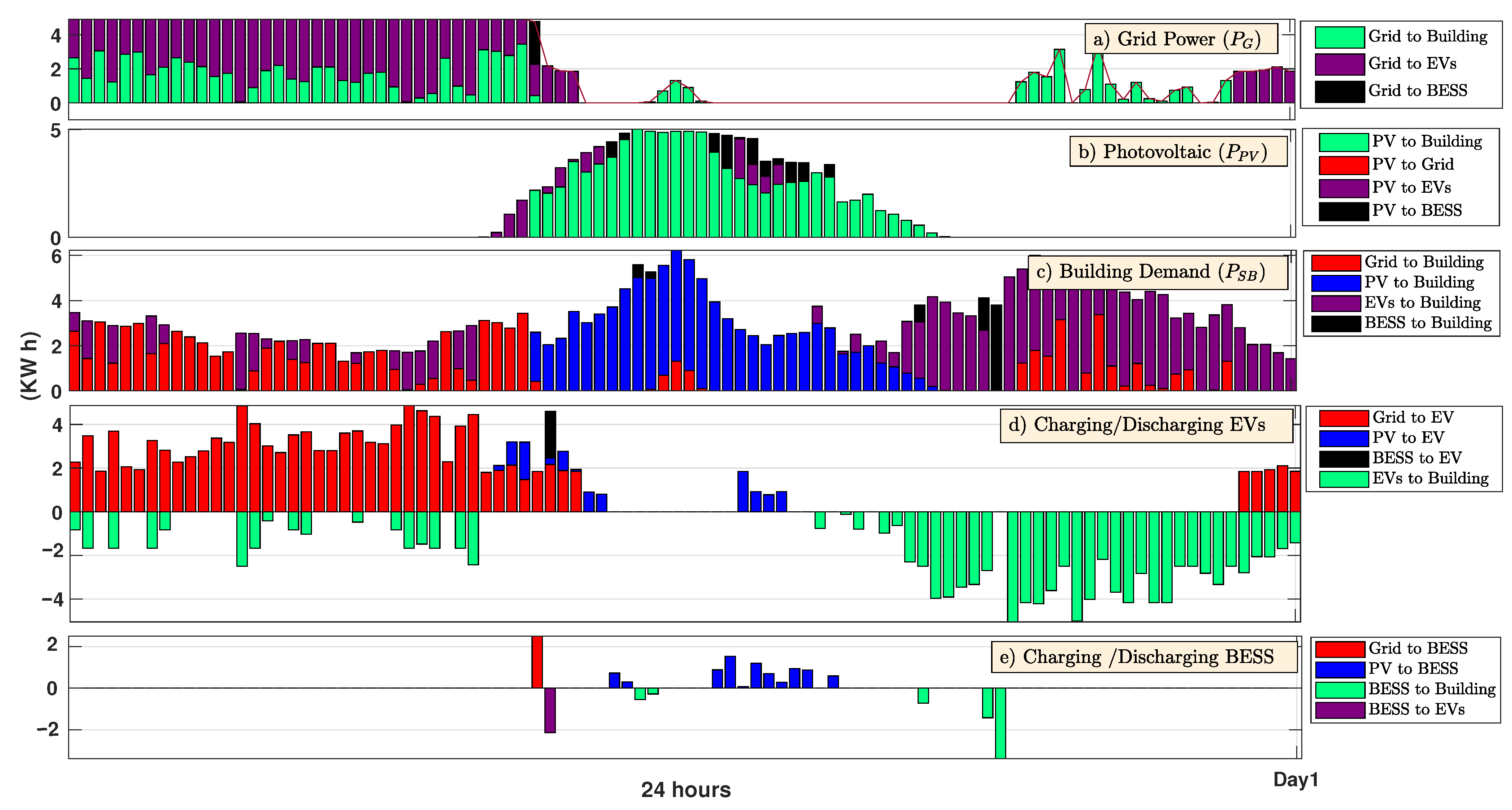
4. Case Study
Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kazerani, M.; Tehrani, K. Grid of Hybrid AC/DC Microgrids: A New Paradigm for Smart City of Tomorrow. In Proceedings of the 2020 IEEE 15th International Conference of System of Systems Engineering (SoSE), Budapest, Hungary, 2–4 June 2020; pp. 175–180. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Ton, D.; Zhou, Y.; Kim, J.; Vyas, A. Impact of plug-in hybrid electric vehicles on power systems with demand response and wind power. Energy Policy 2011, 39, 4016–4021. [Google Scholar] [CrossRef]
- Habib, S.; Kamran, M.; Rashid, U. Impact analysis of vehicle-to-grid technology and charging strategies of electric vehicles on distribution networks—A review. J. Power Sources 2015, 277, 205–214. [Google Scholar] [CrossRef]
- Soares, J.; Pinto, T.; Lezama, F.; Morais, H. Survey on Complex Optimization and Simulation for the New Power Systems Paradigm. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Haidar, N.; Attia, M.; Senouci, S.M.; Aglzim, E.H.; Kribeche, A.; Asus, Z.B. New consumer-dependent energy management system to reduce cost and carbon impact in smart buildings. Sustain. Cities Soc. 2018, 39, 740–750. [Google Scholar] [CrossRef]
- Thomas, D.; Ioakimidis, C.S.; Klonari, V.; Vallée, F.; Deblecker, O. Effect of electric vehicles’ optimal charging-discharging schedule on a building’s electricity cost demand considering low voltage network constraints. In Proceedings of the 2016 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Ljubljana, Slovenia, 9–12 October 2016; pp. 1–6. [Google Scholar]
- Tehrani, K. A smart cyber physical multi-source energy system for an electric vehicle prototype. J. Syst. Archit. 2020, 111, 101804. [Google Scholar] [CrossRef]
- Thomas, D.; Deblecker, O.; Bagheri, A.; Ioakimidis, C.S. A scheduling optimization model for minimizing the energy demand of a building using electric vehicles and a micro-turbine. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016; pp. 1–6. [Google Scholar]
- Thomas, D.; Deblecker, O.; Genikomsakis, K.; Ioakimidis, C.S. Smart house operation under PV and load demand uncertainty considering EV and storage utilization. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3644–3649. [Google Scholar]
- Deepak Mistry, R.; Eluyemi, F.T.; Masaud, T.M. Impact of aggregated EVs charging station on the optimal scheduling of battery storage system in islanded microgrid. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–5. [Google Scholar]
- Chandra Mouli, G.R.; Kefayati, M.; Baldick, R.; Bauer, P. Integrated PV Charging of EV Fleet Based on Energy Prices, V2G, and Offer of Reserves. IEEE Trans. Smart Grid 2019, 10, 1313–1325. [Google Scholar] [CrossRef]
- Zahra, F.; Sérgio, R.; Soares, J.; Fernando, L.; Zita, V.; Antonio, G.; Rodrigo, L.J. A Mixed Binary Linear Programming Model for Optimal Energy Management of Smart Buildings. Energies 2020, 13, 1719. [Google Scholar] [CrossRef]
- Moya, F.D.; Moreno, T.; Álvarez, J.D. Optimal Model for Energy Management Strategy in Smart Building with Energy Storage Systems and Electric Vehicles. Energies 2020, 13, 3605. [Google Scholar] [CrossRef]
- Van der Meer, D.; Mouli, G.R.C.; Elizondo, L.R.; Bauer, P. Energy Management System With PV Power Forecast to Optimally Charge EVs at the Workplace. IEEE Trans. Ind. Inform. 2018, 14, 311–320. [Google Scholar] [CrossRef]
- Erdinc, O.; Paterakis, N.G.; Mendes, T.D.P.; Bakirtzis, A.G.; Catalão, J.P. Smart Household Operation Considering Bi-Directional EV and ESS Utilization by Real-Time Pricing-Based DR. IEEE Trans. Smart Grid 2015, 6, 1281–1291. [Google Scholar] [CrossRef]
- Cox, R.; Walker, S.; van der Velden, J.; Nguyen, P.; Zeiler, W. Flattening the electricity demand profile of office buildings for future-proof smart grids. Energies 2020, 13, 2357. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M.; Jantzen, J.; Kristensen, M.; Ben Othman, S. Energy scheduling of a smart microgrid with shared photovoltaic panels and storage: The case of the Ballen marina in Samsø. Energy 2020, 198. [Google Scholar] [CrossRef]
- Olivieri, Z.; McConky, K. Optimization of residential battery energy storage system scheduling for cost and emissions reductions. Energy Build. 2020, 210. [Google Scholar] [CrossRef]
- Zadeh, L. Optimality and non-scalar-valued performance criteria. IEEE Trans. Autom. Control. 1963, 8, 59–60. [Google Scholar] [CrossRef]
- Haimes, Y. On a Bicriterion Formation of the Problems of Integrated System Identification and System Optimization. IEEE Trans. Syst. Man Cybern. 1971, 1, 296–297. [Google Scholar]
- Messac, A.; Ismail-Yahaya, A.; Mattson, C. The normalized normal constraint method for generating the Pareto frontier. Struct. Multidiscip. Optim. 2003, 25, 86–98. [Google Scholar] [CrossRef]
- Messac, A.; Mattson, C.A. Normal Constraint Method with Guarantee of Even Representation of Complete Pareto Frontier. AIAA J. 2004, 42, 2101–2111. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Kaliszewski, I. A modified weighted tchebycheff metric for multiple objective programming. Comput. Oper. Res. 1987, 14, 315–323. [Google Scholar] [CrossRef]
- Pascoletti, A.; Serafini, P. Scalarizing vector optimization problems. J. Optim. Theory Appl. 1984, 42, 499–524. [Google Scholar] [CrossRef]
- Eichfelder, G. Adaptive Scalarization Methods in Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 2008; Volume 436. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 1998; Volume 12. [Google Scholar] [CrossRef]
| Parameter | Index | Description |
|---|---|---|
| I | Number of time-slots per Time-Study | |
| Time-slot duration (hour) | ||
| J | Number of apartments (or EVs) in the building | |
| , | The number of period-time in which j-th EV enters to the parking | |
| , | The number of period-time in which j-th EV leaves the parking | |
| Maximum allowable State of Charge(SoC) of j-th EV | ||
| , | The initial SoC of j-th EV at the beginning departure in | |
| , | The minimum allowable SoC for j-th EV at exit time | |
| Maximum SoC for BESS | ||
| Initial SoC for BESS at the beginning of time-period | ||
| Total power demand of SB at period i | ||
| Total generated power by PV at period i | ||
| Maximum power that can got from Grid at time-slot i | ||
| Purchased electricity cost from grid in i-th time-slot | ||
| Sell electricity cost to grid in i-th time-slot | ||
| Active power related to the charging process of the j-th EV | ||
| Active power related to the discharging process of the j-th EV | ||
| The charge efficiency of j-th EV | ||
| The discharge efficiency of j-th EV | ||
| Active power of the charging process of the BESS in period i | ||
| Active power of the discharging process of BESS in period i |
| Variable | Type | Index | Description |
|---|---|---|---|
| j-th EV charging process in period i | |||
| j-th EV discharging process in period i | |||
| BESS charging process in period i | |||
| BESS discharging process in period i | |||
| SoC of the j-th EV at the start of period i | |||
| SoC of the BESS at the start of period i | |||
| Active power extracted from the grid in period i | |||
| Active power of charging the BESS by grid in period i | |||
| Active power of charging the j-th EV by grid in period i | |||
| Active power of discharging of j-th EV to SB in period i. | |||
| Active power from PV to SB in period i | |||
| Active power from PV to BESS in period i | |||
| Active power from PV to grid in period i | |||
| Active power from BESS to grid in period i |
| Total Cost | Peak Load (kW h) | |
|---|---|---|
| MOMBLP Model | ||
| Reference Case Study [12] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroozandeh, Z.; Ramos, S.; Soares, J.; Vale, Z. Energy Management in Smart Building by a Multi-Objective Optimization Model and Pascoletti-Serafini Scalarization Approach. Processes 2021, 9, 257. https://doi.org/10.3390/pr9020257
Foroozandeh Z, Ramos S, Soares J, Vale Z. Energy Management in Smart Building by a Multi-Objective Optimization Model and Pascoletti-Serafini Scalarization Approach. Processes. 2021; 9(2):257. https://doi.org/10.3390/pr9020257
Chicago/Turabian StyleForoozandeh, Zahra, Sérgio Ramos, João Soares, and Zita Vale. 2021. "Energy Management in Smart Building by a Multi-Objective Optimization Model and Pascoletti-Serafini Scalarization Approach" Processes 9, no. 2: 257. https://doi.org/10.3390/pr9020257
APA StyleForoozandeh, Z., Ramos, S., Soares, J., & Vale, Z. (2021). Energy Management in Smart Building by a Multi-Objective Optimization Model and Pascoletti-Serafini Scalarization Approach. Processes, 9(2), 257. https://doi.org/10.3390/pr9020257









