Turbulence Enhancement and Mixing Analysis for Multi-Inlet Vortex Photoreactor for CO2 Reduction
Abstract
1. Introduction
2. Methodology
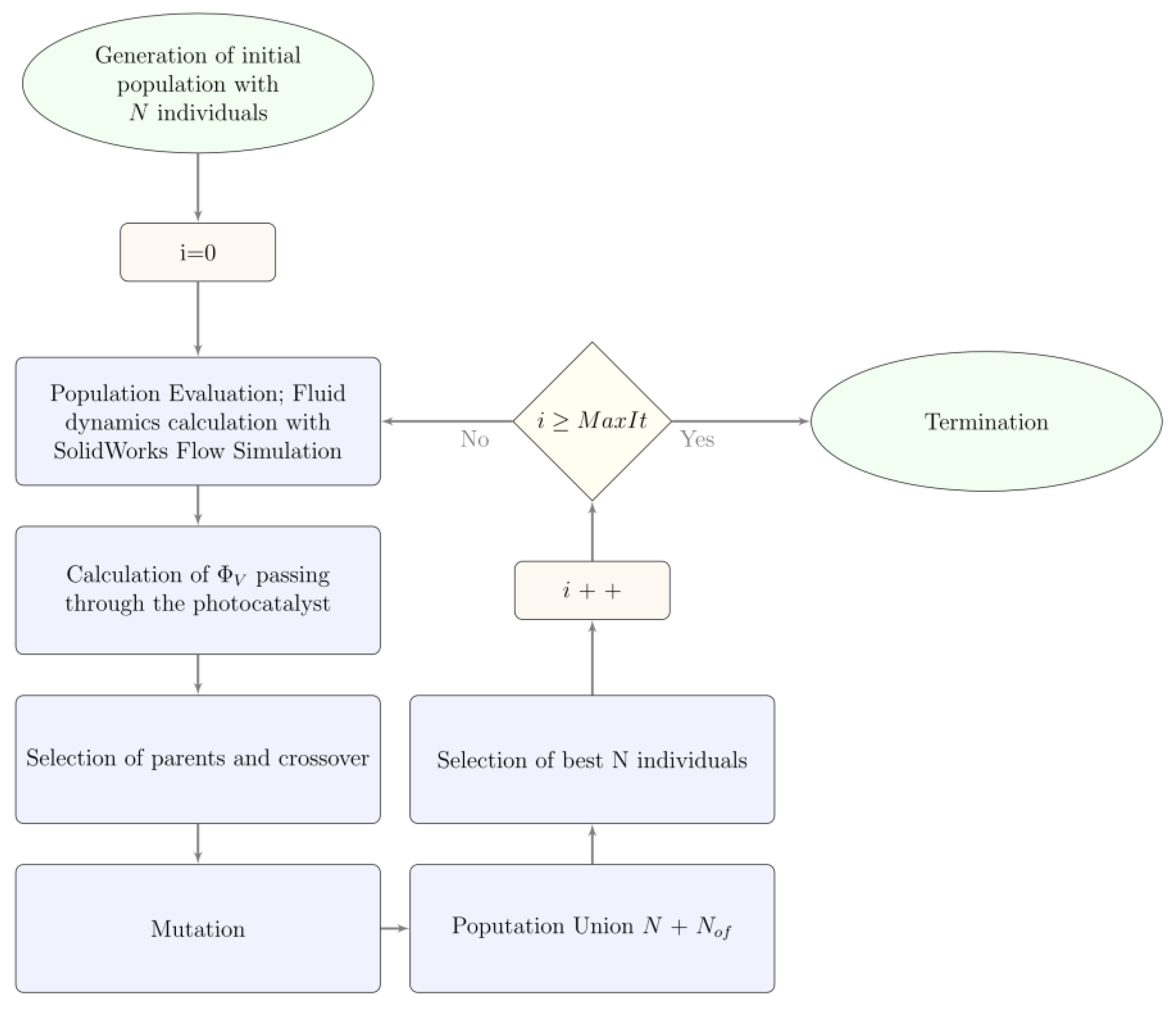
2.1. Optimization Process
Genetic Algorithm
2.2. Tunning Process for the Optimized Photoreactor
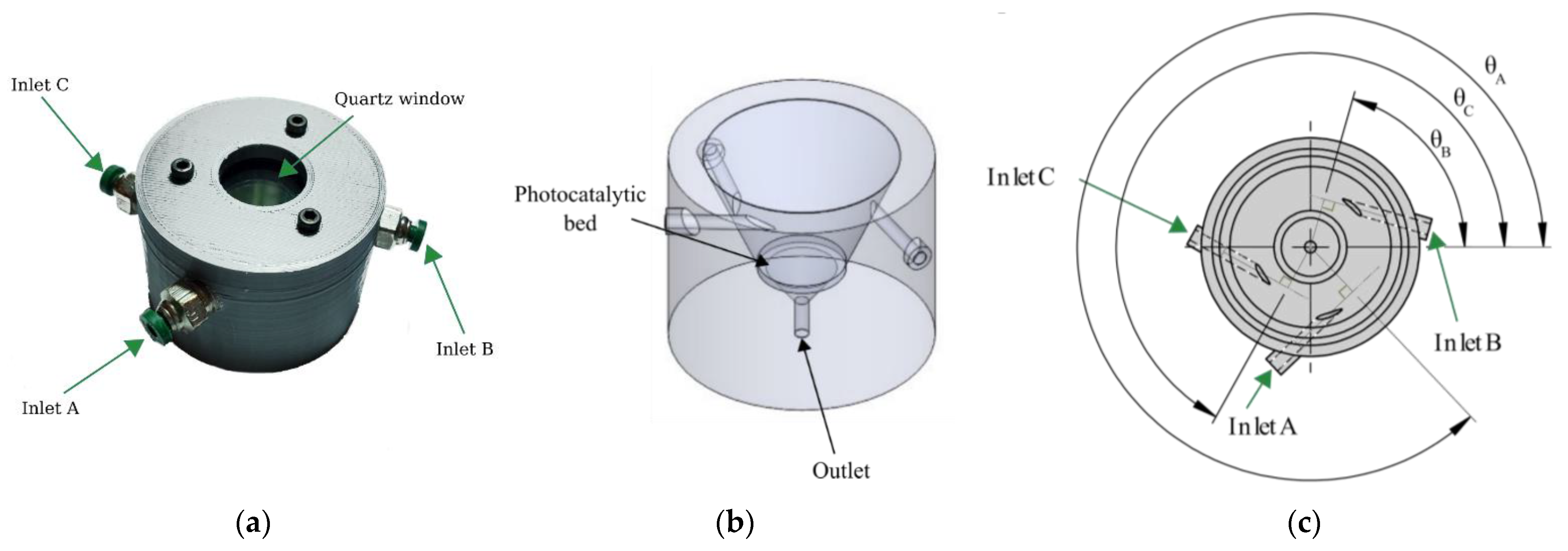
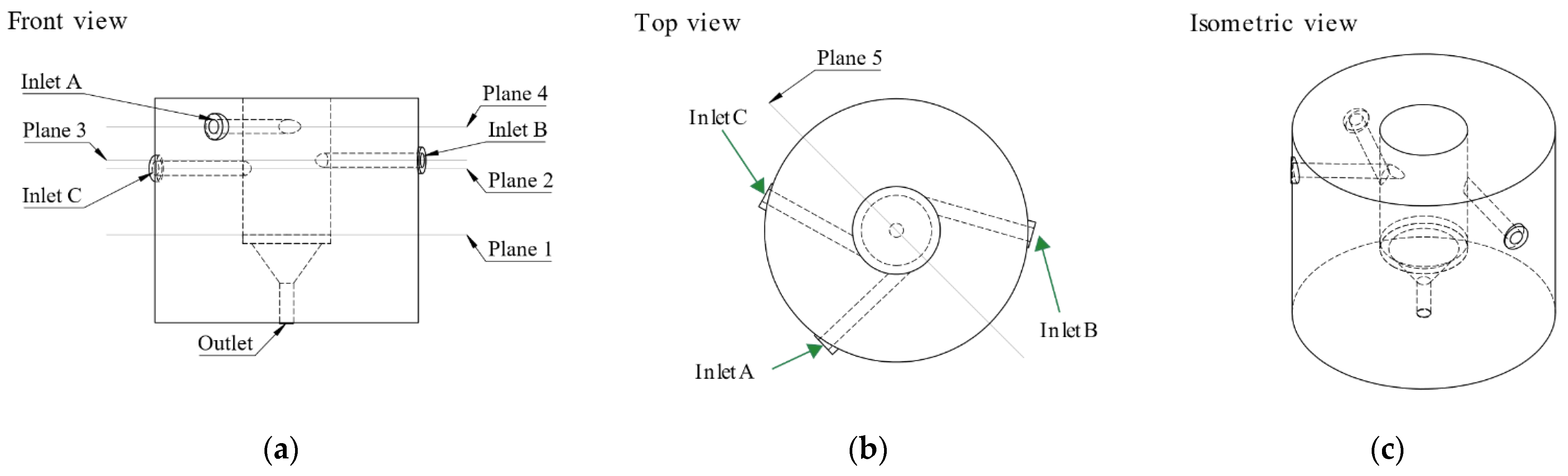
2.2.1. Reactor Configuration
2.2.2. Inlets Gas Flow Considerations
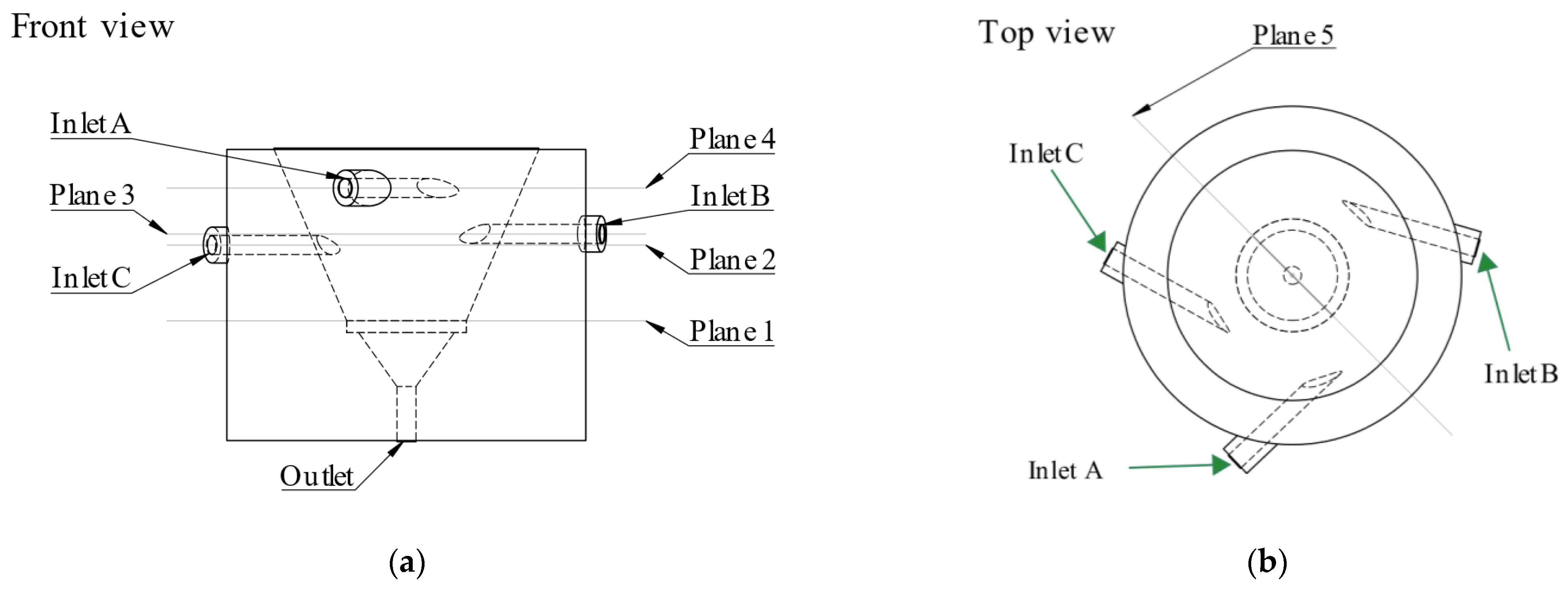
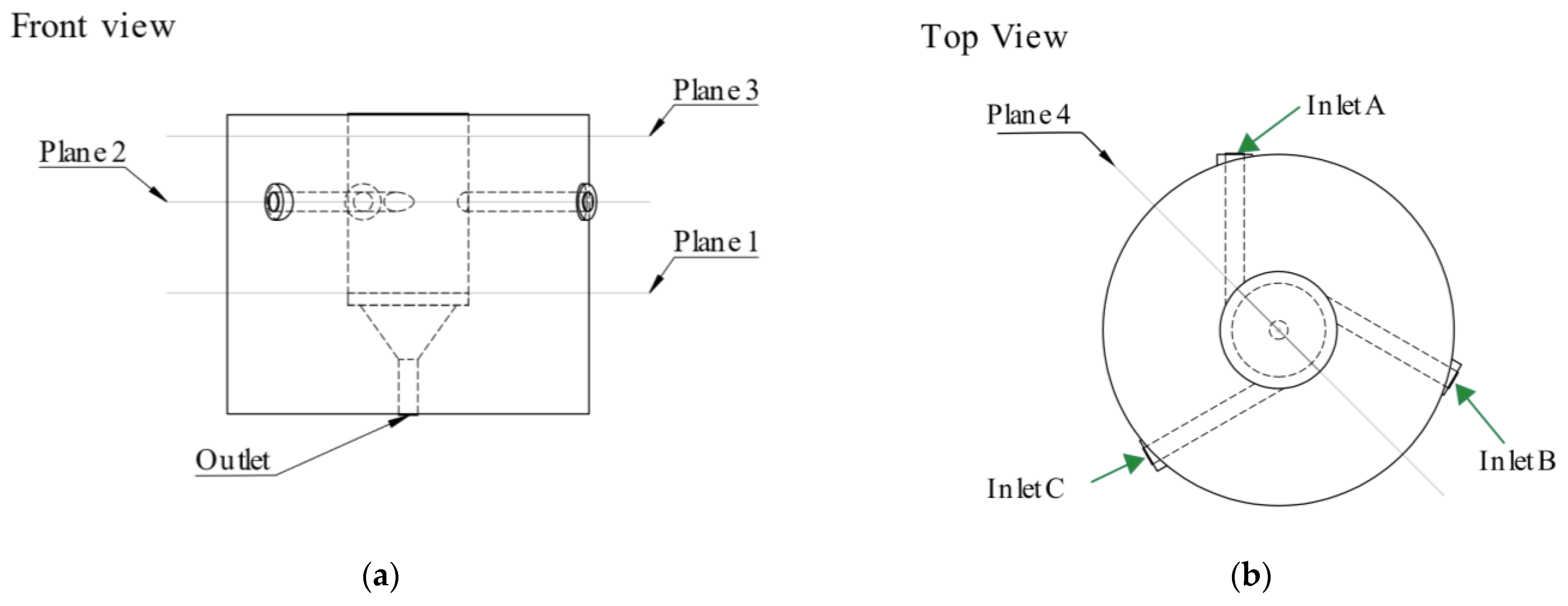
2.3. Computational Fluid Dynamics Simulation
3. Results and Discussion
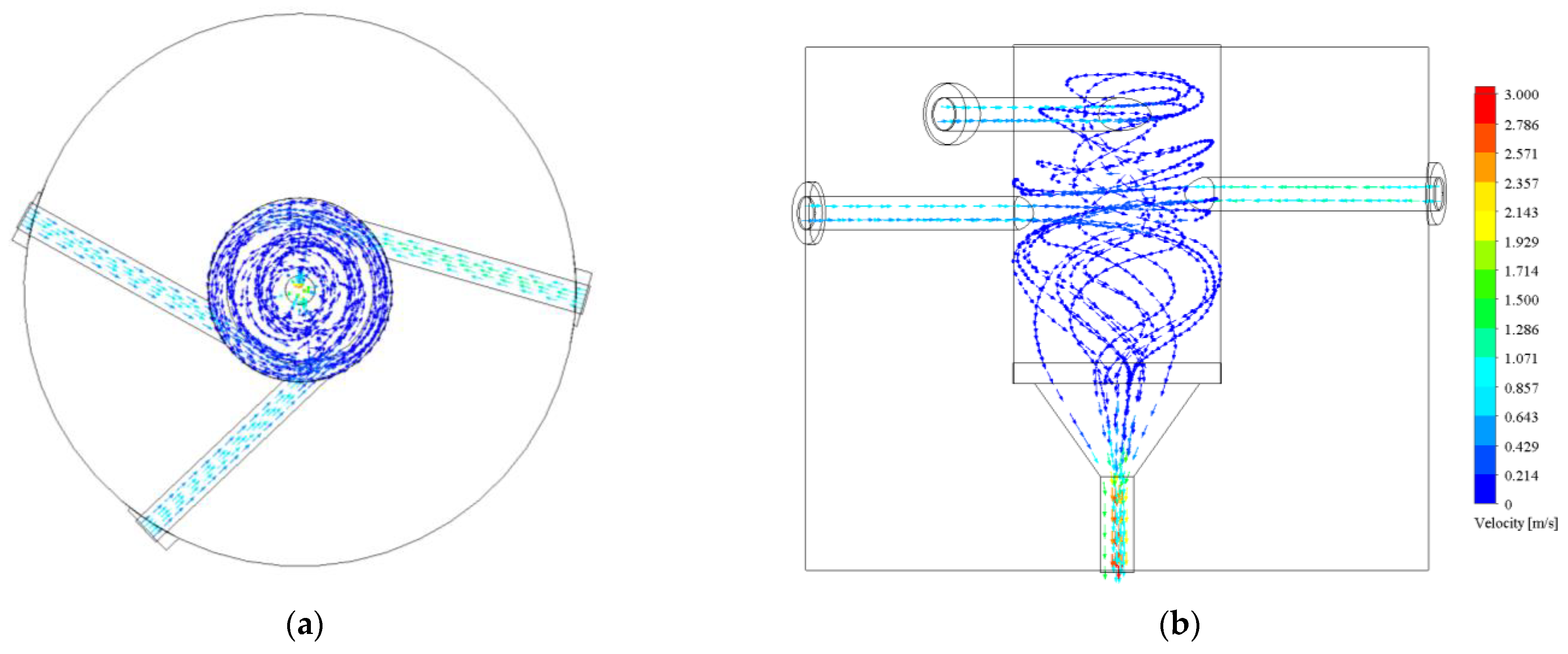
3.1. CFD Simulations Results
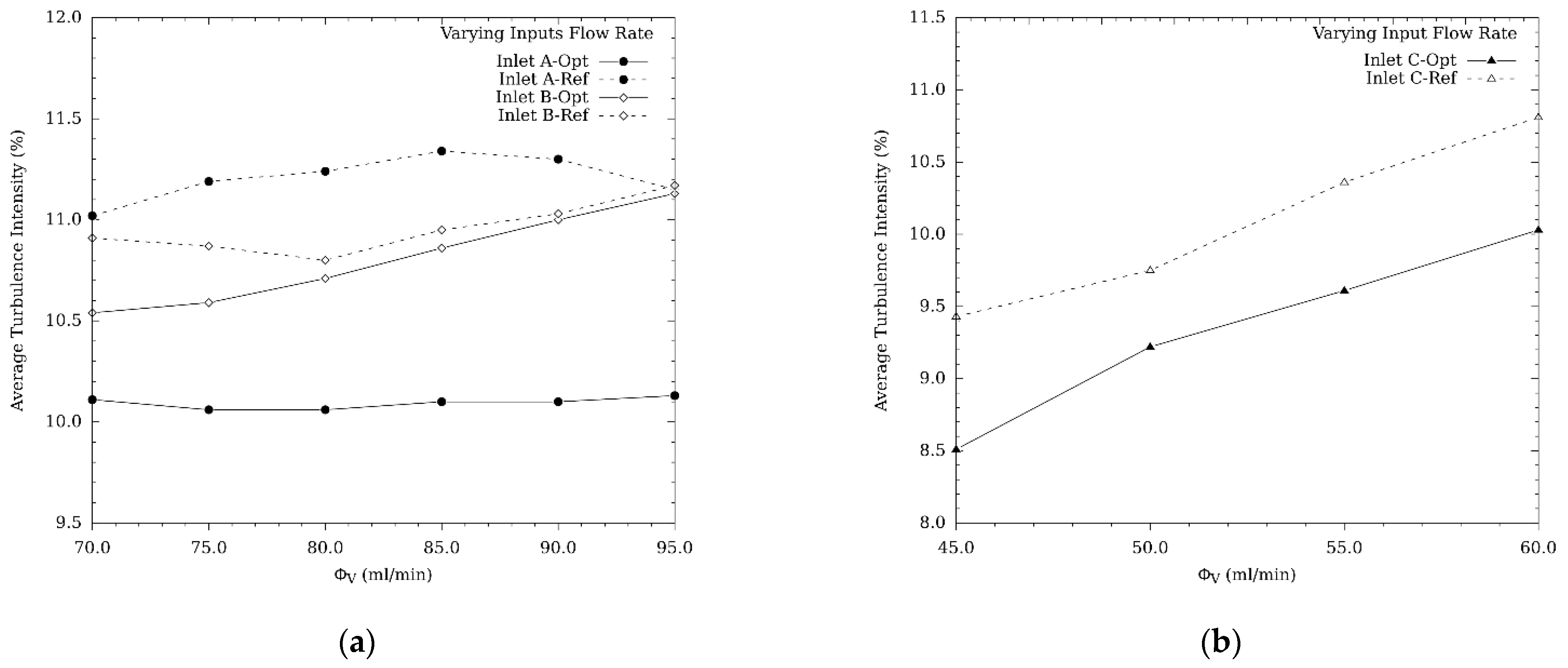
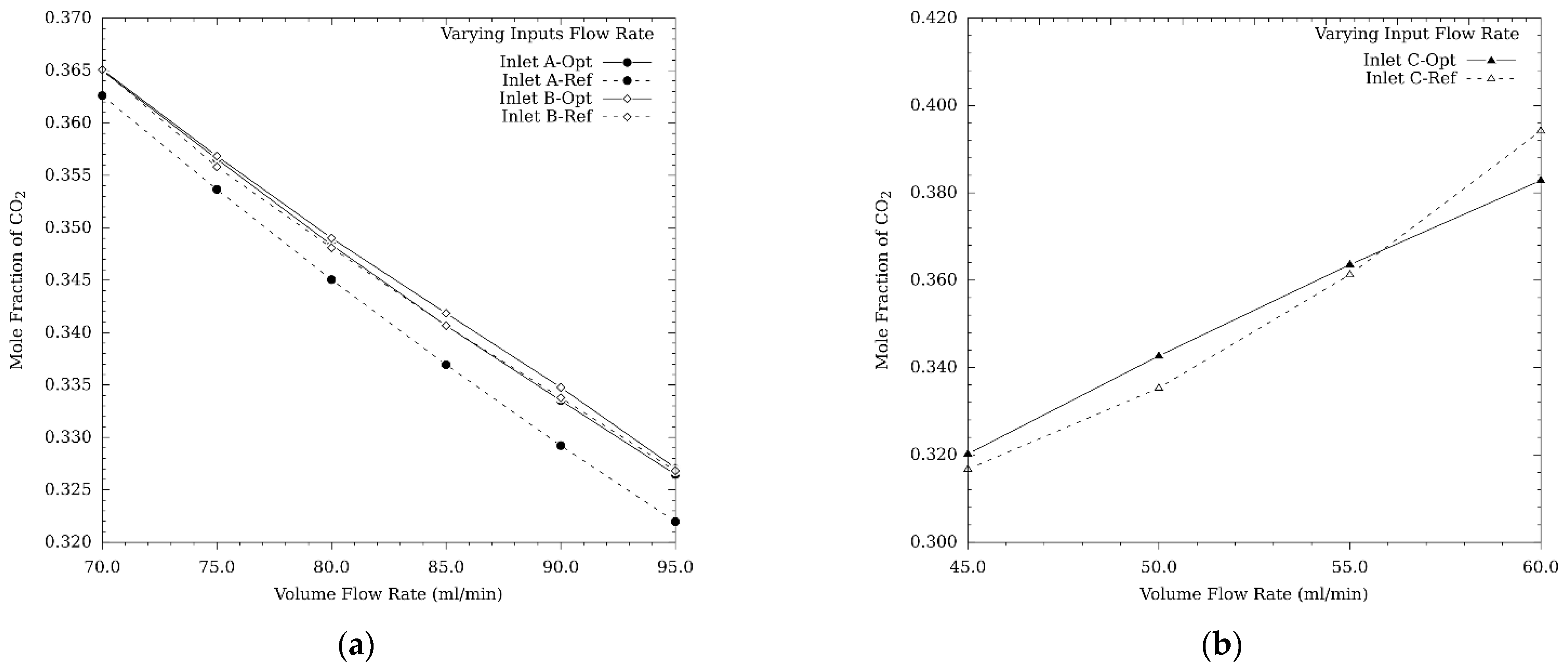
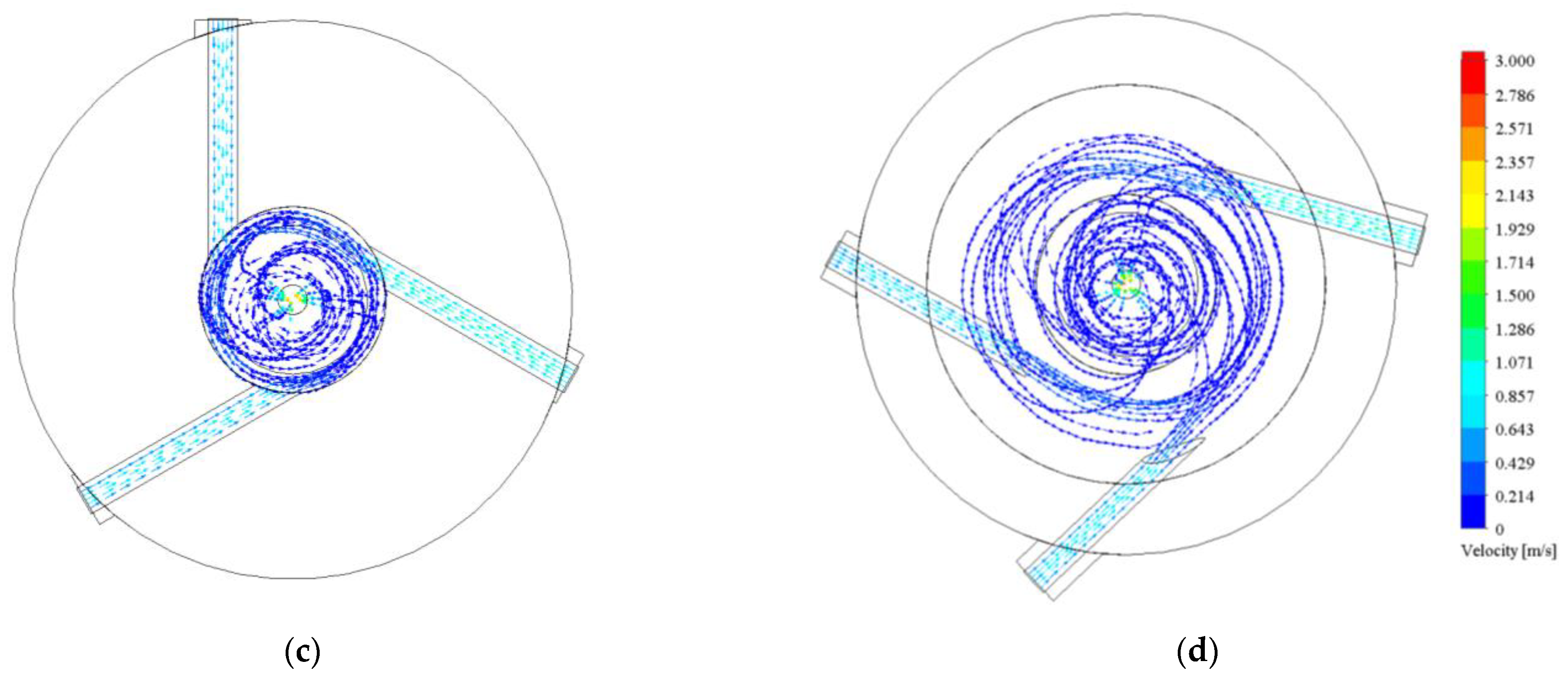
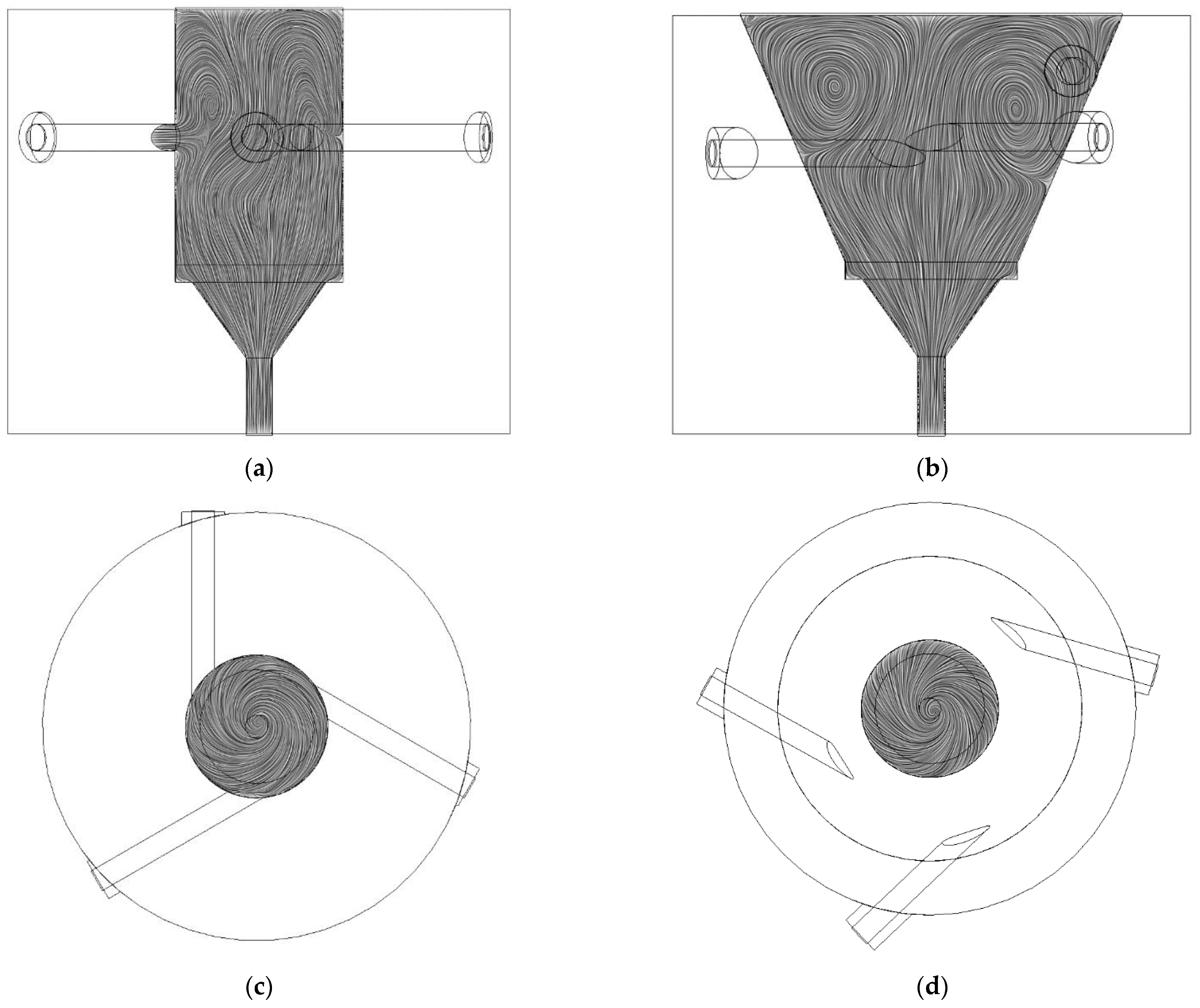
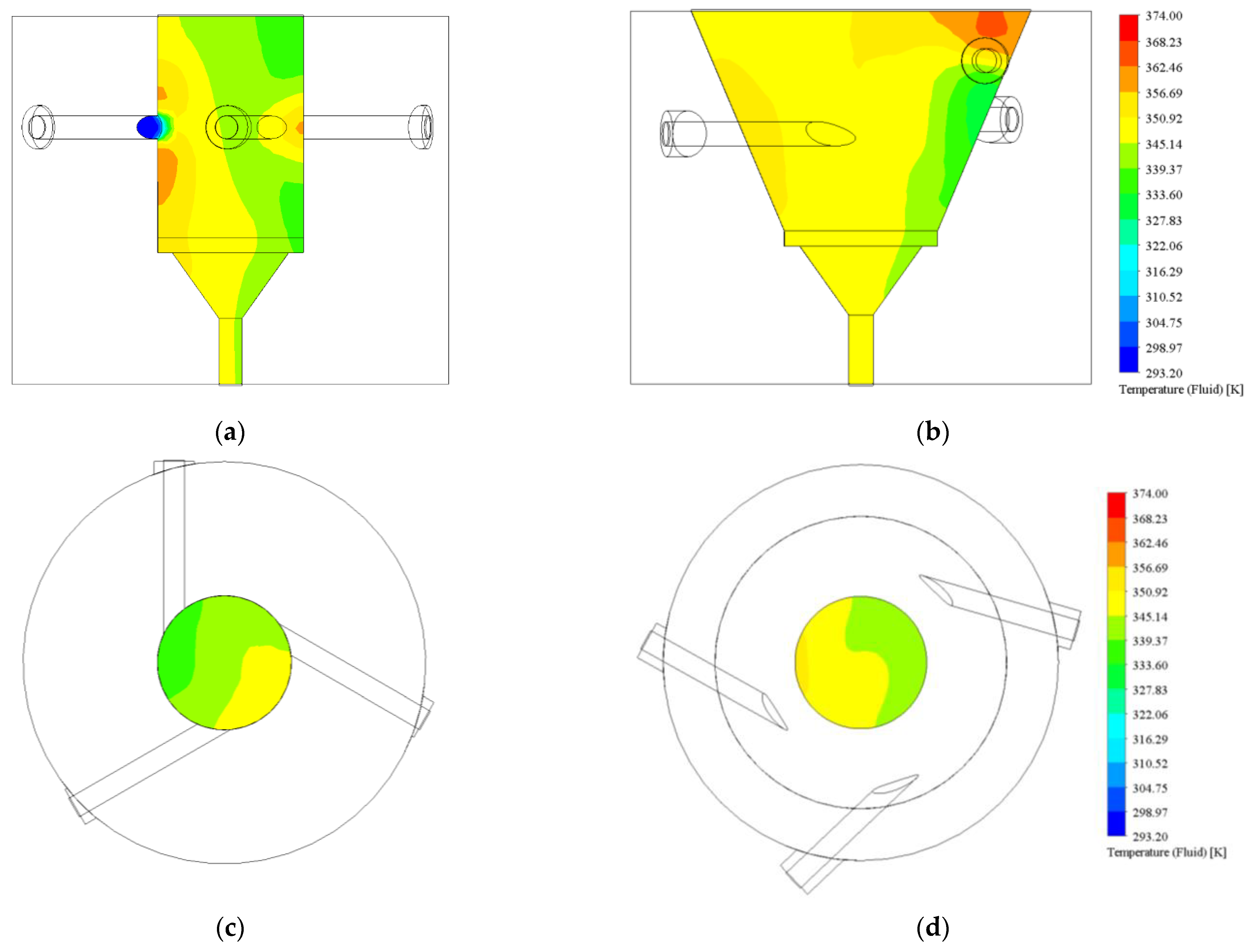
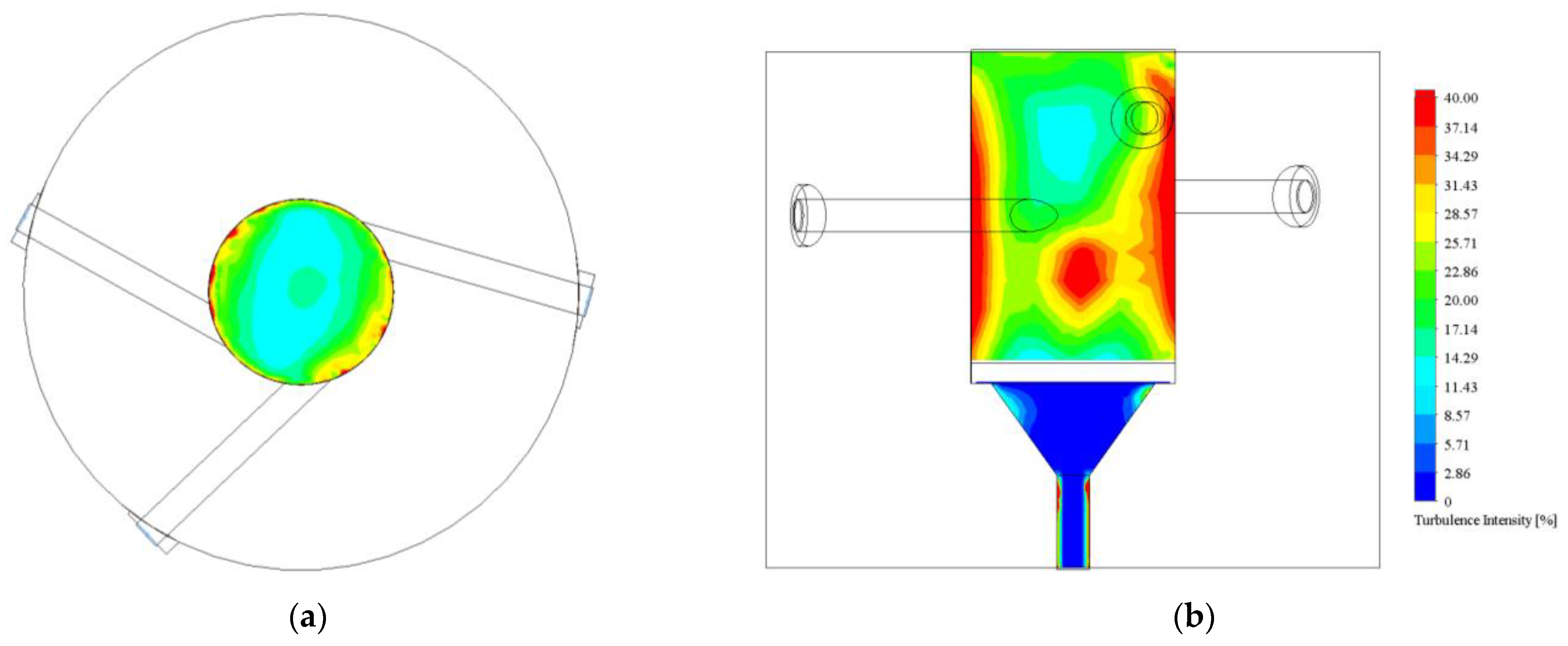
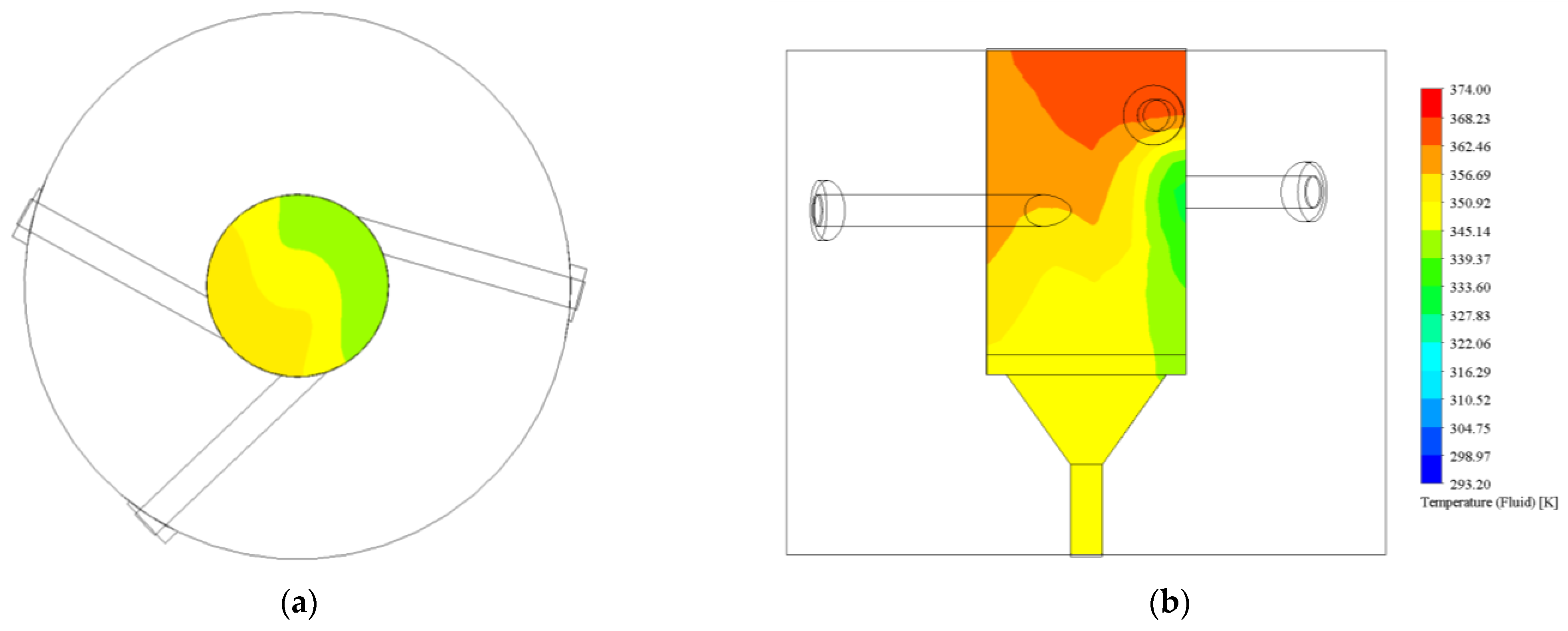
3.1.1. Turbulence Intensity and Mole Fraction Profile
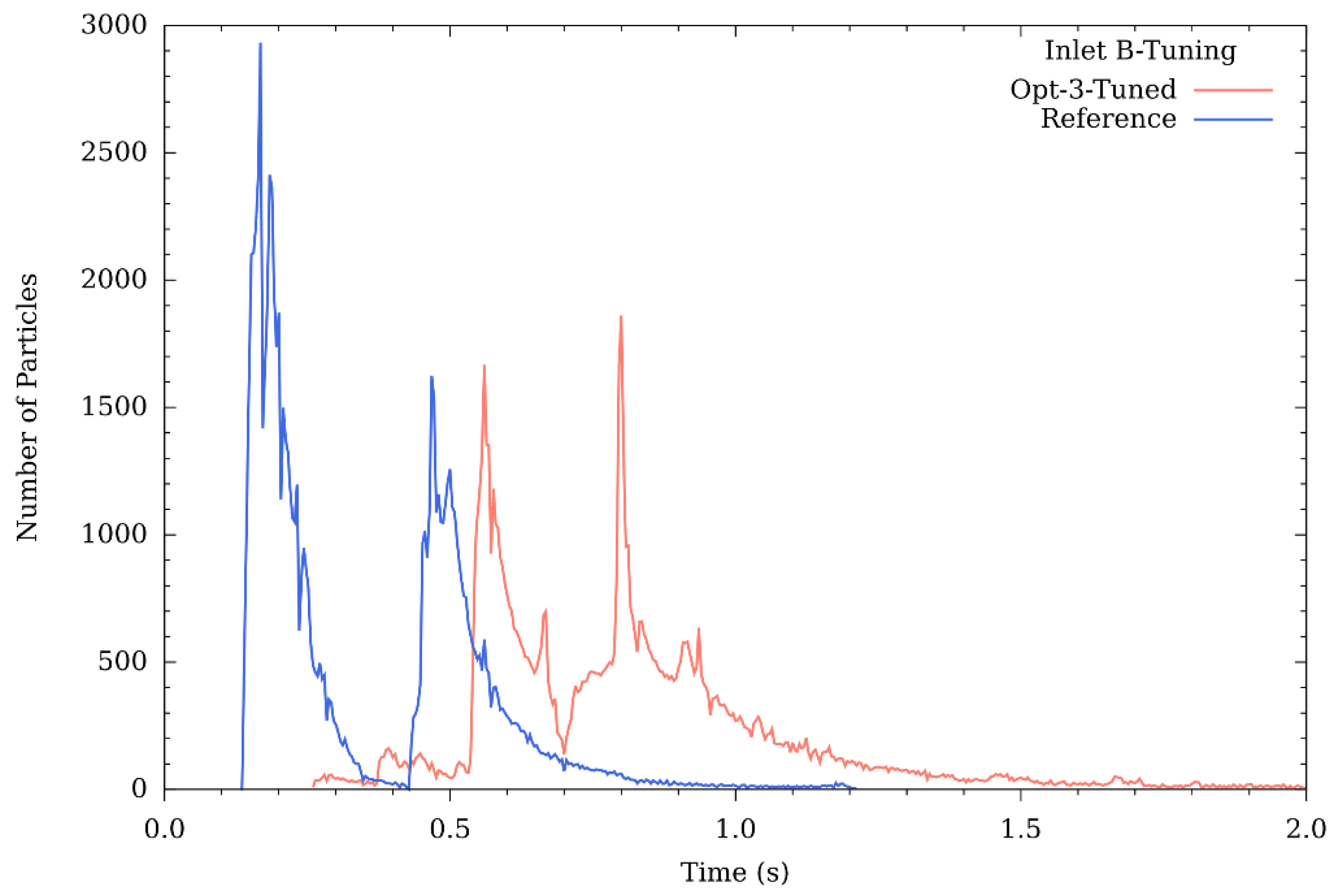
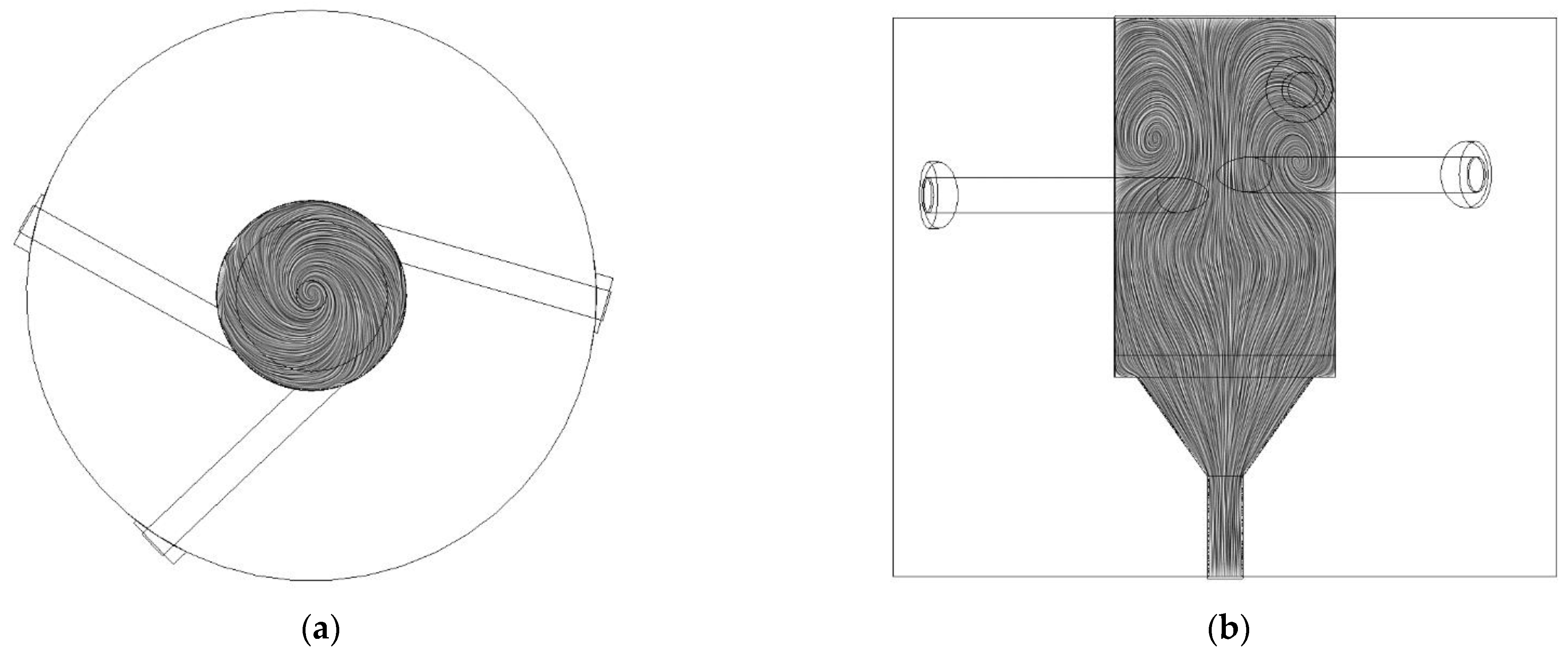
3.1.2. Graphical Profile of Reference and Opt-3-Tuned Reactor
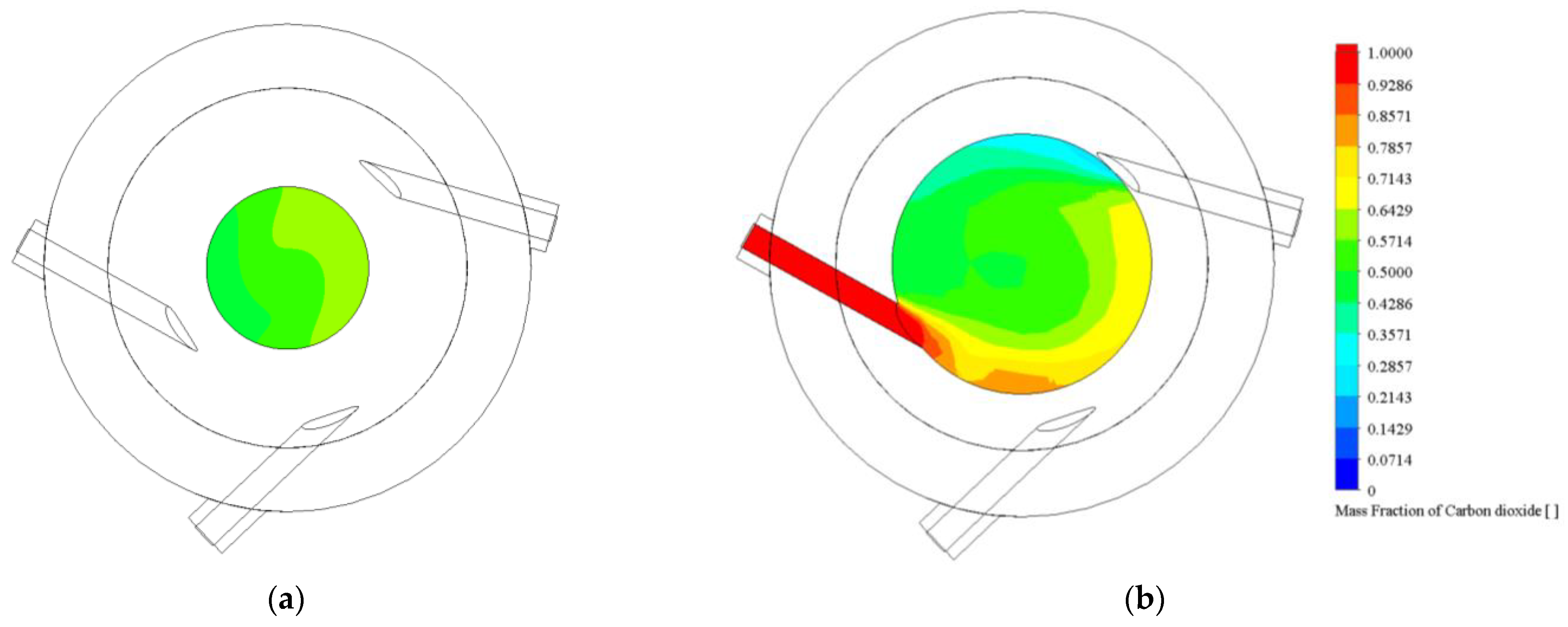
3.1.3. Main Chamber Cone Influence
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rabaia, M.K.H.; Abdelkareem, M.A.; Sayed, E.T.; Elsaid, K.; Chae, K.J.; Wilberforce, T.; Olabi, A. Environmental impacts of solar energy systems: A review. Sci. Total Environ. 2021, 754, 141989. [Google Scholar] [CrossRef]
- Kumar, M.B.H.; Saravanan, B.; Sanjeevikumar, P.; Blaabjerg, F. Review on control techniques and methodologies for maximum power extraction from wind energy systems. IET Renew. Power Gener. 2018, 12, 1609–1622. [Google Scholar] [CrossRef]
- Aleixandre-Tudó, J.L.; Castelló-Cogollos, L.; Aleixandre, J.L.; Aleixandre-Benavent, R. Renewable energies: Worldwide trends in research, funding and international collaboration. Renew. Energy 2019, 139, 268–278. [Google Scholar] [CrossRef]
- Looney, B. Statistical Review of World Energy, 69th ed.; BP: London, UK, 2020; p. 66. [Google Scholar]
- Core Writing Team; Rajendra, K.P. (Eds.) Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Gong, J.; Li, C.; Wasielewski, M.R. Advances in solar energy conversion. Chem. Soc. Rev. 2019, 48, 1862–1864. [Google Scholar] [CrossRef]
- Lewis, N.S. Toward cost-effective solar energy use. Science 2007, 315, 798–801. [Google Scholar] [CrossRef] [PubMed]
- Vu, N.N.; Kaliaguine, S.; Do, T.O. Plasmonic Photocatalysts for Sunlight-Driven Reduction of CO2: Details, Developments, and Perspectives. ChemSusChem 2020, 13, 3967–3991. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Peng, B.; Peng, T. Recent advances in heterogeneous photocatalytic CO2 conversion to solar fuels. ACS Catal. 2016, 6, 7485–7527. [Google Scholar] [CrossRef]
- Green, M.A.; Bremner, S.P. Energy conversion approaches and materials for high-efficiency photovoltaics. Nat. Mater. 2017, 16, 23–34. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, D. Photocatalysis: Basic principles, diverse forms of implementations and emerging scientific opportunities. Adv. Energy Mater. 2017, 7, 1700841. [Google Scholar] [CrossRef]
- Shi, R.; Chen, Y. Controlled formation of defective shell on TiO2 (001) facets for enhanced photocatalytic CO2 reduction. ChemCatChem 2019, 11, 2270–2276. [Google Scholar] [CrossRef]
- Ochedi, F.O.; Liu, D.; Yu, J.; Hussain, A.; Liu, Y. Photocatalytic, electrocatalytic and photoelectrocatalytic conversion of carbon dioxide: A review. Environ. Chem. Lett. 2020, 19, 941–967. [Google Scholar] [CrossRef]
- Zeng, S.; Kar, P.; Thakur, U.K.; Shankar, K. A review on photocatalytic CO2 reduction using perovskite oxide nanomaterials. Nanotechnology 2018, 29, 052001. [Google Scholar] [CrossRef] [PubMed]
- Kistler, T.A.; Larson, D.; Walczak, K.; Agbo, P.; Sharp, I.D.; Weber, A.Z.; Danilovic, N. Integrated Membrane-Electrode-Assembly Photoelectrochemical Cell under Various Feed Conditions for Solar Water Splitting. J. Electrochem. Soc. 2018, 166, H3020. [Google Scholar] [CrossRef]
- Kim, H.R.; Razzaq, A.; Heo, H.J.; In, S.I. Photocatalytic conversion of CO 2 into hydrocarbon fuels with standard titania (Degussa P25) using newly installed experimental setup. Rapid Commun. Photosci. 2013, 2, 64–66. [Google Scholar] [CrossRef][Green Version]
- Dong, Y.; Duchesne, P.; Mohan, A.; Ghuman, K.K.; Kant, P.; Hurtado, L.; Ulmer, U.; Loh, J.Y.; Tountas, A.A.; Wang, L.; et al. Shining light on CO2: From materials discovery to photocatalyst, photoreactor and process engineering. Chem. Soc. Rev. 2020, 49, 5648–5663. [Google Scholar] [CrossRef] [PubMed]
- Valadés-Pelayo, P.J.; Arancibia-Bulnes, C.A.; Salgado-Tránsito, I.; Villafán-Vidales, H.I.; Pena-Cruz, M.I.; Jiménez-González, A.E. Effect of photocatalyst film geometry on radiation absorption in a solar reactor, a multiscale approach. Chem. Eng. Sci. 2017, 161, 24–35. [Google Scholar] [CrossRef]
- Mueses, M.A.; Colina-Márquez, J.; Machuca-Martnez, F.; Puma, G.L. Recent advances on modeling of solar heterogeneous photocatalytic reactors applied for degradation of pharmaceuticals and emerging organic contaminants in water. Curr. Opin. Green Sustain. Chem. 2021, 100486. [Google Scholar] [CrossRef]
- Valadés-Pelayo, P.; Sosa, F.G.; Serrano, B.; De Lasa, H. Eight-lamp externally irradiated bench-scale photocatalytic reactor: Scale-up and performance prediction. Chem. Eng. J. 2015, 282, 142–151. [Google Scholar] [CrossRef]
- Keller, N.; Ivanez, J.; Highfield, J.; Ruppert, A.M. Photo-/thermal synergies in heterogeneous catalysis: Towards low-temperature (solar-driven) processing for sustainable energy and chemicals. Appl. Catal. B Environ. 2021, 296, 120320. [Google Scholar] [CrossRef]
- Nabil, S.; Hammad, A.S.; El-Bery, H.M.; Shalaby, E.A.; El-Shazly, A.H. The CO2 photoconversion over reduced graphene oxide based on Ag/TiO2 photocatalyst in an advanced meso-scale continuous-flow photochemical reactor. Environ. Sci. Pollut. Res. 2021, 28, 36157–36173. [Google Scholar] [CrossRef]
- Fiorenza, R.; Bellardita, M.; Balsamo, S.A.; Spitaleri, L.; Gulino, A.; Condorelli, M.; D’Urso, L.; Scirè, S.; Palmisano, L. A solar photothermocatalytic approach for the CO2 conversion: Investigation of different synergisms on CoO-CuO/brookite TiO2-CeO2 catalysts. Chem. Eng. J. 2022, 428, 131249. [Google Scholar] [CrossRef]
- Ali, S.; Flores, M.C.; Razzaq, A.; Sorcar, S.; Hiragond, C.B.; Kim, H.R.; Park, Y.H.; Hwang, Y.; Kim, H.S.; Kim, H.; et al. Gas phase photocatalytic CO2 reduction, “A brief overview for benchmarking”. Catalysts 2019, 9, 727. [Google Scholar] [CrossRef]
- Mazierski, P.; Bajorowicz, B.; Grabowska, E.; Zaleska-Medynska, A. Photoreactor design aspects and modeling of light. In Heterogeneous Photocatalysis; Springer: Berlin/Heidelberg, Germany, 2016; pp. 211–248. [Google Scholar] [CrossRef]
- Dilla, M.; Schlögl, R.; Strunk, J. Photocatalytic CO2 Reduction Under Continuous Flow High-Purity Conditions: Quantitative Evaluation of CH4 Formation in the Steady-State. ChemCatChem 2017, 9, 696–704. [Google Scholar] [CrossRef]
- Simon, D. Evolutionary Optimization Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Liu, Z.; Passalacqua, A.; Olsen, M.G.; Fox, R.O.; Hill, J.C. Dynamic delayed detached eddy simulation of a multi-inlet vortex reactor. AIChE J. 2016, 62, 2570–2578. [Google Scholar] [CrossRef]
- Fang, R.H.; Chen, K.N.H.; Aryal, S.; Hu, C.M.J.; Zhang, K.; Zhang, L. Large-scale synthesis of lipid–polymer hybrid nanoparticles using a multi-inlet vortex reactor. Langmuir 2012, 28, 13824–13829. [Google Scholar] [CrossRef]
- Dassault-Systemes. Smartcells Enabling Fast and Accurate CFD. Available online: https://www.solidworks.com/sites/default/files/2018-10/DS-18028-Enabling-Fast-Accurate-CFD-Whitepaper-02.pdf (accessed on 28 November 2021).
- Lam, C.K.G.; Bremhorst, K. A modified form of the k-model for predicting wall turbulence. J. Fluids Eng. 1981, 103, 456–460. [Google Scholar] [CrossRef]
- Li, G.; Mukhopadhyay, A.; Cheng, C.Y.; Dai, Y. Various approaches to compute fluid residence time in mixing systems. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting Collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels, Montreal, QC, Canada, 1–5 August 2010; Volume 49484, pp. 295–304. [Google Scholar] [CrossRef]
- Hoch, L.B.; Wood, T.E.; O’Brien, P.G.; Liao, K.; Reyes, L.M.; Mims, C.A.; Ozin, G.A. The Rational Design of a Single-Component Photocatalyst for Gas-Phase CO2 Reduction Using Both UV and Visible Light. Adv. Sci. 2014, 1, 1400013. [Google Scholar] [CrossRef]
- Ohtani, B. Revisiting the fundamental physical chemistry in heterogeneous photocatalysis: Its thermodynamics and kinetics. Phys. Chem. Chem. Phys. 2014, 16, 1788–1797. [Google Scholar] [CrossRef]
- Pan, X.; Yang, M.Q.; Fu, X.; Zhang, N.; Xu, Y.J. Defective TiO2 with oxygen vacancies: Synthesis, properties and photocatalytic applications. Nanoscale 2013, 5, 3601–3614. [Google Scholar] [CrossRef]








| Name | Maximum Value | Minimum Value |
|---|---|---|
| 360.0° | 310.0° | |
| 168.0° | 70.0° | |
| 288.0° | 190.0° | |
| 150.0° | 90.0° | |
| 13.5 mm | 2.0 mm | |
| 13.5 mm | 2.0 mm | |
| 13.5 mm | 2.0 mm |
| Name | Value |
|---|---|
| 313.4° | |
| 74.0° | |
| 240.9° | |
| 23.0° | |
| 11.0 mm | |
| 7.2 mm | |
| 6.3 mm |
| Factor | Level Name | Level Value | |
|---|---|---|---|
| Gas configuration | 1 | Inlet A | CO2 |
| Inlet B | H2O | ||
| Inlet C | H2O | ||
| 2 | Inlet A | H2O | |
| Inlet B | CO2 | ||
| Inlet C | H2O | ||
| 3 | Inlet A | H2O | |
| Inlet B | H2O | ||
| Inlet C | CO2 | ||
| Factor | Level Name | Level Value | Volume Flow Rate (mL/min) | |
|---|---|---|---|---|
| Gas configuration | 3 | Inlet A | H2O | 60 |
| Inlet B | H2O | 90 | ||
| Inlet C | CO2 | 60 | ||
| Reactor | Mean Residence Time (s) |
|---|---|
| Opt-3-Tuned | 0.85 |
| Opt-3-Tuned-No-Cone | 0.35 |
| One Inlet | 0.20 |
| Reference | 0.35 |
| Reactor | Photocatalyst Surface Turbulence Intensity (%) |
|---|---|
| Opt-3-Tuned | 13.07 |
| Opt-3-Tuned-No-Cone | 17.97 |
| One Inlet | 11.10 |
| Reference | 12.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valdés, J.; Domínguez-Juárez, J.L.; Nava, R.; Cuán, Á.; Cortés-Romero, C.M. Turbulence Enhancement and Mixing Analysis for Multi-Inlet Vortex Photoreactor for CO2 Reduction. Processes 2021, 9, 2237. https://doi.org/10.3390/pr9122237
Valdés J, Domínguez-Juárez JL, Nava R, Cuán Á, Cortés-Romero CM. Turbulence Enhancement and Mixing Analysis for Multi-Inlet Vortex Photoreactor for CO2 Reduction. Processes. 2021; 9(12):2237. https://doi.org/10.3390/pr9122237
Chicago/Turabian StyleValdés, Jesús, Jorge Luis Domínguez-Juárez, Rufino Nava, Ángeles Cuán, and Carlos M. Cortés-Romero. 2021. "Turbulence Enhancement and Mixing Analysis for Multi-Inlet Vortex Photoreactor for CO2 Reduction" Processes 9, no. 12: 2237. https://doi.org/10.3390/pr9122237
APA StyleValdés, J., Domínguez-Juárez, J. L., Nava, R., Cuán, Á., & Cortés-Romero, C. M. (2021). Turbulence Enhancement and Mixing Analysis for Multi-Inlet Vortex Photoreactor for CO2 Reduction. Processes, 9(12), 2237. https://doi.org/10.3390/pr9122237






