An Analytic Solution for an Expanding/Contracting Strain-Hardening Viscoplastic Hollow Cylinder at Large Strains and Its Application to Tube Hydroforming Design
Abstract
:1. Introduction
2. Statement of the Problem
3. General Solution
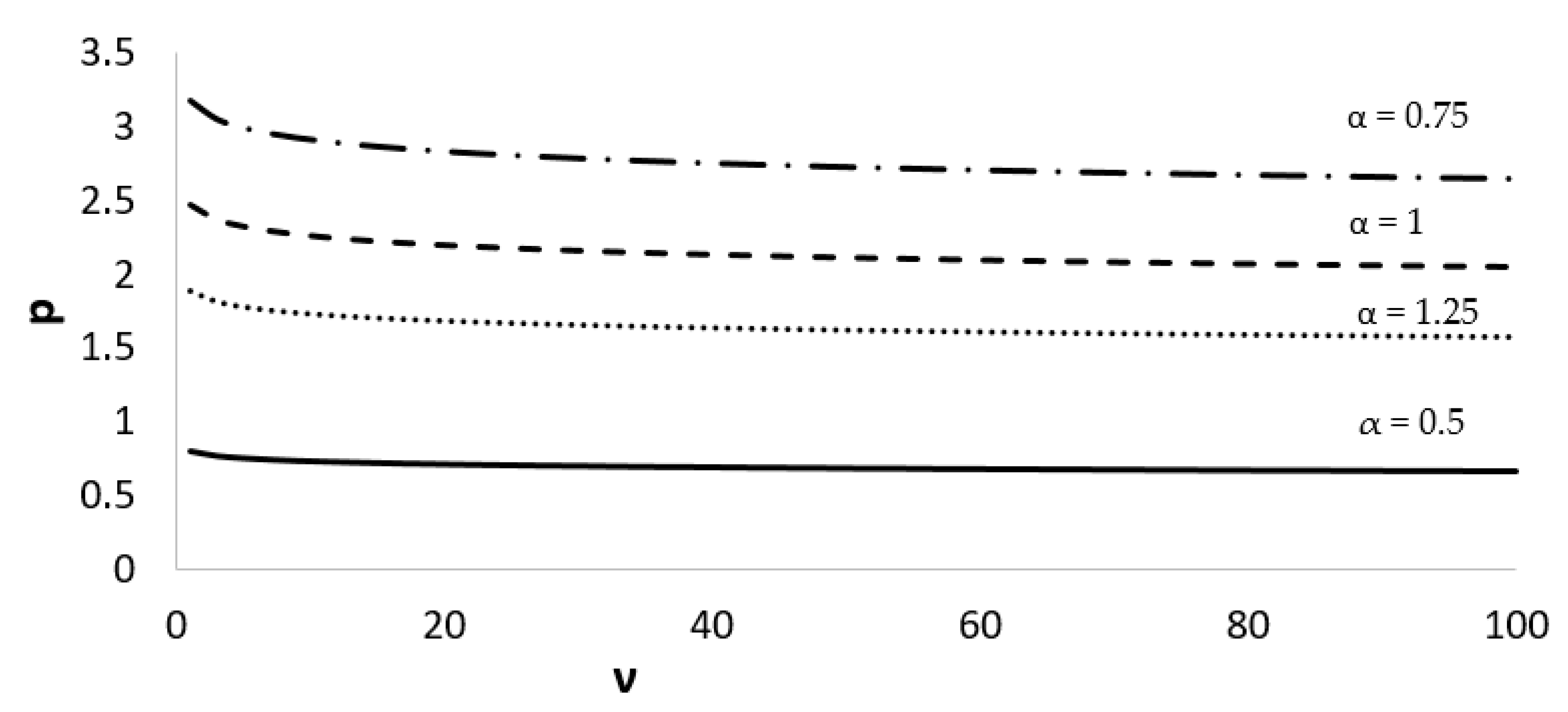
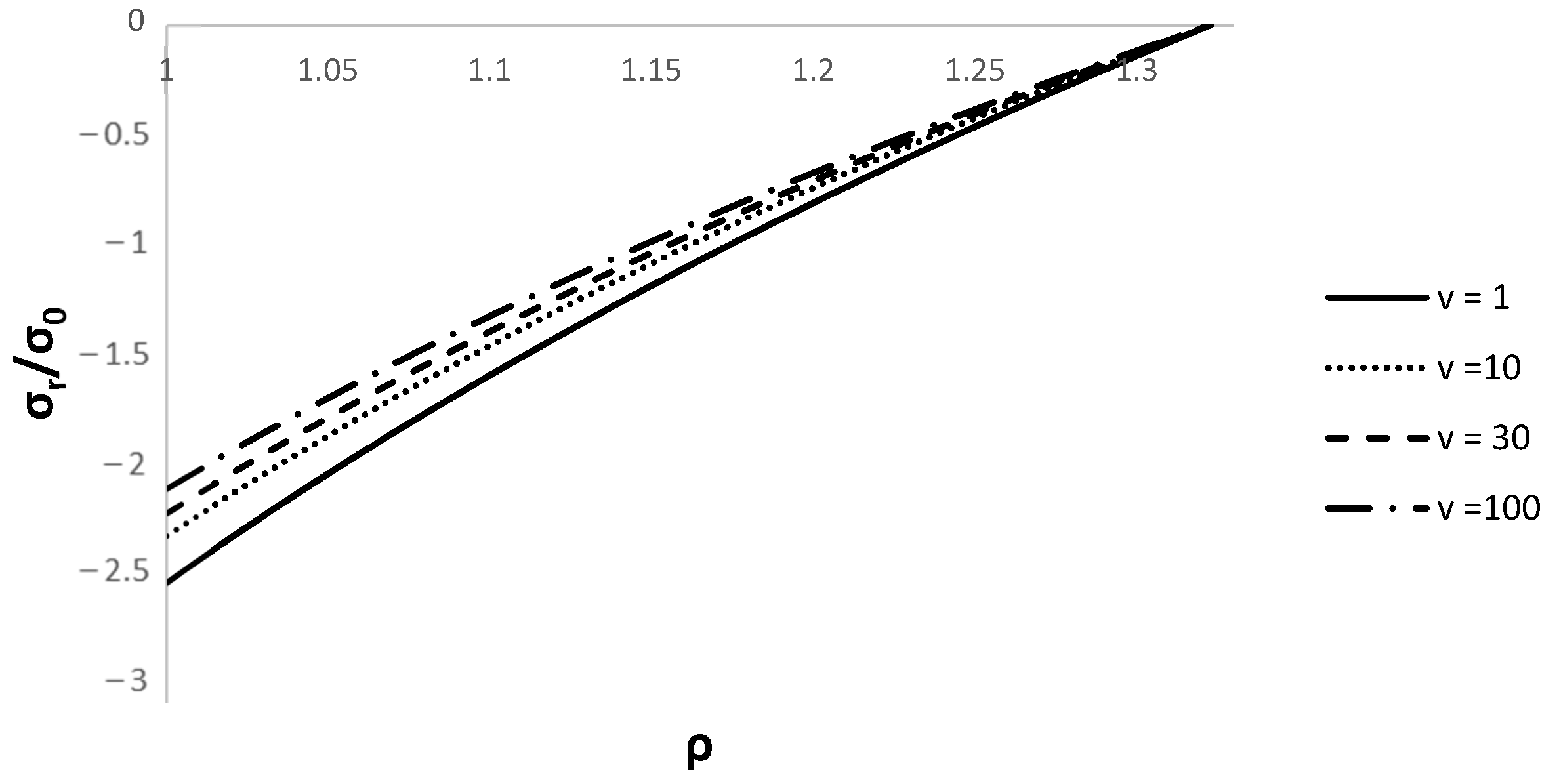
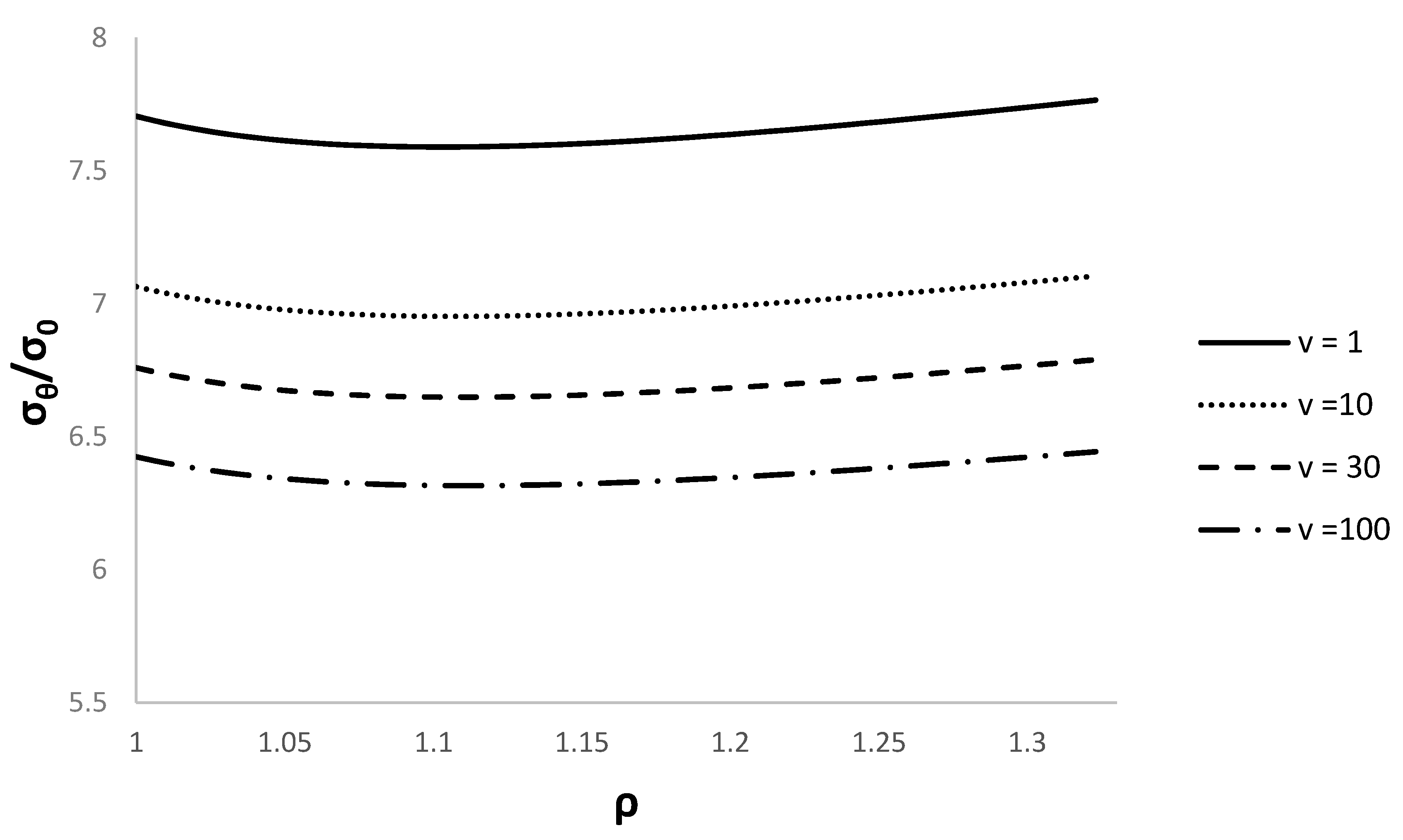
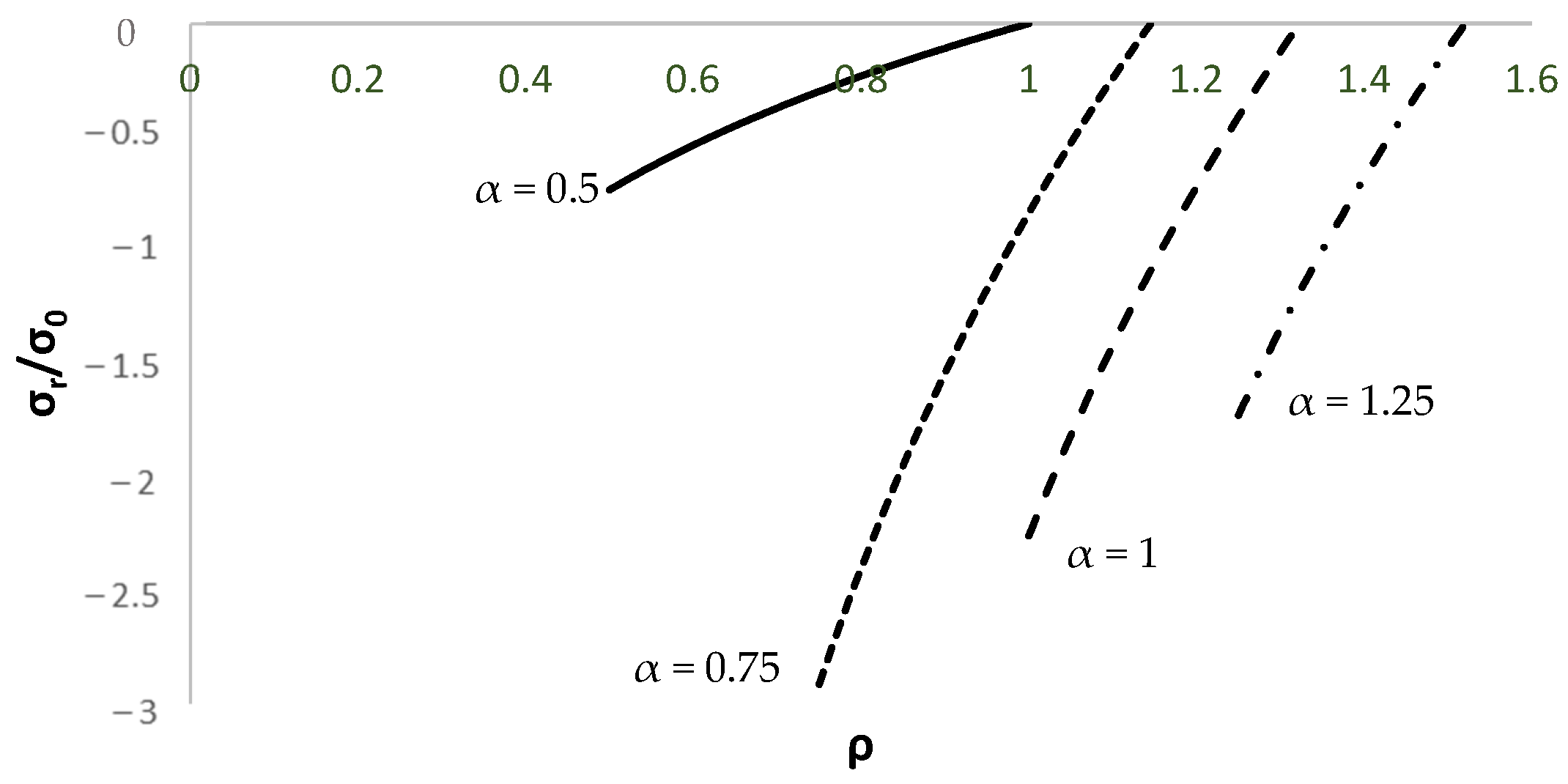
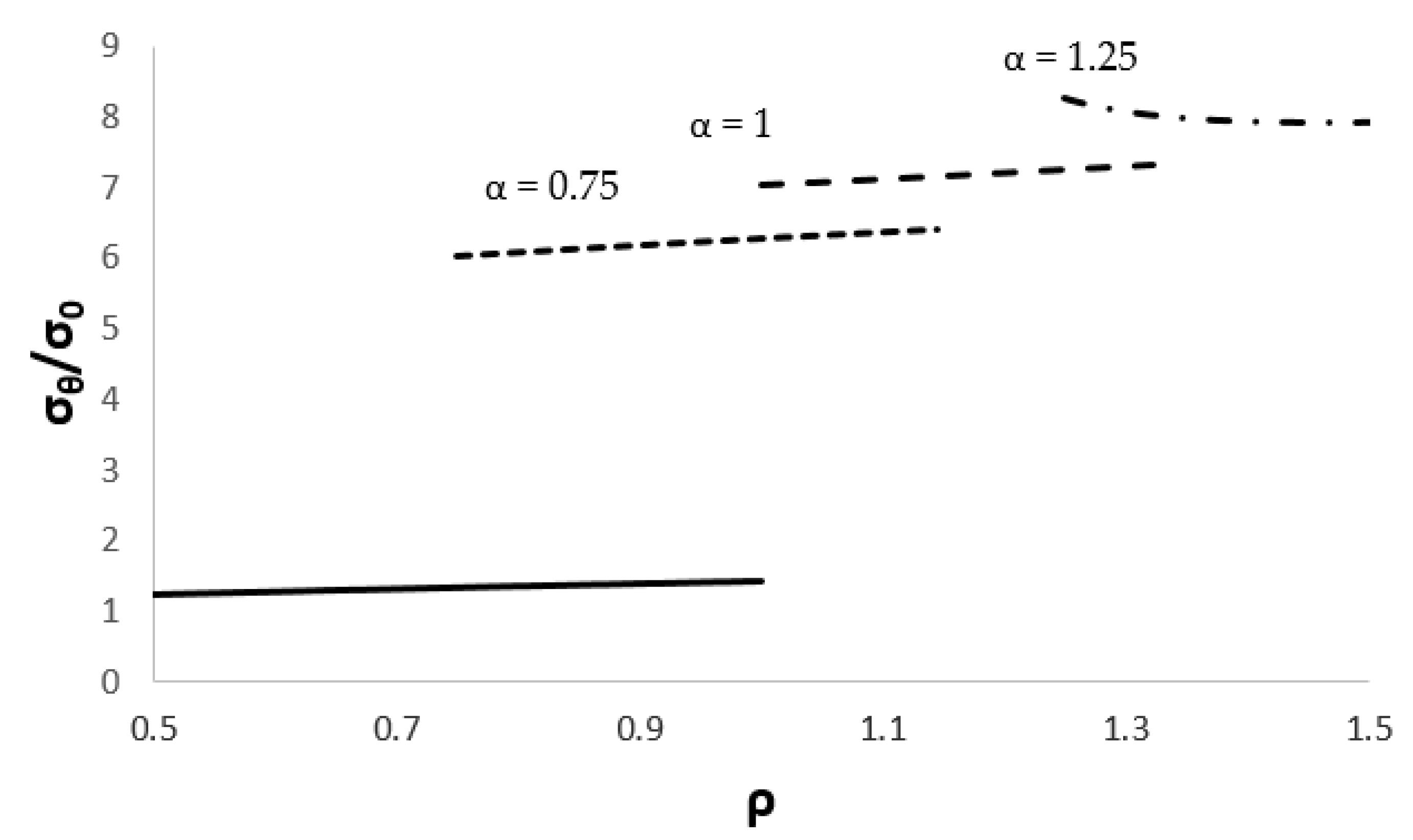
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | current inner radius |
| b | current outer radius |
| a0 | initial inner radius |
| b0 | initial outer radius |
| c0 | dimensionless initial inner radius |
| n | constitutive parameter involved in (32) |
| p | dimensionless inner pressure |
| cylindrical coordinate system | |
| t | time |
| u | radial velocity |
| P | inner pressure |
| R | Lagrangian coordinate |
| U | speed of the expansion/contraction of the inner radius |
| α | dimensionless current inner radius |
| γ | dimensionless equivalent strain rate |
| dimensionless equivalent strain rate at the inner radius | |
| dimensionless equivalent strain rate at the outer radius | |
| equivalent strain | |
| λ | constitutive parameter involved in (32) |
| μ | constitutive parameter involved in (32) |
| ν | dimensionless parameter introduced in (21) |
| radial strain rate | |
| circumferential strain rate | |
| equivalent strain rate | |
| characteristic strain rate | |
| ρ | dimensionless polar radius |
| radial stress | |
| circumferential stress | |
| yield stress | |
| reference stress |
References
- Mendelson, A. Plasticity: Theory and Application; The Macmillan Company: New York, NY, USA, 1968. [Google Scholar]
- Durban, D.; Baruch, M. Analysis of an elasto-plastic thick walled sphere loaded by internal and external pressure. Int. J. Non-Linear Mech. 1977, 12, 9–21. [Google Scholar] [CrossRef]
- Alexandrov, S.; Pirumov, A.; Jeng, Y.-R. Expansion/contraction of a spherical elastic/plastic shell revisited. Contin. Mech. Thermodyn. 2015, 27, 483–494. [Google Scholar] [CrossRef]
- Lee, W.-S.; Yeh, G.-W. The plastic deformation behaviour of AISI 4340 alloy steel subjected to high temperature and high strain rate loading conditions. J. Mater. Process. Technol. 1997, 71, 224–234. [Google Scholar] [CrossRef]
- Shin, H.; Kim, J.-B. A Phenomenological Constitutive Equation to Describe Various Flow Stress Behaviors of Materials in Wide Strain Rate and Temperature Regimes. J. Eng. Mater. Technol. 2010, 132, 021009. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, J.W.; Chung, K.; Lee, M.-G. A multiplicative plastic hardening model in consideration of strain softening and strain rate: Theoretical derivation and characterization of model parameters with simple tension and creep test. Int. J. Mech. Sci. 2020, 187, 105913. [Google Scholar] [CrossRef]
- Altenbach, H.; Gorash, Y.; Naumenko, K. Steady-state creep of a pressurized thick cylinder in both the linear and the power law ranges. Acta Mech. 2008, 195, 263–274. [Google Scholar] [CrossRef]
- Wineman, A.; Min, J.-H. The Pressurized Cylinder Problem for Nonlinear Viscoelastic Materials with a Strain Clock. Math. Mech. Solids 1996, 1, 393. [Google Scholar] [CrossRef] [Green Version]
- Leu, S.-Y. Limit analysis of strain-hardening viscoplastic cylinders under internal pressure by using the velocity control: Analytical and numerical investigation. Int. J. Mech. Sci. 2008, 50, 1578–1585. [Google Scholar] [CrossRef]
- Leu, S.-Y. Static and kinematic limit analysis of orthotropic strain-hardening pressure vessels involving large deformation. Int. J. Mech. Sci. 2009, 51, 508–514. [Google Scholar] [CrossRef]
- Leu, S.-Y.; Li, R.-S. Exact solutions of sequential limit analysis of pressurized cylinders with combined hardening based on a generalized Hölder inequality: Formulation and validation. Int. J. Mech. Sci. 2012, 64, 47–53. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Haghi, M.; Anand, L. Analysis of strain-hardening viscoplastic thick-walled sphere and cylinder under external pressure. Int. J. Plast. 1991, 7, 123–140. [Google Scholar] [CrossRef]
- Leu, S.-Y. Analytical and numerical investigation of strain-hardening viscoplastic thick-walled cylinders under internal pressure by using sequential limit analysis. Comput. Methods Appl. Mech. Eng. 2007, 196, 2713–2722. [Google Scholar] [CrossRef]
- Christopher, T.; Sarma, B.R.; Potti, P.G.; Rao, B.N.; Sankarnarayanasamy, K. A comparative study on failure pressure estimations of unflawed cylindrical vessels. Int. J. Press. Vessel. Pip. 2002, 79, 53–66. [Google Scholar] [CrossRef]
- Güven, U. A comparison on failure pressures of cylindrical pressure vessels. Mech. Res. Commun. 2007, 34, 466–471. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhao, J.; Zhang, C.; Li, Y.; Wang, S. Elastic–Brittle–Plastic Analysis of Double-Layered Combined Thick-Walled Cylinder Under Internal Pressure. J. Press. Vessel. Technol. 2016, 138, 011201. [Google Scholar] [CrossRef]
- Bell, C.; Corney, J.; Zuelli, N.; Savings, D. A state of the art review of hydroforming technology: Its applications, research areas, history, and future in manufacturing. Int. J. Mater. Form. 2019, 13, 789–828. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.-M.; Manabe, K.-I. Latest Hydroforming Technology of Metallic Tubes and Sheets. Metals 2021, 11, 1360. [Google Scholar] [CrossRef]
- Fiorentino, A.; Ginestra, P.S.; Attanasio, A.; Ceretti, E. Numerical optimization of the blank dimensions in tube hydroforming using line-search and bisection methods. Materials 2020, 13, 945. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.-M.; Pham, H.-N.; Tsui, H.-S. Investigation of Punch Shape and Loading Path Design in Hydro-Flanging Processes of Aluminum Alloy Tubes. Metals 2021, 11, 636. [Google Scholar] [CrossRef]
- Manabe, K.; Nishimura, H. Influence of material properties in forming of tubes. Bander Bleche Rohre 1983, 9, 266–269. [Google Scholar]
- Mori, S.; Manabe, K.-I.; Nishimura, H. Hydraulic bulge forming of clad thin-walled tubes. Adv. Technol. Plast. 1990, 3, 1549–1554. [Google Scholar]
- Alexandrov, S.; Lyamina, E.; Lang, L. Description of the expansion of a two-layer tube: An analytic plane-strain solution for arbitrary pressure-independent yield criterion and hardening law. Metals 2021, 11, 793. Available online: https://www.mdpi.com/2075-4701/11/5/793 (accessed on 14 May 2021). [CrossRef]
- Roberts, S.M.; Hall, F.; Van Bael, A.; Hartley, P.; Pillinger, I.; Sturgess, E.N.; Van Houtte, P.; Aernoudt, E. Benchmark tests for 3-D, elasto-plastic, finite-element codes for the modelling of metal forming processe. J. Mater. Process. Technol. 1992, 34, 61–68. Available online: https://www.sciencedirect.com/science/article/abs/pii/092401369290090F (accessed on 14 September 1992). [CrossRef]
- Abali, B.E.; Reich, F.A. Verification of deforming polarized structure computation by using a closed-form solution. Contin. Mech. Thermodyn. 2020, 32, 693–708. Available online: https://link.springer.com/article/10.1007/s00161-018-0709-8 (accessed on 14 September 2018). [CrossRef]
- Rusinek, A.; Zaera, R.; Klepaczko, J.R. Constitutive relations in 3-D for a wide range of strain rates and temperatures—Application to mild steels. Int. J. Solids Struct. 2007, 44, 5611–5634. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, L.; Alexandrov, S.; Rynkovskaya, M. An Analytic Solution for an Expanding/Contracting Strain-Hardening Viscoplastic Hollow Cylinder at Large Strains and Its Application to Tube Hydroforming Design. Processes 2021, 9, 2161. https://doi.org/10.3390/pr9122161
Lang L, Alexandrov S, Rynkovskaya M. An Analytic Solution for an Expanding/Contracting Strain-Hardening Viscoplastic Hollow Cylinder at Large Strains and Its Application to Tube Hydroforming Design. Processes. 2021; 9(12):2161. https://doi.org/10.3390/pr9122161
Chicago/Turabian StyleLang, Lihui, Sergei Alexandrov, and Marina Rynkovskaya. 2021. "An Analytic Solution for an Expanding/Contracting Strain-Hardening Viscoplastic Hollow Cylinder at Large Strains and Its Application to Tube Hydroforming Design" Processes 9, no. 12: 2161. https://doi.org/10.3390/pr9122161
APA StyleLang, L., Alexandrov, S., & Rynkovskaya, M. (2021). An Analytic Solution for an Expanding/Contracting Strain-Hardening Viscoplastic Hollow Cylinder at Large Strains and Its Application to Tube Hydroforming Design. Processes, 9(12), 2161. https://doi.org/10.3390/pr9122161





