Off-Gas-Based Soft Sensor for Real-Time Monitoring of Biomass and Metabolism in Chinese Hamster Ovary Cell Continuous Processes in Single-Use Bioreactors
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Lines
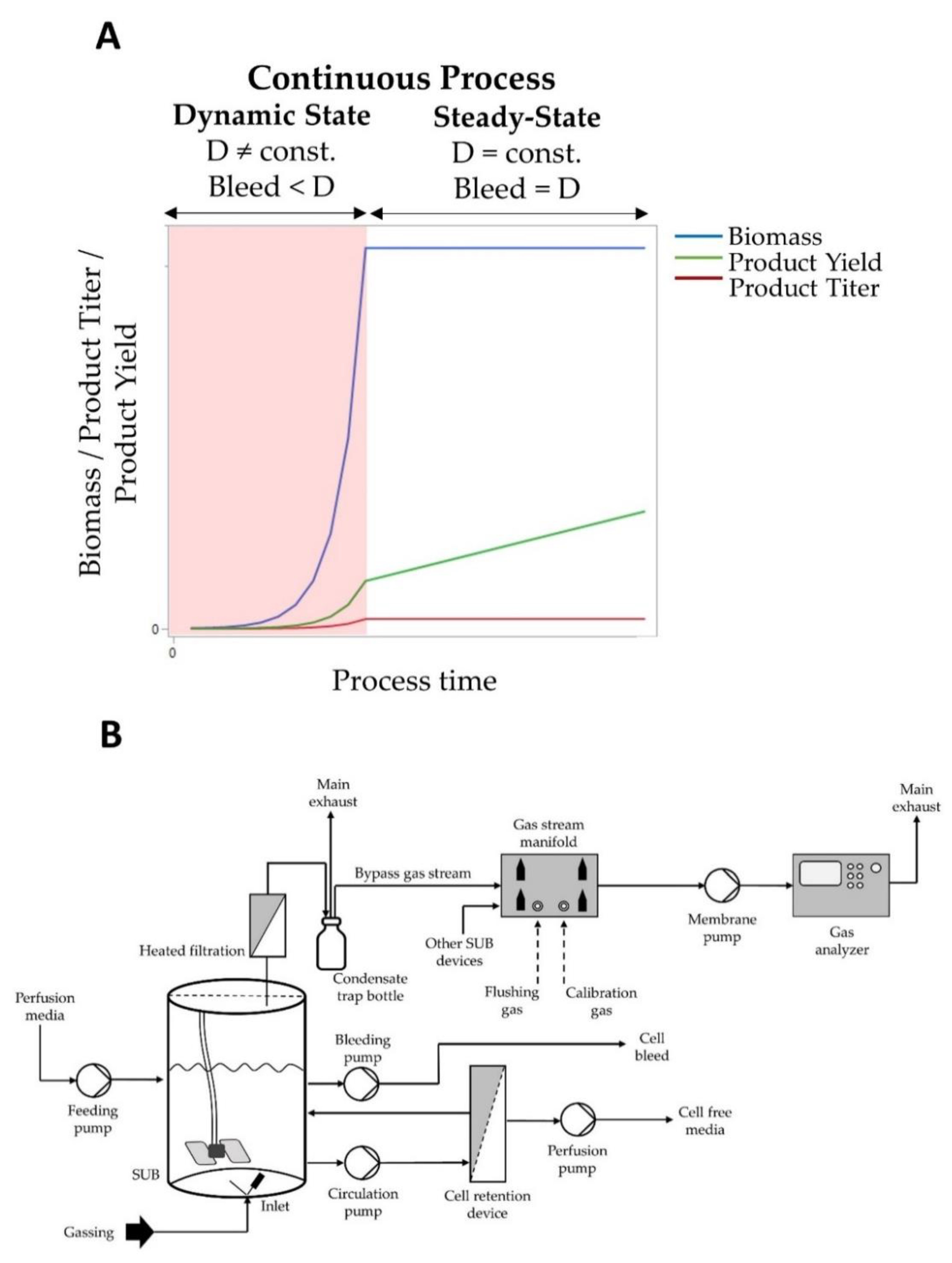
2.2. Cell Cultivation and in Process Control
2.3. Oxygen Balancing and OUR Calculation
2.4. Off-Gas Measurement Set-Up
2.5. Data Collection and Preprocessing
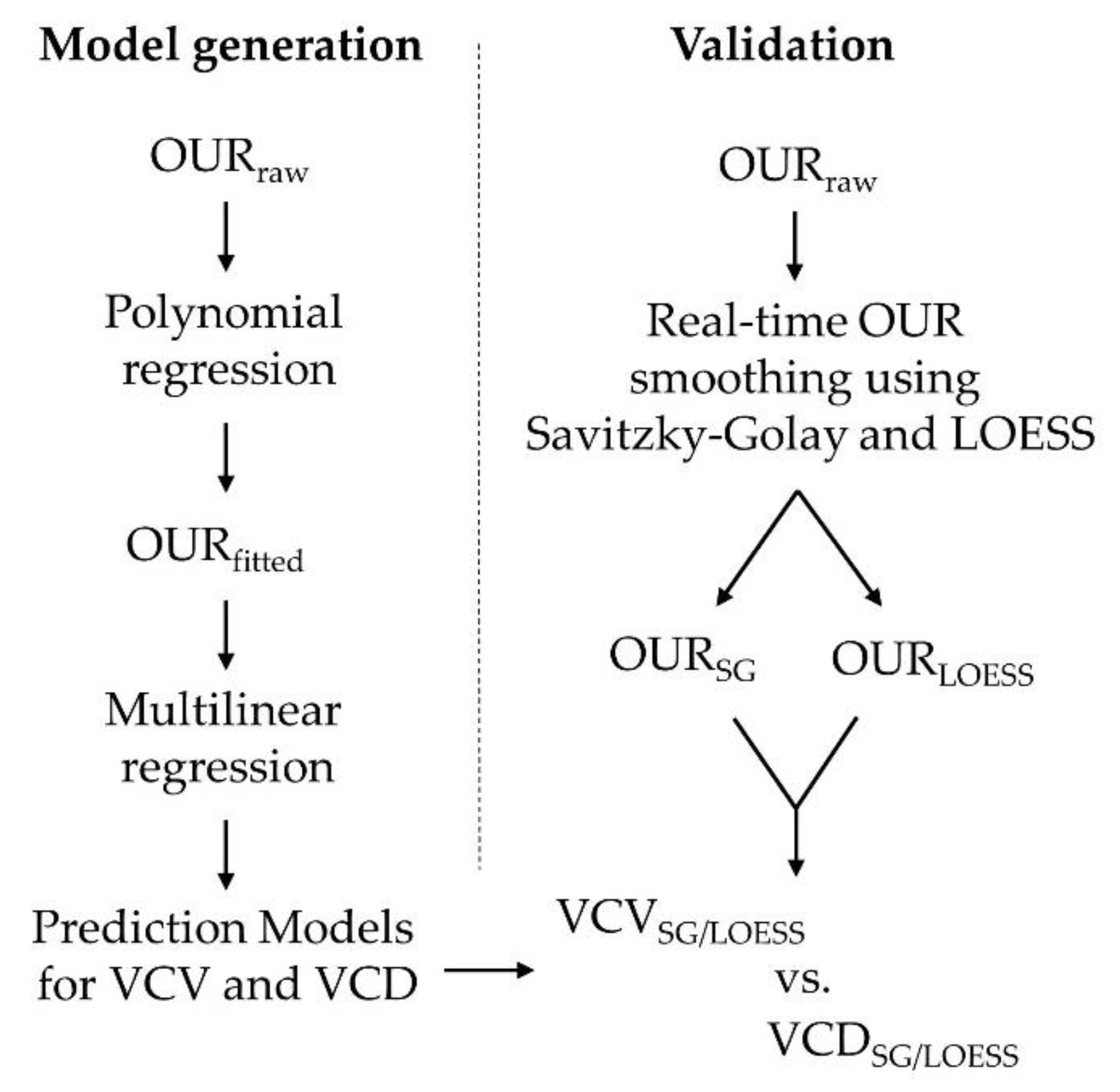
2.6. Model Generation and Assessment
2.7. Real-Time Prediction and Validation
2.8. Off-Line Measurements
2.9. Cell-Specific Substrate and Metabolite Consumption and Production Rate, Product Formation Rate and Yield Calculation
3. Results and Discussion
3.1. Online Parameter Evaluation and Preprocessing
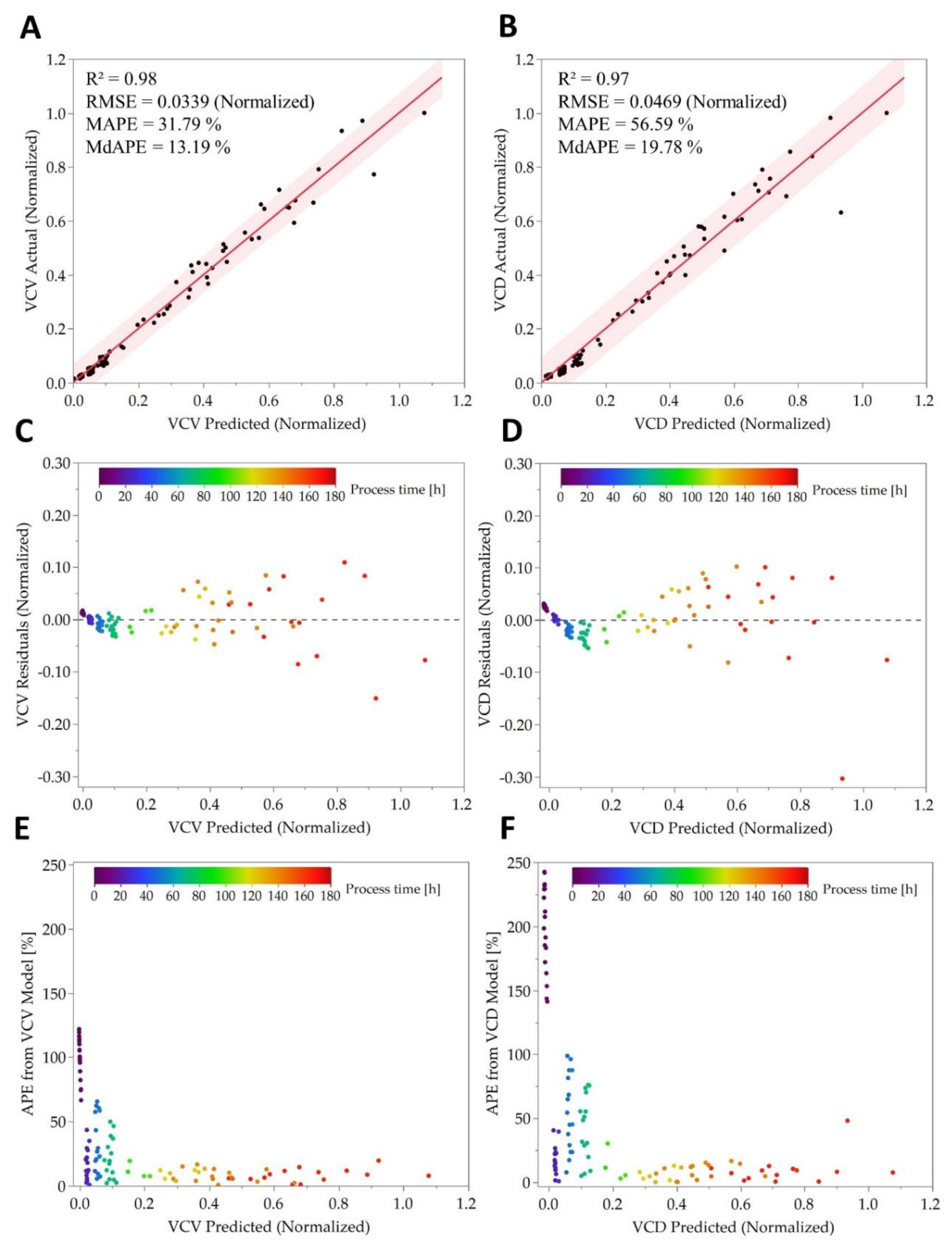
3.2. Biomass Model Generation and Assessment
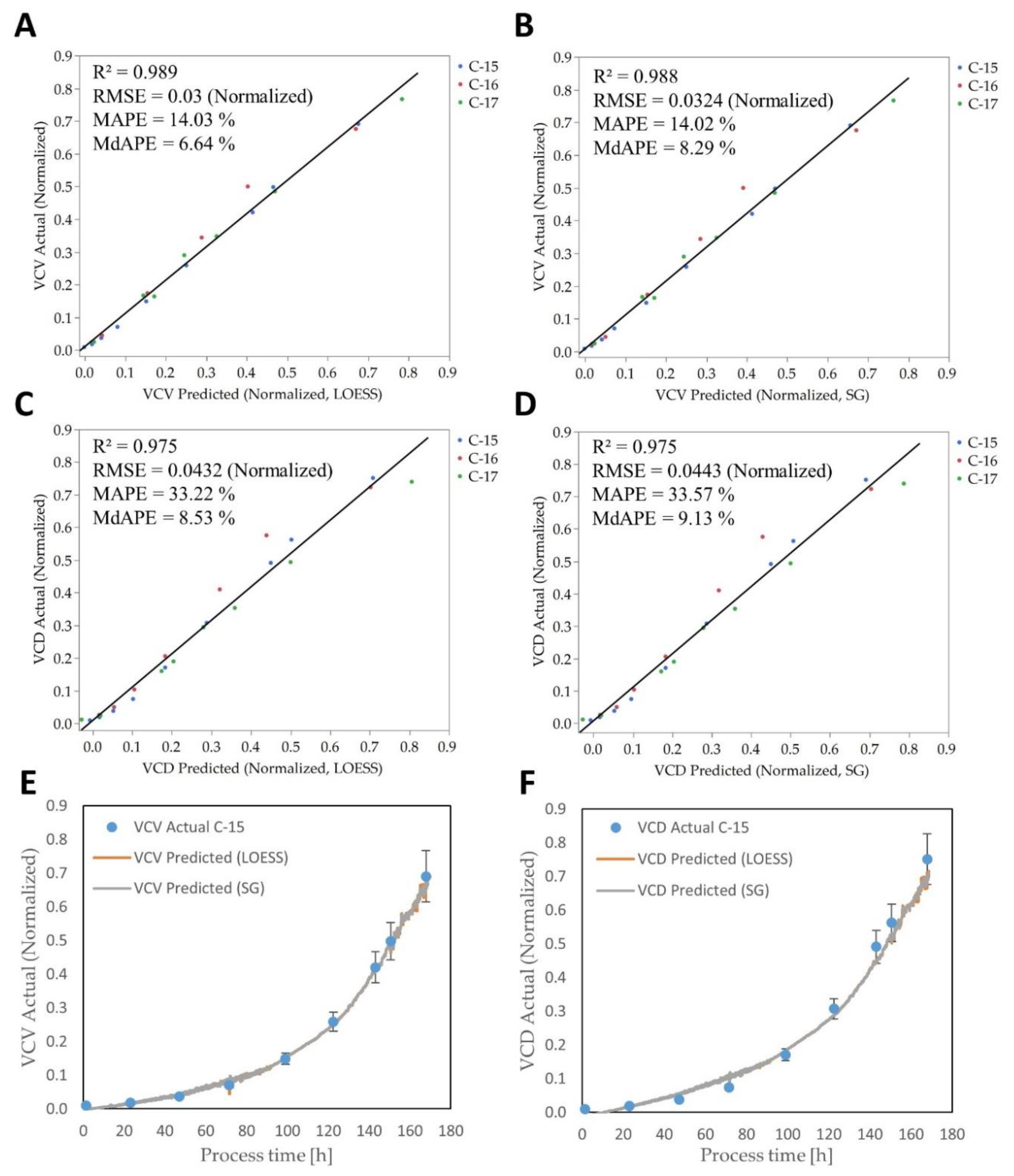
3.3. Real-Time Prediction and Quality of Online OUR Monitoring
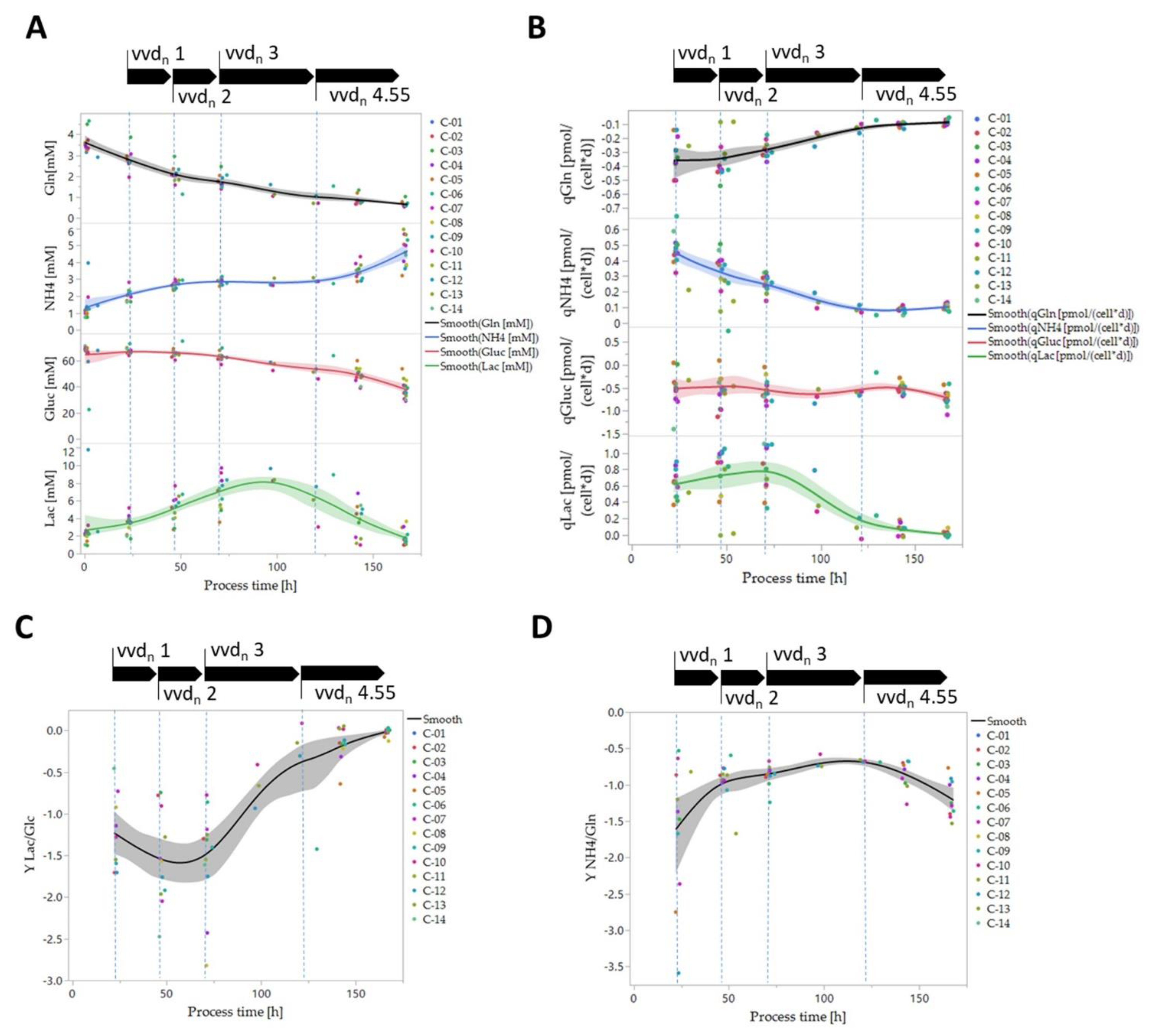
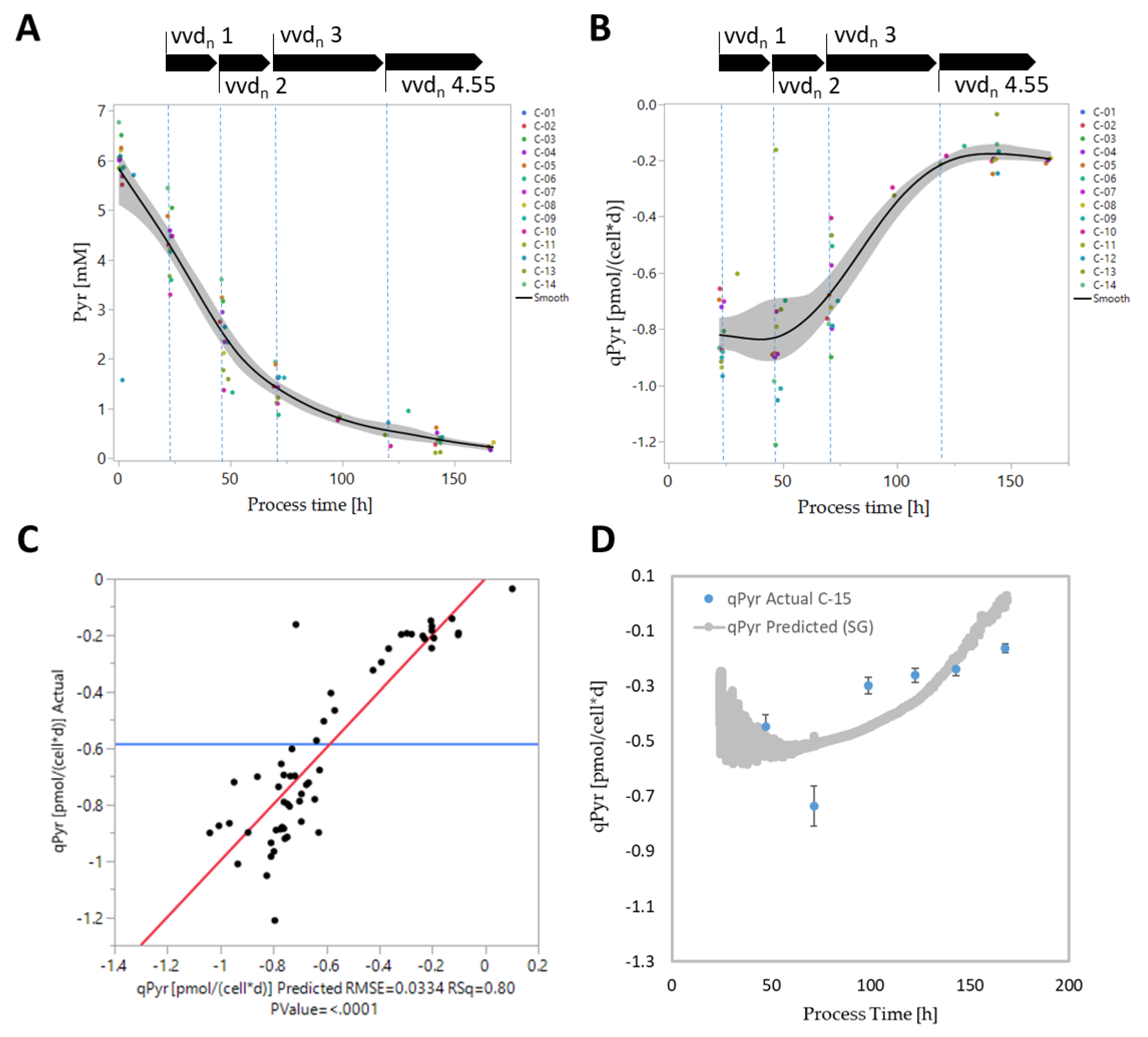
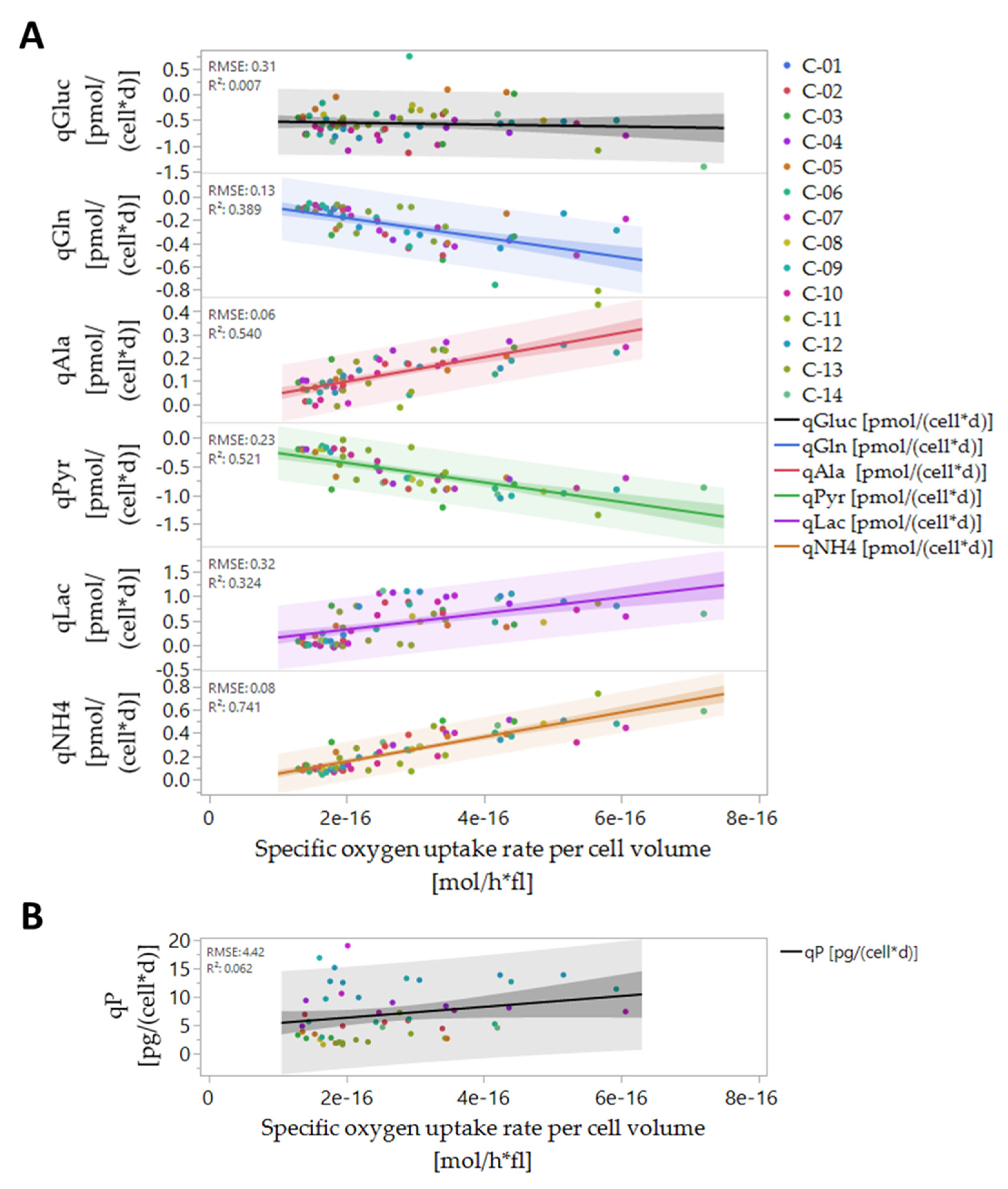
3.4. Biomass-Specific Oxygen Demand and Key Metabolism Analysis
3.5. Online Prediction of Cellular Metabolic Rates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aehle, M.; Kuprijanov, A.; Schaepe, S.; Simutis, R.; Lübbert, A. Increasing batch-to-batch reproducibility of CHO cultures by robust open-loop control. Cytotechnology 2011, 63, 41–47. [Google Scholar] [CrossRef] [PubMed]
- FDA. Guidance for Industry: PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance; FDA: Silver Spring, MD, USA, 2004. [Google Scholar]
- Lopes, A.G. Single-use in the biopharmaceutical industry: A review of current technology impact, challenges and limitations. Food Bioprod. Process. 2015, 93, 98–114. [Google Scholar] [CrossRef]
- Löffelholz, C.; Husemann, U.; Greller, G.; Meusel, W.; Kauling, J.; Ay, P.; Kraume, M.; Eibl, R.; Eibl, D. Bioengineering Parameters for Single-Use Bioreactors: Overview and Evaluation of Suitable Methods. Chem. Ing. Tech. 2013, 85, 40–56. [Google Scholar] [CrossRef]
- Junne, S.; Neubauer, P. How scalable and suitable are single-use bioreactors? Curr. Opin. Biotechnol. 2018, 53, 240–247. [Google Scholar] [CrossRef]
- Mandenius, C.-F. Measurement Technologies for Upstream and Downstream Bioprocessing. Processes 2021, 9, 143. [Google Scholar] [CrossRef]
- Gnoth, S.; Jenzsch, M.; Simutis, R.; Lübbert, A. Process Analytical Technology (PAT): Batch-to-batch reproducibility of fermentation processes by robust process operational design and control. J. Biotechnol. 2007, 132, 180–186. [Google Scholar] [CrossRef]
- Justice, C.; Brix, A.; Freimark, D.; Kraume, M.; Pfromm, P.; Eichenmueller, B.; Czermak, P. Process control in cell culture technology using dielectric spectroscopy. Biotechnol. Adv. 2011, 29, 391–401. [Google Scholar] [CrossRef]
- Busse, C.; Biechele, P.; De Vries, I.; Reardon, K.F.; Solle, D.; Scheper, T. Sensors for disposable bioreactors. Eng. Life Sci. 2017, 17, 940–952. [Google Scholar] [CrossRef]
- Steinwandter, V.; Zahel, T.; Sagmeister, P.; Herwig, C. Propagation of measurement accuracy to biomass soft-sensor estimation and control quality. Anal. Bioanal. Chem. 2016, 409, 693–706. [Google Scholar] [CrossRef][Green Version]
- Kiviharju, K.; Salonen, K.; Moilanen, U.; Eerikäinen, T. Biomass measurement online: The performance of in situ measurements and software sensors. J. Ind. Microbiol. Biotechnol. 2008, 35, 657–665. [Google Scholar] [CrossRef]
- Mandenius, C.-F.; Gustavsson, R. Mini-review: Soft sensors as means for PAT in the manufacture of bio-therapeutics. J. Chem. Technol. Biotechnol. 2015, 90, 215–227. [Google Scholar] [CrossRef]
- Luttmann, R.; Bracewell, D.G.; Cornelissen, G.; Gernaey, K.V.; Glassey, J.; Hass, V.C.; Kaiser, C.; Preusse, C.; Striedner, G.; Mandenius, C.-F. Soft sensors in bioprocessing: A status report and recommendations. Biotechnol. J. 2012, 7, 1040–1048. [Google Scholar] [CrossRef]
- Pappenreiter, M.; Sissolak, B.; Sommeregger, W.; Striedner, G. Oxygen Uptake Rate Soft-Sensing via Dynamic k L a Computation: Cell Volume and Metabolic Transition Prediction in Mammalian Bioprocesses. Front. Bioeng. Biotechnol. 2019, 7, 195. [Google Scholar] [CrossRef] [PubMed]
- Metze, S.; Ruhl, S.; Greller, G.; Grimm, C.; Scholz, J. Monitoring online biomass with a capacitance sensor during scale-up of industrially relevant CHO cell culture fed-batch processes in single-use bioreactors. Bioprocess Biosyst. Eng. 2020, 43, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Aehle, M.; Kuprijanov, A.; Schaepe, S.; Simutis, R.; Lübbert, A. Simplified off-gas analyses in animal cell cultures for process monitoring and control purposes. Biotechnol. Lett. 2011, 33, 2103–2110. [Google Scholar] [CrossRef]
- Zeng, A.-P.; Byun, T.-G.; Deckwer, W.-D. On-line estimation of viable biomass of a microaerobic culture using exit gas analysis. Biotechnol. Tech. 1991, 5, 247–250. [Google Scholar] [CrossRef]
- Dorresteijn, R.C.; Numan, K.H.; De Gooijer, C.D.; Tramper, J.; Beuvery, E.C. On-line estimation of the biomass activity during animal-cell cultivations. Biotechnol. Bioeng. 1996, 51, 206–214. [Google Scholar] [CrossRef]
- Goldrick, S.; Umprecht, A.; Tang, A.; Zakrzewski, R.; Cheeks, M.; Turner, R.; Charles, A.; Les, K.; Hulley, M.; Spencer, C.; et al. High-Throughput Raman Spectroscopy Combined with Innovate Data Analysis Workflow to Enhance Biopharmaceutical Process Development. Processes 2020, 8, 1179. [Google Scholar] [CrossRef]
- Downey, B.J.; Graham, L.J.; Breit, J.F.; Glutting, N.K. A novel approach for using dielectric spectroscopy to predict viable cell volume (VCV) in early process development. Biotechnol. Prog. 2014, 30, 479–487. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Konstantinov, K.B. Continuous, real-time monitoring of the oxygen uptake rate (OUR) in animal cell bioreactors. Biotechnol. Bioeng. 1994, 44, 983–990. [Google Scholar] [CrossRef]
- Wagner, B.A.; Venkataraman, S.; Buettner, G.R. The Rate of Oxygen Utilization by Cells. Free Radic. Biol. Med. 2011, 51, 700–712. [Google Scholar] [CrossRef]
- Ruffieux, P.-A.; von Stockar, U.; Marison, I.W. Measurement of volumetric (OUR) and determination of specific (qO2) oxygen uptake rates in animal cell cultures. J. Biotechnol. 1998, 63, 85–95. [Google Scholar] [CrossRef]
- Goudar, C.T.; Piret, J.M.; Konstantinov, K.B. Estimating cell specific oxygen uptake and carbon dioxide production rates for mammalian cells in perfusion culture. Biotechnol. Prog. 2011, 27, 1347–1357. [Google Scholar] [CrossRef]
- Fleischaker, R.J.; Sinskey, A.J., Jr. Oxygen demand and supply in cell culture. Appl. Microbiol. Biotechnol. 1981, 12, 193–197. [Google Scholar] [CrossRef]
- Pereira, S.; Kildegaard, H.F.; Andersen, M.R. Impact of CHO Metabolism on Cell Growth and Protein Production: An Overview of Toxic and Inhibiting Metabolites and Nutrients. Biotechnol. J. 2018, 13, e1700499. [Google Scholar] [CrossRef] [PubMed]
- Heidemann, R.; Lütkemeyer, D.; Büntemeyer, H.; Lehmann, J. Effects of dissolved oxygen levels and the role of extra- and intracellular amino acid concentrations upon the metabolism of mammalian cell lines during batch and continuous cultures. Cytotechnology 1998, 26, 185–197. [Google Scholar] [CrossRef] [PubMed]
- De Jonge, L.; Heijnen, J.; van Gulik, W. Reconstruction of the oxygen uptake and carbon dioxide evolution rates of microbial cultures at near-neutral pH during highly dynamic conditions. Biochem. Eng. J. 2014, 83, 42–54. [Google Scholar] [CrossRef]
- Moreno, J.J.M.; Pol, A.P.; Abad, A.S. Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema 2013, 25, 500–506. [Google Scholar] [CrossRef]
- Bausch, M.; Schultheiss, C.; Sieck, J.B. Recommendations for Comparison of Productivity Between Fed-Batch and Perfusion Processes. Biotechnol. J. 2019, 14, e1700721. [Google Scholar] [CrossRef]
- Wu, L.; Lange, H.C.; Van Gulik, W.M.; Heijnen, J.J. Determination of in vivo oxygen uptake and carbon dioxide evolution rates from off-gas measurements under highly dynamic conditions. Biotechnol. Bioeng. 2002, 81, 448–458. [Google Scholar] [CrossRef]
- Bloemen, H.H.J.; Wu, L.; van Gulik, W.M.; Heijnen, J.J.; Verhaegen, M.H.G. Reconstruction of the O2 uptake rate and CO2 evolution rate on a time scale of seconds. AIChE J. 2003, 49, 1895–1908. [Google Scholar] [CrossRef]
- Tuveri, A.; Pérez-García, F.; Lira-Parada, P.A.; Imsland, L.; Bar, N. Sensor fusion based on Extended and Unscented Kalman Filter for bioprocess monitoring. J. Process. Control 2021, 106, 195–207. [Google Scholar] [CrossRef]
- Sarkar, S.; Lund, S.P.; Vyzasatya, R.; Vanguri, P.; Elliott, J.T.; Plant, A.L.; Lin-Gibson, S. Evaluating the quality of a cell counting measurement process via a dilution series experimental design. Cytotherapy 2017, 19, 1509–1521. [Google Scholar] [CrossRef] [PubMed]
- Cadena-Herrera, D.; Lara, J.E.E.-D.; Ramírez-Ibañez, N.D.; Lopez-Morales, C.A.; Pérez, N.O.; Flores-Ortiz, L.F.; Medina-Rivero, E. Validation of three viable-cell counting methods: Manual, semi-automated, and automated. Biotechnol. Rep. 2015, 7, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Bassey, E.; Whalley, J.; Sallis, P. An Evaluation of Smoothing Filters for Gas Sensor Signal Cleaning. In Proceedings of the Fourth International Conference on Advanced Communications and Computation, Paris, France, 8–9 February 2014; pp. 19–23. [Google Scholar]
- Sonderhoff, S.A.; Kilburn, D.G.; Piret, J.M. Analysis of mammalian viable cell biomass based on cellular ATP. Biotechnol. Bioeng. 1992, 39, 859–864. [Google Scholar] [CrossRef]
- Pan, X.; Dalm, C.; Wijffels, R.H.; Martens, D.E. Metabolic characterization of a CHO cell size increase phase in fed-batch cultures. Appl. Microbiol. Biotechnol. 2017, 101, 8101–8113. [Google Scholar] [CrossRef]
- Nielsen, L.K.; Reid, S.; Greenfield, P.F. Cell cycle model to describe animal cell size variation and lag between cell number and biomass dynamics. Biotechnol. Bioeng. 1997, 56, 372–379. [Google Scholar] [CrossRef]
- Milo, R. What is the total number of protein molecules per cell volume? A call to rethink some published values. BioEssays 2013, 35, 1050–1055. [Google Scholar] [CrossRef]
- Frame, K.K.; Hu, W.-S. Cell volume measurement as an estimation of mammalian cell biomass. Biotechnol. Bioeng. 1990, 36, 191–197. [Google Scholar] [CrossRef]
- Stettler, M.; Jaccard, N.; Hacker, D.; De Jesus, M.; Wurm, F.M.; Jordan, M. New disposable tubes for rapid and precise biomass assessment for suspension cultures of mammalian cells. Biotechnol. Bioeng. 2006, 95, 1228–1233. [Google Scholar] [CrossRef]
- Popp, O.; Müller, D.; Didzus, K.; Paul, W.; Lipsmeier, F.; Kirchner, F.; Niklas, J.; Mauch, K.; Beaucamp, N. A hybrid approach identifies metabolic signatures of high-producers for chinese hamster ovary clone selection and process optimization. Biotechnol. Bioeng. 2016, 113, 2005–2019. [Google Scholar] [CrossRef]
- Yuk, I.H.; Zhang, J.D.; Ebeling, M.; Berrera, M.; Gomez, N.; Werz, S.; Meiringer, C.; Shao, Z.; Swanberg, J.C.; Lee, K.H.; et al. Effects of copper on CHO cells: Insights from gene expression analyses. Biotechnol. Prog. 2014, 30, 429–442. [Google Scholar] [CrossRef]
- Takagi, M.; Hayashi, H.; Yoshida, T. The effect of osmolarity on metabolism and morphology in adhesion and suspension chinese hamster ovary cells producing tissue plasminogen activator. Cytotechnology 2000, 32, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Noh, S.M.; Woo, J.R.; Kim, J.W.; Lee, G.M. Valeric acid induces cell cycle arrest at G1 phase in CHO cell cultures and improves recombinant antibody productivity. Biotechnol. J. 2016, 11, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Chevallier, V.; Andersen, M.R.; Malphettes, L. Oxidative stress-alleviating strategies to improve recombinant protein production in CHO cells. Biotechnol. Bioeng. 2020, 117, 1172–1186. [Google Scholar] [CrossRef]
- Deshpande, R.R.; Heinzle, E. On-line oxygen uptake rate and culture viability measurement of animal cell culture using microplates with integrated oxygen sensors. Biotechnol. Lett. 2004, 26, 763–767. [Google Scholar] [CrossRef]
- Jorjani, P.; Ozturk, S.S. Effects of cell density and temperature on oxygen consumption rate for different mammalian cell lines. Biotechnol. Bioeng. 1999, 64, 349–356. [Google Scholar] [CrossRef]
- Gray, D.R.; Chen, S.; Howarth, W.; Inlow, D.; Maiorella, B.L. CO2 in large-scale and high-density CHO cell perfusion culture. Cytotechnology 1996, 22, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Super, A.; Jaccard, N.; Marques, M.P.C.; Macown, R.J.; Griffin, L.D.; Veraitch, F.S.; Szita, N. Real-time monitoring of specific oxygen uptake rates of embryonic stem cells in a microfluidic cell culture device. Biotechnol. J. 2016, 11, 1179–1189. [Google Scholar] [CrossRef] [PubMed]
- Genzel, Y.; Ritter, J.B.; König, S.; Alt, R.; Reichl, U. Substitution of Glutamine by Pyruvate to Reduce Ammonia Formation and Growth Inhibition of Mammalian Cells. Biotechnol. Prog. 2008, 21, 58–69. [Google Scholar] [CrossRef]
- Mulukutla, B.C.; Mitchell, J.; Geoffroy, P.; Harrington, C.; Krishnan, M.; Kalomeris, T.; Morris, C.; Zhang, L.; Pegman, P.; Hiller, G.W. Metabolic engineering of Chinese hamster ovary cells towards reduced biosynthesis and accumulation of novel growth inhibitors in fed-batch cultures. Metab. Eng. 2019, 54, 54–68. [Google Scholar] [CrossRef] [PubMed]
- Jeremy, M.; Berg, J.L.T. The Citric Acid Cycle. Biochemistry, 5th ed.; W H Freeman: New York, NY, USA, 2002. [Google Scholar]
- Möller, J.; Bhat, K.; Guhl, L.; Pörtner, R.; Jandt, U.; Zeng, A. Regulation of pyruvate dehydrogenase complex related to lactate switch in CHO cells. Eng. Life Sci. 2021, 21, 100–114. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.K.; Srivastava, S.K.; Sharma, A.; Nalage, V.H.H.; Salvi, D.; Kushwaha, H.; Chitnis, N.B.; Shukla, P. Metabolic engineering of CHO cells for the development of a robust protein production platform. PLoS ONE 2017, 12, e0181455. [Google Scholar] [CrossRef] [PubMed]
- Dhiman, H.; Gerstl, M.P.; Ruckerbauer, D.; Hanscho, M.; Himmelbauer, H.; Clarke, C.; Barron, N.; Zanghellini, J.; Borth, N. Genetic and Epigenetic Variation across Genes Involved in Energy Metabolism and Mitochondria of Chinese Hamster Ovary Cell Lines. Biotechnol. J. 2019, 14, 1800681. [Google Scholar] [CrossRef] [PubMed]
- Klinger, C.; Trinkaus, V.; Wallocha, T. Novel Carbon Dioxide-Based Method for Accurate Determination of pH and pCO2 in Mammalian Cell Culture Processes. Processes 2020, 8, 520. [Google Scholar] [CrossRef]


| No. | Process | Expressed Antibody | Clone | Purpose |
|---|---|---|---|---|
| 1 | P-01 | A-01 | C-01 | Training |
| 2 | P-02 | A-02 | C-02 | Training |
| 3 | P-03 | A-03 | C-03 | Training |
| 4 | P-04 | A-04 | C-04 | Training |
| 5 | P-05 | A-01 | C-05 | Training |
| 6 | P-06 | A-05 | C-06 | Training |
| 7 | P-07 | A-06 | C-07 | Training |
| 8 | P-08 | A-07 | C-08 | Training |
| 9 | P-09 | A-05 | C-09 | Training |
| 10 | P-10 | A-08 | C-10 | Training |
| 11 | P-11 | A-09 | C-11 | Training |
| 12 | P-12 | A-05 | C-12 | Training |
| 13 | P-13 | A-10 | C-13 | Training |
| 14 | P-14 | A-11 | C-14 | Training |
| 15 | P-15 | A-12 | C-15 | Validation |
| 16 | P-16 | A-13 | C-16 | Validation |
| 17 | P-17 | A-14 | C-17 | Validation |
| Process | Polynomial Degree | R2 |
|---|---|---|
| P-01 | 5 | 0.863 |
| P-02 | 4 | 0.983 |
| P-03 | 4 | 0.878 |
| P-04 | 4 | 0.888 |
| P-05 | 4 | 0.712 |
| P-06 | 4 | 0.971 |
| P-07 | 4 | 0.991 |
| P-08 | 3 | 0.892 |
| P-09 | 3 | 0.982 |
| P-10 | 3 | 0.977 |
| P-11 | 3 | 0.918 |
| P-12 | 4 | 0.956 |
| P-13 | 4 | 0.977 |
| P-14 | 4 | 0.954 |
| Process | R2 | RMSE (Normalized) | MAPE [%] | MdAPE [%] | ||||
|---|---|---|---|---|---|---|---|---|
| SG | LOESS | SG | LOESS | SG | LOESS | SG | LOESS | |
| P-15 | 0.999 | 0.998 | 0.017 | 0.015 | 18.13 | 18.15 | 4.93 | 3.85 |
| P-16 | 0.974 | 0.980 | 0.057 | 0.052 | 14.94 | 14.61 | 14.35 | 13.77 |
| P-17 | 0.995 | 0.994 | 0.025 | 0.025 | 7.99 | 8.23 | 6.61 | 6.60 |
| Process | R2 | RMSE (Normalized) | MAPE [%] | MdAPE [%] | ||||
|---|---|---|---|---|---|---|---|---|
| SG | LOESS | SG | LOESS | SG | LOESS | SG | LOESS | |
| P-15 | 0.997 | 0.995 | 0.035 | 0.033 | 33.09 | 32.57 | 9.85 | 8.29 |
| P-16 | 0.965 | 0.971 | 0.072 | 0.068 | 16.75 | 15.21 | 19.43 | 11.16 |
| P-17 | 0.996 | 0.995 | 0.025 | 0.031 | 48.81 | 49.71 | 6.79 | 7.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wallocha, T.; Popp, O. Off-Gas-Based Soft Sensor for Real-Time Monitoring of Biomass and Metabolism in Chinese Hamster Ovary Cell Continuous Processes in Single-Use Bioreactors. Processes 2021, 9, 2073. https://doi.org/10.3390/pr9112073
Wallocha T, Popp O. Off-Gas-Based Soft Sensor for Real-Time Monitoring of Biomass and Metabolism in Chinese Hamster Ovary Cell Continuous Processes in Single-Use Bioreactors. Processes. 2021; 9(11):2073. https://doi.org/10.3390/pr9112073
Chicago/Turabian StyleWallocha, Tobias, and Oliver Popp. 2021. "Off-Gas-Based Soft Sensor for Real-Time Monitoring of Biomass and Metabolism in Chinese Hamster Ovary Cell Continuous Processes in Single-Use Bioreactors" Processes 9, no. 11: 2073. https://doi.org/10.3390/pr9112073
APA StyleWallocha, T., & Popp, O. (2021). Off-Gas-Based Soft Sensor for Real-Time Monitoring of Biomass and Metabolism in Chinese Hamster Ovary Cell Continuous Processes in Single-Use Bioreactors. Processes, 9(11), 2073. https://doi.org/10.3390/pr9112073







