Chaotic Analysis and Prediction of Wind Speed Based on Wavelet Decomposition
Abstract
:1. Introduction
2. Wind Data Description
3. Fractal Analysis
4. Data Analysis Methods Applied
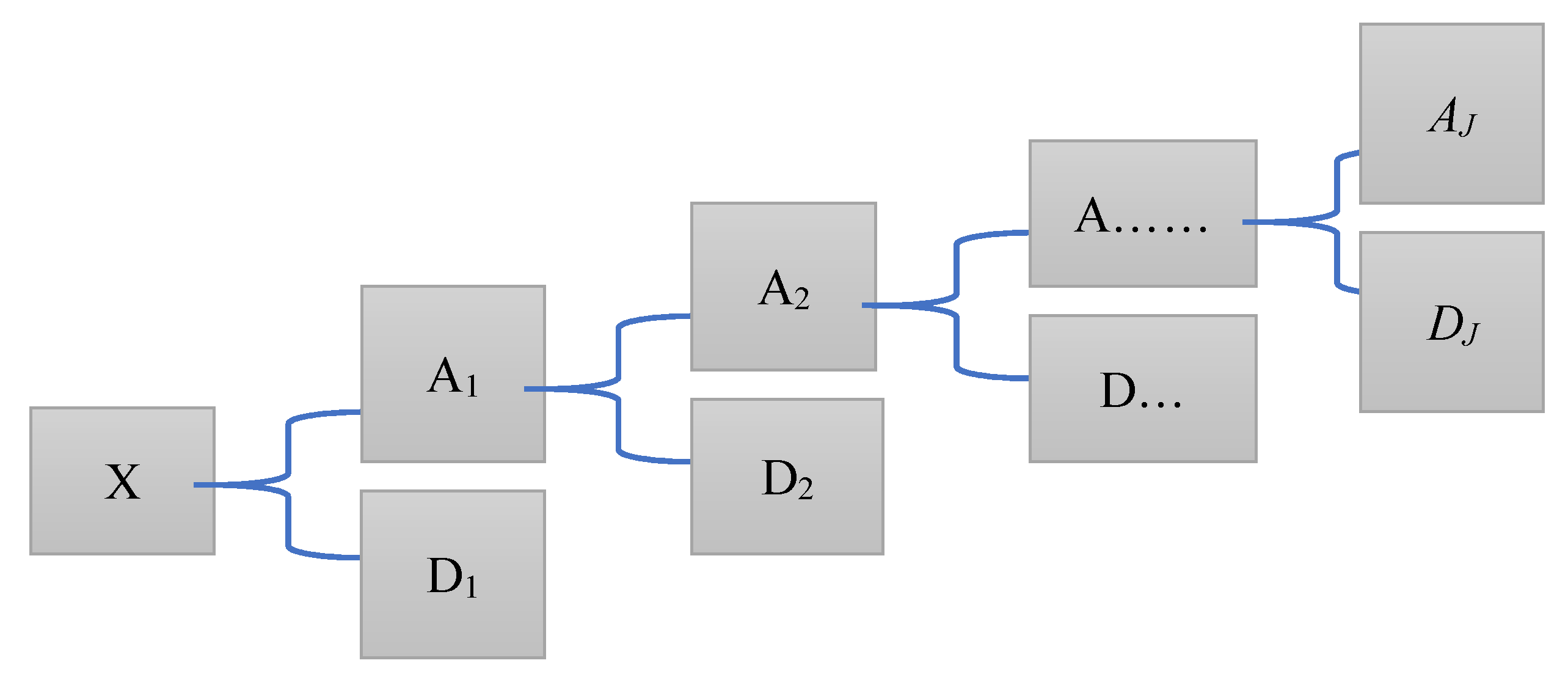
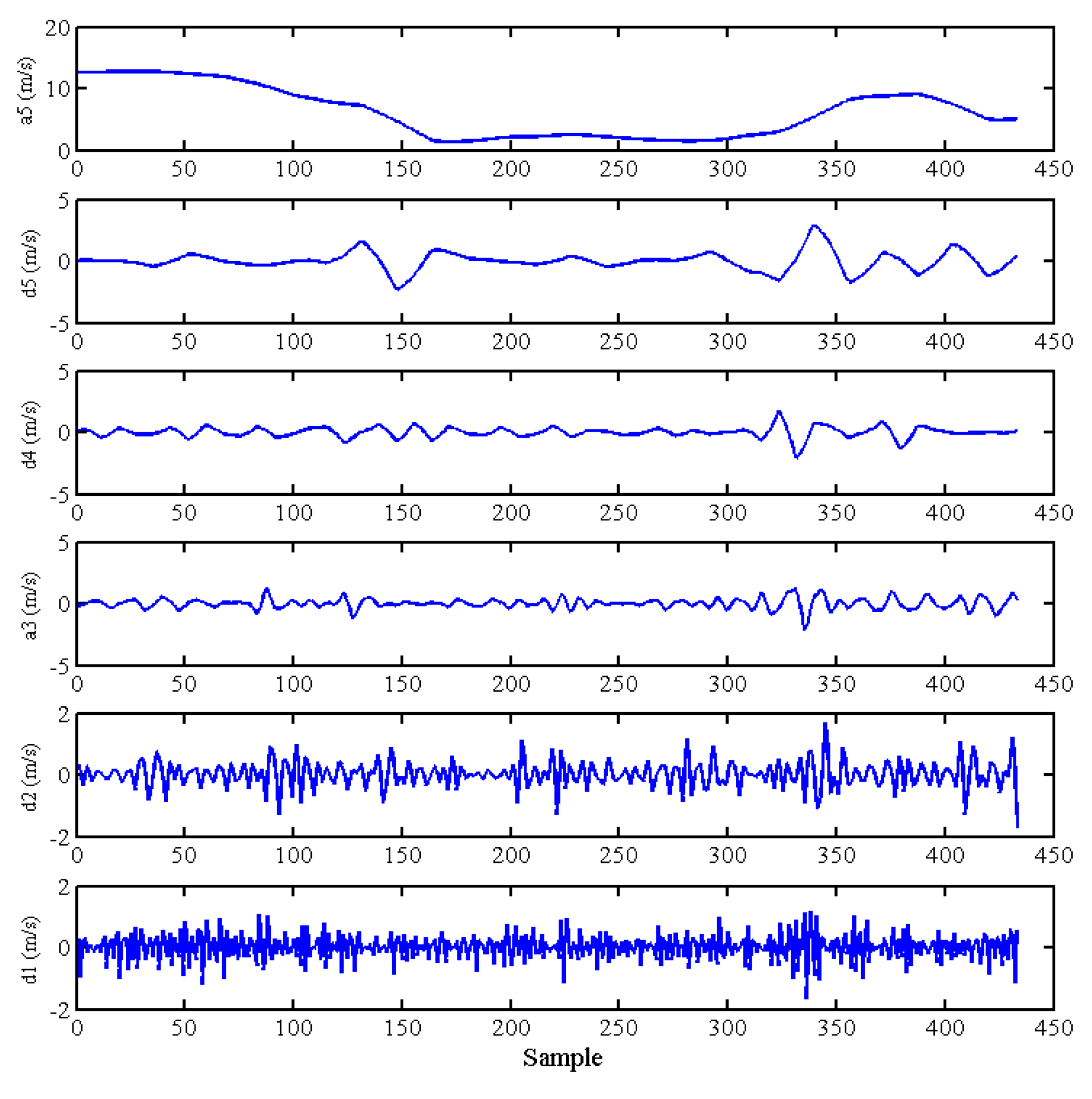
4.1. Wavelet Analysis
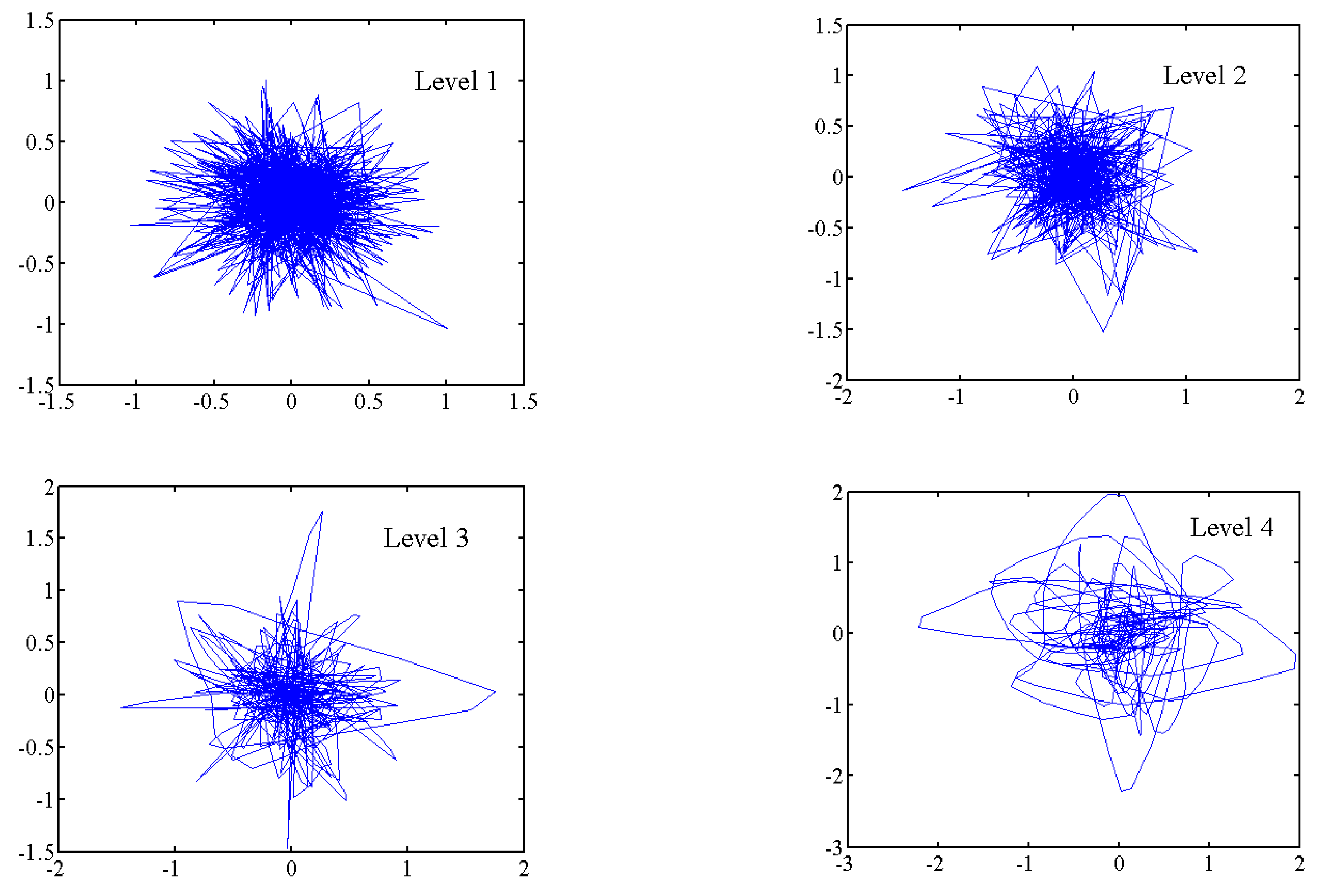
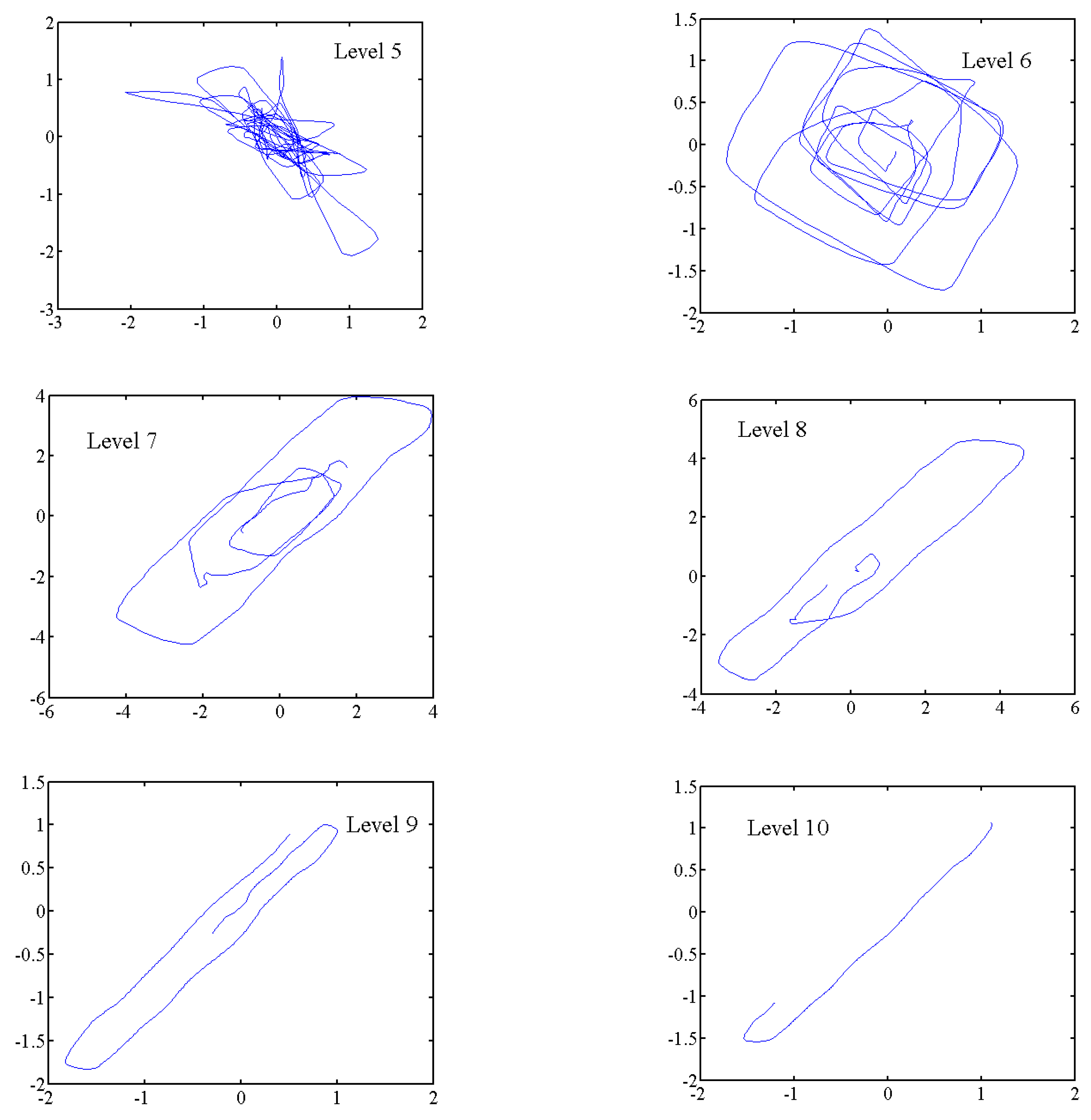
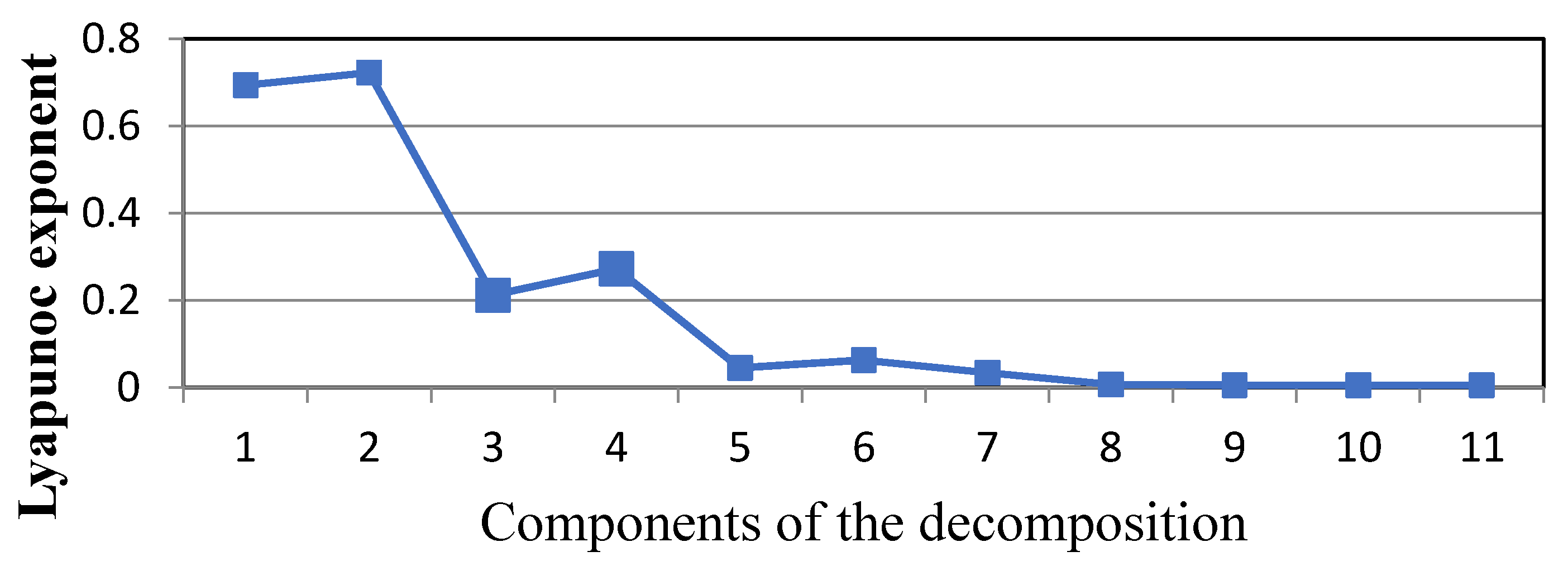
4.2. Chaotic Analysis of the Decomposed Components
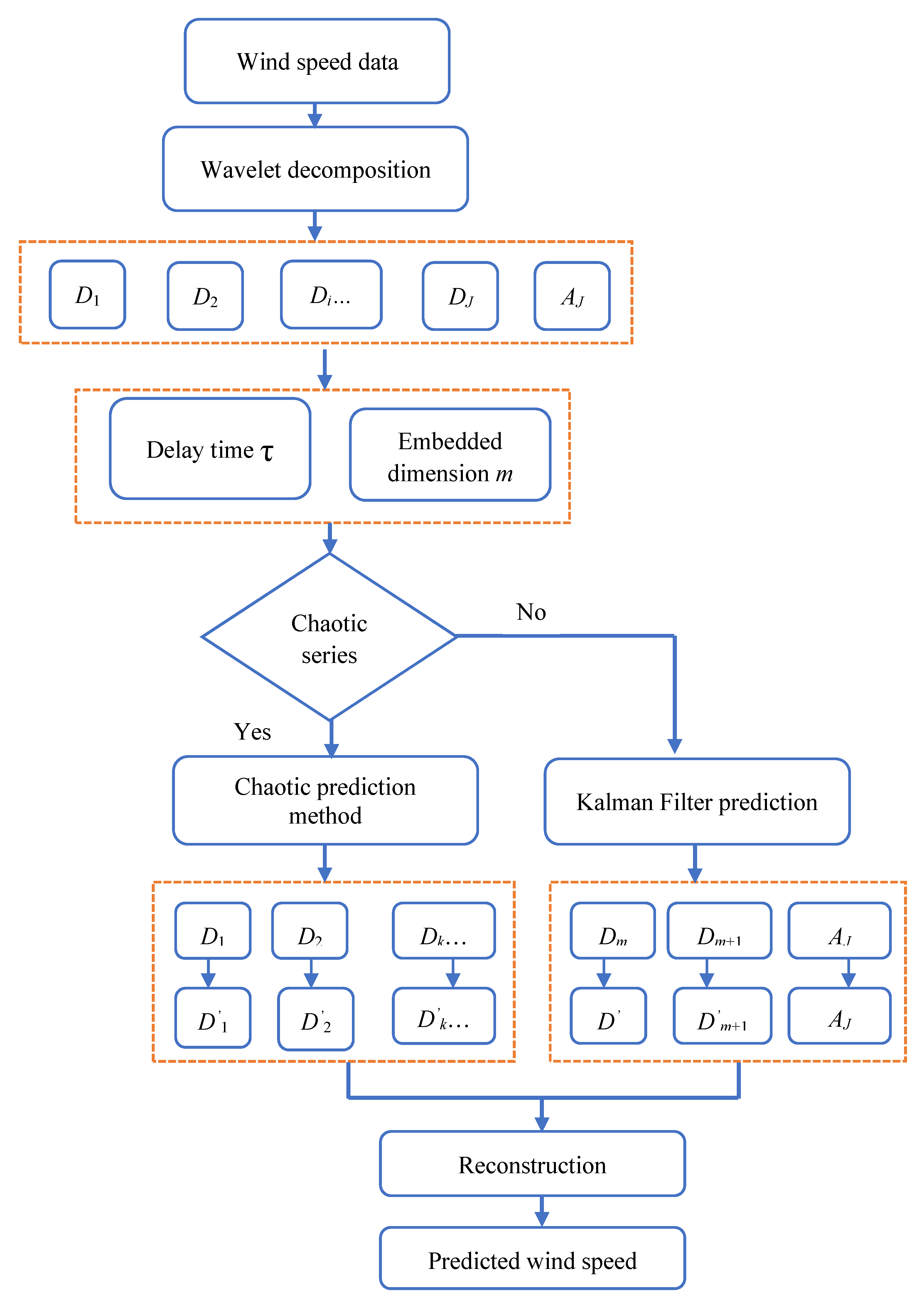
5. Wind Speed Prediction
5.1. Wind Prediction for Non-Chaotic Components
5.2. Wind Prediction for Chaotic Components
5.3. A Hybrid Prediction Method Combining Wavelet Decomposition
6. Results and Discussion
7. Conclusions
- With the application of fractal dimensional analysis, the seasonal and monthly wind speed data were considered random with fractal dimensions of approximately 1.5. The daily wind speed data were proven to have persistence and could be predicted with fractal dimensions between 1.1 and 1.3.
- To study the wind speed at a frequency level, the wavelet decomposition method was applied to separate the wind speed data from components at different frequency levels. Chaotic behaviors were found at high frequency levels.
- With the application of the Kalman filter and Volterra prediction method, the wind speed could be accurately predicted with an improvement of 67.8% compared to other prediction methods.
- For the proposed prediction method, the decomposition levels may affect the predictions. The results showed that with a higher decomposition level, the forecasting level is improved; however, for the considered wind speed, the forecast error changed little after level 7.
- Moreover, the proposed method showed better performance forecasting hourly data than the 10-min data.
Author Contributions
Funding
Conflicts of Interest
References
- Tu, Q.; Betz, R.; Mo, J.L.; Fan, Y.; Liu, Y. Achieving grid parity of wind power in China-Present levelized cost of electricity and future evolution. Appl. Energy 2019, 250, 1053–1064. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.; Li, G.; Yao, B.; Wu, J. Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration. Appl. Energy 2021, 292, 116851. [Google Scholar] [CrossRef]
- Drisya, G.; Asokan, K.; Kumar, K.S. Diverse dynamical characteristics across the frequency spectrum of wind speed fluctuations. Renew. Energy 2018, 119, 540–550. [Google Scholar]
- Wang, X.; Hui, L. Multiscale prediction of wind speed and output power for the wind farm. J. Control Theory Appl. 2012, 10, 251–258. [Google Scholar] [CrossRef]
- Cadenas, E.; Campos-Amezcua, R.; Rivera, W.; Espinosa-Medina, M.A.; Méndez-Gordillo, A.R.; Rangel, E.; Tena, J. Wind speed variability study based on the Hurst coefficient and fractal dimensional analysis. Energy Sci. Eng. 2019, 7, 361–378. [Google Scholar] [CrossRef]
- Chang, T.-P.; Ko, H.-H.; Liu, F.-J.; Chen, P.-H.; Chang, Y.-P.; Liang, Y.-H.; Jang, H.-Y.; Lin, T.-C.; Chen, Y.-H. Fractal dimension of wind speed time series. Appl. Energy 2012, 93, 742–749. [Google Scholar] [CrossRef]
- Harrouni, S.; Guessoum, A. Using a fractal dimension to quantify long-range persistence in global solar radiation. Chaos Solut. Fractal 2009, 41, 1520–1530. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Kanevski, M. Power spectrum and multi-fractal detrended fluctuation analysis of high-frequency wind measurements in mountainous regions. Appl. Energy 2016, 162, 1052–1061. [Google Scholar] [CrossRef]
- Ouyang, T.; Cha, X.; Qin, L. Medium-or long-term wind power prediction with combined models of meteorological multivariable. Power Syst. Technol. 2016, 40, 847–852. [Google Scholar]
- Sun, H.; Qiu, C.; Lu, L.; Gao, X.; Chen, J.; Yang, H. Wind turbine power modeling and optimization using artificial neural network with wind field experimental data. Appl. Energy 2020, 280, 115880. [Google Scholar] [CrossRef]
- Yan, C.; Pan, Y.; Archer, C.L. A general method to estimate wind farm power using artificial neural networks. Wind Energy 2019, 22, 1421–1432. [Google Scholar] [CrossRef]
- Díaz, S.; Carta, J.A.; Matías, J.M. Comparison of several measure-correlate-predict models using support vector regression techniques to estimate wind power densities. A case study. Energy Convers. Manag. 2017, 140, 362–400. [Google Scholar] [CrossRef]
- Sheta, A.F.; Ahmed, S.E.M.; Faris, H. A Comparison between regression, artificial neural networks and support vector machines for predicting stock Market Index. Int. J. Adv. Res. Artif. Intell. 2015, 4, 55–63. [Google Scholar]
- Shirzad, A.; Tabesh, M.; Farmani, R. A comparison between performance of support vector regression and artificial neural network in prediction of pipe burst rate in water distribution networks. KSCE J. Civ. Eng. 2014, 18, 941–948. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Torres, J.L.; García a De Blas, M.; De Francisco, A. Forecast of hourly average wind speed with ARMA models in Navarre (Spain). Sol. Energy 2005, 79, 65–77. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Wang, Y.; Yao, L.; Li, Q.; Li, J.; Pei, S. Long short-term memory network based on neighborhood gates for processing complex causality in wind speed prediction. Energy Convers. Manag. 2019, 192, 37–51. [Google Scholar] [CrossRef]
- Zuluaga, C.D.; Álvarez, M.A.; Giraldo, E. Short-term wind speed prediction based on robust Kalman filtering: An experimental comparison. Appl. Energy 2015, 156, 321–330. [Google Scholar] [CrossRef]
- Okumus, I.; Dinler, A. Current status of wind energy forecasting and a hybrid method for hourly predictions. Energy Convers. Manag. 2016, 123, 362–371. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Qu, Z.X.; Zhang, K.Q.; Mao, W.Q.; Ma, Y.N.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Song, J.J.; Wang, J.Z.; Lu, H.Y. A novel combined model based on advanced optimization algorithm for short-term wind speed forecasting. Appl. Energy 2018, 215, 643–658. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, G.-Q.; Zhou, W.; Du, W.; Lu, K.-D. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers. Manag. 2018, 165, 681–695. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Zhao, M.; Liu, C. Short-term prediction of wind power using EMD and chaotic theory. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 1036–1042. [Google Scholar] [CrossRef]
- Kawauchi, S.; Sugihara, H.; Sasaki, H. Development of very-short-term load forecasting based on chaos theory. Electr. Eng. Jpn. 2004, 148, 55–63. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Yang, Q.; Yan, Z.; Zhang, C. A novel probabilistic wind speed prediction approach using real time refined variational model decomposition and conditional kernel density estimation. Energy Convers. Manag. 2019, 185, 758–773. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Liu, C.; Zhao, M. Wind farm power prediction based on wavelet decomposition and chaotic time series. Expert Syst. Appl. 2011, 38, 11280–11285. [Google Scholar] [CrossRef]
- Harrouni, S. Long term persistence in daily wind speed series using fractal dimension. Int. J. Multiphys. 2016, 7, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Soille, P.; Rivest, J.F. On the validity of fractal dimension measurements in image analysis. J. Vis. Commun. Image Represent. 1996, 7, 217–229. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; Volume 61. [Google Scholar]
- Tutueva, A.V.; Karimov, T.I. Detection of Hidden Oscillations in system without equilibrium. Int. J. Bifurc. Chaos 2021, 31, 20150043. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Grassberger, P. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef] [Green Version]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. Proc. Am. Control Conf. 1995, 128, 1628–1632. [Google Scholar]
- Billings, S.A.; Boaghe, O.M. The Response Spectrum Map, Volterra Series Representations and the Duffing Equation; The Department of Automatic Control & Systems Engineering, The University of Sheffield: Sheffield, UK, 1999. [Google Scholar]

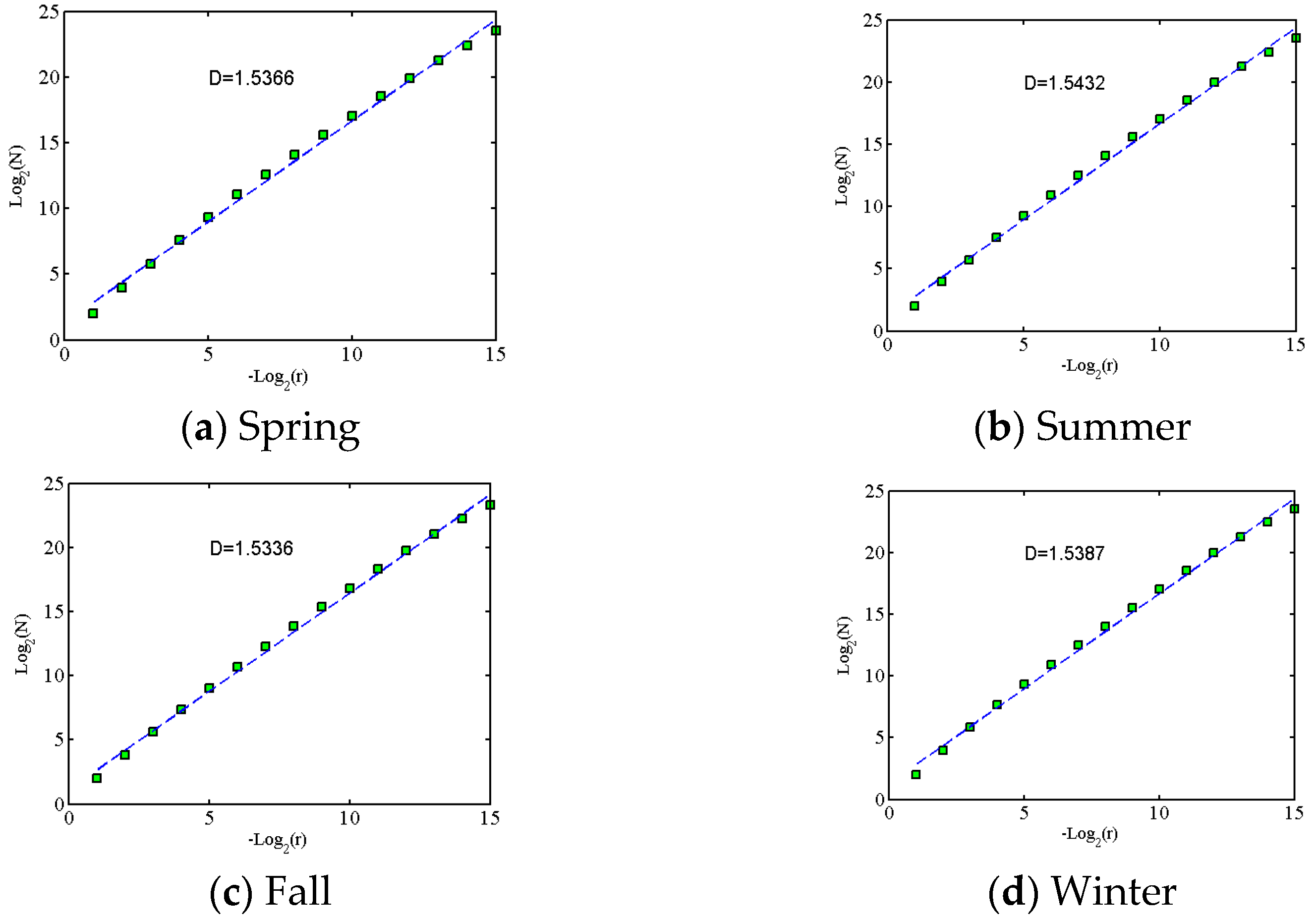
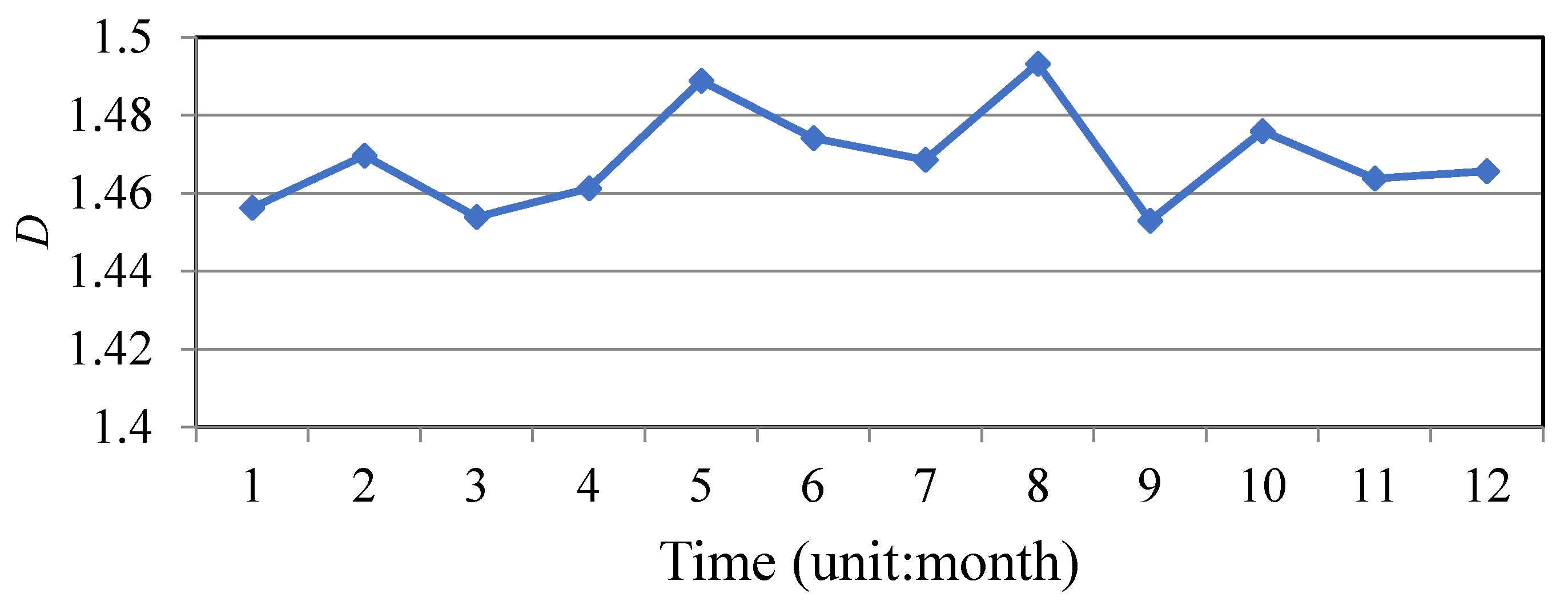
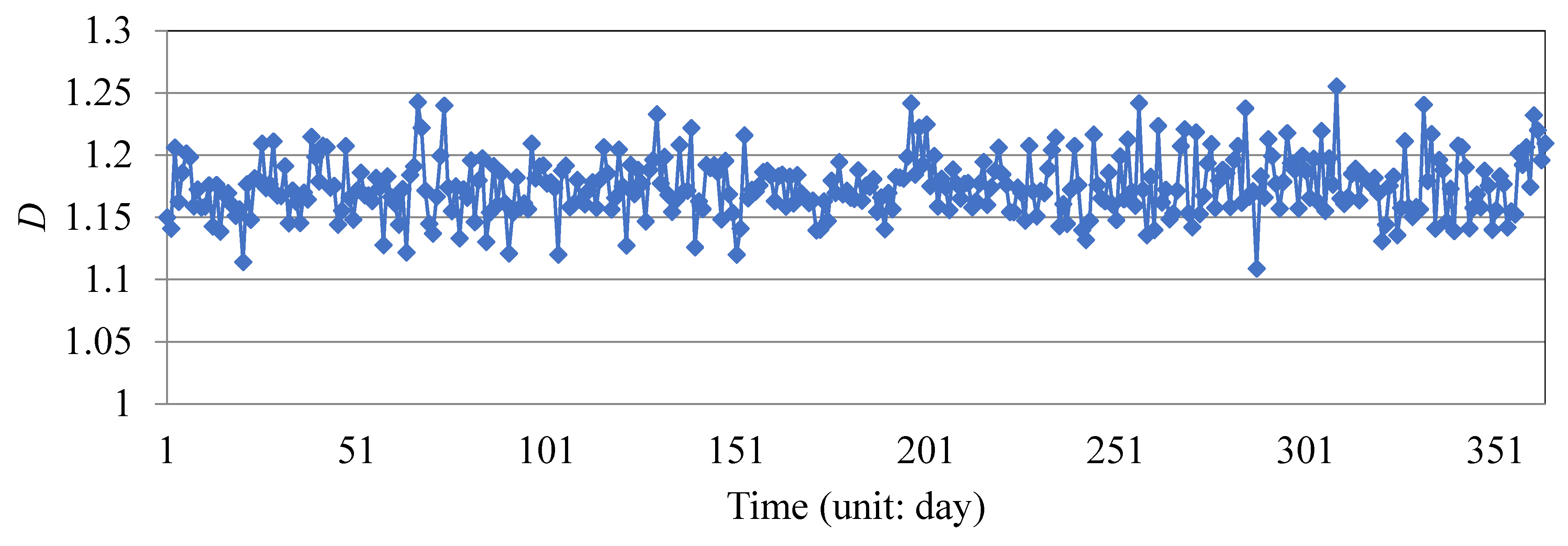


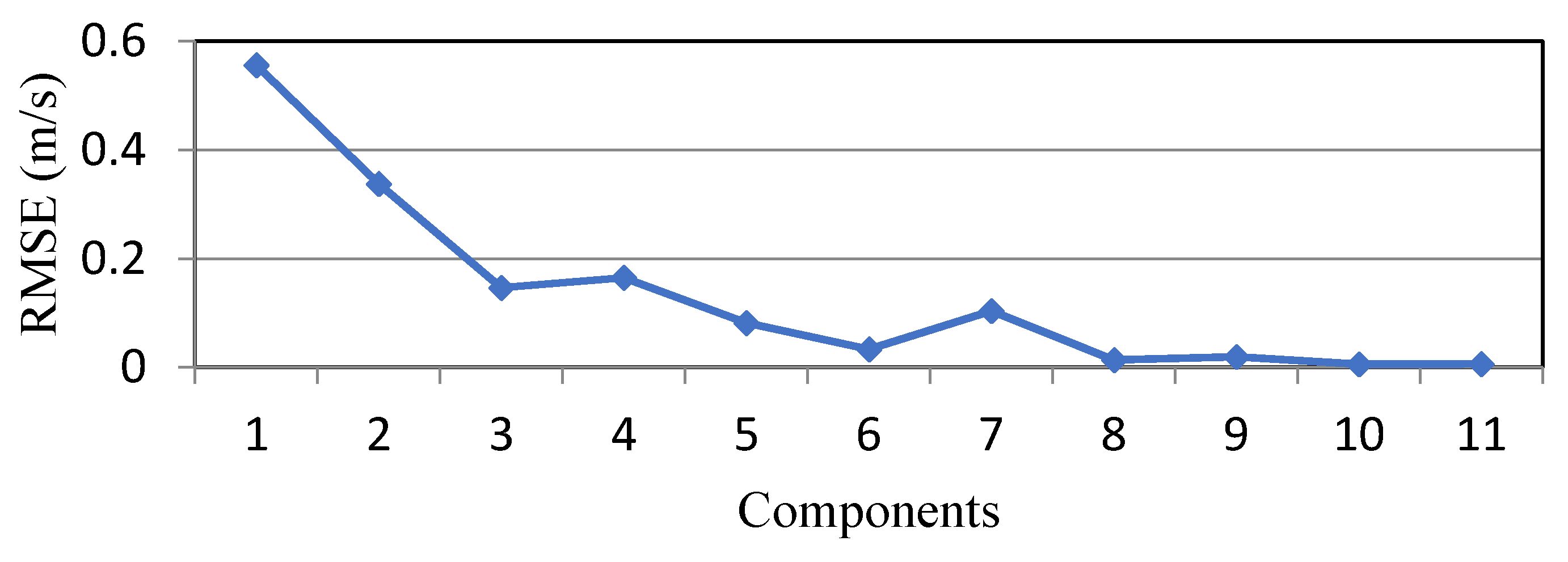
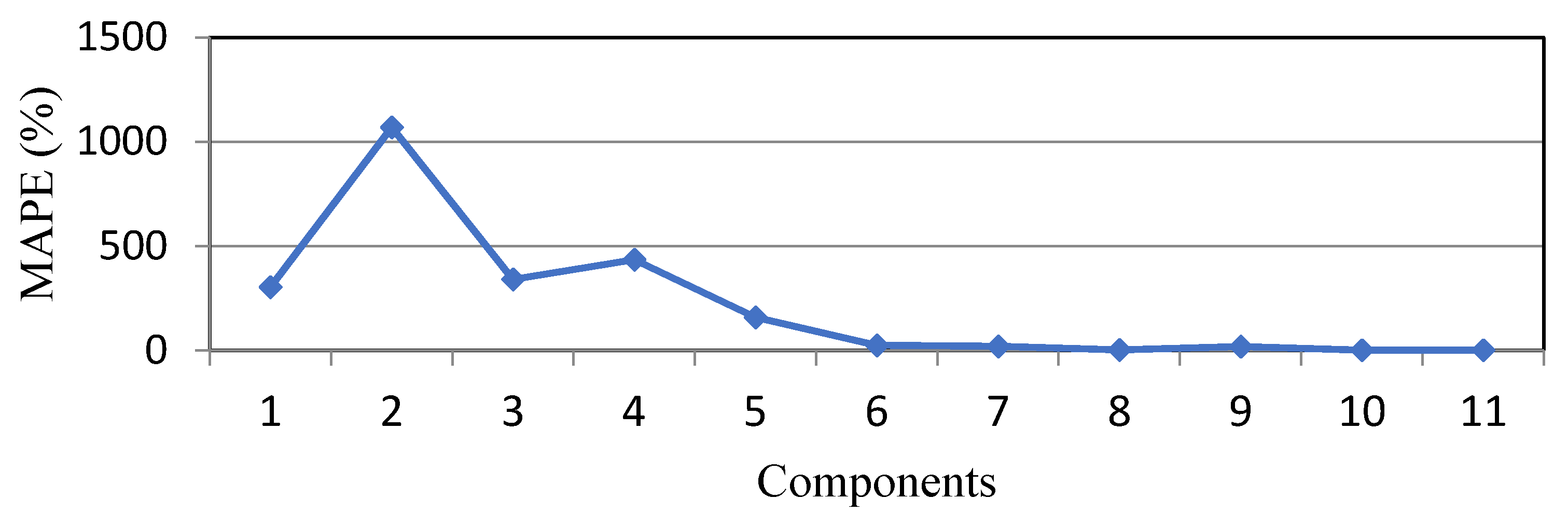
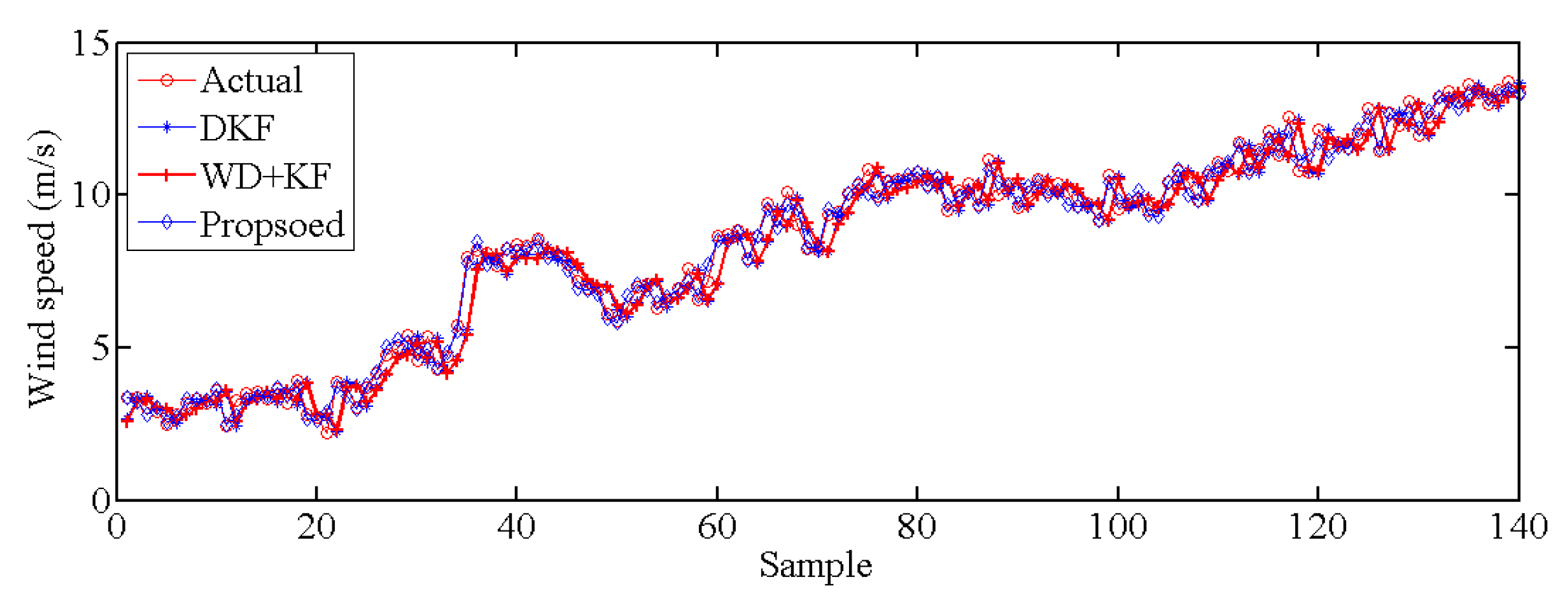
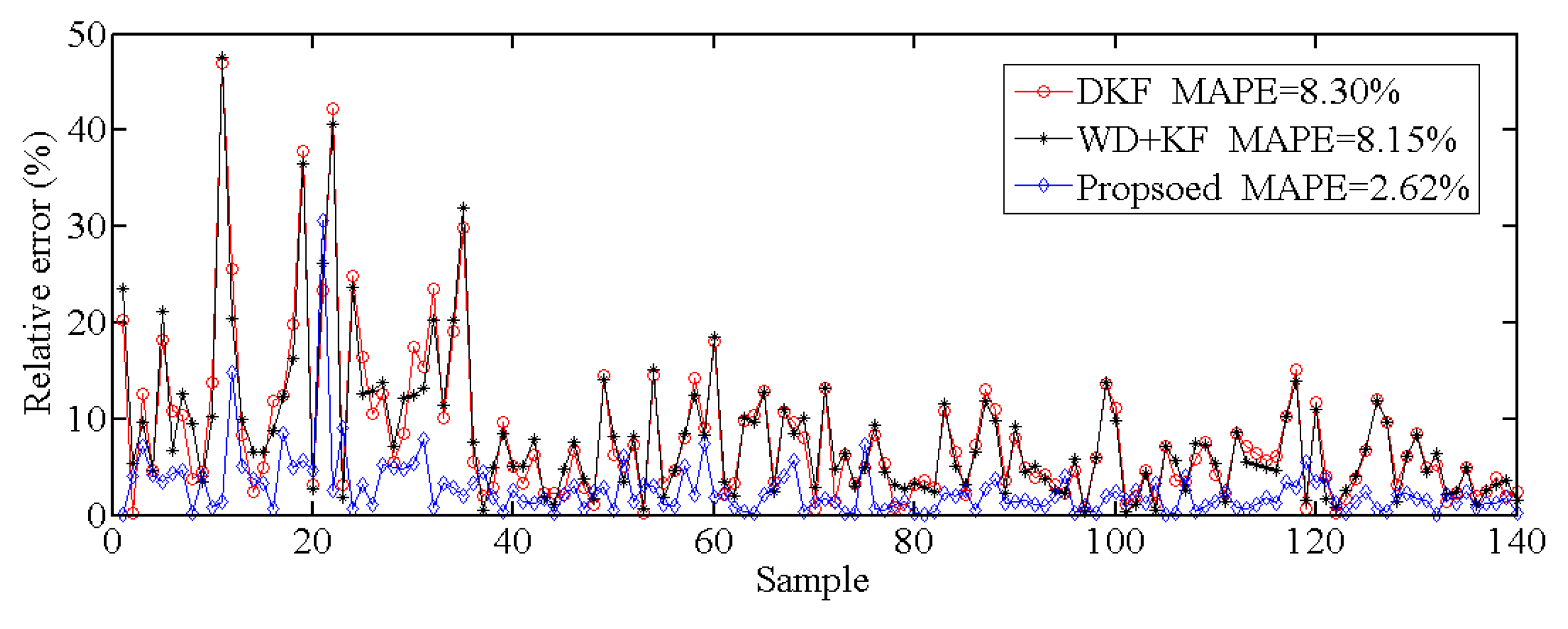
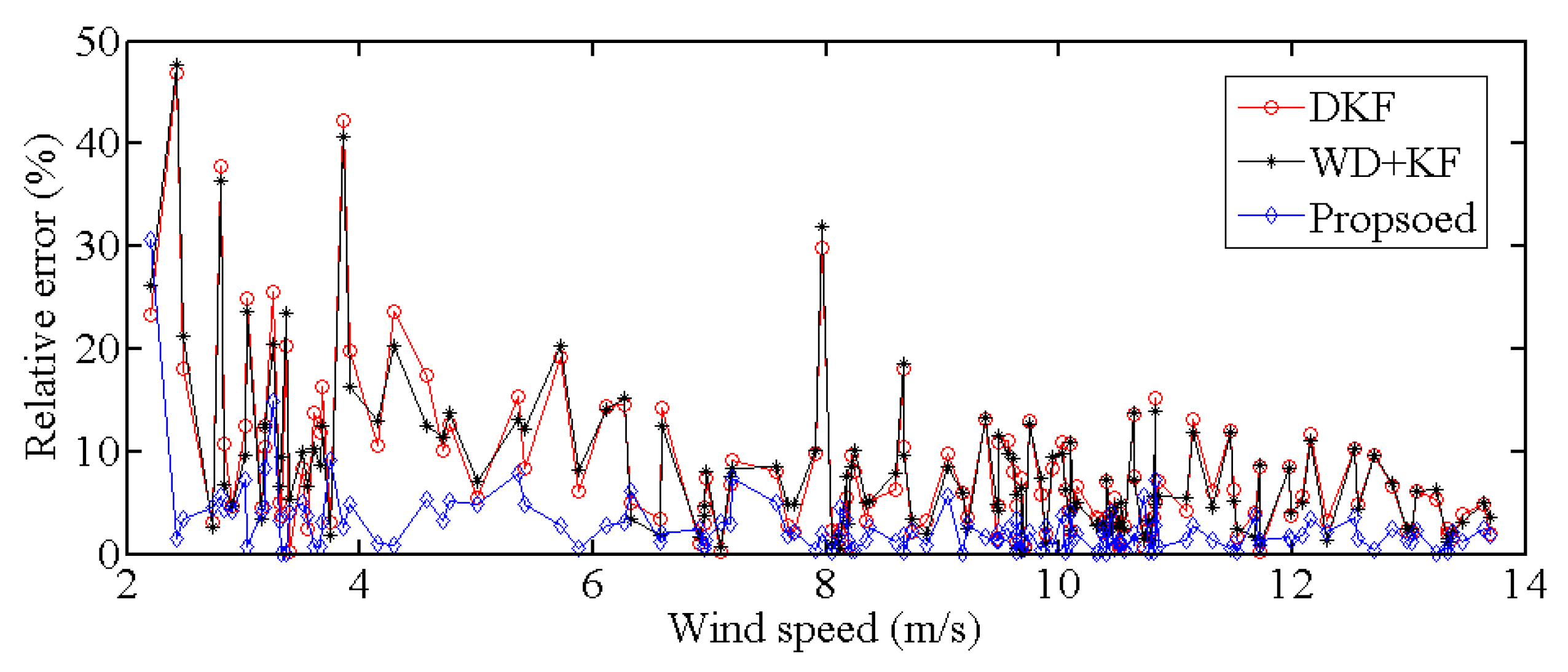

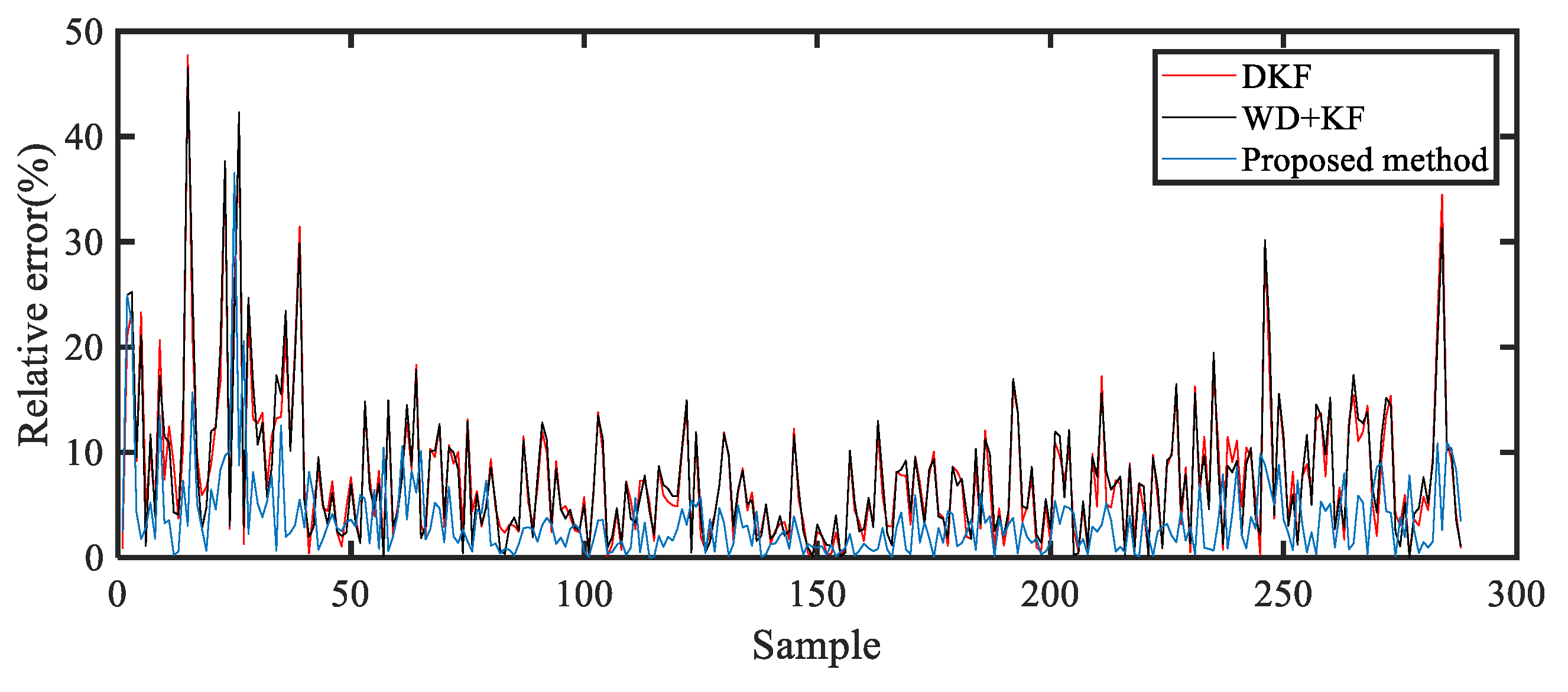


| Prediction Method | MAPE (%) | RMSE (m/s) | MAE (m/s) |
|---|---|---|---|
| DKF | 8.30 | 0.70 | 0.56 |
| WD+KF | 8.15 | 0.65 | 0.46 |
| Proposed | 2.62 | 0.23 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Xia, D.; Dai, L.; Zheng, Q.; Qin, Z. Chaotic Analysis and Prediction of Wind Speed Based on Wavelet Decomposition. Processes 2021, 9, 1793. https://doi.org/10.3390/pr9101793
Lin L, Xia D, Dai L, Zheng Q, Qin Z. Chaotic Analysis and Prediction of Wind Speed Based on Wavelet Decomposition. Processes. 2021; 9(10):1793. https://doi.org/10.3390/pr9101793
Chicago/Turabian StyleLin, Li, Dandan Xia, Liming Dai, Qingsong Zheng, and Zhiqin Qin. 2021. "Chaotic Analysis and Prediction of Wind Speed Based on Wavelet Decomposition" Processes 9, no. 10: 1793. https://doi.org/10.3390/pr9101793
APA StyleLin, L., Xia, D., Dai, L., Zheng, Q., & Qin, Z. (2021). Chaotic Analysis and Prediction of Wind Speed Based on Wavelet Decomposition. Processes, 9(10), 1793. https://doi.org/10.3390/pr9101793






