Abstract
Molecular dynamics (MD) simulations have become increasingly useful in the modern drug development process. In this review, we give a broad overview of the current application possibilities of MD in drug discovery and pharmaceutical development. Starting from the target validation step of the drug development process, we give several examples of how MD studies can give important insights into the dynamics and function of identified drug targets such as sirtuins, RAS proteins, or intrinsically disordered proteins. The role of MD in antibody design is also reviewed. In the lead discovery and lead optimization phases, MD facilitates the evaluation of the binding energetics and kinetics of the ligand-receptor interactions, therefore guiding the choice of the best candidate molecules for further development. The importance of considering the biological lipid bilayer environment in the MD simulations of membrane proteins is also discussed, using G-protein coupled receptors and ion channels as well as the drug-metabolizing cytochrome P450 enzymes as relevant examples. Lastly, we discuss the emerging role of MD simulations in facilitating the pharmaceutical formulation development of drugs and candidate drugs. Specifically, we look at how MD can be used in studying the crystalline and amorphous solids, the stability of amorphous drug or drug-polymer formulations, and drug solubility. Moreover, since nanoparticle drug formulations are of great interest in the field of drug delivery research, different applications of nano-particle simulations are also briefly summarized using multiple recent studies as examples. In the future, the role of MD simulations in facilitating the drug development process is likely to grow substantially with the increasing computer power and advancements in the development of force fields and enhanced MD methodologies.
1. Introduction
The purpose of a computer simulation is to gain insight into the behavior of an actual physical system or process. To achieve that specific objective, a model system is developed that represents or emulates the given physical system. A suitable algorithm subsequently generates a time series or an ensemble of states (“observations”) for the model system. Finally, an analysis is conducted by calculating various system properties from these states (certain properties may also be monitored during a simulation). In the present context, the word “simulation” usually refers to the process of generating states by numerically solving a set of differential equations for the selected degrees of freedom (state variables) of the given model system. Many computed system properties are measured by experiment as well so that an explanation of the observed experimental data is immediately available based on the model system and the simulation results. More importantly, one can also observe behavior that is inaccessible to experiment and test “what-if” scenarios (e.g., mutation studies). As a result, simulation techniques have become invaluable tools for modern research as they complement experimental approaches. With the continuing advance of computing power, such tools will only further increase in importance.
1.1. Classical Molecular Dynamics Simulations
Molecular dynamics (MD) is one such simulation technique [1,2]. It aims at deriving statements about the structural, dynamical, and thermodynamical properties of a molecular system. The latter is typically a biomolecule (solute) such as a protein, an enzyme, or a collection of lipids forming a membrane, immersed in an aqueous solvent (water or electrolyte). In the case of proteins and enzymes, the experimental protein structure as deposited in the Protein Data Bank (PDB) [3] serves as a starting point for MD simulations. If no structure is available, one must resort to modeling (predicting) the structure for which several techniques are available, such as homology or comparative modeling [4]. In atomistic “all-atom” MD (AAMD), the model system consists of a collection of interacting particles represented as atoms, describing both solute and solvent, placed inside a sufficiently large simulation box, where their movements are described by Newton’s laws of motions. An algorithm such as velocity-Verlet or leap-frog [2] is employed to advance over the course of many time steps the state of the model system as a function of time (see Figure 1 for a schematic view of a basic MD algorithm). A single state consists of the combined values of the atoms’ positions and velocities (or momenta). To advance the state, forces acting on particles are computed from a model or empirical potential energy (“force field”), a function of particle positions, which includes all types of “non-bonded” interactions, such as electrostatic and Lennard-Jones forces, but also various types of “bonded” potentials for preserving the structural integrity of the given biomolecular system. The latter include harmonic potentials for maintaining bonds, bond angles, and “improper” dihedrals as well as terms for dihedrals. Some force fields include the Morse potential for a more realistic representation of bonds, while others may account for explicit electronic polarization effects. An extensive discussion of force fields is given by Monticelli and Tieleman [5]. Of note, various force fields have been developed for different types of molecules. In the context of our review, force fields for proteins [5], biological lipids [6], and small molecules [7] are of particular relevance (see Table 1 for examples of current commonly used force fields). Force fields are also employed to compute energies in molecular mechanics (MM) applications [8]. Such simulations are usually conducted under conditions of constant temperature and pressure to mimic laboratory conditions for which special algorithms are available. In addition, to emulate a very large molecular system, several techniques for artificially extending the size of the model system have been developed. The most common one is the periodic boundary condition (PBC). Here, an infinite number of replicas of the central simulation box surrounds the central box. Due to the long-range character of electrostatic interactions, special techniques such as Ewald-based methods are required to include the interactions between the particles in the central box and their replicas. In the course of a simulation, successive states at regular time intervals are stored in a trajectory for later analysis. Typically, in AAMD, the time step is 1–2 fs (1 fs = 10–15 s) and the system size is in the order of tens of thousands of atoms (including solvent). A larger number of software packages for MD of biomolecules are available, for example, GROMACS [9], AMBER [10], NAMD [11], and CHARMM [12].
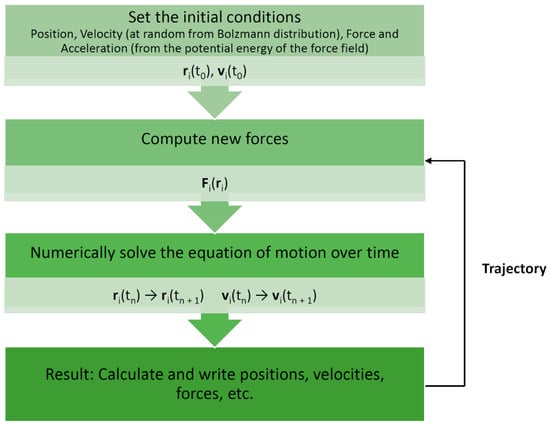
Figure 1.
Basic molecular dynamics simulation algorithm. Each particle moves according to Newton’s second law or the equation of motion, F = ma (where F is the force exerted on the particle, m is its mass, and a is its acceleration under a potential field), such that the particles in the system are captured in the trajectory [1,13]. r—position; v—velocity; t—time.

Table 1.
Examples of commonly used force fields in molecular dynamics simulations.
Early applications of AAMD were concerned with rather simple systems such as liquid argon consisting of just 864 atoms [36] and covered the ps (10−12 s) time scale. The first MD simulation of a biomolecule was achieved by McCammon et al. in 1977; bovine pancreatic trypsin inhibitor (58 residues) was simulated for 9.2 ps [37]. Nowadays, µs (10−6 s) timescale is easily achieved with relatively small proteins [38], wherewith larger systems, this is reachable if state-of-the-art computational power is available [39]. More typically, MD of larger biomolecular systems attain hundreds to thousands of ns (10−9 s). MD excels in focusing on the dynamical aspects of a given protein or enzyme in relation to its function. Applications include, for instance, estimation of affinities ∆bG⊖ (the standard Gibbs free energy of binding) of ligands for proteins using the so-called free energy perturbation (FEP) methods [40], the inclusion of charge fluctuations in constant pH AAMD [41], folding of small proteins [42], and the simulation of ion channels [43]. Additional examples are also listed in the recent reviews by Cavalli and collaborators [44] and Hollingsworth and Dror [45]. Recently, one of the largest atomistic simulations was reported by Rommie Amaro’s group where they simulated an explicitly solvated influenza A viral envelope in a phospholipid bilayer [46], a system of ca. 160 million atoms, for approximately 121 ns. Another study by Jung et al. reported the first atom-scale simulation of an entire gene with a billion atoms [47].
It is worthwhile to stress that MD is meant to explore the configuration space (the set of all values of positions and momenta). In the widely used ligand-protein docking one also needs to sample the configuration space using a similar force field as in MD in order to optimize the location and binding mode (a “pose”) of the ligand on the surface of a given protein (receptor) [48]. However, the sampled configuration space is frequently restricted to a specific region of the protein, while also only specific portions of the protein and/or ligand are allowed to fluctuate (e.g., only the protein’s side chain are displaceable, while the main chain is kept rigid). The outcome of such docking studies is a small set of possible complexes, typically ranked according to the force field employed. Dynamical information is not obtained from ligand-protein docking studies, but some measure for the affinity of the ligand for the protein may be obtained. In fact, the lack of a proper description of systems’ true dynamics is one of the biggest caveats of docking [49]. Therefore, frequently after selecting one of the complexes (usually the highest-ranked complex), an MD simulation is conducted to explore the complex in much greater detail [50].
1.2. Faster and Longer without Atomistic Details: Coarse-Grained Simulations
While the advancements of the “traditional” AAMD have been very impressive, the limited length (nm) and time scales (ns to µs) attainable in AAMD still poses a severe limitation when studying molecular processes that occur on much longer time scales (e.g., protein (un)folding, protein–membrane association) and/or require much larger length scales (e.g., very large protein tertiary structure or protein–membrane systems). In standard AAMD, atoms serve as particles. In coarse-grained MD (CGMD), 4 to 6 atoms (or more) are grouped together to form “beads” that serve as the particles of the model system. A similar procedure may be applied to the solvent as well [51]. For instance, in the Martini force field [52], initially designed for studying biological membranes modeled as lipid bilayers at the coarse-grained level, four water molecules form a single water bead. As a result of such coarse-graining techniques, the number of particles is significantly reduced in comparison to AAMD of the same system, while the interaction potential energy surface is also much smoother so that a much longer time and larger length scales are attainable by CGMD, but at the expense of atomistic details. It otherwise relies on similar algorithms and associated techniques such as PBC in AAMD, with time steps ranging between 20 to 60 fs. The Martini force field, one of the first force fields for CGMD, has seen important applications and developments since its first installment and is now also employed for the analysis of lipid membrane properties, protein–lipid interactions, oligomerization of membrane proteins, the self-assembly of soluble peptides and proteins, the prediction of protein conformational changes, binding and pore-formation in membranes [53,54]. A recent and far more elaborate overview of applications according to the Martini model is also given by Marrink and Tieleman [55]. There exist also more extreme versions of coarse-graining. It is quite possible and even desirable in some applications to completely remove the atomistic details of the solvent and replace it with a structureless polarizable continuum. This approach is commonly employed for the prediction of acid dissociation constants of titrating sites in proteins as well as for the calculation of affinities of ligands for proteins [56].
1.3. Zooming into the Details of Chemical Reactions: Quantum Mechanics Simulations
While MD is extremely useful for the investigation of molecular properties at a longer time and larger length scales, it cannot be used to study the details of chemical reactions in the active site of enzymes, simply because current MD techniques cannot properly handle bond-breaking events. The MM force fields commonly in use for MD enforce links between specific particles to ensure that they remain together to prevent a complete destabilization of the molecular structure. Consequently, changes in the electronic structure are not included in MD simulations. That, however, can be accounted for with quantum mechanics (QM). A typical QM calculation solves the (time-independent) wave equation to estimate single point energies, bond distances and angles, partial charges, spectroscopic properties, various thermodynamic properties, interaction parameters (for instance for use in classical force fields employed in MD), and so forth, thus providing a very detailed description of the given chemical system. This can be completed for any given atom configuration. Because QM is computationally rather demanding, it is not possible and actually not even necessary to treat the full molecular system (i.e., protein and solvent) at the quantum level [57]. Commonly, the enzyme system is divided into a quantum motif (QM part) or region that includes the active site of a given enzyme plus a relevant portion of the substrate or ligand, while the rest of the system including the solvent is considered as part of a classical environment (MM part) adhering to a force field like those in AAMD. The QM part should include all relevant residues and chemical groups that are expected to play a role in the (proposed) reaction mechanism. Failing to do so may result in erroneous statements regarding the reaction mechanism and the binding mode of the substrate. It is also useful to repeat the calculations with different sizes of the QM motif, excluding a particular residue to discover the role of that residue in the mechanism. Numerous applications can be found in the literature on the use of QM/MM for studying the details of enzyme-catalyzed chemical reactions [58]. Relevant to such studies is the identification of the correct protonation states of titrating sites, especially of those residues or chemical groups directly involved in the reaction [59,60,61].
In this review article, we aim to give a broad overview of the current and emerging applications of MD in drug discovery and design-related processes as well as in pharmaceutical formulation/product development. The review introduces the basic concepts of MD, describes the principles of various commonly used methods and approaches in relevant contexts, as well as illustrates many practical aspects and limitations of MD with respect to the particular tasks at hand. However, detailed theoretical accounts of various methodologies are beyond the scope of the review. We hope that this piece of work could serve as an introductory synopsis to many scientists that have no (or little) experience in MD and wish to combine their experimental research with appropriate computations (either in collaboration with computational scientists or if attracted to the method, by themselves). In the following paragraphs, we will discuss how MD can help explore the dynamics and function of different drug targets or evaluate drug-target interactions. We will also look at the intricacies of simulating different biological systems, such as membrane proteins or intrinsically disordered proteins. Moreover, the growing role of MD in the field of computational pharmaceutics is analyzed in light of several examples. Many focused reviews have been recently published on the application of MD in drug discovery [44,45,62,63,64,65,66]. Some recent reviews can also be found on drug formulation and drug delivery aspects, e.g., [67,68,69,70].
2. Molecular Dynamics in Drug Discovery
2.1. Exploring the Dynamics and Function of Drug Targets
Contemporary drug discovery processes start commonly with identifying and validating a biologically relevant target that can be modulated with drug molecules to prevent or cure a disease or alleviate symptoms of sickness (Figure 2). Drug targets are often different proteins, such as receptors or enzymes, but may also be DNA or RNA molecules. Protein conformation is one of the biggest approximations in ligand design because proteins are dynamic and can undergo various conformational changes. Even minor conformational changes that involve movements of residue side chains can affect the complementarity between the ligand and the binding site of a protein. Since protein flexibility crucially affects the range of possible target conformational states for ligand binding, MD simulations can provide important information on the dynamic character of the target with regard to drug design.
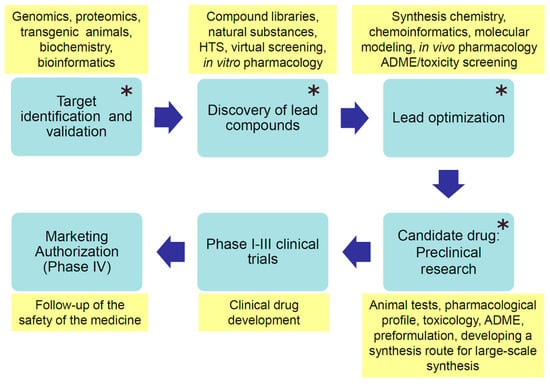
Figure 2.
Phases of modern drug development (blue boxes). The yellow boxes contain characteristic actions, methods, or tools used in the particular development phase. ADME—absorption, distribution, metabolism, and excretion; main steps of a drug in the body. Molecular dynamics simulations can be applied to facilitate research in the phases denoted with a star (*).
The following paragraphs present studies of selected target proteins or protein groups that highlight the flexible nature of proteins. MD simulations have been necessary for studying these proteins’ dynamics and function and understanding how they bind with small molecules or other proteins. Specifically, sirtuins have several ligand-binding sites, and understanding their dynamics may give insights into the development of selective inhibitors or activators. Additionally, one of the ‘Holy Grails’ of cancer drug discovery is direct inhibition of oncogenic RAS proteins [71]. RAS proteins are small, dynamic, and difficult to drug. Therefore, a proper understanding of their dynamics may provide the necessary key for drugging them. The other two examples include a group of highly flexible, intrinsically disordered proteins, and a group of immunological proteins that are currently being actively investigated and developed as biological drugs, i.e., antibodies. Both protein groups play an important role in many therapeutically significant protein-protein interactions. Especially MD simulations of proteins belonging to the former group need improved methodologies to obtain meaningful results.
2.1.1. Ligand-Binding Dynamics of Sirtuins—In Search of Therapeutic Regulators
Sirtuins are a family of proteins that function as nicotinamide adenine dinucleotide (NAD+)-dependent deacetylases. In mammals, there exist seven sirtuin proteins (SIRT1–7) that have histone and non-histone targets. Sirtuins have diverged tissue distribution and subcellular localization; nuclear (SIRT1/6/7), mitochondrial (SIRT3/4/5), and cytosolic (SIRT2) [72]. Sirtuins have an important role in gene silencing and expression, in cell metabolism, and tumorigenesis [73]. The function of sirtuins depends on the physiological conditions and tissues, and they can either stimulate or prevent signaling pathways [74].
The structure of sirtuins contains a conserved catalytic core of about 275 amino acids. The catalytic core is formed by a typical Rossmann fold domain that binds NAD+ and a zinc-binding domain (Figure 3). There are four flexible loops connecting these two domains. These loops form a tunnel in which the substrate interacts with NAD+ in a deacetylation reaction. The binding site of NAD+ is divided into three pockets A–C: The ADP ribose moiety binds in the A and B pocket (residues Asn286, Glu288, Arg97, Ala85, Gln167, His187 in SIRT2) and nicotinamide moiety in the C pocket (residues Ala33, Gly34, Thr37, Phe44, and Asp43 in SIRT2). Inhibitors often bind into the C-pocket. In addition, sirtuins have N- and C-terminal extensions of variable length that can affect the enzymes’ function as these terminals are targets to posttranslational modifications. Over two decades, several compounds have been developed to bind into the pockets A-C and to regulate the function of sirtuins (reviewed in e.g., [75]). However, there is still no approved sirtuin regulator/inhibitor in the clinic. One of the challenges has been the flexible nature of the substrate and cofactor-binding sites.
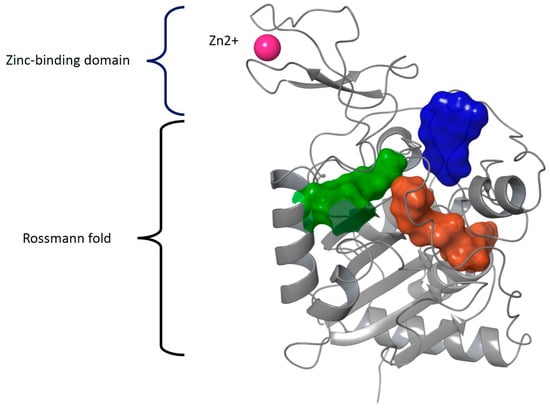
Figure 3.
The structural domains forming the catalytic core of all sirtuins. The large, nucleotide-binding Rossmann fold domain comprises a six-stranded beta-sheet sandwiched between several alpha-helices, whereas the smaller zinc-binding domain is formed by four cysteine residues coordinating the Zn2+ cation (PDB IDs 3GLT and 6QCD). The binding pockets of the substrate (green), co-factor (pockets A and B, both in brown), and inhibitor (pocket C, blue) in SIRT3 are surrounded by flexible loops.
For many years, there was no crystal structure of human sirtuins with any co-crystallized regulator available. The binding site of putative regulators in sirtuins is mostly formed by flexible loops and, thus, the conformational state of these enzymes crucially affects the prediction of binding modes of small-molecule ligands. Therefore, MD simulations have been applied to generate different sirtuin conformers to explore the possible ligand-binding conformations. MD was first used for SIRT2 in the year 2008 to generate multiple conformations for an ensemble docking approach [76]. In another study, a set of short (from 400 ps to 10 ns) MD runs were performed for SIRT2 with GROMACS 3.3.1 employing the GROMOS96 force field [77]. The compounds under investigation were then docked using Gold 3.2 [78] to each SIRT2 snapshot structure in the ensemble. Several binding modes were observed for the SIRT2 inhibitors with an N-(3-phenylpropenoyl)-glycine tryptamide backbone. Interestingly, the MD simulations suggested an extended binding area of C pocket for the SIRT2 inhibitors, which later was experimentally observed for a highly selective SIRT2 inhibitor, SirReal2 [79].
Thereafter, several MD studies of SIRT2 have been carried out by Sakkiah and coworkers [80,81,82,83] using GROMACS with either GROMOS96 or AMBER03 force field [84]. In one study, they performed 5-ns MD simulations for the SIRT2-sirtinol complex and the apo structure of SIRT2 to identify alternative binding pocket conformations for the enzyme [80]. The SIRT2 conformations from the MD runs were clustered and three representative structures were selected for receptor-based pharmacophore modeling in order to screen for novel SIRT2 inhibitors. Their other study on the conformational changes of the SIRT2 substrate and inhibitor binding sites revealed the dynamic role of Phe96 in binding the inhibitor in SIRT2 [81]. They further investigated the role of the inhibitor-binding residues by simulating the docked complexes of five known inhibitors with SIRT2 for 20 ns [82]. The stability of the complexes was evaluated by monitoring the root-mean-square deviation (RMSD) of the protein Cα atoms and the root-mean-square fluctuation (RMSF) of the protein residues as well as the inhibitor-protein hydrogen bonding interactions along the simulation trajectory. All compounds had established favorable binding interactions and stable binding poses after about 10-ns simulation. The detailed analysis of the interactions revealed that hydrogen bonds formed between the inhibitors and especially Arg97 and Gln167 are important for the inhibition of SIRT2 activity. Further MD simulations by the same research group suggested crucial conformational differences between the wild-type SIRT2 and two mutants, thus providing insight into the design of more potent SIRT2 inhibitors [83].
In an attempt to understand more about the role of C- and N-terminals of sirtuins, MD simulations were carried out to explore the terminal regions’ effect on the enzymatic activity of SIRT2 [85]. The results of the simulations performed with GROMACS 4.5.5 and the all-atom AMBER ff99SB-ILDN force field [86] suggest that the C-terminal region of SIRT2 can partially occlude the NAD+ binding pocket or stabilize the NAD+ in a non-productive state, thus functioning as an autoinhibitory region.
MD studies have also been applied to study the dynamics of other sirtuins than SIRT2. For example, SIRT1 simulations have been utilized to screen for novel inhibitors and to study the interactions between ligands and the protein [87,88]. In another study, the binding modes of 2-anilinobenzamide derivatives in SIRT1/2/3 were investigated by 30-ns MD simulations with the AMBER 11.0 simulation package using the ff03.r1 [84] and ff99SB [14] force fields to explain the isoform selectivity of the compounds [89]. According to the RMSD of the ligand-bound structures, the dynamic stability was achieved at 20 ns. Furthermore, Sinha and coworkers [90] studied the stability of sirtuin-inhibitor complexes with the high-speed simulation software Desmond [91] employing the OPLS2005 [17] force field. After carrying out a virtual screening of plant-derived compounds against SIRT1-7 by docking and scoring, they identified sulforaphane, kaempferol, and apigenin as hits. Multiple 20-ns MD simulations were performed for the top-scored poses of these compounds in the respective sirtuin structures. The results suggested that sulforaphane bound stably in SIRT1 and SIRT5, kaempferol in SIRT3 and apigenin in SIRT6, and the critical ligand-protein interactions remained throughout the simulations. In another recent study [92], natural compounds were identified as potential SIRT1 activators. Stable binding of mulberrin, quinine, quinidine, gartanin, and nicotinamide in an allosteric SIRT1 site (i.e., other than the catalytic site) was demonstrated in 50-ns MD simulations with AMBER. These ligands did not disrupt the functionally important hydrogen bonds between Arg234 (allosteric site) and Asp475, His473, or Val459 (catalytic site) of SIRT1, which was concluded to be consistent with their experimentally shown ability to activate the enzyme.
There is only little experimental information on the structure of SIRT7. A recently published study reported a homology model of SIRT7 [93]. Three 1-μs long MD simulations with GROMACS (AMBER03 force field) were used to investigate the stability and dynamics of the model structure. The simulations showed that the model of SIRT7 in complex with NAD+ and acetyl-lysine was stable, suggesting that the model was built properly. In addition, the simulations suggest that the N-terminus of SIRT7 may play an important role in assisting to hold the substrate in the active site during the catalytic reaction.
Additionally, the co-factor binding to sirtuins has been studied with MD simulations. Desmond together with the OPLS3 force field [25] was employed to simulate SIRT1 and SIRT3 in complex with either NAD+ or NADH and an acetyl-lysine substrate for 250–500 ns [94]. The simulations suggested an opening of the enzyme structure and an alternative binding site for the dihydropyridyl moiety of NADH instead of the C pocket. Furthermore, two persistent hydrogen bonds were observed between NAD+ and Ile347/230 and Asp-348/231 in SIRT1/3 whereas the corresponding bonds were missing if NADH was bound.
Our case of sirtuins exemplifies that protein flexibility is important to take into consideration in designing ligands that target dynamic binding sites such as that in sirtuins. Although current flexible docking approaches can take into consideration some features of the target protein flexibility, MD is clearly a useful method for studying not only protein flexibility affecting ligand-binding but also larger structural arrangements in dynamic drug targets. Our next case further highlights how understanding protein dynamics can be a key to facilitate the design of potent therapeutic compounds against highly dynamic drug targets such as RAS proteins.
2.1.2. RAS—Uncovering the Conformational Dynamics of a Challenging Anticancer Drug Target
More than 150 members belong to the Ras superfamily of small guanosine triphosphatases (GTPases) [95]. The subgroup of the Ras family comprises 36 proteins, including the oncogenes HRAS, KRAS, and NRAS. As KRAS may undergo alternative splicing, these three RAS genes encode four proteins: HRAS, KRAS4A, KRAS4B, and NRAS (referred to as RAS from now on). RAS proteins share high sequence similarity and mainly differ in their membrane anchoring hypervariable region (HVR) [96]. GTPases, including RAS proteins, have a built-in switch mechanism that allows the protein to adopt an active conformation, capable of binding effector proteins when GTP is bound [97]. Thus, RAS activity is controlled by the bound nucleotide, GDP, or GTP. The nucleotide exchange from GDP to GTP, i.e., RAS activation is facilitated by guanine exchange factors (GEFs) [98,99]. Inactivation of RAS occurs upon GTP hydrolysis to GDP. RAS bears low intrinsic hydrolytic activity, which is greatly enhanced by GTPase activating proteins (GAPs) [98,99]. For a more comprehensive picture of RAS biology, the reader is referred to review [100].
Hyperactivation in RAS signaling is related to diseases, especially to cancer [100]. Altogether, RAS mutations appear in around 17% of all human cancers, whereas KRAS mutations contribute to the majority (69%) [101]. KRAS mutations are frequently observed in solid tumors of the pancreas, colon, and lung; NRAS in melanomas; HRAS in head and neck as well as in bladder carcinomas. RAS isoforms display different mutation preferences; for instance, KRAS mutations appear most often in Gly12 (81%) whereas NRAS in Gln61 (62%). Not only are RAS isoforms different [102,103], but also oncogenic mutants of the same isoform even at the same position are dissimilar (e.g., KRAS G12D vs. KRAS G12R) [104,105,106,107,108]. Due to their major role in cancer, RAS proteins are highly attractable drug targets and, thus, the focus of major drug discovery efforts [71].
RAS related research has been intense already for several decades since the discovery of these oncogenes in the early 1980s [109]. However, these small GTPases are difficult-to-drug and previously, were considered as undruggable targets [71]. The reason for this is that, first, there is no obvious druggable small-molecule binding pocket in RAS. A pocket beneath the switch-II was revealed only after G12C-targeting covalent compounds were disclosed [110]. Of note, the existence of this pocket (as druggable) was not evident from the available crystal structures at the time. Since then, potential pockets on the effector protein binding interface have been described [111,112,113,114]. Second, RAS proteins are active at the membrane, which plays a significant role in their function [115]. Third, a major obstacle in drugging RAS is its highly dynamic character (Figure 4). These difficulties related to targeting RAS, together with the discrepancy among the oncogenic mutants, clearly highlight the need for a better understanding of these oncoproteins. To this end, mastering RAS conformational dynamics comes into play.
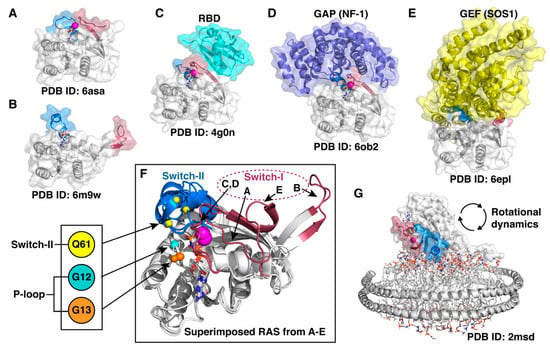
Figure 4.
RAS displays remarkable conformational flexibility and adaptability. (A) State 1 conformation of RAS, also known as an open state [116]. (B) Fully open switch-I conformation that exemplifies the high intrinsic capability of the switch mobility [117]. (C) RAS appears in a closed conformation (also known as state 2) in complex with effector proteins; here demonstrated by a complex of HRAS with RBD (RAS binding domain) of Raf kinase [118]. (D) A closed conformation of RAS is also observed in a GAP–RAS complex [119]. (E) GDP is displaced from RAS upon binding of GEF that binds to an open switch-I RAS conformation and introduces an α-helix into the nucleotide-binding site [120]. (F) Superimposed RAS structures from (A–E) highlight the switch dynamics. Oncogenic mutation hotspot locations (Cα-atoms) are indicated with small spheres. (G) NMR data-driven model of RAS on a lipid nanodisc [121]. In all (A–G): Switch-I (residues 30–40) region is highlighted with red and switch-II (58–72) with blue; Mg2+-ion is displayed as a magenta sphere; the bound nucleotide is shown in sticks.
In order to adopt all potential binding conformations with various effector proteins and with its regulators, RAS needs to be highly dynamic, especially on the switch regions (Figure 4). Even though recent crystal structures have demonstrated multiple conformational states of RAS, in all crystal structures of KRAS, the switch regions, when not disordered, are stabilized by crystal contacts [122]. Therefore, the structural data is unable to fully describe the dynamics of the switches. To capture the dynamics of these cryptic switches, which is beyond the currently available experimental methods, MD simulations can be utilized [123].
Recently, we conducted a comprehensive analysis of KRAS G domain (excluding the HVR) dynamics by classical all-atom MD simulations, including wild-type KRAS and all G12 missense mutants (G12A, G12C, G12D, G12R, G12S, G12V) bound to both nucleotides GDP and GTP [124]. Perhaps unsurprisingly, with an aggregate of 170 μs simulation data, we observed highly dynamic behavior in the switch regions. Interestingly, principal component analysis (PCA) not only highlighted differences among GDP and GTP bound systems but also revealed unique profiles for each mutant. Finally, by utilizing Markov state modeling (MSM), as reviewed in [125], we were able to capture discrepancy among GTP-bound G12D, G12R, G12V, and wild-type KRAS in their long-timescale dynamics. Each system populated MSM derived metastable states differently. We anticipated that the shift in protein dynamics, occurring especially in switch regions, may lead to modulated KRAS mediated signal transduction among the mutants, as was demonstrated before between wild-type HRAS and G12V [126]. Indeed, it was later confirmed that G12R mutant, for which MSM revealed a unique profile, exhibits different effector protein binding compared to G12D; it is defective for interaction with PI3Kα [108]. Our results demonstrated that a G12 mutation located in the P-loop (Figure 4F) is capable of shifting KRAS’ dynamics in distant regions of the protein that are responsible for effector protein binding [124]. How is this possible as no evident direct interactions from this position to switches were observed in the simulations? A putative explanation is that the shift in the dynamics will occur via a hydrophobic interaction network. Through this network, mutant KRAS may alter the protein dynamics in an allosteric manner, inflicting changes in distant sites of the protein. In this interaction network, hydrophobic hubs (displaying more than three hydrophobic interactions) include the residues V14 and A146, which when mutated are associated with altered RAS dynamics [106,127]. In another study, MD simulations revealed highly dynamic characteristics for the switches even when there exists a covalent inhibitor beneath the switch-II [128]. Importantly, the inhibitor AMG 510 appeared extremely stable regardless of the switch movements. These open conformations and high flexibility of the switches that were revealed by the simulations are not observed in the crystal structure (most likely due to the crystal packing effects) [129].
On top of the convoluted switch dynamics, another layer of complexity in KRAS dynamics exists: RAS rotational dynamics on the membrane (Figure 4G). On artificial lipid nanodiscs, monomeric KRAS was shown to exist in different configurations, named occluded and exposed, where the effector protein interaction-surface-forming switch regions are occluded or exposed to RAS effectors [121]. The rotational dynamics of KRAS were captured in single 20 μs MD simulations of KRAS mutants G12D, G12V, and Q61H, where three distinct major orientations of RAS were observed [130,131]. Recently, impressive 1.45 ms MD simulations (290 individual simulations of 5 μs) were conducted to further study dynamic orientations of wild-type KRAS4B at the membrane with different lipid compositions [39]. Still an unclear issue, however, is the relevant oligomerization state of KRAS at the membrane. It may exist in monomeric, dimeric, trimeric, or a higher oligomeric state [132,133,134,135,136]. Overall, small GTPase proteins’ rotational and translational dynamics on the membrane, which has a substantial influence on RAS oligomerization, is not well understood [137]. Importantly, this should not be neglected as RAS dimerization may have an important role in oncogenicity and drug therapy efficacy [138]. Approaches to obtain a better understanding of RAS signaling on the membrane are ongoing, and for instance, a structural model of RAS–RAF signalosome was recently reported by Shaw et al. [139]. For further information on RAS-related MD simulations and dynamics, the reader is referred to reviews [122,140,141].
Taken together, MD simulations have uncovered RAS conformational dynamics at the atomic level and provided further insights into RAS biology. Conformational states derived from MD simulations, which are not captured by experimental methods, could be utilized in RAS targeted drug discovery. Finally, understanding RAS dynamics may be a guide in deciphering mutant RAS functionality and point out potential vulnerabilities of these oncoproteins at the atomic level, which could be targeted directly or indirectly.
In the next section, we will be introducing drug targets of the future, a group of extremely flexible proteins whose dynamics may be investigated with MD simulations to complement the data derived with various experimental approaches.
2.1.3. Extremely Challenging Targets—Intrinsically Disordered Proteins
Intrinsically disordered proteins (IDPs) are the type of proteins that in physiological conditions lack a stable tertiary structural arrangement and instead exist as conformational ensembles. Apart from fully disordered proteins, many folded proteins contain intrinsically disordered regions (IDPRs). IDPs are associated with multifunctional roles as they can undergo conformational arrangements to different folds, depending on the particular binding partner [142]. The formation of ‘fuzzy’ complexes, where the disorder is maintained upon binding to the partner, has also been shown to be important in many biological processes [143]. The structural characteristics and the individual state of conformation in such proteins are dependent upon the type of amino acids forming the disordered segments [142,144,145]. There are many web-servers and computational tools available for accurate prediction of IDPs and their molecular functions (comprehensively reviewed in [146]). In addition, there are databases that store experimentally determined IDPs and IDPRs, e.g., DisProt [147].
The abundance of IDPs in the human genome, their importance in biological functions such as cellular signaling, and their involvement in various pathological conditions make them an attractive target for drug design [148]. Although the lack of a defined tertiary structure poses a challenge for rational structure-based drug design strategies, there is evidence that small molecules and peptides can be designed to target the protein-protein interactions of IDPs with their ordered binding partners (reviewed in [148,149]). Experimental techniques such as NMR spectroscopy or small-angle X-ray scattering (SAXS) can be used to characterize the conformational ensembles of IDPs although the quantitative data on the dynamic processes can be difficult to interpret regarding the unambiguously identified motions [150]. On the other hand, MD simulations suit perfectly for describing atomic motions and, thus, MD-based approaches can be valuable in studying the conformational dynamics of IDPs and their binding mechanisms to the partner proteins. However, there are some challenges that need to be addressed [149].
First, the extremely large number of degrees of freedom present in IDPs poses a challenge for proper sampling of the conformational space of the protein. Therefore, MD algorithms with enhanced sampling techniques such as replica exchange molecular dynamics (REMD) [151] (see Figure 5) are often used to efficiently overcome energy barriers in the IDP conformational landscape.
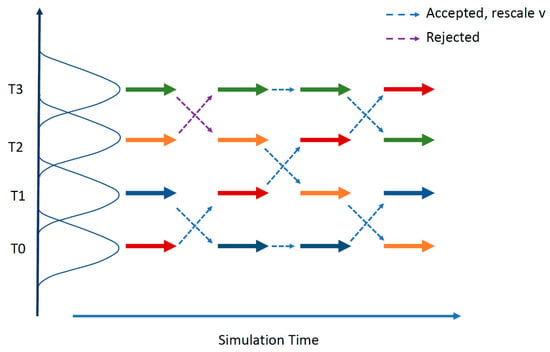
Figure 5.
The replica exchange molecular dynamics (REMD) method. REMD combines multiple MD simulations with the Monte-Carlo-based replica exchange algorithm [152,153]. Several replicas of the same system are simulated in parallel at different temperatures. At specified intervals, replicas with neighboring temperatures are exchanged with the Boltzmann weighted Metropolis criterion. After a successful temperature exchange, velocities are rescaled to those expected in the new temperature condition. Successful swapping between replicas happens when there is some overlap between the potential energy of neighboring replicas over the course of a simulation.
Second, when simulating IDPs, it is crucial is to pay attention to the selection of the applied force field since most of the available protein force fields have been developed for proteins that have stable folded structures. Thus, general protein force fields tend to overpopulate certain secondary structures or compact, collapsed structures over the extended ones [154]. Experimental structural data have been used to guide the development of novel or updated force fields for both all-atom and coarse-grained simulations, such as FF14IDPSFF [155], FF14IDP [156], FF99IDP [157], A99SB-ILDN [158], CHARMM36 IDPSFF [159], and AWSEM-IDP [160]. Third, the applied solvent model needs to be carefully selected as in IDPs, the solvation effect plays a greater role. Novel solvent models such as TIP4P-D [161] facilitate the protein-water interactions and disfavor collapsed protein structures. However, depending on the studied IDP, such models may underestimate the transient tendency of an IDP/IDPR for folded structures, in which case a traditional water model could give better results [162]. Table 2 lists some examples of MD simulation studies of biologically relevant IDPs employing different force fields and solvent models.

Table 2.
Molecular dynamics simulation of intrinsically disordered proteins (IDPs) with various force fields and solvent models.
From the studies listed in Table 2, it is worth discussing in more detail how Jin et al. [163] mapped the conformational ensemble of the unbound disordered dimerization domain of the transcription factor c-Myc using REMD. Subsequent (conventional) MD simulations of the inhibitor-bound c-Myc domain gave the authors valuable insight into the constantly changing binding interactions and binding sites of the inhibitor at c-Myc (the conformational ensembles looked as if there were ‘ligand clouds’ around ‘protein clouds’). The obtained information was later utilized when Yu et al. [172] selected representative conformations of these different c-Myc binding sites to carry out a successful structure-based virtual screening study, which produced four active compounds that block c-Myc function in the cell.
The above example supports the suggested in silico protocol of Bhattacharya and Lin [149] for designing small molecule drugs for IDPs:
- Generate the conformational ensemble for the unbound target protein using enhanced-sampling MD.
- Identify highly populated conformations in the ensemble and extract the representative ones by clustering.
- Detect possible ligand-binding pockets in all the representative conformations of the IDP.
- Select the most druggable pockets using criteria such as hydrophobicity, plasticity, and allosteric coupling to functional sites.
- Carry out conventional virtual screening in each selected pocket and protein conformation exhibiting that pocket.
- Select the virtual hits that show good predicted binding affinity in many IDP conformations.
This general protocol could also work well with other types of targets with flexible binding sites.
Of note, MD generated IDP ensembles are frequently compared with experimental data and vice versa [173,174]. Naturally, since MD and the experimental techniques have their own limitations but produce complementary information, they can be used synergistically to characterize the conformational ensembles of IDPs [150,175,176,177,178]. For example, Shrestha et al. [170] recently reported how their enhanced simulation protocol was able to produce a structural ensemble of the disordered N terminal of c-Src kinase that agreed with the NMR and SAXS data, without reweighting or biasing the simulations.
In the next section, we will briefly look at a fast-growing branch of drug discovery that can also benefit from MD simulations: the design of monoclonal antibodies and antibody fragments.
2.1.4. Molecular Dynamics Simulations in Antibody Design
Antibodies have become an attractive class of biotherapeutics because of their low toxicity and innate ability to recognize and selectively bind to a wide variety of targets [179]. Experimental methods for the discovery of high-affinity antibodies, such as phage display, have proven to be extremely effective in antibody development, but also time-consuming and laborious [180]. Therefore, computational methods, such as MD simulations, have emerged to complement and expand the knowledge obtained from experimental antibody research.
In contrast to many other computational methods that ignore the structural plasticity of molecules, MD simulations can describe the dynamic details of molecular interactions. In antibody design, this can be utilized to identify the so-called “hot-spot” regions at the antibody-antigen interface [181]. As an example of this, Sinha et al. [181] in their work based on anti-lysozyme antibody structures could demonstrate that MD was able to reveal salt-bridges and other functionally important electrostatic forces even though these interactions were left undetected in the static crystal structure of the studied antigen-antibody complex. Naturally, the discovery of functionally important residues is the key to designing mutations in antibodies with improved affinities and selectivity to their targets.
Because MD simulations can reproduce molecular fluctuations at atomic resolution, they are also being employed to improve the scoring of antibody-antigen complex prediction methods. In this regard, MD simulations were used to refine the interactions in docked antigen-antibody complexes to obtain average values for the Generalized Born/Surface Area (GBSA) score that was used for re-ranking the docking results. The averaged GBSA scores derived from the simulations further improved the accuracy of predicting the antigen-antibody complexes [182]. Similarly, conformational ensembles generated with MD simulations can be used in rigid docking calculations, also called ensemble docking [183,184]. Even minor changes in protein conformation can affect docking results. Therefore, the advantage of this approach is that it incorporates backbone flexibility in the docking procedure and can be considered to mimick the conformational selection in antigen-antibody binding [183].
MD simulations can also provide a solution for designing antibodies with enhanced stability [184]. In a recent study, Bekker et al. [185] applied MD simulations to predict the thermal stability of single-domain antibodies and comparing them with experimental data. This allowed them to pinpoint the key residues contributing to the instability and to successfully design a mutated antibody with improved thermal stability [185,186]. Additionally, a major issue encountered in antibody-based therapeutics is that antibodies are prone to aggregate in the high concentration formulations needed for treatment [187]. Spatial aggregation propensity (SAP) is a measure directed to solve this issue. SAP quantifies the hydrophobic patches exposed on the antibody surface, averaged over the snapshot structures obtained from MD simulations with explicit solvent. Identification of regions prone to aggregation can be used to predict targeted mutations to design antibodies with better stability.
Overall, MD simulations can reveal details on antigen-antibody interactions that are not (easily) obtainable with any other methods. MD provides a useful tool to complement both experimental and other computational methods for designing novel antibodies with improved affinity, specificity, and stability.
2.2. Simulating Drug-Target Interactions
In the drug development process, lead compound discovery and subsequent optimization of the identified compounds to candidate drugs follow the target validation (Figure 2). During this phase, the aim is to discover and design compounds that have a good binding affinity and selectivity to the target. Docking and scoring are common tools for fast estimation of favorable ligand binding poses and binding energies. However, the scoring functions of current docking tools have many limitations that result in inaccurate binding affinity predictions [49,188]. With MD, we can tackle these limitations and facilitate a more accurate evaluation of the compound binding affinity as the simulations take into account the effect of water and the dynamics of the binding partners [49]. In this section, we will go through some principal methods that utilize MD in the estimation of ligand binding energies and binding kinetics. In the end, we also discuss how the challenge of docking extremely flexible peptides has been tackled with hybrid approaches combining molecular docking and MD simulations.
2.2.1. Binding Energy Estimation
Molecular recognition is critical to many fundamental biological processes [189]. Binding between two interacting molecules in the cell initiates several biological processes, and the significance of these specific interactions can be judged through the free energy of binding (ΔGbind). In general, the change in free energy (∆G) describes the thermodynamics and the kinetic properties of a system (for our purpose, a ligand binding to a protein in a solvent). ∆G can be described as an amount of energy released or required during a chemical process. The final ∆G value at the state of equilibrium is negative if the chemical process (for our purpose, ligand binding to its target) is spontaneous, while ∆G is positive if the chemical process is non-spontaneous. Conventionally, ΔG is given by the change in Gibbs function:
where ΔH represents the change in enthalpy of the system, T represents the temperature in Kelvin, and ΔS represents the change in the entropy of the system.
ΔG = ΔH − TΔS,
Moreover, ∆G of a system can be used as an overall measure to determine the stability of a given system (for our purpose, the stability of a ligand-receptor complex, or ligand binding affinity) [190]. In case of a ligand-binding event, the standard binding free energy ΔG°bind is related to the binding constant Kb by the relationship:
where R is the universal gas constant (unit: cal·K−1·mol−1), T is the temperature in Kelvin, and ΔG° has been measured at standard conditions: 1 atm pressure, room temperature (298.15 K), and 1 M protein and ligand concentrations. On the other hand, Kb is a ratio of the kinetic rate constants for association and dissociation (kon and koff, respectively) and the inverse of the dissociation constant, Kd.
ΔG°bind = −RTlnKb,
Since the free energy is a state function, binding affinity (or Kd) of a ligand can be obtained from the difference between the two thermodynamic equilibrium states, i.e., the unbound (initial) and the bound (final), without knowing the exact pathway connecting the two states [190]. Computationally, the estimation of ΔGbind requires extensive MD simulations to generate the unbound and the bound equilibrium states. These equilibrium states can also be defined as macrostates, while the macrostates can be further sub-divided into an ensemble of discrete microstates, comprising various intermediate stages of the ligand-receptor probing process (Figure 6).
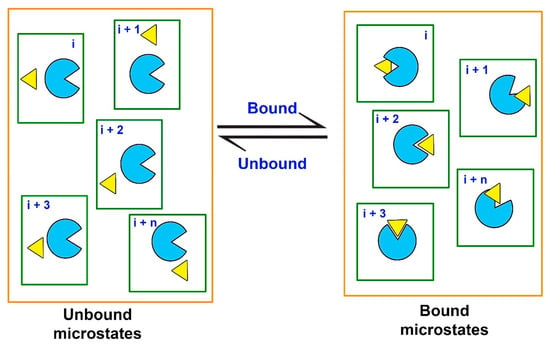
Figure 6.
Equilibrium states (macrostates, delineated by orange lines) are represented by ensembles of discrete microstates for a protein (light blue) and a ligand (yellow) in a solvated system (delineated by green lines).
Assessment of ΔGbind for a series of ligands against a specific target protein can help identify the most promising compounds with higher binding affinities than the rest of the compounds. Therefore, drug design and docking-based virtual screening processes are often followed up by ΔGbind calculations [191] for which several computational methods have been developed. Such methods include rigorous thermodynamic pathway approaches to obtain relative (and recently also absolute) binding free energies of a series ligands [192], as well as less rigorous and computationally faster end-point methods that only sample the macrostates. The accuracy of these methods varies and is inversely correlated with the computational requirements. The most rigorous (alchemical i.e., non-physical) pathway approaches such as free energy perturbation (FEP) methods [192,193], Bennet’s Acceptance Ratio (BAR) [194], and thermodynamic integration (TI) [195] can usually be applied only to a few compounds due to the high computational cost. Somewhat faster approximations include methods that sample the possible physical microstates of the thermodynamic pathway, e.g., the Weighted Histogram Analysis Method (WHAM) [196] applied to predict the potential of mean force (PMF) using enhanced MD techniques such as steered molecular dynamics (SMD) [197,198,199] (Figure 7) and umbrella sampling [200], as well as the multistate BAR estimator (MBAR) [201] and Jarzynski’s non-equilibrium method [202]. For ligand-protein systems, the change in the PMF upon (un)binding is often assumed to be equivalent with the binding free energy profile along the chosen reaction coordinate [203]; there are, however, different theoretical approaches to obtain the free energy from the PMF [203,204,205]. Computationally less expensive end-point methods include the linear interaction energy (LIE) method [206] and the well-established Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA) and Molecular Mechanics Generalized Born Surface Area (MM-GBSA) [207,208] approaches. In the next paragraphs, we focus on the application and limitations of the MM-PB(GB)SA methods that are commonly used for the evaluation of binding free energies of hit compounds from virtual screening experiments (post-docking analysis), e.g., to re-rank the docked poses of the top ligands [209].
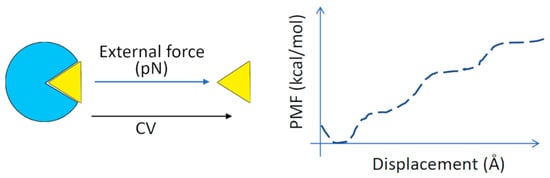
Figure 7.
Steered molecular dynamics (SMD). A continuous external force is used to pull the ligand out of the target protein binding site along the reaction coordinate (‘collective variable’, CV). The free energy of binding is calculated from the relationship between the force used and the displacement of the ligand. The plot of average potential energy versus displacement is called the potential of mean force (PMF) [210]. Enhanced MD simulations (e.g., as umbrella sampling) coupled with the weighted histogram analysis method (WHAM) are used to determine the PMF along the reaction coordinate.
The binding free energy estimation based on MM-PB(GB)SA method employs only the unbound and bound states (i.e., end-points) of the system. The binding free energy of a ligand to a protein is obtained as:
ΔGbind = Gcomplex − Gprotein − Gligand.
The free energy (G) of each individual system (ligand/protein/complex) is calculated from the total molecular mechanics’ energy (EMM) of the system in the gas phase (includes internal bonded and non-bonded electrostatic and van der Waals energies), the solvation free energy (Gsolv) with both polar (computed using implicit solvation models, either Poisson-Boltzmann or generalized Born continuum solvent models), and non-polar contributions (assumed to be proportional to the solvent-accessible surface area, SASA), as well as the entropy (S; includes translational, rotational and vibrational contributions) at a specified temperature T:
G = EMM + Gsolv − TS.
The entropy is estimated from a normal-mode analysis of harmonic frequencies calculated at the molecular mechanics level, which is computationally costly (please, see e.g., [211] for a more detailed description of the theoretical aspects of the methodology).
MM-PB(GB)SA calculations include two conventional approaches: (i) the three-trajectory scheme, and (ii) the single trajectory scheme [212,213,214,215]. The former relies on the snapshots from three MD trajectories, including apoprotein, free ligand, and the ligand-protein complex, which makes it comparatively accurate but computationally expensive [214,216]. Single trajectory strategy, however, includes only one MD simulation for the ligand-protein complex, reducing the computational time significantly [214,215,216,217]. The latter approach, however, neglects any explicit structural relaxation of the protein and ligand upon binding. Besides the strategy chosen, other factors also contribute towards MM-PB(GB)SA calculations, which include: (i) simulation time, (ii) choice of the force field, (iii) solvent model, (iv) solute dielectric constant, and (v) the net charge of the system. It has been reported that several short MD simulations run independently provide better ΔGbind predictions than a single long MD trajectory [213,214,218,219]. On the other hand, charged ligands can hinder the process of making accurate predictions [216,220,221]. Additionally, for obtaining absolute ΔGbind with the MM-PB(GB)SA calculations, the inclusion of conformational entropy (TΔS) remains a challenge. Incorporation of TΔS in the calculation does not guarantee a better accuracy in the final energies due to insufficient conformational sampling [212,213,218,220]. A sufficient number of MD snapshots may lead to a reliable estimate of absolute ΔGbind, however, it is computationally expensive [214,216]. Therefore, relative ΔGbind is generally sufficient to rank compounds against the target protein in structure-based drug design [214] and has a better prediction accuracy than the absolute ΔGbind calculations with this method.
The MM-PB(GB)SA approach has been applied in a number of studies, including the development of anticancer compounds [222,223,224], antibacterial [225,226,227], antiviral [228,229,230,231,232] and antiparasitic drugs [233,234,235], as well as antipsychotics [236,237]. These methods are also often applied to understand and analyze the binding mode and key interactions of small molecules [238,239] as well as peptide [240,241] and protein ligands [242] at their targets. Several comparative studies differentiating between the prediction accuracy of ΔGbind energies of protein-ligand complexes by MM-GBSA and MM-PBSA have been reported [243,244,245,246]. One such study indicated hot-spots in Ras–Raf and Ras–RalGDS protein-protein complexes involved in allosteric activation [244]. In another such study, the prediction of binding affinities of HIV-1 protease inhibitors helped rationalize drug resistance as a result of binding site mutations [245]. MM-PB(GB)SA calculations do not rely only on the parameters employed but also the receptor structures used [216,218,233,247,248]. Specifically, these approaches are believed to be dependent on the system. Hou et al. [214] reported accurate relative ΔGbind for 59 ligands against six different protein targets using the MM-GBSA approach when compared with the MM-PBSA method. Oehme et al. [220] reported that MM-GBSA has better accuracy than MM-PBSA for calculating ΔGbind energies of ligand–HIV protease systems. Hence, to date, no study concludes on which approach is better; instead, the literature suggests that the applied method should be selected on a case-by-case basis.
In conclusion, MD-based binding free energy calculations have a significant impact on the hit identification stage as they can improve the accuracy of the ranking of the hit compounds. As we learned from Equation (2), binding free energy is also related to binding kinetics, i.e., association and dissociation of a ligand to/from its target. We will now look at how MD is used in analyzing the drug binding and unbinding events to facilitate the design of compounds with favorable binding kinetics.
2.2.2. Drug-Protein Binding Kinetics Estimation
There is increasing evidence of the importance of drug-protein binding kinetics to develop improved drugs [249,250,251,252]. The binding kinetics of drug-protein complexes is characterized by the association rate constant (kon; unit: M−1·s−1) and by the dissociation rate constant (koff; unit: s−1) [253]. It is also common to refer to the inverse of koff, the residence time (τ). Recent works have shown that residence times can often be better correlated with the in vivo efficacy of drugs than binding affinities [250,251,254,255]. Drugs with increased residence time interact longer with the target protein, displaying longer physiological effects. Drugs with increased on-rates may bind faster to the target protein than endogenous ligands, being effective competitors. Such drugs would also be less available in the free form, leading to less non-specific binding and fewer side effects. Therefore, modulation of kon and koff values may help in the design of effective and safe drugs.
Computational methods are useful to reveal molecular details about drug-protein binding, providing information on how to modulate binding kinetics. However, obtaining binding and unbinding events from conventional MD simulations is challenging, because they are often infrequent events. One of the ways of sampling such infrequent events is combining MD simulations with enhanced sampling methods [253,255,256,257,258].
This section provides information on how enhanced sampling methods can be used to help in the design of drugs with modified kon or koff values. This is not a comprehensive list of all available enhanced sampling methods. The reader is referred to up-to-date information in the toolbox KBbox [259], which provides a compilation of tutorials and publications of computational methods to predict binding kinetics.
Most computational work done so far is retrospective, aiming at reproducing data for binding kinetics available in the literature. One exception is a recent study that used elABMD, a method to predict relative residence times that combines adiabatic bias MD with an electrostatics-like collective variable [260]. A Spearman coefficient of 0.94 was achieved for a set of 6 glycogen synthase kinase 3 beta inhibitors. Another exception is the study of koff values of inhibitors of the human flavoprotein D-amino acid oxidase using scaled MD [261]. The koff values of 5 compounds were determined by scaled MD and, afterward, experimentally. The correct ranking was obtained for 4 out of 5 compounds.
Methods with low computational cost allow the estimation of relative kinetic rates for a set of drugs. One of these methods is smoothed potential or scaled MD [262], which aims at estimating relative residence times. Scaled MD enhances the sampling of unbinding events by smoothing the potential energy of the system. The method was used to predict relative residence times for 4 78-kDa glucose-regulated protein binders (correlation coefficient, R, of 0.85) [262], 4 adenosine A2A receptor binders (R of 0.95) [262], 7 glucokinase activators (R of 0.92 after removal of one outlier) [263], and 7 HSP90 inhibitors (coefficient of determination, R2, of 0.89 after removal of one outlier) [264]. Scaled MD was also used to understand why the residence time of the drug etoposide is longer for the human type II topoisomerase (TopoII) α, compared to TopoIIβ [265].
τRAMD [266] is another method that aims at computing relative residence times for a set of drugs. τRAMD is based on random acceleration molecular dynamics (RAMD) [267,268], a method where an additional force of constant magnitude and random orientation is applied to the drug to facilitate dissociation. τRAMD was used to predict relative residence times for 70 HSP90 inhibitors (R2 of 0.86 after removal of outliers) [266]. Analysis of inhibitor-protein contacts in the trajectories using machine learning improved residence time estimates and detected that interactions between a halogen or a methyl group in the loop-binder compounds with Phe138 lead to a longer residence time [269]. τRAMD was also recently applied to estimate relative residence times of ligands dissociating from different mutants of T4 lysozyme [270].
Nonequilibrium targeted MD (TMD) [271,272,273] is another method that can be used to compute relative residence times for a set of drugs. In this method, an additional force is applied to the drug to facilitate dissociation, as in τRAMD, but in this case, the magnitude of the force is changed to obtain constant velocity of unbinding. The mean work calculated from TMD simulations was compared to koff values for a set of 26 HSP90 inhibitors [274], resulting in R2 from 0.45 to 0.80 for inhibitors grouped according to binding mode and scaffold. Moreover, the net charge of inhibitors was identified as a factor that could lead to longer residence times.
Brownian dynamics (BD) simulations [275] are suitable for studying drug-protein binding. In this method, the drug and protein are treated as rigid bodies, with no internal motions, and the solvent is represented implicitly, leading to low computational cost. A combination of BD with MD simulations was used to study the binding pathways of two inhibitors to H1N1 neuraminidase [276]. The computed association rates were ranked correctly, and the formation of a salt bridge between the inhibitors’ carboxyl group and Arg368 was revealed as a key step for binding.
Many enhanced sampling methods have moderate to high computational costs, preventing fast computation of residence times for a large set of drugs. However, such methods can reveal molecular details that may help in the design of drugs with modified binding kinetic rates. Methods that depend on the definition of one or more progress coordinates to describe the infrequent event and enhance the sampling, such as metadynamics [277] and weighted ensemble MD (WEMD) [278,279], have been used to reveal mechanistic details of drug-protein association and dissociation. Metadynamics was used to distinguish cyclin-dependent kinase 8 inhibitors with short or long residence times [280] and to study association or dissociation events for relevant pharmacological targets such as HIV reverse transcriptase [281], Src kinase [282,283], p38 MAP kinase [284], the M3 muscarinic receptor [285], the adenosine A2A receptor [285,286] and the β2-adrenergic receptor [287]. WEMD was used to study ligand dissociation from epoxide hydrolase [288] and from proteins used as model systems to study binding kinetics [289,290].
SMD has also been used to uncover molecular mechanisms of ligand association and dissociation. SMD suits for analyzing fast and slow (un)binding events of various ligands (see for example refs [291,292,293]). While applying biasing force restraints on explicit-solvent models allows for faster approximate calculations in SMD simulations, this leads to a non-equilibrium trajectory and could change the underlying physical processes too drastically [294]. A recent work [295] used interaction-energy fingerprints obtained from SMD to predict koff values for 37 HIV protease inhibitors (R2 of 0.75), showing that interactions with residues Asp25, Ile47, and Ile50, located in the active site or in the flap region, are important to modulate koff values. SMD was also used in combination with RAMD to study dissociation from B-RAF kinase [296].
Another enhanced sampling method used for binding kinetics studies is REMD, although with a usually high computational cost. A modification of REMD which employed replica exchange in two dimensions was used to study the binding of an inhibitor to Src kinase [297]. Many binding and unbinding events were sampled. Transient encounter complexes, which are not visible in experimental data but may reveal information to help in the design of drugs with improved kinetic rates, were characterized.
Other methods to obtain (un)binding events include Markov state models [298,299], adaptive sampling [300], fluctuation amplification of specific traits (FAST) approach [301], and the milestoning approach [302].
In summary, there are many examples of works showcasing how computational methods can be used to help in the design of drugs with improved binding kinetics (Figure 8). On one hand, methods with low computational cost, such as τRAMD and scaled MD, can be used to rank tens to hundreds of ligands by residence time. This information can help in the prospective selection of candidate drugs with short or long residence times. On the other hand, methods with high computational cost, such as WEMD, metadynamics, and REMD, can reveal information about transient states and ligand-protein interactions that can be modified to modulate kon or koff values. Therefore, computational methods can be applied to provide mechanistic insights in drug-protein association and dissociation events, helping in the design of drugs with improved kinetic rate constants.
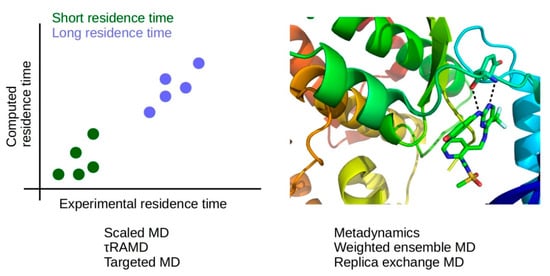
Figure 8.
Methods of low computational cost (scaled MD, τRAMD, targeted MD) allow the prediction of relative residence times (left panel), while methods of high computational cost (metadynamics, weighted ensemble MD, replica-exchange MD) provide information about drug-protein interactions during association and dissociation, which may be modified to modulate binding kinetics (right panel); ligand-protein complex from PDB ID 5TOB [303].
In the next section, we will look at ways to tackle the flexibility of peptides in peptide-protein docking to get more accurate binding poses.
2.2.3. Peptide-Protein Docking: Tackling the Flexibility Challenge with Molecular Dynamics Simulations
Peptides represent a unique class of compounds that differ in their biochemical and therapeutic characteristics from small molecules, proteins, and antibodies [304]. Peptide-protein interactions are essential e.g., for cellular signaling, localization, immune system, and apoptotic pathways. Consequently, these molecules have been attracting attention from pharmaceutical and biological communities, with nearly 20 new peptide-based clinical trials annually [305]. In the computational field, much progress has been achieved in small-molecule docking, but these methods are often not suited for peptides given their size and flexibility [306]. The inherent flexibility of peptides poses a great obstacle toward determining the 3D structure of the complexes they form. In this section, we briefly review the use of MD simulations to tackle the peptide flexibility challenge, its applications, advantages, and fallbacks in the context of peptide-protein interactions.
Computational methods that aim to study protein-peptide interactions can be classified into three categories: (1) template-based docking that uses known structures to build an initial model of the target complex; (2) local docking that performs a search around a user-defined region, and; (3) global docking that concomitantly searches for the binding site and a binding pose. Each approach has its own strategies to deal with the main challenges in protein-peptide docking, namely the modeling of conformational changes, in particular on the peptide side, the integration of experimental or theoretical data into the modeling process, and the selection of the best models out of the plethora of generated models (scoring). The application of flexible refinement in combination with molecular docking software to address the flexibility challenge has been investigated among others by using an enhanced sampling MD method with models obtained from ClusPro Peptidock [307], by combining the default pepATTRACT [308] method with an additional round of MD refinement, and by using MD to generate an ensemble of peptide conformations as input for HADDOCK [309]. A detailed description of several protein-peptide docking software is available elsewhere [310].
The use of MD simulations can provide an improved sampling of protein-peptide conformations; however, it has been observed that for large-scale predictions, heavy computational resources would be needed. A possible approach to circumvent this is to apply enhanced sampling MD methods such as SMD [311], Hamiltonian replica exchange [312], and Gaussian accelerated MD (GaMD) [313] to study protein-peptide binding. GaMD has been successfully used, in combination with the global peptide docking software ClusPro Peptidock, to refine docking poses and explore the binding mechanism of three systems. Initial models of the complexes were obtained by using the standard ClusPro Peptidock webserver protocol from the unbound forms of the peptides and proteins, excluding the PDB entries that contained the bound form of the target systems from the fragment search. For each system, the top-scoring protein-peptide complex was selected and refined using GaMD (described in detail in Supplementary Material of Wang, Alekseenko, Kozakov, and Miao [313]). The selected initial docking models had backbone RMSD of 3.3, 3.5, and 4.8 Å, for peptides 1, 2, and 3 respectively, with no significant conformational changes compared to the starting model observed for peptides 1 and 3. After GaMD refinement, the minimal backbone RMSD from the bound form observed throughout the MD simulations for peptides 1 and 2 was lower than 1 Å, whereas peptide 3 showed high fluctuations, temporarily sampling the near-native conformation (1 Å ≤ i-RMSD ≤ 2 Å). Cluster analysis of the conformations with the lowest free energies yielded backbone RMSDs of 0.94 Å, 0.61 Å, and 2.72 Å for peptides 1, 2, and 3, respectively, adequately capturing conformational changes and noticeably refining the initial docking poses. Despite these promising results, the number of systems tested remains very limited.
HADDOCK, the High Ambiguity-Driven biomolecular DOCKing software has been optimized for protein-peptide docking, taking full advantage of its capacity to handle molecular ensembles and allow for flexible refinement. The protocol starts from three peptide conformations: extended, alpha-helical, and polyproline-II, which, together, cover about 80% of the observed protein-bound peptide conformations in the experimentally determined structures in the PDB [314]. The default HADDOCK protein-protein protocol consists of three stages: (1) From randomized ligand orientations around the protein receptor, rigid-body energy minimization is performed, (2) the top-ranking models are subsequently refined using semi-flexible simulated annealing [315] in torsion angle space, and finally, (3) the resulting docking models are refined with a short restrained MD in explicit solvent. In the case of protein-peptide docking, to allow for more flexibility and potential conformational changes, the length of the semi-flexible refinement is doubled, and the peptides are treated as fully flexible, which increases the conformational sampling. This protocol was tested on peptiDB [316], with 103 non-redundant peptide-protein complexes, including 47 unbound cases. Since HADDOCK is an information-driven method, the binding region was defined in a broad manner, consisting of a binding interface on the protein receptor which was ~3 times larger than the true interface. By doing this, the focus is on the challenge of identifying the correct binding conformation of the peptide. The protocol generated 79.4% high quality (interface-RMSD ≤ 1 Å) models for bound-unbound (i.e., experimental peptide-bound protein/unbound peptide) and 69.4% for unbound-unbound (unbound protein/unbound peptide) docking, the latter representing the most realistic scenario [317]. This ensemble docking approach that includes flexible MD refinement steps is shown to be a valuable strategy to tackle the flexibility challenge in protein-peptide docking. The HADDOCK developers have also provided guides on how to generate peptide ensembles using MD simulations instead of the three common conformation approaches and how these can be used in HADDOCK, both through its webserver and a local installation [304,309].
The flexible peptide-protein docking protocol pepATTRACT combines fast coarse-grained ab initio docking with an atomistic refinement of the most favorable docked models. Combination of the ATTRACT docking protocol with an MD refinement using AMBER 14 [318] led to a 50% increase in the top-10 success rate when compared to a no-refinement scenario [308]. An ensemble of 80 peptide-protein complexes from the peptiDB benchmark was selected for testing. This ensemble includes experimental data and has been used in other docking protocols [317]. The same strategy as previously published for HADDOCK was followed by, using the three main peptide conformations for the docking with some knowledge of the binding site. For each complex, the 1000 best initial rigid-body docking solutions, ranked by the ATTRACT score, were selected for flexible interface refinement [319] and subsequent MD with AMBER 14 using a generalized Born implicit solvent model. The final complexes were clustered by the fraction of common contacts [320] and ranked by the top-four members of each cluster [317] as done in HADDOCK. Interestingly, the authors also considered a “worst-case” scenario in which no knowledge of the binding site is assumed, and a global docking is performed. This is often the case faced by most researchers. After clustering, 97% of the successful cases (56 out of the 80 complexes considered) had at least one cluster with an average top-four interface-RMSD ≤ 2 Å. The AMBER MD refinement step was shown to yield an average improvement of 0.44 Å of the interface-RMSD. There was a striking increase in comparison to the use of only the default interface refinement, which only improved the model’s interface-RMSD by 0.10 Å.
In conclusion, several peptide-protein docking software are continuously being developed and optimized further. While addressing the innate flexibility of peptide-protein complexes remains challenging, researchers are taking advantage of MD simulations for enhanced sampling and refinement. This combination of docking and MD can greatly improve the prediction of peptide-protein complexes and is a powerful asset in the field of peptide therapeutics and drug design.
In our biological context, the cellular environment is of course more complex than just water, ions, and proteins. In the next section, we specifically look at target proteins that are associated with biological membranes. We will discuss how MD is utilized to study their structure, function, and ligand binding properties as well as what the benefits are if we can include the membrane structure explicitly in the simulations.
2.3. Molecular Dynamics Simulations of Membrane Proteins
Most current drug targets are membrane-associated, either integral or peripheral proteins [321,322]. Integral membrane proteins are either polytopic proteins (spanning through the membrane several times) or bitopic proteins (single-pass proteins, spanning through the membrane only once), whereas peripheral proteins are associated with only one side of the membrane. Unfortunately, the structure determination of membrane proteins has been particularly challenging [321]. This has hampered reliable computational studies of several important drug targets. However, recent advances in crystallography and especially in cryogenic electron microscopy (cryo-EM) have resulted in a significant increase of atomistic resolution structures of large membrane-bound macromolecules, thus providing valuable information on these targets for computer-aided drug design.
MD simulations of membrane proteins have often been carried out without the membrane as it is computationally more costly to include a membrane model in the simulation system, especially if the lipid bilayer is represented in atomic detail [323]. However, biological membranes can play significant roles in modulating drug action (e.g., by affecting the substrate selection or receptor function), not only at polytopic integral membrane protein targets but also at bitopic and peripheral membrane protein targets [324]. There are also drugs whose mode of action is to directly target (disrupt) biological membranes [325], and thus, the inclusion of membranes in MD simulations may be crucial for gaining realistic insights. In this section, we focus on MD simulations of particularly important drug targets that are polytopic integral membrane proteins, i.e., G-protein coupled receptors (GPCRs) and ion channels. We also look at what MD simulations can tell about the function of cytochrome P450 (CYP) enzymes that are bitopic membrane proteins playing a significant role in drug metabolism.
2.3.1. Molecular Dynamics Simulations of GPCRs and Ion Channels
With membrane proteins representing around 25% of the total proteome and their experimentally proven importance in various pathophysiological processes, they are highly regarded as targets in small molecule drug discovery. Indeed, approximately one-third of all currently marketed small molecule drugs target membrane proteins to alter downstream cellular signaling pathways. Rhodopsin-like GPCRs, nuclear receptors, ligand- and voltage-gated ion channels are ranked as the top four of all druggable targets by FDA-approved drugs [326,327].
The most targeted class of transmembrane (TM) proteins are the GPCRs. These consist of seven transmembrane-spanning α-helical domains with a characteristic dynamic network connecting the ligand-binding site to the cytosolic Gα signaling subunit. Despite the significant functional importance of GPCRs, spectroscopic techniques remain challenging for these membrane proteins because of their distinct hydrophobic surfaces, high flexibility, and relatively low expression. However, recent advances in the structural biology of GPCRs, with X-ray crystallography, cryo-EM, and X-ray free-electron lasers (XFELs) have resulted in novel overall structural insights and understanding of the structural basis for the induced receptor response upon ligand binding and unbinding [328,329,330]. Because of the highly dynamic nature of GPCRs with multiple, functionally distinct conformational states [331,332], combined spectroscopic and computational studies allow for a detailed atomic analysis of the TM domain dynamics mediating downstream signals [333]. The most recent example is the in-depth characterized structure of GPR52 coupled to its downstream heterotrimeric Gs protein in a previously unknown self-activation state [334]. Additionally, a potential allosteric ligand-bound state was suggested as a potential drug target for Huntington’s disease.
Interestingly, class A GPCRs contain a ‘placeholder’ formed by the N-terminus and the extracellular loop 2 (ECL2) [335,336,337]. While adopting an open conformation in the absence of the ligand, the extracellular loop plays a critical role in lipophilic ligand recognition, access, and selectivity for the orthosteric site [338,339]. In the same class, a consensus amino acid network was described through a comprehensive analysis of X-ray structures by Venkatakrishnan et al. [340]. While the GPCR family allows binding ligands of diverse chemical properties, most ligand-contacting residues are preserved in the TM helices TM3, TM6, and TM7 that form a scaffold for the ligand-binding pocket. This observation explains drug cross-reactivity and allows drug repurposing with tailored ligand specificity based on topologically equivalent positions in the TM helices from structural homologs [341,342,343]. In contrast, class B GPCRs are frequently targeted by highly flexible peptide ligands at a solvent-accessible orthosteric binding pocket [344]. While consensus scaffolds generally guide GPCR ligand recognition, different ligands induce various conformational states of the receptor with a specific downstream signal [345,346].
These observed characteristic dynamics have spurred the use and advanced development of atomic level MD simulation approaches to supplement the increasing amount of static structural information from spectroscopic techniques. The increase in computational resources has enabled the analysis of conformational dynamics up to the microseconds range [347,348]. To date, because of the high structural homology between various TM protein classes even with distant homologs [349], the rational design of novel therapeutic candidates has been facilitated by comparative modeling combined with docking approaches and machine learning algorithms [350,351,352,353]. While currently repurposed ligands generally target primary orthosteric sites [343,354], long unbiased MD simulations have also facilitated the identification of allosteric regions of membrane proteins that may potentiate or inhibit downstream signal transduction [355,356].
Early simulations of membrane proteins were performed without membrane embedding, but today accurate membrane modeling has allowed for the simulation of realistic cellular membrane environments [357,358]. In vitro data on membrane thickness, curvature, fluidity [359], and surface tension [360] has enabled accurate modeling of ligand binding and the corresponding downstream activation of the signaling proteins [361,362]. Furthermore, multiscale MD simulations combining atomistic and coarse-grained MD can also give structural and functional insights into important protein–lipid interactions, protein oligomerization, clustering, and crowding [363]. For example, cholesterol-GPCR interactions and cholesterol’s general influence on membranes can modulate GPCR structure and dimerization, thus affecting e.g., receptor-crosstalk and drug efficacy [364].
Multiple dedicated web servers have been developed to facilitate the highly complex set-up of membrane protein simulations. For example, CG dynamics can benefit from the user-friendly CHARM-GUI [365], the VMD Membrane plugin [366], and the recently developed MERMAID (employing the Martini forcefield) [367]. Alternatively, parameterized phospholipids for coarse-grained simulation of membrane-protein dynamics are available in the SIRAH2.0 forcefield [368] recently implemented in the GROMACS and AMBER simulation packages. Besides these, LipidWrapper and BUMPy allow for geometric transformations towards different curved shapes of lipid bilayers [369,370]. The development of PACKMOL-Memgen for building membrane protein–lipid bilayer systems has enabled accurate atomistic MD simulations with complex lipid mixtures at desired ratios, allowing asymmetric leaflet compositions [371]. While parameters for phosphoinositides and lysophospholipids have recently been added to the AmberTools19 PACKMOL-Memgen release, the range of lipids in the new Lipid17 force field, which is the update of the AMBER Lipid14 forcefield [35], can be further extended. Moreover, various enhanced sampling and biasing simulation methods such as REMD [372], metadynamics [373], milestoning [374], and umbrella sampling [359,375] have been explored successfully for membrane-associated simulations. Another useful resource is the MemProtMD database, which, as of now, contains 3500 resolved membrane protein structures that have been inserted into simulated lipid bilayers using coarse-grained self-assembly MD simulations [376].
Besides gaining general insights into ligand binding modes [377] or quantifying ligand binding energies [378] at membrane-embedded TM receptors, ligand migration from the membrane bilayer to the central GPCR channel has been recently successfully simulated [379]. For example, it has become evident that membrane partitioning characteristics of drug molecules such as quantitative bilayer distribution, permeation depth, and their overall conformational features in the lipid bilayer are crucial for understanding their target GPCR binding kinetics [380,381]. Simulations of membrane permeability of small molecular compounds are useful for predicting drug absorption through cellular membranes, although challenging [382]. Recently, the physics-based PerMM tool and database were developed to facilitate the analysis of passive membrane permeability coefficients and translocation pathways of bioactive molecules [383]. The availability of such advanced computational tools may offer an alternative to the common in vitro membrane diffusion models that include Parallel Artificial Membrane Permeability Assay (PAMPA), phospholipid vesicle-based permeation assay (PVPA), Permeapad®, and the artificial membrane insert system (AMI-system) [384]. From the available data in reported studies, it can be inferred that membrane-embedding significantly affects TM receptor structure and dynamics, ligand diffusion and binding as well as downstream signaling.
MD simulations of ion channels have been used, for example, to explore the mechanism of ion permeation by external stimulants or to investigate the structural and functional effects of disease-causing mutations in the context of genetic disorders such as cystic fibrosis [385,386]. Such studies can give important insights to aid in the drug discovery process. For example, the key conformational changes in the channel pore could be targeted with small molecular compounds [385]. For ion channels (or any other target proteins) that lack a known experimental structure, MD can help select and validate the best homology models for further structural investigations [387,388]. In addition to evaluating the stability of ligand-binding at ion channels (e.g., [387,389]), simulations of agonists, partial agonists, and antagonists in the ligand-binding sites of the ion channel may give an understanding of the structural details crucial for the channel opening (activation) or closing (inhibition). For example, Feng et al. found that an agonist had larger conformational effects on the channel pore profile of human TRPV1 (transient receptor potential vanilloid type 1) than an antagonist [387]. On the other hand, simulations of an ionotropic glutamate receptor GluR2 (iGluR2) suggest that since partial agonists show more flexibility at the binding pocket, they cannot open the channel pore as efficiently as full agonists [390]. Interestingly, water exchange within the iGluR2 binding pocket was shown to be more pronounced when a partial agonist was bound than when a full agonist was present. Simulations of the serotonin 3A receptor (5-HT3AR) with granisetron showed how the binding of this antagonist causes conformational changes in the receptor, thus leading to constricting the channel pore [391]. Similar to Feng et al.’s TRPV1 simulations with agonists and antagonists [387], MD simulation of the cryo-EM structure of rabbit TRPV5 with econazole showed different flexibilities of the inhibitor in the four binding sites of the homotetrameric channel structure [392]. The varying dynamic behavior of the inhibitor in each monomer was shown to be correlated with the direct lipid contacts of econazole at the binding site. The simulation data also suggests how econazole affects the pore profile to inhibit Ca2+ flow through the channel. Wang et al., in their study on allosteric regulation of P2X receptors (ATP-gated cation channels), used metadynamics to determine favorable binding modes of an allosteric regulator AF-353 at human P2X3 receptor (hP2X3) [393]. Moreover, after a short MD refinement of the crystal structure of hP2X3 complexed with another allosteric modulator AF-219, they were able to observe new, stable ligand-receptor hydrogen bonds that were not seen in the original crystal complex.
As in the case of GPCRs, the phospholipid bilayer plays an important role in ligand-ion channel interactions. MD simulations can give insight into the access pathways of ligands to their site of action; e.g., MD was used to elucidate how capsaicin accesses its intracellular TRPV1 binding site by first flipping from the extracellular to the intracellular leaflet of the bilayer [394]. Moreover, MD simulations can efficiently facilitate the identification of structurally and functionally important lipid interaction sites on ion channels and other integral membrane proteins [395]. For example, the crucial role of cholesterol on the structural integrity of nicotinic acetylcholine receptor (nAChR) was demonstrated by MD simulations; in the absence of cholesterol the receptor structure collapses, while the cholesterol molecules present both in the surface sites and buried pockets maintain the original receptor conformation and support the contacts between the pore and the agonist-binding domain [396]. Likewise, MD simulations of the GABA type A receptor (GABAAR) with cholesterol suggest that cholesterol may promote pore opening by binding in the intersubunit sites of the receptor in a wedge-like manner [397]. Insight into such sites may aid in the design of (lipid-like) drug molecules that can modulate the function of therapeutic integral membrane proteins such as ion channels and GPCRs.
We will now look at the key enzymes responsible for drug metabolism and how their membrane interactions significantly affect their ligand-binding and functional properties.
2.3.2. Drug Metabolizing Cytochrome P450 Enzymes
Cytochrome P450 enzymes (CYPs) play an important role in drug metabolism, steroid biosynthesis, and xenobiotic degradation. Human CYPs are bitopic integral membrane proteins with a single TM α-helix that is connected to the globular catalytic domain via a linker region varying in length from 25 to 28 residues. The knowledge of orientation and interactions of CYPs in the membrane and therefore mechanism of substrate entrance and exit after metabolism is scarce due to experimental limitations. The most X-ray structures of CYPs have been resolved after truncating the TM helix residues, or even by mutating residues in the globular domain region that interacts with the membrane. Therefore, significant information on protein-membrane interactions and function has been lost. To date, full-length structures of only fungal (Saccharomyces cerevisiae, Candida albicans, and Candida glabrata) lanosterol 14-alpha demethylases (CYP51) have been reported [398,399,400]. However, there are a number of experiments performed (employing e.g., epitope analysis, mutagenesis, tryptophan fluorescence scanning, and atomic force microscopy) to find the important globular domain and membrane interactions and distance of the globular domain above the membrane [401,402,403,404]. The TM-helix orientation can be measured experimentally using solid-state NMR spectroscopy [405,406]. Furthermore, the orientation of CYPs’ globular domain has been determined by measuring the heme-tilt angle by rotational diffusion and nanodisc experiments [407].
As these experiments have been performed for only certain CYPs and there is a very low sequence identity between different CYP subfamilies, there is little understanding of how sequence differences between CYP isoforms will influence the membrane orientation, interactions of the globular domain with the membrane, and subsequent selection of substrates for metabolism by individual CYPs. As most of the substrates are hydrophobic in nature, it is assumed that the ligand tunnel opening in the membrane would be the favorable route of entry into the catalytic site of CYPs [408,409]. To understand such fine differences, computational modeling, and simulations at various time and length scales have played a significant role in understanding the mechanistic behavior and dynamics of CYPs in their native environment.
Computational methods such as the Orientation of Protein in Membranes (OPM) database (http://opm.phar.umich.edu/) [410] and the Protein Data Bank of Transmembrane Proteins (http://pdbtm.enzim.hu/) [411] can be used to predict the position, insertion, and orientation of membrane proteins in the biological membranes. Some research groups have taken the OPM predicted orientation of the globular domain above the membrane as the starting point and further optimized it using all-atom molecular dynamics (AAMD) simulations in the physiological conditions [412,413]. However, large domain motions or orientational changes of the globular domain are unattainable by AAMD and require coarse-grained (CG) simulations. The CG simulations help us explore large conformational spaces by decreasing the number of degrees of freedom and allowing the extension of simulations beyond the microsecond scale. Different approaches utilizing multiscale simulations, CGMD, and AAMD have been used to study the orientations of several CYPs (CYP2C9, CYP3A4, and human CYP51) in a lipid bilayer [414,415,416]
We have optimized a multiscale simulation protocol to study CYP–membrane interactions [417]. For this, CYP3A4 was used as the test case for the insertion and orientation of a CYP enzyme in a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) bilayer. We then extended the same approach to other major drug-metabolizing CYPs such as CYP2C9, CYP2C19, CYP1A1, CYP1A2, as well as to the human steroidogenic enzymes CYP17 and CYP19 that are [417,418,419]. From the results of our simulations, we have been able to identify differences in the orientations or the distance of the globular domain with respect to the membrane, and important residues at the membrane–protein interface that result in such differences.
Through our optimized multiscale simulation protocol, we identified that the two highly similar CYPs: CYP2C9 and CYP2C19 that share 94% sequence identity, can have not only distinct substrate specificities but also different membrane protein orientations and interactions [419]. Such differences were due to the primary sequence variation in the linker, beta-strand1, the B-C loop, helices F, F’-G’, G regions and their turns. These regions are the flexible substrate recognition sites (SRS1, 2, and 3), located at the entrance to the active site [420]. Furthermore, using our multiscale simulation approach, we identified the effect of mutations in the TM-helix of CYP17 on the interactions and orientation [418]. The original TM-helix sequence was modified to increase the expression of CYP17 in E. coli. The difference in the heme-tilt angles in wildtype and mutant (mt) TM-helix corresponded to the experimental heme-tilt angle measured by Ivan Lenov for mtCYP17 (64 ± 4°) [421], Ohta et al. [404] (47° to 63°), and simulation results by Cui et al. [422]. Furthermore, mutations in the TM-helix of CYP 17A1, especially W2A and E3L, led to a gradual drifting of the TM-helix out of the hydrophobic core of the membrane. This instability of the TM-helix could affect the interactions with the allosteric redox partner, cytochrome b5, required for CYP 17A1’s lyase activity. Truncation of the TM-helix residues in CYP17 has been shown to decrease its catalytic activity 2.4-fold, which could be due to the loss of hydrophobic interactions between CYP17 and its redox partner [423]. Such hydrophobic interactions between TM helices of CYP2B4 and cytochrome b5 have been reported by dynamic nuclear polarization (DNP) NMR spectroscopy under magic angle spinning (MAS) [424]. Therefore, the unstable TM-helix lying parallel to the membrane plane in mtCYP17 could result in the loss of inter-TM helix interactions between mtCYP17 and its redox partner, leading to decreased catalytic activity, or affect membrane anchoring and thereby lead to reduced activity.
Besides understanding the CYP–membrane interactions and orientations, it remains unexplained how the CYPs select different substrates and what route substrates take for entry into the catalytic site, and how the corresponding soluble products exit the site. The study of ligand entrance and exit is beyond the scope of classical MD due to the limited time and length scale one can reach in such simulations. Therefore, enhanced sampling techniques such as RAMD [268,425] and SMD [408,426,427,428] are used. In RAMD simulations, an artificial force with random direction is applied to the center of mass of the ligand while in SMD, a force is applied to the ligand in a specified direction (Figure 7).
Different ligand access/exit tunnels have been observed opening in soluble vs membrane-bound CYPs [425,429]. In mammalian CYPs, the 2a tunnel that opens into the membrane can be used by hydrophobic substrates, whereas tunnel 2c that opens in the solvent may be preferred by hydrophilic products to egress [430]. RAMD simulations of CYP2C9 in complex with flurbiprofen and warfarin and their products by Cojocaru et al. [425] suggest that depending on the physicochemical properties of the ligands, different tunnels were preferred. RAMD simulation of CYP51 by Yu et al. showed, on the other hand, that tunnel 2f is the predominant ligand egress tunnel that leads to the membrane [431].
To conclude, computational prediction, modeling, and simulation have enabled us to a great extent to understand the structure, dynamics, and function of CYPs in general and in particular mammalian CYPs in their native membrane-like environment. However, there is still a need for improving computational algorithms, developing compatible force fields, and facilitating the inclusion of complex membrane systems in MD simulations to help understand fully complex biological questions relating to drug metabolism by CYP enzymes. In the future, elucidating the intricacies of the membrane and ligand interactions of CYPs may, for example, aid in predicting the metabolism of novel drug candidates or understanding the adverse effects of drugs and their metabolites. Moreover, this may give important insights into anticancer drug development that targets CYP enzymes [432].
We have now seen how MD can be used to support the first steps of the drug development process from target identification and validation to lead discovery and optimization (Figure 2). In the last part of this review, we focus on the next phase, the preclinical research and, more specifically, pharmaceutical development or (pre)formulation studies. In this phase, it is important to find suitable formulations (e.g., a tablet or solution) that then will be used in the preclinical toxicity assays and later in clinical trials. If the candidate drug is successful in the trials (safe and effective) and will later obtain the marketing authorization, its formulation needs also to be up-scalable and suitable for industrial manufacturing. Since the solubility of the drug is important for absorption, it is of uttermost importance to ensure the solubility of the solid-state drug formulations. The stability of the chemical compounds is also an important aspect to be considered. To achieve these and any other required properties that are important for the manufacturing process or the final dosage form, drug formulations include many excipients, e.g., wetting agents, preservatives, antioxidants, plasticizers, lubricants. It may also be beneficial to load the drug to different delivery vehicles such as nanoparticles. In the following paragraphs, we get a glimpse of how MD can help in drug formulation and solubility studies, as well as in the characterization and design of nanoparticles for drug delivery and therapeutic purposes.
3. Molecular Dynamics in Pharmaceutical Development
3.1. MD Studies of Crystalline and Amorphous Solids
Pharmaceutical formulations are often crystalline or solid-state in nature, which makes the understanding of such systems critical in pharmaceutical development and manufacturing. The crystalline systems include everything from polymorphic forms, salts, and co-crystals to hydrates [433]. Additionally, recent research has suggested that formulations containing the active pharmaceutical ingredient (API) in an amorphous state are an attractive option for poorly soluble drugs [434].
Many physical phenomena of interest such as dissolution, phase changes, nucleation, and crystal growth happen on large time scales which necessitates the use of molecular mechanics force fields instead of more accurate but more expensive quantum mechanics-based approaches. Force fields typically used in drug discovery such as AMBER, OPLS, and CHARMM can be applied to crystalline systems [435], and other force fields that are developed with crystals in mind also exist [436,437].
Understanding the possible phase changes between different polymorphic forms of the same crystalline drugs is critical because different forms can have radically different behavior during dissolution, storage, and manufacturing. The transition between the β and α forms of DL-norleucine is a typical example of a solid-solid phase change simulated with MD [438]. It was possible to discover different transition pathways and their energy barriers and to determine that the transition proceeded by cooperative movement between the bilayers in the crystal.
Another type of phase change that is often encountered, is dehydration of a hydrate crystal to a lower hydrated form or to the anhydrous state [439,440]. This process has been captured for example for naproxen using MD as the dihydrate form of the sodium salt dehydrated to the monohydrate form during the simulation [441]. Dehydrated products are often of low crystallinity, which makes structure determination difficult with traditional single-crystal X-ray diffraction methods. Solving the molecular structure of such products requires, therefore, X-ray powder diffraction (XRD). Here, MD can assist by simulating the dehydration process; the XRD pattern of the dehydrated state found in the simulation can then be compared with an experimental powder pattern to solve the structure of the new phase [442,443]. Using MD-based free-energy perturbation methods, the free energy of inclusion of a solvated molecule can be calculated, which is relevant for understanding the stability of a hydrate [444].
The morphology of the crystalline phase of an API is very important for its behavior during processing because the shape of the microcrystalline particles influences the powder’s flowability [445]. Several studies have targeted the crystal growth of organic molecules using MD and have been able to predict the morphology of experimental crystals with good accuracy [446]. The growth of a crystal is often modified using additives. MD simulations can be used to quantify the particular additive’s effect on the growth rates of each crystal face [447].
At the macroscopic level, crystals of drug-like molecules often take days to grow but at the nanoscale, the growth of a single crystal layer is much faster and accessible with MD. Such events are typically simulated using enhanced sampling methods such as metadynamics, where a collective variable describing the crystallinity is used to construct a biased potential that enables escaping from local minima (Figure 9). The collective variable is modeled by calculating the orientation of a crystalline molecule with its neighbors. This allows for distinguishing between molecules in the crystal and molecules in the solution. By simulating several different faces of a crystal, the rates of the different ways a molecule can attach and detach to the crystal surface can be computed. The rates are dependent on the MD simulation and therefore parameters such as temperature, solvent composition, and level of supersaturation can be varied. These rates can then be used as an input in a kinetic Monte Carlo simulation to predict the morphology of the crystal [448].
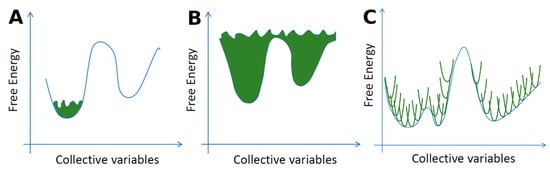
Figure 9.
Collective variable-based enhanced-sampling methods restrain the system along one or more reaction coordinates (so-called collective variables) by introducing an additional bias potential. (A,B) Metadynamics [277]. (A) After the simulation has reached a local minimum and is sampling around it, a biased potential is employed to enhance the sampling in that part of the potential energy surface to be able to push the system away from the local minimum to new regions. (B) In the end, the biased potential becomes larger than the free energy barriers, allowing the system to move freely from one minimum to the other. (C) Umbrella sampling [200]. The reaction coordinate is divided into separate overlapping windows and the biasing potential is applied to each window to efficiently sample the conformational space by multiple simulations along the reaction profile.
Another fundamental problem for crystalline formulations is the nucleation of a crystal from a solution, where changes in the experimental conditions can produce different polymorphic forms of the same API. Here, MD can be used to simulate the nucleation by preparing a simulation box consisting of a supersaturated solution of the API. MD simulations have shown that nucleation sometimes happens by a two-step process where density fluctuations of the solute produce amorphous clusters that can potentially turn crystalline and form the initial crystal nucleus [449]. This contrasts with the classical nucleation theory that assumes that a crystal nucleus forms directly from the solute [450]. For example, the nucleation of DL-norleucine crystals from an octanol solution has been studied by Ectors et al. [451] and they also found that pre-nucleation clusters were formed. The norleucine molecules formed bilayers of enantiopure domains that the authors theorize could transform into the racemic crystal structure.
Nucleation can also happen from a pure amorphous phase that can be created using methods such as ball milling or melting followed by quench cooling [452]. Understanding nucleation at the molecular level is very difficult using experimental techniques because of the small time and length scales involved. Using metadynamics, it is possible to simulate the nucleation event at the molecular level. Giberti et al. [453] were able to simulate the transition of urea from the amorphous phase to the known most stable crystalline polymorph and additionally found a new metastable polymorph.
Coamorphous systems have shown promise in drug delivery due to their enhanced stability compared with the pure amorphous phases [454]. However, MD simulations of such systems are still rare [455]. In the next paragraph, we will look at how MD simulations can facilitate the characterization of drug-polymer formulations that are commonly used for increasing the physical stability of amorphous solid drugs (e.g., preventing nucleation and subsequent crystallization).
3.2. Amorphous Drug-Polymer Formulations
In the field of amorphous drug formulations, the main challenge is the stability of the amorphous solid dispersions (ASD) [456,457]. Once the solid drug is amorphized, via, e.g., spray-drying, the molecules will tend to recrystallize [458], and the physical stability is further reduced if the compound is stored under humid conditions. The water acts as a plasticizer and will lead to time-limited stability of such drugs [459,460]. One way to extend the amorphous stage is the addition of polymers to the ASD. If the polymer is chosen properly, the drugs will have a high affinity to it and that will slow down the drug aggregation and crystallization process [460,461].
Solubility/miscibility and mobility are two of the several factors contributing to the stability of an amorphous formulation. For example, the formation of a hydrogen bond network between the drug and the polymer often plays a significant role in reducing the tendency of the amorphous drug to crystallize [462,463]. Experimentally, the molecular dynamics and crystallization kinetics of amorphous formulations are usually studied with broadband dielectric spectroscopy (BDS) and differential scanning calorimetry (DSC) [464,465,466], whereas the molecular interactions such as hydrogen bond distributions can be studied with Fourier-transform infrared spectroscopy (FTIR) and high-resolution solid-state NMR techniques, although with limited insights due to e.g., poor resolution [462,467].
The past decade has seen an increased interest in computational studies of drug-polymer formulations, Bradley D. Anderson’s group being among the pioneers in employing MD simulations in the field [467,468,469,470,471,472,473,474]. Complementing the experimental methods, MD simulations are particularly useful for providing atomic-level structural insights into drug-polymer-solvent interactions and distributions and for exploring and predicting the thermodynamic and kinetic bulk properties of such formulations [472,475,476,477]. For example, the glass transition temperature (Tg), an important parameter for the stability of amorphous formulations, can be determined dilatometrically from a series of MD simulations performed at different temperatures. Usually, the obtained Tg values agree reasonably with the experiments, although they may be higher due to the faster cooling rates in the simulations [472]. The contribution of various groups of a polymer to the mobility of a drug molecule can be studied by analyzing the atomic fluctuations of the molecules along the simulation trajectories. Another important property to assess for ASD is the miscibility of the drug and the polymer. Despite the concerns about the applicability of the Flory-Huggins (FH) theory [478], a significant number of studies are based on the calculation of chi (χ), the FH interaction parameter [479,480]. In the majority of studies, chi represents how much molecules of type A prefer to interact with molecules of type B rather than both A and B interacting with themselves (applied to a binary system). As the next step, the miscibility can be used to estimate solubility parameters [470]. Importantly, MD allows us to study the formation of the hydrogen bonds between the drug molecules and polymers [473,481]. That, along with radial distribution function and other analysis routines, are powerful tools to quantify the nature of the drug-polymer interactions, for instance, whether hydrogen bonds are formed or whether it is the hydrophobicity that plays the major role in the specific placement of the drug molecules.
The frequent problem with MD simulations in this field is that the polymers are relatively long for the all-atomistic simulations [482]. In some works, researchers represent the polymer by a chain with a lower number of monomers [481]. In others, where atomistic details can be considered negligible, a coarse-graining is applied to get a faster qualitative analysis of the polymeric excipients [483].
3.3. Drug Solubility
According to the biopharmaceutical classification proposed by Amidon et al., active pharmaceutical ingredients can be divided into four groups [484] that define to which extent two main properties of importance for oral absorption, namely permeability and solubility, impact the bioavailability of a specific drug molecule. Absorption is a result of complex, multiphase molecular interactions between the molecules of interest, membrane components, and the environment at the interface between the gastrointestinal (GI) fluid and the cells. A number of computational studies are focused on the permeability issue, targeting for example the passage of small molecular drugs [485,486] or peptides [487,488,489] through the cell membrane, and the effect of permeability enhancers on the membrane permeability [490]. Poor aqueous solubility has emerged as the main problem in the field, with as much as 70–90% of contemporary drug molecules having too low solubility to allow absorption after oral intake [491]. Low drug solubility, therefore, frequently causes erratic exposure and clinical failure after oral dosing [492]. To improve aqueous solubility, a number of advanced strategies have been developed such as the use of co-solvents, surfactants, self-emulsifying drug delivery systems, mesoporous carriers, lipid-based and amorphous formulations [493]. All these techniques have their own pros and cons, but their optimization for a particular poorly water-soluble drug requires a thorough analysis. Not only may the experiments be expensive, but also the molecular level details and mechanisms on the scale of nanoseconds and nanometers often cannot be observed in the wet lab. Thus, computer simulations appear to be a useful tool, capable to predict the interactions of the drug molecules with the formulations and surrounding media of interest, e.g., GI fluids for orally delivered drugs. Apart from MD simulations, there are also other computational methods available; these can be generally classified as machine-learning-based methods requiring training on experimental data [494,495] and empirical methods exploiting the datasets to analyze the contributions of specific descriptors (functional groups) to solubility [496,497]. Nevertheless, classical MD not only allows one to determine the best parameters for the solubility improvement but also sheds light on the underlying mechanisms [471,498,499], thus, providing new ideas for further formulation development [500].
In MD studies, solubility is explored through calculations of the change in Gibbs free energy of the simulation box while the system is being transferred from one state to another. This is visualized in a simplified example provided in Figure 10, where a simulation box filled with only water molecules is compared to a similar box complemented with a hydrophobic molecule or a hydrophilic molecule. As compared to the purely aqueous system, the second box is going to have extra free energy, as the higher repulsion between the insoluble (I) molecule will make the solvent molecules more packed out of the cut-off radius of the I, which essentially moves the system further from the energy minima. In the third system, on the contrary, the stronger attraction will lead to the minimization of the Gibbs free energy, along with more stable placement of the molecules and lower entropy.
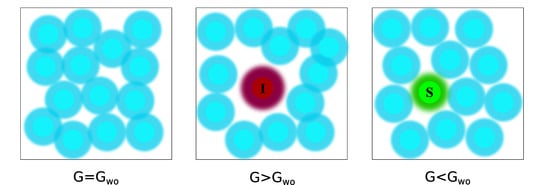
Figure 10.
Schematic representation of three similar simulation boxes. Inner circles represent the regions of strong repulsion (overlapping electronic clouds), outer stand for van der Waals attraction (except for the red, insoluble I molecule). On the left panel, a purely aqueous system is presented; in the middle, a hydrophobic molecule is put into an aqueous environment; the right panel demonstrates the system with a hydrophilic molecule.
The absolute value of solubility is not trivial to observe as it is difficult to compute the residual chemical potential of the solid form [501,502]. On the other hand, if the experimental value of solubility for one compound is known in the chosen media, it can serve as a reference for comparison in simulations: the reference system is simulated, its free energy is calculated and the same is repeated for a similar system with another compound. In the same way, the impact of various solvents can be estimated from a set of simulations where the reference system is compared with other simulation boxes containing the same molecule but different solvents [503]. The solubility of a compound can be evaluated in any solvent of interest based on the experimentally found solubility of the compound in another solvent, and the relevant free energies of solvation computed with MD. For instance, Chebil et al. [504] reproduced the solubility of quercetin in chloroform, water, acetonitrile, acetone, and tert-amyl alcohol within 0.5 log unit using the equation:
Here c2 and c1 are solubilities in two different media (unknown and known, respectively), ΔGsolv is the computed free energies of solvation in these media, R is the gas constant, and T is the temperature in Kelvin.
A similar approach is used for the calculation of excess solubility—the solubility in the actual solution relative to an ideal solution [505]. Nevertheless, several important assumptions need to be taken, the most important being that the amount of the solvent should not influence the solubility of the drug molecule. In practice, this is implemented by introducing just one molecule of the solute to the box with solvent (usually the periodic boundary condition is applied), which represents the infinite dilution [503].
Several computational approaches exist to calculate relative solubility values for such systems. The firsthand choice is to perform free energy calculations, for example, using free energy perturbation (FEP) [193,506], thermodynamic integration (TI) [195], or Bennett’s acceptance ratio [194]. The underlying concept in them is based on the change of the energy of the system while the solute molecule is introduced to the solvent. For example, the solute molecule can be gradually inserted in (or deleted from) the box. This is implemented by reducing the strength of the Lennard-Jones and electrostatic interactions between the molecule of interest and the solvent molecules. The gap between the two states (the presence and absence of the solute molecule in the solvent) can then be subdivided into more configurations, so that the difference between the adjacent ones would be small, thus improving the accuracy of the method.
The Widom insertion method is an alternative approach where the solute particle is randomly inserted into various places across the box and the averaged energy of the interaction is used to calculate the excess chemical potential [507]. The main disadvantage of the method is the significant overlaps between the atoms, which makes it less suitable for relatively big solute molecules in the dense solvents. On the other hand, the method has shown a good agreement with experimental data for smaller molecules. Further, solubility can also be calculated through Grand Canonical Ensemble MD simulations [508,509]. The partition coefficient is yet another important value that can be observed from MD. It represents the difference in solubility of the solute in water and organic phases. Calculating partition coefficients can be as valuable as the solubility calculations, as it allows to evaluate the affinity of the solute molecule to the media at the interface with water [510]. For more details and methods, the reader is recommended to read the review on MD simulations for solubility calculations by Hossain et al. [511].
3.4. Nanoparticle Simulations
Recent advances in nanotechnology and applications of nanomedicines for site-specific drug delivery have increased the interest in nanoparticles (NPs) for drug discovery and pharmaceutical applications [69,512,513]. Currently, a number of different NPs with their unique physical properties are being investigated for pharmaceutical applications, including but not limited to, liposomes [514], inorganic or polymer-based nanoparticles [515,516,517], and carbon nanotubes [518]. The typical size of various nanoparticles can range between 1 and 100 nm. Due to this smaller length scale, molecular simulation is particularly suitable and extensively used in a number of studies for investigating different NPs’ molecular structure [514,515,516,517], drug loading capacity [519,520], drug release mechanism [521,522,523], interaction with cell membrane, and membrane penetration process [524,525,526,527,528,529,530]. A number of excellent review articles are already available in the literature on the application of MD on various aspects of NP-based drug delivery systems [512,531,532,533,534]. However, in this section, we will provide a review of recent articles where MD simulations have been applied to study some of the key structural and functional properties of different NPs that are necessary for the NPs to become successful in pharmaceutical applications.
3.4.1. Structural Characteristics
Structural characteristics of lipid-based NPs composed of stearic acid, oleic acid, and sodium dodecyl sulfate (SDS) have been studied by coarse-grained (CG) MD simulations [514]. Formation of vesicle-like structures with water entrapped inside the lipid droplet was observed. Such lipid-based NPs were proposed to be suitable for the delivery of both hydrophilic and hydrophobic drugs. MD simulations were used by Connell et al. to study the adsorption of gonadotropin-releasing hormone I (GnRH-I) and a cysteine-tagged modification of GnRH-I (cys-GnRH-I) to modeled silica surfaces [516]. The simulations revealed that a specific orientation of the peptides at the silica surface was the reason behind different immunological responses of two different peptide-silica NP systems. The simulations also showed that when the peptides were conjugated with bovine serum albumin, they formed more interaction points with the surrounding molecules which resulted in improved immunological responses. In another study, Monti et al. investigated the stability, aggregation, and sintering of gold (Au)-NPs functionalized with cysteine-based peptides using MD simulations with reactive force fields (ReaxFF) [517]. Their molecular level analysis suggested that the Au-NPs functionalized with peptides are physically stable and the peptide chains adsorbed to the gold surface hindered sintering of the particles. The stability of fluticasone NPs was studied by Ahmed and coworkers [515] with MD simulations. Fluticasone is a poorly water-soluble corticosteroid and six different polymers were used to prepare fluticasone nano polymeric particles. The MD simulations and calculated MM-GBSA binding free energies confirmed the experimental results, showing better binding of the drug to a copolymer as compared to the individual respective polymers.
3.4.2. Drug Loading and Release
MD has been employed to investigate the loading of cyclosporin A (CyA) by lipid-based NPs composed of medium-chain fatty acids and poly (ethylene glycol) molecules at various compositions [519]. The simulations showed that the increase of drug loading did not significantly change the NP nanostructure and drug exposure to the aqueous environment. The CyA molecules prefer to localize at the NP surface. However, if the particle is overloaded with CyA (increasing the number of drug molecules from 1 to 10), a submerged localization of CyA inside the NP was observed. The drug loading capacity of chitosan NPs was investigated by Mousavi et al. for donepezil and rivastigmine molecules [520]. Their simulation showed that in the presence of ions, the overall drug loading capacity of rivastigmine is relatively lower compared to donepezil in chitosan NPs.
Thota et al. [522] performed CGMD simulations to investigate the loading and release of ibuprofen in the amphiphilic peptide (AF)6H5K15 (FA32) and its derivatives (F12H5K15 and F16H5K15). The simulations showed that the FA32 formed quasi-spherical NPs and the derivatives of FA32 formed nanofibers, respectively, when loaded with ibuprofen. It was also found that the release of ibuprofen was slower from the NPs than the nanofibers.
MD simulations can be employed to investigate the interaction of NPs with drug compounds as a function of the NPs’ various functional and structural properties, i.e. surface modification with coating polymers, morphology, and size. For example, PEGylation of NPs, a process where NPs are coated with polyethylene glycol (PEG) polymers, can enhance the loading of hydrophobic drug molecules [535]. However, the binding affinities of such NPs and drug compounds should then be evaluated properly to better understand the release capabilities from such NPs. MD with ReaxFF has also been used to explore the structure, dynamics and drug release of Au-NPs functionalized with chitosan and loaded with gentamicin [521]. The simulations revealed that the loading of the drug is dependent on the size of the carrier and chitosan polymer chain length. The simulations also showed a slower release mechanism by a delayed gentamicin migration towards the solvent.
The size and internal microstructure of the NPs are also important in terms of drug release from the NPs. Depending on the binding affinity of the drug compounds with the NP constituent components, the drug can be loaded in the core or corona of the NPs. The release of drug compounds will highly depend on the location of the drug loaded at the NPs. Free energy calculations using SMD can play a vital role in understanding drug components’ location inside the NP and their release mechanism. Such free energy calculations by Vukovic et al. [536] revealed the exact location of the hydrophobic bexarotene and a highly charged drug, human vasoactive intestinal peptide, inside a PEGylated NP. In a recent study by Kabedev et al. [537], it was shown that an NP composed of intestinal fluid components loaded with a hydrophobic drug, danazol, requires significantly less energy to release the danazol molecules from the NP surface to the membrane center than into the water phase. Unrestrained CGMD was employed to investigate the mixed polymeric-surfactant NP structure by Wu et al. [538]. The authors observed that the particle microstructure was affected by the different polymer-surfactant ratios, which subsequently affected the particles’ drug loading ability.
MD simulations have also been used to evaluate the effect of the system pH and drug concentration required to achieve an optimal drug release and loading. Chitosan NPs were evaluated as carriers for the controlled release of cytarabine at pH 6.4 and 7.4 [523]. The release of cytarabine was found to be higher at pH 6.4 than 7.4, which agreed well with the experimental results. Koochaki et al. [539] investigated the self-assembly behavior of dual-responsive block copolymer and the resulting micelles’ loading ability of doxorubicin (DOX) using both AAMD and CGMD simulations. The results of CGMD simulations showed that DOX can be efficiently loaded in the polymeric micelles. However, the loading efficiency was slightly decreased with the increasing drug concentration, mainly due to the decrease in particle size.
Overall, MD simulations can reveal important information on the size and internal molecular structure of NPs as well as on the system parameters such as pH and overall drug concentration, which can be utilized to achieve optimal NP design characteristics for desired drug loading and release.
3.4.3. Diffusion through Cell Protecting Layers
MD simulations were used by Yu and colleagues to better understand the diffusion behavior of lipid-based NPs in a biological hydrogel mimicking a mucus layer [540,541]. The simulations revealed that lipid-based NPs with moderate rigidity have higher diffusivity through the mucus layer compared to their soft and hard counterparts. NPs with moderate rigidity can deform into an ellipsoidal shape and diffuse through the mucus layer with rotational motions. MD simulations also captured the temperature-dependent diffusion mechanism where lipid-based NPs show higher diffusivity near the phase transition temperature or the temperature at which the liposome membrane transforms from a solid-like gel to liquid crystalline phase [541]. MD simulations were also employed to study NP diffusion through endothelial glycocalyx [542]. It was estimated that the force required to indent the glycocalyx surface increases significantly with the increase in NP size. The results also suggested that an improved diffusivity of the glycocalyx layer will be possible with positively charged NPs.
3.4.4. Direct Membrane Penetration
One of the attractive functional properties of NPs (more specifically cationic NPs) is their capability of direct translocation into the membrane without a significant toxic effect at lower concentrations [524]. However, the direct translocation mechanism is not clearly understood, and the knowledge of the molecular insertion mechanism(s) would be beneficial in designing NPs for efficient cellular uptake. MD simulations have shown a significant promise in modeling the direct insertion process. For example, SMD combined with umbrella sampling has been applied in a number of studies to understand the effect of particle size and shape [525], surface charge [525,526], and properties of ligands used as particle coatings [527,543] on cellular uptake of the NPs.
Regular or unrestrained MD has also been applied to investigate NP translocation through the membrane by taking some additional measures in the simulations such as using multiple NPs [528], applying an external electric [529] or magnetic field [530], or applying gradients of ionic concentration across the cell membrane [524]. In one such study, CGMD simulations were performed to investigate the interaction of multiple peptide-NP conjugates with the cell membrane [528]. The simulations showed that some NPs form a transmembrane pore and then the other NPs can permeate the membrane through that pore. Direct translocation of cationic Au-NPs was investigated by applying an external electric field using CGMD simulations [529,544]. The simulation results suggested that translocation of NPs can occur under a weak external electric field without permanently damaging the membrane. The effect of the magnetic field for the permeation of NPs through the blood-brain barrier endothelial cell membrane was studied by Pedram et al. [530]. They used iron oxide as the core and gold as the shell of the NPs in all-atom MD simulations. The results showed that the NPs of size between 5-45 nm can cross the cell membrane with the application of very week magnetic force (<5000 pN). Lin and Alexander-Katz showed that ionic concentration gradient across the cell membrane can induce the penetration of Au-NPs using CGMD simulations [524]. After the insertion process, the pore was self-resealed and the ionic concentration across the membrane was equilibrated. This study suggested that the gradient of different properties, such as pH or osmotic pressure across the membrane can be important for the direct permeation of NP.
3.4.5. Interactions with Viruses and Biomacromolecules
In addition to functioning as a drug delivery system, NPs can also interact with a relevant receptor and act like a drug itself [534]. In a recent study, it was found that Au-NPs coated with long and flexible ligands mimicking heparan sulfate proteoglycan (HSPG) molecules can associate with different classes of viruses and induce irreversible viral deformation [545]. To better understand the finding, all-atom MD simulations were performed to investigate the interaction of different NPs and viruses at physiological conditions. NPs were initially placed close to the virus capsid and the simulation showed that multivalent binding develops between the negative sulfonate group of the NP ligands and the positively charged L1 protein of the virus. The total binding energy and force applied on the L1 protein by each NP was calculated to be about −34 kcal/mol and 189 pN, respectively. Such force was able to deform the L1 protein, disturb the arrangement of L1 proteins of the virus, and ultimately destabilized the virus [545].
MD simulations have also been used to investigate the inhibition process of amyloid β (Aβ) fibrillation by using Au-NPs [546]. The simulations showed that Au-NPs can influence the conformational change of the peptides and reduce inter-peptide interactions which can in turn prevent the β-Sheet formation of Aβ peptides and prolong the progress of Aβ aggregation. The interaction of NPs covered with different types of ligands (i.e., positively and negatively charged, peptide, and synthetic inhibitor ligands) with Aβ40 peptides and their fibrils were also investigated using MD [547]. The simulations revealed that the peptide-NPs and negatively charged-NPs attached to the free peptides and fibril tips, respectively, which can potentially restrict peptide fibrillization and fibril growth. Positively charged NPs, on the other hand, attached to the peptide and fibril surface and deformed it [547].
Altogether, this section identifies a number of studies where MD simulations were used to investigate various structural characteristics and functionalities of NPs. MD simulations were also applied to improve the understanding of NPs’ interaction with membranes, viruses, and macromolecules. The molecular-level description obtained using MD simulations might facilitate the successful NP-based product development in drug discovery and pharmaceutical applications.
4. Conclusions
Over the past 50 years, MD simulation techniques have established their relevance in modern drug discovery and development processes. With the increasing computer power and development of new force fields and enhanced sampling methods, it is now possible to simulate even big and complex (bio)molecular systems in time scales that can give important insights into real-life molecular events and interactions. Our example cases of sirtuins and RAS show how MD simulations can be successfully used to uncover the conformational dynamics of highly flexible target proteins, thus providing valuable insights for drug discovery and design. Moreover, MD-generated conformational ensembles can be helpful in ligand design against extremely flexible intrinsically disordered proteins. Enhanced MD approaches and force field development are key in tackling such challenging targets. MD simulations can also reveal important details of antibody-antigen interactions and help design novel antibody therapeutics with improved properties.
MD-based binding free energy calculations are widely used in the hit identification phase to improve the accuracy of ranking the putative hits. In addition, the design of drugs with improved binding kinetics benefits from various enhanced MD techniques that probe the drug residence times at the target site. Similarly, MD simulations can facilitate peptide docking by enhancing the conformational sampling and refinement of peptide-protein complexes in the development of peptide therapeutics.
MD simulations of membrane proteins embedded in a relevant cell membrane model have been challenging due to the big size of the simulation system, but especially coarse-graining has helped to reduce the computational cost. Inclusion of the membrane in MD simulations has revealed important insights into lipid-protein interactions, the function of membrane proteins, as well as the ligand entry and exit into the target binding site.
Apart from the first steps of the drug discovery process, MD simulations have also shown to be useful in pharmaceutical development and formulations studies. For example, crystalline and amorphous drugs, drug-polymer formulations, or drug-loaded nanoparticles can be studied by MD simulations to complement experimental studies. Molecular-level insights into such systems can help in improving the solubility, stability, or other properties of drug formulations.
In conclusion, MD simulations can serve as a powerful tool in facilitating the early phases of the modern drug discovery and development process. In the future, MD simulations will likely gain even more importance due to the theoretical and technological advancements in the field.
Author Contributions
O.M.H.S.-A. coordinated and compiled the review. Specifically, O.M.H.S.-A., I.A., R.B., P.M., A.S., R.V.H., S.H., A.K., A.H.J., M.L.-K., T.P., A.S.L., M.U.M., M.V., G.M., A.N.-A. and K.S. wrote the manuscript. E.L. supervised and contributed to the chapters describing binding energy calculations and GPCR simulations. A.M.J.J.B. supervised and contributed to the chapter about peptide-protein docking. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the BioExcel CoE (www.bioexcel.eu), a project funded by the European Horizon 2020 program under grant agreements 675728 and 823830 (R.V.H.); the Åbo Akademi University research mobility program in the research profiling area of Drug Development and Diagnostics (R.B.); Åbo Akademi University research grant (A.S.); Tor, Joe and Pentti Borg’s Foundation in 2020 (P.M.); the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes, process number 88881.162167/2017-01), the Alexander von Humboldt Foundation, and the Klaus Tschira Foundation (A.N.A.); the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 839230 and Orion Research Foundation sr. (T.P.); Vinnova (Dnr 2017-02690), the European Research Council Grant 638965 (A.K. and S.H.) and the Academy of Finland grant number 315824 (M.L.-K.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We acknowledge the NordForsk Nordic POP (Patient Oriented Products) university consortium, the joint Drug Development and Diagnostics research profiling area of the University of Turku and Åbo Akademi University, and the science program of the Swedish Drug Delivery Forum (SDDF). A.N.A. thanks Rebecca Wade for suggestions on the manuscript (drug binding kinetics section). M.L.-K. acknowledges CSC—IT Center for Science, Finland, for computational resources.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the writing of the manuscript, or in the decision to publish the results.
| Contents | |
| 1. Introduction...................................................................................................................................................................................................................................... | 2 |
| 1.1. Classical Molecular Dynamics Simulations............................................................................................................................................................................ | 2 |
| 1.2. Faster and Longer Without Atomistic Details: Coarse-Grained Simulations..................................................................................................................... | 4 |
| 1.3. Zooming Into the Details of Chemical Reactions: Quantum Mechanics Simulations....................................................................................................... | 5 |
| 2. Molecular Dynamics in Drug Discovery....................................................................................................................................................................................... | 6 |
| 2.1. Exploring the Dynamics and Function of Drug Targets....................................................................................................................................................... | 6 |
| 2.1.1. Ligand-Binding Dynamics of Sirtuins—in Search of Therapeutic Regulators............................................................................................................ | 7 |
| 2.1.2. RAS—Uncovering the Conformational Dynamics of a Challenging Anticancer Drug Target.................................................................................. | 10 |
| 2.1.3. Extremely Challenging Targets—Intrinsically Disordered Proteins............................................................................................................................ | 12 |
| 2.1.4. Molecular Dynamics Simulations in Antibody Design.................................................................................................................................................. | 15 |
| 2.2. Simulating Drug-Target Interactions...................................................................................................................................................................................... | 16 |
| 2.2.1. Binding Energy Estimation............................................................................................................................................................................................... | 16 |
| 2.2.2. Drug-Protein Binding Kinetics Estimation...................................................................................................................................................................... | 20 |
| 2.2.3. Peptide-Protein Docking: Tackling the Flexibility Challenge with Molecular Dynamics Simulations.................................................................... | 23 |
| 2.3. Molecular Dynamics Simulations of Membrane Proteins.................................................................................................................................................... | 25 |
| 2.3.1. Molecular Dynamics Simulations of GPCRs and Ion channels.................................................................................................................................... | 25 |
| 2.3.2. Drug Metabolizing Cytochrome P450 Enzymes............................................................................................................................................................. | 28 |
| 3. Molecular Dynamics in Pharmaceutical Development............................................................................................................................................................... | 30 |
| 3.1. MD Studies of Crystalline and Amorphous Solids............................................................................................................................................................... | 30 |
| 3.2. Amorphous Drug-Polymer Formulations.............................................................................................................................................................................. | 32 |
| 3.3. Drug Solubility.......................................................................................................................................................................................................................... | 33 |
| 3.4. Nanoparticle Simulations......................................................................................................................................................................................................... | 35 |
| 3.4.1. Structural Characteristics.................................................................................................................................................................................................. | 35 |
| 3.4.2. Drug Loading and Release................................................................................................................................................................................................ | 36 |
| 3.4.3. Diffusion through Cell Protecting Layers....................................................................................................................................................................... | 37 |
| 3.4.4. Direct Membrane Penetration.......................................................................................................................................................................................... | 37 |
| 3.4.5. Interactions with Viruses and Biomacromolecules........................................................................................................................................................ | 38 |
| 4. Conclusions...................................................................................................................................................................................................................................... | 38 |
| References............................................................................................................................................................................................................................................ | 41 |
References
- Leach, A.R. Molecular Modelling: Principles and Applications, 2nd ed.; Pearson Education: Harlow, UK, 2001. [Google Scholar]
- Van Gunsteren, W.F.; Berendsen, H.J.C. Computer Simulation of Molecular Dynamics: Methodology, Applications, and Perspectives in Chemistry. Angew. Chem. Int. Ed. Engl. 1990, 29, 992–1023. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Kuhlman, B.; Bradley, P. Advances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol. 2019, 20, 681–697. [Google Scholar] [CrossRef] [PubMed]
- Monticelli, L.; Tieleman, D.P. Force fields for classical molecular dynamics. Methods Mol. Biol. 2013, 924, 197–213. [Google Scholar] [CrossRef] [PubMed]
- Lyubartsev, A.P.; Rabinovich, A.L. Force Field Development for Lipid Membrane Simulations. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2483–2497. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.Y.; MacKerell, A.D., Jr. Force Fields for Small Molecules. Methods Mol. Biol. 2019, 2022, 21–54. [Google Scholar] [CrossRef]
- Hubbard, R.E. Molecular graphics and modeling: Tools of the trade. In Guidebook on Molecular Modeling in Drug Design; Cohen, N.C., Ed.; Academic Press: New York, NY, USA, 1996; pp. 19–54. [Google Scholar]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.C.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks III, C.L.; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. II. MMFF94 van der Waals and electrostatic parameters for intermolecular interactions. J. Comput. Chem. 1996, 17, 520–552. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. III. Molecular geometries and vibrational frequencies for MMFF94. J. Comput. Chem. 1996, 17, 553–586. [Google Scholar] [CrossRef]
- Halgren, T.A.; Nachbar, R.B. Merck molecular force field. IV. Conformational energies and geometries for MMFF94. J. Comput. Chem. 1996, 17, 587–615. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. V. Extension of MMFF94 using experimental data, additional computational data, and empirical rules. J. Comput. Chem. 1996, 17, 616–641. [Google Scholar] [CrossRef]
- Harder, E.; Damm, W.; Maple, J.; Wu, C.; Reboul, M.; Xiang, J.Y.; Wang, L.; Lupyan, D.; Dahlgren, M.K.; Knight, J.L.; et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput. 2016, 12, 281–296. [Google Scholar] [CrossRef] [PubMed]
- Daura, X.; Mark, A.E.; Van Gunsteren, W.F. Parametrization of aliphatic CHn united atoms of GROMOS96 force field. J. Comput. Chem. 1998, 19, 535–547. [Google Scholar] [CrossRef]
- Schuler, L.D.; Daura, X.; Van Gunsteren, W.F. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 2001, 22, 1205–1218. [Google Scholar] [CrossRef]
- Horta, B.A.C.; Fuchs, P.F.J.; van Gunsteren, W.F.; Hünenberger, P.H. New interaction parameters for oxygen compounds in the GROMOS force field: Improved pure-liquid and solvation properties for alcohols, ethers, aldehydes, ketones, carboxylic acids, and esters. J. Chem. Theory Comput. 2011, 7, 1016–1031. [Google Scholar] [CrossRef] [PubMed]
- Horta, B.A.C.; Merz, P.T.; Fuchs, P.F.J.; Dolenc, J.; Riniker, S.; Hünenberger, P.H. A GROMOS-compatible force field for small organic molecules in the condensed phase: The 2016H66 parameter set. J. Chem. Theory Comput. 2016, 12, 3825–3850. [Google Scholar] [CrossRef]
- Marzuoli, I.; Margreitter, C.; Fraternali, F. Lipid Head Group Parameterization for GROMOS 54A8: A Consistent Approach with Protein Force Field Description. J. Chem. Theory Comput. 2019, 15, 5175–5193. [Google Scholar] [CrossRef] [PubMed]
- Berger, O.; Edholm, O.; Jähnig, F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997, 72, 2002–2013. [Google Scholar] [CrossRef]
- Venable, R.M.; Sodt, A.J.; Rogaski, B.; Rui, H.; Hatcher, E.; MacKerell, A.D., Jr.; Pastor, R.W.; Klauda, J.B. CHARMM all-atom additive force field for sphingomyelin: Elucidation of hydrogen bonding and of positive curvature. Biophys. J. 2014, 107, 134–145. [Google Scholar] [CrossRef]
- Lee, S.; Tran, A.; Allsopp, M.; Lim, J.B.; Hénin, J.; Klauda, J.B. CHARMM36 United Atom Chain Model for Lipids and Surfactants. J. Phys. Chem. B 2014, 118, 547–556. [Google Scholar] [CrossRef] [PubMed]
- Jämbeck, J.P.M.; Lyubartsev, A.P. Another Piece of the Membrane Puzzle: Extending Slipids Further. J. Chem. Theory Comput. 2013, 9, 774–784. [Google Scholar] [CrossRef] [PubMed]
- Dickson, C.J.; Madej, B.D.; Skjevik, Å.A.; Betz, R.M.; Teigen, K.; Gould, I.R.; Walker, R.C. Lipid14: The Amber Lipid Force Field. J. Chem. Theory Comput. 2014, 10, 865–879. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411. [Google Scholar] [CrossRef]
- McCammon, J.G. Dynamics of folded proteins. Nature 1977, 267, 585–590. [Google Scholar] [CrossRef]
- Zou, Y.; Qian, Z.; Chen, Y.; Qian, H.; Wei, G.; Zhang, Q. Norepinephrine Inhibits Alzheimer’s Amyloid-β Peptide Aggregation and Destabilizes Amyloid-β Protofibrils: A Molecular Dynamics Simulation Study. ACS Chem. Neurosci. 2019, 10, 1585–1594. [Google Scholar] [CrossRef]
- Neale, C.; García, A.E. The Plasma Membrane as a Competitive Inhibitor and Positive Allosteric Modulator of KRas4B Signaling. Biophys. J. 2020. [Google Scholar] [CrossRef]
- Abel, R.; Wang, L.; Harder, E.D.; Berne, B.J.; Friesner, R.A. Advancing Drug Discovery through Enhanced Free Energy Calculations. Acc. Chem. Res. 2017, 50, 1625–1632. [Google Scholar] [CrossRef]
- Donnini, S.; Ullmann, R.T.; Groenhof, G.; Grubmüller, H. Charge-Neutral Constant pH Molecular Dynamics Simulations Using a Parsimonious Proton Buffer. J. Chem. Theory Comput. 2016, 12, 1040–1051. [Google Scholar] [CrossRef]
- Duan, L.; Guo, X.; Cong, Y.; Feng, G.; Li, Y.; Zhang, J.Z.H. Accelerated Molecular Dynamics Simulation for Helical Proteins Folding in Explicit Water. Front. Chem. 2019, 7, 540. [Google Scholar] [CrossRef]
- Maffeo, C.; Bhattacharya, S.; Yoo, J.; Wells, D.; Aksimentiev, A. Modeling and Simulation of Ion Channels. Chem. Rev. 2012, 112, 6250–6284. [Google Scholar] [CrossRef] [PubMed]
- De Vivo, M.; Masetti, M.; Bottegoni, G.; Cavalli, A. Role of Molecular Dynamics and Related Methods in Drug Discovery. J. Med. Chem. 2016, 59, 4035–4061. [Google Scholar] [CrossRef] [PubMed]
- Hollingsworth, S.A.; Dror, R.O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [PubMed]
- Durrant, J.D.; Kochanek, S.E.; Casalino, L.; Ieong, P.U.; Dommer, A.C.; Amaro, R.E. Mesoscale All-Atom Influenza Virus Simulations Suggest New Substrate Binding Mechanism. ACS Cent. Sci. 2020, 6, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Nishima, W.; Daniels, M.; Bascom, G.; Kobayashi, C.; Adedoyin, A.; Wall, M.; Lappala, A.; Phillips, D.; Fischer, W.; et al. Scaling molecular dynamics beyond 100,000 processor cores for large-scale biophysical simulations. J. Comput. Chem. 2019, 40, 1919–1930. [Google Scholar] [CrossRef] [PubMed]
- Brooijmans, N.; Kuntz, I.D. Molecular recognition and docking algorithms. Annu Rev. Biophys. Biomol. Struct. 2003, 32, 335–373. [Google Scholar] [CrossRef] [PubMed]
- Pantsar, T.; Poso, A. Binding Affinity via Docking: Fact and Fiction. Molecules 2018, 23, 1899. [Google Scholar] [CrossRef]
- Salmaso, V.; Moro, S. Bridging Molecular Docking to Molecular Dynamics in Exploring Ligand-Protein Recognition Process: An Overview. Front. Pharmacol. 2018, 9, 923. [Google Scholar] [CrossRef]
- Riniker, S.; van Gunsteren, W.F. A simple, efficient polarizable coarse-grained water model for molecular dynamics simulations. J. Chem. Phys. 2011, 134, 084110. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Ruskamo, S.; Yadav, R.P.; Sharma, S.; Lehtimäki, M.; Laulumaa, S.; Aggarwal, S.; Simons, M.; Bürck, J.; Ulrich, A.S.; Juffer, A.H. Atomic resolution view into the structure–function relationships of the human myelin peripheral membrane protein P2. Acta Cryst. Sect. D Biol. Cryst. 2014, 70, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [PubMed]
- Donnini, S.; Juffer, A.H. Calculation of affinities of peptides for proteins. J. Comput. Chem. 2004, 25, 393–411. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Truhlar, D.G. Quantum mechanical methods for enzyme kinetics. Annu Rev. Phys. Chem. 2002, 53, 467–505. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM studies of enzymes. Curr. Opin. Chem. Biol. 2007, 11, 182–187. [Google Scholar] [CrossRef]
- Sharma, S.; Rauk, A.; Juffer, A.H. A DFT Study on the Formation of a Phosphohistidine Intermediate in Prostatic Acid Phosphatase. J. Am. Chem. Soc. 2008, 130, 9708–9716. [Google Scholar] [CrossRef]
- Sharma, S.; Bhaumik, P.; Schmitz, W.; Venkatesan, R.; Hiltunen, J.K.; Conzelmann, E.; Juffer, A.H.; Wierenga, R.K. The Enolization Chemistry of a Thioester-Dependent Racemase: The 1.4 Å Crystal Structure of a Reaction Intermediate Complex Characterized by Detailed QM/MM Calculations. J. Phys. Chem. B 2012, 116, 3619–3629. [Google Scholar] [CrossRef]
- Sharma, S.; Pirilä, P.; Kaija, H.; Porvari, K.; Vihko, P.; Juffer, A.H. Theoretical investigations of prostatic acid phosphatase. Proteins 2005, 58, 295–308. [Google Scholar] [CrossRef]
- Liu, X.; Shi, D.; Zhou, S.; Liu, H.; Liu, H.; Yao, X. Molecular dynamics simulations and novel drug discovery. Exp. Opin. Drug Discov. 2018, 13, 23–37. [Google Scholar] [CrossRef]
- Bera, I.; Payghan, P.V. Use of Molecular Dynamics Simulations in Structure-Based Drug Discovery. Curr. Pharm. Des. 2019, 25, 3339–3349. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Rosell, G.; Giorgino, T.; Harvey, M.J.; de Fabritiis, G. Drug Discovery and Molecular Dynamics: Methods, Applications and Perspective Beyond the Second Timescale. Curr. Top. Med. Chem. 2017, 17, 2617–2625. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, A.; Coote, M.L.; Barakat, K. Molecular dynamics-driven drug discovery: Leaping forward with confidence. Drug Discov. Today 2017, 22, 249–269. [Google Scholar] [CrossRef] [PubMed]
- Fox, S.J.; Li, J.; Tan, Y.S.; Nguyen, M.N.; Pal, A.; Ouaray, Z.; Yadahalli, S.; Kannan, S. The Multifaceted Roles of Molecular Dynamics Simulations in Drug Discovery. Curr. Pharm. Des. 2016, 22, 3585–3600. [Google Scholar] [CrossRef] [PubMed]
- Lee, H. Molecular Simulations of PEGylated Biomolecules, Liposomes, and Nanoparticles for Drug Delivery Applications. Pharmaceutics 2020, 12, 533. [Google Scholar] [CrossRef] [PubMed]
- Al-Qattan, M.N.; Deb, P.K.; Tekade, R.K. Molecular dynamics simulation strategies for designing carbon-nanotube-based targeted drug delivery. Drug Discov. Today 2018, 23, 235–250. [Google Scholar] [CrossRef]
- Bunker, A.; Róg, T. Mechanistic Understanding From Molecular Dynamics Simulation in Pharmaceutical Research 1: Drug Delivery. Front. Mol. Biosci. 2020, 7, 604770. [Google Scholar] [CrossRef]
- Rocco, P.; Cilurzo, F.; Minghetti, P.; Vistoli, G.; Pedretti, A. Molecular Dynamics as a tool for in silico screening of skin permeability. Eur. J. Pharm. Sci. 2017, 106, 328–335. [Google Scholar] [CrossRef]
- Spencer-Smith, R.; O’Bryan, J.P. Direct inhibition of RAS: Quest for the Holy Grail? Semin. Cancer Biol. 2019, 54, 138–148. [Google Scholar] [CrossRef]
- Martínez-Redondo, P.; Vaquero, A. The diversity of histone versus nonhistone sirtuin substrates. Genes Cancer 2013, 4, 148–163. [Google Scholar] [CrossRef]
- Mei, Z.; Zhang, X.; Yi, J.; Huang, J.; He, J.; Tao, Y. Sirtuins in metabolism, DNA repair and cancer. J. Exp. Clin. Cancer Res. 2016, 35, 182. [Google Scholar] [CrossRef] [PubMed]
- Carafa, V.; Rotili, D.; Forgione, M.; Cuomo, F.; Serretiello, E.; Hailu, G.S.; Jarho, E.; Lahtela-Kakkonen, M.; Mai, A.; Altucci, L. Sirtuin functions and modulation: From chemistry to the clinic. Clin. Epigenetics 2016, 8, 61. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Sinclair, D.A.; Ellis, J.L.; Steegborn, C. Sirtuin activators and inhibitors: Promises, achievements, and challenges. Pharmacol. Ther. 2018, 188, 140–154. [Google Scholar] [CrossRef] [PubMed]
- Kiviranta, P.; Salo, H.S.; Leppänen, J.; Rinne, V.M.; Kyrylenko, S.; Kuusisto, E.; Suuronen, T.; Salminen, A.; Poso, A.; Lahtela-Kakkonen, M.; et al. Characterization of the binding properties of SIRT2 inhibitors with a N-(3-phenylpropenoyl)-glycine tryptamide backbone. Bioorg. Med. Chem. 2008, 16, 8054–8062. [Google Scholar] [CrossRef]
- van Gunsteren, W.F.; Billeter, S.R.; Eising, A.A.; Hünenberger, P.H.; Krüger, P.; Mark, A.E.; Scott, W.; Tironi, I.G. Biomolecular Simulation: The GROMOS96 Manual and User Guide; Vdf Hochschulverlag AG an der ETH Zürich: Zürich, Switzerland, 1996. [Google Scholar]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef]
- Rumpf, T.; Schiedel, M.; Karaman, B.; Roessler, C.; North, B.J.; Lehotzky, A.; Oláh, J.; Ladwein, K.I.; Schmidtkunz, K.; Gajer, M.; et al. Selective Sirt2 inhibition by ligand-induced rearrangement of the active site. Nat. Commun. 2015, 6, 6263. [Google Scholar] [CrossRef]
- Sakkiah, S.; Thangapandian, S.; Park, C.; Son, M.; Lee, K.W. Molecular docking and dynamics simulation, receptor-based hypothesis: Application to identify novel sirtuin 2 inhibitors. Chem. Biol. Drug Design 2012, 80, 315–327. [Google Scholar] [CrossRef]
- Sakkiah, S.; Chandrasekaran, M.; Lee, Y.; Kim, S.; Lee, K.W. Molecular modeling study for conformational changes of Sirtuin 2 due to substrate and inhibitor binding. J. Biomol. Struct. Dyn. 2012, 30, 235–254. [Google Scholar] [CrossRef]
- Sakkiah, S.; Arooj, M.; Kumar, M.R.; Eom, S.H.; Lee, K.W. Identification of inhibitor binding site in human sirtuin 2 using molecular docking and dynamics simulations. PLoS ONE 2013, 8, e51429. [Google Scholar] [CrossRef]
- Sakkiah, S.; Arooj, M.; Cao, G.P.; Lee, K.W. Insight the C-site pocket conformational changes responsible for sirtuin 2 activity using molecular dynamics simulations. PLoS ONE 2013, 8, e59278. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Flick, F.; Verheugd, P.; Carloni, P.; Lüscher, B.; Rossetti, G. Insight into the Mechanism of Intramolecular Inhibition of the Catalytic Activity of Sirtuin 2 (SIRT2). PLoS ONE 2015, 10, e0139095. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Jian, Y.; Sun, M.; Chang, T.; Lee, C.; Chen, C.Y. Investigation of silent information regulator 1 (Sirt1) agonists from Traditional Chinese Medicine. J. Biomol. Struct. Dyn. 2013, 31, 1207–1218. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, B.; Ramu, M.; Mathur, S.; Unni, S.; Thiyagarajan, S. Identification of new inhibitors for human SIRT1: An in-silico approach. Med. Chem. 2016, 12, 347–361. [Google Scholar] [CrossRef]
- Chuang, Y.; Chang, C.; Lin, J.; Yang, C. Molecular modelling studies of sirtuin 2 inhibitors using three-dimensional structure-activity relationship analysis and molecular dynamics simulations. Mol. BioSyst. 2015, 11, 723–733. [Google Scholar] [CrossRef]
- Sinha, S.; Patel, S.; Athar, M.; Vora, J.; Chhabria, M.T.; Jha, P.C.; Shrivastava, N. Structure-based identification of novel sirtuin inhibitors against triple negative breast cancer: An in silico and in vitro study. Int. J. Biol. Macromol. 2019, 140, 454–468. [Google Scholar] [CrossRef]
- Bowers, K.J.; Chow, D.E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; Klepeis, J.L.; Kolossvary, I.; Moraes, M.A.; Sacerdoti, F.D.; et al. Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters, SC 06. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006; p. 43. [Google Scholar]
- Azminah, A.; Erlina, L.; Radji, M.; Mun’im, A.; Syahdi, R.R.; Yanuar, A. In silico and in vitro identification of candidate SIRT1 activators from Indonesian medicinal plants compounds database. Comput. Biol. Chem. 2019, 83, 107096. [Google Scholar] [CrossRef]
- Hałasa, M.; Bartuzi, D.; Cieślak, D.; Kaczor, A.A.; Miziak, P.; Stepulak, A.; Matosiuk, D. Role of N-terminus in function and dynamics of sirtuin 7: An in silico study. J. Biomol. Struct. Dyn. 2019. [Google Scholar] [CrossRef]
- Madsen, A.S.; Andersen, C.; Daoud, M.; Anderson, K.A.; Laursen, J.S.; Chakladar, S.; Huynh, F.K.; Colaço, A.R.; Backos, D.S.; Fristrup, P.; et al. Investigating the Sensitivity of NAD+-dependent Sirtuin Deacylation Activities to NADH. J. Biol. Chem. 2016, 291, 7128–7141. [Google Scholar] [CrossRef]
- Wennerberg, K.; Rossman, K.L.; Der, C.J. The Ras superfamily at a glance. J. Cell Sci. 2005, 118, 843–846. [Google Scholar] [CrossRef] [PubMed]
- Hancock, J.F. Ras proteins: Different signals from different locations. Nat. Rev. Mol. Cell Biol. 2003, 4, 373–384. [Google Scholar] [CrossRef]
- Vetter, I.R.; Wittinghofer, A. The guanine nucleotide-binding switch in three dimensions. Science 2001, 294, 1299–1304. [Google Scholar] [CrossRef] [PubMed]
- Hennig, A.; Markwart, R.; Esparza-Franco, M.; Ladds, G.; Rubio, I. Ras activation revisited: Role of GEF and GAP systems. Biol. Chem. 2015, 396, 831–848. [Google Scholar] [CrossRef] [PubMed]
- Bos, J.L.; Rehmann, H.; Wittinghofer, A. GEFs and GAPs: Critical elements in the control of small G proteins. Cell 2007, 129, 865–877. [Google Scholar] [CrossRef] [PubMed]
- Simanshu, D.K.; Nissley, D.V.; McCormick, F. RAS Proteins and Their Regulators in Human Disease. Cell 2017, 170, 17–33. [Google Scholar] [CrossRef]
- Mo, S.P.; Coulson, J.M.; Prior, I.A. RAS variant signalling. Biochem. Soc. Trans. 2018, 46, 1325–1332. [Google Scholar] [CrossRef]
- Johnson, C.W.; Reid, D.; Parker, J.A.; Salter, S.; Knihtila, R.; Kuzmic, P.; Mattos, C. The small GTPases K-Ras, N-Ras, and H-Ras have distinct biochemical properties determined by allosteric effects. J. Biol. Chem. 2017, 292, 12981–12993. [Google Scholar] [CrossRef]
- Parker, J.A.; Mattos, C. The K-Ras, N-Ras, and H-Ras Isoforms: Unique Conformational Preferences and Implications for Targeting Oncogenic Mutants. Cold Spring Harbor Perspect. Med. 2018, 8, a031427. [Google Scholar] [CrossRef]
- Hunter, J.C.; Manandhar, A.; Carrasco, M.A.; Gurbani, D.; Gondi, S.; Westover, K.D. Biochemical and Structural Analysis of Common Cancer-Associated KRAS Mutations. Mol. Cancer Res. MCR 2015, 13, 1325–1335. [Google Scholar] [CrossRef]
- Haigis, K.M. KRAS Alleles: The Devil Is in the Detail. Trends Cancer 2017, 3, 686–697. [Google Scholar] [CrossRef]
- Poulin, E.J.; Bera, A.K.; Lu, J.; Lin, Y.; Strasser, S.D.; Paulo, J.A.; Huang, T.Q.; Morales, C.; Yan, W.; Cook, J.; et al. Tissue-Specific Oncogenic Activity of KRASA146T. Cancer Discov. 2019, 9, 738–755. [Google Scholar] [CrossRef] [PubMed]
- Winters, I.P.; Chiou, S.; Paulk, N.K.; McFarland, C.D.; Lalgudi, P.V.; Ma, R.K.; Lisowski, L.; Connolly, A.J.; Petrov, D.A.; Kay, M.A.; et al. Multiplexed in vivo homology-directed repair and tumor barcoding enables parallel quantification of Kras variant oncogenicity. Nat. Commun. 2017, 8, 2053. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, G.A.; Baker, N.M.; Miermont, A.M.; Thurman, R.D.; Pierobon, M.; Tran, T.H.; Anderson, A.O.; Waters, A.M.; Diehl, J.N.; Papke, B.; et al. Atypical KRASG12R Mutant Is Impaired in PI3K Signaling and Macropinocytosis in Pancreatic Cancer. Cancer Discov. 2019. [Google Scholar] [CrossRef] [PubMed]
- Chang, E.H.; Gonda, M.A.; Ellis, R.W.; Scolnick, E.M.; Lowy, D.R. Human genome contains four genes homologous to transforming genes of Harvey and Kirsten murine sarcoma viruses. Proc. Natl. Acad. Sci. USA 1982, 79, 4848–4852. [Google Scholar] [CrossRef] [PubMed]
- Ostrem, J.M.; Peters, U.; Sos, M.L.; Wells, J.A.; Shokat, K.M. K-Ras(G12C) inhibitors allosterically control GTP affinity and effector interactions. Nature 2013, 503, 548–551. [Google Scholar] [CrossRef]
- Cruz-Migoni, A.; Canning, P.; Quevedo, C.E.; Bataille, C.J.R.; Bery, N.; Miller, A.; Russell, A.J.; Phillips, S.E.V.; Carr, S.B.; Rabbitts, T.H. Structure-based development of new RAS-effector inhibitors from a combination of active and inactive RAS-binding compounds. Proc. Natl. Acad. Sci. USA 2019, 116, 2545–2550. [Google Scholar] [CrossRef]
- Quevedo, C.E.; Cruz-Migoni, A.; Bery, N.; Miller, A.; Tanaka, T.; Petch, D.; Bataille, C.J.R.; Lee, L.Y.W.; Fallon, P.S.; Tulmin, H.; et al. Small molecule inhibitors of RAS-effector protein interactions derived using an intracellular antibody fragment. Nat. Commun. 2018, 9, 3169. [Google Scholar] [CrossRef]
- Sun, Q.; Burke, J.P.; Phan, J.; Burns, M.C.; Olejniczak, E.T.; Waterson, A.G.; Lee, T.; Rossanese, O.W.; Fesik, S.W. Discovery of small molecules that bind to K-Ras and inhibit Sos-mediated activation. Angew. Chem. 2012, 51, 6140–6143. [Google Scholar] [CrossRef]
- Kessler, D.; Gmachl, M.; Mantoulidis, A.; Martin, L.J.; Zoephel, A.; Mayer, M.; Gollner, A.; Covini, D.; Fischer, S.; Gerstberger, T.; et al. Drugging an undruggable pocket on KRAS. Proc. Natl. Acad. Sci. USA 2019, 116, 15823–15829. [Google Scholar] [CrossRef]
- Nussinov, R.; Tsai, C.; Jang, H. Oncogenic Ras Isoforms Signaling Specificity at the Membrane. Cancer Res. 2018, 78, 593–602. [Google Scholar] [CrossRef]
- Lu, J.; Bera, A.K.; Gondi, S.; Westover, K.D. KRAS Switch Mutants D33E and A59G Crystallize in the State 1 Conformation. Biochemistry 2018, 57, 324–333. [Google Scholar] [CrossRef]
- Dharmaiah, S.; Tran, T.H.; Messing, S.; Agamasu, C.; Gillette, W.K.; Yan, W.; Waybright, T.; Alexander, P.; Esposito, D.; Nissley, D.V.; et al. Structures of N-terminally processed KRAS provide insight into the role of N-acetylation. Sci. Rep. 2019, 9, 10512. [Google Scholar] [CrossRef]
- Fetics, S.K.; Guterres, H.; Kearney, B.M.; Buhrman, G.; Ma, B.; Nussinov, R.; Mattos, C. Allosteric effects of the oncogenic RasQ61L mutant on Raf-RBD. Structure 2015, 23, 505–516. [Google Scholar] [CrossRef] [PubMed]
- Rabara, D.; Tran, T.H.; Dharmaiah, S.; Stephens, R.M.; McCormick, F.; Simanshu, D.K.; Holderfield, M. KRAS G13D sensitivity to neurofibromin-mediated GTP hydrolysis. Proc. Natl. Acad. Sci. USA 2019, 116, 22122–22131. [Google Scholar] [CrossRef] [PubMed]
- Hillig, R.C.; Sautier, B.; Schroeder, J.; Moosmayer, D.; Hilpmann, A.; Stegmann, C.M.; Werbeck, N.D.; Briem, H.; Boemer, U.; Weiske, J.; et al. Discovery of potent SOS1 inhibitors that block RAS activation via disruption of the RAS-SOS1 interaction. Proc. Natl. Acad. Sci. USA 2019, 116, 2551–2560. [Google Scholar] [CrossRef] [PubMed]
- Mazhab-Jafari, M.; Marshall, C.B.; Smith, M.J.; Gasmi-Seabrook, G.; Stathopulos, P.B.; Inagaki, F.; Kay, L.E.; Neel, B.G.; Ikura, M. Oncogenic and RASopathy-associated K-RAS mutations relieve membrane-dependent occlusion of the effector-binding site. Proc. Natl. Acad. Sci. USA 2015, 112, 6625. [Google Scholar] [CrossRef] [PubMed]
- Pantsar, T. The current understanding of KRAS protein structure and dynamics. Comput. Struct. Biotechnol. J. 2020, 18, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Bermudez, M.; Mortier, J.; Rakers, C.; Sydow, D.; Wolber, G. More than a look into a crystal ball: Protein structure elucidation guided by molecular dynamics simulations. Drug Discov. Today 2016, 21, 1799–1805. [Google Scholar] [CrossRef]
- Pantsar, T.; Rissanen, S.; Dauch, D.; Laitinen, T.; Vattulainen, I.; Poso, A. Assessment of mutation probabilities of KRAS G12 missense mutants and their long-timescale dynamics by atomistic molecular simulations and Markov state modeling. PLoS Comput. Biol. 2018, 14, e1006458. [Google Scholar] [CrossRef]
- Husic, B.E.; Pande, V.S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140, 2386–2396. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.J.; Ikura, M. Integrated RAS signaling defined by parallel NMR detection of effectors and regulators. Nat. Chem. Biol. 2014, 10, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Bera, A.K.; Lu, J.; Wales, T.E.; Gondi, S.; Gurbani, D.; Nelson, A.; Engen, J.R.; Westover, K.D. Structural basis of the atypical activation mechanism of KRASV14I. J. Biol. Chem. 2019, 294, 13964–13972. [Google Scholar] [CrossRef]
- Pantsar, T. KRAS(G12C)–AMG 510 interaction dynamics revealed by all-atom molecular dynamics simulations. Sci. Rep. 2020, 10, 11992. [Google Scholar] [CrossRef] [PubMed]
- Canon, J.; Rex, K.; Saiki, A.Y.; Mohr, C.; Cooke, K.; Bagal, D.; Gaida, K.; Holt, T.; Knutson, C.G.; Koppada, N.; et al. The clinical KRAS(G12C) inhibitor AMG 510 drives anti-tumour immunity. Nature 2019, 575, 217–223. [Google Scholar] [CrossRef] [PubMed]
- Prakash, P.; Gorfe, A.A. Probing the Conformational and Energy Landscapes of KRAS Membrane Orientation. J. Phys. Chem. B 2019, 123, 8644–8652. [Google Scholar] [CrossRef]
- Prakash, P.; Litwin, D.; Liang, H.; Sarkar-Banerjee, S.; Dolino, D.; Zhou, Y.; Hancock, J.F.; Jayaraman, V.; Gorfe, A.A. Dynamics of Membrane-Bound G12V-KRAS from Simulations and Single-Molecule FRET in Native Nanodiscs. Biophys. J. 2019, 116, 179–183. [Google Scholar] [CrossRef]
- Barklis, E.; Stephen, A.G.; Staubus, A.O.; Barklis, R.L.; Alfadhli, A. Organization of Farnesylated, Carboxymethylated KRAS4B on Membranes. J. Mol. Biol 2019, 431, 3706–3717. [Google Scholar] [CrossRef]
- Chung, J.K.; Lee, Y.K.; Denson, J.; Gillette, W.K.; Alvarez, S.; Stephen, A.G.; Groves, J.T. K-Ras4B Remains Monomeric on Membranes over a Wide Range of Surface Densities and Lipid Compositions. Biophys. J. 2018, 114, 137–145. [Google Scholar] [CrossRef]
- Sarkar-Banerjee, S.; Sayyed-Ahmad, A.; Prakash, P.; Cho, K.; Waxham, M.N.; Hancock, J.F.; Gorfe, A.A. Spatiotemporal Analysis of K-Ras Plasma Membrane Interactions Reveals Multiple High Order Homo-oligomeric Complexes. J. Am. Chem. Soc. 2017, 139, 13466–13475. [Google Scholar] [CrossRef]
- Muratcioglu, S.; Chavan, T.; Freed, B.; Jang, H.; Khavrutskii, L.; Freed, R.; Dyba, M.; Stefanisko, K.; Tarasov, S.; Gursoy, A.; et al. GTP-Dependent K-Ras Dimerization. Structure 2015, 23, 1325–1335. [Google Scholar] [CrossRef]
- Lee, K.; Fang, Z.; Enomoto, M.; Gasmi-Seabrook, G.; Zheng, L.; Koide, S.; Ikura, M.; Marshall, C.B. Two Distinct Structures of Membrane-Associated Homodimers of GTP- and GDP-Bound KRAS4B Revealed by Paramagnetic Relaxation Enhancement. Angew. Chem. Int. Ed. 2020, 59, 11037–11045. [Google Scholar] [CrossRef] [PubMed]
- Nussinov, R.; Tsai, C.; Jang, H. Oncogenic KRas mobility in the membrane and signaling response. In Seminars in Cancer Biology; Academic Press: Cambridge, UK, 2019; Volume 54, pp. 109–113. [Google Scholar] [CrossRef] [PubMed]
- Ambrogio, C.; Köhler, J.; Zhou, Z.; Wang, H.; Paranal, R.; Li, J.; Capelletti, M.; Caffarra, C.; Li, S.; Lv, Q.; et al. KRAS Dimerization Impacts MEK Inhibitor Sensitivity and Oncogenic Activity of Mutant KRAS. Cell 2018, 172, 857–868. [Google Scholar] [CrossRef] [PubMed]
- Mysore, V.P.; Zhou, Z.; Ambrogio, C.; Li, L.; Kapp, J.N.; Lu, C.; Wang, Q.; Tucker, M.R.; Okoro, J.J.; Nagy-Davidescu, G.; et al. A structural model of a Ras-Raf signalosome. bioRxiv 2020. [Google Scholar] [CrossRef]
- Prakash, P.; Gorfe, A.A. Lessons from computer simulations of Ras proteins in solution and in membrane. Biochim. Biophys. Acta 2013, 1830, 5211–5218. [Google Scholar] [CrossRef]
- Pálfy, G.; Menyhárd, D.K.; Perczel, A. Dynamically encoded reactivity of Ras enzymes: Opening new frontiers for drug discovery. Cancer Metastasis Rev. 2020. [Google Scholar] [CrossRef]
- Dunker, A.K.; Silman, I.; Uversky, V.N.; Sussman, J.L. Function and structure of inherently disordered proteins. Curr. Opin. Struct. Biol. 2008, 18, 756–764. [Google Scholar] [CrossRef]
- Sharma, R.; Raduly, Z.; Miskei, M.; Fuxreiter, M. Fuzzy complexes: Specific binding without complete folding. FEBS Lett. 2015, 589, 2533–2542. [Google Scholar] [CrossRef]
- Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Uversky, V.N.; Kurgan, L. Comprehensive review of methods for prediction of intrinsic disorder and its molecular functions. Cell Mol. Life Sci. 2017, 74, 3069–3090. [Google Scholar] [CrossRef] [PubMed]
- Sickmeier, M.; Hamilton, J.A.; LeGall, T.; Vacic, V.; Cortese, M.S.; Tantos, A.; Szabo, B.; Tompa, P.; Chen, J.; Uversky, V.N.; et al. DisProt: The Database of Disordered Proteins. Nucleic Acids Res. 2007, 35, 786. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Intrinsically disordered proteins and novel strategies for drug discovery. Exp. Opin. Drug Discov. 2012, 7, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Lin, X. Recent Advances in Computational Protocols Addressing Intrinsically Disordered Proteins. Biomolecules 2019, 9, 146. [Google Scholar] [CrossRef] [PubMed]
- Fisette, O.; Lagüe, P.; Gagné, S.; Morin, S. Synergistic applications of MD and NMR for the study of biological systems. J. Biomed. Biotechnol. 2012, 2012, 254208. [Google Scholar] [CrossRef]
- Zhou, R. Replica exchange molecular dynamics method for protein folding simulation. Methods Mol. Biol. 2007, 350, 205–223. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Geyer, C.J. Markov chain Monte Carlo maximum likelihood. Comput. Sci Stat. 1991, 23, 156–163. [Google Scholar]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Song, D.; Luo, R.; Chen, H.F. The IDP-Specific Force Field ff14IDPSFF Improves the Conformer Sampling of Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2017, 57, 1166–1178. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Wang, W.; Ye, W.; Ji, D.; Luo, R.; Chen, H.F. ff14IDPs force field improving the conformation sampling of intrinsically disordered proteins. Chem. Biol. Drug Des. 2017, 89, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Ji, D.; Wang, W.; Luo, R.; Chen, H.F. Test and Evaluation of ff99IDPs Force Field for Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2015, 55, 1021–1029. [Google Scholar] [CrossRef] [PubMed]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef]
- Liu, H.; Song, D.; Zhang, Y.; Yang, S.; Luo, R.; Chen, H.F. Extensive tests and evaluation of the CHARMM36IDPSFF force field for intrinsically disordered proteins and folded proteins. Phys. Chem. Chem. Phys. 2019, 21, 21918–21931. [Google Scholar] [CrossRef]
- Wu, H.; Wolynes, P.G.; Papoian, G.A. AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins. J. Phys. Chem. B 2018, 122, 11115–11125. [Google Scholar] [CrossRef]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Bomblies, R.; Luitz, M.P.; Scanu, S.; Madl, T.; Zacharias, M. Transient helicity in intrinsically disordered Axin-1 studied by NMR spectroscopy and molecular dynamics simulations. PLoS ONE 2017, 12, e0174337. [Google Scholar] [CrossRef]
- Jin, F.; Yu, C.; Lai, L.; Liu, Z. Ligand clouds around protein clouds: A scenario of ligand binding with intrinsically disordered proteins. PLoS Comput. Biol. 2013, 9, e1003249. [Google Scholar] [CrossRef]
- Fichou, Y.; Heyden, M.; Zaccai, G.; Weik, M.; Tobias, D.J. Molecular Dynamics Simulations of a Powder Model of the Intrinsically Disordered Protein Tau. J. Phys. Chem. B 2015, 119, 12580–12589. [Google Scholar] [CrossRef]
- Castro, T.G.; Munteanu, F.D.; Cavaco-Paulo, A. Electrostatics of Tau Protein by Molecular Dynamics. Biomolecules 2019, 9, 116. [Google Scholar] [CrossRef] [PubMed]
- Missimer, J.H.; Steinmetz, M.O.; van Gunsteren, W.F.; Dolenc, J. Influence of 63Ser Phosphorylation and Dephosphorylation on the Structure of the Stathmin Helical Nucleation Sequence: A Molecular Dynamics Study. Biochemistry 2012, 51, 8455–8463. [Google Scholar] [CrossRef] [PubMed]
- Cino, E.A.; Wong-ekkabut, J.; Karttunen, M.; Choy, W.Y. Microsecond molecular dynamics simulations of intrinsically disordered proteins involved in the oxidative stress response. PLoS ONE 2011, 6, e27371. [Google Scholar] [CrossRef] [PubMed]
- Apicella, A.; Marascio, M.; Colangelo, V.; Soncini, M.; Gautieri, A.; Plummer, C.J.G. Molecular dynamics simulations of the intrinsically disordered protein amelogenin. J. Biomol. Struct. Dyn. 2017, 35, 1813–1823. [Google Scholar] [CrossRef]
- Henriques, J.; Skepo, M. Molecular Dynamics Simulations of Intrinsically Disordered Proteins: On the Accuracy of the TIP4P-D Water Model and the Representativeness of Protein Disorder Models. J. Chem. Theory Comput. 2016, 12, 3407–3415. [Google Scholar] [CrossRef]
- Shrestha, U.R.; Juneja, P.; Zhang, Q.; Gurumoorthy, V.; Borreguero, J.M.; Urban, V.; Cheng, X.; Pingali, S.V.; Smith, J.C.; O’Neill, H.M.; et al. Generation of the configurational ensemble of an intrinsically disordered protein from unbiased molecular dynamics simulation. Proc. Natl. Acad. Sci. USA 2019, 116, 20446–20452. [Google Scholar] [CrossRef]
- Kasahara, K.; Shiina, M.; Higo, J.; Ogata, K.; Nakamura, H. Phosphorylation of an intrinsically disordered region of Ets1 shifts a multi-modal interaction ensemble to an auto-inhibitory state. Nucleic Acids Res. 2018, 46, 2243–2251. [Google Scholar] [CrossRef]
- Yu, C.; Niu, X.; Jin, F.; Liu, Z.; Jin, C.; Lai, L. Structure-based Inhibitor Design for the Intrinsically Disordered Protein c-Myc. Sci. Rep. 2016, 6, 22298. [Google Scholar] [CrossRef]
- Ball, K.A.; Wemmer, D.E.; Head-Gordon, T. Comparison of structure determination methods for intrinsically disordered amyloid-β peptides. J. Phys. Chem. B 2014, 118, 6405–6416. [Google Scholar] [CrossRef]
- Bottaro, S.; Lindorff-Larsen, K. Biophysical experiments and biomolecular simulations: A perfect match? Science 2018, 361, 355–360. [Google Scholar] [CrossRef]
- Fawzi, N.L.; Phillips, A.H.; Ruscio, J.Z.; Doucleff, M.; Wemmer, D.E.; Head-Gordon, T. Structure and dynamics of the Abeta(21-30) peptide from the interplay of NMR experiments and molecular simulations. J. Am. Chem. Soc. 2008, 130, 6145–6158. [Google Scholar] [CrossRef] [PubMed]
- Graen, T.; Klement, R.; Grupi, A.; Haas, E.; Grubmüller, H. Transient Secondary and Tertiary Structure Formation Kinetics in the Intrinsically Disordered State of α-Synuclein from Atomistic Simulations. Chem. Phys. Chem. 2018, 19, 2507–2511. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Luo, Y.; Ma, B.; Nussinov, R.; Wei, G. Conformational distribution and α-helix to β-sheet transition of human amylin fragment dimer. Biomacromolecules 2014, 15, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Chan-Yao-Chong, M.; Durand, D.; Ha-Duong, T. Molecular Dynamics Simulations Combined with Nuclear Magnetic Resonance and/or Small-Angle X-ray Scattering Data for Characterizing Intrinsically Disordered Protein Conformational Ensembles. J. Chem. Inform. Model. 2019, 59, 1743–1758. [Google Scholar] [CrossRef]
- Peng, H.P.; Lee, K.H.; Jian, J.W.; Yang, A.S. Origins of specificity and affinity in antibody-protein interactions. Proc. Natl. Acad. Sci. USA 2014, 111, 2656. [Google Scholar] [CrossRef]
- Bradbury, A.R.; Sidhu, S.; Dubel, S.; McCafferty, J. Beyond natural antibodies: The power of in vitro display technologies. Nat. Biotechnol. 2011, 29, 245–254. [Google Scholar] [CrossRef]
- Sinha, N.; Li, Y.; Lipschultz, C.A.; Smith-Gill, S.J. Understanding antibody-antigen associations by molecular dynamics simulations: Detection of important intra- and inter-molecular salt bridges. Cell Biochem. Biophys. 2007, 47, 361–375. [Google Scholar] [CrossRef]
- Shimba, N.; Kamiya, N.; Nakamura, H. Model Building of Antibody-Antigen Complex Structures Using GBSA Scores. J. Chem. Inf. Model. 2016, 56, 2005–2012. [Google Scholar] [CrossRef]
- Yamashita, T. Toward rational antibody design: Recent advancements in molecular dynamics simulations. Int. Immunol. 2018, 30, 133–140. [Google Scholar] [CrossRef]
- Kuroda, D.; Shirai, H.; Jacobson, M.P.; Nakamura, H. Computer-aided antibody design. Protein Eng. Des. Sel. 2012, 25, 507–521. [Google Scholar] [CrossRef]
- Bekker, G.J.; Ma, B.; Kamiya, N. Thermal stability of single-domain antibodies estimated by molecular dynamics simulations. Protein Sci. 2019, 28, 429–438. [Google Scholar] [CrossRef] [PubMed]
- Zabetakis, D.; Shriver-Lake, L.; Olson, M.A.; Goldman, E.R.; Anderson, G.P. Experimental evaluation of single-domain antibodies predicted by molecular dynamics simulations to have elevated thermal stability. Protein Sci. Public. Protein Soc. 2019, 28, 1909–1912. [Google Scholar] [CrossRef] [PubMed]
- Chennamsetty, N.; Voynov, V.; Kayser, V.; Helk, B.; Trout, B.L. Design of therapeutic proteins with enhanced stability. Proc. Natl. Acad. Sci. USA 2009, 106, 11937–11942. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Fu, A.; Zhang, L. An Overview of Scoring Functions Used for Protein-Ligand Interactions in Molecular Docking. Interdiscip. Sci. 2019, 11, 320–328. [Google Scholar] [CrossRef]
- Yu-ming, M.; Chen, W.; Potter, M.J.; Chia-en, A. Insights from free-energy calculations: Protein conformational equilibrium, driving forces, and ligand-binding modes. Biophys. J. 2012, 103, 342–351. [Google Scholar] [CrossRef]
- Du, X.; Li, Y.; Xia, Y.L.; Ai, S.M.; Liang, J.; Sang, P.; Ji, X.L.; Liu, S.Q. Insights into Protein-Ligand Interactions: Mechanisms, Models, and Methods. Int J. Mol. Sci. 2016, 17, 144. [Google Scholar] [CrossRef]
- Ge, H.; Wang, Y.; Li, C.; Chen, N.; Xie, Y.; Xu, M.; He, Y.; Gu, X.; Wu, R.; Gu, Q. Molecular dynamics-based virtual screening: Accelerating the drug discovery process by high-performance computing. J. Chem. Inform. Model. 2013, 53, 2757–2764. [Google Scholar] [CrossRef]
- Li, Z.; Huang, Y.; Wu, Y.; Chen, J.; Wu, D.; Zhan, C.G.; Luo, H.B. Absolute Binding Free Energy Calculation and Design of a Subnanomolar Inhibitor of Phosphodiesterase-10. J. Med. Chem. 2019, 62, 2099–2111. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Grubmüller, H.; Heymann, B.; Tavan, P. Ligand binding: Molecular mechanics calculation of the streptavidin-biotin rupture force. Science 1996, 271, 997–999. [Google Scholar] [CrossRef] [PubMed]
- Izrailev, S.; Stepaniants, S.; Balsera, M.; Oono, Y.; Schulten, K. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 1997, 72, 1568–1581. [Google Scholar] [CrossRef]
- Park, S.; Schulten, K. Calculating potentials of mean force from steered molecular dynamics simulations. J. Chem. Phys. 2004, 120, 5946–5961. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Doudou, S.; Burton, N.A.; Henchman, R.H. Standard Free Energy of Binding from a One-Dimensional Potential of Mean Force. J. Chem. Theory Comput. 2009, 5, 909–918. [Google Scholar] [CrossRef]
- Wong, K.; York, D.M. Exact Relation between Potential of Mean Force and Free-Energy Profile. J. Chem. Theory Comput. 2012, 8, 3998–4003. [Google Scholar] [CrossRef]
- den Otter, W.K. Revisiting the Exact Relation between Potential of Mean Force and Free-Energy Profile. J. Chem. Theory Comput. 2013, 9, 3861–3865. [Google Scholar] [CrossRef]
- Åqvist, J.; Medina, C.; Samuelsson, J.E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng. 1994, 7, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, J.; Cheatham, T.E.; Cieplak, P.; Kollman, P.A.; Case, D.A. Continuum Solvent Studies of the Stability of DNA, RNA, and Phosphoramidate−DNA Helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Barakat, K.; Mane, J.; Friesen, D.; Tuszynski, J. Ensemble-based virtual screening reveals dual-inhibitors for the p53–MDM2/MDMX interactions. J. Mol. Graph. Model. 2010, 28, 555–568. [Google Scholar] [CrossRef]
- Williams-Noonan, B.; Yuriev, E.; Chalmers, D.K. Free Energy Methods in Drug Design: Prospects of “Alchemical Perturbation” in Medicinal Chemistry. J. Med. Chem. 2018, 61, 638–649. [Google Scholar] [CrossRef]
- Hayes, J.M.; Archontis, G. MM-GB(PB)SA Calculations of Protein-Ligand Binding Free Energies. In Molecular Dynamics—Studies of Synthetic and Biological Macromolecules, 1st ed.; Wang, L., Ed.; IntechOpen: Rijeka, Croatia, 2012; pp. 171–190. [Google Scholar]
- Kalyaanamoorthy, S.; Chen, Y.P. Modelling and enhanced molecular dynamics to steer structure-based drug discovery. Prog. Biophys. Mol. Biol. 2014, 114, 123–136. [Google Scholar] [CrossRef]
- Su, P.; Tsai, C.; Mehboob, S.; Hevener, K.E.; Johnson, M.E. Comparison of radii sets, entropy, QM methods, and sampling on MM-PBSA, MM-GBSA, and QM/MM-GBSA ligand binding energies of F. tularensis enoyl-ACP reductase (F abI). J. Comput. Chem. 2015, 36, 1859–1873. [Google Scholar] [CrossRef]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J. Chem. Inform. Model. 2011, 51, 69–82. [Google Scholar] [CrossRef]
- Kerrigan, J.E. Molecular dynamics simulations in drug design. In Silico Models for Drug Discovery. Methods in Molecular Biology (Methods and Protocols); Kortagere, S., Ed.; Humana Press: Totowa, NJ, USA, 2013; Volume 993, pp. 95–113. [Google Scholar]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef]
- Hou, X.; Du, J.; Zhang, J.; Du, L.; Fang, H.; Li, M. How to improve docking accuracy of AutoDock4. 2: A case study using different electrostatic potentials. J. Chem. Inform. Model. 2013, 53, 188–200. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Exp. Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. How to obtain statistically converged MM/GBSA results. J. Comput. Chem. 2010, 31, 837–846. [Google Scholar] [CrossRef]
- Oehme, D.P.; Brownlee, R.T.C.; Wilson, D.J.D. Effect of atomic charge, solvation, entropy, and ligand protonation state on MM-PB (GB) SA binding energies of HIV protease. J. Comput. Chem. 2012, 33, 2566–2580. [Google Scholar] [CrossRef]
- Kalyaanamoorthy, S.; Chen, Y.P. Quantum polarized ligand docking investigation to understand the significance of protonation states in histone deacetylase inhibitors. J. Mol. Graph. Model. 2013, 44, 44–53. [Google Scholar] [CrossRef]
- Arba, M.; Ihsan, S.; Tjahjono, D.H. In silico study of porphyrin-anthraquinone hybrids as CDK2 inhibitor. Comput. Biol. Chem. 2017, 67, 9–14. [Google Scholar] [CrossRef]
- Chen, J. Clarifying binding difference of ATP and ADP to extracellular signal-regulated kinase 2 by using molecular dynamics simulations. Chem. Biol. Drug Design 2017, 89, 548–558. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, G.; Xiang, S.; Gao, D.; Zeng, C. In silico analysis of the effect of mutation on epidermal growth factor receptor in non-small-cell lung carcinoma: From mutational analysis to drug designing. J. Biomol. Struct. Dyn. 2017, 35, 427–434. [Google Scholar] [CrossRef]
- Biswas, A.; Shukla, A.; Vijayan, R.; Jeyakanthan, J.; Sekar, K. Crystal structures of an archaeal thymidylate kinase from Sulfolobus tokodaii provide insights into the role of a conserved active site Arginine residue. J. Struct. Biol 2017, 197, 236–249. [Google Scholar] [CrossRef]
- Yang, X.; Lu, J.; Ying, M.; Mu, J.; Li, P.; Liu, Y. Docking and molecular dynamics studies on triclosan derivatives binding to FabI. J. Mol. Model. 2017, 23, 25. [Google Scholar] [CrossRef]
- Moreira, C.; Ramos, M.J.; Fernandes, P.A. Glutamine synthetase drugability beyond its active site: Exploring oligomerization interfaces and pockets. Molecules 2016, 21, 1028. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, C.E.P.; Silva, P.J. Computational development of rubromycin-based lead compounds for HIV-1 reverse transcriptase inhibition. PeerJ 2014, 2, e470. [Google Scholar] [CrossRef] [PubMed]
- Sroczyński, D.; Malinowski, Z.; Szcześniak, A.K.; Pakulska, W. New 1 (2 H)-phthalazinone derivatives as potent nonpeptidic HIV-1 protease inhibitors: Molecular docking studies, molecular dynamics simulation, oral bioavailability and ADME prediction. Mol. Simul. 2016, 42, 628–641. [Google Scholar] [CrossRef]
- Phanich, J.; Rungrotmongkol, T.; Kungwan, N.; Hannongbua, S. Role of R292K mutation in influenza H7N9 neuraminidase toward oseltamivir susceptibility: MD and MM/PB (GB) SA study. J. Comput. Aided Mol. Des. 2016, 30, 917–926. [Google Scholar] [CrossRef]
- Meeprasert, A.; Hannongbua, S.; Kungwan, N.; Rungrotmongkol, T. Effect of D168V mutation in NS3/4A HCV protease on susceptibilities of faldaprevir and danoprevir. Mol. BioSyst. 2016, 12, 3666–3673. [Google Scholar] [CrossRef]
- Pethe, M.A.; Rubenstein, A.B.; Khare, S.D. Large-scale structure-based prediction and identification of novel protease substrates using computational protein design. J. Mol. Biol. 2017, 429, 220–236. [Google Scholar] [CrossRef]
- Abbat, S.; Jain, V.; Bharatam, P.V. Origins of the specificity of inhibitor P218 toward wild-type and mutant Pf DHFR: A molecular dynamics analysis. J. Biomol. Struct. Dyn. 2015, 33, 1913–1928. [Google Scholar] [CrossRef]
- Omotuyi, O.I. Methyl-methoxylpyrrolinone and flavinium nucleus binding signatures on falcipain-2 active site. J. Mol. Model. 2014, 20, 2386. [Google Scholar] [CrossRef]
- Mokmak, W.; Chunsrivirot, S.; Hannongbua, S.; Yuthavong, Y.; Tongsima, S.; Kamchonwongpaisan, S. Molecular Dynamics of Interactions between Rigid and Flexible Antifolates and Dihydrofolate Reductase from Pyrimethamine-Sensitive and Pyrimethamine-Resistant Plasmodium falciparum. Chem. Biol. Drug Design 2014, 84, 450–461. [Google Scholar] [CrossRef]
- Ekhteiari Salmas, R.; Seeman, P.; Aksoydan, B.; Stein, M.; Yurtsever, M.; Durdagi, S. Biological insights of the dopaminergic stabilizer ACR16 at the binding pocket of dopamine D2 receptor. ACS Chem. Neurosci. 2017, 8, 826–836. [Google Scholar] [CrossRef]
- Koukoulitsa, C.; Villalonga-Barber, C.; Csonka, R.; Alexi, X.; Leonis, G.; Dellis, D.; Hamelink, E.; Belda, O.; Steele, B.R.; Micha-Screttas, M. Biological and computational evaluation of resveratrol inhibitors against Alzheimer’s disease. J. Enzym. Inhib. Med. Chem. 2016, 31, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Jordheim, L.P.; Barakat, K.H.; Heinrich-Balard, L.; Matera, E.; Cros-Perrial, E.; Bouledrak, K.; El Sabeh, R.; Perez-Pineiro, R.; Wishart, D.S.; Cohen, R. Small molecule inhibitors of ERCC1-XPF protein-protein interaction synergize alkylating agents in cancer cells. Mol. Pharmacol. 2013, 84, 12–24. [Google Scholar] [CrossRef] [PubMed]
- Barakat, K.H.; Anwar-Mohamed, A.; Tuszynski, J.A.; Robins, M.J.; Tyrrell, D.L.; Houghton, M. A refined model of the HCV NS5A protein bound to daclatasvir explains drug-resistant mutations and activity against divergent genotypes. J. Chem. Inform. Model. 2015, 55, 362–373. [Google Scholar] [CrossRef]
- Marimuthu, P.; Singaravelu, K. Prediction of Hot Spots at Myeloid Cell Leukemia-1-Inhibitors Interface using Energy Estimation and Alanine Scanning Mutagenesis. Biochemistry 2018, 57, 1249–1261. [Google Scholar] [CrossRef]
- Marimuthu, P.; Singaravelu, K. Deciphering the crucial residues involved in heterodimerization of Bak peptide and anti-apoptotic proteins for apoptosis. J. Biomol. Struct. Dyn. 2018, 36, 1637–1648. [Google Scholar] [CrossRef] [PubMed]
- Viricel, C.; Ahmed, M.; Barakat, K. Human PD-1 binds differently to its human ligands: A comprehensive modeling study. J. Mol. Graph. Model. 2015, 57, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Ferri, N.; Corsini, A.; Bottino, P.; Clerici, F.; Contini, A. Virtual screening approach for the identification of new Rac1 inhibitors. J. Med. Chem. 2009, 52, 4087–4090. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein–protein binding by binding free energy calculation and free energy decomposition for the Ras–Raf and Ras–RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Hou, T.; Yu, R. Molecular dynamics and free energy studies on the wild-type and double mutant HIV-1 protease complexed with amprenavir and two amprenavir-related inhibitors: Mechanism for binding and drug resistance. J. Med. Chem. 2007, 50, 1177–1188. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Yao, X. Understanding the molecular basis of MK2–p38α signaling complex assembly: Insights into protein–protein interaction by molecular dynamics and free energy studies. Mol. BioSyst. 2012, 8, 2106–2118. [Google Scholar] [CrossRef]
- Xu, L.; Sun, H.; Li, Y.; Wang, J.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 3. The impact of force fields and ligand charge models. J. Phys. Chem. B 2013, 117, 8408–8421. [Google Scholar] [CrossRef]
- Sun, H.; Duan, L.; Chen, F.; Liu, H.; Wang, Z.; Pan, P.; Zhu, F.; Zhang, J.Z.H.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 7. Entropy effects on the performance of end-point binding free energy calculation approaches. Phys. Chem. Chem. Phys. 2018, 20, 14450–14460. [Google Scholar] [CrossRef]
- Copeland, R.A.; Pompliano, D.L.; Meek, T.D. Drug-target residence time and its implications for lead optimization. Nat. Rev. Drug Discov. 2006, 5, 730–739. [Google Scholar] [CrossRef]
- Copeland, R.A. The drug-target residence time model: A 10-year retrospective. Nat. Rev. Drug Discov. 2016, 15, 87–95. [Google Scholar] [CrossRef]
- Schuetz, D.A.; Witte, W.E.A.; Wong, Y.C.; Knasmueller, B.; Richter, L.; Kokh, D.B.; Sadiq, S.K.; Bosma, R.; Nederpelt, I.; Heitman, L.H.; et al. Kinetics for Drug Discovery: An industry-driven effort to target drug residence time. Drug Discov. Today 2017, 22, 896–911. [Google Scholar] [CrossRef]
- Tang, Z.; Roberts, C.C.; Chang, C.A. Understanding ligand-receptor non-covalent binding kinetics using molecular modeling. Front. Biosci. 2017, 22, 960–981. [Google Scholar] [CrossRef]
- Romanowska, J.; Kokh, D.B.; Fuller, J.C.; Wade, R.C. Computational approaches for studying drug binding kinetics. In Thermodynamics and Kinetics of Drug Binding; Keserü, G.M., Swinney, D.C., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 211–235. [Google Scholar]
- Lu, H.; Tonge, P.J. Drug-target residence time: Critical information for lead optimization. Curr. Opin. Chem. Biol. 2010, 14, 467–474. [Google Scholar] [CrossRef]
- Bernetti, M.; Cavalli, A.; Mollica, L. Protein-ligand (un)binding kinetics as a new paradigm for drug discovery at the crossroad between experiments and modelling. Med. Chem. Commun. 2017, 8, 534–550. [Google Scholar] [CrossRef]
- Bruce, N.J.; Ganotra, G.K.; Kokh, D.B.; Sadiq, S.K.; Wade, R.C. New approaches for computing ligand-receptor binding kinetics. Curr. Opin. Struct. Biol. 2018, 49, 1–10. [Google Scholar] [CrossRef]
- Ribeiro, J.M.L.; Tsai, S.-T.; Pramanik, D.; Wang, Y.; Tiwary, P. Kinetics of ligand-protein dissociation from all-atom simulations: Are we there yet? Biochemistry 2019, 58, 156–165. [Google Scholar] [CrossRef]
- Nunes-Alves, A.; Kokh, D.B.; Wade, R.C. Recent progress in molecular simulation methods for drug binding kinetics. Curr. Opin. Struct. Biol. 2020, 64, 126–133. [Google Scholar] [CrossRef]
- Bruce, N.J.; Ganotra, G.K.; Richter, S.; Wade, R.C. KBbox: A toolbox of computational methods for studying the kinetics of molecular binding. J. Chem. Inf. Model. 2019, 59, 3630–3634. [Google Scholar] [CrossRef]
- Gobbo, D.; Piretti, V.; Di Martino, R.M.C.; Tripathi, S.K.; Giabbai, B.; Storici, P.; Demitri, N.; Girotto, S.; Decherchi, S.; Cavalli, A. Investigating drug-target residence time in kinases through enhanced sampling simulations. J. Chem. Theory Comput. 2019, 15, 4646–4659. [Google Scholar] [CrossRef]
- Bernetti, M.; Rosini, E.; Mollica, L.; Masetti, M.; Pollegioni, L.; Recanatini, M.; Cavalli, A. Binding residence time through scaled molecular dynamics: A prospective application to hDAAO inhibitors. J. Chem. Inf. Model. 2018, 58, 2255–2265. [Google Scholar] [CrossRef]
- Mollica, L.; Decherchi, S.; Zia, S.R.; Gaspari, R.; Cavalli, A.; Rocchia, W. Kinetics of protein-ligand unbinding via smoothed potential molecular dynamics simulations. Sci. Rep. 2015, 5, 11539. [Google Scholar] [CrossRef]
- Mollica, L.; Theret, I.; Antoine, M.; Perron-Sierra, F.; Charton, Y.; Fourquez, J.; Wierzbicki, M.; Boutin, J.A.; Ferry, G.; Decherchi, S.; et al. Molecular dynamics simulations and kinetic measurements to estimate and predict protein-ligand residence times. J. Med. Chem. 2016, 59, 7167–7176. [Google Scholar] [CrossRef]
- Schuetz, D.A.; Bernetti, M.; Bertazzo, M.; Musil, D.; Eggenweiler, H.; Recanatini, M.; Masetti, M.; Ecker, G.F.; Cavalli, A. Predicting residence time and drug unbinding pathway through scaled molecular dynamics. J. Chem. Inf. Model. 2019, 59, 535–549. [Google Scholar] [CrossRef]
- Kuriappan, J.A.; Osheroff, N.; De Vivo, M. Smoothed potential MD simulations for dissociation kinetics of etoposide to unravel isoform specificity in targeting human topoisomerase II. J. Chem. Inf. Model. 2019, 59, 4007–4017. [Google Scholar] [CrossRef]
- Kokh, D.B.; Amaral, M.; Bomke, J.; Grädler, U.; Musil, D.; Buchstaller, H.-P.; Dreyer, M.K.; Frech, M.; Lowinski, M.; Vallee, F.; et al. Estimation of drug-target residence times by tau-random acceleration molecular dynamics simulations. J. Chem. Theory Comput. 2018, 14, 3859–3869. [Google Scholar] [CrossRef]
- Lüdemann, S.K.; Carugo, O.; Wade, R.C. Substrate access to cytochrome P450cam: A comparison of a thermal motion pathway analysis with molecular dynamics simulation data. Mol. Model. Annu. 1997, 3, 369–374. [Google Scholar] [CrossRef]
- Lüdemann, S.K.; Lounnas, V.; Wade, R.C. How do substrates enter and products exit the buried active site of cytochrome P450cam? 1. Random expulsion molecular dynamics investigation of ligand access channels and mechanisms. J. Mol. Biol. 2000, 303, 797–811. [Google Scholar] [CrossRef] [PubMed]
- Kokh, D.B.; Kaufmann, T.; Kister, B.; Wade, R.C. Machine learning analysis of tau-RAMD trajectories to decipher molecular determinants of drug-target residence times. Front. Mol. Biosci. 2019, 6, 36. [Google Scholar] [CrossRef] [PubMed]
- Nunes-Alves, A.; Kokh, D.B.; Wade, R.C. Comprehensive characterization of ligand unbinding mechanisms and kinetics for T4 lysozyme mutants using tauRAMD. arXiv 2020, arXiv:2010.08763. [Google Scholar]
- Schlitter, J.; Engels, M.; Krüger, P. Targeted molecular dynamics: A new approach for searching pathways of conformational transitions. J. Mol. Graph. 1994, 12, 84–89. [Google Scholar] [CrossRef]
- Wolf, S.; Stock, G. Targeted molecular dynamics calculations of free energy profiles using a nonequilibrium friction correction. J. Chem. Theory Comput. 2018, 14, 6175–6182. [Google Scholar] [CrossRef]
- Wolf, S.; Lickert, B.; Bray, S.; Stock, G. Multisecond ligand dissociation dynamics from atomistic simulations. Nat. Commun. 2020, 11, 2918. [Google Scholar] [CrossRef]
- Wolf, S.; Amaral, M.; Lowinski, M.; Vallée, F.; Musil, D.; Güldenhaupt, J.; Dreyer, M.K.; Bomke, J.; Frech, M.; Schlitter, J.; et al. Estimation of Protein–Ligand Unbinding Kinetics Using Non-Equilibrium Targeted Molecular Dynamics Simulations. J. Chem. Inf. Model. 2019, 59, 5135–5147. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Zeller, F.; Luitz, M.P.; Bomblies, R.; Zacharias, M. Multiscale simulation of receptor-drug association kinetics: Application to neuraminidase inhibitors. J. Chem. Theory Comput. 2017, 13, 5097–5105. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Huber, G.A.; Kim, S. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophys. J. 1996, 70, 97–110. [Google Scholar] [CrossRef]
- Zuckerman, D.M.; Chong, L.T. Weighted ensemble simulation: Review of methodology, applications, and software. Annu Rev. Biophys. 2017, 46, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Callegari, D.; Lodola, A.; Pala, D.; Rivara, S.; Mor, M.; Rizzi, A.; Capelli, A.M. Metadynamics simulations distinguish short- and long-residence-time inhibitors of cyclin-dependent kinase 8. J. Chem. Inf. Model. 2017, 57, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Dodda, L.S.; Tirado-Rives, J.; Jorgensen, W.L. Unbinding dynamics of non-nucleoside inhibitors from HIV-1 reverse transcriptase. J. Phys. Chem. B 2019, 123, 1741–1748. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, P.; Mondal, J.; Berne, B.J. How and when does an anticancer drug leave its binding site? Sci. Adv. 2017, 3, 1700014. [Google Scholar] [CrossRef] [PubMed]
- Haldar, S.; Comitani, F.; Saladino, G.; Woods, C.; van der Kamp, M.W.; Mulholland, A.J.; Gervasio, F.L. A multiscale simulation approach to modeling drug-protein binding kinetics. J. Chem. Theory Comput. 2018, 14, 6093–6101. [Google Scholar] [CrossRef] [PubMed]
- Casasnovas, R.; Limongelli, V.; Tiwary, P.; Carloni, P.; Parrinello, M. Unbinding kinetics of a p38 MAP kinase type II inhibitor from metadynamics simulations. J. Am. Chem. Soc. 2017, 139, 4780–4788. [Google Scholar] [CrossRef]
- Bortolato, A.; Deflorian, F.; Weiss, D.R.; Mason, J.S. Decoding the role of water dynamics in ligand-protein unbinding: CRF1R as a test case. J. Chem. Inf. Model. 2015, 55, 1857–1866. [Google Scholar] [CrossRef]
- Deganutti, G.; Zhukov, A.; Deflorian, F.; Federico, S.; Spalluto, G.; Cooke, R.M.; Moro, S.; Mason, J.S.; Bortolato, A. Impact of protein-ligand solvation and desolvation on transition state thermodynamic properties of adenosine A2A ligand binding kinetics. In Silico Pharmacol. 2017, 5, 16. [Google Scholar] [CrossRef]
- Bernetti, M.; Masetti, M.; Recanatini, M.; Amaro, R.E.; Cavalli, A. An integrated Markov state model and path metadynamics approach to characterize drug binding processes. J. Chem. Theory Comput. 2019, 15, 5689–5702. [Google Scholar] [CrossRef]
- Lotz, S.D.; Dickson, A. Unbiased molecular dynamics of 11 min timescale drug unbinding reveals transition state stabilizing interactions. J. Am. Chem. Soc. 2018, 140, 618–628. [Google Scholar] [CrossRef] [PubMed]
- Nunes-Alves, A.; Zuckerman, D.M.; Arantes, G.M. Escape of a small molecule from inside T4 lysozyme by multiple pathways. Biophys. J. 2018, 114, 1058–1066. [Google Scholar] [CrossRef] [PubMed]
- Dickson, A.; Lotz, S.D. Multiple ligand unbinding pathways and ligand-induced destabilization revealed by WExplore. Biophys. J. 2017, 112, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Madeo, J.; Mihajlovic, M.; Lazaridis, T.; Gunner, M.R. Slow Dissociation of a Charged Ligand: Analysis of the Primary Quinone QA Site of Photosynthetic Bacterial Reaction Centers. J. Am. Chem. Soc. 2011, 133, 17375–17385. [Google Scholar] [CrossRef] [PubMed]
- Nicolini, P.; Frezzato, D.; Gellini, C.; Bizzarri, M.; Chelli, R. Toward quantitative estimates of binding affinities for protein-ligand systems involving large inhibitor compounds: A steered molecular dynamics simulation route. J. Comput. Chem. 2013, 34, 1561–1576. [Google Scholar] [CrossRef]
- Capelli, A.M.; Costantino, G. Unbinding Pathways of VEGFR2 Inhibitors Revealed by Steered Molecular Dynamics. J. Chem. Inf. Model. 2014, 54, 3124–3136. [Google Scholar] [CrossRef]
- Wong, C.F. Steered molecular dynamics simulations for uncovering the molecular mechanisms of drug dissociation and for drug screening: A test on the focal adhesion kinase. J. Comput. Chem. 2018, 39, 1307–1318. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, D.; Mei, H.; Kevin, M.; Qu, S.; Pan, X.; Lu, L. SMD-based interaction-energy fingerprints can predict accurately the dissociation rate constants of HIV-1 protease inhibitors. J. Chem. Inf. Model. 2019, 59, 159–169. [Google Scholar] [CrossRef]
- Niu, Y.; Li, S.; Pan, D.; Liu, H.; Yao, X. Computational study on the unbinding pathways of B-RAF inhibitors and its implication for the difference of residence time: Insight from random acceleration and steered molecular dynamics simulations. Phys. Chem. Chem. Phys. 2016, 18, 5622–5629. [Google Scholar] [CrossRef]
- Re, S.; Oshima, H.; Kasahara, K.; Kamiya, M.; Sugita, Y. Encounter complexes and hidden poses of kinase-inhibitor binding on the free-energy landscape. Proc. Natl. Acad. Sci. USA 2019, 116, 18404–18409. [Google Scholar] [CrossRef]
- Harrigan, M.P.; Sultan, M.M.; Hernandez, C.X.; Husic, B.E.; Eastman, P.; Schwantes, C.R.; Beauchamp, K.A.; McGibbon, R.T.; Pande, V.S. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophys. J. 2017, 112, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Shukla, D.; Hernandez, C.X.; Weber, J.K.; Pande, V.S. Markov state models provide insights into dynamic modulation of protein function. Acc. Chem. Res. 2015, 48, 414–422. [Google Scholar] [CrossRef] [PubMed]
- Gregory, R.B.; Daniel, L.E.; Vijay, S.P. Enhanced modeling via network theory: Adaptive sampling of Markov state models. J. Chem. Theory Comput. 2010, 6, 787–794. [Google Scholar] [CrossRef]
- Zimmerman, M.I.; Bowman, G.R. FAST Conformational Searches by Balancing Exploration/Exploitation Trade-Offs. J. Chem. Theory Comput. 2015, 11, 5747–5757. [Google Scholar] [CrossRef]
- Votapka, L.W.; Jagger, B.R.; Heyneman, A.L.; Amaro, R.E. SEEKR: Simulation Enabled Estimation of Kinetic Rates, A Computational Tool to Estimate Molecular Kinetics and Its Application to Trypsin-Benzamidine Binding. J. Phys. Chem. B 2017, 121, 3597–3606. [Google Scholar] [CrossRef]
- Farand, J.; Mai, N.; Chandrasekhar, J.; Newby, Z.E.; Van Veldhuizen, J.; Loyer-Drew, J.; Venkataramani, C.; Guerrero, J.; Kwok, A.; Li, N.; et al. Selectivity switch between FAK and Pyk2: Macrocyclization of FAK inhibitors improves Pyk2 potency. Bioorg. Med. Chem. Lett. 2016, 26, 5926–5930. [Google Scholar] [CrossRef]
- Geng, C.; Narasimhan, S.; Rodrigues, J.P.; Bonvin, A.M. Information-Driven, Ensemble Flexible Peptide Docking Using HADDOCK. Methods Mol. Biol. 2017, 1561, 109–138. [Google Scholar] [CrossRef]
- Lee, A.C.; Harris, J.L.; Khanna, K.K.; Hong, J.H. A Comprehensive Review on Current Advances in Peptide Drug Development and Design. Int. J. Mol. Sci. 2019, 20, 2383. [Google Scholar] [CrossRef]
- London, N.; Raveh, B.; Schueler-Furman, O. Druggable protein-protein interactions from hot spots to hot segments. Curr. Opin. Chem. Biol. 2013, 17, 952–959. [Google Scholar] [CrossRef]
- Porter, K.A.; Xia, B.; Beglov, D.; Bohnuud, T.; Alam, N.; Schueler-Furman, O.; Kozakov, D. ClusPro PeptiDock: Efficient global docking of peptide recognition motifs using FFT. Bioinformatics 2017, 33, 3299–3301. [Google Scholar] [CrossRef]
- Schindler, C.E.M.; de Vries, S.J.; Zacharias, M. Fully Blind Peptide-Protein Docking with pepATTRACT. Structure 2015, 23, 1507–1515. [Google Scholar] [CrossRef] [PubMed]
- Trellet, M.; Melquiond, A.S.; Bonvin, A.M. Information-driven modeling of protein-peptide complexes. Methods Mol. Biol. 2015, 1268, 221–239. [Google Scholar] [CrossRef] [PubMed]
- Ciemny, M.; Kurcinski, M.; Kamel, K.; Kolinski, A.; Alam, N.; Schueler-Furman, O.; Kmiecik, S. Protein-peptide docking: Opportunities and challenges. Drug Discov. Today 2018, 23, 1530–1537. [Google Scholar] [CrossRef] [PubMed]
- Cuendet, M.A.; Zoete, V.; Michielin, O. How T cell receptors interact with peptide-MHCs: A multiple steered molecular dynamics study. Proteins Struct. Funct. Bioinform. 2011, 79, 3007–3024. [Google Scholar] [CrossRef] [PubMed]
- Morrone, J.A.; Perez, A.; Deng, Q.; Ha, S.N.; Holloway, M.K.; Sawyer, T.K.; Sherborne, B.S.; Brown, F.K.; Dill, K.A. Molecular Simulations Identify Binding Poses and Approximate Affinities of Stapled alpha-Helical Peptides to MDM2 and MDMX. J. Chem. Theory Comput. 2017, 13, 863–869. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Alekseenko, A.; Kozakov, D.; Miao, Y. Improved Modeling of Peptide-Protein Binding Through Global Docking and Accelerated Molecular Dynamics Simulations. Front. Mol. Biosci. 2019, 6, 112. [Google Scholar] [CrossRef]
- Diella, F.; Haslam, N.; Chica, C.; Budd, A.; Michael, S.; Brown, N.P.; Trave, G.; Gibson, T.J. Understanding eukaryotic linear motifs and their role in cell signaling and regulation. Front. Biosci. 2008, 13, 6580–6603. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- London, N.; Movshovitz-Attias, D.; Schueler-Furman, O. The structural basis of peptide-protein binding strategies. Structure 2010, 18, 188–199. [Google Scholar] [CrossRef]
- Trellet, M.; Melquiond, A.S.; Bonvin, A.M. A unified conformational selection and induced fit approach to protein-peptide docking. PLoS ONE 2013, 8, e58769. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed]
- Schindler, C.E.; de Vries, S.J.; Zacharias, M. iATTRACT: Simultaneous global and local interface optimization for protein-protein docking refinement. Proteins 2015, 83, 248–258. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, J.P.; Trellet, M.; Schmitz, C.; Kastritis, P.; Karaca, E.; Melquiond, A.S.; Bonvin, A.M. Clustering biomolecular complexes by residue contacts similarity. Proteins 2012, 80, 1810–1817. [Google Scholar] [CrossRef] [PubMed]
- Arinaminpathy, Y.; Khurana, E.; Engelman, D.M.; Gerstein, M.B. Computational analysis of membrane proteins: The largest class of drug targets. Drug Discov. Today 2009, 14, 1130–1135. [Google Scholar] [CrossRef] [PubMed]
- Hubert, P.; Sawma, P.; Duneau, J.; Khao, J.; Hénin, J.; Bagnard, D.; Sturgis, J. Single-spanning transmembrane domains in cell growth and cell-cell interactions: More than meets the eye? Cell Adhes. Migr. 2010, 4, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Goossens, K.; De Winter, H. Molecular Dynamics Simulations of Membrane Proteins: An Overview. J. Chem. Inf. Model. 2018, 58, 2193–2202. [Google Scholar] [CrossRef]
- Magarkar, A.; Parkkila, P.; Viitala, T.; Lajunen, T.; Mobarak, E.; Licari, G.; Cramariuc, O.; Vauthey, E.; Rog, T.; Bunker, A. Membrane bound COMT isoform is an interfacial enzyme: General mechanism and new drug design paradigm. Chem. Commun. 2018, 54, 3440–3443. [Google Scholar] [CrossRef]
- Koivuniemi, A.; Fallarero, A.; Bunker, A. Insight into the antimicrobial mechanism of action of beta(2,2)-amino acid derivatives from molecular dynamics simulation: Dancing the can-can at the membrane surface. Biochim. Biophys. Acta Biomembr. 2019, 1861, 183028. [Google Scholar] [CrossRef]
- Santos, R.; Ursu, O.; Gaulton, A.; Bento, A.P.; Donadi, R.S.; Bologa, C.G.; Karlsson, A.; Al-Lazikani, B.; Hersey, A.; Oprea, T.I.; et al. A comprehensive map of molecular drug targets. Nat. Rev. Drug Discov. 2017, 16, 19–34. [Google Scholar] [CrossRef]
- John, P.O.; Bissan, A.; Andrew, L.H. How many drug targets are there? Nat. Rev. Drug Discov. 2006, 5, 993–996. [Google Scholar] [CrossRef]
- Coudrat, T.; Christopoulos, A.; Sexton, P.M.; Wootten, D. Structural features embedded in G protein-coupled receptor co-crystal structures are key to their success in virtual screening. PLoS ONE 2017, 12, e0174719. [Google Scholar] [CrossRef] [PubMed]
- Ishchenko, A.; Gati, C.; Cherezov, V. Structural biology of G protein-coupled receptors: New opportunities from XFELs and cryoEM. Curr. Opin. Struct. Biol. 2018, 51, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Doerr, A. The new XFELs. Nat. Methods 2018, 15, 33. [Google Scholar] [CrossRef]
- Hilger, D.; Masureel, M.; Kobilka, B.K. Structure and dynamics of GPCR signaling complexes. Nat. Struct. Mol. Biol. 2018, 25, 4–12. [Google Scholar] [CrossRef]
- Manglik, A.; Kim, T.H.; Masureel, M.; Altenbach, C.; Yang, Z.; Hilger, D.; Lerch, M.T.; Kobilka, T.S.; Thian, F.S.; Hubbell, W.L.; et al. Structural Insights into the Dynamic Process of beta2-Adrenergic Receptor Signaling. Cell 2015, 161, 1101–1111. [Google Scholar] [CrossRef]
- Latorraca, N.R.; Venkatakrishnan, A.J.; Dror, R.O. GPCR Dynamics: Structures in Motion. Chem. Rev. 2017, 117, 139–155. [Google Scholar] [CrossRef]
- Lin, X.; Li, M.; Wang, N.; Wu, Y.; Luo, Z.; Guo, S.; Han, G.; Li, S.; Yue, Y.; Wei, X.; et al. Structural basis of ligand recognition and self-activation of orphan GPR52. Nature 2020, 579, 152–157. [Google Scholar] [CrossRef]
- Peeters, M.C.; van Westen, G.J.; Li, Q.; IJzerman, A.P. Importance of the extracellular loops in G protein-coupled receptors for ligand recognition and receptor activation. Trends Pharmacol. Sci. 2011, 32, 35–42. [Google Scholar] [CrossRef]
- David, W.; Günther, B.; Stefan, D.; Armin, B. The Extracellular Loop 2 (ECL2) of the Human Histamine H4 Receptor Substantially Contributes to Ligand Binding and Constitutive Activity. PLoS ONE 2015, 10, 1–14. [Google Scholar] [CrossRef]
- Woolley, M.J.; Watkins, H.A.; Taddese, B.; Karakullukcu, Z.G.; Barwell, J.; Smith, K.J.; Hay, D.L.; Poyner, D.R.; Reynolds, C.A.; Conner, A.C. The role of ECL2 in CGRP receptor activation: A combined modelling and experimental approach. J. R. Soc. Interface 2013, 10, 20130589. [Google Scholar] [CrossRef]
- Andrews, S.P.; Brown, G.A.; Christopher, J.A. Structure-based and fragment-based GPCR drug discovery. Chem. Med. Chem. 2014, 9, 256–275. [Google Scholar] [CrossRef] [PubMed]
- Payghan, P.V.; Bera, I.; Bhattacharyya, D.; Ghoshal, N. Computational Studies for Structure-Based Drug Designing Against Transmembrane Receptors: pLGICs and Class A GPCRs. Front. Phys. 2018, 6, 52. [Google Scholar] [CrossRef]
- Venkatakrishnan, A.J.; Deupi, X.; Lebon, G.; Tate, C.G.; Schertler, G.F.; Babu, M.M. Molecular signatures of G-protein-coupled receptors. Nature 2013, 494, 185–194. [Google Scholar] [CrossRef]
- Lebon, G.; Warne, T.; Edwards, P.C.; Bennett, K.; Langmead, C.J.; Leslie, A.G.; Tate, C.G. Agonist-bound adenosine A2A receptor structures reveal common features of GPCR activation. Nature 2011, 474, 521–525. [Google Scholar] [CrossRef] [PubMed]
- Fei, X.; Huixian, W.; Vsevolod, K.; Gye, W.H.; Kenneth, A.J.; Zhan-Guo, G.; Vadim, C.; Raymond, C.S. Structure of an Agonist-Bound Human A2A Adenosine Receptor. Science 2011, 332, 322–327. [Google Scholar] [CrossRef]
- Basith, S.; Cui, M.; Macalino, S.J.Y.; Park, J.; Clavio, N.A.B.; Kang, S.; Choi, S. Exploring G Protein-Coupled Receptors (GPCRs) Ligand Space via Cheminformatics Approaches: Impact on Rational Drug Design. Front. Pharmacol. 2018, 9, 128. [Google Scholar] [CrossRef]
- Liang, Y.L.; Khoshouei, M.; Radjainia, M.; Zhang, Y.; Glukhova, A.; Tarrasch, J.; Thal, D.M.; Furness, S.G.B.; Christopoulos, G.; Coudrat, T.; et al. Phase-plate cryo-EM structure of a class B GPCR-G-protein complex. Nature 2017, 546, 118–123. [Google Scholar] [CrossRef]
- Dror, R.O.; Green, H.F.; Valant, C.; Borhani, D.W.; Valcourt, J.R.; Pan, A.C.; Arlow, D.H.; Canals, M.; Lane, J.R.; Rahmani, R.; et al. Structural basis for modulation of a G-protein-coupled receptor by allosteric drugs. Nature 2013, 503, 295–299. [Google Scholar] [CrossRef]
- Yin, H.; Flynn, A.D. Drugging Membrane Protein Interactions. Annu. Rev. Biomed. Eng. 2016, 18, 51–76. [Google Scholar] [CrossRef]
- Li, Y.; Deng, L.; Liang, J.; Dong, G.H.; Xia, Y.L.; Fu, Y.X.; Liu, S.Q. Molecular dynamics simulations reveal distinct differences in conformational dynamics and thermodynamics between the unliganded and CD4-bound states of HIV-1 gp120. Phys. Chem. Chem. Phys. 2020, 22, 5548–5560. [Google Scholar] [CrossRef]
- Narayanan, C.; Bernard, D.N.; Bafna, K.; Gagne, D.; Chennubhotla, C.S.; Doucet, N.; Agarwal, P.K. Conservation of Dynamics Associated with Biological Function in an Enzyme Superfamily. Structure 2018, 26, 426–436. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.Y.; Sun, J.; Salvo, J.S.; Baker, D.; Barth, P. High-resolution modeling of transmembrane helical protein structures from distant homologues. PLoS Comput. Biol. 2014, 10, e1003636. [Google Scholar] [CrossRef] [PubMed]
- Prakash, P.; Sayyed-Ahmad, A.; Gorfe, A.A. pMD-Membrane: A Method for Ligand Binding Site Identification in Membrane-Bound Proteins. PLoS Comput. Biol. 2015, 11, e1004469. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, Y.; Song, Y.; Dai, D.; Zhao, Z.; Zhang, Q.; Zhong, W.; Hu, L.A.; Ma, Y.; Li, X.; et al. Fragment-Based Computational Method for Designing GPCR Ligands. J. Chem. Inf. Model. 2019. [Google Scholar] [CrossRef] [PubMed]
- Raschka, S.; Kaufman, B. Machine learning and AI-based approaches for bioactive ligand discovery and GPCR-ligand recognition. Methods 2020, 180, 89–110. [Google Scholar] [CrossRef]
- Varga, J.; Dobson, L.; Remenyi, I.; Tusnady, G.E. TSTMP: Target selection for structural genomics of human transmembrane proteins. Nucleic Acids Res. 2017, 45, D325–D330. [Google Scholar] [CrossRef][Green Version]
- Kappel, K.; Miao, Y.; McCammon, J.A. Accelerated molecular dynamics simulations of ligand binding to a muscarinic G-protein-coupled receptor. Q. Rev. Biophys. 2015, 48, 479–487. [Google Scholar] [CrossRef]
- Toda, Y.; Nakagita, T.; Hirokawa, T.; Yamashita, Y.; Nakajima, A.; Narukawa, M.; Ishimaru, Y.; Uchida, R.; Misaka, T. Positive/Negative Allosteric Modulation Switching in an Umami Taste Receptor (T1R1/T1R3) by a Natural Flavor Compound, Methional. Nat. Sci. Rep. 2018, 8, 11796. [Google Scholar] [CrossRef]
- Schneider, S.; Provasi, D.; Filizola, M. How Oliceridine (TRV-130) Binds and Stabilizes a mu-Opioid Receptor Conformational State That Selectively Triggers G Protein Signaling Pathways. Biochemistry 2016, 55, 6456–6466. [Google Scholar] [CrossRef]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingolfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational Modeling of Realistic Cell Membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef]
- Klauda, J.B. Perspective: Computational modeling of accurate cellular membranes with molecular resolution. J. Chem. Phys. 2018, 149, 220901. [Google Scholar] [CrossRef] [PubMed]
- Domanski, J.; Hedger, G.; Best, R.B.; Stansfeld, P.J.; Sansom, M.S.P. Convergence and Sampling in Determining Free Energy Landscapes for Membrane Protein Association. J. Phys. Chem. B 2017, 121, 3364–3375. [Google Scholar] [CrossRef]
- Reddy, A.S.; Warshaviak, D.T.; Chachisvilis, M. Effect of membrane tension on the physical properties of DOPC lipid bilayer membrane. Biochim. Biophys. Acta 2012, 1818, 2271–2281. [Google Scholar] [CrossRef] [PubMed]
- Conrard, L.; Tyteca, D. Regulation of Membrane Calcium Transport Proteins by the Surrounding Lipid Environment. Biomolecules 2019, 9, 513. [Google Scholar] [CrossRef] [PubMed]
- Guixa-Gonzalez, R.; Albasanz, J.L.; Rodriguez-Espigares, I.; Pastor, M.; Sanz, F.; Marti-Solano, M.; Manna, M.; Martinez-Seara, H.; Hildebrand, P.W.; Martin, M.; et al. Membrane cholesterol access into a G-protein-coupled receptor. Nat. Commun. 2017, 8, 14505. [Google Scholar] [CrossRef] [PubMed]
- Chavent, M.; Duncan, A.L.; Sansom, M.S. Molecular dynamics simulations of membrane proteins and their interactions: From nanoscale to mesoscale. Curr. Opin. Struct. Biol. 2016, 40, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, D.; Chattopadhyay, A. Molecular dynamics simulations of GPCR–cholesterol interaction: An emerging paradigm. Biochim. Biophys. Acta Biomembr. 2015, 1848, 1775–1782. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Guixà-González, R.; Rodriguez-Espigares, I.; Ramírez-Anguita, J.M.; Carrió-Gaspar, P.; Martinez-Seara, H.; Giorgino, T.; Selent, J. MEMBPLUGIN: Studying membrane complexity in VMD. Bioinformatics 2014, 30, 1478–1480. [Google Scholar] [CrossRef]
- Damre, M.; Marchetto, A.; Giorgetti, A. MERMAID: Dedicated web server to prepare and run coarse-grained membrane protein dynamics. Nucleic Acids Res. 2019, 47, W456–W461. [Google Scholar] [CrossRef]
- Machado, M.R.; Barrera, E.E.; Klein, F.; Sonora, M.; Silva, S.; Pantano, S. The SIRAH 2.0 Force Field: Altius, Fortius, Citius. J. Chem. Theory Comput. 2019, 15, 2719–2733. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.D.; Rommie, E.A. LipidWrapper: An Algorithm for Generating Large-Scale Membrane Models of Arbitrary Geometry. PLoS Comput. Biol. 2014, 10, 1–11. [Google Scholar] [CrossRef]
- Boyd, K.J.; May, E.R. BUMPy: A Model-Independent Tool for Constructing Lipid Bilayers of Varying Curvature and Composition. J. Chem. Theory Comput. 2018, 14, 6642–6652. [Google Scholar] [CrossRef] [PubMed]
- Schott-Verdugo, S.; Gohlke, H. PACKMOL-Memgen: A Simple-To-Use, Generalized Workflow for Membrane-Protein-Lipid-Bilayer System Building. J. Chem. Inf. Model. 2019, 59, 2522–2528. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Garcia, A.E. Acceleration of Lateral Equilibration in Mixed Lipid Bilayers Using Replica Exchange with Solute Tempering. J. Chem. Theory Comput. 2014, 10, 4264–4272. [Google Scholar] [CrossRef] [PubMed]
- Lelimousin, M.; Limongelli, V.; Sansom, M.S. Conformational Changes in the Epidermal Growth Factor Receptor: Role of the Transmembrane Domain Investigated by Coarse-Grained MetaDynamics Free Energy Calculations. J. Am. Chem. Soc. 2016, 138, 10611–10622. [Google Scholar] [CrossRef]
- Elber, R. A new paradigm for atomically detailed simulations of kinetics in biophysical systems. Q. Rev. Biophys. 2017, 50, e8. [Google Scholar] [CrossRef]
- Mori, T.; Miyashita, N.; Im, W.; Feig, M.; Sugita, Y. Molecular dynamics simulations of biological membranes and membrane proteins using enhanced conformational sampling algorithms. Biochim. Biophys. Acta 2016, 1858, 1635–1651. [Google Scholar] [CrossRef]
- Newport, T.D.; Sansom, M.S.P.; Stansfeld, P.J. The MemProtMD database: A resource for membrane-embedded protein structures and their lipid interactions. Nucleic Acids Res. 2019, 47, D390–D397. [Google Scholar] [CrossRef]
- Lin, F.; Li, F.; Wang, C.; Wang, J.; Yang, Y.; Yang, L.; Li, Y. Mechanism Exploration of Arylpiperazine Derivatives Targeting the 5-HT2A Receptor by In Silico Methods. Molecules 2017, 22, 1064. [Google Scholar] [CrossRef]
- Salari, R.; Joseph, T.; Lohia, R.; Henin, J.; Brannigan, G. A Streamlined, General Approach for Computing Ligand Binding Free Energies and Its Application to GPCR-Bound Cholesterol. J. Chem. Theory Comput. 2018, 14, 6560–6573. [Google Scholar] [CrossRef] [PubMed]
- Stanley, N.; Pardo, L.; Fabritiis, G.D. The pathway of ligand entry from the membrane bilayer to a lipid G protein-coupled receptor. Sci. Rep. 2016, 6, 22639. [Google Scholar] [CrossRef] [PubMed]
- Sykes, D.A.; Stoddart, L.A.; Kilpatrick, L.E.; Hill, S.J. Binding kinetics of ligands acting at GPCRs. Mol. Cell Endocrinol. 2019, 485, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Raniolo, S.; Limongelli, V.; Xu, Y. The Molecular Mechanism Underlying Ligand Binding to the Membrane-Embedded Site of a G-Protein-Coupled Receptor. J. Chem. Theory Comput. 2018, 14, 2761–2770. [Google Scholar] [CrossRef]
- Venable, R.M.; Kramer, A.; Pastor, R.W. Molecular Dynamics Simulations of Membrane Permeability. Chem. Rev. 2019, 119, 5954–5997. [Google Scholar] [CrossRef]
- Lomize, A.L.; Hage, J.M.; Schnitzer, K.; Golobokov, K.; LaFaive, M.B.; Forsyth, A.C.; Pogozheva, I.D. PerMM: A Web Tool and Database for Analysis of Passive Membrane Permeability and Translocation Pathways of Bioactive Molecules. J. Chem. Inf. Model. 2019, 59, 3094–3099. [Google Scholar] [CrossRef]
- Berben, P.; Bauer-Brandl, A.; Brandl, M.; Faller, B.; Flaten, G.E.; Jacobsen, A.; Brouwers, J.; Augustijns, P. Drug permeability profiling using cell-free permeation tools: Overview and applications. Eur. J. Pharm. Sci. 2018, 119, 219–233. [Google Scholar] [CrossRef]
- Linsdell, P. Structural Changes Fundamental to Gating of the Cystic Fibrosis Transmembrane Conductance Regulator Anion Channel Pore. Adv. Exp. Med. Biol. 2017, 925, 13–32. [Google Scholar] [CrossRef]
- Callebaut, I.; Hoffmann, B.; Lehn, P.; Mornon, J.P. Molecular modelling and molecular dynamics of CFTR. Cell Mol. Life Sci 2017, 74, 3–22. [Google Scholar] [CrossRef]
- Feng, Z.; Pearce, L.V.; Xu, X.; Yang, X.; Yang, P.; Blumberg, P.M.; Xie, X.Q. Structural insight into tetrameric hTRPV1 from homology modeling, molecular docking, molecular dynamics simulation, virtual screening, and bioassay validations. J. Chem. Inf. Model. 2015, 55, 572–588. [Google Scholar] [CrossRef]
- Amiri, S.; Shimomura, M.; Vijayan, R.; Nishiwaki, H.; Akamatsu, M.; Matsuda, K.; Jones, A.K.; Sansom, M.S.P.; Biggin, P.C.; Sattelle, D.B. A role for Leu118 of loop E in agonist binding to the alpha 7 nicotinic acetylcholine receptor. Mol. Pharmacol. 2008, 73, 1659–1667. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Saito, S.; Mori, Y.; Itoh, S.G.; Okumura, H.; Tominaga, M. Structural basis of TRPA1 inhibition by HC-030031 utilizing species-specific differences. Sci. Rep. 2016, 6, 37460. [Google Scholar] [CrossRef] [PubMed]
- Arinaminpathy, Y.; Sansom, M.S.P.; Biggin, P.C. Binding site flexibility: Molecular simulation of partial and full agonists within a glutamate receptor. Mol. Pharmacol. 2006, 69, 11–18. [Google Scholar] [CrossRef]
- Basak, S.; Gicheru, Y.; Kapoor, A.; Mayer, M.L.; Filizola, M.; Chakrapani, S. Molecular mechanism of setron-mediated inhibition of full-length 5-HT3A receptor. Nat. Commun. 2019, 10, 3225–3228. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.E.T.; Lodowski, D.T.; Huynh, K.W.; Yazici, A.; Del Rosario, J.; Kapoor, A.; Basak, S.; Samanta, A.; Han, X.; Chakrapani, S.; et al. Structural basis of TRPV5 channel inhibition by econazole revealed by cryo-EM. Nat. Struct. Mol. Biol. 2018, 25, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Y.; Cui, W.W.; Huang, Y.; Yang, Y.; Liu, Y.; Zhao, W.S.; Cheng, X.Y.; Sun, W.S.; Cao, P.; et al. Druggable negative allosteric site of P2X3 receptors. Proc. Natl. Acad. Sci. USA 2018, 115, 4939–4944. [Google Scholar] [CrossRef] [PubMed]
- Hanson, S.M.; Newstead, S.; Swartz, K.J.; Sansom, M.S.P. Capsaicin interaction with TRPV1 channels in a lipid bilayer: Molecular dynamics simulation. Biophys. J. 2015, 108, 1425–1434. [Google Scholar] [CrossRef]
- Hedger, G.; Sansom, M.S.P. Lipid interaction sites on channels, transporters and receptors: Recent insights from molecular dynamics simulations. Biochim. Biophys. Acta 2016, 1858, 2390–2400. [Google Scholar] [CrossRef]
- Brannigan, G.; Hénin, J.; Law, R.; Eckenhoff, R.; Klein, M.L. Embedded cholesterol in the nicotinic acetylcholine receptor. Proc. Natl. Acad. Sci. USA 2008, 105, 14418–14423. [Google Scholar] [CrossRef]
- Hénin, J.; Salari, R.; Murlidaran, S.; Brannigan, G. A Predicted Binding Site for Cholesterol on the GABAA Receptor. Biophys. J. 2014, 106, 1938–1949. [Google Scholar] [CrossRef]
- Monk, B.C.; Tomasiak, T.M.; Keniya, M.V.; Huschmann, F.U.; Tyndall, J.D.; OConnell, J.D.; Cannon, R.D.; McDonald, J.G.; Rodriguez, A.; Finer-Moore, J.; et al. Architecture of a single membrane spanning cytochrome P450 suggests constraints that orient the catalytic domain relative to a bilayer. Proc. Natl. Acad. Sci. USA 2014, 111, 3865–3870. [Google Scholar] [CrossRef] [PubMed]
- Tyndall, J.D.A.; Sabherwal, M.; Sagatova, A.A.; Keniya, M.V.; Negroni, J.; Wilson, R.K.; Woods, M.A.; Tietjen, K.; Monk, B.C. Structural and Functional Elucidation of Yeast Lanosterol 14α-Demethylase in Complex with Agrochemical Antifungals. PLoS ONE 2016, 11, e0167485. [Google Scholar] [CrossRef] [PubMed]
- Keniya, M.V.; Sabherwal, M.; Wilson, R.K.; Woods, M.A.; Sagatova, A.A.; Tyndall, J.D.A.; Monk, B.C. Crystal Structures of Full-Length Lanosterol 14α-Demethylases of Prominent Fungal Pathogens Candida albicans and Candida glabrata Provide Tools for Antifungal Discovery. Antimicrob. Agents Chemother. 2018, 62, 1134. [Google Scholar] [CrossRef] [PubMed]
- De Lemos-Chiarandini, C.; Frey, A.B.; Sabatini, D.D.; Kreibich, G. Determination of the membrane topology of the phenobarbital-inducible rat liver cytochrome P-450 isoenzyme PB-4 using site-specific antibodies. J. Cell Biol. 1987, 104, 209–219. [Google Scholar] [CrossRef]
- Black, S.D. Membrane topology of the mammalian P450 cytochromes. FASEB J. Off. Public. Fed. Am. Soc. Exp. Biol. 1992, 6, 680–685. [Google Scholar] [CrossRef]
- Ozalp, C.; Szczesna-Skorupa, E.; Kemper, B. Identification of Membrane-Contacting Loops of the Catalytic Domain of Cytochrome P450 2C2 by Tryptophan Fluorescence Scanning. Biochemistry 2006, 45, 4629–4637. [Google Scholar] [CrossRef]
- Ohta, Y.; Kawato, S.; Tagashira, H.; Takemori, S.; Kominami, S. Dynamic structures of adrenocortical cytochrome P-450 in proteoliposomes and microsomes: Protein rotation study. Biochemistry 1992, 31, 12680–12687. [Google Scholar] [CrossRef]
- Yamamoto, K.; Gildenberg, M.; Ahuja, S.; Im, S.; Pearcy, P.; Waskell, L.; Ramamoorthy, A. Probing the Transmembrane Structure and Topology of Microsomal Cytochrome-P450 by Solid-State NMR on Temperature-Resistant Bicelles. Sci. Rep. 2013, 3, 2556. [Google Scholar] [CrossRef]
- Huang, R.; Yamamoto, K.; Zhang, M.; Popovych, N.; Hung, I.; Im, S.; Gan, Z.; Waskell, L.; Ramamoorthy, A. Probing the Transmembrane Structure and Dynamics of Microsomal NADPH-cytochrome P450 oxidoreductase by Solid-State NMR. Biophys. J. 2014, 106, 2126–2133. [Google Scholar] [CrossRef]
- Denisov, I.G.; Sligar, S.G. Cytochromes P450 in Nanodiscs. Biochim. Biophys. Acta Protein. Proteom. 2011, 1814, 223–229. [Google Scholar] [CrossRef]
- Lüdemann, S.K.; Lounnas, V.; Wade, R.C. How do substrates enter and products exit the buried active site of cytochrome P450cam? 2. Steered molecular dynamics and adiabatic mapping of substrate pathways. J. Mol. Biol. 2000, 303, 813–830. [Google Scholar] [CrossRef] [PubMed]
- Winn, P.J.; Lüdemann, S.K.; Gauges, R.; Lounnas, V.; Wade, R.C. Comparison of the dynamics of substrate access channels in three cytochrome P450s reveals different opening mechanisms and a novel functional role for a buried arginine. Proc. Natl. Acad. Sci. USA 2002, 99, 5361–5366. [Google Scholar] [CrossRef] [PubMed]
- Lomize, M.a.; Lomize, A.L.; Pogozheva, I.D.; Mosberg, H.I. OPM: Orientations of proteins in membranes database. Bioinformatics 2006, 22, 623–625. [Google Scholar] [CrossRef] [PubMed]
- Gábor, E.; Dosztányi, T.Z.; Simon, I. Transmembrane proteins in the Protein Data Bank: Identification and classification. Bioinformatics 2004, 20, 2964–2972. [Google Scholar] [CrossRef]
- Ash, W.L.; Zlomislic, M.R.; Oloo, E.O.; Tieleman, D.P. Computer simulations of membrane proteins. Biochim. Biophys. Acta Biomembr. 2004, 1666, 158–189. [Google Scholar] [CrossRef] [PubMed]
- Kandt, C.; Ash, W.L.; Peter Tieleman, D. Setting up and running molecular dynamics simulations of membrane proteins. Methods 2007, 41, 475–488. [Google Scholar] [CrossRef]
- Cojocaru, V.; Balali-Mood, K.; Sansom, M.S.P.; Wade, R.C. Structure and Dynamics of the Membrane-Bound Cytochrome P450 2C9. PLoS Comput. Biol. 2011, 7, e1002152. [Google Scholar] [CrossRef]
- Lonsdale, R.; Rouse, S.L.; Sansom, M.S.P.; Mulholland, A.J. A multiscale approach to modelling drug metabolism by membrane-bound cytochrome P450 enzymes. PLoS Comput. Biol. 2014, 10, e1003714. [Google Scholar] [CrossRef]
- Yu, X.; Cojocaru, V.; Mustafa, G.; Salo-Ahen, O.M.H.; Lepesheva, G.I.; Wade, R.C. Dynamics of CYP51: Implications for function and inhibitor design. J. Mol. Recognit. 2015, 28, 59–73. [Google Scholar] [CrossRef]
- Mustafa, G.; Nandekar, P.P.; Yu, X.; Wade, R.C. On the application of the MARTINI coarse-grained model to immersion of a protein in a phospholipid bilayer. J. Chem. Phys. 2015, 143, 243139. [Google Scholar] [CrossRef]
- Mustafa, G.; Nandekar, P.P.; Camp, T.J.; Bruce, N.J.; Gregory, M.C.; Sligar, S.G.; Wade, R.C. Influence of Transmembrane Helix Mutations on Cytochrome P450-Membrane Interactions and Function. Biophys. J. 2019, 116, 419–432. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, G.; Nandekar, P.P.; Bruce, N.J.; Wade, R.C. Differing Membrane Interactions of Two Highly Similar Drug-Metabolizing Cytochrome P450 Isoforms: CYP 2C9 and CYP 2C19. Int. J. Mol. Sci. 2019, 20, 4328. [Google Scholar] [CrossRef] [PubMed]
- Zawaira, A.; Ching, L.Y.; Coulson, L.; Blackburn, J.; Wei, Y.C. An expanded, unified substrate recognition site map for mammalian cytochrome P450s: Analysis of molecular interactions between 15 mammalian CYP450 isoforms and 868 substrates. Curr. Drug Metab. 2011, 12, 684–700. [Google Scholar] [CrossRef] [PubMed]
- Lenov, I.L. Methodologies for the Analysis of Membrane Systems Using Lipid Nanodiscs; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2016. [Google Scholar]
- Cui, Y.; Zheng, Q.; Zhang, J.; Xue, Q.; Wang, Y.; Zhang, H. Molecular Dynamic Investigations of the Mutational Effects on Structural Characteristics and Tunnel Geometry in CYP17A1. J. Chem. Inform. Model. 2013, 53, 3308–3317. [Google Scholar] [CrossRef]
- Pechurskaya, T.A.; Lukashevich, O.P.; Gilep, A.A.; Usanov, S.A. Engineering, expression, and purification of "soluble" human cytochrome P45017alpha and its functional characterization. Biochemistry 2008, 73, 806–811. [Google Scholar] [CrossRef]
- Yamamoto, K.; Caporini, M.A.; Im, S.; Waskell, L.; Ramamoorthy, A. Transmembrane Interactions of Full-length Mammalian Bitopic Cytochrome-P450-Cytochrome-b5 Complex in Lipid Bilayers Revealed by Sensitivity-Enhanced Dynamic Nuclear Polarization Solid-state NMR Spectroscopy. Sci. Rep. 2017, 7, 4116. [Google Scholar] [CrossRef]
- Cojocaru, V.; Winn, P.J.; Wade, R.C. Multiple, ligand-dependent routes from the active site of cytochrome P450 2C9. Curr. Drug Metab. 2012, 143–154. [Google Scholar] [CrossRef]
- Shen, Z.; Cheng, F.; Xu, Y.; Fu, J.; Xiao, W.; Shen, J.; Liu, G.; Li, W.; Tang, Y. Investigation of indazole unbinding pathways in CYP2E1 by molecular dynamics simulations. PLoS ONE 2012, 7, e33500. [Google Scholar] [CrossRef]
- Li, W.; Shen, J.; Liu, G.; Tang, Y.; Hoshino, T. Exploring coumarin egress channels in human cytochrome P450 2A6 by random acceleration and steered molecular dynamics simulations. Proteins 2011, 79, 271–281. [Google Scholar] [CrossRef]
- Fishelovitch, D.; Shaik, S.; Wolfson, H.J.; Nussinov, R. Theoretical characterization of substrate access/exit channels in the human cytochrome P450 3A4 enzyme: Involvement of phenylalanine residues in the gating mechanism. J. Phys. Chem. B 2009, 113, 13018–13025. [Google Scholar] [CrossRef]
- Wade, R.C.; Motiejunas, D.; Schleinkofer, K.; Sudarko; Winn, P.J.; Banerjee, A.; Kariakin, A.; Jung, C. Multiple molecular recognition mechanisms. Cytochrome P450—A case study. Biochim. Biophys. Acta 2005, 1754, 239–244. [Google Scholar] [CrossRef]
- Schleinkofer, K.; Winn, P.J.; Lüdemann, S.K.; Wade, R.C. Do mammalian cytochrome P450s show multiple ligand access pathways and ligand channelling? EMBO Rep. 2005, 6, 584–589. [Google Scholar] [CrossRef]
- Yu, X.; Nandekar, P.; Mustafa, G.; Cojocaru, V.; Lepesheva, G.I.; Wade, R.C. Ligand tunnels in T. brucei and human CYP51: Insights for parasite-specific drug design. Biochim. Biophys. Acta Gen. Subj. 2016, 1860, 67–78. [Google Scholar] [CrossRef]
- Bruno, R.D.; Njar, V.C.O. Targeting cytochrome P450 enzymes: A new approach in anti-cancer drug development. Bioorgan. Med. Chem. 2007, 15, 5047–5060. [Google Scholar] [CrossRef]
- Datta, S.; Grant, D.J.W. Crystal structures of drugs: Advances in determination, prediction and engineering. Nat. Rev. Drug Discov. 2004, 3, 42–57. [Google Scholar] [CrossRef]
- Grohganz, H.; Löbmann, K.; Priemel, P.; Tarp Jensen, K.; Graeser, K.; Strachan, C.; Rades, T. Amorphous drugs and dosage forms. J. Drug Deliv. Sci. Technol. 2013, 23, 403–408. [Google Scholar] [CrossRef]
- Nemkevich, A.; Bürgi, H.; Spackman, M.A.; Corry, B. Molecular dynamics simulations of structure and dynamics of organic molecular crystals. Phys. Chem. Chem. Phys. 2010, 12, 14916–14929. [Google Scholar] [CrossRef]
- Nyman, J.; Pundyke, O.S.; Day, G.M. Accurate force fields and methods for modelling organic molecular crystals at finite temperatures. Phys. Chem. Chem. Phys. 2016, 18, 15828–15837. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.C.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef]
- Van den Ende, J.; Smets, M.M.H.; de Jong, D.T.; Brugman, S.J.T.; Ensing, B.; Tinnemans, P.T.; Meekes, H.; Cuppen, H.M. Do solid-to-solid polymorphic transitions in dl-norleucine proceed through nucleation? Faraday Discuss. 2015, 179, 421–436. [Google Scholar] [CrossRef]
- Giron, D.; Goldbronn, C.; Mutz, M.; Pfeffer, S.; Piechon, P.; Schwab, P. Solid State Characterizations of Pharmaceutical Hydrates. J. Therm. Anal. Calorim. 2002, 68, 453–465. [Google Scholar] [CrossRef]
- Healy, A.M.; Worku, Z.A.; Kumar, D.; Madi, A.M. Pharmaceutical solvates, hydrates and amorphous forms: A special emphasis on cocrystals. Eng. Pharm. Cocryst. Salts Polym. Adv. Chall. 2017, 117, 25–46. [Google Scholar] [CrossRef]
- Larsen, A.S.; Ruggiero, M.T.; Johansson, K.E.; Zeitler, J.A.; Rantanen, J. Tracking Dehydration Mechanisms in Crystalline Hydrates with Molecular Dynamics Simulations. Cryst. Growth Design 2017, 17, 5017–5022. [Google Scholar] [CrossRef]
- Larsen, A.S.; Olsen, M.A.; Moustafa, H.; Larsen, F.H.; Sauer, S.P.A.; Rantanen, J.; Madsen, A.Ø. Determining short-lived solid forms during phase transformations using molecular dynamics. Cryst. Eng. Commun. 2019, 21, 4020–4024. [Google Scholar] [CrossRef]
- van de Streek, J.; Alig, E.; Parsons, S.; Vella-Zarb, L. A jumping crystal predicted with molecular dynamics and analysed with TLS refinement against powder diffraction data. IUCrJ 2019, 6, 136–144. [Google Scholar] [CrossRef]
- Rexrode, N.R.; Orien, J.; King, M.D. Effects of Solvent Stabilization on Pharmaceutical Crystallization: Investigating Conformational Polymorphism of Probucol Using Combined Solid-State Density Functional Theory, Molecular Dynamics, and Terahertz Spectroscopy. J. Phys. Chem. A 2019, 123, 6937–6947. [Google Scholar] [CrossRef]
- Mirza, S.; Miroshnyk, I.; Heinämäki, J.; Antikainen, O.; Rantanen, J.; Vuorela, P.; Vuorela, H.; Yliruusi, J. Crystal morphology engineering of pharmaceutical solids: Tabletting performance enhancement. AAPS Pharm. Sci. Tech. 2009, 10, 113–119. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Vetter, T.; Mazzotti, M.; Parrinello, M. Controlling and Predicting Crystal Shapes: The Case of Urea. Angew. Chem. Int. Ed. 2013, 52, 13369–13372. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Vetter, T.; Giberti, F.; Mazzotti, M.; Parrinello, M. Uncovering Molecular Details of Urea Crystal Growth in the Presence of Additives. J. Am. Chem. Soc. 2012, 134, 17221–17233. [Google Scholar] [CrossRef]
- Piana, S.; Reyhani, M.; Gale, J.D. Simulating micrometre-scale crystal growth from solution. Nature 2005, 438, 70–73. [Google Scholar] [CrossRef]
- Whiteman, G.; Walker, B.; Perego, P. Planetary boundaries: Ecological foundations for corporate sustainability. J. Manag. Stud. 2013, 50, 307–336. [Google Scholar] [CrossRef]
- Karthika, S.; Radhakrishnan, T.K.; Kalaichelvi, P. A Review of Classical and Nonclassical Nucleation Theories. Cryst. Growth Design 2016, 16, 6663–6681. [Google Scholar] [CrossRef]
- Ectors, P.; Duchstein, P.; Zahn, D. From oligomers towards a racemic crystal: Molecular simulation of dl-norleucine crystal nucleation from solution. Cryst. Eng. Commun. 2015, 17, 6884–6889. [Google Scholar] [CrossRef]
- Löbmann, K.; Laitinen, R.; Grohganz, H.; Gordon, K.C.; Strachan, C.; Rades, T. Coamorphous Drug Systems: Enhanced Physical Stability and Dissolution Rate of Indomethacin and Naproxen. Mol. Pharm. 2011, 8, 1919–1928. [Google Scholar] [CrossRef]
- Giberti, F.; Salvalaglio, M.; Mazzotti, M.; Parrinello, M. Insight into the nucleation of urea crystals from the melt. Chem. Eng. Sci. 2015, 121, 51–59. [Google Scholar] [CrossRef]
- Knapik-Kowalczuk, J.; Tu, W.; Chmiel, K.; Rams-Baron, M.; Paluch, M. Co-Stabilization of Amorphous Pharmaceuticals-The Case of Nifedipine and Nimodipine. Mol. Pharm. 2018, 15, 2455–2465. [Google Scholar] [CrossRef]
- Russo, M.G.; Baldoni, H.A.; Dávila, Y.A.; Brusau, E.V.; Ellena, J.A.; Narda, G.E. Rational Design of a Famotidine-Ibuprofen Coamorphous System: An Experimental and Theoretical Study. J. Phys. Chem. B 2018, 122, 8772–8782. [Google Scholar] [CrossRef]
- Sareen, S.; Mathew, G.; Joseph, L. Improvement in solubility of poor water-soluble drugs by solid dispersion. Int. J. Pharm. Invest. 2012, 2, 12. [Google Scholar] [CrossRef]
- Grohganz, H.; Priemel, P.A.; Löbmann, K.; Nielsen, L.H.; Laitinen, R.; Mullertz, A.; Van den Mooter, G.; Rades, T. Refining stability and dissolution rate of amorphous drug formulations. Exp. Opin. Drug Deliv. 2014, 11, 977–989. [Google Scholar] [CrossRef]
- Van den Mooter, G. The use of amorphous solid dispersions: A formulation strategy to overcome poor solubility and dissolution rate. Drug Discov. Today Technol. 2012, 9, e79–e85. [Google Scholar] [CrossRef]
- Rumondor, A.C.F.; Stanford, L.A.; Taylor, L.S. Effects of polymer type and storage relative humidity on the kinetics of felodipine crystallization from amorphous solid dispersions. Pharm. Res. 2009, 26, 2599. [Google Scholar] [CrossRef] [PubMed]
- Prudic, A.; Ji, Y.; Luebbert, C.; Sadowski, G. Influence of humidity on the phase behavior of API/polymer formulations. Eur. J. Pharm. Biopharm. 2015, 94, 352–362. [Google Scholar] [CrossRef] [PubMed]
- Lehmkemper, K.; Kyeremateng, S.O.; Heinzerling, O.; Degenhardt, M.; Sadowski, G. Impact of polymer type and relative humidity on the long-term physical stability of amorphous solid dispersions. Mol. Pharm. 2017, 14, 4374–4386. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.S.; Zografi, G. Spectroscopic Characterization of Interactions Between PVP and Indomethacin in Amorphous Molecular Dispersions. Pharm. Res. 1997, 14, 1691–1698. [Google Scholar] [CrossRef]
- Matsumoto, T.; Zografi, G. Physical Properties of Solid Molecular Dispersions of Indomethacin with Poly(vinylpyrrolidone) and Poly(vinylpyrrolidone-co-vinyl-acetate) in Relation to Indomethacin Crystallization. Pharm. Res. 1999, 16, 1722–1728. [Google Scholar] [CrossRef]
- Pacułt, J.; Rams-Baron, M.; Chrząszcz, B.; Jachowicz, R.; Paluch, M. Effect of Polymer Chain Length on the Physical Stability of Amorphous Drug–Polymer Blends at Ambient Pressure. Mol. Pharm. 2018, 15, 2807–2815. [Google Scholar] [CrossRef]
- Szczurek, J.; Rams-Baron, M.; Knapik-Kowalczuk, J.; Antosik, A.; Szafraniec, J.; Jamróz, W.; Dulski, M.; Jachowicz, R.; Paluch, M. Molecular Dynamics, Recrystallization Behavior, and Water Solubility of the Amorphous Anticancer Agent Bicalutamide and Its Polyvinylpyrrolidone Mixtures. Mol. Pharm. 2017, 14, 1071–1081. [Google Scholar] [CrossRef]
- Knapik, J.; Wojnarowska, Z.; Grzybowska, K.; Tajber, L.; Mesallati, H.; Paluch, K.J.; Paluch, M. Molecular Dynamics and Physical Stability of Amorphous Nimesulide Drug and Its Binary Drug–Polymer Systems. Mol. Pharm. 2016, 13, 1937–1946. [Google Scholar] [CrossRef]
- Yuan, X.; Xiang, T.; Anderson, B.D.; Munson, E.J. Hydrogen Bonding Interactions in Amorphous Indomethacin and Its Amorphous Solid Dispersions with Poly(vinylpyrrolidone) and Poly(vinylpyrrolidone-co-vinyl acetate) Studied Using 13C Solid-State NMR. Mol. Pharm. 2015, 12, 4518–4528. [Google Scholar] [CrossRef]
- Xiang, T.X.; Anderson, B.D. A molecular dynamics simulation of reactant mobility in an amorphous formulation of a peptide in poly(vinylpyrrolidone). J. Pharm. Sci. 2004, 93, 855–876. [Google Scholar] [CrossRef]
- Xiang, T.X.; Anderson, B.D. Water uptake, distribution, and mobility in amorphous poly(D,L-lactide) by molecular dynamics simulation. J. Pharm. Sci. 2014, 103, 2759–2771. [Google Scholar] [CrossRef] [PubMed]
- Xiang, T.; Anderson, B.D. Molecular dynamics simulation of amorphous indomethacin-poly (vinylpyrrolidone) glasses: Solubility and hydrogen bonding interactions. J. Pharm. Sci. 2013, 102, 876–891. [Google Scholar] [CrossRef] [PubMed]
- Xiang, T.; Anderson, B.D. Molecular dynamics simulation of amorphous hydroxypropyl-methylcellulose acetate succinate (HPMCAS): Polymer model development, water distribution, and plasticization. Mol. Pharm. 2014, 11, 2400–2411. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.D.; Xiang, T. Molecular Dynamics Simulations of Amorphous Systems. In Computational Pharmaceutical Solid State Chemistry, 1st ed.; Abramov, Y.A., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 331–373. [Google Scholar]
- Xiang, T.; Anderson, B.D. Molecular dynamics simulation of amorphous hydroxypropylmethylcellulose and its mixtures with felodipine and water. J. Pharm. Sci. 2017, 106, 803–816. [Google Scholar] [CrossRef]
- Xiang, T.X.; Anderson, B.D. Effects of Molecular Interactions on Miscibility and Mobility of Ibuprofen in Amorphous Solid Dispersions with Various Polymers. J. Pharm. Sci. 2019, 108, 178–186. [Google Scholar] [CrossRef]
- Brunsteiner, M.; Khinast, J.; Paudel, A. Relative contributions of Solubility and Mobility to the Stability of Amorphous Solid Dispersions of poorly soluble drugs: A Molecular Dynamics Simulation study. Pharmaceutics 2018, 10, 101. [Google Scholar] [CrossRef]
- Gupta, J.; Nunes, C.; Vyas, S.; Jonnalagadda, S. Prediction of solubility parameters and miscibility of pharmaceutical compounds by molecular dynamics simulations. J. Phys. Chem. B 2011, 115, 2014–2023. [Google Scholar] [CrossRef]
- Barmpalexis, P.; Karagianni, A.; Katopodis, K.; Vardaka, E.; Kachrimanis, K. Molecular modelling and simulation of fusion-based amorphous drug dispersions in polymer/plasticizer blends. Eur. J. Pharm. Sci. 2019, 130, 260–268. [Google Scholar] [CrossRef]
- Anderson, B.D. Predicting solubility/miscibility in amorphous dispersions: It is time to move beyond regular solution theories. J. Pharm. Sci. 2018, 107, 24–33. [Google Scholar] [CrossRef]
- Marsac, P.J.; Li, T.; Taylor, L.S. Estimation of drug–polymer miscibility and solubility in amorphous solid dispersions using experimentally determined interaction parameters. Pharm. Res. 2009, 26, 139. [Google Scholar] [CrossRef]
- Marsac, P.J.; Shamblin, S.L.; Taylor, L.S. Theoretical and practical approaches for prediction of drug–polymer miscibility and solubility. Pharm. Res. 2006, 23, 2417. [Google Scholar] [CrossRef] [PubMed]
- Edueng, K.; Mahlin, D.; Larsson, P.; Bergström, C.A.S. Mechanism-based selection of stabilization strategy for amorphous formulations: Insights into crystallization pathways. J. Controll. Release 2017, 256, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Jha, P.K.; Larson, R.G. Assessing the efficiency of polymeric excipients by atomistic molecular dynamics simulations. Mol. Pharm. 2014, 11, 1676–1686. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Johnston, B.F.; Mackay, S.P.; Schatzlein, A.G.; Gellert, P.; Sengupta, D.; Uchegbu, I.F. In silico modelling of drug–polymer interactions for pharmaceutical formulations. J. Royal Soc. Interface 2010, 7, S423–S433. [Google Scholar] [CrossRef] [PubMed]
- Amidon, G.L.; Lennernäs, H.; Shah, V.P.; Crison, J.R. A theoretical basis for a biopharmaceutic drug classification: The correlation of in vitro drug product dissolution and in vivo bioavailability. Pharm. Res. 1995, 12, 413–420. [Google Scholar] [CrossRef]
- Meng, F.; Xu, W. Drug permeability prediction using PMF method. J. Mol. Model. 2013, 19, 991–997. [Google Scholar] [CrossRef]
- Awoonor-Williams, E.; Rowley, C.N. Molecular simulation of nonfacilitated membrane permeation. Biochim. Biophys. Acta Biomembr. 2016, 1858, 1672–1687. [Google Scholar] [CrossRef]
- Herce, H.D.; Garcia, A.E. Molecular dynamics simulations suggest a mechanism for translocation of the HIV-1 TAT peptide across lipid membranes. Proc. Natl. Acad. Sci. USA 2007, 104, 20805–20810. [Google Scholar] [CrossRef]
- Im, W.; Brooks, C.L. Interfacial folding and membrane insertion of designed peptides studied by molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6771–6776. [Google Scholar] [CrossRef]
- Larsson, P.; Kasson, P.M. Lipid tail protrusion in simulations predicts fusogenic activity of influenza fusion peptide mutants and conformational models. PLoS Comput. Biol. 2013, 9, e1002950. [Google Scholar] [CrossRef]
- Notman, R.; den Otter, W.K.; Noro, M.G.; Briels, W.J.; Anwar, J. The permeability enhancing mechanism of DMSO in ceramide bilayers simulated by molecular dynamics. Biophys. J. 2007, 93, 2056–2068. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.H.; Keck, C.M. Twenty years of drug nanocrystals: Where are we, and where do we go? Eur. J. Pharm. Biopharm. Off. J. Arb. Pharm. Verfahr. 2012, 80, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.M.; Cullis, P.R. Drug delivery systems: Entering the mainstream. Science 2004, 303, 1818–1822. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, A.; Nagaich, U.; Gulati, N.; Sharma, V.K.; Khosa, R.L.; Partapur, M.U. Enhancement of solubilization and bioavailability of poorly soluble drugs by physical and chemical modifications: A recent review. J. Adv. Pharm. Educ. Res. 2012, 2, 32–67. [Google Scholar]
- Hewitt, M.; Cronin, M.T.D.; Enoch, S.J.; Madden, J.C.; Roberts, D.W.; Dearden, J.C. In silico prediction of aqueous solubility: The solubility challenge. J. Chem. Inform. Model. 2009, 49, 2572–2587. [Google Scholar] [CrossRef]
- Hughes, L.D.; Palmer, D.S.; Nigsch, F.; Mitchell, J.B.O. Why are some properties more difficult to predict than others? A study of QSPR models of solubility, melting point, and Log P. J. Chem. Inform. Model. 2008, 48, 220–232. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Wittig, R.; Lohmann, J.; Gmehling, J. Vapor-liquid equilibria by UNIFAC group contribution. 6. Revision and extension. Ind. Eng. Chem. Res. 2003, 42, 183–188. [Google Scholar] [CrossRef]
- Cao, P.; Short, M.P.; Yip, S. Understanding the mechanisms of amorphous creep through molecular simulation. Proc. Natl. Acad. Sci. USA 2017, 114, 13631–13636. [Google Scholar] [CrossRef]
- Chan, T.; Ouyang, D. Investigating the molecular dissolution process of binary solid dispersions by molecular dynamics simulations. Asian J. Pharm. Sci. 2018, 13, 248–254. [Google Scholar] [CrossRef]
- Edueng, K.; Mahlin, D.; Bergström, C.A.S. The need for restructuring the disordered science of amorphous drug formulations. Pharm. Res. 2017, 34, 1754–1772. [Google Scholar] [CrossRef] [PubMed]
- Schnieders, M.J.; Baltrusaitis, J.; Shi, Y.; Chattree, G.; Zheng, L.; Yang, W.; Ren, P. The structure, thermodynamics, and solubility of organic crystals from simulation with a polarizable force field. J. Chem. Theory Comput. 2012, 8, 1721–1736. [Google Scholar] [CrossRef] [PubMed]
- Noya, E.G.; Conde, M.M.; Vega, C. Computing the free energy of molecular solids by the Einstein molecule approach: Ices XIII and XIV, hard-dumbbells and a patchy model of proteins. J. Chem. Phys. 2008, 129, 104704. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Cao, S.; Hoang, K.; Young, K.L.; Paluch, A.S.; Mobley, D.L. Using MD Simulations to Calculate How Solvents Modulate Solubility. J. Chem. Theory Comput. 2016, 12, 1930–1941. [Google Scholar] [CrossRef]
- Chebil, L.; Chipot, C.; Archambault, F.; Humeau, C.; Engasser, J.M.; Ghoul, M.; Dehez, F. Solubilities Inferred from the Combination of Experiment and Simulation. Case Study of Quercetin in a Variety of Solvents. J. Phys. Chem. B 2010, 114, 12308–12313. [Google Scholar] [CrossRef]
- Paluch, A.S.; Parameswaran, S.; Liu, S.; Kolavennu, A.; Mobley, D.L. Predicting the excess solubility of acetanilide, acetaminophen, phenacetin, benzocaine, and caffeine in binary water/ethanol mixtures via molecular simulation. J. Chem. Phys. 2015, 142, 044508. [Google Scholar] [CrossRef]
- Torrie, G.; Valleau, J. Monte Carlo Free-Energy Estimates Using Non-Boltzmann Sampling—Application to Subcritical Lennard-Jones Fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. Molecular dynamics simulation in the grand canonical ensemble. J. Comput. Chem. 2007, 28, 1763–1773. [Google Scholar] [CrossRef]
- Eslami, H.; Mehdipour, N. Grand canonical ensemble molecular dynamics simulation of water solubility in polyamide-6, 6. Phys. Chem. Chem. Phys. 2011, 13, 669–673. [Google Scholar] [CrossRef]
- Bannan, C.C.; Calabró, G.; Kyu, D.Y.; Mobley, D.L. Calculating partition coefficients of small molecules in octanol/water and cyclohexane/water. J. Chem. Theory Comput. 2016, 12, 4015–4024. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Kabedev, A.; Parrow, A.; Bergström, C.A.S.; Larsson, P. Molecular simulation as a computational pharmaceutics tool to predict drug solubility, solubilization processes and partitioning. Eur. J. Pharm. Biopharm. Off. J. Arb. Pharm. Verfahr. 2019, 137, 46–55. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, H.; Watano, S. Direct permeation of nanoparticles across cell membrane: A review. KONA Powder Part. J. 2018, 2018, 49–65. [Google Scholar] [CrossRef]
- Patra, J.K.; Das, G.; Fraceto, L.F.; Campos, E.V.R.; Rodriguez-Torres, M.; Acosta-Torres, L.; Diaz-Torres, L.; Grillo, R.; Swamy, M.K.; Sharma, S.; et al. Nano based drug delivery systems: Recent developments and future prospects. J. Nanobiotechnol. 2018, 16, 1–33. [Google Scholar] [CrossRef]
- Khalkhali, M.; Mohammadinejad, S.; Khoeini, F.; Rostamizadeh, K. Vesicle-like structure of lipid-based nanoparticles as drug delivery system revealed by molecular dynamics simulations. Int. J. Pharm. 2019, 559, 173–181. [Google Scholar] [CrossRef]
- Ahmed, S.; Govender, T.; Khan, I.; ur Rehman, N.; Ali, W.; Shah, S.M.H.; Khan, S.; Hussain, Z.; Ullah, R.; Alsaid, M.S. Experimental and molecular modeling approach to optimize suitable polymers for fabrication of stable fluticasone nanoparticles with enhanced dissolution and antimicrobial activity. Drug Design Dev. Ther. 2018, 12, 255–269. [Google Scholar] [CrossRef]
- Connell, D.J.; Gebril, A.; Khan, M.A.H.; Patwardhan, S.V.; Kubiak-Ossowska, K.; Ferro, V.A.; Mulheran, P.A. Rationalising drug delivery using nanoparticles: A combined simulation and immunology study of GnRH adsorbed to silica nanoparticles. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Monti, S.; Barcaro, G.; Sementa, L.; Carravetta, V.; Ågren, H. Dynamics and self-assembly of bio-functionalized gold nanoparticles in solution: Reactive molecular dynamics simulations. Nano Res. 2018, 11, 1757–1767. [Google Scholar] [CrossRef]
- Ketabi, S.; Rahmani, L. Carbon nanotube as a carrier in drug delivery system for carnosine dipeptide: A computer simulation study. Mater. Sci. Eng. C 2017, 73, 173–181. [Google Scholar] [CrossRef]
- Benson, S.P.; Pleiss, J. Molecular dynamics simulations of self-emulsifying drug-delivery systems (SEDDS): Influence of excipients on droplet nanostructure and drug localization. Langmuir 2014, 30, 8471–8480. [Google Scholar] [CrossRef]
- Mousavi, S.V.; Hashemianzadeh, S.M. Molecular dynamics approach for behavior assessment of chitosan nanoparticles in carrying of donepezil and rivastigmine drug molecules. Mater. Res. Express 2019, 6, 045069. [Google Scholar] [CrossRef]
- Monti, S.; Jose, J.; Sahajan, A.; Kalarikkal, N.; Thomas, S. Structure and dynamics of gold nanoparticles decorated with chitosan-gentamicin conjugates: ReaxFF molecular dynamics simulations to disclose drug delivery. Phys. Chem. Chem. Phys. 2019, 21, 13099–13108. [Google Scholar] [CrossRef] [PubMed]
- Thota, N.; Hu, Z.; Jiang, J. Ibuprofen loading and release in amphiphilic peptide FA32 and its derivatives: A coarse-grained molecular dynamics simulation study. Mol. Simul. 2016, 42, 679–687. [Google Scholar] [CrossRef]
- Deepa, G.; Sivakumar, K.C.; Sajeevan, T.P. Molecular simulation and in vitro evaluation of chitosan nanoparticles as drug delivery systems for the controlled release of anticancer drug cytarabine against solid tumours. 3 Biotech. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Lin, J.; Alexander-Katz, A. Cell Membranes Open “Doors” for Cationic Nanoparticles/Biomolecules: Insights into Uptake Kinetics. ACS Nano 2013, 7, 10799–10808. [Google Scholar] [CrossRef]
- Nangia, S.; Sureshkumar, R. Effects of nanoparticle charge and shape anisotropy on translocation through cell membranes. Langmuir 2012, 28, 17666–17671. [Google Scholar] [CrossRef]
- Gupta, R.; Rai, B. Effect of Size and Surface Charge of Gold Nanoparticles on their Skin Permeability: A Molecular Dynamics Study. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef]
- Mhashal, A.R.; Roy, S. Free Energy of Bare and Capped Gold Nanoparticles Permeating through a Lipid Bilayer. Chem. Phys. Chem. 2016, 17, 3504–3514. [Google Scholar] [CrossRef]
- Li, Z.L.; Ding, H.M.; Ma, Y.Q. Translocation of polyarginines and conjugated nanoparticles across asymmetric membranes. Soft Matter 2013, 9, 1281–1286. [Google Scholar] [CrossRef]
- Shimizu, K.; Nakamura, H.; Watano, S. MD simulation study of direct permeation of a nanoparticle across the cell membrane under an external electric field. Nanoscale 2016, 8, 11897–11906. [Google Scholar] [CrossRef]
- Pedram, M.Z.; Shamloo, A.; Alasty, A.; Ghafar-Zadeh, E. Optimal magnetic field for crossing super-para-magnetic nanoparticles through the Brain Blood Barrier: A computational approach. Biosensors 2016, 6, 25. [Google Scholar] [CrossRef] [PubMed]
- Thota, N.; Jiang, J. Computational amphiphilic materials for drug delivery. Front. Mater. 2015, 2, 1–15. [Google Scholar] [CrossRef]
- Ramezanpour, M.; Leung, S.S.W.; Delgado-Magnero, K.; Bashe, B.Y.M.; Thewalt, J.; Tieleman, D.P. Computational and experimental approaches for investigating nanoparticle-based drug delivery systems. Biochim. Biophys. Acta Biomembr. 2016, 1858, 1688–1709. [Google Scholar] [CrossRef] [PubMed]
- Shillcock, J.; Lipowsky, R. Visualizing soft matter: Mesoscopic simulations of membranes, vesicles and nanoparticles. Biophys. Rev. Lett. 2007, 2, 33–55. [Google Scholar] [CrossRef]
- Sen, S.; Han, Y.; Rehak, P.; Vuković, L.; Král, P. Computational studies of micellar and nanoparticle nanomedicines. Chem. Soc. Rev. 2018, 47, 3849–3860. [Google Scholar] [CrossRef]
- Bunker, A. Poly(Ethylene Glycol) in Drug Delivery, Why Does it Work, and Can We do Better? All Atom Molecular Dynamics Simulation Provides Some Answers. Phys. Proc. 2012, 34, 24–33. [Google Scholar] [CrossRef]
- Vuković, L.; Madriaga, A.; Kuzmis, A.; Banerjee, A.; Tang, A.; Tao, K.; Shah, N.; Král, P.; Onyuksel, H. Solubilization of Therapeutic Agents in Micellar Nanomedicines. Langmuir 2013, 29, 15747–15754. [Google Scholar] [CrossRef][Green Version]
- Kabedev, A.; Hossain, S.; Hubert, M.; Larsson, P.; Bergström, C.A.S. Molecular Dynamics Simulations Reveal Membrane Interactions for Poorly Water-Soluble Drugs: Impact of Bile Solubilization and Drug Aggregation. J. Pharm. Sci. 2020. [Google Scholar] [CrossRef]
- Wu, W.; Zou, Z.; Yang, S.; Wu, Q.; Li, W.; Ding, Q.; Guan, Z.; Zhu, W. Coarse-Grained Molecular Dynamic and Experimental Studies on Self-Assembly Behavior of Nonionic F127/HS15 Mixed Micellar Systems. Langmuir 2020, 36, 2082–2092. [Google Scholar] [CrossRef]
- Koochaki, A.; Moghbeli, M.R.; Nikkhah, S.J.; Ianiro, A.; Tuinier, R. Dual responsive PMEEECL–PAE block copolymers: A computational self-assembly and doxorubicin uptake study. RSC Adv. 2020, 10, 3233–3245. [Google Scholar] [CrossRef]
- Yu, M.; Song, W.; Tian, F.; Dai, Z.; Zhu, Q.; Ahmad, E.; Guo, S.; Zhu, C.; Zhong, H.; Yuan, Y.; et al. Temperature- and rigidity-mediated rapid transport of lipid nanovesicles in hydrogels. Proc. Natl. Acad. Sci. USA 2019, 116, 5362–5369. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Xu, L.; Tian, F.; Su, Q.; Zheng, N.; Yang, Y.; Wang, J.; Wang, A.; Zhu, C.; Guo, S.; et al. Rapid transport of deformation-tuned nanoparticles across biological hydrogels and cellular barriers. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kabedev, A.; Lobaskin, V. Structure and elasticity of bush and brush-like models of the endothelial glycocalyx. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Van Lehn, R.C.; Alexander-Katz, A. Energy landscape for the insertion of amphiphilic nanoparticles into lipid membranes: A computational study. PLoS ONE 2019, 14, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, H.; Sezawa, K.; Hata, M.; Ohsaki, S.; Watano, S. Direct translocation of nanoparticles across a model cell membrane by nanoparticle-induced local enhancement of membrane potential. Phys. Chem. Chem. Phys. 2019, 21, 18830–18838. [Google Scholar] [CrossRef] [PubMed]
- Cagno, V.; Andreozzi, P.; D’Alicarnasso, M.; Silva, P.J.; Mueller, M.; Galloux, M.; Goffic, R.L.; Jones, S.T.; Vallino, M.; Hodek, J.; et al. Broad-spectrum non-toxic antiviral nanoparticles with a virucidal inhibition mechanism. Nat. Mater. 2018, 17, 195–203. [Google Scholar] [CrossRef]
- Song, M.; Sun, Y.; Luo, Y.; Zhu, Y.; Liu, Y.; Li, H. Exploring the mechanism of inhibition of au nanoparticles on the aggregation of amyloid-β(16-22) peptides at the atom level by all-atom molecular dynamics. Int. J. Mol. Sci. 2018, 19, 1815. [Google Scholar] [CrossRef]
- Sen, S.; Vuković, L.; Král, P. Computational screening of nanoparticles coupling to Aβ40 peptides and fibrils. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).