Model Predictive Control for First-Order Hyperbolic System Based on Quasi-Shannon Wavelet Basis

Abstract

In this paper, we consider a class of first-order hyperbolic distributed parameter systems. Our focus is on the design of a new class of model predictive control schemes using a quasi-Shannon wavelet basis. First, the first-order hyperbolic distributed parameter system is transformed into an equivalent system using collocation techniques for the approximation of spatial derivatives and Euler forward difference method for the approximation of the time component. Then, a model reduction method is applied to obtain a reduced-order system on which a nonlinear model predictive controller is designed through solving a nonlinear quadratic programming problem with input constraints. For illustration, the temperature control of a flow-control long-duct heating system is considered to be an example. A comparative simulation study is conducted to demonstrate the effectiveness of the proposed method.

1. Introduction

Modeling and control of systems governed by partial differential equations (PDEs) have attracted the interest of many researchers. See, for example, [1] and the references cited therein. These systems are known as distributed parameter systems (DPSs). Among the controller synthesis methods for DPSs, there are direct design strategies [2], post-centralized strategies [3], and prior-centralized strategies. For these three strategies, the prior-centralized strategy is easier to be understood, so it has been widely used to deal with DPSs. With the prior-centralized approach, a DPS is first approximated by a system of ordinary differential equations, referred to as a lumped parameter system (LPS) [4]. However, the obtained LPS tends to have a high dimension, and hence it is essential to get a low-order representation of the LPS and use it for the design of the controller. There are many effective control schemes in the literature for the design of the controller.

For a system described by hyperbolic PDEs, the eigenspectrums of its differential operator contain almost all the energy. As a consequence, the order of the model is higher than that of the parabolic system [4]. The classical finite difference method (FDM) has long been recognized as a popular numerical method for DPSs among the control community. For example, several FDM numerical models have been developed to deal with various control problems, including optimal control problems governed by first-order hyperbolic systems. A coupled system involving PDE and ODE is transformed into a zero-order neutral system with distributed delays [5]. An optimal boundary control problem, where its underlying dynamical system is governed by linear hyperbolic partial differential equations with a turnpike structure, is being applied to solve a control problem in gas pipeline operation [6]. A boundary input-to-state stability of a class of coupled systems involving hyperbolic PDE and ODE in the presence of uncertainties and external disturbances is investigated and the results obtained is applied to an interconnected continuous stirred tank reactor coupled with a plug-flow reactor [7]. Furthermore, the weighted residual methods (WRMs), such as the Galerkin method, collocation method, and finite element method (FEM), have also attracted the attention of many researchers among the control community. WRM has been widely used in various industrial applications due to its high computational efficiency and flexibility in handling complex geometries and boundaries [8]. For control problems governed by various DPSs, the weighted residual method based on a wavelet basis is found to be effective, showing great potential [9]. The collocation method involves finding a functional basis for the solution space of the equation, then making the residual zero at n points within the domain [10]. Generally, wavelet-collocation method (WCM), created by choosing a wavelet and some grid structure, is most appropriate for solving nonlinear PDEs with general boundary conditions [11]. The computational model of hyperbolic wave equations is proposed by using Haar wavelet operation matrix [12]. A non-Fourier heat conduction problem is solved through the use of Haar wavelet basis implicitly in combination of finite difference and pseudospectral methods, thereby avoiding numerical oscillations near wavefront jumping discontinuities [13]. Although the Haar wavelet function has an explicit expression, it is non-differentiable. Thus, an integral smoothing calculation is introduced. Furthermore, since the Haar wavelet has only one vanishing moment, it does not perform well for the approximation of a smooth function. The Pennes bioheat transfer equation is solved by the WCM and a multiresolution analysis is conducted using Daubechies wavelets [14]. The Daubechies wavelet is tightly supported, smooth, and has n-order vanishing moments, but its differential operator is difficult to obtain due to the lack of analytical expression. By combining the operation matrix of integration for Legendre and Chebyshev wavelets with the collocation method, an approximate solution of a one-dimensional hyperbolic PDEs with given initial conditions is derived [15]. By the operation matrix of fractional integration combined with the Galerkin method and the collocation method, a coupled system of Burgers’ equations with the time-fractional derivative of Gegenbauer wavelets is obtained [16]. The operation matrix of Hermite wavelet is derived, and on this basis a direct numerical method is developed for solving optimal control problems [17]. By combining WRM with Shannon wavelet basis, a numerical method is proposed to calculate the stationary solution of Fokker-Planck-Kolmogorov equation [18]. Shannon wavelet is continuous, smooth, and infinitely differentiable, but it is not tightly supported. For the quasi-Shannon wavelet [19], it is also tightly supported.

Model predictive control (MPC) is a successful method for the control of industrial processes modeled as LPSs or DPSs with constraints and time delays. For the control of hyperbolic systems, such as long duct heating systems [20], and convection-dominated chemical reactor [21], the need to handle constraints and time delays is unavoidable. The key step in the design of an MPC algorithm for DPSs is to build a prediction model through model reduction. For DPS, a linear MPC scheme using Cayley-Tustin transformation is proposed in [22]. The FDM has also become a popular method for constructing prediction models. MPC using FDM’s prediction model has been successfully applied to several industrial processes, such as convection-dominated transport-reaction processes [21], cocurrent fluid flow problems [22], non-isothermal plug-flow reactor [23,24], wind tunnel propagation delay problems [25], and open irrigation canals [26]. The characteristic line method (CLM) is a spatio-temporal discretization method. It has been applied to the study of control problems, where the $S{O}_2$ concentration is to be controlled in a circulating fluidized bed [27]. It has also been applied to uncertain hyperbolic systems [28], and a counterflow plug-flow reactor [29]. On the other hand, model predictive control based on the weighted residual method is being developed for hyperbolic systems. The control problem of selective catalytic reduction in diesel-powered vehicles is solved by CLM combined with spectral decomposition [30]. Wavelet-based numerical methods have great potential in MPC application design, but there is little related literature. A prediction model based on Haar wavelet basis has been applied to the design of the MPC controller of discrete DPS [31]. However, in order to improve the computational efficiency, it is necessary to develop a more suitable wavelet-based method.

In this paper, the WCM is used to construct the reduced-order model of first-order hyperbolic system. The interval quasi-Shannon wavelet scaling function is used as a basis function to suppress the boundary error. Then, a nonlinear MPC scheme is developed based on the above prediction model. Nonlinear MPC schemes are also developed based on the models obtained by FDM and the Haar wavelet transformation proposed in [31]. They are applied to solve the disturbance rejection problem of long duct heating systems. Their computational efficiency has been compared.

The rest of the paper is organized as follows. In Section 2, the first-order hyperbolic system and its control objective are introduced. Then, the interval quasi-Shannon wavelet is introduced, and a nonlinear model predictive control scheme is developed based on the wavelet-collocation method for the first-order hyperbolic system in Section 3. In Section 4, a simulation study involving a long duct heating system is performed to verify the effectiveness of the algorithm proposed in Section 3. Some concluding remarks are given in Section 5.

2. Problem Formulation

We consider the following class of distributed parameter systems described by first-order hyperbolic evolution equations:

$$y_t(x,t)=f_1(x,t)y_x(x,t)+f_2(y,u,x,t)$$

(1)

subject to initial condition $y(x,0)=y_0\left(x\right)$ and boundary condition $y(\alpha ,t)=L\left(t\right)$, where $x\in [\alpha ,\beta ]\subset \mathcal{R}$ is the spatial variable, $\mathcal{R}$ is the set of real numbers, $t\in [0,\infty )$ is the time variable, $y(x,t)\in \mathcal{H}\left[\right(\alpha ,\beta ),\mathcal{R}]$ is the controlled variable, $\mathcal{H}\left[\right(\alpha ,\beta ),\mathcal{R}]$ is an infinite-dimensional Hilbert space containing integrable spatial differentiable functions defined in the interval $[\alpha ,\beta ]$, $y(x,t)$ is differentiable with respect to x and t, $y_t(x,t)=\partial y(x,t)/\partial t$, $y_x(x,t)=\partial y(x,t)/\partial x$, $u(x,t)$ is a smooth and bounded manipulatable variable, $f_1,f_2$ are sufficiently smooth nonlinear functions of x and t, $L\left(t\right)$ is a smooth and bounded function of time t, $\parallel f_1{\parallel }_2\le A<+\infty$, $\parallel f_2{\parallel }_2\le B<+\infty$, where ${\parallel ·\parallel }_2$ is ${\mathcal{L}}_2$-norm.

The optimal control problem may now be stated as follows:

$$\begin{array}{cc}\hfill J\left(u\right):=& {\int }_{\alpha }^{\beta }{\int }_0^t\left(\parallel r(x,t)-\widehat{y}(x,t)\parallel +\lambda ·\parallel \Delta u(x,t)\parallel \right),\hfill \\ \hfill s.t.& y_t(x,t)=f_1(x,t)y_x(x,t)+f_2(y,u,x,t),\hfill \\ & u_{min}\le u(x,t)\le u_{max},\hfill \\ & \Delta u_{min}\le \Delta u(x,t)\le \Delta u_{max}\hfill \end{array}$$

(2)

where $J\left(u\right)$ is the objective function, and $r(x,t)$, $\hat{y}(x,t)$, $u(x,t)$ and $\Delta u(x,t)$ are, respectively, the reference trajectory, the prediction output and the control increment at position x and time t. $u_{min}$ and $u_{max}$ represent, respectively, the upper bound and the lower bound of the control variables, while $\Delta u_{min}$ and $\Delta u_{max}$ represent, respectively, the upper bound and the lower bound of the control increment. $\lambda$ is the weighting coefficient.

To proceed further, let us consider an actual situation, which is referred to as Problem (P), as stated below.

Consider the situation where there are $M=2^J+1$ sensors, which are uniformly located, and l actuators, and let $u(x,t)={\sum }_{i=0}^{l-1}{b}_i\left(x\right)·u_i\left(t\right),b_i\left(x\right)=H(x-(i-1)\pi /4)-H(x-i\pi /4),(i=1,\cdots ,4)$, where H is the standard Heaviside function.

The discrete forms of the system and the cost function will be constructed using the wavelet-collocation method to be described in Section 3.

3. Model Predictive Control Using Quasi-Shannon Interpolating Wavelet

This section describes the principle and design process of the proposed MPC schemes using a quasi-Shannon wavelet basis. After a brief introduction of the principle of FDM and WCM, the given first-order hyperbolic system is transformed into an equivalent system using a collocation technique for spatial derivatives combined with the Euler forward difference method for the approximation of the time component. On this basis, the resulting prediction model is constructed. Since the quasi-Shannon wavelet scaling function has advantages in approximating continuous functions, the quasi-Shannon wavelet scaling function on a finite interval is selected as the basis function. On this basis, a prediction model is constructed, which is then applied to design the MPC scheme for the first-order hyperbolic system such that the discrete objective function is minimized.

3.1. Model Reduction for First-Order Hyperbolic Systems

There are various model reduction methods in the literature, such as the eigenfunction method, Green’s function method, and WRMs [4]. For WRMs, they include Galerkin method, the collocation method, the FEM, and the spectral method. We will consider the latter two methods because the eigenfunction method and Green’s function method are not suitable for nonlinear DPSs.

3.1.1. Finite Difference Method

The FDM is the earliest and most popular approach to approximate PDE by difference equations (in which the derivatives are approximated by finite differences) [32]. Based on the Taylor series expansion, the PDE system is approximated by a system of difference equations. These difference equations are obtained based on forward, backward or central differences. The accuracy of the algorithm is determined by the grid size and the scheme for constructing the difference equations. This scheme must satisfy the Courant-Friedrichs-Lewy (CFL) condition to ensure the stability of the discretization.

We consider the first-order hyperbolic system (1). The mesh of the solution region is as shown in Figure 1. Let the space discretization interval be $\Delta x$ and the time discretization interval be $\Delta t$. Then, $x_m=\alpha +m·\Delta x,m=0,2,\cdots ,M-1$, $t_n=n·\Delta t,n=0,1,\cdots ,\infty$, and $y_m^n=y(x_m,t_n)$, $f{\mid }_m^n=f(x_m,t_n)$ are, respectively, the approximations of $y(x,t)$ and $f(x,t)$ at $x_m$ and $t_n$. The upwind discretized form of system (1) can be expressed as:

$$y_m^{n+1}=y_m^n+\Delta t/\Delta x·f_1{\mid }_m^n(y_{m+1}^n-y_m^n)+\Delta t·f_2{\mid }_m^n$$

(3)

where the accuracy of the upwind discretized form is first-order, and the CFL condition is $\Delta t\le \Delta x/max\left\{f_1{\mid }_m^n\right\}$. The FDM-based MPC scheme will be compared with the proposed method in Section 4.

FDM has two disadvantages. It is more complicated when solving PDEs on irregular domains, and the mathematical analysis is difficult for nonlinear PDEs with FDM [11].

3.1.2. Wavelet-Collocation Method

The wavelet-collocation method is derived based on the WRM, which is one of the most effective numerical methods for solving PDE systems. The numerical method obtained based on WRM is conceptually different from those obtained using FDM because WRM assumes that the solution can be expressed analytically. It is well known that a continuous spatio-temporal variable can be approximated in terms of a set of spatial basis functions

$$y(x,t)=\sum _{i=1}^{\infty }\phi \left(x\right)·y_i\left(t\right).$$

(4)

Equation (4) is truncated as:

$$y(x,t)\approx y^M(x,t)=\sum _{i=0}^{M-1}\phi \left(x\right)·y_i\left(t\right).$$

(5)

For (1), we can express the residual $R(x,t)$ as:

$$R(x,t)=y_t^M(x,t)-f_1{y}_x^M(x,t)-f_2\left(y^M,u,x,t\right).$$

(6)

To minimize $R(x,t)$, we let

$$\left(R(x,t),{\phi }_i\right)=0,i=1,2,...,j$$

(7)

where ${\left\{{\phi }_i\right\}}_{i=0}^{M-1}$ is a set of weighting functions. The residual $R(x,t)$ is converted to its projection onto the space of weighting functions. The key to the accuracy and efficiency of WRM is the selection of the basis functions and the weighting functions.

The two most popular approaches to procure the weighting functions are Galerkin method and the collocation method. For Galerkin method, only the basis functions ${\left\{{\varphi }_i\right\}}_{i=0}^{M-1}$ need to be chosen because the weighting functions ${\left\{{\phi }_i\right\}}_{i=0}^{M-1}$ are the same as the basis functions ${\left\{{\varphi }_i\right\}}_{i=0}^{M-1}$. The residual is orthogonal to each basis function, so Galerkin method is simple and has been successfully applied, especially in parabolic systems. The Dirac delta functions $\delta (x-x_i)$ are chosen as the weighting functions ${\left\{{\phi }_i\right\}}_{i=0}^{M-1}$ in the collocation method. The residuals vanish at the collocation nodes and the collocation nodes can be specified optimally. Both Galerkin method and the collocation method, which are linear reduction methods, are applicable to nonlinear DPSs.

The selection of the basis functions ${\left\{{\varphi }_i\right\}}_{i=0}^{M-1}$ is also crucial for the application of WRM. The basis functions ${\left\{{\varphi }_i\right\}}_{i=0}^{M-1}$ can be classified as global and local types. Typical basis functions include Fourier functions, orthogonal polynomials, and wavelet functions. Various model reduction approaches have been proposed through the application of Galerkin method and the collocation method using different basis functions [4].

Because of the collocation nature of the WCM, it is a simple task to deal with nonlinearities. Compare with wavelet-Galerkin method, the collocation method is more practical for implementation [11] (see Figure 2).

3.2. Interval Quasi-Shannon Wavelet

In this section, the quasi-Shannon wavelets are used as the basis functions of the proposed prediction model taking into account its normalization conditions. Then, the choice of the parameters is discussed. To eliminate the boundary effect, the interval quasi-Shannon wavelets are adopted.

Shannon wavelet functions are, which have analytic expressions, orthogonal, smooth, and differentiable. However, they are not tightly supported. To derive a wavelet function with compact support, Shannon wavelet is multiplied by Gauss window function, forming a semi-orthogonal wavelet function with compact support. This wavelet function is called the quasi-Shannon wavelet [19]. The scaling function ${\varphi }^{\Delta ,\sigma }$ and the wavelet function ${\psi }^{\Delta ,\sigma }$ of the quasi-Shannon wavelet are, respectively, given by

$${\varphi }^{\Delta ,\sigma }\left(x\right)=\left\{\begin{array}{cc}1& x=0\\ \frac{sin(\pi x/\Delta )}{\pi x/\Delta }exp\left(-\frac{x^2}{2{\sigma }^2}\right)& x\ne 0\end{array}\right.,$$

(8)

$${\psi }^{\Delta ,\sigma }\left(x\right)=\left\{\begin{array}{cc}1& x=0\\ \frac{sin(\pi x/\Delta )-sin(2\pi x/\Delta )}{\pi x/\Delta }exp\left(-\frac{x^2}{2{\sigma }^2}\right)& x\ne 0\end{array}\right.$$

(9)

where $\Delta$ is the spatial mesh size, while $\sigma$ is the window size.

The first-order derivative of the quasi-Shannon scaling function is depicted in Figure 3 obtained by $Matlab2016b$, and it is expressed as:

$${\varphi }_x^{{}_{\Delta ,\sigma }}\left(x\right)=\left\{\begin{array}{cc}0& x=0\\ \left(\frac{cos(\pi x/\Delta )}{x}-\frac{sin(\pi x/\Delta )}{\pi x^2/\Delta }-\frac{sin(\pi x/\Delta )}{\pi {\sigma }^2/\Delta }\right)·exp\left(-\frac{x^2}{2{\sigma }^2}\right)& x\ne 0.\end{array}\right.$$

(10)

To guarantee normalization conditions being satisfied, the following lemma [19] is given.

Lemma 1.

Suppose that $\tilde{r}=\sigma /\Delta \gg \sqrt{2}/\pi$. Then the normalization condition ${\int }_{-\infty }^{+\infty }{\varphi }^{\Delta ,\sigma }\left(x\right)dx\propto 1$ is satisfied.

Proof. 

$${\int }_{-\infty }^{+\infty }{\varphi }^{\Delta ,\sigma }\left(x\right)dx=erf\left(\frac{\pi \sigma }{\sqrt{2}\Delta }\right)=1-erfc\left(\frac{\pi \sigma }{\sqrt{2}\Delta }\right)$$

$$={\int }_{-\infty }^{+\infty }\frac{sin(\pi x/\Delta )}{\pi x/\Delta }exp\left(-\frac{x^2}{2{\sigma }^2}\right)dx=\sqrt{2\pi }·\frac{\sigma }{\Delta }\sum _{k=0}^{+\infty }\frac{{(-1)}^k}{k!(2k+1)}{\left(\frac{\pi \sigma }{\sqrt{2}\Delta }\right)}^{2k}$$

$$=1-\sqrt{\frac{2}{\pi }}\frac{1}{\sigma }exp\left(-\frac{{\sigma }^2{\pi }^2}{2{\Delta }^2}\times {\int }_0^{+\infty }exp\left(-\frac{t^2}{2{\sigma }^2}-\frac{\pi }{\Delta }\right)dt\right)$$

where the error function $erf\left(z\right)=2/\sqrt{\pi }·{\int }_0^z{e}^{-t^2}dt$. The residue term $erfc(\pi \sigma /\sqrt{2}\Delta )$ approaches zero extremely fast when $\tilde{r}=\sigma /\Delta \gg \sqrt{2}/\pi$, so that $erf(\pi \sigma /\sqrt{2}\Delta )$ is extremely close to unity. This phenomenon is observed in practical applications. □

The choice of the parameter $\tilde{r}$ and the nature of the curve being described with wavelet as the basis function will affect the accuracy of wavelet representation. A guide for the choice of $\tilde{r}$ and the resulting mathematical estimation of the approximation error are given in [19]. When $\tilde{r}\to \infty ,$ the tight support property of the wavelet is completely lost. On the other hand, when $\tilde{r}\to \sqrt{2}/\pi ,$ the normalization conditions will fail to be satisfied.

Empirically, the parameter $\tilde{r}$ should be chosen in the interval $\left[2.12.3\right]$ (respectively, $\left[2.63.8\right]$) when approaching a linear function (respectively, a nonlinear function).

The wavelet transform is defined in the bilateral infinite interval, but the signals appearing in real life are usually in a finite interval. The interval wavelets are often used to reduce boundary effects. The interval quasi-Shannon wavelets based on the difference method [33] are given by

$${\varphi }^{jk}=\left\{\begin{array}{ccc}\hfill \varphi (2^{j}x-k& )+2\sum _{i=1}^N\varphi (2^{j}x+i)\hfill & \hfill k=0\\ \hfill \varphi (2^{j}x-& k)-\varphi (2^{j}x+k)\hfill & \hfill k=1,...,N\\ \hfill \varphi & (2^{j}x-k)\hfill & \hfill k=N+1,...,2^j-N-1\\ \hfill \varphi (2^{j}x-k& )-\varphi (2^{j}x-2^{j+1}+k)\hfill & \hfill k=2^j-N,...,2^j-1\\ \hfill \varphi (2^{j}x-k& )+2\sum _{i=2^j+1}^{2^j+N}\varphi (2^{j}x-i)\hfill & \hfill k=2^j\end{array}\left(11\right)\right.$$

where j is an integer, $\varphi (2^{j}x-k)$ is the quasi-Shannon wavelet scaling function, N is the number of the outer wavelet scale function on each side of the boundary.

3.3. The Prediction Model Developed Based on WCM

Based on WCM under the situation referred to as Problem (P). The spatio-temporal variable $y(x,t)$ in (1) is approximated by

$$y(x,t)\approx y^M(x,t)=\sum _{m=0}^{2^j}{y}^M(x_i,t)·{\varphi }^j{\mid }_{x-x_m}$$

(12)

where $y^M(x,t)$ is the approximation at the spatial location x and the time t. Let $\varphi \left(x\right)$ be the scaling function of the quasi-Shannon wavelet, and let ${\varphi }^j{\mid }_{x-x_m}={\varphi }^j(x-x_m)$. Then, the first derivative of the spatio-temporal variable $y(x,t)$ at any time t is given by

$$y_x(x,t)\approx y_x^M(x,t)=\sum _{m=0}^{2^j}{y}^M(x_m,t)·{\varphi }_x^j{\mid }_{x-x_m}.$$

(13)

By Euler forward difference method, it gives explicit format and a first-order accuracy approximation to $y_t(x_m,t)$, meaning that the error is proportional to $h.$ Let $y^M(x_m,t)\approx y^M{\mid }_m^n,n=1,2,\dots ,\infty$. Then, we obtain

$$y_t(x_m,t)\approx y_t^M{\mid }_m^n=\frac{y^M{\mid }_m^{n+1}-y^M{\mid }_m^n}{\Delta t}.$$

(14)

Let $\mathcal{F}{\mid }_m^n=f_1{\mid }_m^n·{\sum }_{n=0}^{2^j}{y}^M{\mid }_m^n·{\varphi }_x^j{\mid }_{x-x_m}+f_2{\mid }_m^n$, and substituting (13) and (14) into (1) yields

$$\frac{y^M{\mid }_m^{n+1}-y^M{\mid }_m^n}{\Delta t}=\mathcal{F}{\mid }_m^n.$$

(15)

From (15), we can express the prediction value $y^M{\mid }_m^{n+1}$ as:

$$y^M{\mid }_m^{n+1}=y^M{\mid }_m^n+\Delta t·\mathcal{F}{\mid }_m^n.$$

(16)

Since the sensor is located at $x_m$, the approximation $y^M{\mid }_m^n$ can be replaced by the actual output $y{\mid }_m^n$, where the approximation $y^M{\mid }_m^{n+1}$ is the prediction output $\widehat{y}{\mid }_m^{n+1}.$ Iteratively, the recurrence formula of the P-step forward prediction output $y(x,t)$ is given by

$$\begin{array}{c}\hfill \widehat{y}{\mid }_m^{n+p}=y^M{\mid }_m^{n+p-1}+\Delta t·\mathcal{F}{\mid }_m^{n+p-1},p=1,2,\cdots ,P.\end{array}$$

(17)

3.4. Wavelet-Based Nonlinear Model Predictive Control

We consider (16), which is an approximation of (1). The discrete version of the objective function (2) is used to design the MPC controller. It is given by

$$\begin{array}{cc}\hfill J(\Delta u):=\sum _{m=0}^{2^j}& \sum _{p=N_1}^{N_2}\parallel r{\mid }_m^{n+p}-{\widehat{y}}_c{\mid }_m^{n+p}{\parallel }^2+\sum _{i=1}^{N_c}{\lambda }_i·{\parallel \Delta u{\mid }^{n+i}\parallel }^2,\hfill \\ \hfill s.t.& \widehat{y}{\mid }_m^{n+p}=y{\mid }_m^{n+p-1}+\Delta t·\mathcal{F}{\mid }_m^{n+p-1},\hfill \\ & u_{min}\le u{\mid }^{n+i}\le u_{max},\hfill \\ & \Delta u_{min}\le \Delta u{\mid }^{n+i}(x,t)\le \Delta u_{max}\hfill \end{array}$$

(18)

where $J(\Delta u)$ is the objective function, and $r{\mid }_m^{n+p}$ and ${\hat{y}}_c{\mid }_m^{n+p}$ are, respectively, the reference trajectory and the correction prediction output defined at time $t_{n+p}$ and position $x_m$. $\Delta u{\mid }^{n+i}$ is the increment of the control signal at time $n+i$, $u_{min}$ and $u_{max}$ represent, respectively, the upper bound and the lower bound of the control variables, $\Delta u_{min}$ and $\Delta u_{max}$ represent, respectively, the upper bound and lower bound of the control increment. $N_1$ is the minimum cost horizon, $N_2$ is the prediction horizon, $N_c$ is the control horizon, ${\lambda }_i,i=1,\cdots ,N_c$, are the weighting factors for the prediction error and control signal.

The reference trajectory $r{\mid }_m^{n+p}$ is defined as:

$$r{\mid }_m^{n+p}=a{\mid }_m^{n+p}·y{\mid }_m^{n+p}+(1-a{\mid }_m^{n+p})·y_{sp}{\mid }_m^{n+p}$$

(19)

where $y_{sp}{\mid }_m^{n+p}$ are the output and pre-specified value of the output function at position $x_m$ and time $t_{n+p}$. $a{\mid }_m^{n+p}$ is the softening factor. For a real system, the presence of unknown disturbance and model mismatch is unavoidable. Thus, the control action is required to be taken to compensate the deviation of the control. Let $d{\mid }_m^{n+p}=y{\mid }_m^{n+p}-\widehat{y}{\mid }_m^{n+p}$. Then, the correction prediction output ${\widehat{y}}_c{\mid }_m^{n+p}$ is given by

$${\widehat{y}}_c{\mid }_m^{n+p}=\widehat{y}{\mid }_m^{n+p}+H{\mid }_m^{n+p}·d{\mid }_m^{n+p}$$

(20)

where H is the error weight vector, which is usually chosen to be the identity vector ${\mathbf{I}}_{{}_{M\times 1}}$.

At every sample time $t_n$, the $N_c$-step optimal control actions $\Delta u^{*}{\mid }^{n+1},\cdots ,$$\Delta u^{*}{\mid }^{n+N_c}$ over the prediction horizon are calculated through solving the optimization problem (18). This optimization problem is, in general, much too complicated to admit an analytical solution and hence numerical solutions are to be obtained. For this, the original problem is approximated by a series of quadratic programming subproblems, and each of which is solved by using the sequential quadratic programming (SQP) algorithm [34], which is recognized as one of the most efficient algorithms for solving nonlinear optimization problems of small and moderate size. In this way, the increment of the optimal control signal is obtained. The structure of the nonlinear MPC is depicted in Figure 4.

4. Case Study

In this section, we consider the temperature control problem of a long duct heating system based on flow control [20], as shown in Figure 5.

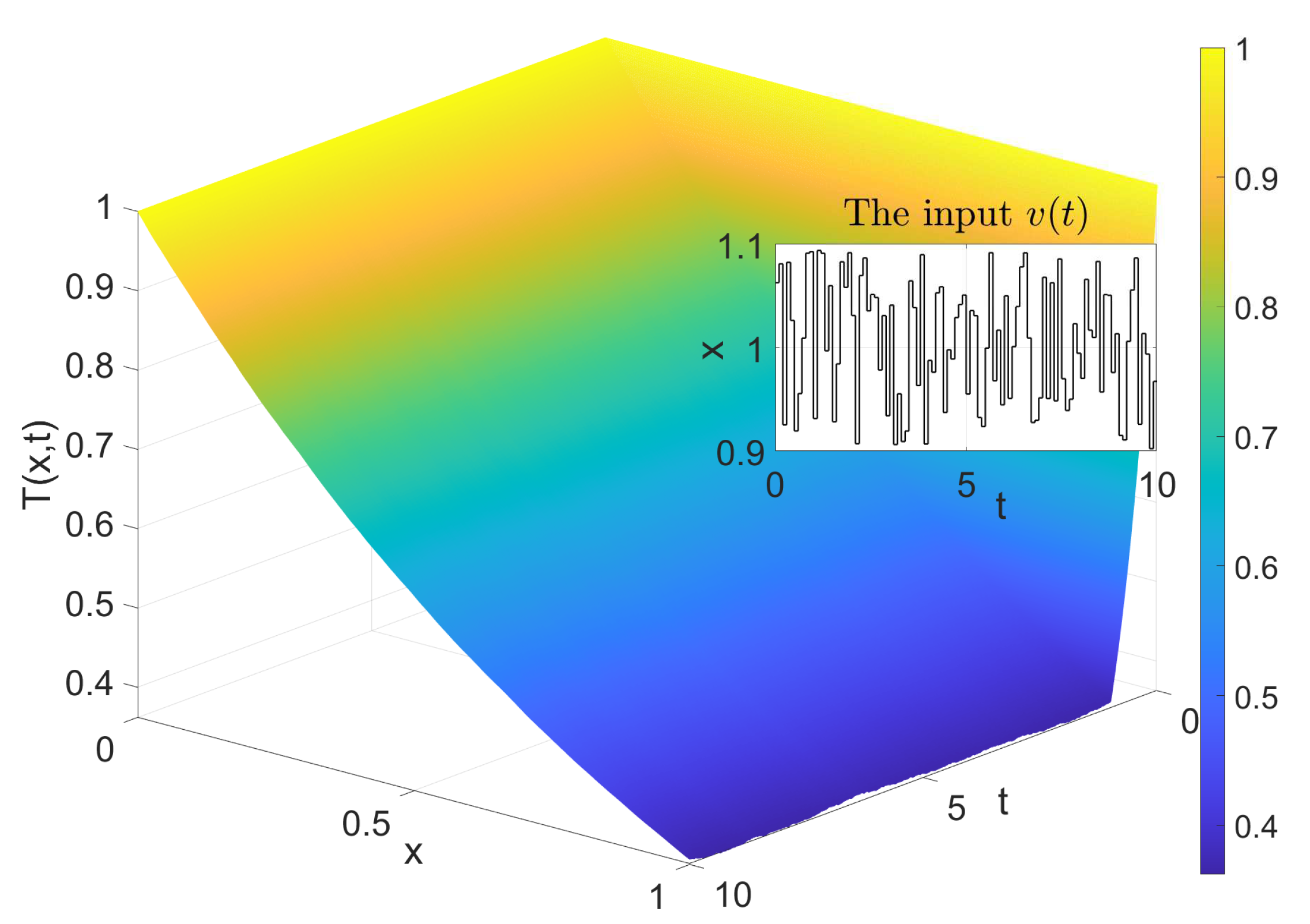
This is a one-dimensional incompressible convection heat transfer process. The fluid flows from one end of the long duct to the other end. We assume that the axial direction of the long duct is the cylindrical surface of the same diameter and that the ambient temperature of the entire system, the inlet temperature and the thermal conductivity of the fluid in the long duct are constant. Furthermore, both the fluid flow and the convection heat transfer are fully developed flows, and the diffusion phenomenon is neglected. Under the above assumptions, the temperature distribution in the duct depends only on the flow velocity. This problem is divided into three categories, corresponding to the different relationships between the flow velocity and the delay time $\tau \left(t\right)$: (i). The flow velocity is high, but the delay time is short. In this case, the influence of the flow velocity on the temperature is fast; (ii). The flow velocity is slow, but the delay time is large. In this case, the influence of the flow velocity on the temperature is slow; and (iii). The flow velocity is particularly slow. In this case, the change of the temperature in response to the flow velocity is negligible. In practice, the first two treatments are similar, and the last case is rare. In actual industrial systems, the flow velocity is often affected by unknown disturbances. When the flow velocity is affected, the axial temperature of the long tube will be affected. The purpose of the controller is to quickly restore the axial temperature of the long duct back to the equilibrium state by adjusting the opening of the regulating valve.

The dimensionless form of the dynamical model can be expressed as:

$$T_t(x,t)+v\left(t\right)·T_x(x,t)+T(x,t)=0$$

(21)

where $T(x,t)$ is the axis temperature of the long duct, $v\left(t\right)$ is the fluid velocity, $T_t(x,t)$ and $T_x(x,t)$ are, respectively, the partial derivative with respect to t and $x.$

The numerical solution is to be obtained by using FDM as described in [32]. The spatial region is evenly divided by uniform grid points $\left\{m\right|m=1,2,\cdots ,M\}$, and $\Delta x=1/(M-1)$. Similarly, let the time step be fixed as $\Delta t_n$, $n=1,2,\cdots ,N$. Then, the discretized temperature value is $T{\mid }_m^n=T(x_m,t_n)$ at the space location $x_m$ and the time $t_n$. The brackets are used to distinguish between time points and indices. Let Krone number be $CFL=v{\mid }^n\Delta t_n/\Delta x_m$. Then, the discretized version of system (21) can be expressed as:

$$T{\mid }_m^{n+1}=(1-CFL-\Delta t)·T{\mid }_m^n+CFL·T_{m-1}^n.$$

(22)

The temperature value of the long duct is calculated iteratively by (22). The sensors are evenly located in a sufficiently small interval $\Delta x$ to measure the real temperature value, whereas the time interval $\Delta t$ is chosen such that Krone stability condition is satisfied, that is $CFL\le 1$. Thus, to ensure that the stability condition is satisfied, we choose $\Delta t\le \Delta x/max\left\{v{\mid }^n\right\}$, where $max\left\{v{\mid }^n\right\}$ is the maximum flow velocity of the fluid in the long duct. The mesh is chosen to be more refine than that in [20] with the same flow velocity. Thus, the numerical solution obtained is more accurate. The length of the spatial interval $\Delta x$ is chosen to be $1/2^{13}$, which is small enough to minimize the inaccuracy to be an integer power of $1/2$ such that it is consistent with the binary wavelet. Meanwhile, the discrete time step $\Delta t$ is chosen to be $0.0001$ such that the inaccuracy is minimized and the CFL condition is satisfied. The flow velocity $v\left(t\right)\sim O\left(1\right)$ is selected randomly between $0.9$ to $1.1$. All the experiments work on IBM PC-Intel Core I5-2500K using $Matlab2016b$. The actual temperature in the long duct after 10-time units is depicted in Figure 6.

4.1. The Performance of the Prediction Model

In this subsection, we will test the performance of the prediction model using the method proposed in Section 3.3. Assume that there are $M=2^j+1$ temperature sensors evenly located along the long duct. $\mathcal{T}{\mid }_m^{n+p-1}=v{\mid }^n·{\sum }_{n=0}^{2^j}{T}^M{\mid }_m^{n+p-1}·{\varphi }_x^j{\mid }_{x-x_m}+T{\mid }_m^{n+p-1}$. The P-step prediction of the temperature value of (21) given by (17) is

$$\begin{array}{c}\hfill T{\mid }_m^{n+p}=T{\mid }_m^{n+p-1}-\Delta t·\mathcal{T}{\mid }_m^{n+p-1},p=1,2,\cdots ,P.\end{array}$$

(23)

The choice of the parameters $j,r,N$ of the interval quasi-Shannon interpolating wavelet will significantly affect the performance. In

Table 1. The prediction performance obtained by the proposed method.

$\mathsf{\Delta }{\mathit{t}}_{\mathit{s}}$	j	N	r	Single-Step Prediction Error		3-Step Prediction Error
				${\mathit{L}}_{\infty }$	$\mathit{MSE}$	${\mathit{L}}_{\infty }$	$\mathit{MSE}$
0.1	2	2	2.2	0.01792	1.90 × 10${}^{-3}$	0.1158	3.70 × 10${}^{-3}$
			2.8	0.2152	2.60 × 10${}^{-3}$	0.1525	5.60 × 10${}^{-3}$
			3.4	0.2347	3.00 × 10${}^{-3}$	0.1848	6.50 × 10${}^{-3}$
	3	3	2.2	0.0143	4.29 × 10${}^{-5}$	0.0449	3.43 × 10${}^{-4}$
			2.8	0.0248	1.64 × 10${}^{-4}$	0.0851	2.20 × 10${}^{-3}$
			3.4	0.0381	4.03 × 10${}^{-4}$	0.1267	6.80 × 10${}^{-3}$
	4	7	2.2	0.0185	2.66 × 10${}^{-5}$	0.2394	4.83 × 10${}^{-4}$
			2.8	0.017	2.70 × 10${}^{-5}$	0.2611	5.82 × 10${}^{-4}$
			3.4	0.019	2.89 × 10${}^{-5}$	0.2771	7.63 × 10${}^{-4}$
0.01	2	2	2.2	0.0181	1.86 × 10${}^{-5}$	0.0478	1.43 × 10${}^{-4}$
			2.8	0.0216	2.60 × 10${}^{-5}$	0.0567	1.99 × 10${}^{-4}$
			3.4	0.0235	2.93 × 10${}^{-5}$	0.0614	2.26 × 10${}^{-4}$
	3	3	2.2	0.0033	5.38 × 10${}^{-7}$	0.0087	3.71 × 10${}^{-6}$
			2.8	0.0041	1.72 × 10${}^{-6}$	0.0107	1.44 × 10${}^{-5}$
			3.4	0.0051	4.08 × 10${}^{-6}$	0.0134	3.65 × 10${}^{-5}$
	4	7	2.2	0.0035	3.31 × 10${}^{-7}$	0.0092	1.86 × 10${}^{-6}$
			2.8	0.0033	3.30 × 10${}^{-7}$	0.0087	1.85 × 10${}^{-6}$
			3.4	0.0033	3.47 × 10${}^{-7}$	0.0075	2.00 × 10${}^{-6}$

, we show the $L_{\infty }$-error and the mean square error (MSE) under two different sample times $\Delta t_s=0.1and0.01$ for three different meshes $j=2,3,4$ with $N=2,3,7$. Based on the results obtained in Section 3.2, the quasi-wavelet parameters $r=2.2,2.8,and3.4$ are chosen. Let the $L_{\infty }$ error function be defined as follows:

$$L_{\infty }=max|T-\hat{T}|$$

(24)

and let the MSE function be given by:

$$MSE=\frac{1}{N}\sum _{n=1}^N{(T-\hat{T})}^2.$$

(25)

From Table 1, we can see that the sample time $\Delta t_s$ has a significant impact on the prediction performance. The single-step prediction performance meets the control requirements for both the cases of $\Delta t_s=0.1$ and $0.01$. On the other hand, the multi-step prediction performance fails to meet the control requirements for the case of $\Delta t_s=0.1$. As j is increased from 2 to 3, the $L_{\infty }$ error is deduced significantly. However, as j continues to increase, the decrease of the error is no longer significantly. The optimal value of the parameter r is around $2.2$. The $L_{\infty }$ error and MSE are the smallest for $j=2$ and 3. However, the parameter r becomes insensitive to prediction performance when $j=4$.

The WCM, which is developed based on Haar wavelet basis in [31] and the FDM developed in [32], are selected for comparison with the method proposed in this paper. The sample time $\Delta t_s$ is chosen small enough such that all errors are mainly originated from the spatial discretization. Without loss of generality, we choose $\Delta t_s=0.01$. In

Table 2. A comparison of the three method.

Method	j	Single-Step Prediction Error		3-Step Prediction Error
		${\mathit{L}}_{\infty }$	$\mathit{MSE}$	${\mathit{L}}_{\infty }$	$\mathit{MSE}$
FDM	2	0.0075	1.05 × 10${}^{-6}$	0.0222	8.29 × 10${}^{-6}$
	3	0.0089	6.04 × 10${}^{-7}$	0.022	4.17 × 10${}^{-6}$
	4	0.0082	4.30 × 10${}^{-7}$	0.017	2.58 × 10${}^{-6}$
Haar	2	$inf$	$inf$	$inf$	$inf$
	3	0.063	6.35 × 10${}^{-4}$	0.0956	9.60 × 10${}^{-4}$
	4	0.1086	3.90 × 10${}^{-3}$	0.1217	1.90 × 10${}^{-3}$
Proposed method	2	0.0181	1.86 × 10${}^{-5}$	0.0478	1.43 × 10${}^{-4}$
	3	0.0033	5.38 × 10${}^{-7}$	0.0087	3.71 × 10${}^{-6}$
	4	0.0033	3.30 × 10${}^{-7}$	0.0087	1.85 × 10${}^{-6}$

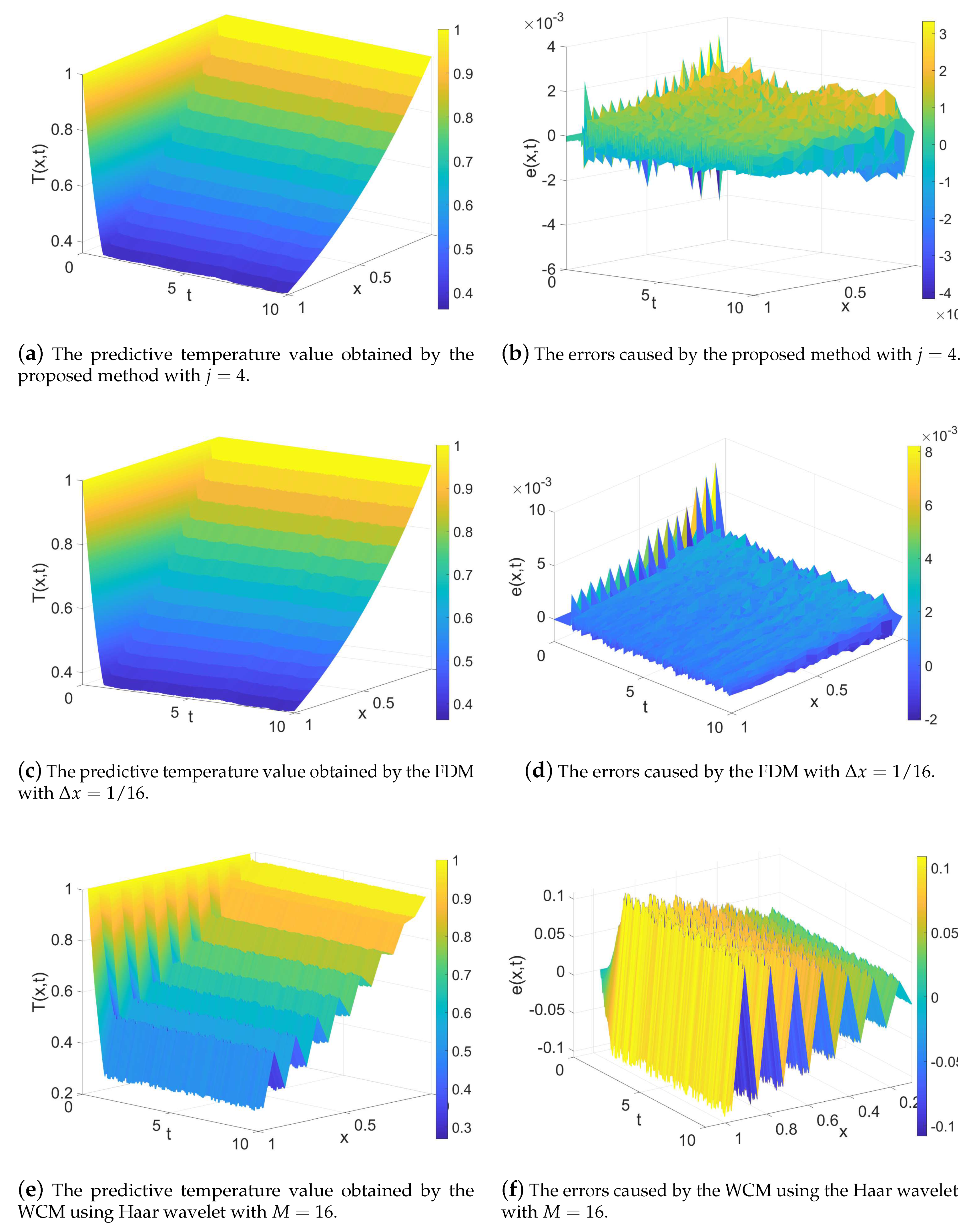
, a comparison of performance between the FDM with $\Delta x=1/4,1/8,1/16$, the WCM using Haar wavelet basis with $M=4,8,16$, and the proposed method with $j=2,3,4$ is given. The parameters of the interval quasi-Shannon interpolating wavelet are selected as $N=2,r=2.2$ for $j=2$; $N=3,r=2.2$ for $j=3$; and $N=7,r=2.8$ for $j=4$. The predictive temperature and the error of the model, which are obtained by the FDM with $\Delta x=1/16$, the WCM using Haar wavelet basis with $M=16$, and the proposed method with $j=4$, are depicted in Figure 7.

In Table 2, the prediction errors obtained by FDM and WCM using Haar wavelet basis decrease slowly when M increases. On the other hand, the prediction errors obtained by the proposed method decrease exponentially when $j=2$ is increased to $j=3$. Please note that with the increase of the integer j, the truncation error of the proposed method using the regularized Shannon’s kernel decays exponentially, but the Euler forward difference method has only the first-order accuracy [35]. Therefore, we can see that the prediction performance of the model using the proposed method is better than those obtained by using the other two methods. The model based on the WCM using Haar wavelet basis with $M=4$ is divergent, and the prediction performance is the worst among the three methods. From Figure 7, the error caused by using the proposed method is smaller than those induced by using the FDM and the WCM using Haar wavelet basis. The errors of the models caused by using the proposed method and the FDM are smoother than that obtained by the WCM using Haar wavelet basis. This is because Haar wavelet basis is discontinuous.

4.2. The Performance of the Proposed MPC Scheme

Based on the above prediction model, a nonlinear predictive controller is designed to deal with the temperature control problem. The controller is required to adjust the flow velocity to drive the temperature back to the desired initial steady state. Assume that the quadratic criterion to be minimized is given by

$$\begin{array}{cc}\hfill J(\Delta v):=\sum _{m=0}^{2^j}& \sum _{p=N_1}^{N_2}\parallel T_r{\mid }_m^{n+p}-{\hat{T}}_c{\mid }_m^{n+p}{\parallel }^2+\sum _{i=1}^{N_c}{\lambda }_i·{\parallel \Delta v{\mid }^{n+i}\parallel }^2,\hfill \\ \hfill s.t.& T{\mid }_m^{n+1}=(1-CFL-\Delta t)·T{\mid }_m^n+CFL·T_{m-1}^n,\hfill \\ & v_{min}\le v{\mid }^{n+i}\le v_{max},\hfill \\ & \Delta v_{min}\le \Delta v{\mid }^{n+i}\le \Delta v_{max}\hfill \end{array}$$

(26)

where $J(\Delta v)$ is the objective function, and $T_r{\mid }_m^{n+p}$ and ${\hat{T}}_c{\mid }_m^{n+p}$ are, respectively, the reference temperature value and the correction prediction temperature value defined at time $t_{n+p}$ and position $x_m$. $\Delta v{\mid }^{n+i}$ is the increment of the flow velocity at time $n+i$, $v_{min}$ and $v_{max}$ represent, respectively, the upper bound and the lower bound of the flow velocity, $\Delta v_{min}$ and $\Delta v_{max}$ represent, respectively, the upper bound and lower bound of the increment of the flow velocity. $N_1$,$N_2$, $N_c$, and ${\lambda }_i$ are defined in (18).

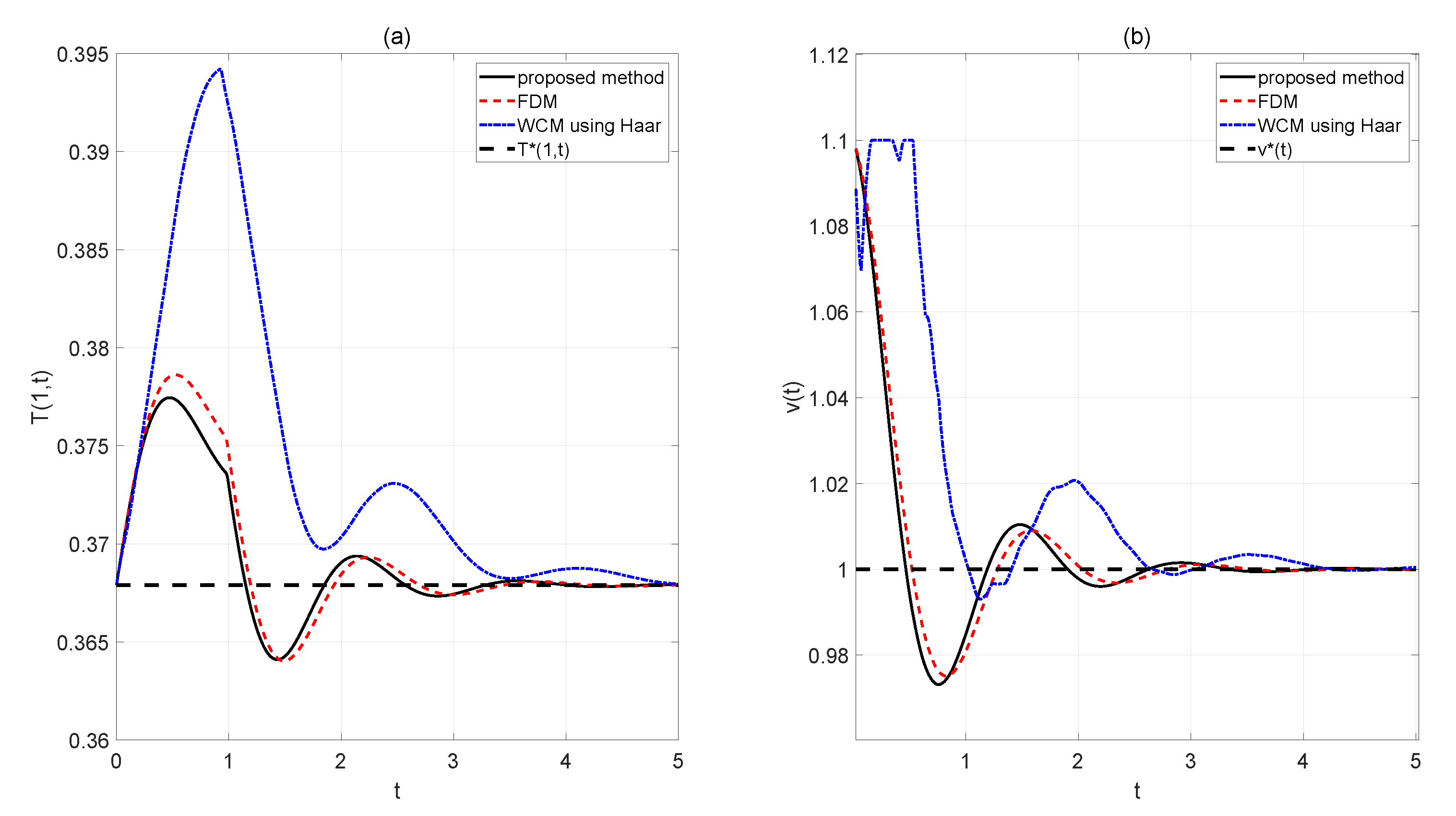
In this section, using the proposed method, the FDM, and the WCM using Haar wavelet basis, three sets of comparison experiments are performed. The purpose is to estimate the temperature at various spatial points along the long duct when the flow velocity $v\left(t\right)$ is suddenly increased by $10\%$ from 1 to 1.1 at the entrance. We suppose that there are 17 temperature sensors when the proposed method and the FDM are used, while there are 16 controlled temperature sensors when the WCM using Haar wavelet basis is used. Assume that $v_{min}=0.9$, $v_{max}=1.1$, $\Delta v_{min}=-0.1\times {10}^{-3}$, $\Delta v_{max}=0.1\times {10}^{-3}$. The predictive horizon $N_1=1,N_2=10$, and the control horizon $N_c=3$, the weighting factors ${\lambda }_i=1,i=1,2,3$ in the quadratic criterion expressed by (26) are chosen. 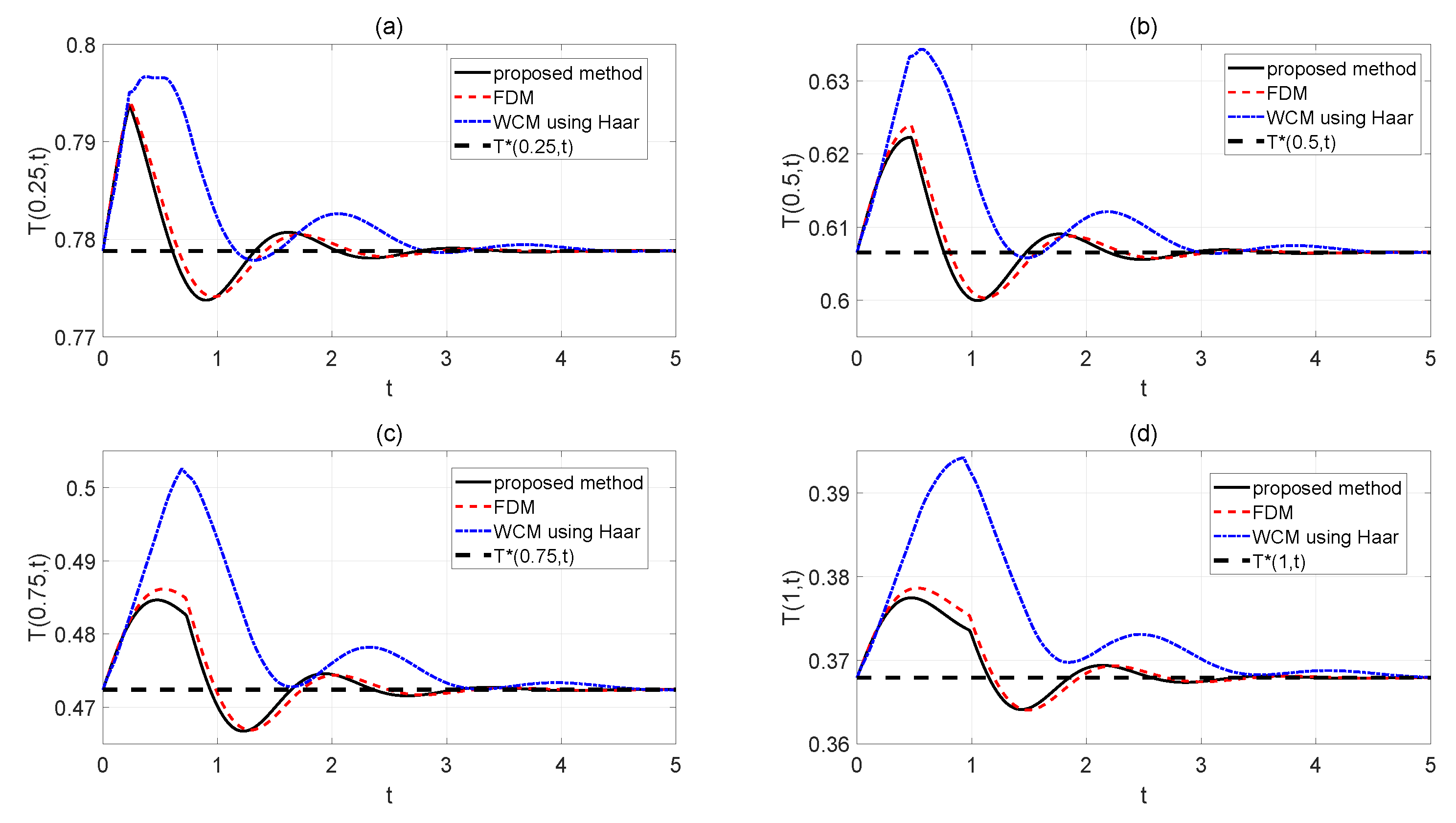The temperature response at the terminal position and the flow velocity $v\left(t\right)$ are depicted in Figure 8, and the response curves of the temperature values at other positions $x=\{0.25,0.5,0.75,1\}$ are depicted in Figure 9.

From Figure 8 to Figure 9, we see that the flow velocity $v\left(t\right)$ changes smoothly, and the temperature values at positions $x=\{0.25,0.5,0.75,1\}$ are driven back to the steady state position for all the three methods. The results show that all the controllers obtained can solve the temperature control problem at any measured position along the long duct. However, for the proposed method, the temperature is driven back to the steady state position at a faster rate with smaller overshoots.

5. Conclusions

In this paper, a first-order hyperbolic system is considered, for which an equivalent system is constructed based on the collocation technique for spatial derivatives and Euler forward difference method for the approximations of the time component. The nonlinearities are handled by the collocation method, while the accuracy of the approximate solution on the finite interval is guaranteed using the interval quasi-Shannon wavelet basis. Then, a nonlinear model predictive controller is designed through solving a nonlinear quadratic programming problem with input constraints. The FDM, the WCM using Haar wavelet basis, and the proposed method are applied to the temperature control problem of a flow-control long-duct heating system. In comparison, the multi-step prediction accuracy of the model approximation using the proposed approach is distinctly higher, and hence producing a superior control performance. From the simulation study, it is observed that the WCM has a strong potential for dealing with singular problems. For future research, it will be of interest to investigate the control of systems in the presence of local dramatic changes.