A Multi-Scale Approach to Modeling the Interfacial Reaction Kinetics of Lipases with Emphasis on Enzyme Adsorption at Water-Oil Interfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.1.1. Substrates
2.1.2. Biocatalyst
2.2. Numerical Integration
3. Single Drop
3.1. Experimental Set-Up and Analysis: The Pendant Drop Method
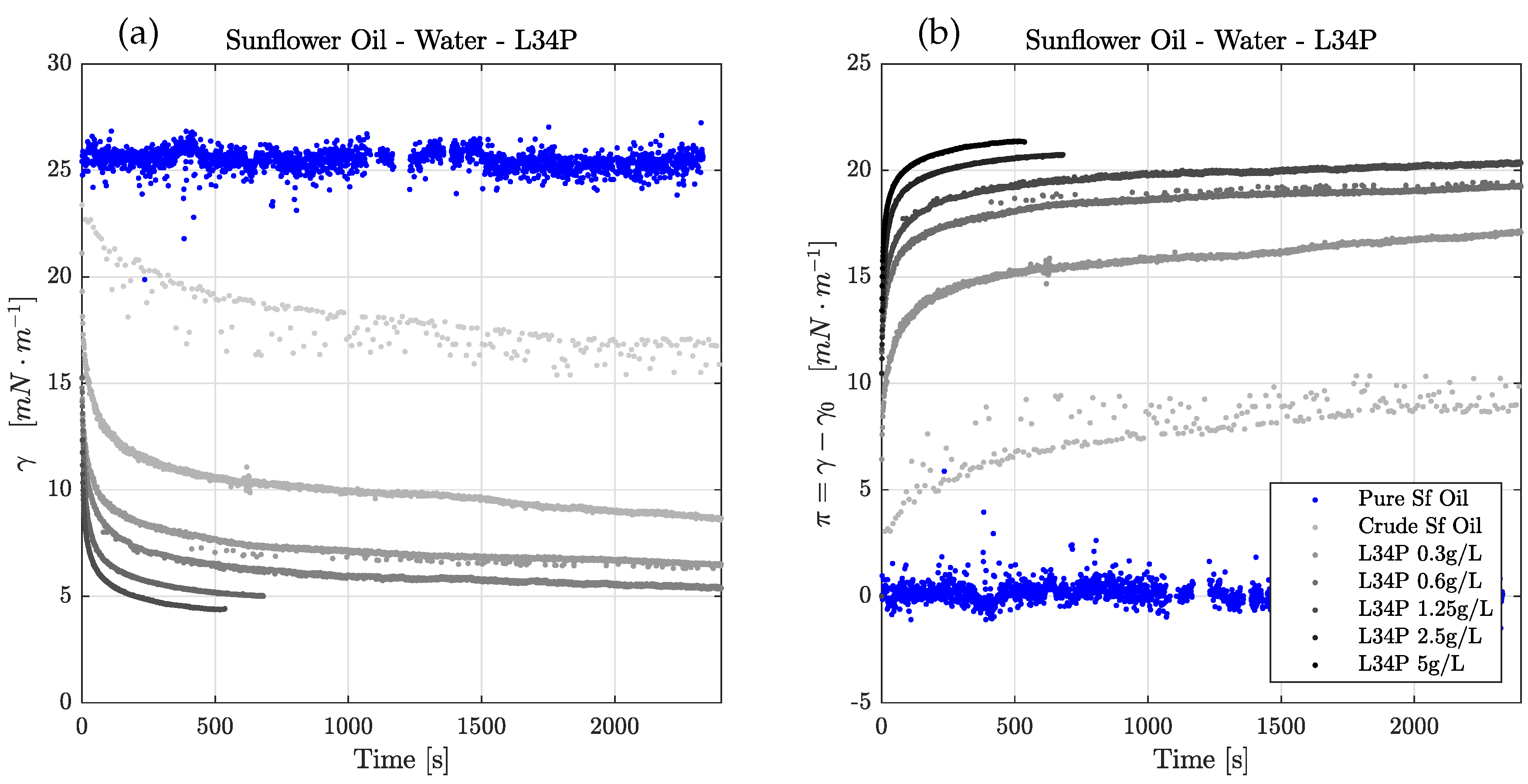
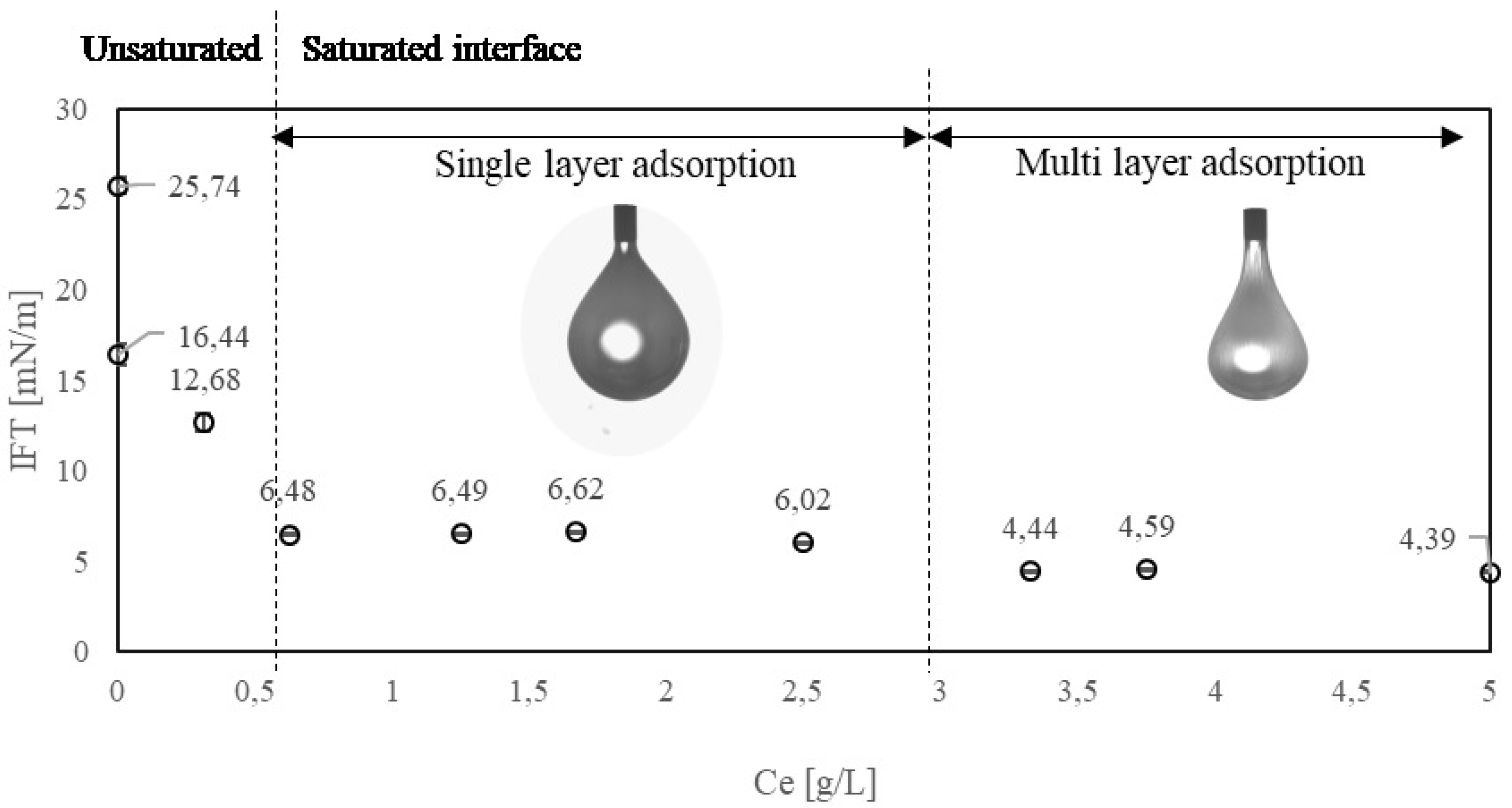
3.2. Experimental Result: Effect of Enzyme Concentration
3.3. Modeling of Enzyme Adsorption Kinetics
- Enzymes are adsorbed in single layer configuration.
- One molecule occupies one adsorption site and is assumed to be globular without molecular unfolding.
- No adsorption competition from other interfacial active components such as DG, MG and FA.
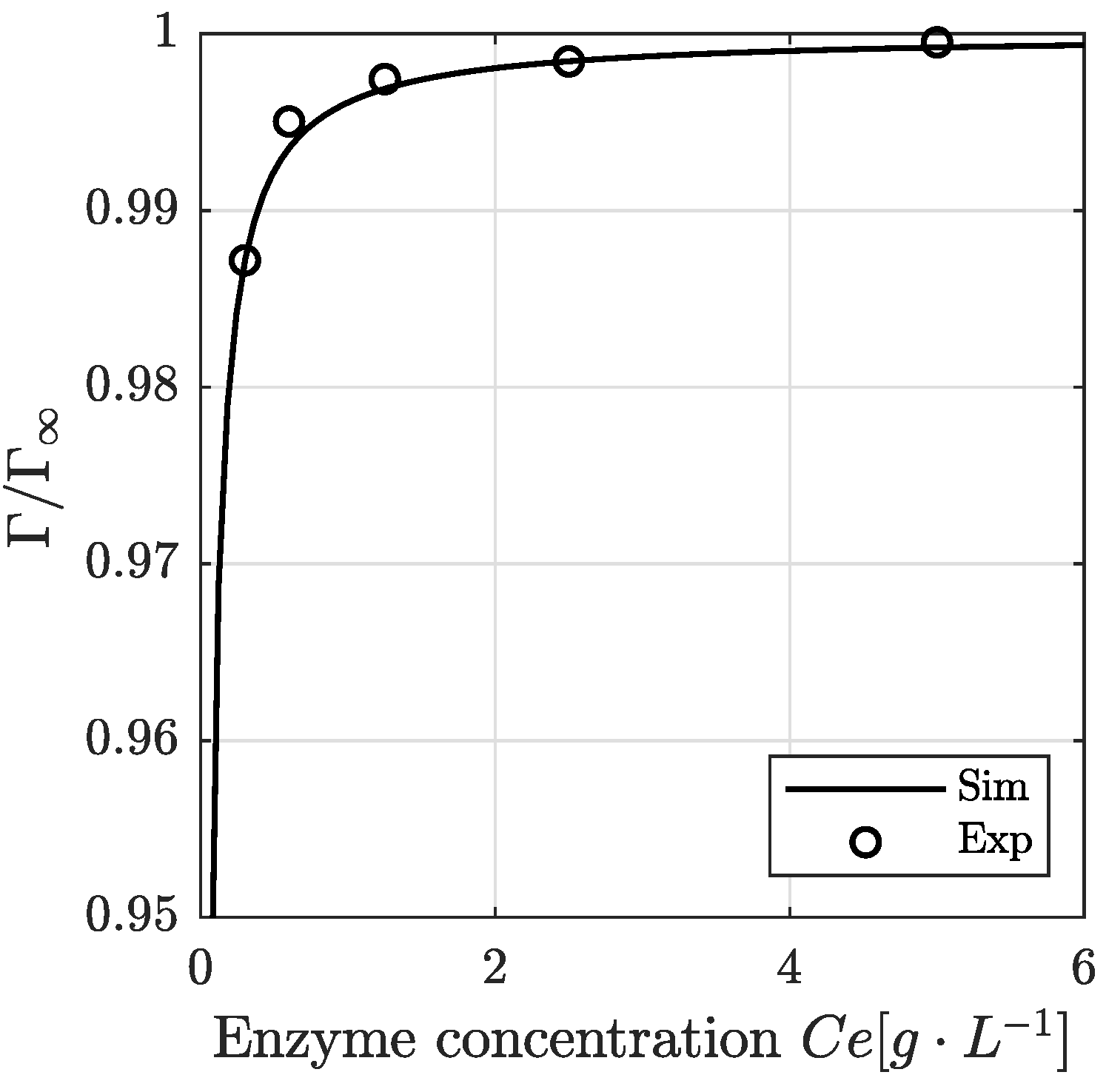
3.4. Modeling Result: Enzyme Adsorption Kinetics
4. Hydrolysis Reaction in Emulsion Reactor
4.1. Experimental Methodology
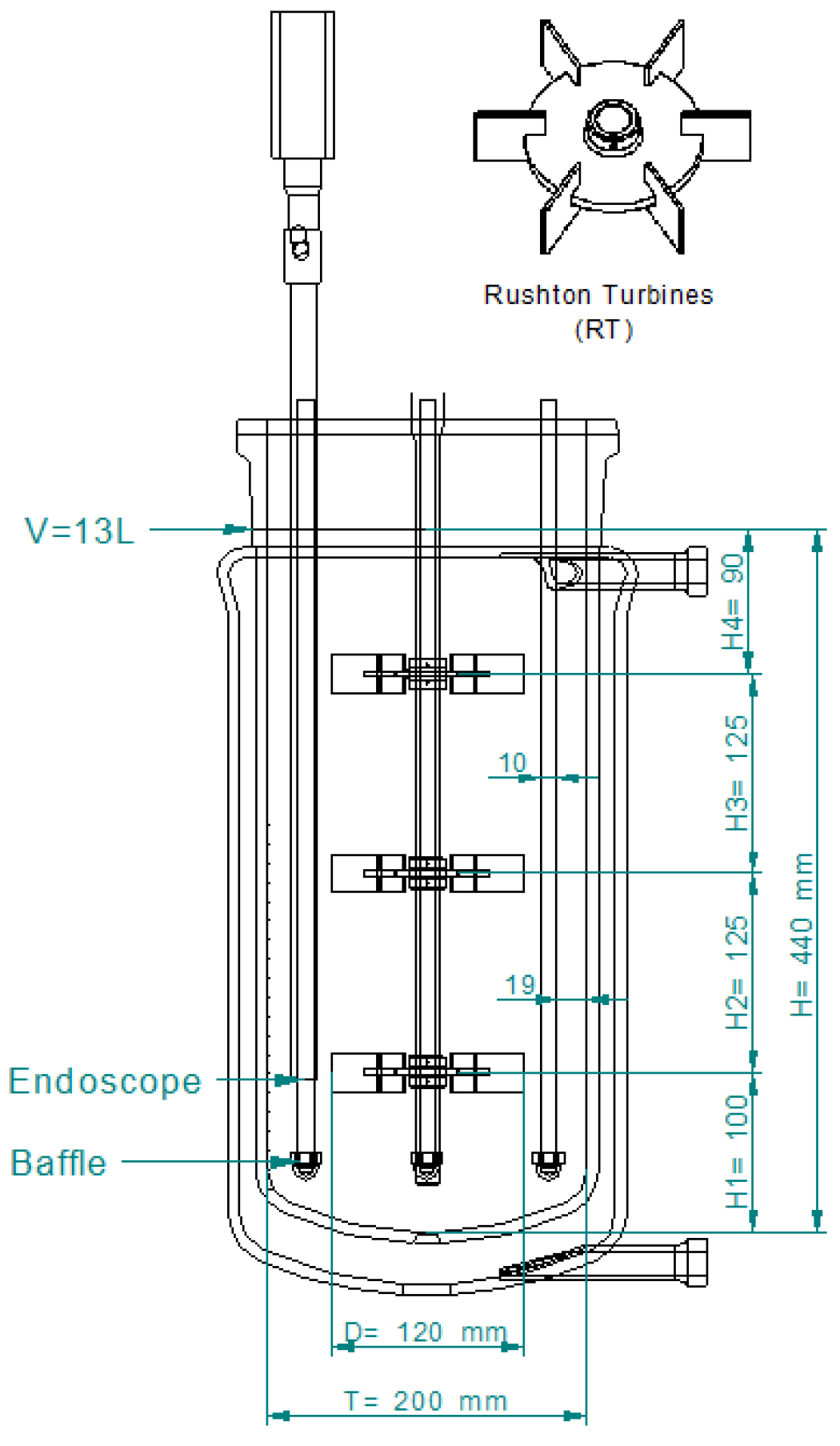
4.1.1. Batch Reaction in STR
4.1.2. Analysis Methods
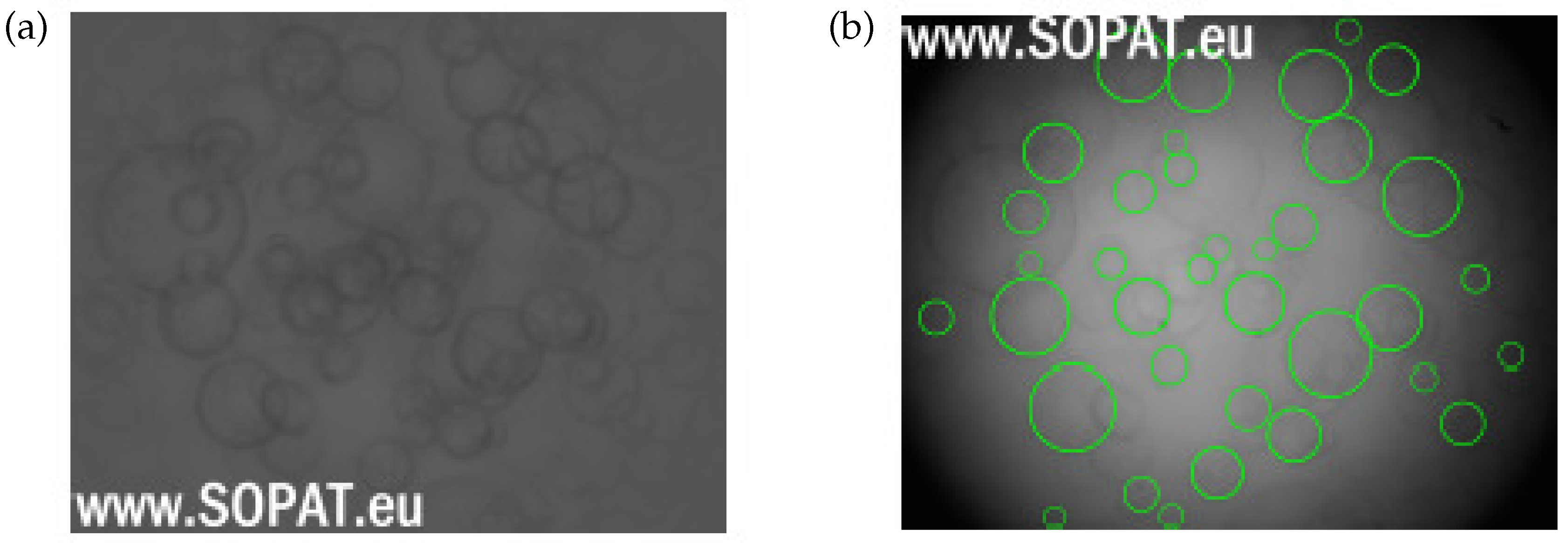
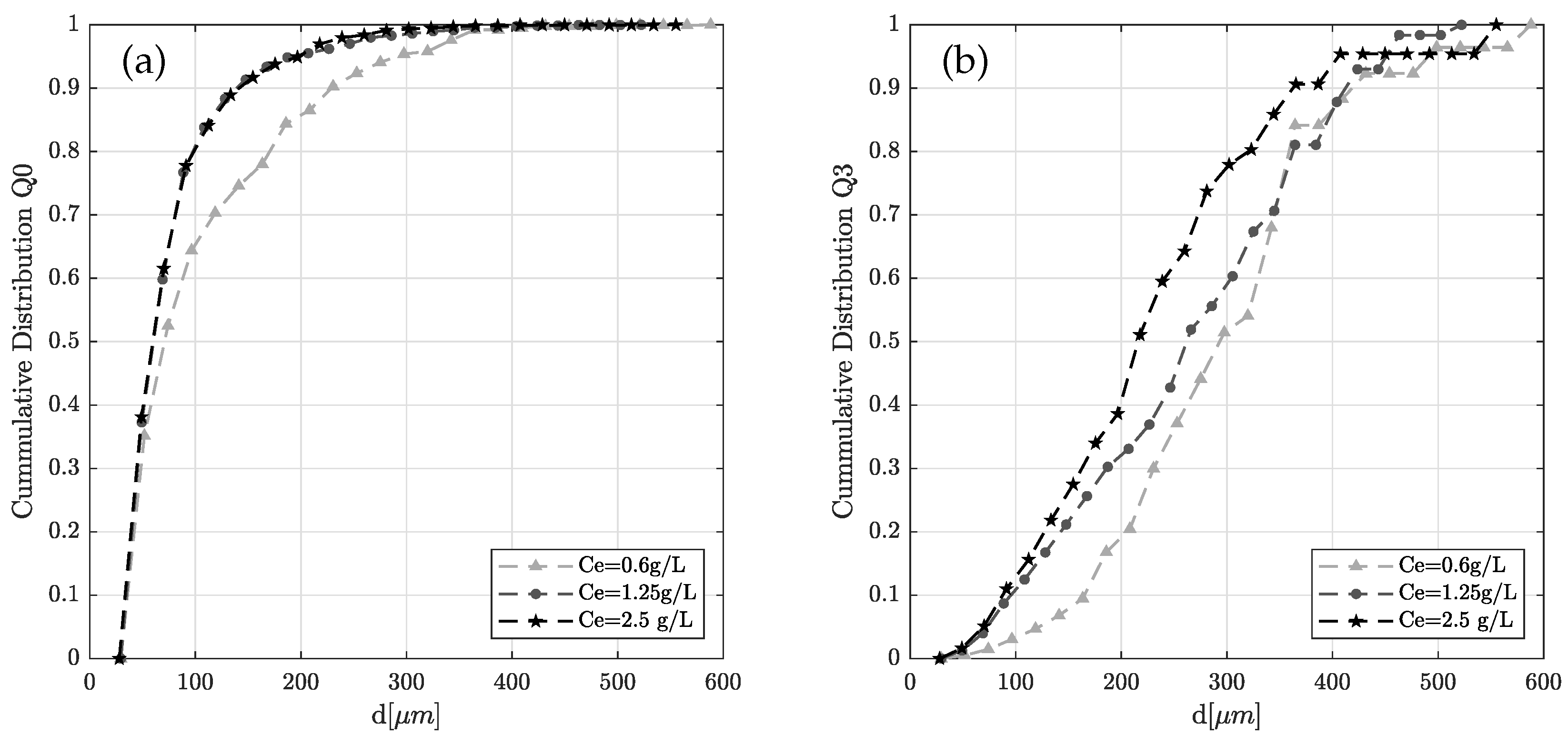
Drop Size Distribution
Concentration Analysis
Determination of Reaction Rate and Hydrolysis Degree
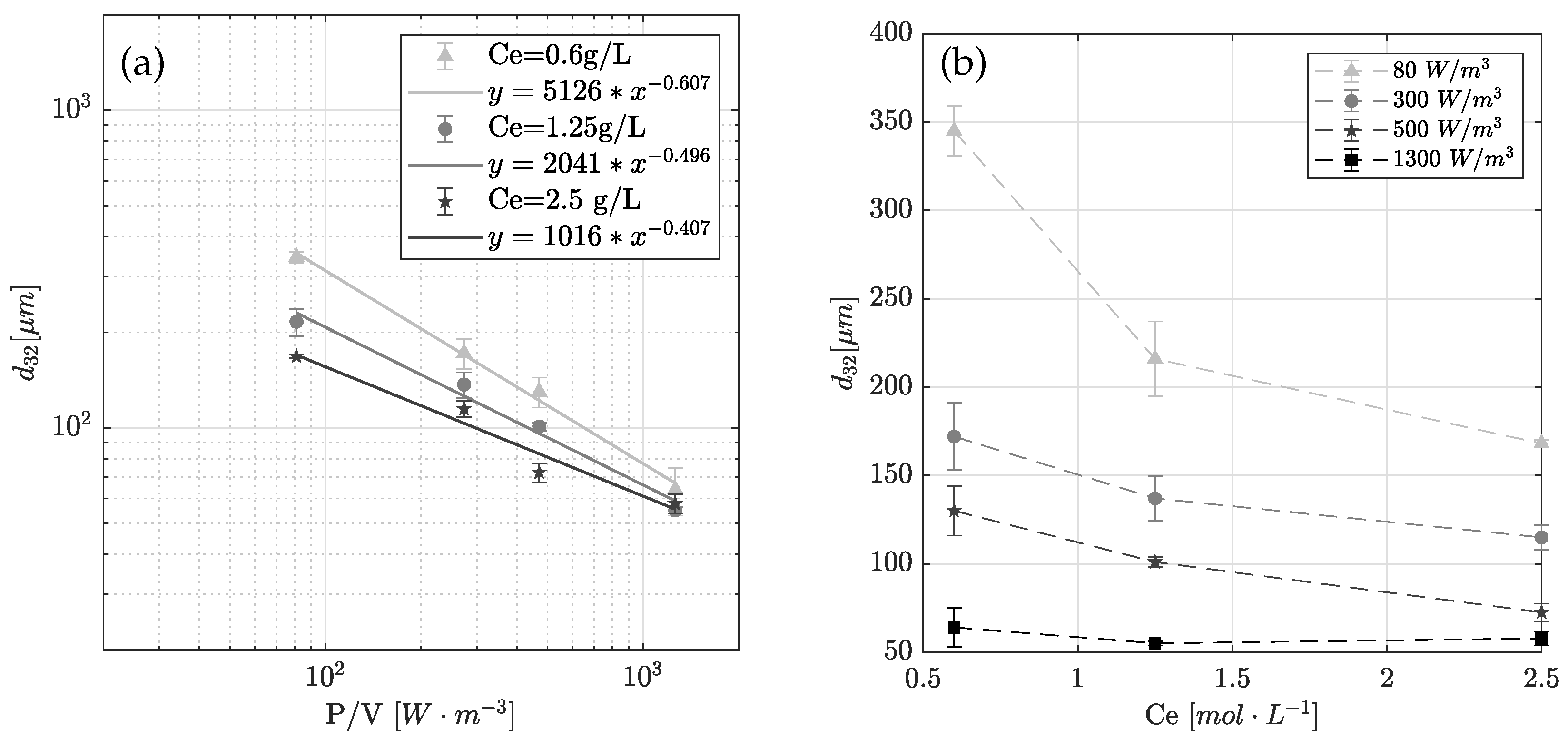
4.2. Experimental Result: Emulsification and Drop Size Distribution
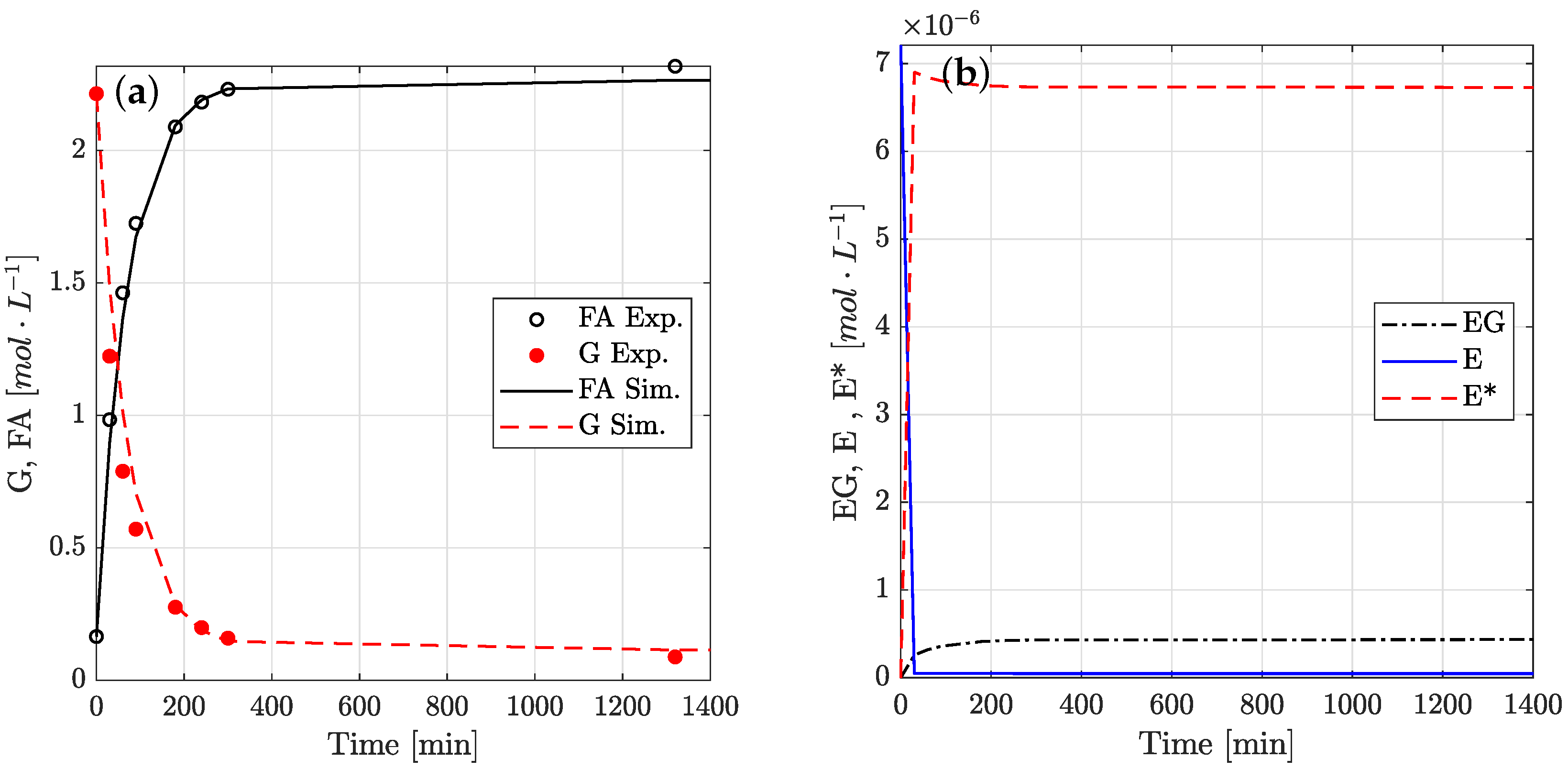
4.3. Modeling of Enzymatic Reaction Kinetics
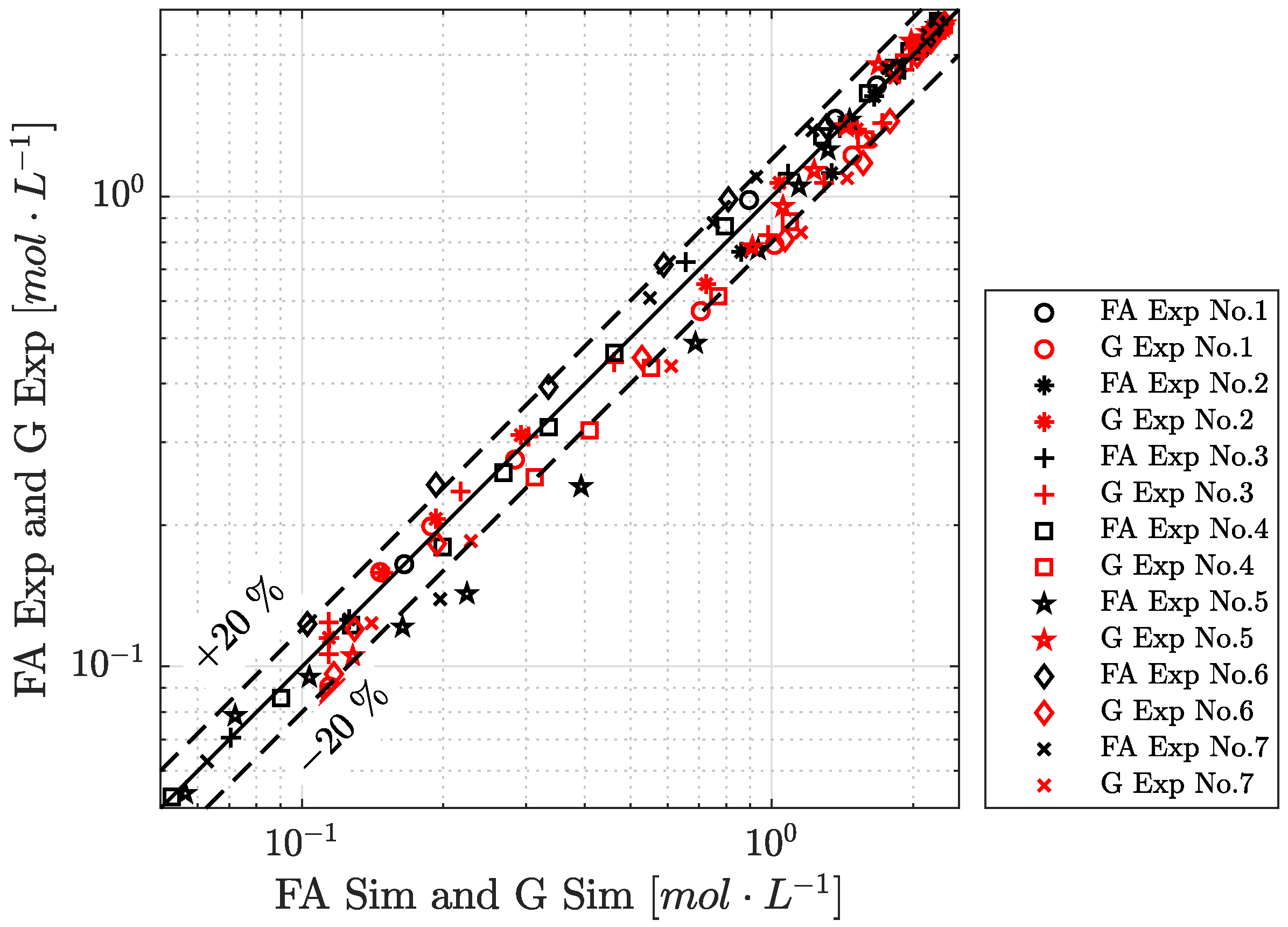
4.4. Reaction Time Course
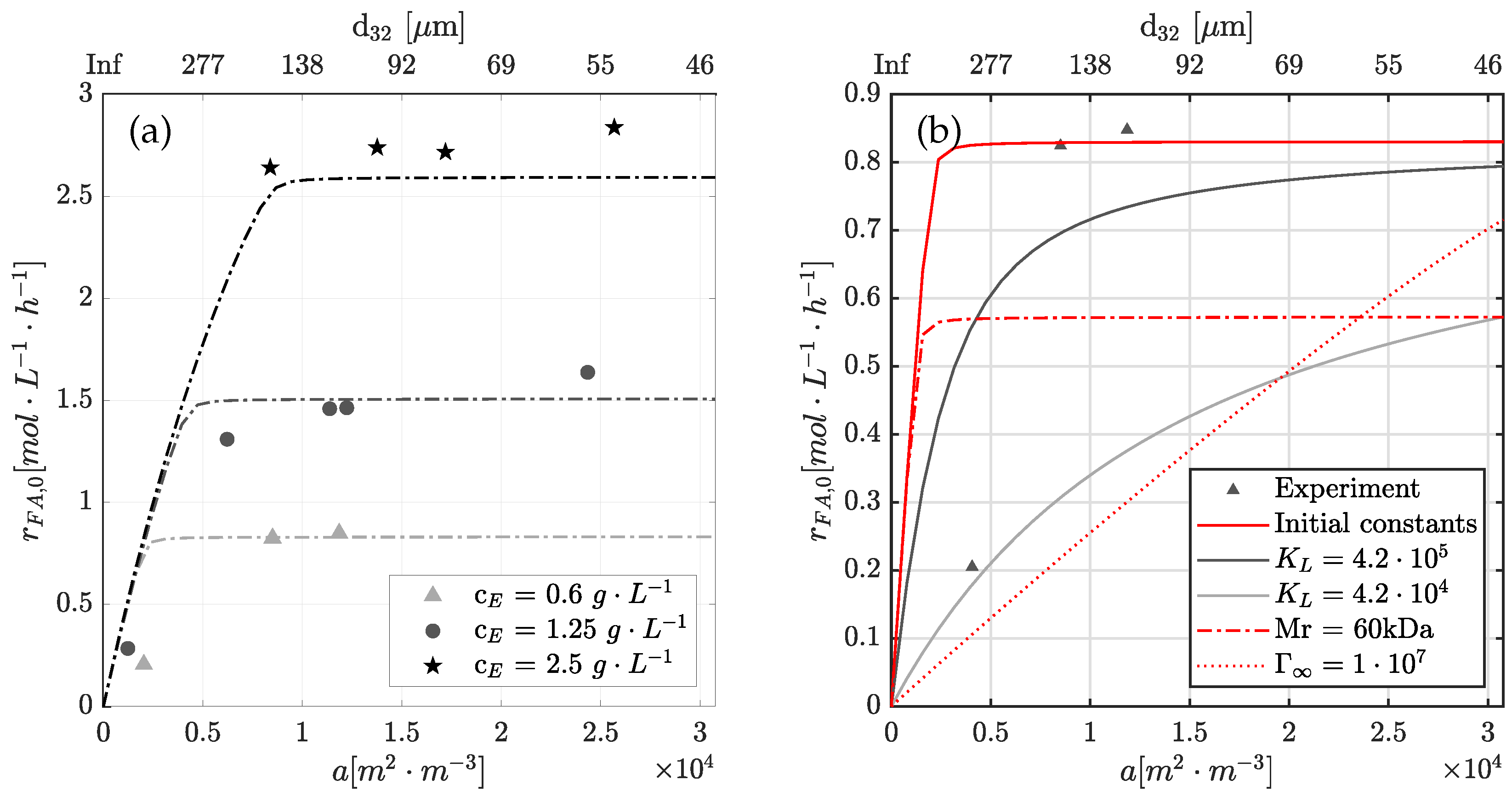
4.5. Limitation of Interfacial Area to Reaction Rate
4.6. Physical Significance of Rate Constants
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DG | Diglyceride |
| DH | Degree of Hydrolysis |
| FA | Fatty Acid |
| G | Glyceride moiety |
| Gly | Glycerol |
| HPLC | High Performance Liquid Chromatography |
| L34P | Lipase enzyme Lipomod 34P |
| MG | Monoglyceride |
| MM | Michaelis Menten |
| ODE | Ordinary Differential Equation |
| PPBB | Ping Pong Bi Bi |
| TG | Triglyceride |
| SSE | Sum of Square Error |
References
- Brady, C.; Metcalfe, L.; Slaboszewski, D.; Frank, D. Lipase immobilized on a hydrophobic, microporous support for the hydrolysis of fats. J. Am. Oil Chem. Soc. 1988, 65, 917–921. [Google Scholar] [CrossRef]
- Paiva, A.L.; Balcão, V.M.; Malcata, F.X. Kinetics and mechanisms of reactions catalyzed by immobilized lipases. Enzym. Microb. Technol. 2000, 27, 187–204. [Google Scholar] [CrossRef]
- Andrade, T.A.; Errico, M.; Christensen, K.V. Evaluation of Reaction Mechanisms and Kinetic Parameters for the Transesterification of Castor Oil by Liquid Enzymes. Ind. Eng. Chem. Res. 2017, 56, 9478–9488. [Google Scholar] [CrossRef]
- Price, J.; Hofmann, B.; Silva, V.T.L.; Nordblad, M.; Woodley, J.M.; Huusom, J.K. Mechanistic modeling of biodiesel production using a liquid lipase formulation. Biotechnol. Prog. 2014, 30, 1277–1290. [Google Scholar] [CrossRef]
- Reis, P.; Holmberg, K.; Watzke, H.; Leser, M.E.; Miller, R. Lipases at interfaces: A review. Adv. Colloid Interface Sci. 2009, 147–148, 237–250. [Google Scholar] [CrossRef]
- Straathof, A.J. Enzymatic catalysis via liquid-liquid interfaces. Biotechnol. Bioeng. 2003, 83, 371–375. [Google Scholar] [CrossRef]
- Verger, R. ‘Interfacial activation’ of lipases: Facts and artifacts. Trends Biotechnol. 1997, 15, 32–38. [Google Scholar] [CrossRef]
- Verger, R.; de Haas, G.H. Interfacial enzyme kinetics of lipolysis. Annu. Rev. Biophys. Bioeng. 1976, 5, 77–117. [Google Scholar] [CrossRef]
- Saktaweewong, S.; Phinyocheep, P.; Ulmer, C.; Marie, E.; Durand, A.; Inprakhon, P. Lipase activity in biphasic media: Why interfacial area is a significant parameter? J. Mol. Catal. B Enzym. 2011, 70, 8–16. [Google Scholar] [CrossRef]
- Mukataka, S.; Kobayashi, T.; Takahashi, J. Kinetics of Enzymatic Hydrolysis of Lipids in Biphasic Organic-Aqueous Systems. J. Ferment. Technol. 1985, 63, 461–466. [Google Scholar]
- Martinez, C.; De Geus, P.; Lauwereys, M.; Matthyssens, G.; Cambillau, C. Fusarium solani cutinase is a lipolytic enzyme with a catalytic serine accessible to solvent. Nature 1992, 356, 615–618. [Google Scholar] [CrossRef] [PubMed]
- Hermansyah, H.; Kubo, M.; Shibasaki-Kitakawa, N.; Yonemoto, T. Mathematical model for stepwise hydrolysis of triolein using Candida rugosa lipase in biphasic oil–water system. Biochem. Eng. J. 2006, 31, 125–132. [Google Scholar] [CrossRef]
- Jurado, E.; Camacho, F.; Luzón, G.; Fernández-Serrano, M.; García-Román, M. Kinetic model for the enzymatic hydrolysis of tributyrin in O/W emulsions. Chem. Eng. Sci. 2006, 61, 5010–5020. [Google Scholar] [CrossRef]
- Al-Zuhair, S.; Ramachandran, K.B.; Hasan, M. High enzyme concentration model for the kinetics of hydrolysis of oils by lipase. Chem. Eng. J. 2004, 103, 7–11. [Google Scholar] [CrossRef]
- Al-Zuhair, S.; Ramachandran, K.B.; Hasan, M. Effect of enzyme molecules covering of oil-water interfacial area on the kinetic of oil hydrolysis. Chem. Eng. J. 2008, 139, 540–548. [Google Scholar] [CrossRef]
- Jurado, E.; Camacho, F.; Luzón, G.; Fernández-Serrano, M.; García-Román, M. Kinetics of the enzymatic hydrolysis of triglycerides in o/w emulsions. Study of the initial rates and the reaction time course. Biochem. Eng. J. 2008, 40, 473–484. [Google Scholar] [CrossRef]
- Brijwani, K.; Vadlani, P.V. Lipase-mediated hydrolysis of corn DDGS oil: Kinetics of linoleic acid production. Biochem. Eng. J. 2010, 52, 289–295. [Google Scholar] [CrossRef]
- Keleti, T. Two rules of enzyme kinetics for reversible Michaelis-Menten mechanisms. FEBS Lett. 1986, 208, 109–112. [Google Scholar] [CrossRef]
- Briggs, G.; Haldane, J. A Note on the Kinetics of Enzyme Action. Biochem. J. 1925, 19, 338–339. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.; Johnson, K.; Goody, R. The Original Michaelis Constant: Translation of the 1913 Michaelis-Menten Paper. Biochemistry 2011, 50, 8264–8269. [Google Scholar] [CrossRef]
- Andrade, T.A.; Martín, M.; Errico, M.; Christensen, K.V. Biodiesel production catalyzed by liquid and immobilized enzymes: Optimization and economic analysis. Chem. Eng. Res. Des. 2019, 141, 1–14. [Google Scholar] [CrossRef]
- Albasi, C.; Bertrand, N.; Riba, J.P. Enzymatic hydrolysis of sunflower oil in a standardized agitated tank reactor. Bioprocess Eng. 1999, 20, 77–81. [Google Scholar] [CrossRef]
- Reis, P.; Miller, R.; Leser, M.; Watzke, H. Lipase-catalyzed reactions at interfaces of two-phase systems and microemulsions. Appl. Biochem. Biotechnol. 2009, 158, 706–721. [Google Scholar] [CrossRef]
- Heyse, A.; Plikat, C.; Grün, M.; Delaval, S.; Ansorge-Schumacher, M.; Drews, A. Impact of enzyme properties on drop size distribution and filtration of water-in-oil Pickering emulsions for application in continuous biocatalysis. Process Biochem. 2018, 72, 86–95. [Google Scholar] [CrossRef]
- Sarkar, A.; Murray, B.; Holmes, M.; Ettelaie, R.; Abdalla, A.; Yang, X. In vitro digestion of Pickering emulsions stabilized by soft whey protein microgel particles: Influence of thermal treatment. Soft Matter 2016, 12, 3558–3569. [Google Scholar] [CrossRef]
- Tripp, B.C.; Magda, J.J.; Andrade, J.D. Adsorption of Globular Proteins at the Air/Water Interface as Measured via Dynamic Surface Tension: Concentration Dependence, Mass-Transfer Considerations, and Adsorption Kinetics. J. Colloid Interface Sci. 1995. [Google Scholar] [CrossRef]
- Latour, R.A. The langmuir isotherm: A commonly applied but misleading approach for the analysis of protein adsorption behavior. J. Biomed. Mater. Res. Part A 2015, 103, 949–958. [Google Scholar] [CrossRef]
- Li, J.B. Multilayer formation on a curved drop surface. Angew. Chem.-Int. Ed. 2001, 40, 891–894. [Google Scholar] [CrossRef]
- Nury, S.; Piéroni, G.; Rivière, C.; Gargouri, Y.; Bois, A.; Verger, R. Lipase kinetics at the triacylglycerol-water interface using surface tension measurements. Chem. Phys. Lipids 1987, 45, 27–37. [Google Scholar] [CrossRef]
- Labourdenne, S.; Cagna, A.; Delorme, B.; Esposito, G.; Verger, R.; Rivière, C. Oil-drop tensiometer: Applications for studying the kinetics of lipase action. Methods Enzymol. 1997, 286, 306–326. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, E.; Murray, B.S.; Stainsby, G. Coalescence stability of emulsion-sized droplets at a planar oil-water interface and the relationship to protein film surface rheology. J. Chem. Soc. Faraday Trans. 1 1988, 84, 871. [Google Scholar] [CrossRef]
- Beverung, C.; Radke, C.; Blanch, H. Protein adsorption at the oil/water interface: Characterization of adsorption kinetics by dynamic interfacial tension measurements. Biophys. Chem. 1999, 81, 59–80. [Google Scholar] [CrossRef]
- Oberholzer, M.R.; Lenhoff, A.M. Protein adsorption isotherms through colloidal energetics. Langmuir 1999, 15, 3905–3914. [Google Scholar] [CrossRef]
- Maldonado-Valderrama, J.; Fainerman, V.B.; Aksenenko, J.; Cabrerizo-Vilchez, M.A.; Miller, R. Dynamics of protein adsorption at the oil-water interface: Comparison with a theoretical model. Colloids Surf. A Physicochem. Eng. Asp. 2005, 261, 85–92. [Google Scholar] [CrossRef]
- Miller, R.; Grigoriev, D.O.; Krägel, J.; Makievski, A.V.; Maldonado-Valderrama, J.; Leser, M.; Michel, M.; Fainerman, V.B. Experimental studies on the desorption of adsorbed proteins from liquid interfaces. Food Hydrocoll. 2005, 19, 479–483. [Google Scholar] [CrossRef]
- Reis, P.; Holmberg, K.; Miller, R.; Krägel, J.; Grigoriev, D.O.; Leser, M.E.; Watzke, H.J. Competition between lipases and monoglycerides at interfaces. Langmuir 2008, 24, 7400–7407. [Google Scholar] [CrossRef]
- He, Q.; Zhang, Y.; Lu, G.; Miller, R.; Möhwald, H.; Li, J. Dynamic adsorption and characterization of phospholipid and mixed phospholipid/protein layers at liquid/liquid interfaces. Adv. Colloid Interface Sci. 2008, 140, 67–76. [Google Scholar] [CrossRef]
- Baldursdottir, S.G.; Fullerton, M.S.; Nielsen, S.H.; Jorgensen, L. Adsorption of proteins at the oil/water interface-Observation of protein adsorption by interfacial shear stress measurements. Colloids Surf. B Biointerfaces 2010, 79, 41–46. [Google Scholar] [CrossRef]
- Duarte, J.G.; Leone-Ignacio, K.; Fernandez-Lafuente, R.; Freire, D.M. Rapid determination of the synthetic activity of lipases/esterases via transesterification and esterification zymography. Fuel 2016, 177, 123–129. [Google Scholar] [CrossRef]
- Pernas, M.; Lopez, C.; Pastrana, L. Purification and characterization of Lip2 and Lip3 isoenzymes from a Candida rugosa pilot-plant scale fed-batch fermentation. J. Biotechnol. 2000, 84, 163–174. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Melo-Espinosa, E.A.; Sánchez-Borroto, Y.; Errasti, M.; Piloto-Rodríguez, R.; Sierens, R.; Roger-Riba, J.; Christopher-Hansen, A. Surface tension prediction of vegetable oils using artificial neural networks and multiple linear regression. Energy Procedia 2014, 57, 886–895. [Google Scholar] [CrossRef]
- Gaonkar, A.G. Interfacial tensions of vegetable oil/water systems: Effect of oil purification. J. Am. Oil Chem. Soc. 1989, 66, 1090–1092. [Google Scholar] [CrossRef]
- Yeung, A.; Zhang, L. Shear effects in interfacial rheology and their implications on oscillating pendant drop experiments. Langmuir 2006, 22, 693–701. [Google Scholar] [CrossRef] [PubMed]
- Lucassen-Reynders, E.H.; Fainerman, V.B.; Miller, R. Surface dilational modulus or gibbs’ elasticity of protein adsorption layers. J. Phys. Chem. B 2004, 108, 9173–9176. [Google Scholar] [CrossRef]
- Mitropoulos, V.; Mütze, A.; Fischer, P. Mechanical properties of protein adsorption layers at the air/water and oil/water interface: A comparison in light of the thermodynamical stability of proteins. Adv. Colloid Interface Sci. 2014, 206, 195–206. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Lucassen-Reynders, E.H.; Miller, R. Description of the adsorption behaviour of proteins at water/fluid interfaces in the framework of a two-dimensional solution model. Adv. Colloid Interface Sci. 2003, 106, 237–259. [Google Scholar] [CrossRef]
- Saad, S.M.; Policova, Z.; Neumann, A.W. Design and accuracy of pendant drop methods for surface tension measurement. Colloids Surf. A Physicochem. Eng. Asp. 2011, 384, 442–452. [Google Scholar] [CrossRef]
- Dickinson, E. Mixed biopolymers at interfaces: Competitive adsorption and multilayer structures. Food Hydrocoll. 2011, 25, 1966–1983. [Google Scholar] [CrossRef]
- Mucic, N.; Javadi, A.; Kovalchuk, N.; Aksenenko, E.; Miller, R. Dynamics of interfacial layers—Experimental feasibilities of adsorption kinetics and dilational rheology. Adv. Colloid Interface Sci. 2011, 168, 167–178. [Google Scholar] [CrossRef]
- Miller, R.; Fainerman, V.B.; Leser, M.E.; Michel, M. Kinetics of adsorption of proteins and surfactants. Curr. Opin. Colloid Interface Sci. 2004, 9, 350–356. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Kretzschmar, G.; Miller, R. Dynamics of Adsorption at Liquid Interfaces: Theory, Experiment, Application; Studies in Interface Science; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Ward, A.F.H.; Tordai, L. Time-Dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-Effects. J. Chem. Phys. 1946, 14, 453–461. [Google Scholar] [CrossRef]
- Stasiak, M.; Andrzejewski, A.; Prochaska, K. Determination of surfactant effective diffusion coefficient using inverse problem for Ward-Tordai equation. Math. Model. 2018, 2, 119–121. [Google Scholar]
- Maaß, S.; Wollny, S.; Voigt, A.; Kraume, M. Experimental comparison of measurement techniques for drop size distributions in liquid/liquid dispersions. Exp. Fluids 2011, 50, 259–269. [Google Scholar] [CrossRef]
- Schoenfelder, W. Determination of monoglycerides, diglycerides, triglycerides and glycerol in fats by means of gel permeation chromatography [C-VI 5b(02)]. Eur. J. Lipid Sci. Technol. 2003, 105, 45–48. [Google Scholar] [CrossRef]
- Hari Krishna, S.; Karanth, N.G. Lipase-catalyzed synthesis of isoamyl butyrate: A kinetic study. Biochim. Et Biophys. Acta-Protein Struct. Mol. Enzymol. 2001, 1547, 262–267. [Google Scholar] [CrossRef]
- Firdaus, M.Y.; Brask, J.; Nielsen, P.M.; Guo, Z.; Fedosov, S. Kinetic model of biodiesel production catalyzed by free liquid lipase from Thermomyces lanuginosus. J. Mol. Catal. B Enzym. 2016, 133, 55–64. [Google Scholar] [CrossRef]
- Li, Y.; Du, W.; Dai, L.; Liu, D. Kinetic study on free lipase NS81006-catalyzed biodiesel production from soybean oil. J. Mol. Catal. B Enzym. 2015, 121, 22–27. [Google Scholar] [CrossRef]

| Parameter | Value | Unit | |
|---|---|---|---|
| Langmuir constant | 10021 | m3 mol−1 | |
| Max enzyme loading | 1.65 × 10−6 | mol m−2 | |
| Pure IFT | 25.74 | mN m−1 | |
| Error | SSE | 3.84 × 10−4 | mol m−2 |
| Exp No. | Stirring Speed | Power Input | Enzyme Concentration | Drop Diameter | Adsorption Site | Error SSE | |
|---|---|---|---|---|---|---|---|
| n | P/V | (+) | |||||
| s | W m | g L | mol L | m | mol L | mol L | |
| 1 | 4.17 | 1300 | 1.25 | 7.21 × 10−6 | 61.85 | 4.14 × 10−5 | 0.0586 |
| 2 | 2.5 | 300 | 1.25 | 7.21 × 10−6 | 115.64 | 1.93 × 10−5 | 0.0419 |
| 3 | 1.67 | 80 | 1.25 | 7.21 × 10−6 | 199.16 | 8.25 × 10−6 | 0.0555 |
| 4 | 2.5 | 300 | 0.6 | 3.46 × 10−6 | 162.81 | 1.45 × 10−5 | 0.0590 |
| 5 | 1.67 | 80 | 0.6 | 3.46 × 10−6 | 340.82 | 2.99 × 10−6 | 0.0675 |
| 6 | 2.5 | 300 | 2.5 | 1.44 × 10−5 | 100.59 | 2.34 × 10−5 | 0.0794 |
| 7 | 1.67 | 80 | 2.5 | 1.44 × 10−5 | 165.05 | 1.42 × 10−5 | 0.0990 |
| Parameter | Value | Unit | |
|---|---|---|---|
| Molecular mass | 40,000 | ||
| Enzyme loading | 1.65 × 10−6 | m3 mol−1 | |
| Adsorption rate constant | 1.86 × 1011 | L mol −1 min−1 | |
| Desorption rate constant | 4.43 × 104 | min−1 | |
| Forward reaction rate constant | 1.97 × 103 | L mol−1 min−1 | |
| Backward reaction rate constant | 3.50 × 103 | min−1 | |
| Forward reaction rate constant | 2.36 × 105 | min−1 | |
| Backward reaction rate constant | 6.73 × 103 | L mol−1 min−1 | |
| Langmuir constant | 4.20 × 107 | L mol−1 | |
| Substrate Michaelis Menten constant | 121.26 | mol L−1 | |
| Product Michaelis Menten constant | 35.61 | mol L−1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusli, S.; Grabowski, J.; Drews, A.; Kraume, M. A Multi-Scale Approach to Modeling the Interfacial Reaction Kinetics of Lipases with Emphasis on Enzyme Adsorption at Water-Oil Interfaces. Processes 2020, 8, 1082. https://doi.org/10.3390/pr8091082
Rusli S, Grabowski J, Drews A, Kraume M. A Multi-Scale Approach to Modeling the Interfacial Reaction Kinetics of Lipases with Emphasis on Enzyme Adsorption at Water-Oil Interfaces. Processes. 2020; 8(9):1082. https://doi.org/10.3390/pr8091082
Chicago/Turabian StyleRusli, Sherly, Janna Grabowski, Anja Drews, and Matthias Kraume. 2020. "A Multi-Scale Approach to Modeling the Interfacial Reaction Kinetics of Lipases with Emphasis on Enzyme Adsorption at Water-Oil Interfaces" Processes 8, no. 9: 1082. https://doi.org/10.3390/pr8091082
APA StyleRusli, S., Grabowski, J., Drews, A., & Kraume, M. (2020). A Multi-Scale Approach to Modeling the Interfacial Reaction Kinetics of Lipases with Emphasis on Enzyme Adsorption at Water-Oil Interfaces. Processes, 8(9), 1082. https://doi.org/10.3390/pr8091082







