Improvement of Fast Kurtogram Combined with PCA for Multiple Weak Fault Features Extraction
Abstract
1. Introduction
2. Methodology
2.1. The Overview of Fast Kurtogram
2.2. P-Kurtogram
2.2.1. Multiband Selection Based on Kurtogram
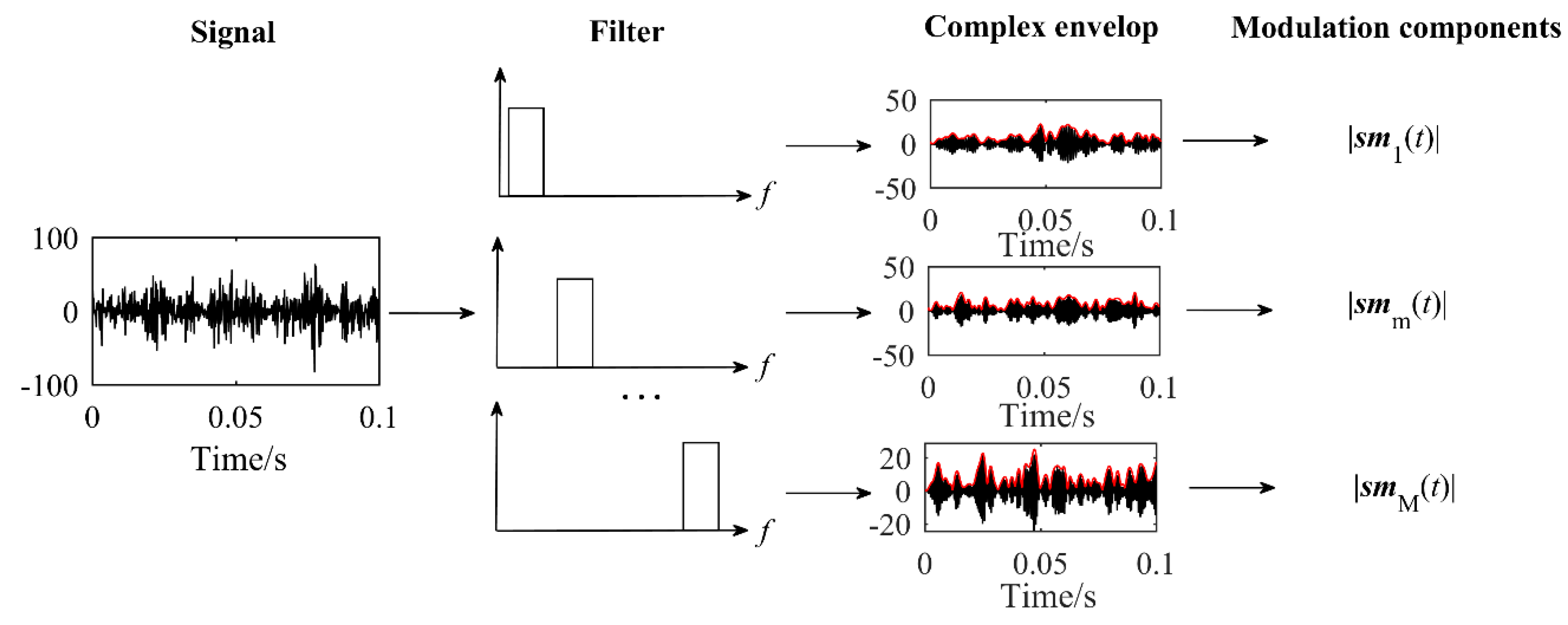
2.2.2. Principal Component Analysis
2.2.3. Feature Extraction
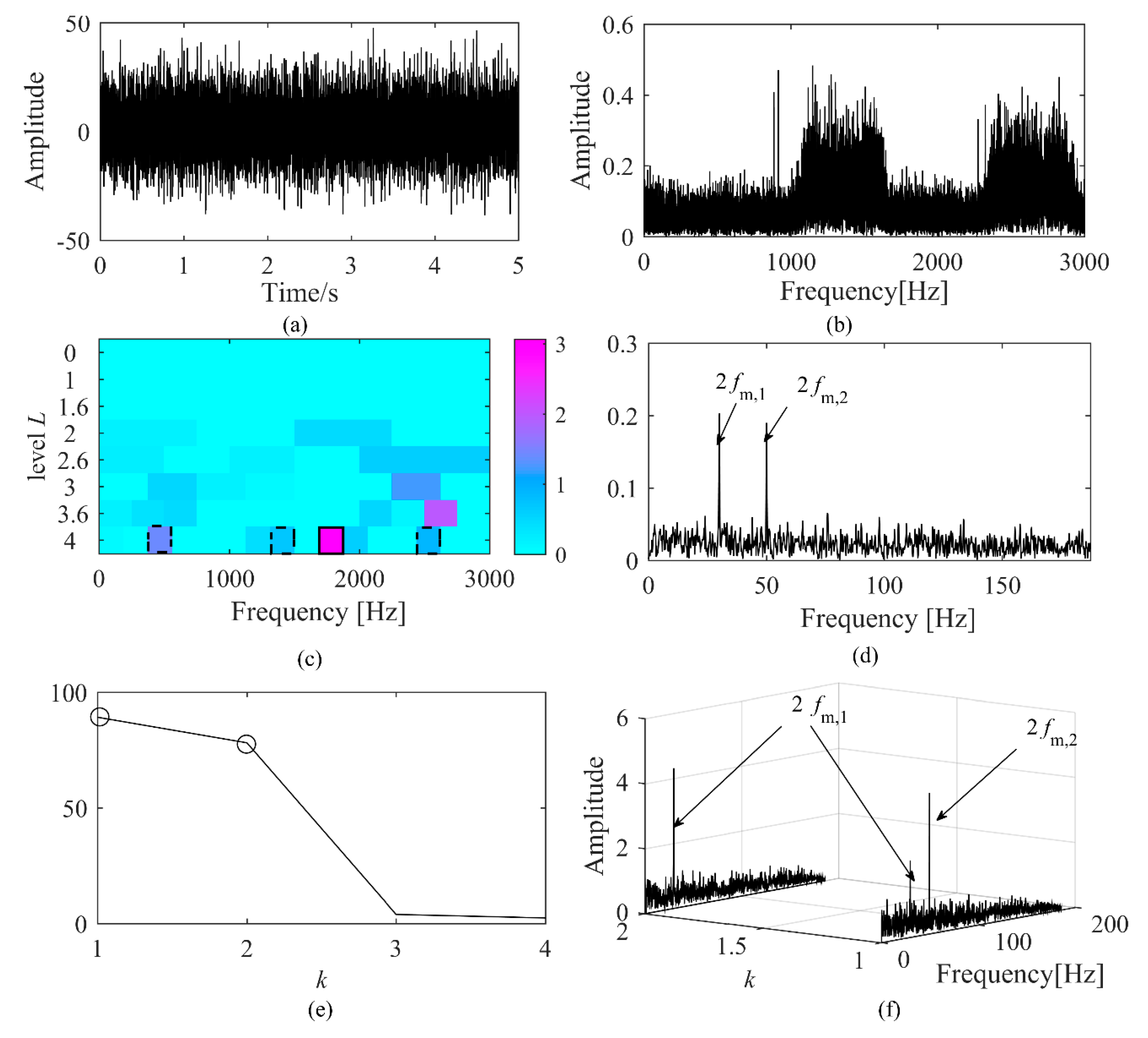
3. Simulations
4. Experiment and Analysis
4.1. Application of P-Kurtogram for Bearing Fault Signals
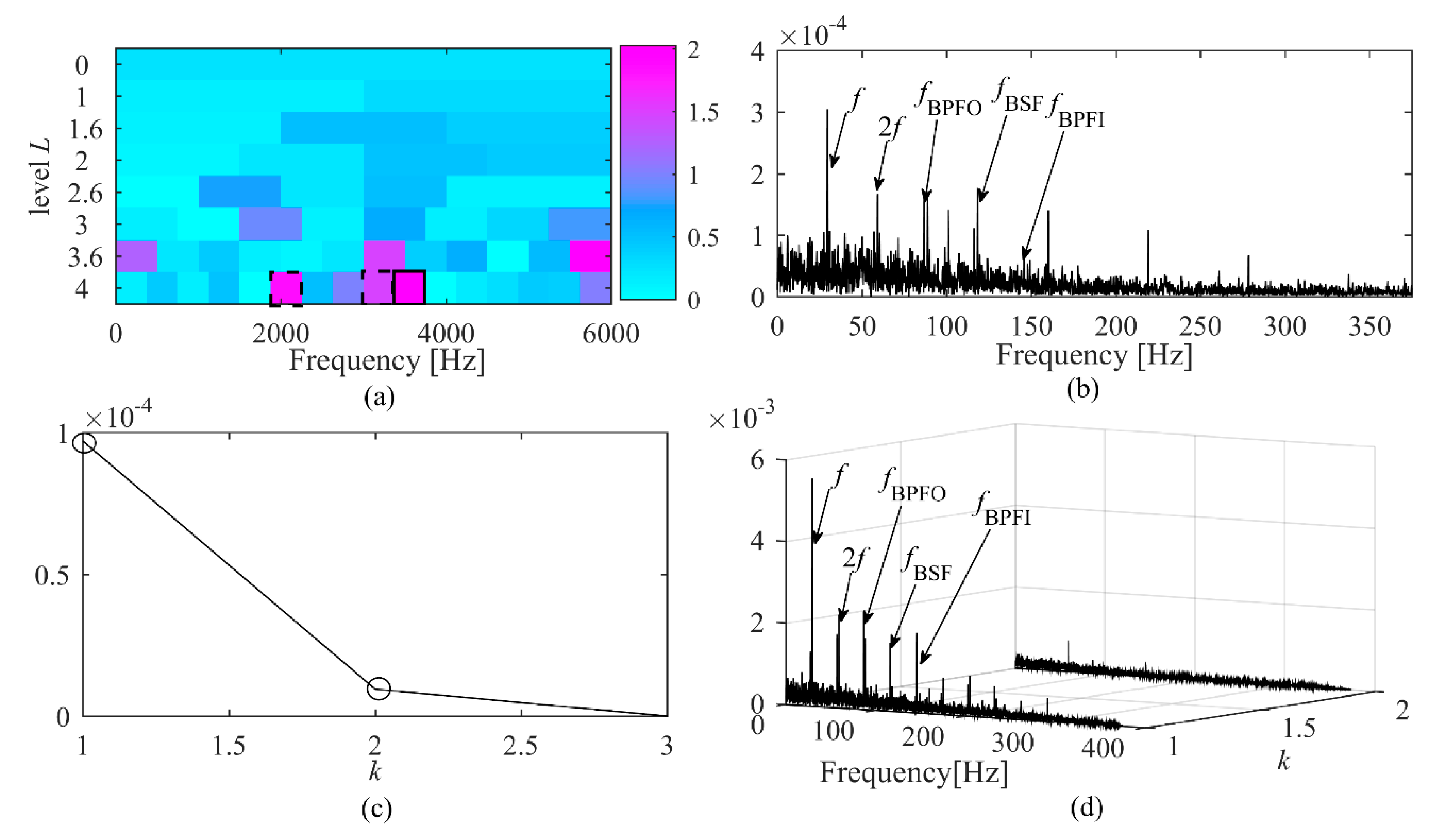
4.1.1. Case 1: Fan End Bearing Inner Race Fault
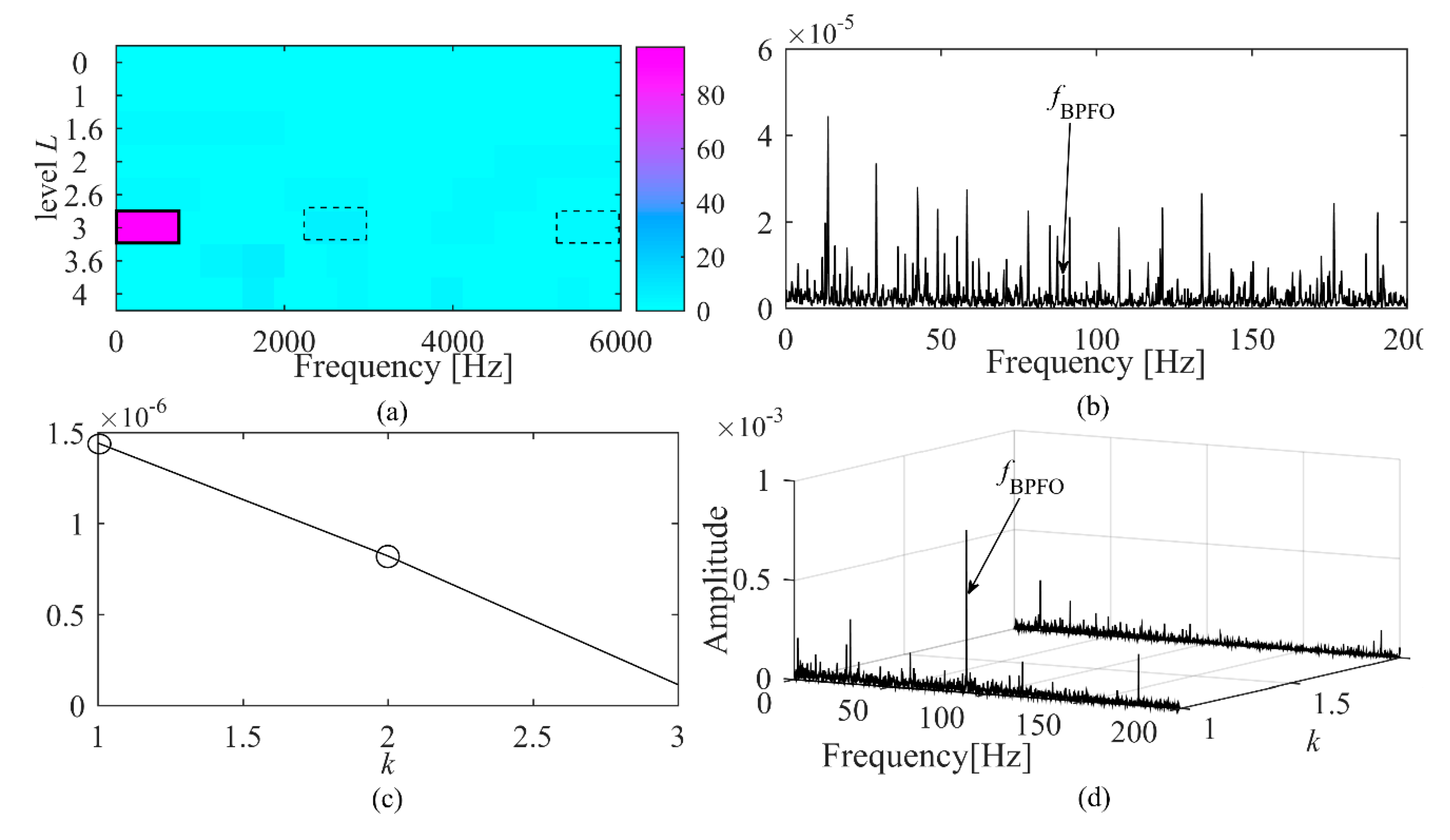
4.1.2. Case 2: Fan End Bearing Outer Race Fault
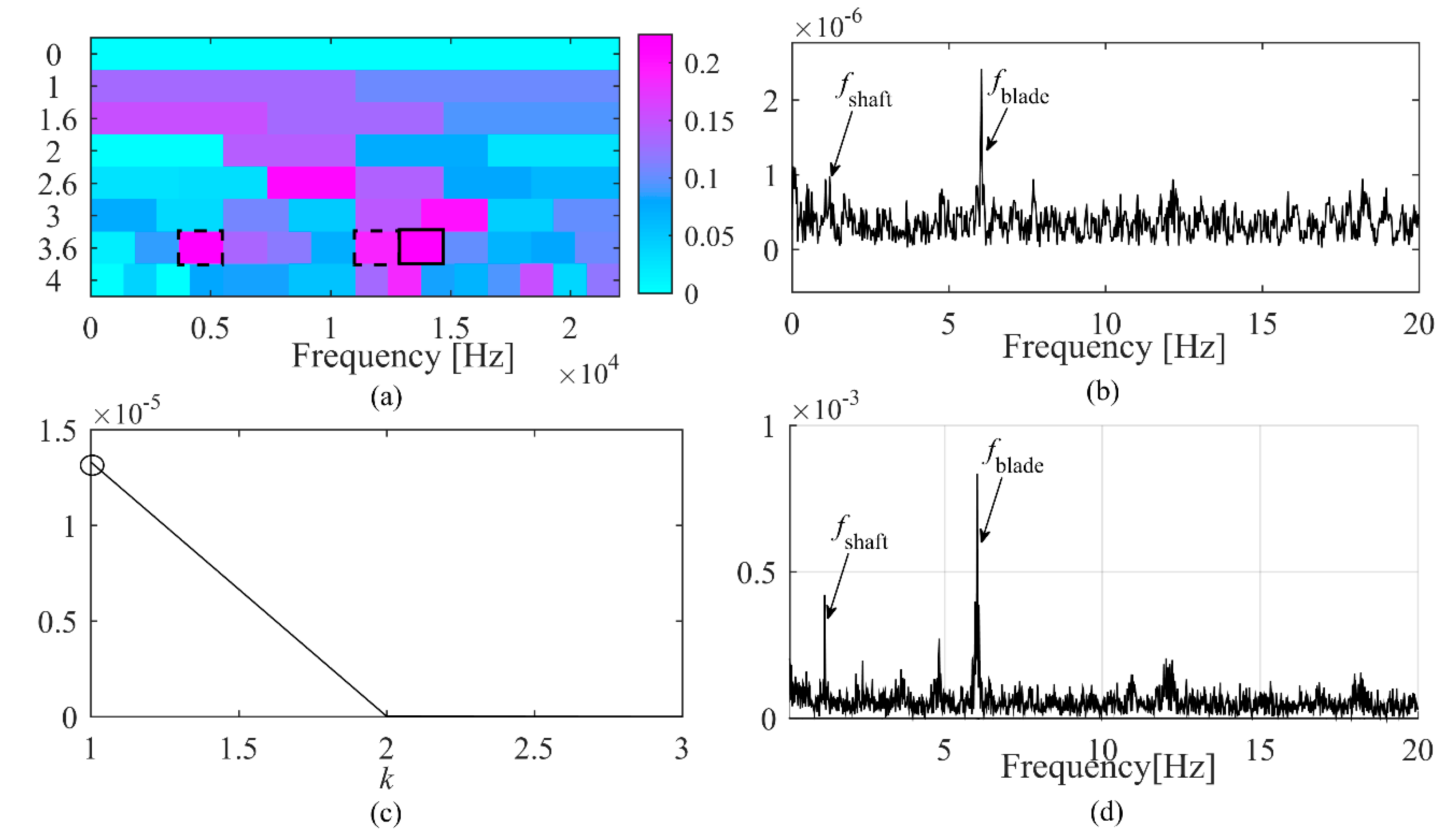
4.2. Application of P-Kurtogram for Acoustic Signals of Propeller
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumar, S.; Goyal, D.; Dang, R.K.; Dhami, S.S.; Pabla, B.S. Condition based maintenance of bearings and gears for fault detection-A review. Mater. Today Proc. 2018, 5, 6128–6137. [Google Scholar]
- Yunusa-Kaltungo, A.; Cao, R. Towards Developing an Automated Faults Characterisation Framework for Rotating Machines. Part 1: Rotor-Related Faults. Energies 2020, 13, 1394. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. HOS analysis of measured vibration data on rotating machines with different simulated faults. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2014; pp. 81–89. [Google Scholar]
- Shahriar, R.; Borghesani, P.; Randall, R.B.; Tan, A.C.C. An assessment of envelope-based demodulation in case of proximity of carrier and modulation frequencies. Mech. Syst. Signal Process. 2017, 96, 176–200. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Han, Q.; Kong, Y. Compound faults detection in gearbox via meshing resonance and spectral kurtosis methods. J. Sound Vib. 2017, 392, 367–381. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the spectral correlation. Mech. Syst. Signal Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Li, S.; Chu, N.; Yan, P.; Wu, D.; Antoni, J. Cyclostationary approach to detect flow-induced effects on vibration signals from centrifugal pumps. Mech. Syst. Signal Process. 2019, 114, 275–289. [Google Scholar] [CrossRef]
- Gu, X.; Yang, S.; Liu, Y.; Rujiang, H. Rolling element bearing faults diagnosis based on kurtogram and frequency domain correlated kurtosis. Meas. Sci. Technol. 2016, 27, 125019. [Google Scholar] [CrossRef]
- Dwyer, R.F. A technique for improving detection and estimation of signals contaminated by under ice noise a. J. Acoust. Soc. Am. 1990, 124, 124–130. [Google Scholar]
- Systems, M.; Maintenance, S.; Vibration, D.; Supe, E.N.; Cedex, L.; January, R. Crest factor and kurtosis contributions. Mech. Syst. Signal Process. 1997, 11, 903–916. [Google Scholar]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Leite, V.C.M.N.; Borges, J.G.; Eduardo, L.; Veloso, G.F.C.; Lambert-torres, G.; Bonaldi, E.L.; De, L.E.L.; Bonaldi, E.L. Oliveira Experimental Bearing Fault Detection, Identification, and Prognosis through Spectral Kurtosis and Envelope Spectral Analysis. Electr. Power Compon. Syst. 2016, 44, 2121–2132. [Google Scholar] [CrossRef]
- Elforjani, M.; Bechhoefer, E. Analysis of extremely modulated faulty wind turbine data using spectral kurtosis and signal intensity estimator. Renew. Energy 2018, 127, 258–268. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.; Shin, Y. Hyperbolic localization of incipient tip vortex cavitation in marine propeller using spectral kurtosis. Mech. Syst. Signal Process. 2018, 110, 442–457. [Google Scholar] [CrossRef]
- Han, H.S.; Lee, C.N.; Jeon, S.H.; Lee, K.H.; Park, S.H. Development of an evaluation method to determine cavitation inception speed with aft hull vibration using kurtosis of the DEMON spectrum. Ocean Eng. 2018, 152, 167–180. [Google Scholar] [CrossRef]
- Zhang, B.; Khawaja, T.; Patrick, R.; Vachtsevanos, G. Blind deconvolution denoising for helicopter vibration signals. IEEE/ASME Trans. Mechatron. 2008, 13, 558–565. [Google Scholar] [CrossRef]
- An, X.; Yang, J. Denoising of hydropower unit vibration signal based on variational mode decomposition and approximate entropy. Trans. Inst. Meas. Control 2016, 38, 282–292. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mech. Syst. Signal Process. 2010, 1, 119–137. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Bao, X. Wavelet denoising method for improving detection performance of distributed vibration sensor. IEEE Photonics Technol. Lett. 2012, 3, 542–544. [Google Scholar] [CrossRef]
- Sun, M.; Wang, H.; Liu, P.; Huang, S.; Fan, P. A sparse stacked denoising autoencoder with optimized transfer learning applied to the fault diagnosis of rolling bearings. Measurement 2019, 1, 305–314. [Google Scholar] [CrossRef]
- Jiang, G.; He, H.; Xie, P.; Tang, Y. Stacked multilevel-denoising autoencoders: A new representation learning approach for wind turbine gearbox fault diagnosis. IEEE Trans. Instrum. Meas. 2017, 23, 2391–2402. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Sensitivity analysis of higher order coherent spectra in machine faults diagnosis. Struct. Health Monit. 2016, 15, 555–567. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Feng, Z. Meshing frequency modulation (MFM) index-based kurtogram for planet bearing fault detection. J. Sound Vib. 2018, 432, 437–453. [Google Scholar] [CrossRef]
- Wang, Y.; Tse, P.W.; Tang, B.; Qin, Y.; Deng, L.; Huang, T. Kurtogram manifold learning and its application to rolling bearing weak signal detection. Measurement 2018, 127, 533–545. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J.; Lei, Y. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2017, 92, 173–195. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y.; Gao, H. Rolling element bearing fault detection using PPCA and spectral kurtosis. Measurement 2015, 75, 180–191. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram’ ski. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Ali Moshrefzadeh, A.F. The Autogram An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis.pdf. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Fuentes-garcía, M.; Maci, G. Evaluation of diagnosis methods in PCA-based Multivariate Statistical Process Control. Chemom. Intell. Lab. Syst. 2018, 172, 194–210. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Liu, Y.; Jiang, N.; Wang, H.; Duan, Z. Fault detection, identification and reconstruction of sensors in nuclear power plant with optimized PCA method. Ann. Nucl. Energy 2018, 113, 105–117. [Google Scholar] [CrossRef]
- Wang, D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification. Mech. Syst. Signal Process. 2016, 80, 19–30. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 8 March 2019).




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Liu, J.; Zhang, L.; Wu, D. Improvement of Fast Kurtogram Combined with PCA for Multiple Weak Fault Features Extraction. Processes 2020, 8, 1059. https://doi.org/10.3390/pr8091059
Song Y, Liu J, Zhang L, Wu D. Improvement of Fast Kurtogram Combined with PCA for Multiple Weak Fault Features Extraction. Processes. 2020; 8(9):1059. https://doi.org/10.3390/pr8091059
Chicago/Turabian StyleSong, Yongxing, Jingting Liu, Linhua Zhang, and Dazhuan Wu. 2020. "Improvement of Fast Kurtogram Combined with PCA for Multiple Weak Fault Features Extraction" Processes 8, no. 9: 1059. https://doi.org/10.3390/pr8091059
APA StyleSong, Y., Liu, J., Zhang, L., & Wu, D. (2020). Improvement of Fast Kurtogram Combined with PCA for Multiple Weak Fault Features Extraction. Processes, 8(9), 1059. https://doi.org/10.3390/pr8091059





