Decoupling Adaptive Smith Prediction Model of Flatness Closed-Loop Control and Its Application
Abstract
:1. Introduction
2. Flatness Decoupling Control System
2.1. Principle of Flatness Control
2.2. Flatness Open-Loop Control Model
2.3. Flatness Closed-Loop Decoupling Control Model
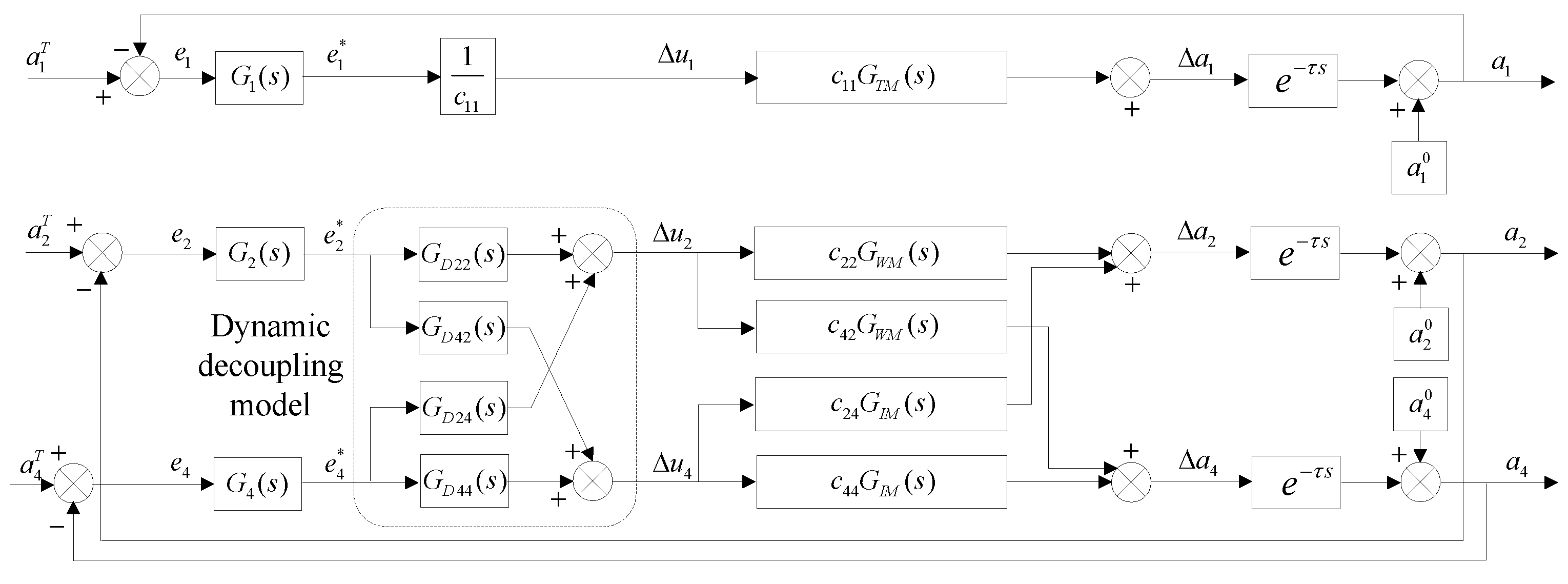
3. Flatness Decoupling Adaptive Smith Predictive Control
3.1. Primary Flatness Adaptive Smith Predictive Control
3.2. Quadratic and Quartic Flatness Decoupling Adaptive Smith Predictive Control
4. Simulation Comparison and Industrial Application
4.1. Simulation Comparison
4.2. Industrial Application
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, L.P.; Yu, H.X.; Zhang, Y.S.; Liu, H.M. Shape Detection and Control System of Cold Rolling Strip Based on the Virtual Instrument and Its Industrial Application. J. Mech. Eng. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Li, X.; Luan, F.; Wu, Y.A. Comparative Assessment of Six Machine Learning Models for Prediction of Bending Force in Hot Strip Rolling Process. Metals 2020, 10, 685. [Google Scholar] [CrossRef]
- Pin, G.; Francesconi, V.; Cuzzola, F.A.; Parisini, T. Adaptive task-space metal strip-flatness control in cold multi-roll mill stands. J. Process Control 2013, 23, 108–119. [Google Scholar] [CrossRef]
- Jin, X.; Li, C.S.; Wang, Y.; Li, X.G.; Xiang, Y.; Gu, T. Investigation and Optimization of Load Distribution for Tandem Cold Steel Strip Rolling Process. Metals 2020, 10, 677. [Google Scholar] [CrossRef]
- Ogasahara, T.; Kitamura, T.; Aoe, S.I.; Tateno, J.I.; Asano, K. Dynamic Control of Flatness and Elongation of the Strip in a Skin Pass Mill. Tetsu Hagane 2019, 105, 512–521. [Google Scholar] [CrossRef]
- Xie, H.B.; Li, L.J.; Liu, T.W.; Wang, E.R.; Liu, X.; Jiang, Z.Y. Three Dimensional Finite Element Simulation of Strip Shape and Flatness of High Strength Steel. Key Eng. Mater. 2019, 794, 232–245. [Google Scholar] [CrossRef]
- Kozhevnikov, A.; Kozhevnikov, I.; Bolobanova, N. Dynamic model of cold strip rolling. Metalurgija 2018, 57, 99–102. [Google Scholar]
- Ataka, M. Rolling Technology and Theory for the Last 100 Years: The Contribution of Theory to Innovation in Strip Rolling Technology. ISIJ Int. 2015, 55, 89–102. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.M.; He, H.T.; Shan, X.Y.; Jiang, G.B. Flatness Control Based on Dynamic Effective Matrix for Cold Strip Mills. J. Mech. Eng. 2009, 22, 41–75. [Google Scholar] [CrossRef]
- Yang, L.P.; Yu, H.Y.; Wang, D.C.; Zhang, Z.; Jiang, Z.Y. Intelligent Shape Regulation Cooperative Model of Cold Rolling Strip and Its Application. Steel Res. Int. 2017, 88, 1600383. [Google Scholar] [CrossRef]
- Wang, P.F.; Peng, Y.; Wang, D.C.; Sun, J.; Zhang, D.H.; Liu, H.M. Flatness Control Strategy Based on Delay Compensation for Cold Rolling Mill. Steel Res. Int. 2017, 88, 1600065. [Google Scholar]
- Ma, L. Strategy of Flatness Control System Lag Compensation. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2014. [Google Scholar]
- Liu, J.W.; Jiang, D.P.; Wu, H.L.; Chen, R.J. Algorithm Research and Application of dynamic variable gain controller based on flatness control in cold mill. In Proceedings of the 8th Youth Academic Annual Meeting of China Metal Society, Beijing, China, 23–25 October 2013; pp. 1–6. [Google Scholar]
- Wang, P.F.; Zhang, Z.J.; Sun, J.; Zhang, D.H.; Liu, H.M.; Gao, X.L. Flatness control of cold rolled strip based on relay optimization. Ironmak. Steelmak. 2016, 45, 166–175. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Q.D. Study on Flatness Predictive Control for CVC-4th Cold Mill. Metall. Equip. 2008, 4, 9–12. [Google Scholar]
- Zhang, R.C.; Zheng, X. Automatic flatness control strategy with a Smith predictor for steel strip rolling. In Proceedings of the 2011 International Conference on Photonics, 3D-Imaging, and Visualization, Guangzhou, China, 30–31 October 2011; pp. 1–6. [Google Scholar]
- Xing, Z.W.; Ding, B.J. Intelligent Control Method for Aircraft Deicing Fluid temperature Based on a New Adaptive Smith Predictor. Adv. Mater. Res. 2012, 424, 936–940. [Google Scholar] [CrossRef]
- Song, M.M.; Wang, D.C.; Zhang, S.; Xu, Y.H.; Liu, H.M. Flatness pattern recognition based on recurrent neural network. Iron Steel 2018, 53, 56–62. [Google Scholar]
- Yang, L.P.; Zhang, Z.; Wang, D.C.; Li, R.M.; Yu, H.X.; Zhang, Y.S. Mechanism-intelligent coordination shape control model of cold strip. Iron Steel 2017, 52, 52–57. [Google Scholar]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute stability condition derivation for position closed-loop system in hydraulic automatic gauge control. Processes 2019, 7, 766. [Google Scholar] [CrossRef] [Green Version]
- Song, M.M.; Liu, H.M.; Wang, D.C.; Xu, Y.H. Decoupling Strategy and Dynamic Decoupling Model of Flatness Control in Cold Rolling Strip. ISIJ Int. 2020, 60, 286–296. [Google Scholar] [CrossRef]
- Wang, J.; Yan, W.; Shao, H. Performance improvement of VAV air conditioning control system through diagonal matrix decoupling and Lonworks technology. Energy Build. 2005, 37, 911–919. [Google Scholar] [CrossRef]
- Chou, J.H.; Chang, J.F.; Lin, D.B.; Wu, T.L. Dual-band WLAN MIMO antenna with a decoupling element for full-metallic bottom cover tablet computer applications. Microw. Opt. Technol. Lett. 2018, 60, 1245–1251. [Google Scholar] [CrossRef]
- Xu, S.; Hashimoto, S.; Jiang, W. Pole-Zero Cancellation Method for Multi Input Multi Output (MIMO) Temperature Control in Heating Process System. Processes 2019, 7, 497. [Google Scholar] [CrossRef] [Green Version]
- Kaya, I. Improving performance using cascade control and a Smith predictor. ISA Trans. 2001, 40, 223–234. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Sun, F.; Liu, J.; Sun, M.H.; Xie, Y.H. Application of Smith Predictor Based on Single Neural Network in Cold Rolling Shape Control. Chin. J. Mech. Eng. 2009, 22, 282–286. [Google Scholar] [CrossRef]
- Zhang, P.; Yuan, M.Z.; Wang, H. Self-adaptive Fuzzy-Smith Control for a Long Time-delay System. Comput. Simul. 2006, 23, 88–90. [Google Scholar]
- Li, X.; Song, D.Q.; Yu, S.Y.; Gui, W.H. Feedback automatic gauge control system using model reference adaptive Smith predictor. Control Theory Appl. 2009, 26, 999–1003. [Google Scholar]
- Gao, H.J.; Lam, J.; Chen, T.W.; Wang, C.H. Stability analysis of uncertain discrete-time systems with time-varying state delay: A parameter-dependent Lyapunov function approach. Asian J. Control 2010, 8, 433–440. [Google Scholar] [CrossRef]
- Zheng, D.Z. Liner System Theory; Tsinghua University Press: Beijing, China, 1990; pp. 213–242. [Google Scholar]
- Zhou, Y.; Song, D.D.; Nie, P.P.; Hao, H.M. Application of model reference adaptive control-improved Smith-predictor in temperature control of fermentation. J. Hebei Univ. Tech. 2011, 40, 5–9. [Google Scholar]
- Song, Y.X.; Zhu, X.F. An Improved Adaptive Smith Predictor System. Meas. Control Tech. 2002, 8, 37–40. [Google Scholar]
- Wang, D.C.; Liu, H.M. A Model Coupling Method for Shape Prediction. J. Iron Steel Res. Int. 2012, 19, 22–27. [Google Scholar] [CrossRef]
- Rodríguez-Miranda, E.; Beschi, M.; Guzmán, J.L.; Berenguel, M.; Visioli, A. Daytime/Nighttime Event-Based PI Control for the pH of a Microalgae Raceway Reactor. Processes 2019, 7, 247. [Google Scholar] [CrossRef] [Green Version]



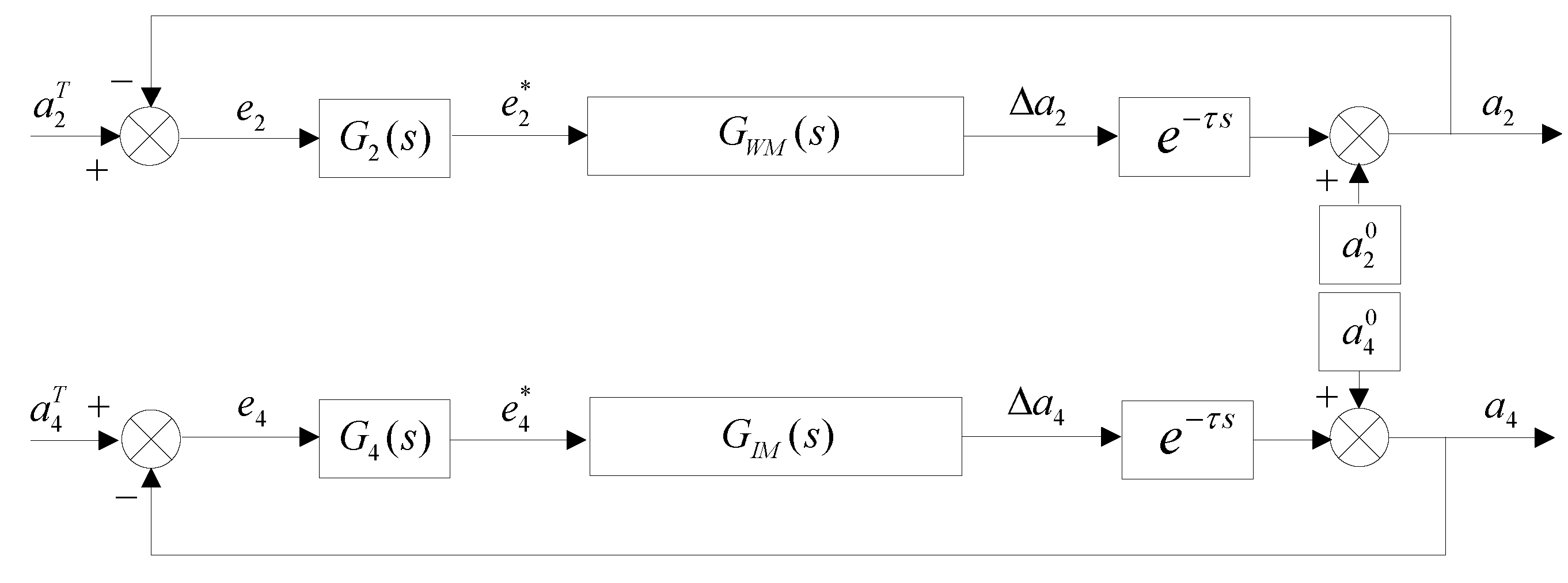




| Strip Width /mm | Rolling Force /10kN | Entry Thickness /mm | Exit Thickness /mm | Front Force /kN | Post Tension /kN | IRS /mm | Calculating Matrix C0 |
|---|---|---|---|---|---|---|---|
| 1230 | 864 | 1.04 | 0.79 | 107 | 80 | 115 |
| KP1 | KI1 | λ1 | λ1* | KP2 | KI2 | λ2 | λ2* | KP4 | KI4 | λ4 | λ4* |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.033 | 0.01 | 0.5 | 0.6 | 0.107 | 0.03 | 0.45 | 0.5 | 0.167 | 0.02 | 0.40 |
| C0 | C1 | C2 |
|---|---|---|
| Curve label | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Calculating matrix | C0 | C0 | C0 | C0 | C0 | C0 |
| Actual matrix | C0 | C0 | C1 | C1 | C2 | C2 |
| Control method | PI | PI-Smith | PI-Smith | PI-adaptive Smith | PI-Smith | PI-adaptive Smith |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, M.; Liu, H.; Xu, Y.; Wang, D.; Huang, Y. Decoupling Adaptive Smith Prediction Model of Flatness Closed-Loop Control and Its Application. Processes 2020, 8, 895. https://doi.org/10.3390/pr8080895
Song M, Liu H, Xu Y, Wang D, Huang Y. Decoupling Adaptive Smith Prediction Model of Flatness Closed-Loop Control and Its Application. Processes. 2020; 8(8):895. https://doi.org/10.3390/pr8080895
Chicago/Turabian StyleSong, Mingming, Hongmin Liu, Yanghuan Xu, Dongcheng Wang, and Yangyang Huang. 2020. "Decoupling Adaptive Smith Prediction Model of Flatness Closed-Loop Control and Its Application" Processes 8, no. 8: 895. https://doi.org/10.3390/pr8080895
APA StyleSong, M., Liu, H., Xu, Y., Wang, D., & Huang, Y. (2020). Decoupling Adaptive Smith Prediction Model of Flatness Closed-Loop Control and Its Application. Processes, 8(8), 895. https://doi.org/10.3390/pr8080895




