Numerical Study of Shear Banding in Flows of Fluids Governed by the Rolie-Poly Two-Fluid Model via Stabilized Finite Volume Methods

Abstract

The flow of viscoelastic fluids may, under certain conditions, exhibit shear-banding characteristics that result from their susceptibility to unusual flow instabilities. In this work, we explore both the existing shear banding mechanisms in the literature, namely; constitutive instabilities and flow-induced inhomogeneities. Shear banding due to constitutive instabilities is modelled via either the Johnson–Segalman or the Giesekus constitutive models. Shear banding due to flow-induced inhomogeneities is modelled via the Rolie–Poly constitutive model. The Rolie–Poly constitutive equation is especially chosen because it expresses, precisely, the shear rheometry of polymer solutions for a large number of strain rates. For the Rolie–Poly approach, we use the two-fluid model wherein the stress dynamics are coupled with concentration equations. We follow a computational analysis approach via an efficient and versatile numerical algorithm. The numerical algorithm is based on the Finite Volume Method (FVM) and it is implemented in the open-source software package, OpenFOAM. The efficiency of our numerical algorithms is enhanced via two possible stabilization techniques, namely; the Log-Conformation Reformulation (LCR) and the Discrete Elastic Viscous Stress Splitting (DEVSS) methodologies. We demonstrate that our stabilized numerical algorithms accurately simulate these complex (shear banded) flows of complex (viscoelastic) fluids. Verification of the shear-banding results via both the Giesekus and Johnson-Segalman models show good agreement with existing literature using the DEVSS technique. A comparison of the Rolie–Poly two-fluid model results with existing literature for the concentration and velocity profiles is also in good agreement.

1. Introduction

Shear banding in flow of polymer solutions has been largely investigated in simple shear geometries. Such flows may, under certain conditions of, say, the prevailing shear rates, develop localized bands in response to the development of flow instabilities. Therefore, these localized bands are aptly referred to as shear bands, see Figure 1.

Shear banding investigations in the shear flow of polymeric liquids are of fundamental industrial importance. As explained, for example, in [1], the processes of emulsion polymerization and polymer blending are of great importance in the manufacture of a wide variety of everyday products, such as margarine. The industrial processes of emulsion polymerization and polymer blending involve, for example, the break-up of droplets contained in a matrix fluid subjected to shear flow. The size and distribution of final droplets determine the quality of the final product. The shear strength is of fundamental importance to the rate of break-up of the drops as well as the size and distribution of the final mini-droplets. Highly shear banded flows lead to plug flows, see, for example [2], with the high shear rate flow regimes confined to thin wall regions but with otherwise significantly diminished shear strengths within the bulk (matrix) flow. In emulsion polymerization and polymer blending processes, it would therefore be crucially important to avoid using matrix fluids that are susceptible to shear banding, as these would lead to very low shear strengths in the bulk flow.

Examples of polymeric fluids in which shear banding has been observed include worm-like micelle solutions [3,4,5], foams [6], granular flows [7], soft glasses [8], telechelic polymers [9], polymer solutions [10], and polymer melts [11]. An excellent review of shear banding with a focus on polymer fluids and soft glass materials is conducted in [12].

Experimental methods that have been employed to study shear banding include Particle Tracking Velocimetry (PTV) [13], Particle Image Velocimetry (PIV) [14], PIV combined with global rheology [15], Optical Coherence Tomography Velocimetry (OCTV) [16], and Flow-Induced Birefringence (FIB) [17,18]. Other experimental methods, such as Nuclear Magnetic Resonance (NMR) velocity imaging, make possible the direct determination of the flow velocity and, consequently, also the flow shear rates [19].

An experimental approach designed and validated by Helgeson et al. [20] enabled the direct measurement of the local fluid make-up for complex fluids in shear flow. They conclusively demonstrated that, for worm-like micelle (WLM) fluids under shear flow, the coupling with flow-concentration has an effect on the concentration gradient. In the concentration results, it was observed that the development of a concentrated para-nematic phase had an effect on the isotropic phase.

The growing literature on shear banding notwithstanding, the exact mechanisms that gives rise to shear bands in the flow of semi-dilute polymers are not always the same and indeed are still not well understood [21]. A number of studies have attributed the shear banding phenomena to constitutive instabilities in shear flow, which manifest as non-monotonic stress–strain relationships. To this end, the Johnson–Segalman constitutive model (and its variant, the diffusive Johnson–Segalman model) has therefore been one of the most extensively used shear banding models, see for example [2,22,23,24] and the references therein. The behaviour of Johnson-Segalman fluids in Couette flow is also investigated in [25] via a combination of analytical techniques, numerical simulations, and controlled experiments with the purpose of explaining spurt phenomena, which is a physical manifestation of shear banding. Numerical computations with the Johnson–Segalman model, implemented in the OpenFOAM software platform, are conducted in Paul et al. [26]. Their numerical results show good agreement with experiments.

In addition to constitutive instabilities via non-monotonic stress–strain models, an alternative mechanism to explain shear banding in flows of polymer solutions is flow-induced concentration fluctuations. The premise of this concept is the Helfand–Fredrickson formalism. This allows for polymer migration due to the stress gradient resulting, in turn, in concentration inhomogeneity. The polymer concentration therefore becomes non-uniform [27]. Hua et al. [28] explore the open question regarding whether or not small scale concentration fluctuations are responsible for the transition from shear-thinning to shear-banding. However, we were able to conclusively demonstrate that large scale fluctuations were not the reason or mechanism for shear banding, this being the case due to the fact that the relaxation time from such fluctuations would be much greater than the life span of the shear bands. They observed steady–state shear banding only via the constitutional instability framework, global polymer migration otherwise had no significant effect on the shear banding.

The effect on shear band formation of coupling the concentration profile to the stress profile, via a two-fluid model, is investigated and explained in [29]. In particular, it was observed from the phase diagrams that increased concentration, in turn, leads to steeper normal micellar strain component gradients, and hence therefore affects shear banding. Using a similar concentration-stress coupling via a two-fluid model for the Rolie–Poly constitutive equation, Cromer et al. [30] were also able to reproduce shear banded velocity profiles. In particular, a modified Rolie-Poly model that takes into account finite extensibility was used since it provides a realistic rheological projection for entangled polymeric solutions. In an extension to this study, [31], they further demonstrated that flow-induced inhomogeneities in polymer solutions under extensional flow can trigger shear banding, even under monotonic stress-strain conditions. In [31], it was further demonstrated that, with an imposed initial defect in the polymer concentration, the velocity would still reach a banded steady-state despite undergoing a non-trivial temporal evolution. For the Taylor–Couette geometry, shear bands have been observed at significantly lower times, hence making the Taylor–Couette geometry ideally suited for experimental studies, [32].

The Rolie–Poly constitutive model was also employed by Adams et al. [33] to capture instabilities related to shear banding. Shear bands were observed for flows with sufficiently non-homogeneous aggregate stress. Transient phenomena were also observed to display flow inhomogeneities similar to shear banding, even for weakly stable fluids, [33]. In an extension to these studies, they used the same model to study transient shear banding in entangled polymer solutions and showed that the inherent instabilities were triggered by perturbations that were caused by inhomogeneous stress profiles, [34].

The above summary demonstrates that shear banding investigations via the flow-induced inhomogeneities mechanism and, hence, using the Rolie–Poly constitutive model, are still largely limited to only a handful of research groups. Indeed, a number of these research groups have worked collaboratively in these investigations, therefore limiting the diversity of research methodologies for such studies even further. Given that the presence of shear banding in experimental flows as well as the exact mechanisms for shear banding on both steady and transient flows are all still open questions, [32], our present investigation therefore seeks to add to the diversity of the body of research methodologies. In particular, we employ finite volume methodologies, on the OpenFOAM software platform, in order to investigate shear banding in the transient shear flow of polymer solutions as modelled via the two-fluid Rolie-Poly constitutive equation. In line with the two-fluid formalism, the concentration profile is coupled to the stress profile in much the same way as in [31].

All investigations in the existing literature thus far each focuses their analytical methodologies as applied to a specific constitutive model and, consequently also, on a specific shear banding mechanism. Given that universal consensus on the exact shear banding mechanisms still does not exist and that the controversy and debate on the issue are still quite considerable, caution therefore needs to be exercised in interpreting the results in the literature, to date, that each focus on a single shear banding model or mechanism. Our present investigation attempts to cover this gap, we indeed demonstrate that our numerical algorithms are not specific to the two-fluid formalism or to the Rolie–Poly constitutive model. Indeed, we test our algorithm against all three viscoelastic shear banding models that exist in the literature, i.e. the Giesekus, Johnson–Segalman, and the Rolie–Poly models. Therefore, we also naturally test our algorithms against both the constitutive instabilities (non-monotonic) shear banding mechanism as well as the flow-induced inhomogeneities framework for shear banding.

Given the obvious differences in material composition of polymer solutions on the one hand and polymer melts on the other hand, investigations, such as the present one, are indeed invaluable. For example, a polymer melt would generally be composed of chemically identical polymer molecules and, hence, also expectedly form a homogeneous mixture at equilibrium. One may then reasonably assume that the shear banding processes in the shear flow of such polymer melts should, therefore, expectedly be largely driven by non-monotonic stress-strain profiles and, hence, modelled as constitutive instabilities. However, the experimental evidence for this does not exist and, hence, the exact mechanism for shear banding, even for polymer melts, still remains elusive.

Therefore, it is important to develop reliable and versatile algorithms capable of simulating shear banding dynamics via any of the existing shear banding mechanisms and also using any of the existing viscoelastic models. To our knowledge, our robust and versatile algorithm is the first to be tested in investigating the various shear banding characteristics in this way.

2. Governing Equations for the Rolie-Poly Model

We follow a two-fluid model approach in which the polymer and solvent fluids are considered as two separate but inter-penetrating fluids. The velocities of the solvent (${\mathit{v}}_s$) and that of the polymer (${\mathit{v}}_p)$ are coupled by a friction term. A more detailed modelling of the equations can be found in [31,35]. The volume-averaged velocity is given as $\mathit{v}={\varphi }_s{\mathit{v}}_s+{\varphi }_p{\mathit{v}}_p$, where ${\varphi }_s$ and ${\varphi }_p$ denote the volume fractions of the solvent and polymer respectively with ${\varphi }_s+{\varphi }_p=1$. In this article, the material derivative $D/Dt$ for a quantity $\Pi$ is defined as,

$$\frac{D\Pi }{Dt}=\frac{\partial \Pi }{\partial t}+\mathit{v}·\nabla \Pi .$$

The fluid is viscoelastic and incompressible and, hence, the continuity equation takes the form,

$$\nabla ·\mathit{v}=0.$$

(1)

The momentum equations for the solvent and polymer fluids are, respectively,

$$\frac{D}{Dt}\left({\rho }_s{\varphi }_s{\mathit{v}}_s\right)={\eta }_s{\nabla }^2{\mathit{v}}_s-\nabla p-\zeta (\mathit{v}-{\mathit{v}}_p),$$

(2)

and

$$\frac{D}{Dt}\left({\rho }_p{\varphi }_p{\mathit{v}}_p\right)=\nabla ·{\mathit{\sigma }}_p-\nabla {\pi }_0+\zeta (\mathit{v}-{\mathit{v}}_p).$$

(3)

Here, ${\pi }_0$ is the osmotic pressure, ${\mathit{\sigma }}_p$ is the polymer elastic stress, $\zeta$ is a friction coefficient, and $\varphi$ is the local volume fraction, and the subscripts s and p stand for solvent and polymer, respectively. For $\varphi \ll 1$, it is assumed that the polymer inertia is negligible, in which case the total inertia in the system can be ignored under certain flow conditions. The left hand side of Equations (2) and (3) are therefore usually set to zero. The two equations can be combined to obtain an overall momentum balance equation, which is written as,

$${\eta }_s{\nabla }^2\mathit{v}+\nabla ·{\mathit{\sigma }}_p-\nabla (p+{\pi }_0)=0.$$

(4)

In this case, the polymer velocity can be recovered from,

$${\mathit{v}}_p=\mathit{v}+\left({\displaystyle \frac{1}{\zeta }}\right)\left(\nabla ·{\mathit{\sigma }}_p-\nabla {\pi }_0\right).$$

(5)

The osmotic pressure ${\pi }_0$ is determined from the mixed free energy, see, for example [31],

$${\pi }_0={\chi }_0^{-1}\left[{\displaystyle \frac{1}{2}}{\varphi }^2-\xi \varphi {\nabla }^2\varphi +{\displaystyle \frac{1}{2}}\left(\varphi {\displaystyle \frac{\partial {\xi }^2}{\partial \varphi }}-{\xi }^2\right){|\nabla \varphi |}^2\right],$$

(6)

where ${\chi }_0$ is the osmotic susceptibility and $\xi$ is the correlation length. For the stress equation, we will employ, among other viscoelastic models that allow for shear banding, the Rolie–Poly constitutive equation of Likhtman and Graham [36]. At present, the Rolie–Poly model remains the most advanced differential constitutive formulation of the Doi–Edwards tube models for linear entangled polymer melts. The Rolie–Poly constitutive equation is modified to include the relative motion between the solvent and the polymer, thus the configuration tensor equation is given as,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathit{Q}}{\partial t}}& +\mathit{v}·\nabla \mathit{Q}-\mathit{Q}·\nabla \mathit{v}-{(\nabla \mathit{v})}^T·\mathit{Q}\hfill \\ \hfill & +\left\{{\displaystyle \frac{1}{\zeta }}\left[\nabla ·{\mathit{\sigma }}_p-\nabla {\pi }_0\right]·\nabla \mathit{Q}-{\left(\nabla {\displaystyle \frac{1}{\zeta }}\left[\nabla ·{\mathit{\sigma }}_p-\nabla {\pi }_0\right]\right)}^T·\mathit{Q}-\mathit{Q}·\nabla {\displaystyle \frac{1}{\zeta }}\left[\nabla ·{\mathit{\sigma }}_p-\nabla {\pi }_0\right]\right\}\hfill \\ \hfill & =-{\tau }_d^{-1}\left(\varphi \right)(\mathit{Q}-\mathit{I})-2{\tau }_R^{-1}(1-{\lambda }^{-1})\left[\mathit{Q}+\beta {\lambda }^{2\delta }(\mathit{Q}-\mathit{I})\right],\hfill \end{array}$$

(7)

where $\mathit{Q}$ is the conformation tensor, $\lambda$ is the stretch parameter, which is defined as $\sqrt{\mathrm{tr}\left(\mathit{Q}\right)/3}$, ${\tau }_d$ is the relaxation time, ${\tau }_R$ is the Rouse relaxation time, and $\beta$ is the convective-constraint release (CCR) parameter that varies from 0 to 1, $\mathrm{tr}$ denotes the trace, and $\mathit{I}$ is the identity tensor. To ensure the monotonicity of the polymer stress, the CCR parameter, $\beta$, is set to 1. The empirical parameter, $\delta$, is obtained from experimental data and usually takes the value of $-1/2$.

To enable comparison with the results in the existing literature, we use the non-dimensional set of equations, as given in [31]. The polymer stress equations, Equation (7), is non-dimensionalized via the polymer velocity equation, Equation (5). The resultant set of non-dimensional equations are,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathit{Q}}{\partial t}}& +{\mathit{v}}_p·\nabla \mathit{Q}-\mathit{Q}·\nabla {\mathit{v}}_p-{(\nabla {\mathit{v}}_p)}^T·\mathit{Q}=-{\tau }_d^{-1}\left(\varphi \right)(\mathit{Q}-\mathit{I})-2\theta (1-{\lambda }^{-1})\left[\mathit{Q}+{\lambda }^{-1}(\mathit{Q}-\mathit{I})\right].\hfill \end{array}$$

(8)

The polymer stress tensor, ${\mathit{\sigma }}_p$, is related to the conformation tensor, $\mathit{Q}$, via the relation,

$${\mathit{\sigma }}_p=G_0\left(\varphi \right)(\mathit{Q}-I),$$

(9)

where $G_0\left(\varphi \right)$ is a relaxation modulus. The values of the parameters used in this study are as given in [31]. The ratio of the reptation to rouse parameter, ${\tau }_d/{\tau }_r=\theta =10$, $\zeta ={\varphi }^{3/2}$, the ratio of elastic to osmotic moduli, $E=G_0/\left({\chi }^{-1}{\varphi }^2\right)=0.33$. The reptation time is given as ${\tau }_d\left(\varphi \right)={\varphi }^{\beta }$ and the relaxation modulus as $G_0\left(\varphi \right)={\varphi }^{\alpha }$, where $\alpha$ and $\beta$ are taken as $2.25$ and $1.5$, respectively.

3. Geometry and Boundary Conditions

For this study, we consider flow between two infinite (in the x-direction) parallel plates with the upper plate moving with a constant velocity, see Figure 1. The bottom plate is kept fixed. No-slip boundary and impermeability conditions are ascribed to the velocity at the walls. The upper plate is assigned a velocity of $H\mathrm{We}tanh\left(at\right)$, where H is the channel width in the y direction, $\mathrm{We}$ is the Weissenberg number and a is the ramp speed parameter assigned the values of 1 and $0.01$ as in [31].

Zero normal gradient boundary conditions are assigned for pressure, p. The polymeric extra stresses are linearly extrapolated at the walls. An initial defect is imposed in the polymer concentration of the order of $\varphi =1+\delta cos(\pi ky/H)$. We take $k=1$ to enable comparisons with the results of [31].

4. Numerical Method

The Finite volume method (FVM) implemented in OpenFOAM is used to discretize the governing equations. For more details, please refer to [37]. The viscoelastic constitutive models, in particular, the Johnson–Segalman, Giesekus, and Rolie–Poly models are added to the viscoelastic solver and the appropriate momentum equations are also built into the solver as necessary.

The SIMPLE algorithm is used for the pressure-velocity coupling in the solver. To solve the pressure equation, we use the preconditioned conjugate gradient (PCG) method. The velocity and volume fraction equations are solved via the Bi-Conjugate Gradient Stabilized (BICGSTAB) method. The preconditioner used is the simplified Diagonal-based Incomplete Cholesky (DIC) for pressure and simplified Diagonal-based Incomplete LU (DILU) for velocity and ILUO for the volume fraction.

The summary steps for the iterative algorithm are given as;

• the variables are initialized;
• the (Log-Conformation Reformulation (LCR) stabilized) stress equations are solved for the conformation tensor $\mathit{Q}$;
• the (DEVSS stabilized) momentum equations are solved for the intermediate velocity field;
• the pressure equation is then solved and the under-relaxation applied, with an under-relaxation factor of 0.3;
• both pressure and velocity are corrected via the SIMPLE algorithm;
• the volume fraction is obtained; and,
• the solutions at the next time level, $t_{new}=t_{old}+\delta t$, are obtained and the processes is repeated from step 2 until either the predetermined final time is reached or certain predetermined conditions are met. The rheoFOAM solver was used in all computations.

4.1. DEVSS Stabilization

The Discrete Elastic Viscous Stress Splitting (DEVSS) technique can be (and indeed is) implemented to improve numerical stability by introducing an additional diffusion term on each side of the momentum equations. The momentum equations are then rewritten as,

$$\rho {\displaystyle \frac{D\mathit{v}}{Dt}}-\left({\eta }_s+\mathit{k}\right)\nabla ·\left(\nabla \mathit{v}\right)=-\nabla p-\mathit{k}\nabla ·\left(\nabla \mathit{v}\right)+\nabla ·{\sigma }_p,$$

(10)

where k is a positive constant related to the parameters of the constitutive model. As in Abuga et al. [37], we take $k={\eta }_p$, where ${\eta }_p$ is the polymer viscosity.

4.2. LCR Stabilization

In this approach to numerical stability, a logarithmic transformation known as the Log-Conformation Reformulation (LCR) technique is used. The approach consists in a change of variable from the polymeric stress ${\mathit{\sigma }}_p$ to the conformation tensor $\mathit{Q}$, as given in Equation (9).

The viscoelastic constitutive equation is written in terms of the conformation tensor, as shown in Equation (8). Because the conformation tensor $\mathit{Q}$ is a positive-definite matrix, it can be diagonalized according to

$$\mathit{Q}=\mathit{R}·\Lambda ·{\mathit{R}}^T,$$

(11)

where $\Lambda$ is a diagonal matrix consisting of the eigenvalues of $\mathit{Q}$ and where the matrix $\mathit{R}$ is orthogonal and contains the corresponding eigenvectors. The polymer stress/conformation equation is reformulated in terms of the natural logarithm of the conformation tensor,

$$\Psi =log\left(\mathit{Q}\right)=\mathit{R}·log(\Lambda )·{\mathit{R}}^T.$$

(12)

$\Psi$ then becomes our new variable and the velocity gradient $\nabla \mathit{v}$ is decomposed as

$$\nabla \mathit{v}=\Omega +\mathit{B}+\mathit{N}·{\mathit{Q}}^{-1},$$

(13)

where $\Omega$ and $\mathit{N}$, which both account for rotations, are anti-symmetric tensors. $\mathit{B}$ is a diagonal tensor that accounts for pure extensions. The eigen-decomposition of the conformation tensor in a two-dimensional flow is given as

$$\mathit{Q}=\mathit{R}\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]{\mathit{R}}^T,$$

(14)

where ${\lambda }_1$ and ${\lambda }_2$ are the eigenvalues and $\mathit{R}$ the orthogonal matrix containing the eigenvectors. The change of the base of velocity gradient is given as

$${\mathit{R}}^T(\nabla \mathit{U})\mathit{R}=\left[\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right].$$

(15)

The pure extension and rotation matrices are obtained as,

$$\mathit{B}=\mathit{R}\left[\begin{array}{cc}{m}_{11}& 0\\ 0& m_{22}\end{array}\right]{\mathit{R}}^T,\Omega =\mathit{R}\left[\begin{array}{cc}0& \zeta \\ -\zeta & 0\end{array}\right]{\mathit{R}}^T,$$

(16)

where $\zeta =(m_{12}+m_{21})/({\lambda }_2-{\lambda }_1)$. For the first time step, $\Omega$ is set to be zero and $\mathit{B}=1/2\left[\nabla \mathit{U}+{(\nabla \mathit{U})}^T\right]$, since $\mathit{Q}=\mathit{I}$ leads to ${\lambda }_2={\lambda }_1$ would result in an undefined division by zero.

The conformation tensor $\mathit{Q}$ is recovered from the matrix exponential of $\Psi$, see Equation (12), once the equations for the log-conformation tensor ($\Psi$) has been solved. The condition $det\left(\mathit{Q}\right)>0$ must, at all times, be satisfied in order to verify the positive-definiteness of the conformation tensor.

5. Code Verification

The verification of our shear banding results is conducted against the existing results [24,31,35,38,39] for the Johnson–Segalman, the Giesekus, and the Rolie–Poly two-fluid constitutive models. The shear banding mechanism as modelled by the Johnson–Segalman and the Giesekus constitutive models is a result of constitutive instabilities. The Johnson–Segalman model exhibits either monotonic or non-monotonic relationship between the shear-stress and the shear-rate, depending on the parameter $\xi$ as well as on the ratio of solvent to polymer viscosities, ${\eta }_s$ and ${\eta }_p$, respectively. Similarly, the Giesekus model can exhibit either monotonic or non-monotonic stress-strain relationships, depending on the value of the anisotropy parameter, $\alpha$, as well as on the ratio of solvent to polymer viscosities. The shear banding mechanism as modelled by the Rolie–Poly two-fluid constitutive model is a result of flow-induced inhomogeneities.

The various viscoelastic constitutive models for the extra stress tensor ${\mathit{\sigma }}_p$ appearing in the momentum equations,

$$\rho {\displaystyle \frac{D\mathit{v}}{Dt}}=-\nabla p+\nabla ·({\eta }_s[\nabla \mathit{v}+{(\nabla \mathit{v})}^T]+{\mathit{\sigma }}_p),$$

(17)

will be described in each of the following sections.

6. Johnson–Segalman Model

For Johnson–segalman fluids, the stress constitutive equation takes the form,

$${\mathit{\sigma }}_p+\lambda \stackrel{\square }{{\mathit{\sigma }}_p}=2{\eta }_p\mathit{D},$$

(18)

where ${}^{\square }$ represents the Gordon-Schowalter derivative, defined as,

$$\stackrel{\square }{{\mathit{\sigma }}_p}=\frac{\xi }{2}\left({\displaystyle \frac{D{\mathit{\sigma }}_p}{Dt}}+{\mathit{\sigma }}_p·{(\nabla \mathit{v})}^T+\nabla \mathit{v}·{\mathit{\sigma }}_p\right)+\left(1-\frac{\xi }{2}\right)\left({\displaystyle \frac{D{\mathit{\sigma }}_p}{Dt}}-{\mathit{\sigma }}_p·{(\nabla \mathit{v})}^T-\nabla \mathit{v}·{\mathit{\sigma }}_p\right).$$

(19)

In keeping with the verification literature, we consider plane shear flow of a Johnson-Segalman fluid in a rectangular geometry. The flow is between two infinite parallel plates located at $y=0$ and $y=1$, as in Figure 1. The upper plate moves with a constant velocity while the lower plate is fixed. Also in keeping with the verification literature, we consider non-dimensional equations and track the flow dynamics via the two (dimensionless) parameters, namely the Reynolds and Weissenberg numbers, respectively, defined as,

$$\mathrm{Re}=\frac{\rho V^{*}H}{\eta },$$

(20)

and

$$\mathrm{We}=\frac{\lambda V^{*}}{H},$$

(21)

where H is a typical length scale, in this case the channel width in the y direction, and $\eta ={\eta }_p+{\eta }_s$ is the total fluid viscosity. We employ both the DEVSS and LCR stabilization techniques in our verification simulations. The LCR results are labelled as LogT on the graphs. We compare our results with those of [24] while using the parameters values; $\mathrm{Re}=1$, $\mathrm{We}=1$, $\Delta t=0.005$, $\Delta y=0.002$, ${\eta }_S=0.05$, ${\eta }_P=0.95$, and $\xi =0.8$.

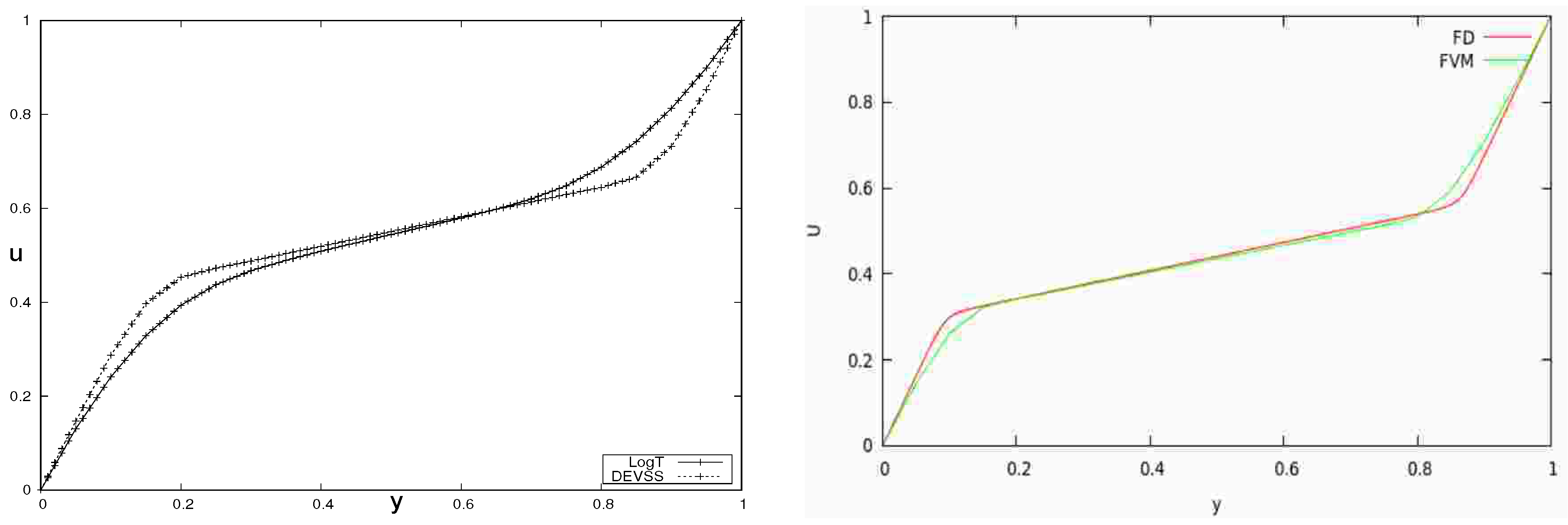
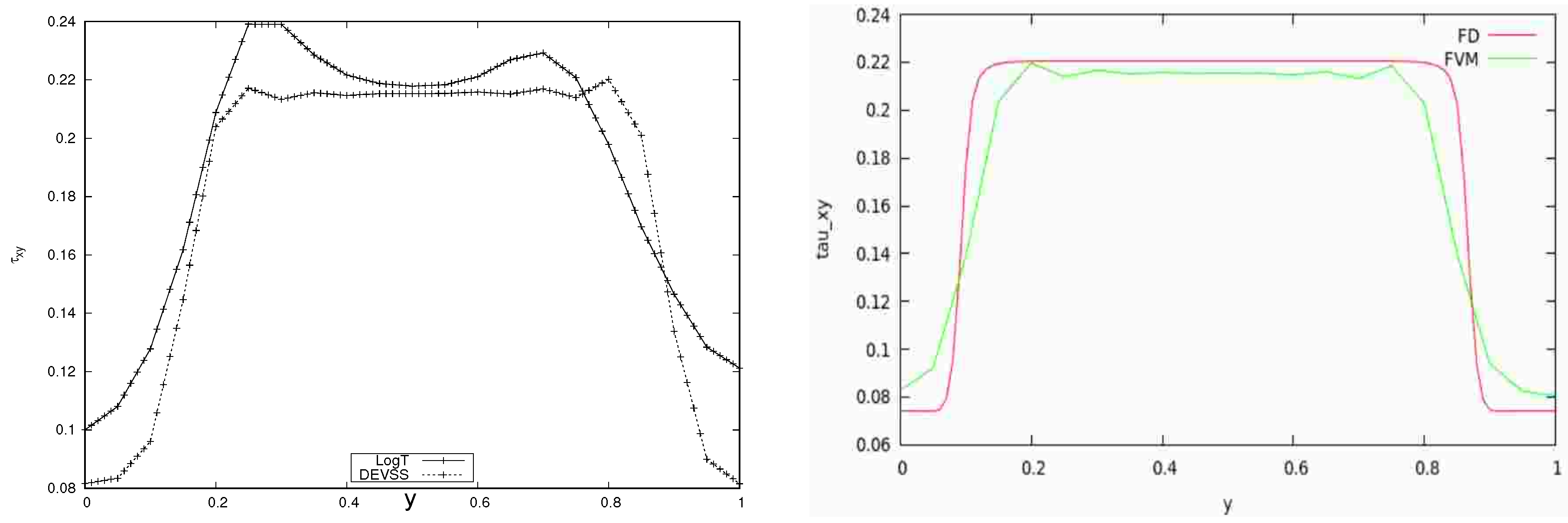
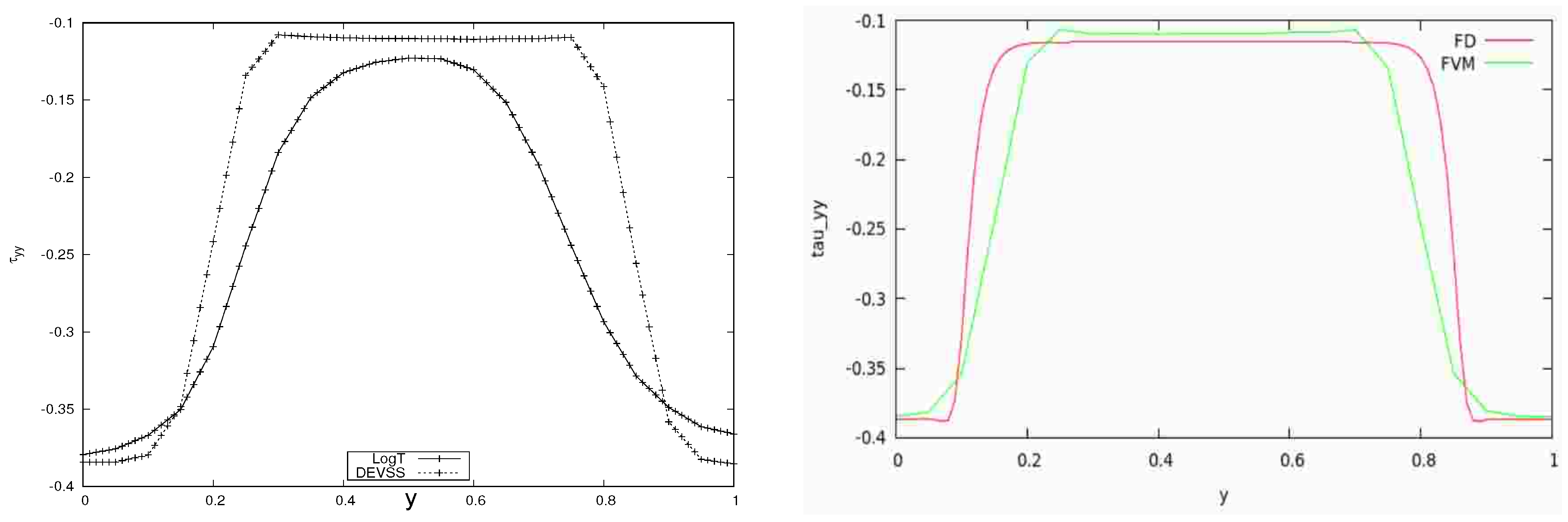
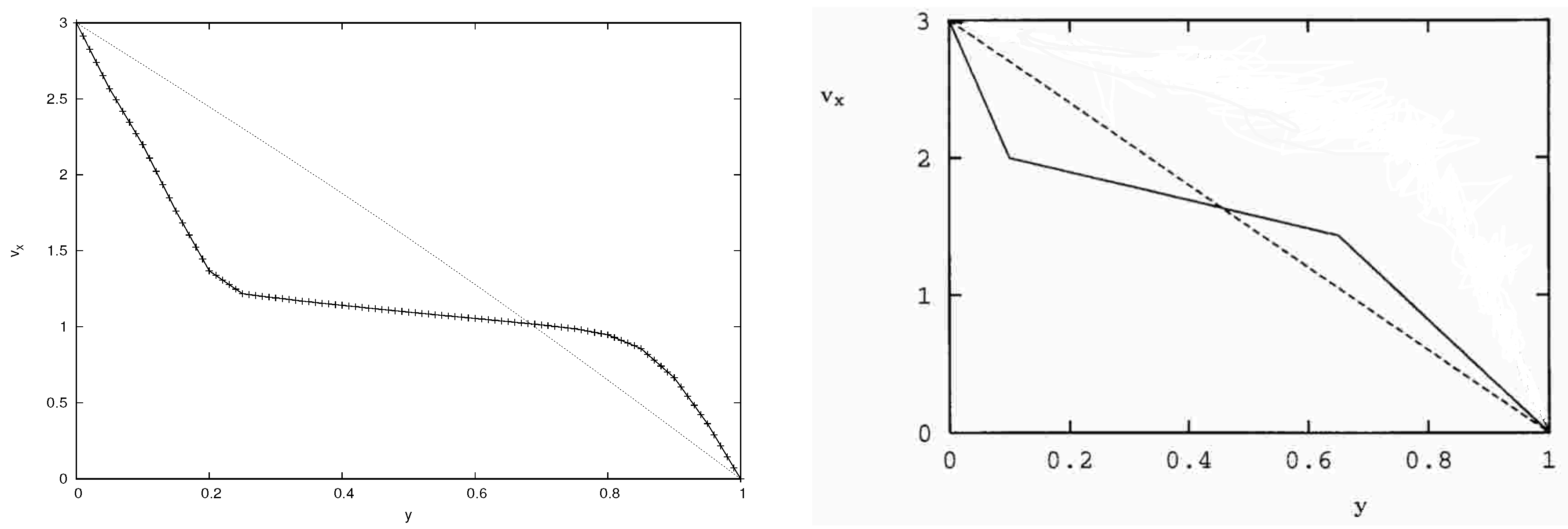
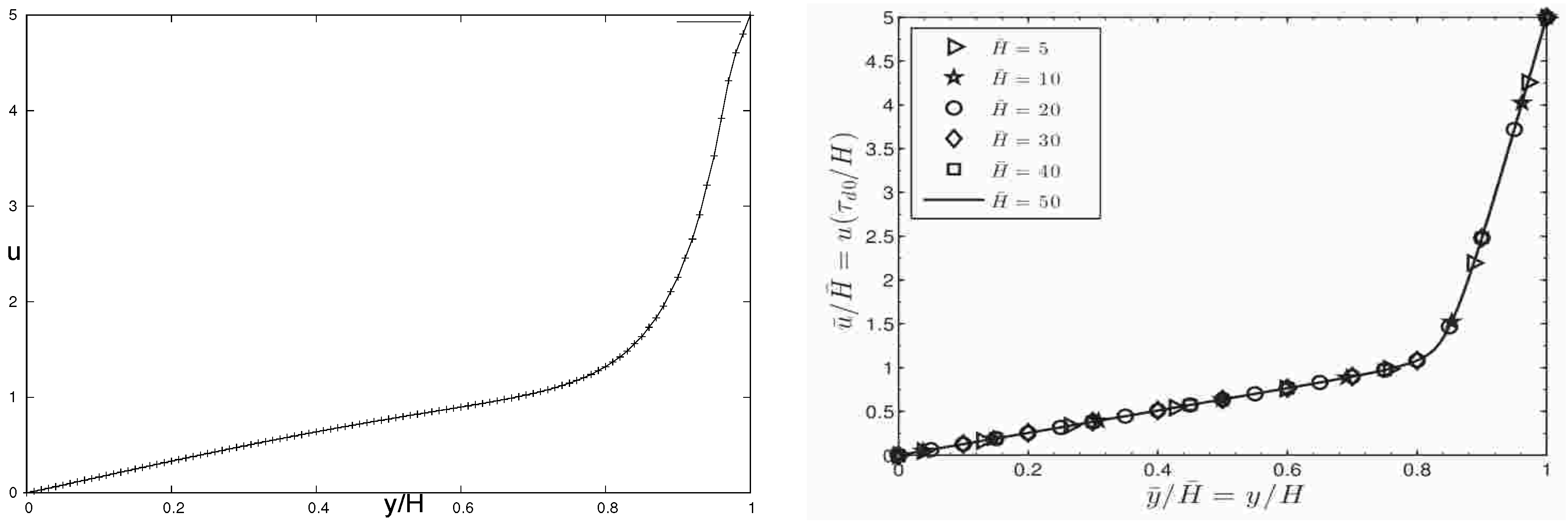
The results for the velocity and stress profiles show good qualitative agreement, see Figure 2, Figure 3, Figure 4 and Figure 5. As also observed in [24] as well as in practically all of the existing shear banding literature, Figure 2 for the velocity profiles shows that the high shear rate bands are located in the vicinity of the channel walls. As also explained in the introduction, the bulk main flow is close to a plug flow with much lower shear rates as compared to the high shear rates at the walls. Shear banding polymeric fluids and flows are, therefore, ill-suited for important applications, such as emulsion polymerization, polymer blending, and shear mixing.

The comparatives results obtained with the DEVSS stabilization techniques give results that are in closer/better agreement with those in [24]. However, we caution at this stage that we will not read too much into these differences. Our focus is on successfully reproducing the qualitative shear banding characteristics. As will be explained in the discussion and conclusion section, quantitative investigations may still be inappropriate at this stage.

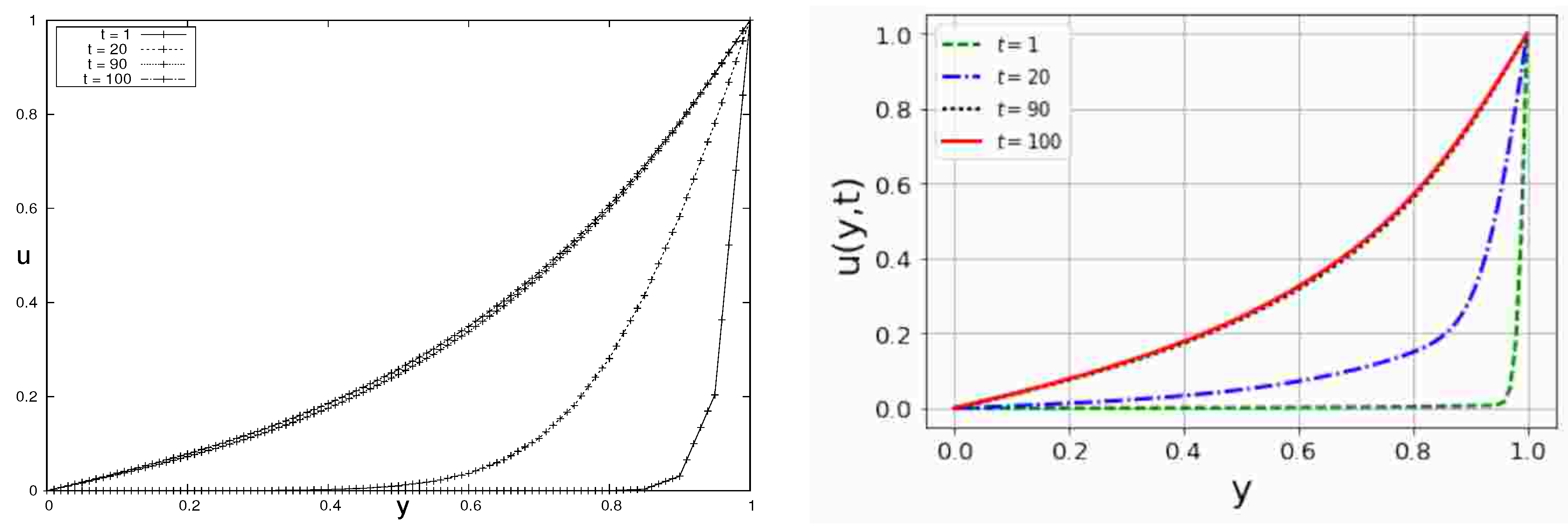
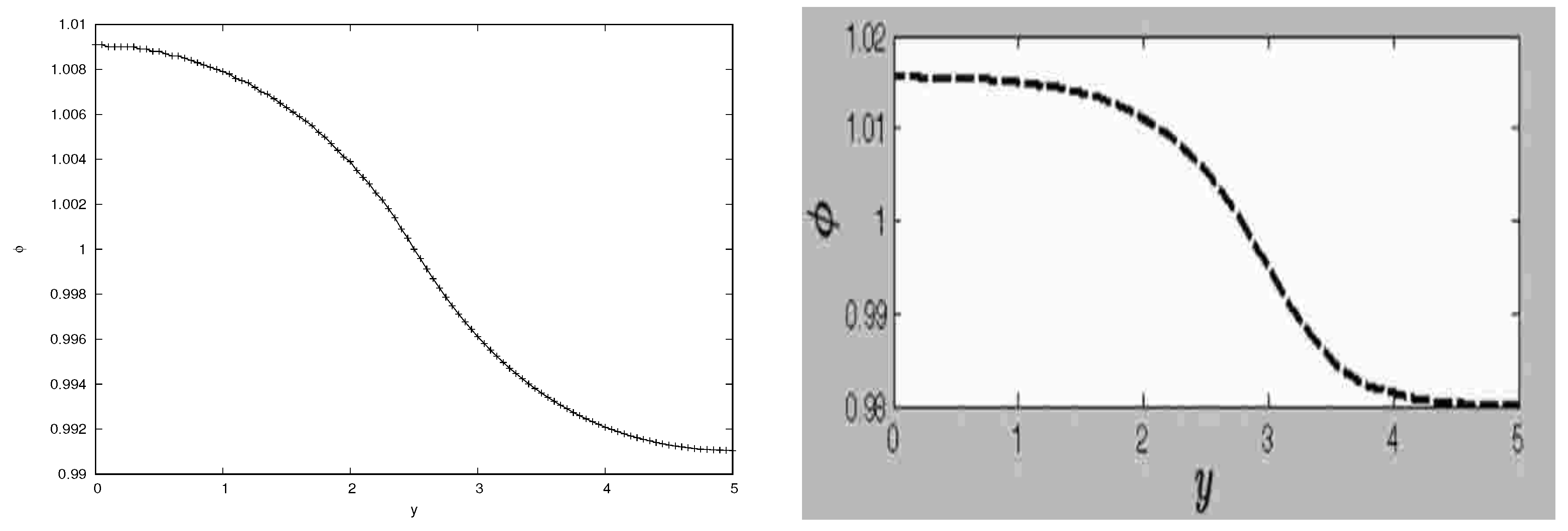
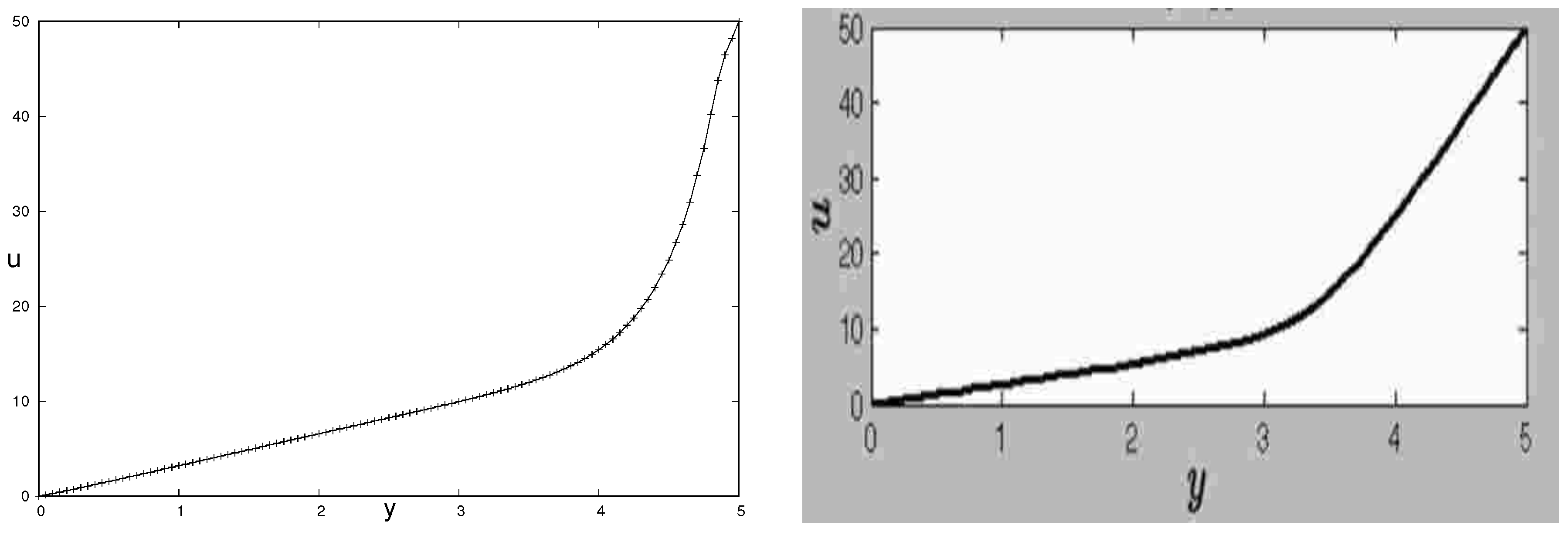
To compare our results with the analytical solutions given in [38], the values of ${\eta }_S=0.05$, $\mathrm{We}=1$, $\xi =0.2$, $\mathrm{Re}=0$, and $V=3$ are employed. Figure 6 and Figure 7 show good qualitative agreement with the results of [38].

7. Giesekus Model

The stress constitutive equation for the Giesekus model in terms of the conformation tensor, $\mathit{Q}$, is given, as in [40];

$${\displaystyle \frac{D\mathit{Q}}{Dt}}=-\mathit{v}·\nabla \mathit{Q}+\mathit{Q}·\nabla \mathit{v}+{(\nabla \mathit{v})}^T·\mathit{Q}-\frac{1}{\lambda }\left[(1-\alpha )\mathit{I}+\alpha \xi \mathit{Q}\right]·\left(\mathit{Q}-\xi \mathit{I}\right)+D{\nabla }^2\mathit{Q}.$$

(22)

The equation for the deviatoric stress, $\mathit{T}=2{\eta }_s\mathit{D}+{\mathit{\sigma }}_p$, is,

$$\mathit{T}=G_0\left(\frac{K}{k_{B}T}\mathit{Q}-\mathit{I}\right)+{\eta }_s\left[\nabla \mathit{v}+{(\nabla \mathit{v})}^T\right].$$

(23)

In keeping with the verification literature [39,40], we employ parameters values for the Giesekus models that were obtained using small amplitude oscillatory shear data. Such data are used to determine the effective relaxation time and the anisotropy factor estimated by fitting the Giesekus model to the steady-state shear stress and first normal stress difference plotted as a function of the shear rate. This procedure is outlined in detail in [40].

Comparative verification of our results against those of [39,40] will therefore be based on the parameters values given in

Table 1. Giesekus parameters.

Parameter	Symbol	Value
Solvent viscosity	${\eta }_S$	0.099 Pa
Plateau Modulus	$G_0$	150 Pa
Relaxation time	$\lambda$	0.013 s
Anisotropy factor	$\alpha$	0.91
Viscoelastic parameter	$\xi$	1
Diffusion coefficient	D	5 m2/s

.

The viscoelastic parameter, $\xi$ in Table 1 corresponds to the ratio,

$$\xi =\frac{K}{k_{B}T}.$$

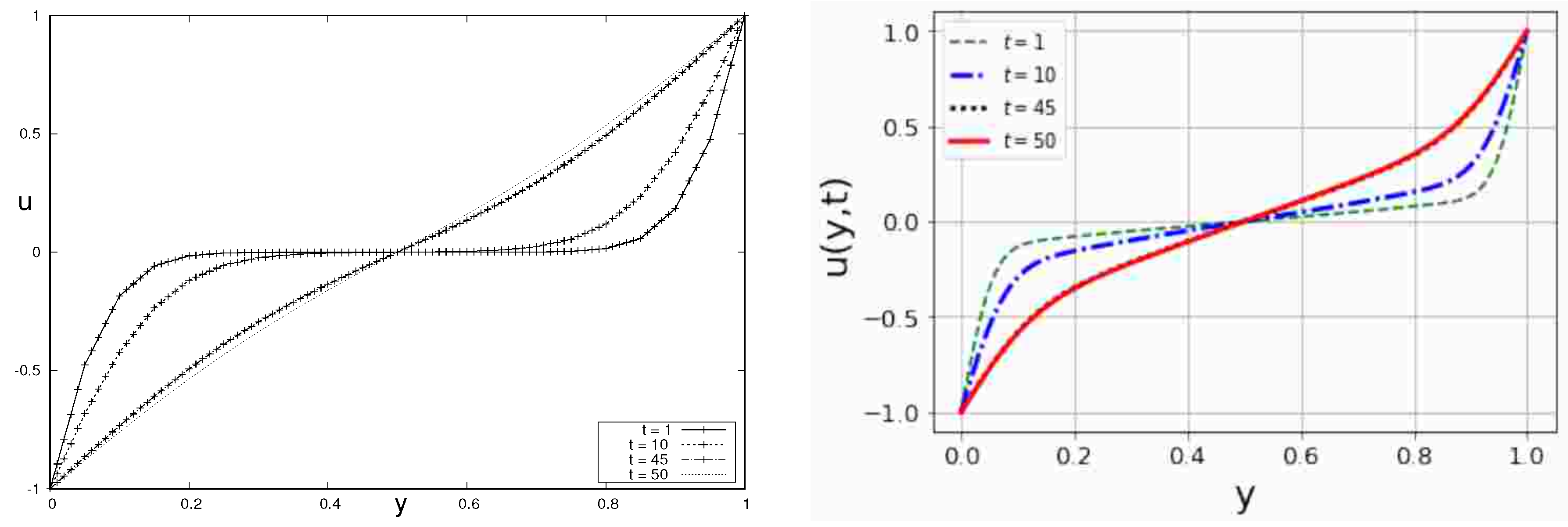
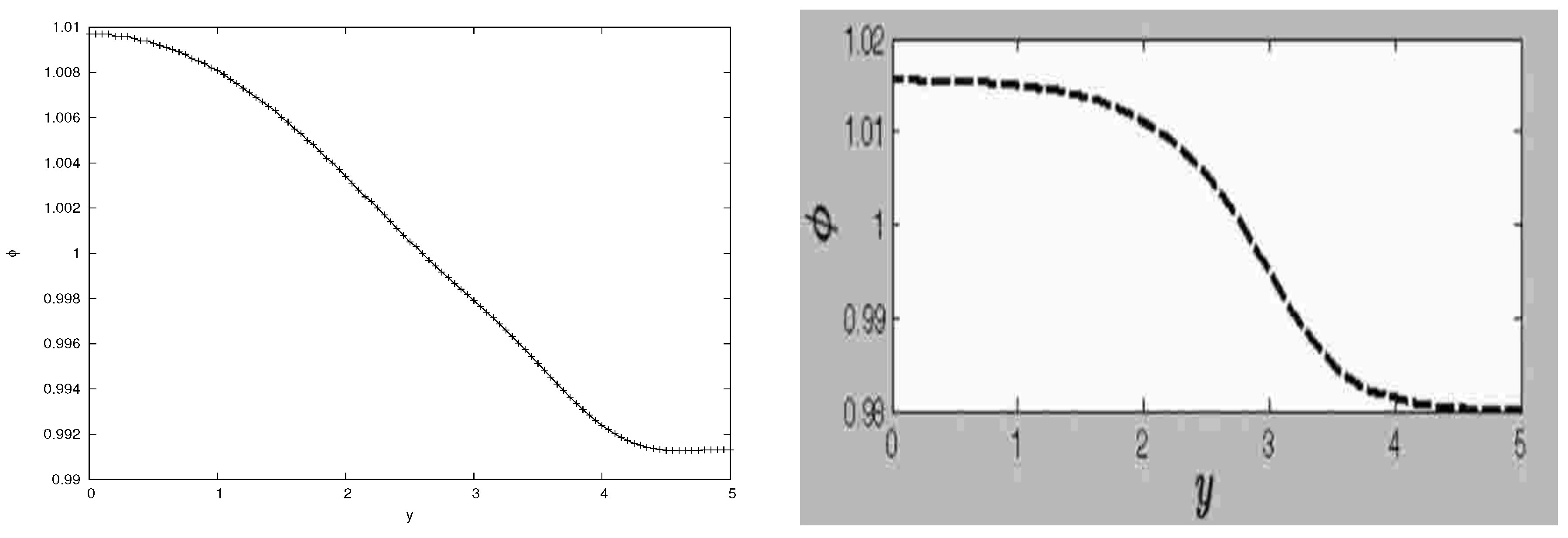
Simulated results are for the Couette flow for both anti-symmetric and symmetric cases. In the anti-symmetric case, the upper plate moves with a velocity of $1\mathrm{m}/\mathrm{s}$, whereas the lower plate is fixed. In the symmetric case, the upper and lower plates move in opposite directions with velocities $1\mathrm{m}/\mathrm{s}$ and $-1\mathrm{m}/\mathrm{s}$, respectively.

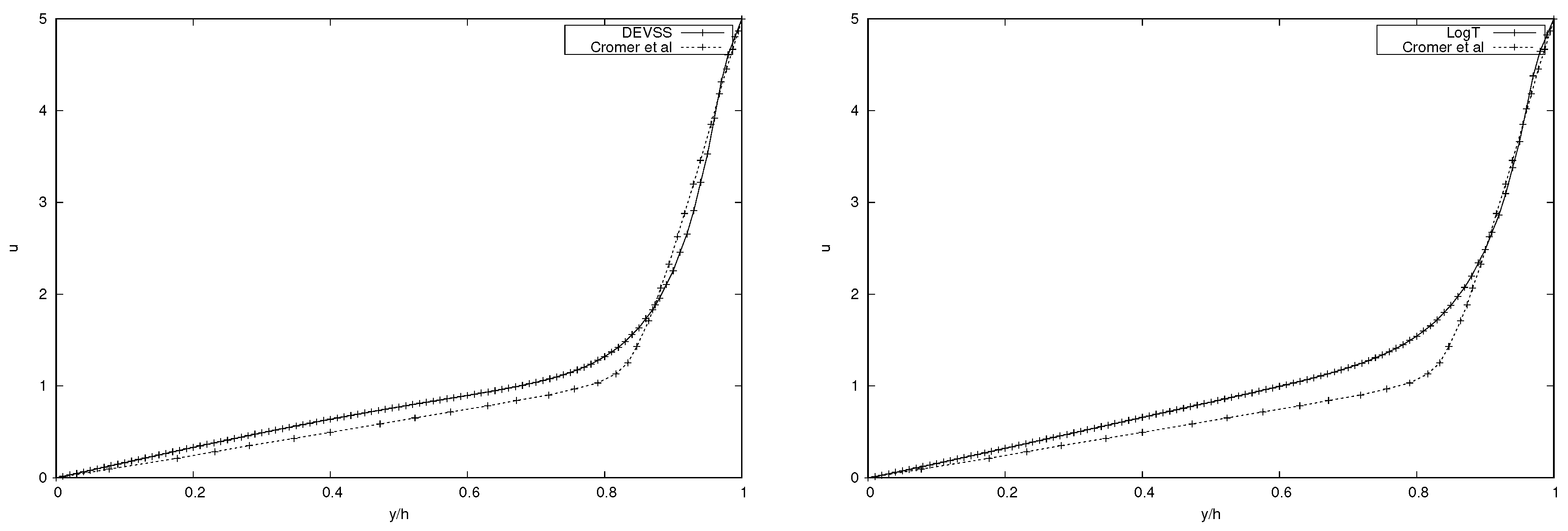
The velocity profiles are obtained at different times and qualitatively compared with those of [39]. A mesh size of $\Delta y=0.002\mathrm{m}$ was used. The time taken to obtain similar results, as in [39], was double the time they took and with a smaller time step of $\Delta T=0.001\mathrm{s}$. Thus, the time given in our graphs is scaled by $1/2$. As illustrated in Figure 8 and Figure 9, we observe good qualitative comparisons with the results of [39].

8. Rolie–Poly Two-Fluid Model

The results for the Rolie–Poly two-fluid model constitutive model are qualitatively compared against those in [31] for $k=1$. As in [31,35], our simulations employ non-dimensional equations and dimensionless parameters. A very small time step of $\Delta t=0.000001$ was used in addition to the mesh size $\Delta y=0.002$.

Figure 10 and Figure 11 show, as in the Johnson–Segalman case, that the DEVSS stabilization technique leads to “better” qualitative results for concentration, $\varphi$, in relation to the existing results in the literature as compared to the LCR stabilization technique. However, there is no signification difference in terms of the results for the velocity profiles between the DEVSS and LCR stabilization technique, refer to Figure 12 and Figure 13.

Our results are also compared to those of [35], see Figure 14 and Figure 15, and they show good qualitative agreement. In this case, the DEVSS and LCR simulations show no significant differences. Due to the restrictively high computational costs involved, we were unable to resolve the simulations when using the small values of H as used in [31,35]. This could also explain the slight quantitative differences between the results.

9. Discussion and Concluding Remarks

In this work, we deploy a robust, efficient, and versatile numerical algorithm, based on the finite volume methodology and implemented on the OpenFOAM software platform, in irder to simulate the complex dynamics (shear banding) of polymeric fluids in shear flow. Shear banding has been observed in the shear flow of polymer solutions as well as polymer melts. The viscoelastic constitutive modelling of these various polymeric fluids, i.e. those that display shear banding characteristics in shear flow, remains an open question. This is also intrinsically linked to the exact mechanisms for shear banding, which also remains a topic of considerable controversy and debate [32].

Two main contesting mechanisms currently exist in order to explain shear banding, namely flow-induced inhomogeneities and constitutive instabilities manifesting as non-monotonic stress-strain relationships. Shear banding in polymer melts (with otherwise homogeneous polymer composition at equilibrium) may reasonably be modelled as constitutive instabilities. However, this is not conclusive, especially given that flow-induced inhomogeneities may still arise in such polymer melts due to non-uniform polymer orientations in the various regions of the flow field. Modelling of shear banding for polymer solutions on the other hand is not so straightforward. No conclusive experimental evidence exists to explain the precise mechanism of shear banding for polymer solutions, and consequently, also, no consensus exists in the existing literature as to which mechanism is the most appropriate, see for example [32]. Both shear banding mechanisms have therefore been variously used in the literature to successfully explain shear banding characteristics in the shear flow of polymer solutions.

Various researchers and research groups have conducted investigations on shear banding in shear flow of polymeric fluids. The common theme in all such investigations is that each of these focus on applying a particular research methodology to a specific shear banding mechanism and hence also to a specific viscoelastic constitutive model. Our present investigation is the first to deploy a robust and versatile numerical algorithm to reproduce shear banding results across both the existing mechanism and across all of the existing viscoelastic constitutive models. Indeed, comparison and verification of our results against those in the existing literature, [24] and [39], for the Johnson–Segalman and Giesekus constitutive models respectively show good qualitative agreement. Good qualitative agreement is also observed between our results, for the non-homogeneous Rolie–Poly two-fluid model, and those in [31,35].

Given that there is as yet no consensus on the exact mechanism of shear banding or the subsequent viscoelastic constitutive modelling of the inherent polymeric fluids, quantitative comparative investigations at this stage would be premature. This is especially so, given that the shear banded solutions are in fact weak solutions, see for example [2] and, hence, the uniqueness of solutions is expectedly still also an open question. Various researchers have made attempts to mathematically investigate the uniqueness of solutions by adding artificial stress diffusion to their viscoelastic stress constitutive models, see for example [23,33]. However, no experimental or empirical evidence exists to support these artificial diffusion formalisms. Once conclusive experimental evidence is established in the future regarding the exact mechanism of shear banding and empirical evidence is equally established regarding the appropriate viscoelastic stress constitutive modelling, quantitative investigations would become pertinent, in particular to establish the accuracy of the various existing methodologies, including our otherwise versatile algorithm.