Robust Data-Driven Soft Sensors for Online Monitoring of Volatile Fatty Acids in Anaerobic Digestion Processes
Abstract
1. Introduction
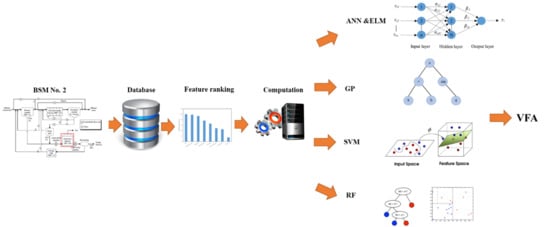
2. Materials and Methods
2.1. Benchmark Simulation Model No. 2
2.2. Data Collection
2.3. Pre-Processing of the Data
3. Data-Driven Methods
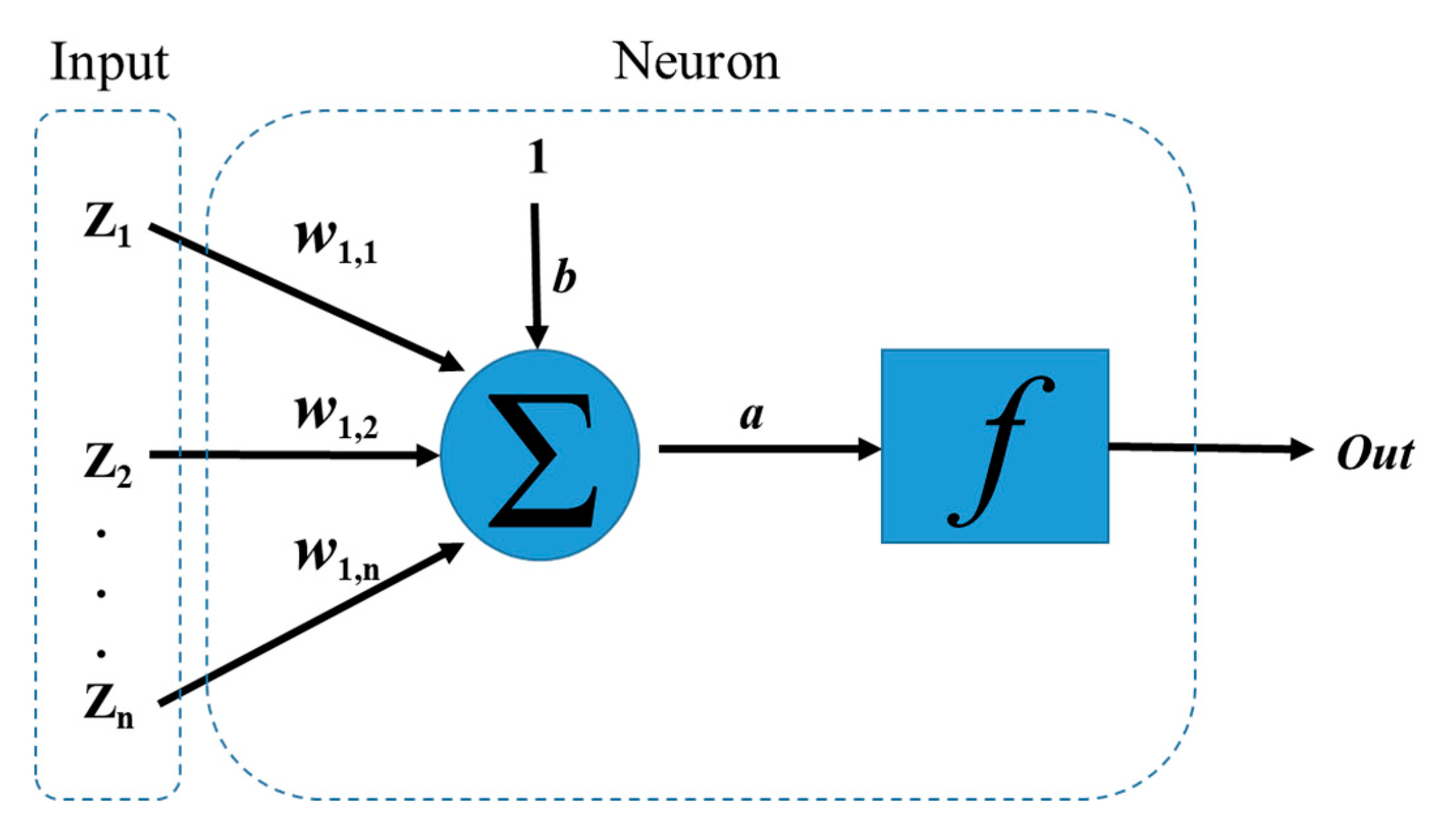
3.1. Artificial Neural Network (ANN)
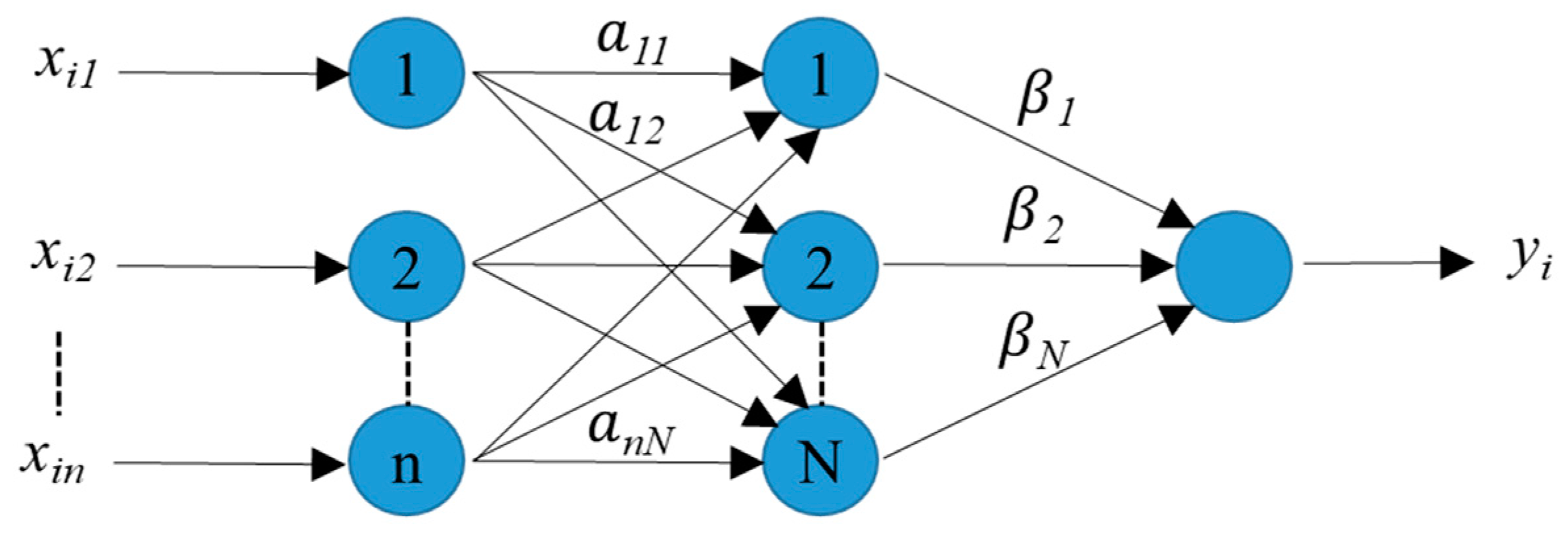
3.2. Extreme Learning Machine (ELM)
3.3. Random Forest (RF)
3.4. Support Vector Machine (SVM)
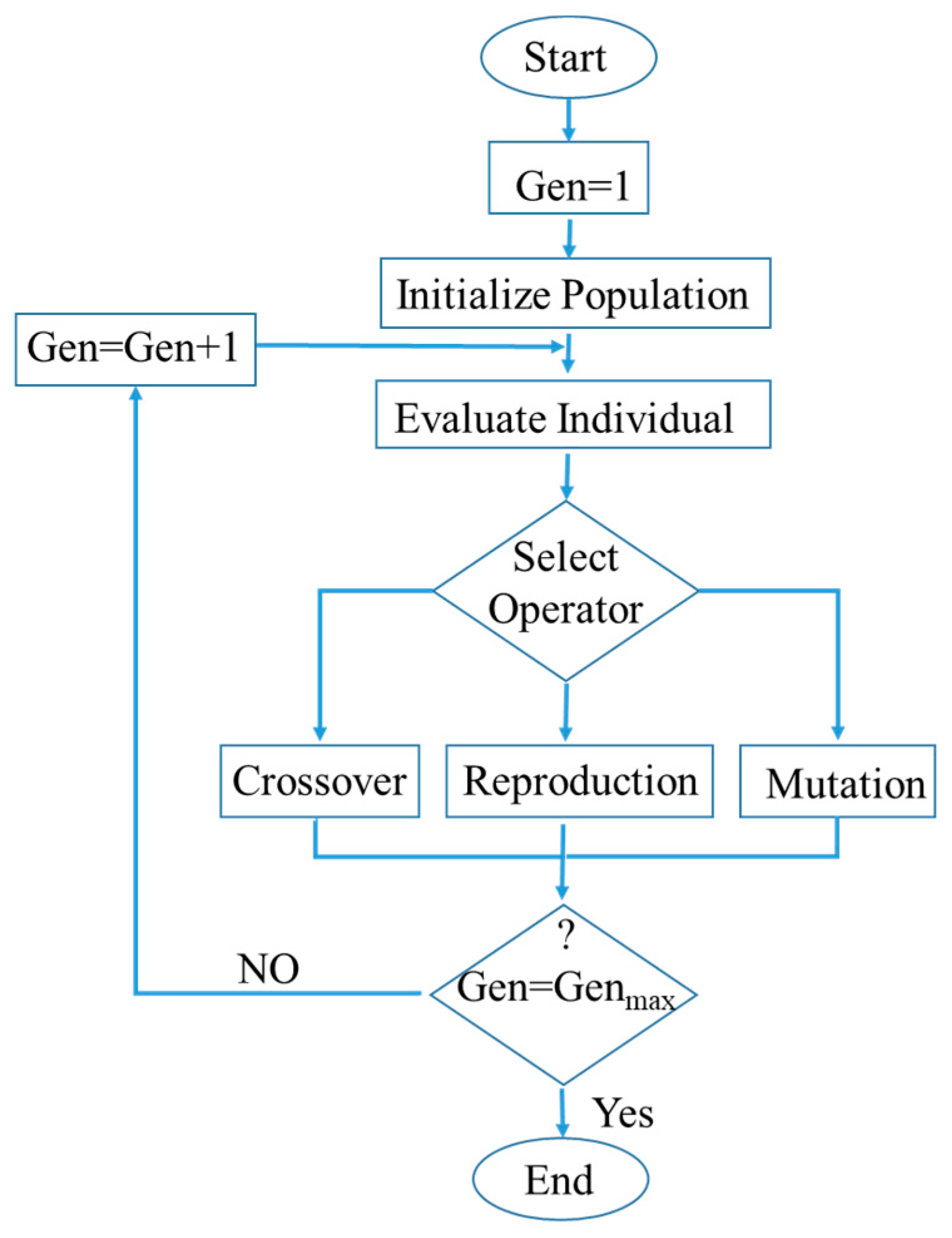
3.5. Genetic Programming (GP)
3.6. Feature Ranking
4. Results and Discussion
4.1. Studying the Relationship between Input and Output Data
4.2. Choosing the Most Influential Variables Using the Feature Ranking Method
4.3. Soft Sensor Design
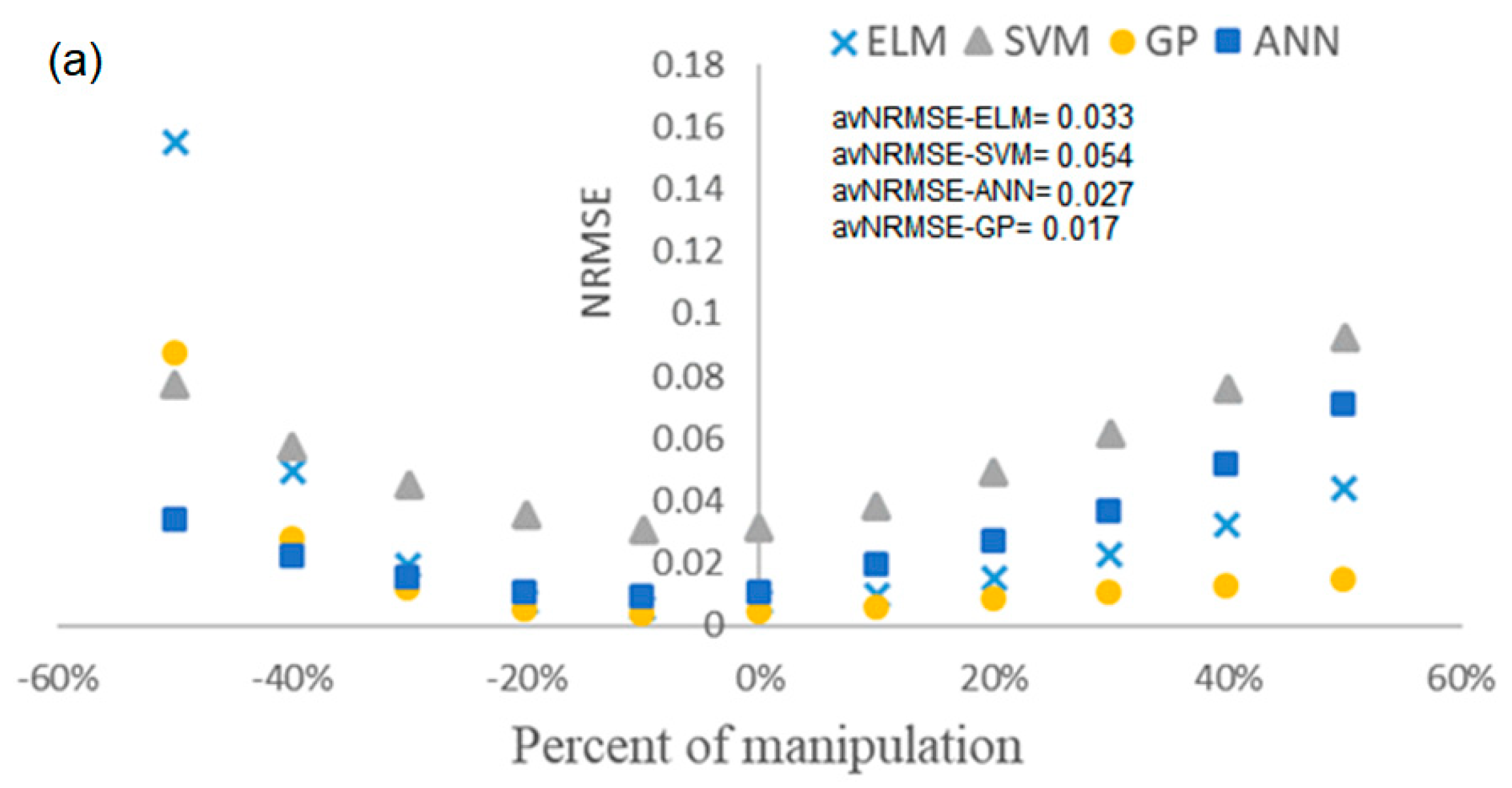
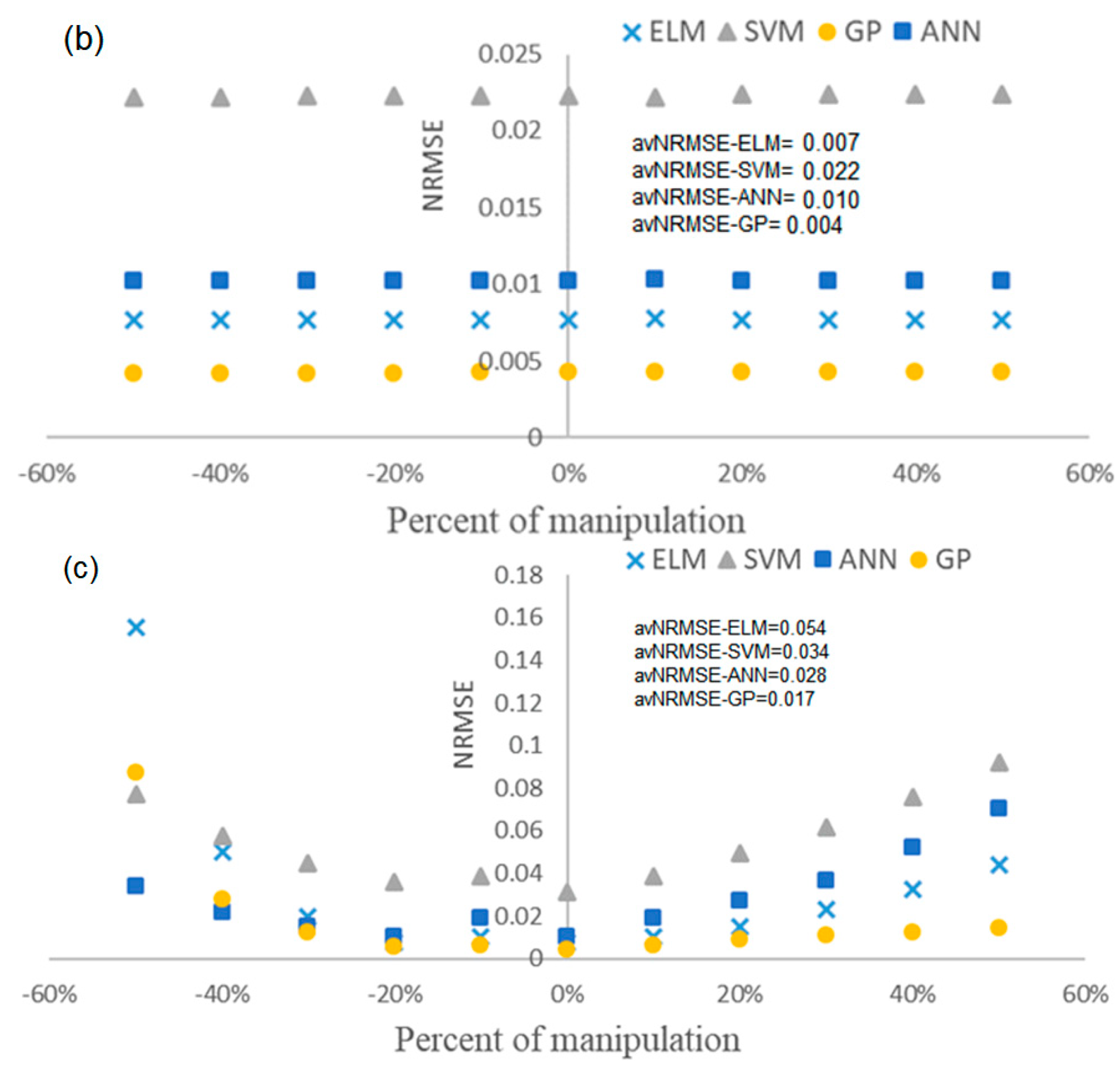
4.4. Evaluation of the Robustness of Soft Sensors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abu Qdais, H.; Bani Hani, K.; Shatnawi, N. Modeling and optimization of biogas production from a waste digester using artificial neural network and genetic algorithm. Resour. Conserv. Recycl. 2010, 54, 359–363. [Google Scholar] [CrossRef]
- Yordanova, S.; Noikova, N.; Petrova, R.; Tzvetkov, P. Neuro-Fuzzy Modelling on Experimental Data in Anaerobic Digestion of Organic Waste in Waters. In Proceedings of the 2005 IEEE Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Sofia, Bulgaria, 5–7 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 84–88. [Google Scholar]
- Franke-Whittle, I.H.; Walter, A.; Ebner, C.; Insam, H. Investigation into the effect of high concentrations of volatile fatty acids in anaerobic digestion on methanogenic communities. Waste Manag. 2014, 34, 2080–2089. [Google Scholar] [CrossRef] [PubMed]
- Haimi, H.; Mulas, M.; Corona, F.; Vahala, R. Data-derived soft-sensors for biological wastewater treatment plants: An overview. Environ. Model. Softw. 2013, 47, 88–107. [Google Scholar] [CrossRef]
- Dürrenmatt, D.J.; Gujer, W. Data-driven modeling approaches to support wastewater treatment plant operation. Environ. Model. Softw. 2012, 30, 47–56. [Google Scholar] [CrossRef]
- Corona, F.; Mulas, M.; Haimi, H.; Sundell, L.; Heinonen, M.; Vahala, R. Monitoring nitrate concentrations in the denitrifying post-filtration unit of a municipal wastewater treatment plant. J. Process Control 2013, 23, 158–170. [Google Scholar] [CrossRef]
- Jimenez, J.; Latrille, E.; Harmand, J.; Robles, A.; Ferrer, J.; Gaida, D.; Wolf, C.; Mairet, F.; Bernard, O.; Alcaraz-Gonzalez, V.; et al. Instrumentation and control of anaerobic digestion processes: A review and some research challenges. Rev. Environ. Sci. Bio/Technol. 2015, 14, 615–648. [Google Scholar] [CrossRef]
- James, S.C.; Legge, R.L.; Budman, H. On-line estimation in bioreactors: A review. Rev. Chem. Eng. 2000, 16, 311–340. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Van Loosdrecht, M.C.M.; Henze, M.; Lind, M.; Jørgensen, S.B. Activated sludge wastewater treatment plant modelling and simulation: State of the art. Environ. Model. Softw. 2004, 19, 763–783. [Google Scholar] [CrossRef]
- Newhart, K.B.; Holloway, R.W.; Hering, A.S.; Cath, T.Y. Data-driven performance analyses of wastewater treatment plants: A review. Water Res. 2019, 157, 498–513. [Google Scholar] [CrossRef]
- Corominas, L.; Garrido-Baserba, M.; Villez, K.; Olsson, G.; Cort Es, U.; Poch, M. Transforming data into knowledge for improved wastewater treatment operation: A critical review of techniques. Environ. Model. Softw. 2018, 106, 89–103. [Google Scholar] [CrossRef]
- Tay, J.-H.; Zhang, X. A fast predicting neural fuzzy model for high-rate anaerobic wastewater treatment systems. Water Res. 2000, 34, 2849–2860. [Google Scholar] [CrossRef]
- Mullai, P.; Arulselvi, S.; Ngo, H.-H.; Sabarathinam, P.L. Experiments and ANFIS modelling for the biodegradation of penicillin-G wastewater using anaerobic hybrid reactor. Bioresour. Technol. 2011, 102, 5492–5497. [Google Scholar] [CrossRef] [PubMed]
- Güçlü, D.; Yılmaz, N.; Ozkan-Yucel, U.G. Application of neural network prediction model to full-scale anaerobic sludge digestion. J. Chem. Technol. Biotechnol. 2011, 86, 691–698. [Google Scholar] [CrossRef]
- Rangasamy, P.; Pvr, I.; Ganesan, S. Anaerobic tapered fluidized bed reactor for starch wastewater treatment and modeling using multilayer perceptron neural network. J. Environ. Sci. 2007, 19, 1416–1423. [Google Scholar] [CrossRef]
- Huang, M.; Han, W.; Wan, J.; Ma, Y.; Chen, X. Multi-objective optimisation for design and operation of anaerobic digestion using GA-ANN and NSGA-II. J. Chem. Technol. Biotechnol. 2016, 91, 226–233. [Google Scholar] [CrossRef]
- Beltramo, T.; Klocke, M.; Hitzmann, B. Prediction of the biogas production using GA and ACO input features selection method for ANN model. Inf. Process. Agric. 2019, 6, 349–356. [Google Scholar] [CrossRef]
- Jeppsson, U.; Rosen, C.; Alex, J.; Copp, J.; Gernaey, K.V.; Pons, M.-N.; Vanrolleghem, P.A. Towards a benchmark simulation model for plant-wide control strategy performance evaluation of WWTPs. Water Sci. Technol. 2006, 53, 287–295. [Google Scholar] [CrossRef]
- Nopens, I.; Benedetti, L.; Jeppsson, U.; Pons, M.-N.; Alex, J.; Copp, J.B.; Gernaey, K.V.; Rosen, C.; Steyer, J.-P.; Vanrolleghem, P.A. Benchmark Simulation Model No 2: Finalisation of plant layout and default control strategy. Water Sci. Technol. 2010, 62, 1967–1974. [Google Scholar] [CrossRef]
- Hota, H.S.; Handa, R.; Shrivas, A.K. Time series data prediction using sliding window based Rbf neural network. Int. J. Comput. Intell. Res. 2017, 13, 1145–1156. [Google Scholar]
- Gil, J.D.; Ruiz-Aguirre, A.; Roca, L.; Zaragoza, G.; Berenguel, M. Prediction models to analyse the performance of a commercial-scale membrane distillation unit for desalting brines from RO plants. Desalination 2018, 445, 15–28. [Google Scholar] [CrossRef]
- Eskandarian, S.; Bahrami, P.; Kazemi, P. A comprehensive data mining approach to estimate the rate of penetration: Application of neural network, rule based models and feature ranking. J. Pet. Sci. Eng. 2017, 156, 605–615. [Google Scholar] [CrossRef]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Candel, A.; Ledell, E.; Bartz, A. Deep Learning with H2O. Available online: https://h2o-release.s3.amazonaws.com/h2o/rel-wright/9/docs-website/h2o-docs/booklets/DeepLearningBooklet.pdf (accessed on 11 November 2019).
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, pp. 985–990. [Google Scholar]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Q.; Wu, Q.; Zheng, Y.; Zhou, J.; Tu, Z.; Chan, S.H. Modelling of solid oxide electrolyser cell using extreme learning machine. Electrochim. Acta 2017, 251, 137–144. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad-Shahidi, A.; Lim, S.Y. Scour prediction in long contractions using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Liu, L.; Lei, Y. An accurate ecological footprint analysis and prediction for Beijing based on SVM model. Ecol. Inform. 2018, 44, 33–42. [Google Scholar] [CrossRef]
- Koza, J. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Bahrami, P.; Kazemi, P.; Mahdavi, S.; Ghobadi, H. A novel approach for modeling and optimization of surfactant/polymer flooding based on Genetic Programming evolutionary algorithm. Fuel 2016, 179, 289–298. [Google Scholar] [CrossRef]
- Sonolikar, R.R.; Patil, M.P.; Mankar, R.B.; Tambe, S.S.; Kulkarni, B.D. Genetic Programming based Drag Model with Improved Prediction Accuracy for Fluidization Systems. Int. J. Chem. React. Eng. 2017, 15. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: New York, NY, USA, 2013; Volume 103, ISBN 978-1-4614-7137-0. [Google Scholar]
- Szlęk, J.; Mendyk, A. Fscaret: Automated Feature Selection from ‘Caret’ [Software]. Available online: https://cran.r-project.org/web/packages/fscaret/index.html (accessed on 10 March 2018).
- Szlęk, J.; Pacławski, A.; Lau, R.; Jachowicz, R.; Kazemi, P.; Mendyk, A. Empirical search for factors affecting mean particle size of PLGA microspheres containing macromolecular drugs. Comput. Methods Programs Biomed. 2016, 134, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Lipson, H. Distilling Free-Form Natural Laws from Experimental Data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Hod, L.; Schmidt, M.; Lipson, H. Eureqa (Version 0.98 Beta) [Software]. 2013. Available online: http://www.eureqa.com/ (accessed on 4 May 2018).



| Parameters | Unit | Parameters | Unit |
|---|---|---|---|
| Effluent COD | g m−3 | CH4 mol_fraction | - |
| Effluent alkalinity | Mol m−3 | CO2 mol_fraction | - |
| Influent TSS | g m−3 | H2 mol_fraction | - |
| Effluent TSS | g m−3 | Pressure | bar |
| Effluent pH | - | Effluent ammonia | g m−3 |
| Effluent BOD | g m−3 | Influent Flow | m3 d−1 |
| Gas flow | m3 d−1 |
| All_Inputs | All_Input_Except _TSS | All_Input_Except _Ammonia | All_Input_Except _TSS & Ammonia | |
|---|---|---|---|---|
| Training_NRMSE | 0.028 | 0.029 | 0.028 | 0.029 |
| Test_NRMSE | 0.039 | 0.039 | 0.038 | 0.038 |
| Training_R2 | 0.981 | 0.978 | 0.979 | 0.976 |
| Test_R2 | 0.967 | 0.966 | 0.967 | 0.968 |
| Default Values | Modified Values | |||||||
|---|---|---|---|---|---|---|---|---|
| Sin (kmol m−3) | Xc (kg m−3) | Xch (kg m−3) | Flow (m3 d−1) | Sin (kmol m−3) | Xc (kg m−3) | Xch (kg m−3) | Flow (m3 d−1) | |
| Min. | 0.0006 | 0 | 0.000 | 56.55 | 0.0006 | 0.00 | 0.000 | 1.993 |
| 1st Qu. | 0.0015 | 0 | 2.941 | 137.07 | 0.0019 | 0.00 | 3.293 | 82.257 |
| Median | 0.0019 | 0 | 3.952 | 175.81 | 0.1156 | 22.54 | 4.897 | 138.704 |
| Mean | 0.0020 | 0 | 3.830 | 183.57 | 0.0957 | 16.41 | 7.256 | 140.602 |
| 3rd Qu. | 0.0022 | 0 | 4.833 | 217.90 | 0.1584 | 28.71 | 9.684 | 193.301 |
| Max. | 0.0325 | 0 | 8.607 | 479.96 | 0.2718 | 39.52 | 40.464 | 477.957 |
| All_Inputs | All_Input_Except _TSS | All_Input_Except _Ammonia | All_Input_Except _TSS & Ammonia | |
|---|---|---|---|---|
| Training_NRMSE | 0.103 | 0.133 | 0.143 | 0.189 |
| Test_NRMSE | 0.197 | 0.213 | 0.122 | 0.304 |
| Training_R2 | 0.865 | 0.794 | 0.748 | 0.586 |
| Test_R2 | 0.654 | 0.511 | 0.841 | 0.663 |
| Inputs | R2 | NRMSE |
|---|---|---|
| pH + Ammonia_conc + pressure | 0.813 | 0.182 |
| pH + Ammonia_conc + pressure + CO2_mol fraction | 0.990 | 0.033 |
| pH + Ammonia_conc + pressure + CO2_mol_fraction + TSS_out | 0.972 | 0.058 |
| pH + Ammonia_conc + pressure + CO2_mol_fraction + TSS_out+Flow | 0.977 | 0.044 |
| pH + Ammonia_conc + pressure + CO2_mol_fraction + TSS_out + Flow + H2_mol_fraction | 0.971 | 0.049 |
| Algorithm | Tuning Parameters | ||||
|---|---|---|---|---|---|
| ANN | Neuron Size | Transfer Function | Number of Hidden Layers | L1 | L2 |
| 108 | Tanh | 1 | 1 × 10−5 | 1 × 10−5 | |
| RF | mtry | Number of trees | Maximum nodes | ||
| 4 | 1600 | 20 | |||
| ELM | Neuron size | Transfer function | |||
| 126 | Sigmoid | ||||
| SVM | Sigma | C | |||
| 0.2 | 500 | ||||
| Algorithm | NRMSE Training | R2 Training | NRMSE Validation | R2 Validation |
|---|---|---|---|---|
| ANN | 0.0089 | 0.9992 | 0.0192 | 0.9969 |
| RF | 0.1432 | 0.7533 | 0.3419 | 0.5784 |
| ELM | 0.0003 | 0.9999 | 0.0169 | 0.9977 |
| SVM | 0.0165 | 0.9966 | 0.0390 | 0.9941 |
| GP | 0.0025 | 0.9999 | 0.0037 | 0.9998 |
| Term * | Coef | Term * | Coef |
|---|---|---|---|
| constant | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazemi, P.; Steyer, J.-P.; Bengoa, C.; Font, J.; Giralt, J. Robust Data-Driven Soft Sensors for Online Monitoring of Volatile Fatty Acids in Anaerobic Digestion Processes. Processes 2020, 8, 67. https://doi.org/10.3390/pr8010067
Kazemi P, Steyer J-P, Bengoa C, Font J, Giralt J. Robust Data-Driven Soft Sensors for Online Monitoring of Volatile Fatty Acids in Anaerobic Digestion Processes. Processes. 2020; 8(1):67. https://doi.org/10.3390/pr8010067
Chicago/Turabian StyleKazemi, Pezhman, Jean-Philippe Steyer, Christophe Bengoa, Josep Font, and Jaume Giralt. 2020. "Robust Data-Driven Soft Sensors for Online Monitoring of Volatile Fatty Acids in Anaerobic Digestion Processes" Processes 8, no. 1: 67. https://doi.org/10.3390/pr8010067
APA StyleKazemi, P., Steyer, J.-P., Bengoa, C., Font, J., & Giralt, J. (2020). Robust Data-Driven Soft Sensors for Online Monitoring of Volatile Fatty Acids in Anaerobic Digestion Processes. Processes, 8(1), 67. https://doi.org/10.3390/pr8010067