Modeling and Exploiting Microbial Temperature Response
Abstract
1. Introduction
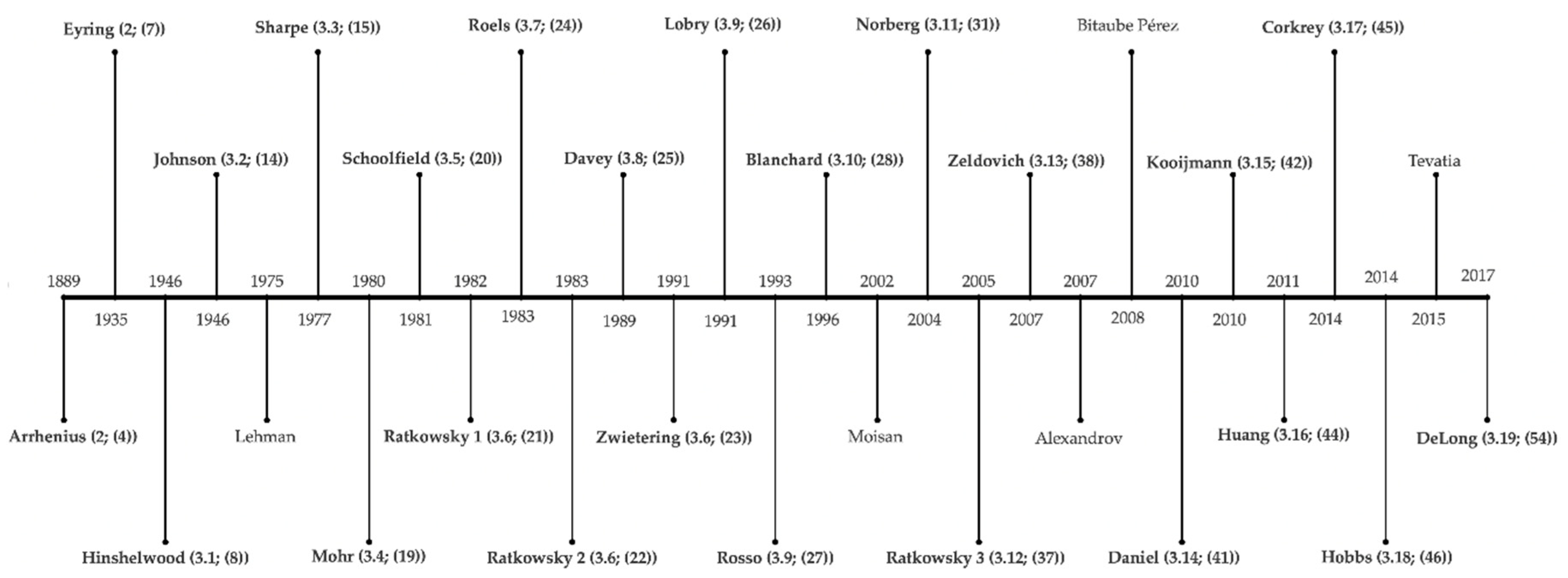
2. History of Temperature Modeling—17th–20th Century
2.1. Temperature in Biological Systems—The History Began with Arrhenius
2.2. Biological Mechanisms Involved in Temperature Responses
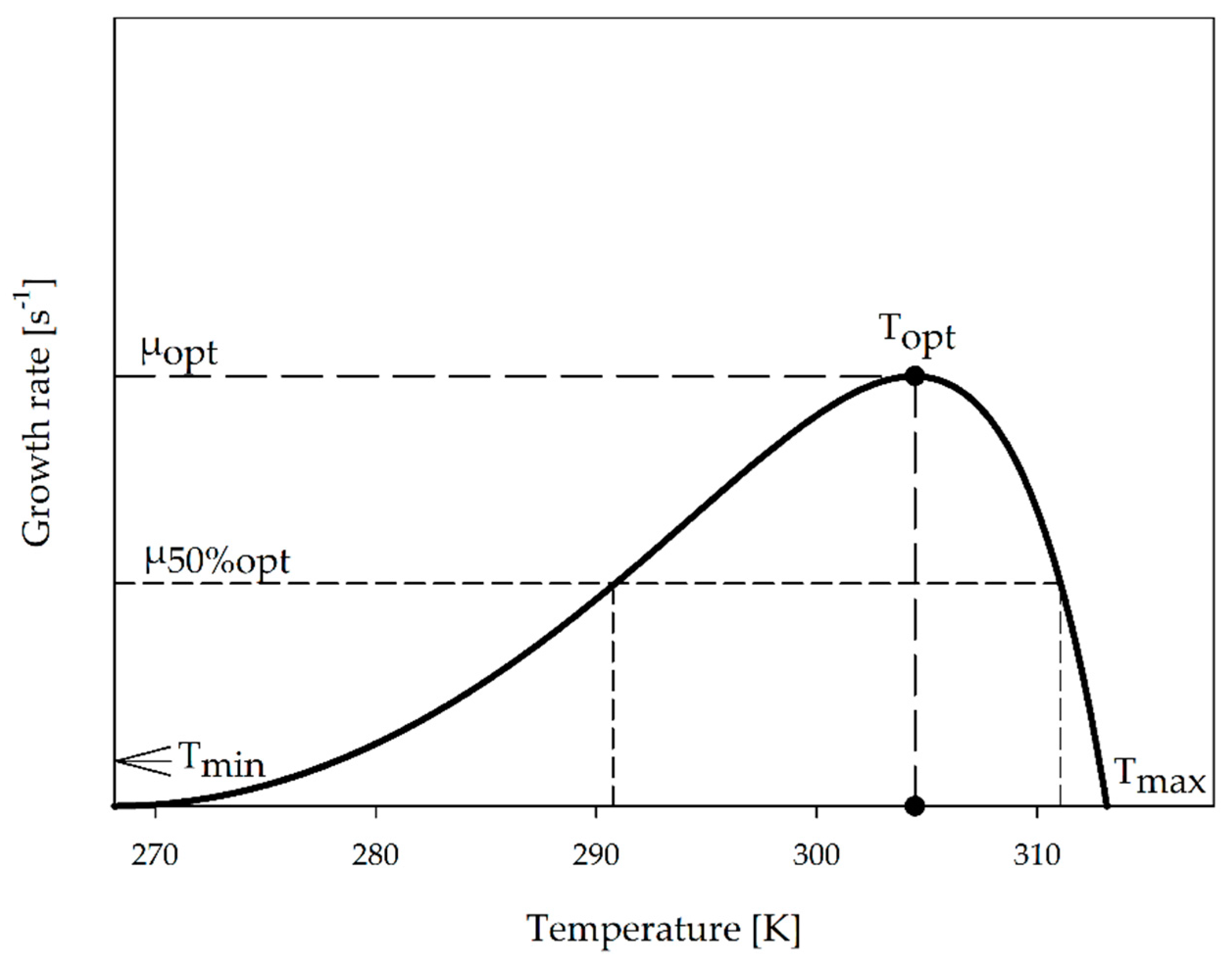
2.3. Characteristic Graph for Growth as a Function of Temperature
2.4. Mechanistic Versus Empirical Models
3. Temperature Modeling—From the 20th Century until Today
3.1. The Model of Hinshelwood (1946)
3.2. The Model of Johnson (1946)
3.3. The Model of Sharpe (1977)
3.4. The Model of Mohr (1980)
3.5. The Model of Schoolfield (1981)
3.6. The Models of Ratkowsky and Zwietering (1982–1991)
3.7. The Model of Roels (1983)
3.8. The Model of Davey (1989)
3.9. The Models of Lobry and Rosso (1991–1993)
3.10. The Model of Blanchard (1996)
3.11. The Models of Eppley and Norberg (2004)
3.12. The Modified Master Reaction Model (2005)
3.13. The Model of Zeldovich (2007–2016)
3.14. The Model of Daniel (2010)
3.15. The Model of Kooijman (2010)
3.16. The Model of Huang (2011)
3.17. The Model of Corkrey (2014)
3.18. The Model of Hobbs (2014)
3.19. The Model of DeLong (2017)
3.20. Additional Temperature Models
4. Biotechnological Applications for Targeted Temperature Variation Assisted by Temperature Models
4.1. Temperature with Potential for Bioprocess Design
4.2. Application of Temperature Models and Temperature for Bioprocesses Design
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hausmann, R.; Henkel, M.; Hecker, F.; Hitzmann, B. Present Status of Automation for Industrial Bioprocesses; Elsevier, B.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 9780444636744. [Google Scholar]
- Klinkert, B.; Narberhaus, F. Microbial thermosensors. Cell. Mol. Life Sci. 2009, 66, 2661–2676. [Google Scholar] [CrossRef] [PubMed]
- Noll, P.; Treinen, C.; Müller, S.; Senkalla, S.; Lilge, L.; Hausmann, R.; Henkel, M. Evaluating temperature-induced regulation of a ROSE-like RNA-thermometer for heterologous rhamnolipid production in Pseudomonas putida KT2440. AMB Express 2019, 9, 154. [Google Scholar] [CrossRef] [PubMed]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. Phys. Chem. 1889, 4, 226–248. [Google Scholar] [CrossRef]
- Von Stockar, U.; Duboc, P.; Menoud, L.; Marison, I.W. On-line calorimetry as a technique for process monitoring and control in biotechnology. Thermochim. Acta 1997, 300, 225–236. [Google Scholar] [CrossRef]
- Voisard, D.; Von Stockar, U.; Marison, I.W. Quantitative calorimetric investigation of fed-batch cultures of Bacillus sphaericus 1593M. Thermochim. Acta 2002, 394, 99–111. [Google Scholar] [CrossRef]
- Schaepe, S.; Kuprijanov, A.; Aehle, M.; Simutis, R.; Lübbert, A. Simple control of fed-batch processes for recombinant protein production with E. coli. Biotechnol. Lett. 2011, 33, 1781–1788. [Google Scholar] [CrossRef]
- Zwietering, M.H.; De Koos, J.T.; Hasenack, B.E.; De Witt, J.C.; Van’t Riet, K. Modeling of bacterial growth as a function of temperature. Appl. Environ. Microbiol. 1991, 57, 1094–1101. [Google Scholar] [CrossRef]
- De Oliveira Filho, P.B.; Nascimento, M.L.F.; Pontes, K.V. Optimal Design of a Dividing Wall Column for the Separation of Aromatic Mixtures Using the Response Surface Method; Elsevier Masson SAS: Paris, France, 2018; Volume 43, ISBN 9780444642356. [Google Scholar]
- MathWorks, Inc. Matlab-Documentation. 2019. Available online: https://de.mathworks.com/help/stats/response-surface-designs.html (accessed on 5 January 2020).
- Restaino, O.F.; Borzacchiello, M.G.; Scognamiglio, I.; Fedele, L.; Alfano, A.; Porzio, E.; Manco, G.; De Rosa, M.; Schiraldi, C. High yield production and purification of two recombinant thermostable phosphotriesterase-like lactonases from Sulfolobus acidocaldarius and Sulfolobus solfataricus useful as bioremediation tools and bioscavengers. BMC Biotechnol. 2018, 18, 18. [Google Scholar] [CrossRef]
- Aucoin, M.G.; McMurray-Beaulieu, V.; Poulin, F.; Boivin, E.B.; Chen, J.; Ardelean, F.M.; Cloutier, M.; Choi, Y.J.; Miguez, C.B.; Jolicoeur, M. Identifying conditions for inducible protein production in E. coli: Combining a fed-batch and multiple induction approach. Microb. Cell Fact. 2006, 5, 27. [Google Scholar] [CrossRef]
- Biener, R.; Steinkämper, A.; Hofmann, J. Calorimetric control for high cell density cultivation of a recombinant Escherichia coli strain. J. Biotechnol. 2010, 146, 45–53. [Google Scholar] [CrossRef]
- Biener, R.; Steinkämper, A.; Horn, T. Calorimetric control of the specific growth rate during fed-batch cultures of Saccharomyces cerevisiae. J. Biotechnol. 2012, 160, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Jensen, W.B.; Kuhlmann, J.; Brush, S.G.; Tyndall, J. Leopold Pfaundler and the origins of the kinetic theory of chemical reactions. Bull. Hist. Chem. 2012, 37, 29–41. [Google Scholar]
- Bernoulli, D. Hydrodynamica, Sive de Viribus et Motibus Fluidorum Commentarii; Johannis Reinholdi Dulseckeri: Strasbourg, France, 1738. [Google Scholar]
- Mikhailov, G.K. Daniel Bernoulli, Hydrodynamica (1738). In Landmark Writings in Western Mathematics 1640–1940; Grattan-Guinness, I., Corry, L., Guicciardini, N., Cooke, R., Crépel, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 131–142. ISBN 9780444508713. [Google Scholar]
- Clapeyron, P.E. Puissance motrice de la chaleur. J. l’École Polytech. 1834, 14, 153–190. [Google Scholar]
- Jensen, W.B. The universal gas constant R. J. Chem. Educ. 2003, 80, 731–732. [Google Scholar] [CrossRef]
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Laidler, K.J. A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC recommendations 1996). Pure Appl. Chem. 1996, 68, 149–192. [Google Scholar] [CrossRef]
- Chalk, S.J. Enthalpy of activation, Δ‡H°. In IUPAC Compendium of Chemical Terminology; Nič, M., Jirát, J., Košata, B., Jenkins, A., McNaught, A., Eds.; IUPAC: Research Triagle Park, NC, USA, 2009; ISBN 0-9678550-9-8. [Google Scholar]
- Johnson, F.H.; Eyring, H.; Stover, B.J. The Theory of Rate Processes in Biology and Medicine; John Wiley & Sons: New York, NY, USA, 1974; ISBN 9780471444855. [Google Scholar]
- Mohr, P.W.; Krawiec, S. Temperature characteristics and Arrhenius plots for nominal psychrophiles, mesophiles and thermophiles. J. Gen. Microbiol. 1980, 121, 311–317. [Google Scholar] [CrossRef]
- Smith, T.P.; Thomas, T.J.H.; Garcia-Carreras, B.; Sal, S.; Yvon-Durocher, G.; Bell, T.; Pawar, S. Metabolic rates of prokaryotic microbes may inevitably rise with global warming. BioRxiv 2019, 524264. [Google Scholar] [CrossRef]
- Ratkowsky, D.A.; Olley, J.; McMeekin, T.A.; Ball, A. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 1982, 149, 1–5. [Google Scholar] [CrossRef]
- Shapiro, R.S.; Cowen, L.E. Thermal Control of Microbial Development and Virulence: Molecular Mechanisms of Microbial Temperature Sensing. MBio 2012, 3, e00238-12. [Google Scholar] [CrossRef]
- Sengupta, P.; Garrity, P. Sensing temperature. Curr. Biol. 2013, 23, R304–R307. [Google Scholar] [CrossRef]
- Pruss, G.J.; Drlica, K. DNA supercoiling and prokaryotic transcription. Cell 1989, 56, 521–523. [Google Scholar] [CrossRef]
- López-García, P.; Forterre, P. DNA topology and the thermal stress response, a tale from mesophiles and hyperthermophiles. BioEssays 2000, 22, 738–746. [Google Scholar] [CrossRef]
- Forterre, P.; Bergerat, A.; Lopez-Garcia, P. The unique DNA topology and DNA topoisomerases of hyperthermophilic archaea. FEMS Microbiol. Rev. 1996, 18, 237–248. [Google Scholar] [CrossRef]
- López-García, P.; Forterre, P. DNA topology in hyperthermophilic archaea: Reference states and their variation with growth phase, growth temperature, and temperature stresses. Mol. Microbiol. 1997, 23, 1267–1279. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Goldberg, M.D.; Olsson, T.; Esposito, D.; Hinton, J.C.D.; Ladbury, J.E. H-NS is a part of a thermally controlled mechanism for bacterial gene regulation. Biochem. J. 2005, 391, 203–213. [Google Scholar] [CrossRef]
- White-Ziegler, C.A.; Davis, T.R. Genome-wide identification of H-NS-controlled, temperature-regulated genes in Escherichia coli K-12. J. Bacteriol. 2009, 191, 1106–1110. [Google Scholar] [CrossRef] [PubMed]
- Schröder, O.; Wagner, R. The bacterial DNA-binding protein H-NS represses ribosomal RNA transcription by trapping RNA polymerase in the initiation complex. J. Mol. Biol. 2000, 298, 737–748. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.; Song, M.; Joon, H.R.; Hong, Y.; Kim, Y.J.; Seok, Y.J.; Ha, K.S.; Jung, S.H.; Choy, H.E. DNA looping-mediated repression by histone-like protein H-NS: Specific requirement of Eσ70 as a cofactor for looping. Genes Dev. 2005, 19, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.J.; Lee, S.Y.; Kenney, L.J.; Yan, J. Nucleoprotein filament formation is the structural basis for bacterial protein H-NS gene silencing. Sci. Rep. 2012, 2, 509. [Google Scholar] [CrossRef]
- Kotlajich, M.V.; Hron, D.R.; Boudreau, B.A.; Sun, Z.; Lyubchenko, Y.L.; Landick, R. Bridged filaments of histone-like nucleoid structuring protein pause RNA polymerase and aid termination in bacteria. Elife 2015, 4, e04970. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Maris, C.; Allain, F.H.T.; Narberhaus, F. Molecular basis for temperature sensing by an RNA thermometer. EMBO J. 2006, 25, 2487–2497. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Murphy, E.R. Temperature-Dependent Regulation of Bacterial Gene Expression by RNA Thermometers. In Nucleic Acids: From Basic Aspects to Laboratory Tools; IntechOpen: London, UK, 2016; pp. 157–181. [Google Scholar]
- Grosso-Becerra, M.V.; Croda-Garcia, G.; Merino, E.; Servin-Gonzalez, L.; Mojica-Espinosa, R.; Soberon-Chavez, G. Regulation of Pseudomonas aeruginosa virulence factors by two novel RNA thermometers. Proc. Natl. Acad. Sci. USA 2014, 111, 15562–15567. [Google Scholar] [CrossRef] [PubMed]
- Waldminghaus, T.; Fippinger, A.; Alfsmann, J.; Narberhaus, F. RNA thermometers are common in α- and γ-proteobacteria. Biol. Chem. 2005, 386, 1279–1286. [Google Scholar] [CrossRef] [PubMed]
- Narberhaus, F.; Waldminghaus, T.; Chowdhury, S. RNA thermometers. FEMS Microbiol. Rev. 2006, 30, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Waldminghaus, T.; Heidrich, N.; Brantl, S.; Narberhaus, F. FourU: A novel type of RNA thermometer in Salmonella. Mol. Microbiol. 2007, 65, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Sen, S.; Apurva, D.; Satija, R.; Siegal, D.; Murray, R.M. Design of a Toolbox of RNA Thermometers. ACS Synth. Biol. 2017, 6, 1461–1470. [Google Scholar] [CrossRef]
- Elsholz, A.K.W.; Michalik, S.; Zühlke, D.; Hecker, M.; Gerth, U. CtsR, the Gram-positive master regulator of protein quality control, feels the heat. EMBO J. 2010, 29, 3621–3629. [Google Scholar] [CrossRef]
- Krell, T.; Lacal, J.; Busch, A.; Silva-Jiménez, H.; Guazzaroni, M.-E.; Ramos, J.L. Bacterial Sensor Kinases: Diversity in the Recognition of Environmental Signals. Annu. Rev. Microbiol. 2010, 64, 539–559. [Google Scholar] [CrossRef]
- Nishiyama, S.I.; Umemura, T.; Nara, T.; Homma, M.; Kawagishi, I. Conversion of a bacterial warm sensor to a cold sensor by methylation of a single residue in the presence of an attractant. Mol. Microbiol. 1999, 32, 357–365. [Google Scholar] [CrossRef]
- Cedervall, T.; Johansson, M.U.; Åkerström, B. Coiled-coil structure of group A streptococcal M proteins. Different temperature stability of class A and C proteins by hydrophobic-nonhydrophobic amino acid substitutions at heptad positions a and d. Biochemistry 1997, 36, 4987–4994. [Google Scholar] [CrossRef] [PubMed]
- Franzmann, T.M.; Menhorn, P.; Walter, S.; Buchner, J. Activation of the Chaperone Hsp26 Is Controlled by the Rearrangement of Its Thermosensor Domain. Mol. Cell 2008, 29, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Haslbeck, M.; Walke, S.; Stromer, T.; Ehrnsperger, M.; White, H.E.; Chen, S.; Saibil, H.R.; Buchner, J. Hsp26: A temperature-regulated chaperone. EMBO J. 1999, 18, 6744–6751. [Google Scholar] [CrossRef] [PubMed]
- Seel, W.; Derichs, J.; Lipski, A. Increased biomass production by mesophilic food-associated bacteria through lowering the growth temperature from 30 °C to 10 °C. Appl. Environ. Microbiol. 2016, 82, 3754–3764. [Google Scholar] [CrossRef] [PubMed]
- Huey, R.B.; Stevenson, R.D. Integrating Thermal Physiology and Ecology of Ectothenns: A Discussion of Approaches Department. Am. Zool. 1979, 19, 357–366. [Google Scholar] [CrossRef]
- Bennett, A.F.; Lenski, R.E. Evolutionary Adaptation to Temperature II. Thermal Niches of Experimental Lines of Escherichia coli. Evolution 1993, 47, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Travisano, M.; Lenski, R.E. Long-term experimental evolution in Escherichia coli. IV. Targets of selection and the specificity of adaptation. Genetics 1996, 143, 15–26. [Google Scholar]
- Cullum, A.J.; Bennett, A.F.; Lenski, R.E. Evolutionary adaptation to temperature. IX. Preadaptation to novel stressful environments of Escherichia coli adapted to high temperature. Evolution 2001, 55, 2194–2202. [Google Scholar] [CrossRef]
- Takai, K.; Nakamura, K.; Toki, T.; Tsunogai, U.; Miyazaki, M.; Miyazaki, J.; Hirayama, H.; Nakagawa, S.; Nunoura, T.; Horikoshi, K. Cell proliferation at 122 °C and isotopically heavy CH4 production by a hyperthermophilic methanogen under high-pressure cultivation. Proc. Natl. Acad. Sci. USA 2008, 105, 10949–10954. [Google Scholar] [CrossRef]
- Corkrey, R.; McMeekin, T.A.; Bowman, J.P.; Ratkowsky, D.A.; Olley, J.; Ross, T. Protein thermodynamics can be predicted directly from biological growth rates. PLoS ONE 2014, 9, e96100. [Google Scholar] [CrossRef][Green Version]
- Ratkowsky, D.A.; Lowry, R.K.; McMeekin, T.A.; Stokes, A.N.; Chandler, R.E. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 1983, 154, 1222–1226. [Google Scholar] [CrossRef] [PubMed]
- Johnson, F.H.; Lewin, I. The growth rate of E. coli in relation to temperature, quinine and coenzyme. J. Cell. Comp. Physiol. 1946, 28, 47–75. [Google Scholar] [CrossRef] [PubMed]
- Grimaud, G.M.; Mairet, F.; Sciandra, A.; Bernard, O. Modeling the temperature effect on the specific growth rate of phytoplankton: A review. Rev. Environ. Sci. Biotechnol. 2017, 16, 625–645. [Google Scholar] [CrossRef]
- Hinshelwood, C.N. Influence of temperature on the growth of bacteria. In The Chemical Kinetics of the Bacterial Cell; Clarendon Press: Oxford, UK, 1946; pp. 254–257. [Google Scholar]
- Sharpe, P.J.H.; Curry, G.L.; DeMichele, D.W.; Cole, C.L. Distribution model of organism development times. J. Theor. Biol. 1977, 66, 21–38. [Google Scholar] [CrossRef]
- Sharpe, P.J.H.; DeMichele, D.W. Reaction kinetics of poikilotherm development. J. Theor. Biol. 1977, 64, 649–670. [Google Scholar] [CrossRef]
- Eyring, H.; Stearn, A.E. The application of the theory of absolute reaction rates to proteins. Chem. Rev. 1939, 24, 253–270. [Google Scholar] [CrossRef]
- Hultin, E. The influence of temperature on the rate of enzymic processes. Acta Chem. Scand. 1955, 9, 1700–1710. [Google Scholar] [CrossRef]
- Lamanna, C.; Mallette, M.F.; Zimmermann, L.N. Basic Bacteriology, 4th ed.; Williams & Wilkins: Baltimore, MD, USA, 1973. [Google Scholar]
- Schoolfield, R.M.; Sharpe, P.J.H.; Magnuson, C.E. Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J. Theor. Biol. 1981, 88, 719–731. [Google Scholar] [CrossRef]
- Roels, J. Energetics and Kinetics in Biotechnology; Elsevier Biomedical Press: Amsterdam, The Netherlands, 1983; ISBN 0444804420. [Google Scholar]
- Davey, K.R. A predictive model for combined temperature and water activity on microbial growth during the growth phase. J. Appl. Bacteriol. 1989, 67, 483–488. [Google Scholar] [CrossRef]
- Davey, K.R. Modelling the combined effect of temperature and pH on the rate coefficient for bacterial growth. Int. J. Food Microbiol. 1994, 23, 295–303. [Google Scholar] [CrossRef]
- Davey, K.R. Applicability of the Davey (linear Arrhenius) predictive model to the lag phase of microbial growth. J. Appl. Bacteriol. 1991, 70, 253–257. [Google Scholar] [CrossRef]
- Lobry, J.R.; Rosso, L.; Flandrois, J.-P. A FORTRAN Subroutine for the Determination of Parameter Confidence Limits in non-linear models. Binary 1991, 3, 86–93. [Google Scholar]
- Rosso, L.; Lobry, J.R.; Flandrois, J.P. An Unexpected Correlation between Cardinal Temperatures of Microbial Growth Highlighted by a New Model. J. Theor. Biol. 1993, 162, 447–463. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, G.F.; Guarini, J.M.; Richard, P.; Gros, P.; Mornet, F. Quantifying the short-term temperature effect on light- saturated photosynthesis of intertidal microphytobenthos. Mar. Ecol. Prog. Ser. 1996, 134, 309–313. [Google Scholar] [CrossRef]
- Eppley, R.W. Temperature and phytoplankton growth in the sea. Fish Bull. 1972, 70, 1063–1085. [Google Scholar]
- Norberg, J. Biodiversity and ecosystem functioning: A complex adaptive systems approach. Limnol. Oceanogr. 2004, 49, 1269–1277. [Google Scholar] [CrossRef]
- Brandts, J.F. Heat effects on proteins and enzymes. In Thermobiology; Academic Press: London, UK, 1967; pp. 25–72. [Google Scholar]
- Ratkowsky, D.A.; Olley, J.; Ross, T. Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 2005, 233, 351–362. [Google Scholar] [CrossRef]
- Privalov, P.L.; Khechinashvili, N.N. A thermodynamic approach to the problem of stabilization of globular protein structure: A calorimetric study. J. Mol. Biol. 1974, 86, 665–684. [Google Scholar] [CrossRef]
- Murphy, K.P.; Privalov, P.L.; Gill, S.J. Common features of protein unfolding and dissolution of hydrophobic compounds. Science 1990, 247, 559–561. [Google Scholar] [CrossRef]
- Murphy, K.P.; Gill, S.J. Solid model compounds and the thermodynamics of protein unfolding. J. Mol. Biol. 1991, 222, 699–709. [Google Scholar] [CrossRef]
- Robertson, A.D.; Murphy, K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997, 97, 1251–1267. [Google Scholar] [CrossRef]
- Baldwin, R.L. Temperature dependence of the hydrophobic interaction in protein folding. Proc. Natl. Acad. Sci. USA 1986, 83, 8069–8072. [Google Scholar] [CrossRef]
- Ross, T. Assessment of a theoretical model for the effects of temperature on bacterial growth rate. In Proceedings of the Refrigeration Science and Technology Proceedings, Quimper, France, 16–18 June 1997; pp. 64–71. [Google Scholar]
- Ross, T. A Philosophy for the Development of Kinetic Models in Predictive Microbiology. Ph.D. Thesis, University of Tasmania, Hobart, Australia, 1993. [Google Scholar]
- Zeldovich, K.B.; Chen, P.; Shakhnovich, E.I. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc. Natl. Acad. Sci. USA 2007, 104, 16152–16157. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, K.; De Graff, A.M.R.; Sawle, L.; Dill, K.A. Role of Proteome Physical Chemistry in Cell Behavior. J. Phys. Chem. B 2016, 120, 9549–9563. [Google Scholar] [CrossRef] [PubMed]
- Sawle, L.; Ghosh, K. How do thermophilic proteins and proteomes withstand high temperature? Biophys. J. 2011, 101, 217–227. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, K.; Dill, K.A. Computing protein stabilities from their chain lengths. Proc. Natl. Acad. Sci. USA 2009, 106, 10649–10654. [Google Scholar] [CrossRef] [PubMed]
- Daniel, R.M.; Danson, M.J. A new understanding of how temperature affects the catalytic activity of enzymes. Trends Biochem. Sci. 2010, 35, 584–591. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Energy budgets can explain body size relations. J. Theor. Biol. 1986, 121, 269–282. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Dynamic Energy Budget theory for metabolic organisation: Summary of concepts of the third edition. Water 2010, 365, 68. [Google Scholar]
- Kooijman, S.A.L.M. Dynamic Energy Budgets in Biological Systems: Theory and Applications in Ecotoxicology; Cambridge University Press: Cambridge, UK, 1993; ISBN 0-521-45223-6. [Google Scholar]
- Huang, L.; Hwang, A.; Phillips, J. Effect of Temperature on Microbial Growth Rate-Mathematical Analysis: The Arrhenius and Eyring-Polanyi Connections. J. Food Sci. 2011, 76, 553–560. [Google Scholar] [CrossRef]
- Hobbs, J.K.; Jiao, W.; Easter, A.D.; Parker, E.J.; Schipper, L.A.; Arcus, V.L. Change in heat capacity for enzyme catalysis determines temperature dependence of enzyme catalyzed rates. ACS Chem. Biol. 2013, 8, 2388–2393. [Google Scholar] [CrossRef] [PubMed]
- Schipper, L.A.; Hobbs, J.K.; Rutledge, S.; Arcus, V.L. Thermodynamic theory explains the temperature optima of soil microbial processes and high Q10 values at low temperatures. Glob. Chang. Biol. 2014, 20, 3578–3586. [Google Scholar] [CrossRef] [PubMed]
- DeLong, J.P.; Gibert, J.P.; Luhring, T.M.; Bachman, G.; Reed, B.; Neyer, A.; Montooth, K.L. The combined effects of reactant kinetics and enzyme stability explain the temperature dependence of metabolic rates. Ecol. Evol. 2017, 7, 3940–3950. [Google Scholar] [CrossRef] [PubMed]
- Lehman, J.T.; Botkin, D.B.; Likens, G.E. The assumptions and rationales of a computer model of phytoplankton population dynamics. Limnol. Oceanogr. 1975, 20, 343–364. [Google Scholar] [CrossRef]
- Moisan, J.R.; Moisan, T.A.; Abbott, M.R. Modelling the effect of temperature on the maximum growth rates of phytoplankton populations. Ecol. Model. 2002, 153, 197–215. [Google Scholar] [CrossRef]
- Bitaubé Pérez, E.; Caro Pina, I.; Pérez Rodríguez, L. Kinetic model for growth of Phaeodactylum tricornutum in intensive culture photobioreactor. Biochem. Eng. J. 2008, 40, 520–525. [Google Scholar] [CrossRef]
- Alexandrov, G.A.; Yamagata, Y. A peaked function for modeling temperature dependence of plant productivity. Ecol. Model. 2007, 200, 189–192. [Google Scholar] [CrossRef]
- Quinn, J.; de Winter, L.; Bradley, T. Microalgae bulk growth model with application to industrial scale systems. Bioresour. Technol. 2011, 102, 5083–5092. [Google Scholar] [CrossRef]
- Tevatia, R.; Demirel, Y.; Rudrappa, D.; Blum, P. Effects of thermodynamically coupled reaction diffusion in microalgae growth and lipid accumulation: Model development and stability analysis. Comput. Chem. Eng. 2015, 75, 28–39. [Google Scholar] [CrossRef]
- Mukhtar, H.; Lin, Y.-P.; Lin, C.-M.; Petway, J.R. Assessing thermodynamic parameter sensitivity for simulating temperature responses of soil nitrification. Environ. Sci. Process. Impacts 2019, 21, 1596–1608. [Google Scholar] [CrossRef]
- Schipper, L.A.; Robertson, W.D.; Gold, A.J.; Jaynes, D.B.; Cameron, S.C. Denitrifying bioreactors-An approach for reducing nitrate loads to receiving waters. Ecol. Eng. 2010, 36, 1532–1543. [Google Scholar] [CrossRef]
- Nordström, A.; Herbert, R.B. Identification of the temporal control on nitrate removal rate variability in a denitrifying woodchip bioreactor. Ecol. Eng. 2019, 127, 88–95. [Google Scholar] [CrossRef]
- Feller, G.; Gerday, C. Psychrophilic enzymes: Hot topics in cold adaptation. Nat. Rev. Microbiol. 2003, 1, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Feller, G. Life at low temperatures: Is disorder the driving force? Extremophiles 2007, 11, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Jaouen, T.; Dé, E.; Chevalier, S.; Orange, N. Pore size dependence on growth temperature is a common characteristic of the major outer membrane protein OprF in psychrotrophic and mesophilic Pseudomonas species. Appl. Environ. Microbiol. 2004, 70, 6665–6669. [Google Scholar] [CrossRef] [PubMed]
- D’Amico, S.; Collins, T.; Marx, J.C.; Feller, G.; Gerday, C. Psychrophilic microorganisms: Challenges for life. EMBO Rep. 2006, 7, 385–389. [Google Scholar] [CrossRef]
- Margesin, R.; Fonteyne, P.A.; Redl, B. Low-temperature biodegradation of high amounts of phenol by Rhodococcus spp. and basidiomycetous yeasts. Res. Microbiol. 2005, 156, 68–75. [Google Scholar] [CrossRef]
- Corkrey, R.; Olley, J.; Ratkowsky, D.; McMeekin, T.; Ross, T. Universality of thermodynamic constants governing biological growth rates. PLoS ONE 2012, 7, e32003. [Google Scholar] [CrossRef]
- Hannig, G.; Makrides, S.C. Strategies for optimizing heterologous protein expression in Escherichia coli. Stud. Health Technol. Inform. 1998, 16, 54–60. [Google Scholar] [CrossRef]
- Gombert, A.K.; Kilikian, B.V. Recombinant gene expression in Escherichia coli cultivation using lactose as inducer. J. Biotechnol. 1998, 60, 47–54. [Google Scholar] [CrossRef]
- Schmidt, M.; Babu, K.R.; Khanna, N.; Marten, S.; Rinas, U. Temperature-induced production of recombinant human insulin in high-cell density cultures of recombinant Escherichia coli. J. Biotechnol. 1999, 68, 71–83. [Google Scholar] [CrossRef]
- Nalley, J.O.; O’Donnell, D.R.; Litchman, E. Temperature effects on growth rates and fatty acid content in freshwater algae and cyanobacteria. Algal Res. 2018, 35, 500–507. [Google Scholar] [CrossRef]
- Jacquet, P.; Daudé, D.; Bzdrenga, J.; Masson, P.; Elias, M.; Chabrière, E. Current and emerging strategies for organophosphate decontamination: Special focus on hyperstable enzymes. Environ. Sci. Pollut. Res. 2016, 23, 8200–8218. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.K. Organophosphorus-degrading bacteria: Ecology and industrial applications. Nat. Rev. Microbiol. 2009, 7, 156–164. [Google Scholar] [CrossRef] [PubMed]
- Horne, I.; Qiu, X.; Russell, R.J.; Oakeshott, J.G. The phosphotriesterase gene opdA in Agrobacterium radiobacter P230 is transposable. FEMS Microbiol. Lett. 2003, 222, 1–8. [Google Scholar] [CrossRef]
- Zellner, M.; Winkler, W.; Hayden, H.; Diestinger, M.; Eliasen, M.; Gesslbauer, B.; Miller, I.; Chang, M.; Kungl, A.; Roth, E.; et al. Quantitative validation of different protein precipitation methods in proteome analysis of blood platelets. Electrophoresis 2005, 26, 2481–2489. [Google Scholar] [CrossRef]
- Cimini, D.; Restaino, O.F.; Catapano, A.; De Rosa, M.; Schiraldi, C. Production of capsular polysaccharide from Escherichia coli K4 for biotechnological applications. Appl. Microbiol. Biotechnol. 2010, 85, 1779–1787. [Google Scholar] [CrossRef]
- McAlindon, T.E.; LaValley, M.P.; Gulin, J.P.; Felson, D.T. Glucosamine and chondroitin for treatment of osteoarthritis: A systematic quality assessment and meta-analysis. JAMA 2000, 283, 1469–1475. [Google Scholar] [CrossRef]
- Whitfield, C.; Roberts, I.S. Structure, assembly and regulation of expression of capsules in Escherichia coli. Mol. Microbiol. 1999, 31, 1307–1319. [Google Scholar] [CrossRef]
- Restaino, O.F.; Marseglia, M.; Diana, P.; Borzacchiello, M.G.; Finamore, R.; Vitiello, M.; D’Agostino, A.; De Rosa, M.; Schiraldi, C. Advances in the 16α-hydroxy transformation of hydrocortisone by Streptomyces roseochromogenes. Process Biochem. 2016, 51, 1–8. [Google Scholar] [CrossRef]
- Restaino, O.F.; Bhaskar, U.; Paul, P.; Li, L.; De Rosa, M.; Dordick, J.S.; Linhardt, R.J. High cell density cultivation of a recombinant E. coli strain expressing a key enzyme in bioengineered heparin production. Appl. Microbiol. Biotechnol. 2013, 97, 3893–3900. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, F.L.; Liu, Y.; Kiesel, B.; Maskow, T. An enhanced bioindicator for calorimetric monitoring of prophage-activating chemicals in the trace concentration range. Eng. Life Sci. 2018, 18, 475–483. [Google Scholar] [CrossRef]
- Schubert, T.; Breuer, U.; Harms, H.; Maskow, T. Calorimetric bioprocess monitoring by small modifications to a standard bench-scale bioreactor. J. Biotechnol. 2007, 130, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Bakermans, C.; Nealson, K.H. Relationship of Critical Temperature to Macromolecular Synthesis and Growth Yield in Psychrobacter cryopegella. J. Bacteriol. 2004, 186, 2340–2345. [Google Scholar] [CrossRef] [PubMed]
| Model | Equation | Source |
|---|---|---|
| Lehman et al. | [99] | |
| Moison et al. | [100] | |
| Bitaube Pérez et al. | [101] | |
| Alexandrov et al. | [102,103] | |
| Tevatia et al. | [104] |
| Purpose | Process | Biological Basis | Applied Model/Temperature Adjustment | Outcome | Source |
|---|---|---|---|---|---|
| Control | Rec. protein production | Lower protein production rates | Downshift in T | Correctly folded proteins | [114,116,126] |
| Control | Rec. protein production | Thermo-inducible promotor | Upshift in T | Induced promoter | [12] |
| Monitoring | Antibiotic biosynthesis | Metabolic heat metabolic state | Calorimetry | Estimation of metabolic activity | [5] |
| Monitoring and control | Insecticidal crystal proteins production | Metabolic heat metabolic state | Calorimetry | Estimation of metabolic state, control of nutrient feed | [6] |
| Control | Biomass production | Metabolic heat metabolic state | Calorimetry | Calorimetric control of nutrient feed | [13,14] |
| Monitoring | Evaluating prophage activating chemicals | Metabolic heat difference activity state of prophage | Calorimetry | Detection of prophage activation + release | [127] |
| Optimization | Denitrification of wastewaters | Reducing microbial consortia | Eyring model (Equation (7)) | Derive (shifts of) Topt for NO3− removal rate | [106,107] |
| Control | Biomass production | Arguably more stable RNA + correctly folded protein + lower degradation rates at low T | Downshift in T, ~Assumptions of Corkrey’s model (see 3.17) | Increased biomass yield, improved nutrient assimilation | [52,129] |
| Control | Fatty acid production for biofuel | Shorter und more unsaturated fatty acids at low T ~modulate membrane fluidity | Norberg model (Equation (31)) | Temperature-specific fatty acid production (profile) | [117] |
| Optimization | Downstream processing | Thermostable extremozyme | RSM/Thermo precipitation | Purified phosphotriesterase-like lactonases | [11] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noll, P.; Lilge, L.; Hausmann, R.; Henkel, M. Modeling and Exploiting Microbial Temperature Response. Processes 2020, 8, 121. https://doi.org/10.3390/pr8010121
Noll P, Lilge L, Hausmann R, Henkel M. Modeling and Exploiting Microbial Temperature Response. Processes. 2020; 8(1):121. https://doi.org/10.3390/pr8010121
Chicago/Turabian StyleNoll, Philipp, Lars Lilge, Rudolf Hausmann, and Marius Henkel. 2020. "Modeling and Exploiting Microbial Temperature Response" Processes 8, no. 1: 121. https://doi.org/10.3390/pr8010121
APA StyleNoll, P., Lilge, L., Hausmann, R., & Henkel, M. (2020). Modeling and Exploiting Microbial Temperature Response. Processes, 8(1), 121. https://doi.org/10.3390/pr8010121





