Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation
Abstract
:1. Introduction
- (a)
- The large parameter tuning burden of conventional NAC can be efficiently resolved via MSSA, which can efficiently and effectively seek the optimal controller and observer parameters with a high stability;
- (b)
- Various modelling uncertainties can be effectively estimated by HGPO in the real-time, which is then fully compensated by the controller online, such that great robustness can be realized;
- (c)
- A dSpace based hardware experiment was undertaken which validates the implementation feasibility of ONAC.
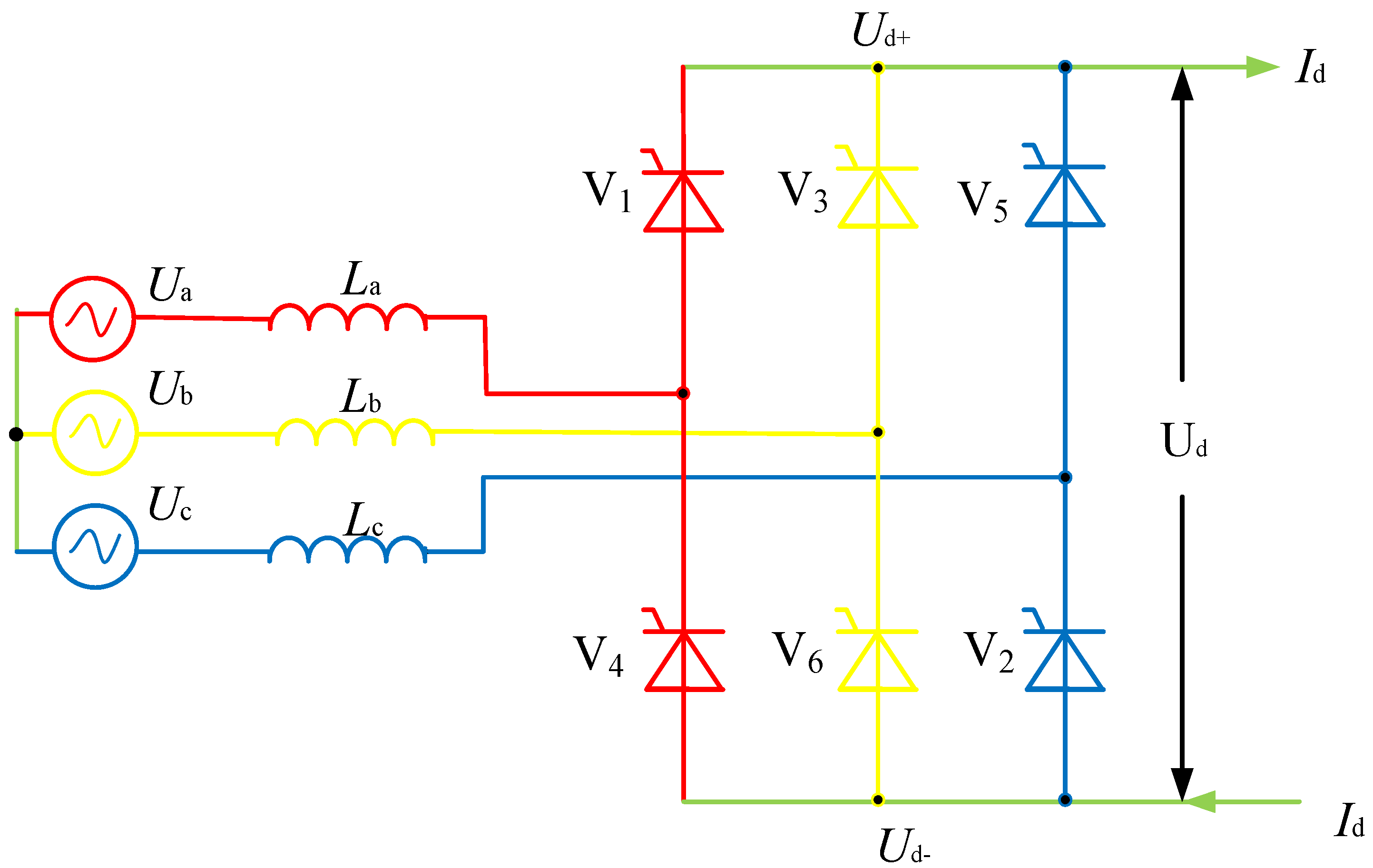
2. VSC Modelling
3. Optimal Nonlinear Adaptive Control
3.1. Nonlinear Adaptive Control
- A.1
- The selection of b0 needs to satisfy certain constraint: , where θ is a positive constant.
- A.2
- The function and are locally Lipschitz in their arguments with a bounded domain of interest, with (0,0,0) = 0 and (0,0,0) = 0.
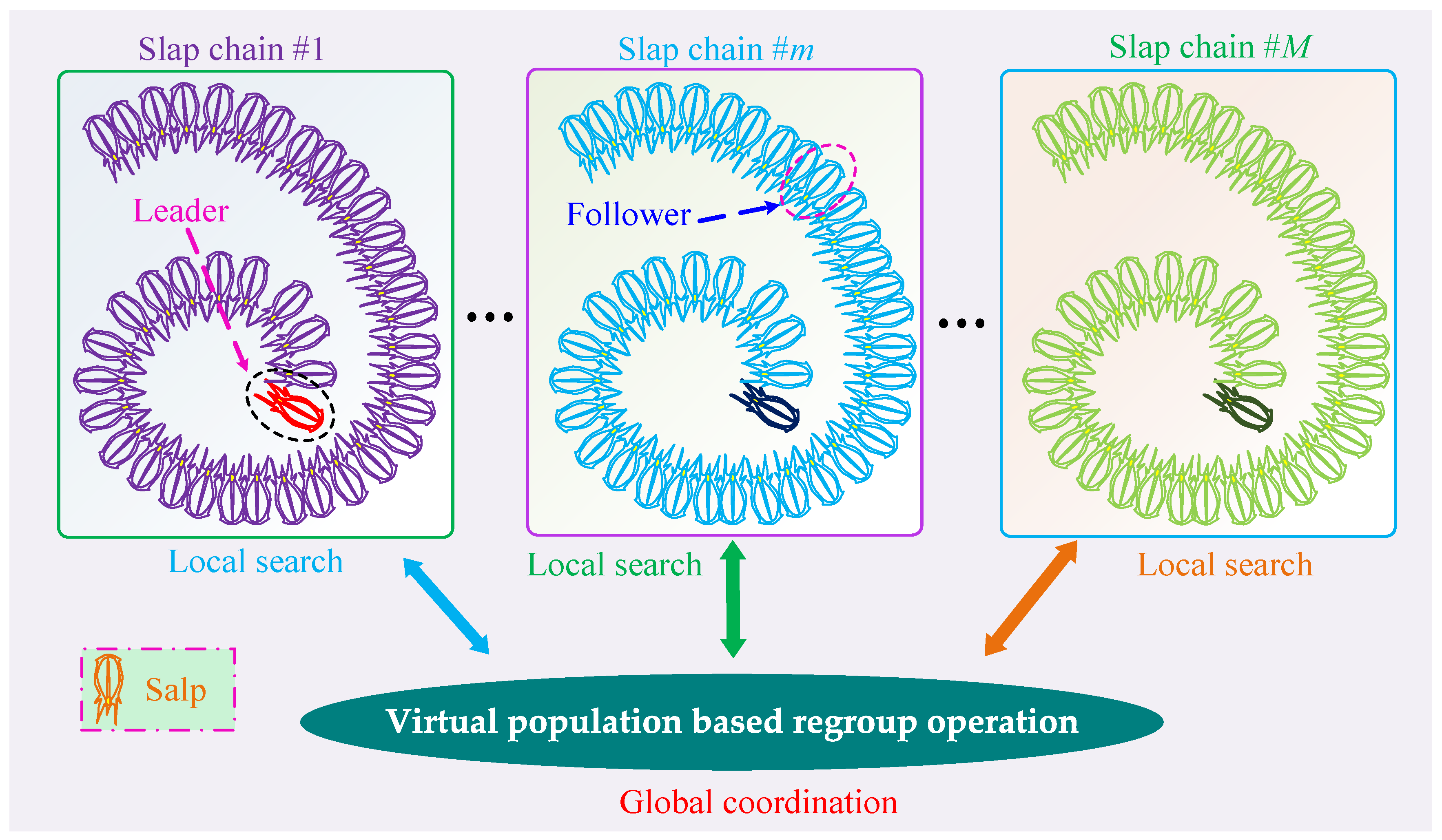
3.2. Memetic Salp Swarm Algorithm
3.2.1. Optimization Framework
- Local search in each chain: Several various salp chains are connected in parallel to constitute MSSA, in which a single salp chain consists of a host of salps. At each iteration, on the basis of foraging behavior of SSA, all the salp chains will undertake a local search while this process is independently carried out in each salp chain.
- Global coordination in virtual population: The whole species group of MSSA can merely be considered as a large number of memes, in which each meme is deemed as a unit of cultural evolution [23]. In particular, positive strategy is adopted in the selection of memes to enhance the communication ability among the salps in MSSA (memetic salp swarm algorithm). Besides, each individual can keep its own physical characteristics stable during the process of global coordination. Therefore, the salps gather together can be considered as a virtual population, where all individuals need to rearrange into many new salp chains, thus various salp chains can achieve a global coordination.
3.2.2. Local Search in Each Chain
3.2.3. Global Coordination in Virtual Population
3.2.4. Optimization Procedure of MSSA
4. ONAC Design for VSC Based Rectifier and Inverter
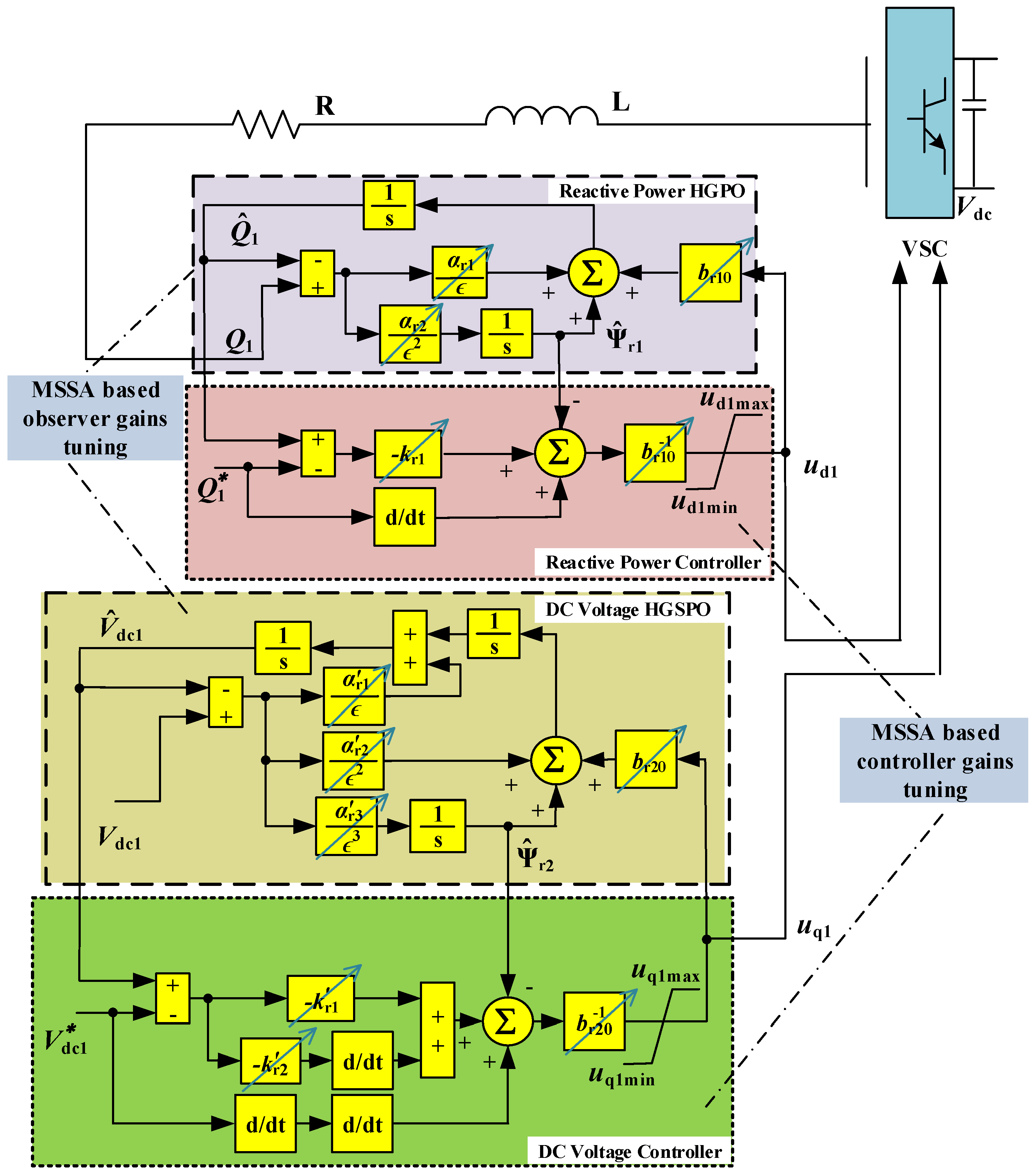
4.1. Rectifier Controller Design
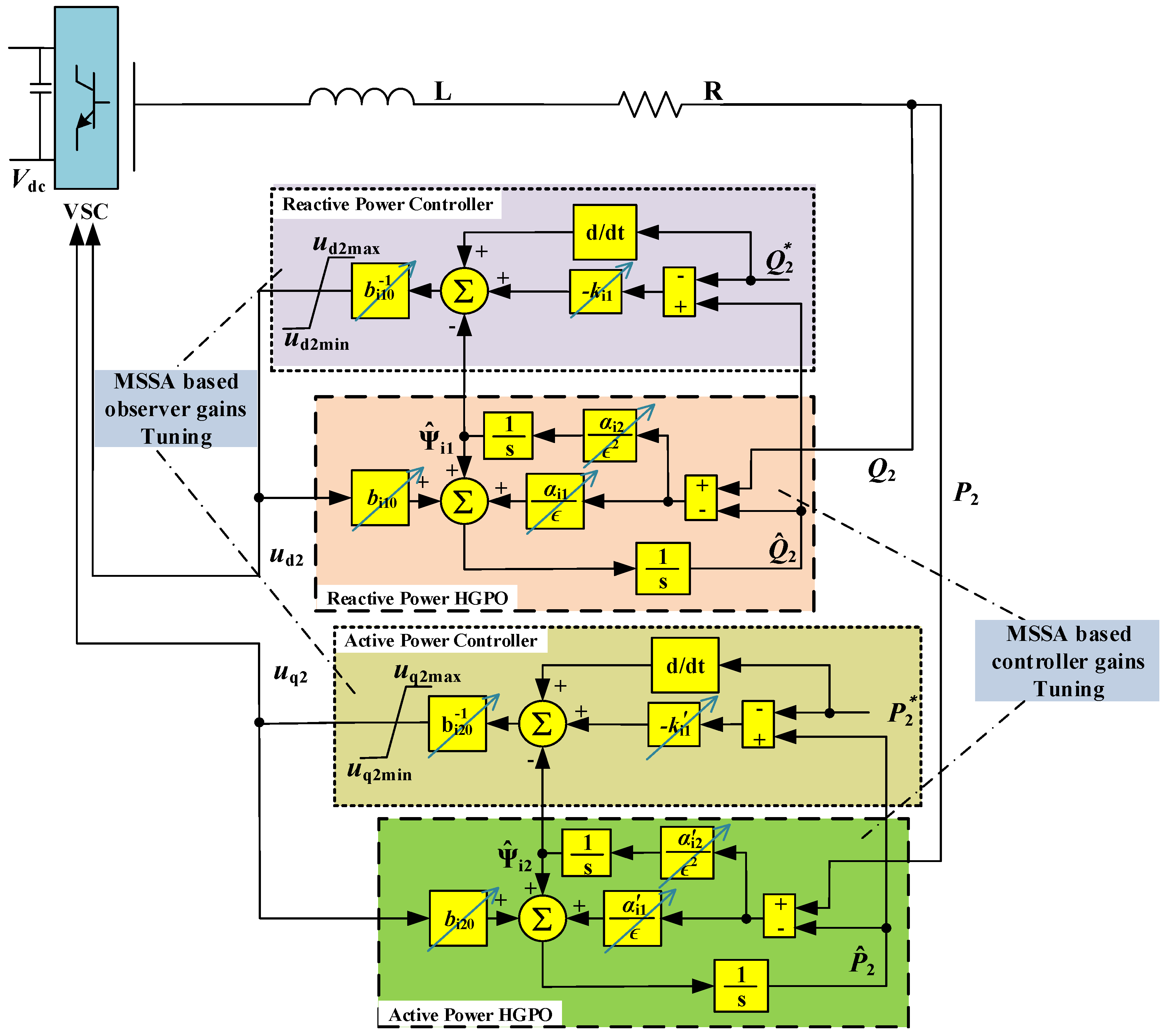
4.2. Inverter Controller Design
4.3. Optimal Control Parameter Tuning
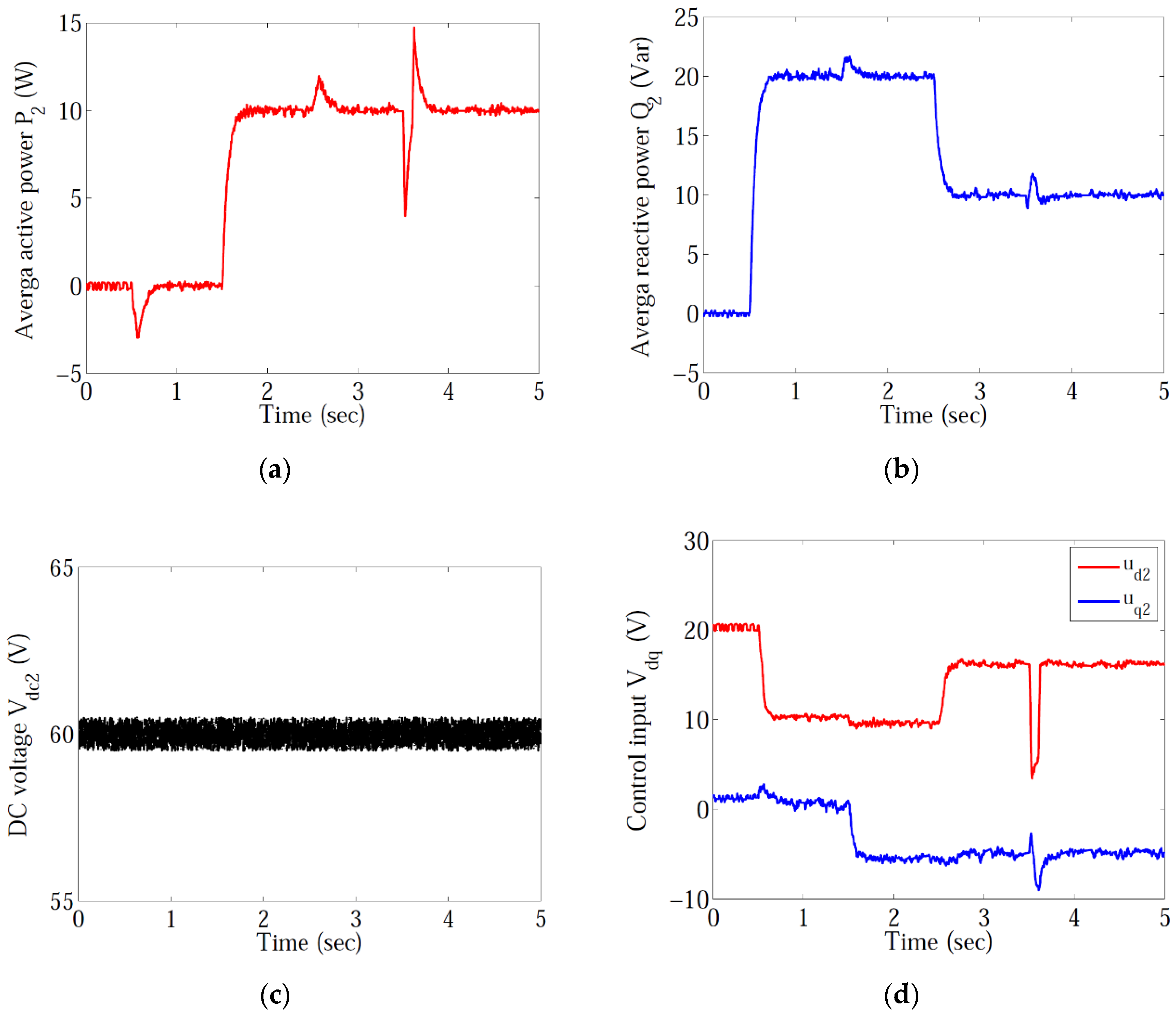
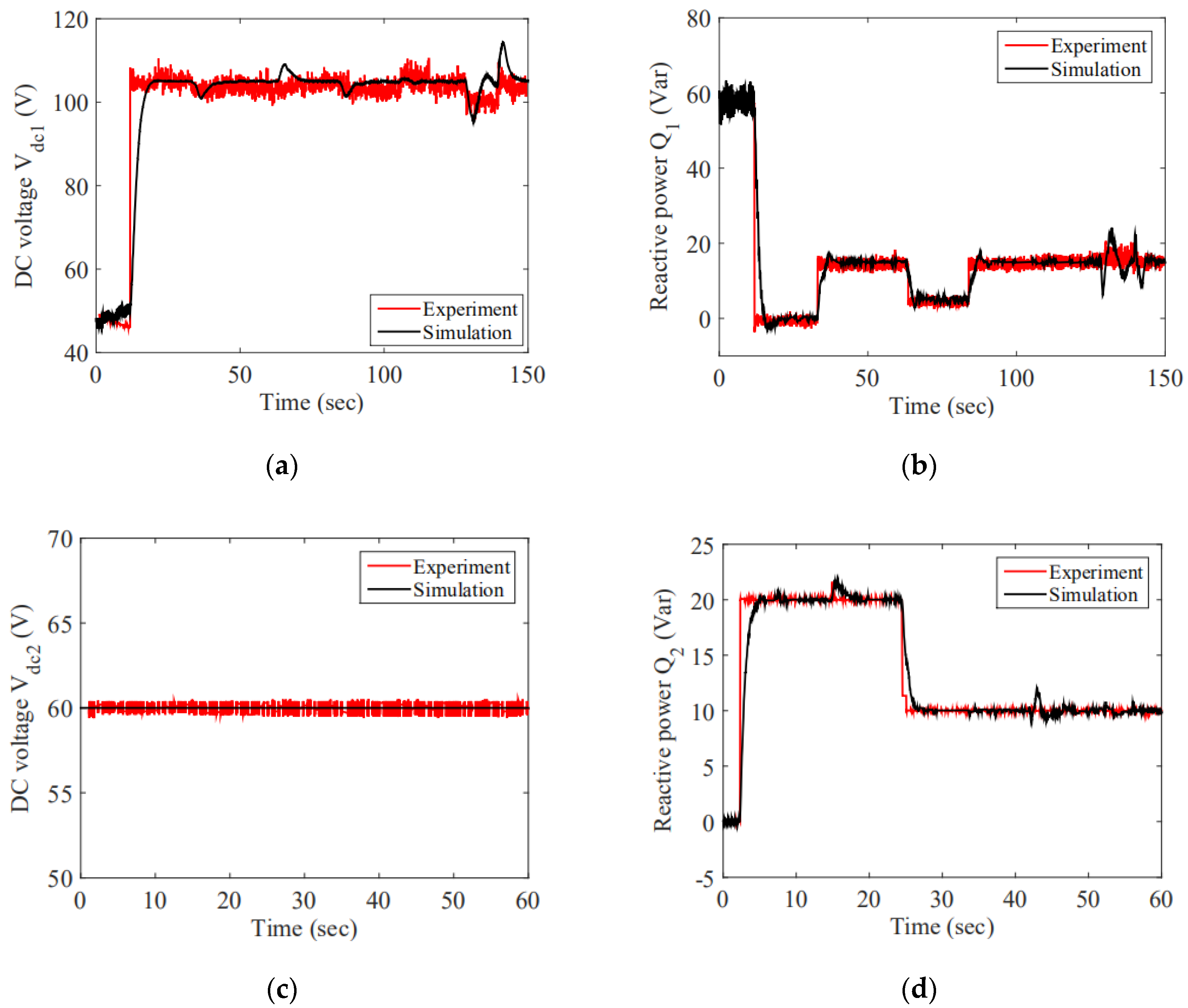
5. Experiment Results
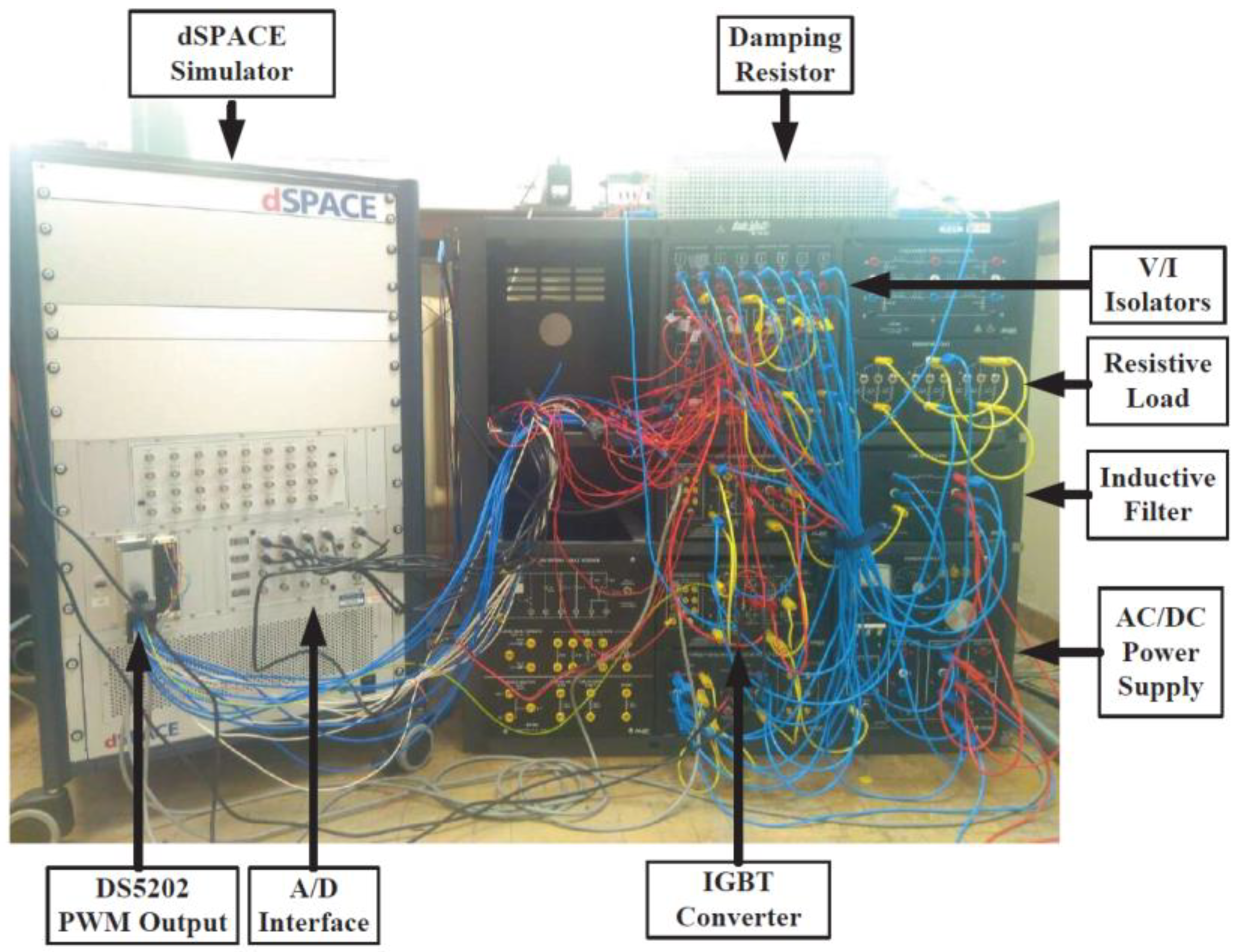
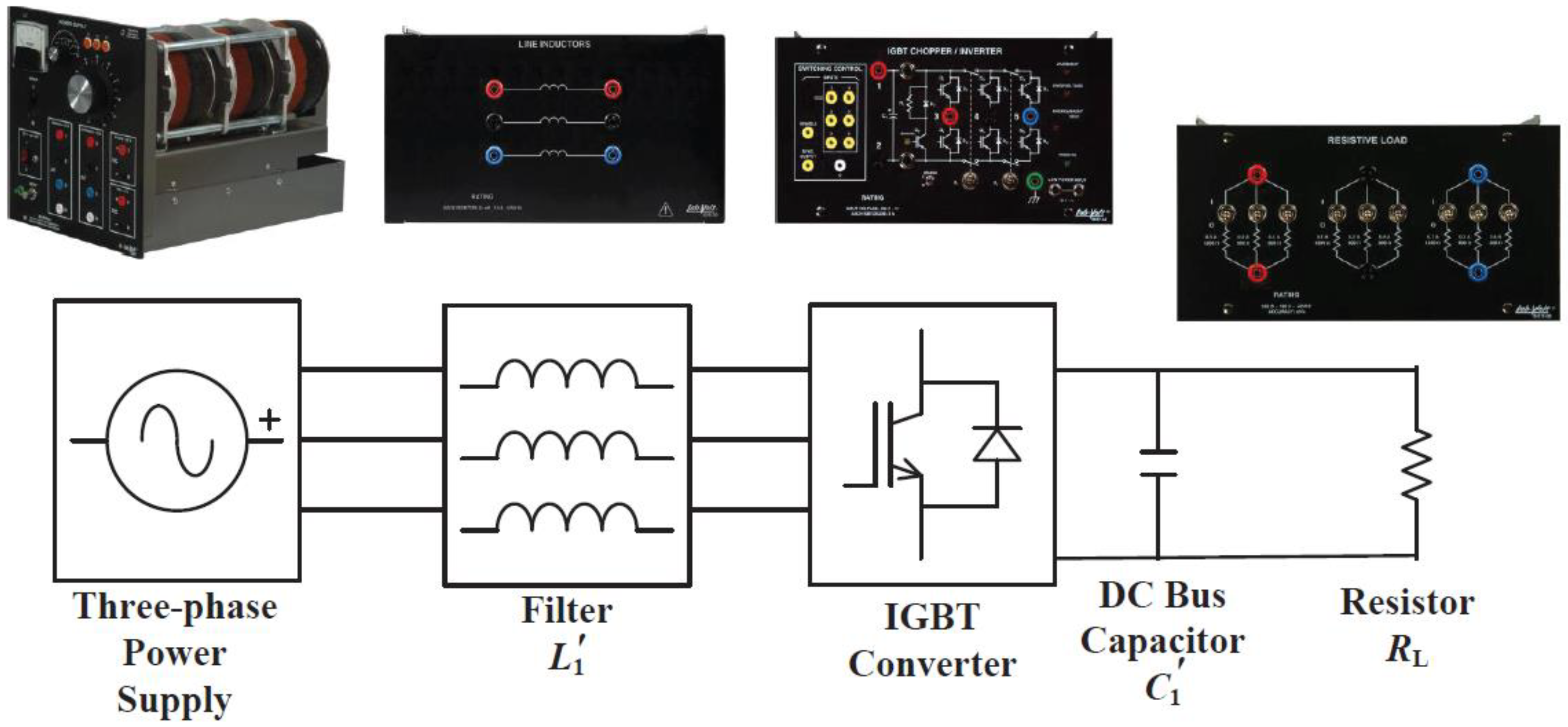
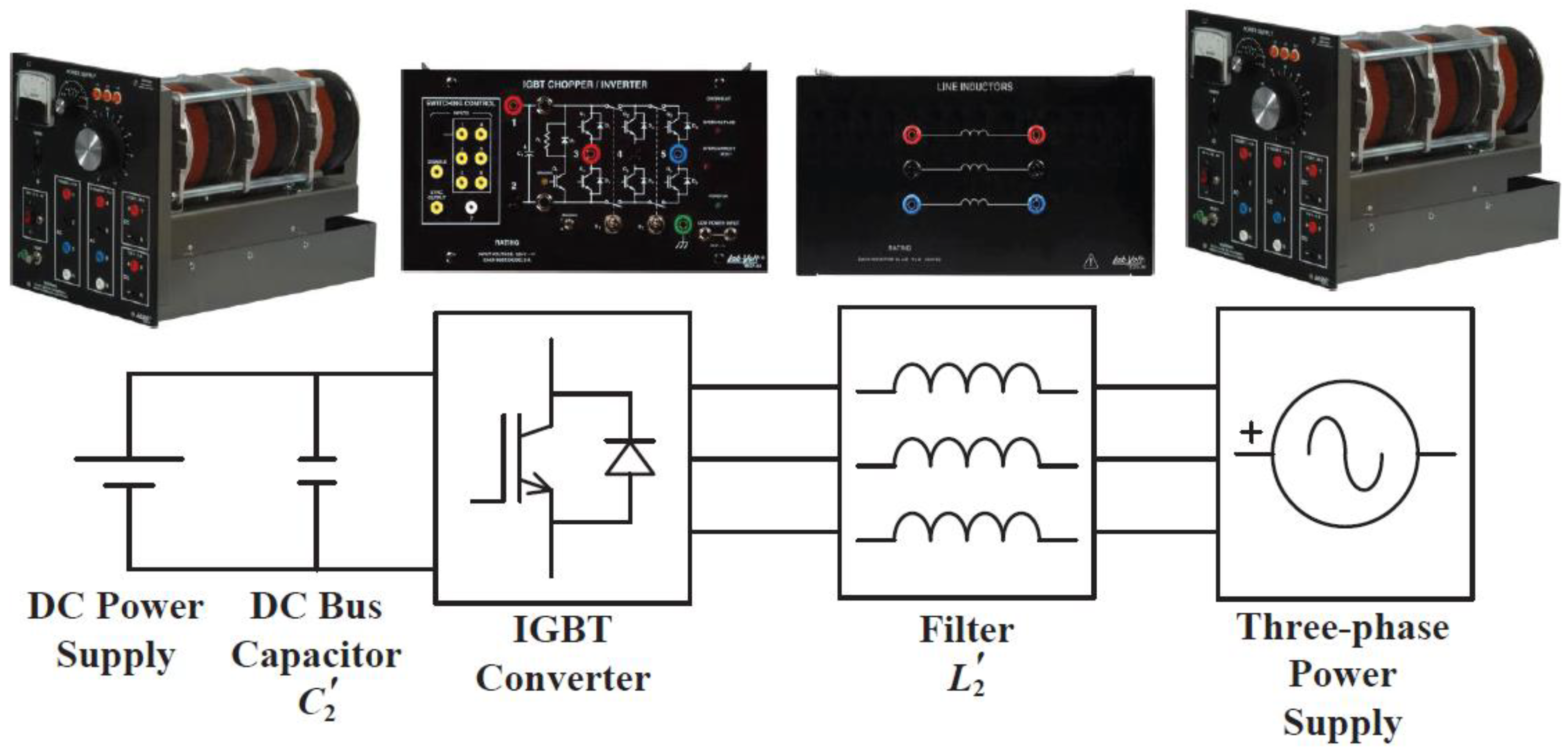
5.1. Experimental Platform
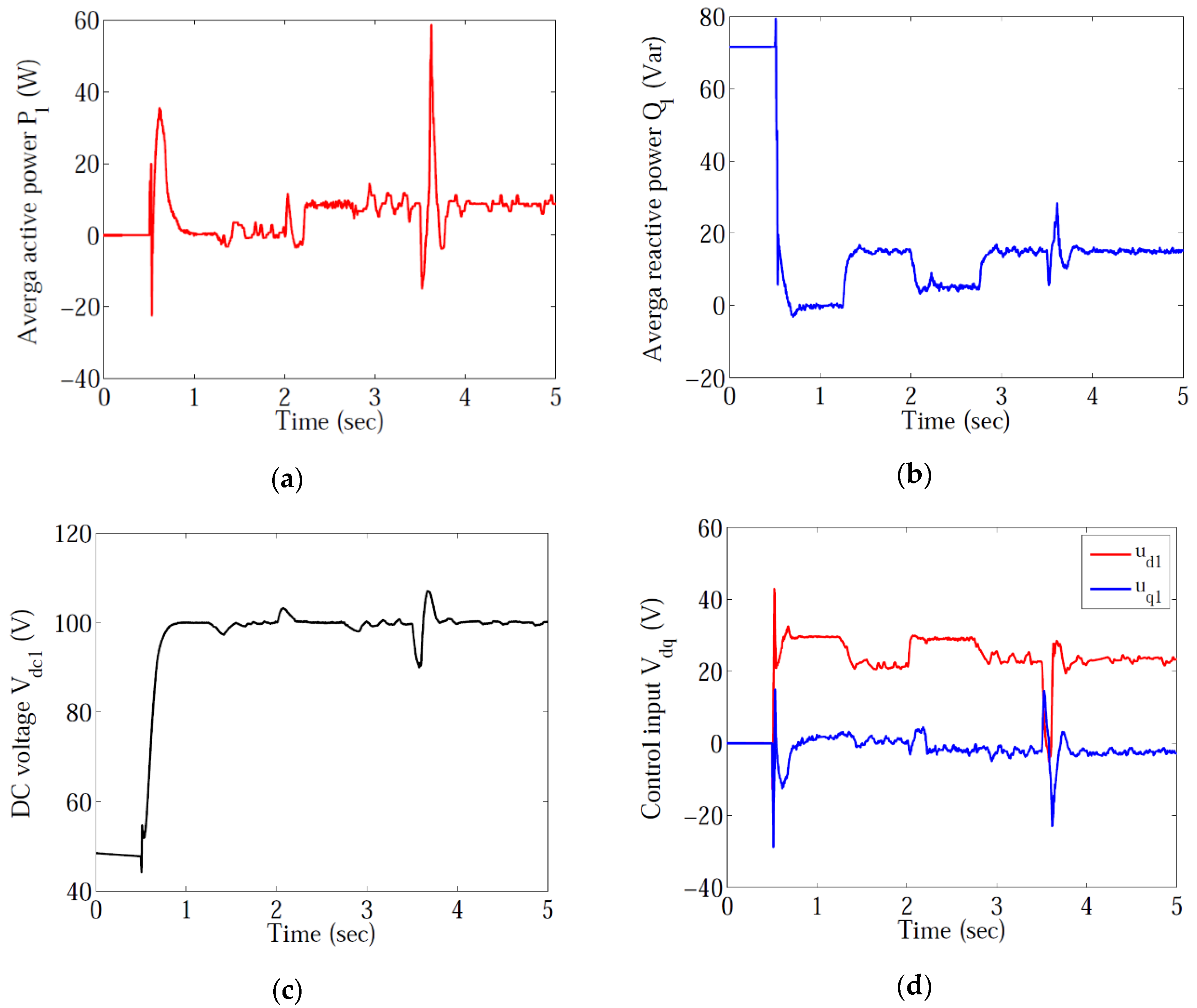
5.2. Rectifier Controller Experiment
5.3. Inverter Controller Experiment
5.4. Set point Tracking
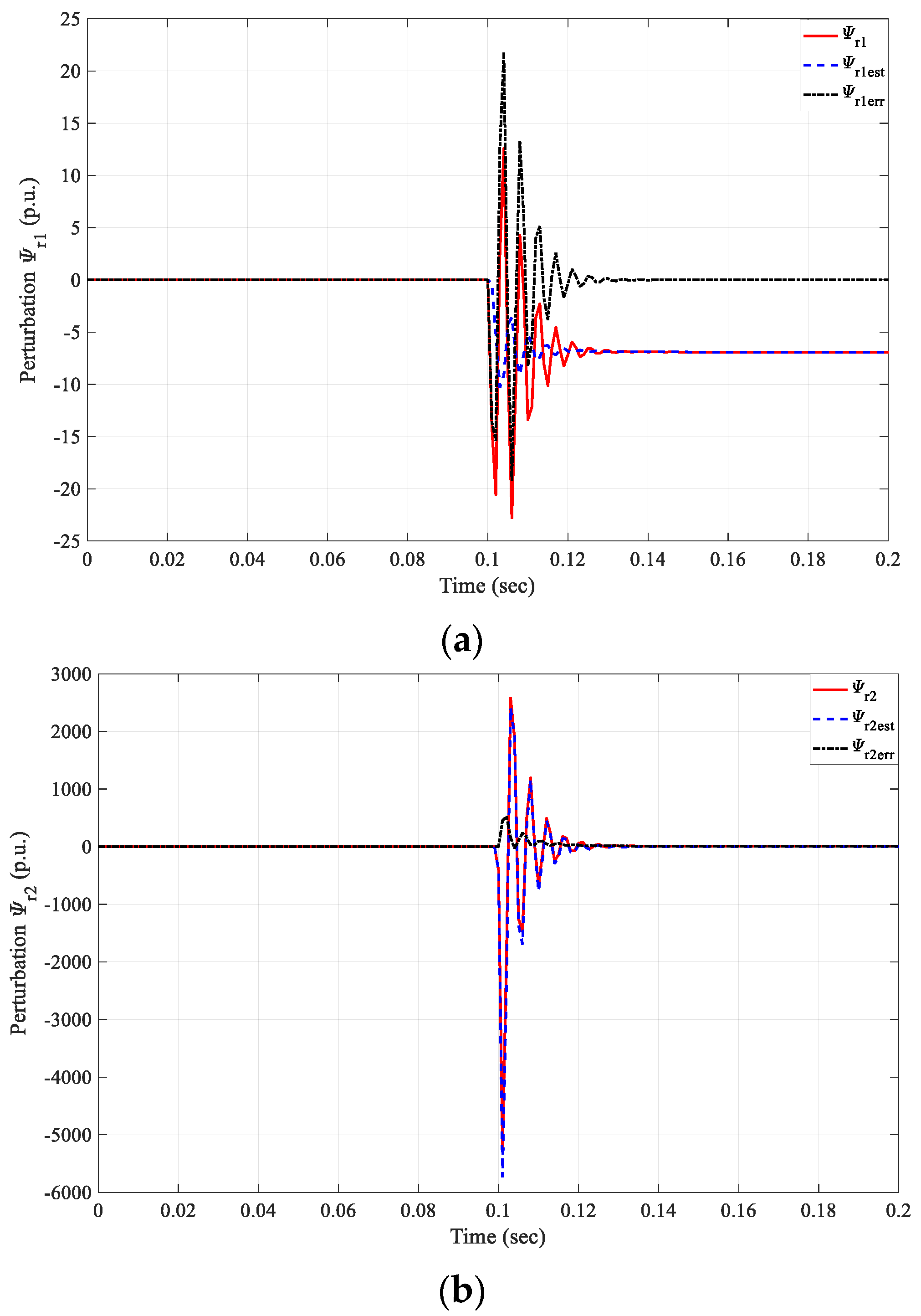
5.5. Disturbance Rejection
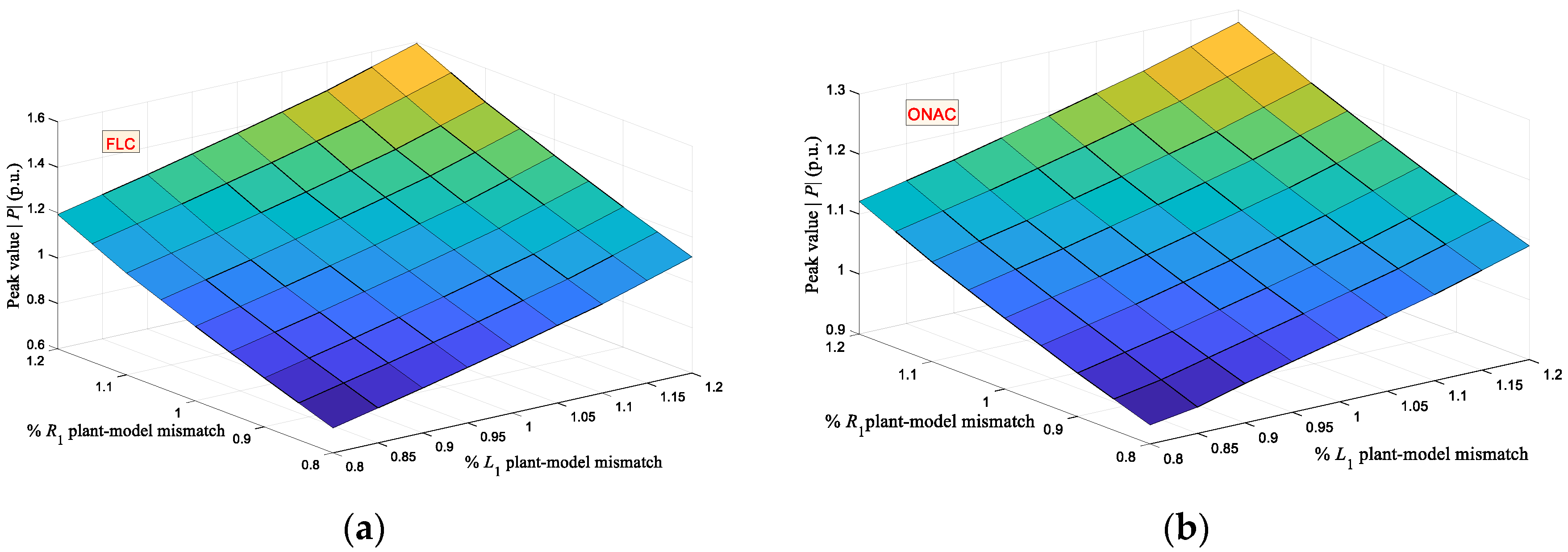
5.6. Robustness to Parameter Uncertainties
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Variables | Abbreviations | ||
| R1, R2 | equivalent resistance, Ω | VSC | voltage source converter |
| L1, L2 | equivalent inductance, mH | CSC | current source converter |
| , | d-axes components of the line currents, A | VSC-HVDC | VSC based high voltage direct current |
| , | q-axes components of the line currents, A | DFIG | doubly fed induction generation |
| , | d-axes components of the line voltages, V | PMSG | permanent magnetic synchronous generator |
| , | q-axes components of the line voltages, V | PV | photovoltaic |
| , | DC voltages, V | DG | distributed generation |
| , | d-axes components of the respective AC grid voltages, V | PID | proportional-integral-derivative |
| , | q-axes components of the respective AC grid voltages, V | FLC | feedback linearization control |
| C1, C2 | capacitance of DC bus, µF | SMC | sliding-mode control |
| , | d-axes components of the converter input voltages, V | PBSMC | passivity-based sliding-mode control |
| , | q-axes components of the converter input voltages, V | MPPT | maximum power point tracking |
| Ua, Ub, Uc | abc three-phase voltages at AC side, V | RSMC | robust sliding-mode control |
| La, Lb, Lc | abc three-phase inductances at AC side, mH | MPC | model predictive control |
| V1~V6 | #1-#6 valves of IGBT | ESO | extended state observer |
| Ud | DC-link voltage, V | NAC | nonlinear adaptive control |
| Id | DC-link current, A | HGPO | high-gain perturbation observer |
| P1, P2 | active powers transmitted from the AC grid to the VSC, W | MSSA | memetic salp swarm algorithm |
| Q1, Q2 | reactive powers transmitted from the AC grid to the VSC, W | PWM | pulse width modulation |
| System parameters | SPWM | sinusoidal pulse width modulation | |
| P0 | rated active power, W | SVM | space vector modulation |
| V0 | rated rms voltage, V | SSA | salp swarm algorithm |
| I0 | rated rms current, A | DC | direct current |
| f0 | rated frequency, Hz | AC | alternating current |
| , | filter inductance, mH | MSSA parameters | |
| fpwm | PWM frequency, kHz | c1, c2, c3 | random numbers |
| fs | Sampling frequency, kHz | n | population size of each salp chain |
| , | DC bus capacitance, µF | M | number of salp chains |
| RL | load resistance, Ω | kmax | maximum iteration number |
References
- He, Y.Q.; Chen, Y.H.; Yang, Z.Q.; He, H.B.; Li, L. A review on the influence of intelligent power consumption technologies on the utilization rate of distribution network equipment. Prot. Control Mod. Power Syst. 2018, 3, 183–193. [Google Scholar] [CrossRef]
- Ruan, S.Y.; Li, G.J.; Jiao, X.H.; Sun, Y.Z.; Lie, T. Adaptive control design for VSC-HVDC systems based on backstepping method. Electr. Power Syst. Res. 2007, 77, 559–565. [Google Scholar] [CrossRef]
- Nguyen, T.T. A rotor-sync signal-based control system of a doubly-fed induction generator in the shaft generation of a ship. Processes 2019, 7, 188. [Google Scholar] [CrossRef]
- Li, J.H.; Wang, S.; Ye, L.; Fang, J.K. A coordinated dispatch method with pumped-storage and battery-storage for compensating the variation of wind power. Prot. Control Mod. Power Syst. 2018, 3, 21–34. [Google Scholar] [CrossRef]
- Han, P.P.; Fan, G.J.; Sun, W.Z.; Shi, B.L.; Zhang, X.A. Research on identification of LVRT characteristics of photovoltaic inverters based on data testing and PSO algorithm. Processes 2019, 7, 250. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, X.S.; Yu, T.; Shu, H.C.; Fang, Z.H. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Convers. Manag. 2017, 133, 427–443. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, L.; Wang, L.; Yao, W.; Wu, Q.H. Nonlinear maximum power point tracking control and modal analysis of DFIG based wind turbine. Int. J. Electr. Power Energy Syst. 2016, 74, 429–436. [Google Scholar] [CrossRef] [Green Version]
- Dash, P.K.; Patnaik, R.K.; Mishra, S.P. Adaptive fractional integral terminal sliding mode power control of UPFC in DFIG wind farm penetrated multimachine power system. Prot. Control Mod. Power Syst. 2018, 3, 79–92. [Google Scholar] [CrossRef]
- Ruan, S.Y.; Li, G.J.; Peng, L.; Sun, Y.Z.; Lie, T.T. A nonlinear control for enhancing HVDC light transmission system stability. Int. J. Electr. Power Energy Syst. 2007, 29, 565–570. [Google Scholar] [CrossRef]
- Moharana, A.; Dash, P.K. Input-output linearization and robust sliding-mode controller for the VSC-HVDC transmission link. IEEE Trans. Power Deliv. 2010, 25, 1952–1961. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Xu, L. Control of HVDC light system using conventional and direct current vector control approaches. IEEE Trans. Power Electron. 2010, 25, 3106–3118. [Google Scholar]
- Yang, B.; Yu, T.; Shu, H.C.; Zhang, Y.M.; Chen, J.; Sang, Y.Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.C.; Dong, J.; Jiang, L. Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Tang, R.L.; Wu, Z.; Fang, Y.J. On figuration of marine photovoltaic system and its MPPT using model predictive control. Sol. Energy 2017, 158, 995–1005. [Google Scholar] [CrossRef]
- Mohomad, H.; Saleh, S.A.M.; Chang, L. Disturbance estimator-based predictive current controller for single-phase interconnected PV systems. IEEE Trans. Ind. Appl. 2017, 53, 4201–4209. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping. IEEE Trans. Power Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. Adrc with adaptive extended state observer and its application to air–fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Cui, R.X.; Chen, L.P.; Yang, C.G.; Chen, M. Correction to extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities. IEEE Trans. Ind. Electron. 2017, 64, 6785–6795. [Google Scholar] [CrossRef]
- Wu, Q.H.; Jiang, L.; Wen, J.Y. Decentralized adaptive control of interconnected non-linear systems using high gain observer. Int. J. Control 2004, 77, 703–712. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, Q.H.; Wen, J.Y. Decentralized nonlinear adaptive control for multi-machine power systems via high-gain perturbation observer. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 2052–2059. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, L.; Wei, Y.; Wu, Q.H. Perturbation estimation based nonlinear adaptive control of a full-rated converter wind turbine for fault ride-through capability enhancement. IEEE Trans. Power Syst. 2014, 29, 2733–2743. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.E.; Yu, T.; Li, H.F.; Zhang, X.S.; Shu, H.C.; Sang, Y.Y.; Jiang, L. Novel bio-inspired memetic salp mswarm algorithm and application to MPPT for PV systems considering partial shading condition. J. Clean. Prod. 2019, 215, 1203–1222. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of water distribution network design using the shuffled frog leaping algorithm. J. Water Resour. Plan. Manag. 2015, 129, 210–225. [Google Scholar] [CrossRef]
- Bharatiraja, C.; Jeevananthan, S.; Latha, R. FPGA based practical implementation of NPC-MLI with SVPWM for an autonomous operation PV system with capacitor balancing. Int. J. Electr. Power Energy Syst. 2014, 61, 489–509. [Google Scholar] [CrossRef]
- Xia, Y.; Gou, B.; Xu, Y. A new ensemble-based classifier for IGBT open-circuit fault diagnosis in three-phase PWM converter. Prot. Control Mod. Power Syst. 2018, 3, 364–372. [Google Scholar] [CrossRef]
- Smith, M. DSpace: An Open Source Dynamic Digital Repository. 2003. Available online: https://dspace.mit.edu/handle/1721.1/29465 (accessed on 9 July 2019).
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Single-Board Hardware /DS1104 R&D Controller Board. Available online: https://www.dspace.com/shared/data/pdf/2018/dSPACE_DS1104_Catalog2018.pdf (accessed on 25 May 2019).
- Gao, Z.; Saxen, H.; Gao, C. Special Section on Data-Driven Approaches for Complex Industrial Systems. IEEE Trans. Ind. Inform. 2013, 9, 2210–2212. [Google Scholar] [CrossRef]
- Gao, Z.; Nguang, S.K.; Kong, D.X. Advances in Modelling, monitoring, and control for complex industrial systems. Complexity 2019, 2019. [Google Scholar] [CrossRef]
- Cao, H.Z.; Yu, T.; Zhang, X.S.; Yang, B.; Wu, Y.X. Reactive power optimization of large-scale power systems: A transfer bees optimizer application. Processes 2019, 7, 321. [Google Scholar] [CrossRef]
|
| Component Parameters | A/D Converter | D/A Converter |
|---|---|---|
| Offset error | ±5 mV | ±1 mV |
| Gain error | Multiplexed channels: ±0.25% | ±0.1% |
| Parallel channels: ±0.5% | ||
| Offset drift | 40 μV/K | 130 μV/K |
| Gain drift | 25 ppm/K | 25 ppm/K |
| Signal-to-noise ratio | Multiplexed channels: >80 dB | >80 dB |
| Parallel channels: >65 dB |
| Rated Active Power | P0 | 300 W |
|---|---|---|
| Rated rms voltage | V0 | 30 V |
| Rated rms current | I0 | 10 A |
| Rated frequency | f0 | 50 Hz |
| Filter inductance | L1′, L2′ | 60 mH |
| PWM frequency | fPWM | 2 kHz |
| Sampling frequency | fs | 10 kHz |
| DC bus capacitance | C1′, C2′ | 1320 µF |
| Load resistance | RL | 1200 Ω |
| Rectifier Controller | |||
|---|---|---|---|
| Controller gains | |||
| Observer gains | |||
| ε = 0.1 | |||
| Inverter controller | |||
| Controller gains | |||
| Observer gains | |||
| ε = 0.1 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Jin, X.; Wang, H.; Fu, Y.; Ge, W.; Yang, B.; Yu, T. Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation. Processes 2019, 7, 490. https://doi.org/10.3390/pr7080490
Jiang Y, Jin X, Wang H, Fu Y, Ge W, Yang B, Yu T. Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation. Processes. 2019; 7(8):490. https://doi.org/10.3390/pr7080490
Chicago/Turabian StyleJiang, Yueping, Xue Jin, Hui Wang, Yihao Fu, Weiliang Ge, Bo Yang, and Tao Yu. 2019. "Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation" Processes 7, no. 8: 490. https://doi.org/10.3390/pr7080490
APA StyleJiang, Y., Jin, X., Wang, H., Fu, Y., Ge, W., Yang, B., & Yu, T. (2019). Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation. Processes, 7(8), 490. https://doi.org/10.3390/pr7080490






