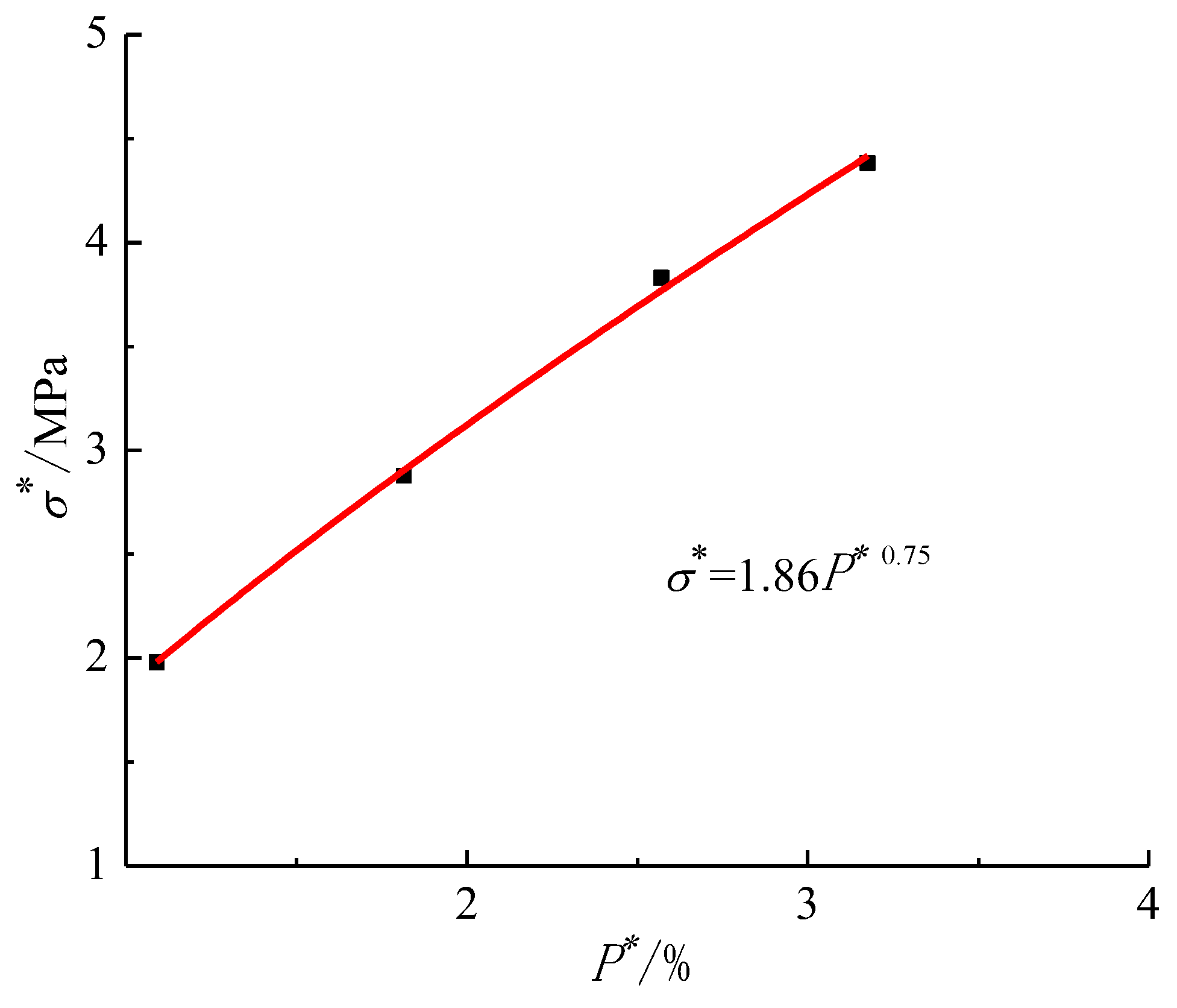
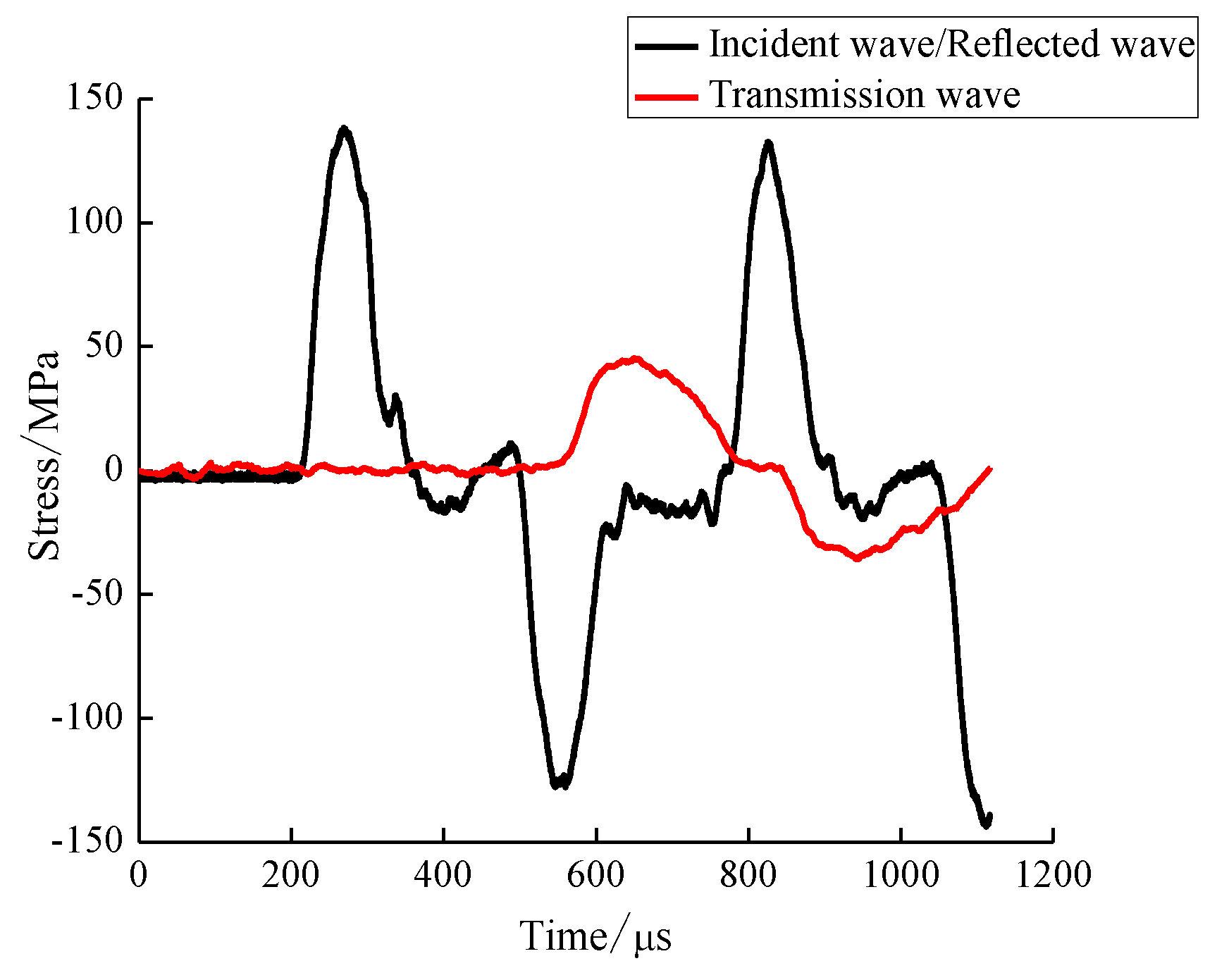
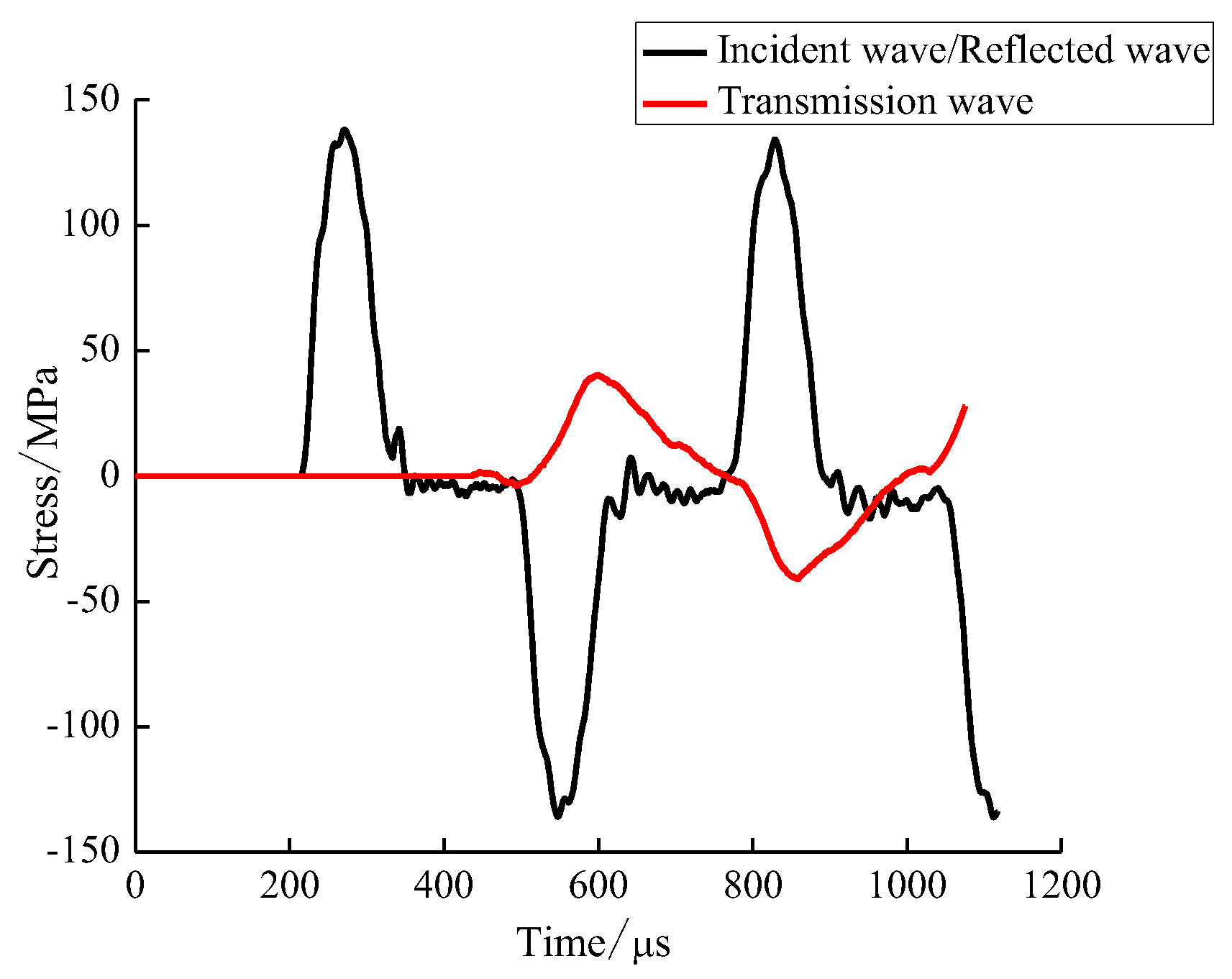
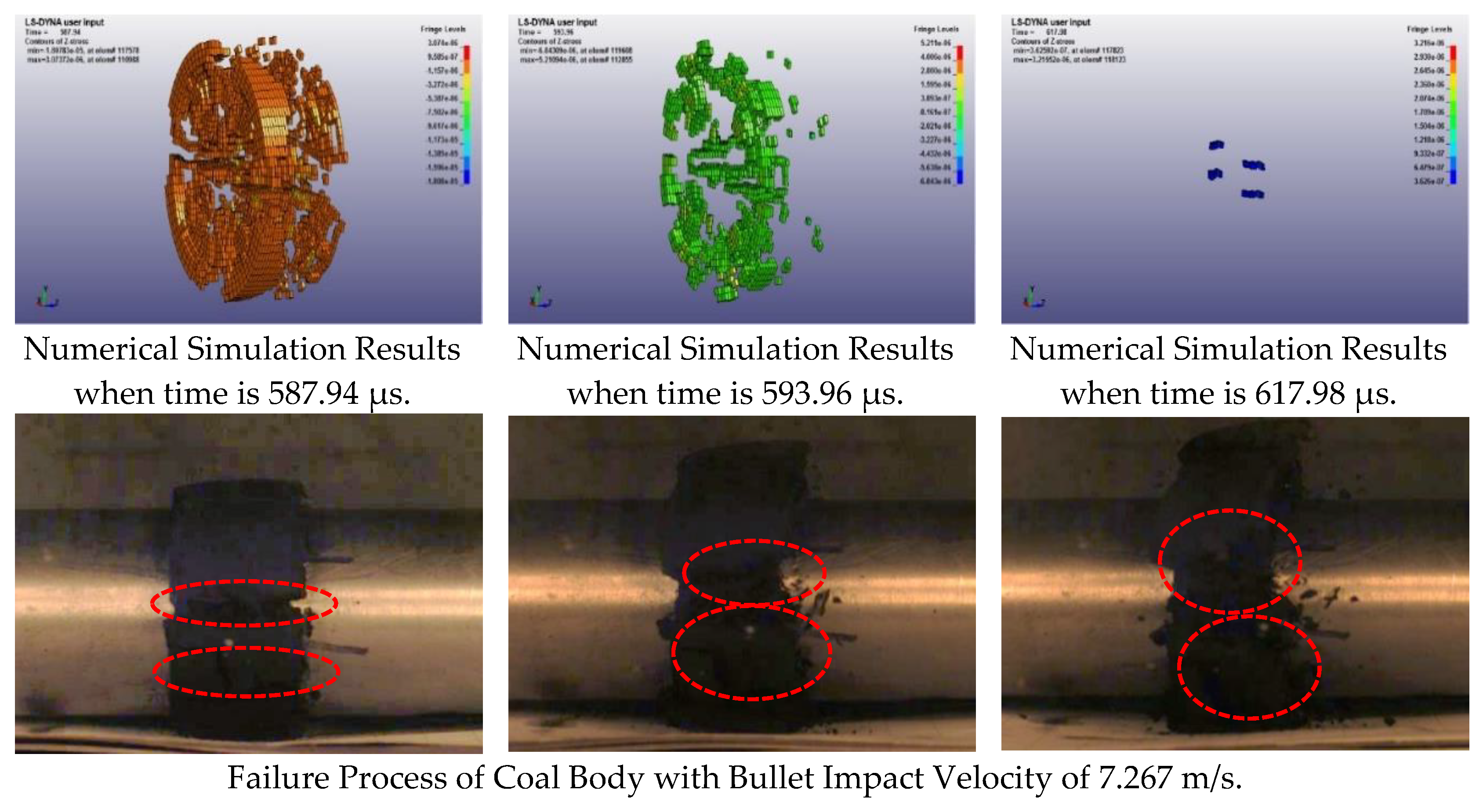
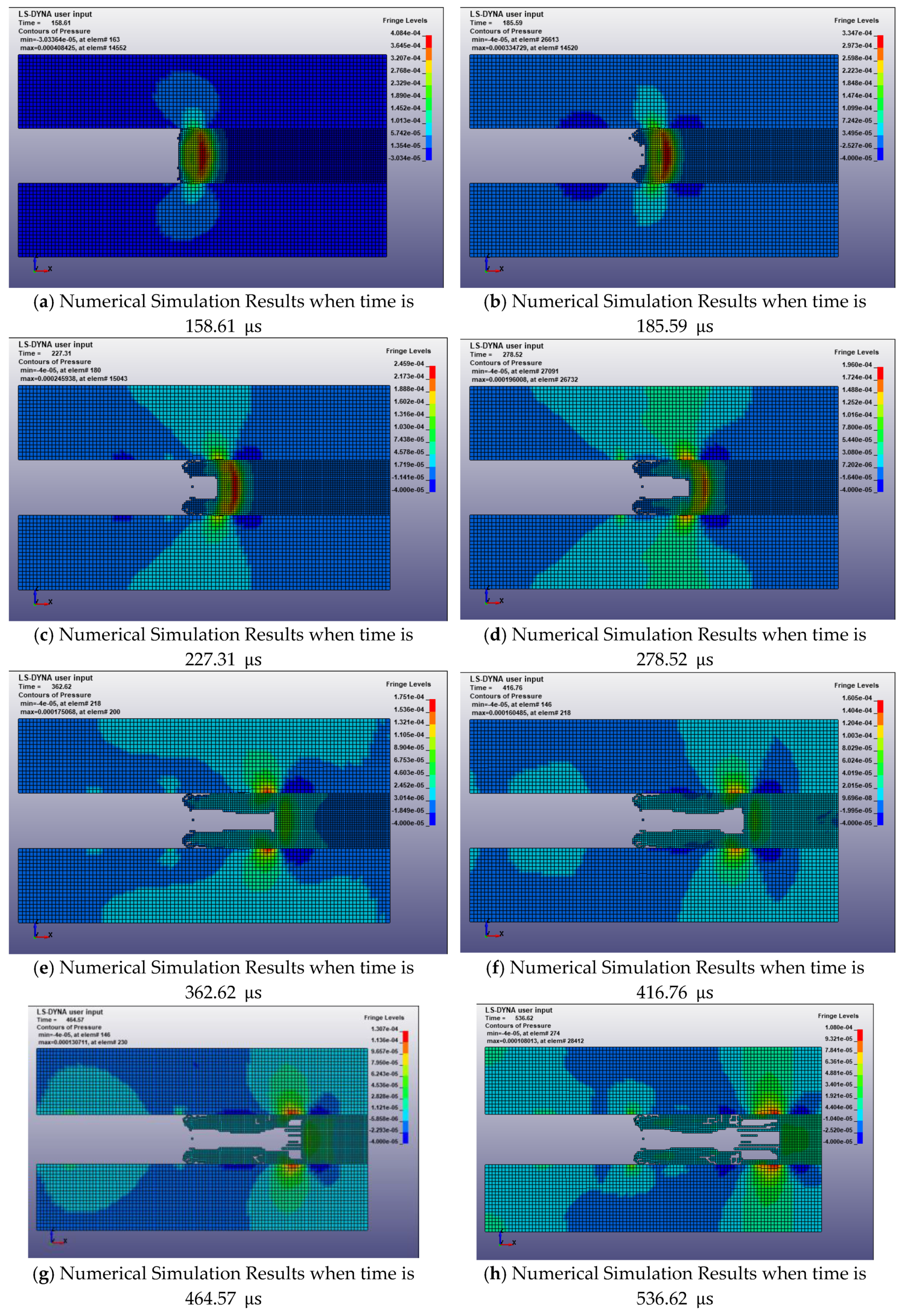
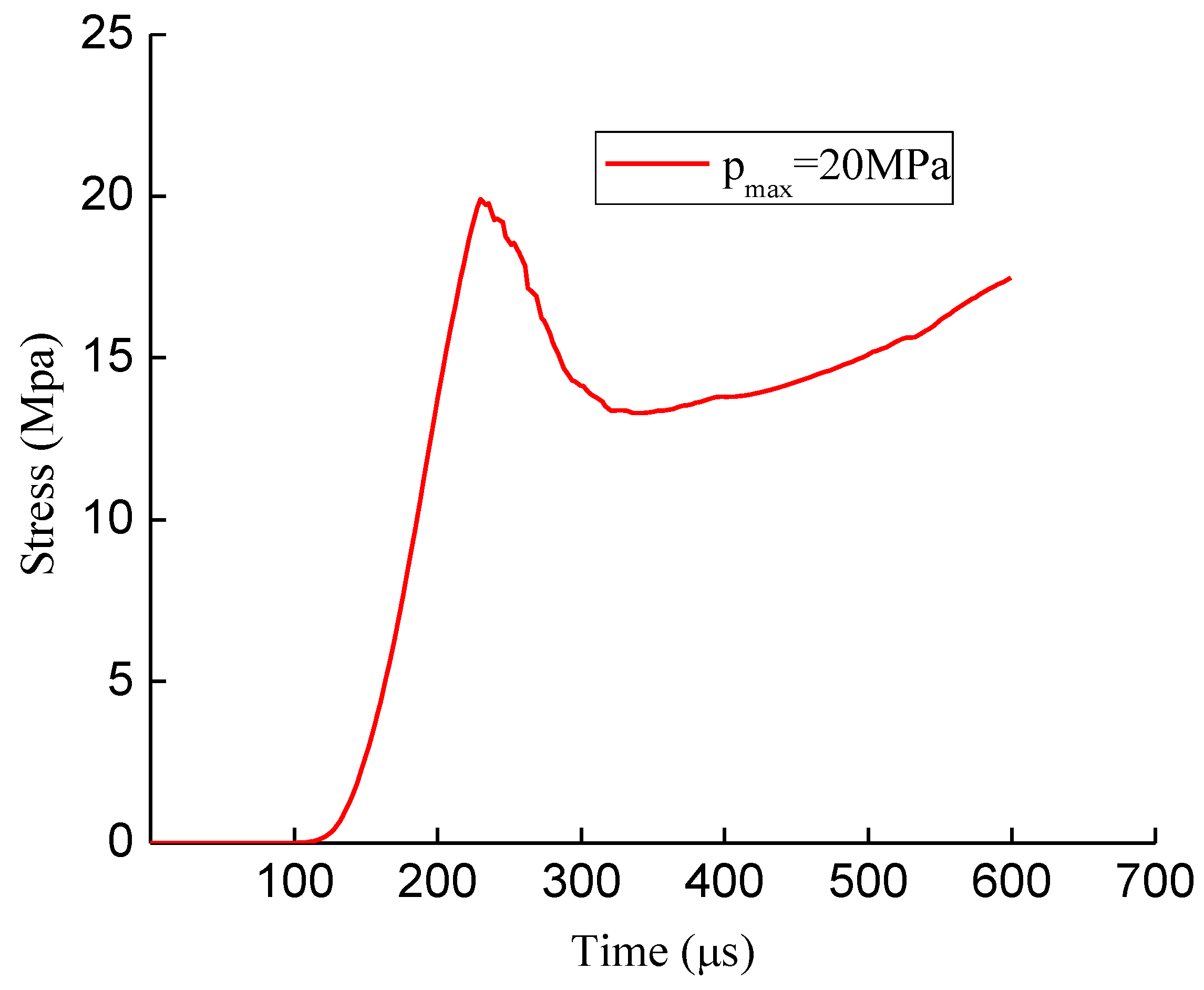
1. Introduction
China is the largest energy consumer in the world and its main energy resource is coal. With the increase in the depth and intensity of coal mining activities, a variety of coal-rock dynamic disasters such as coal and gas outbursts, rock bursts, and large-scale pressure on stope, have become more serious and safety production problems have also arisen [
1,
2]. Coal and gas outbursts and rock bursts are common dynamic disasters in coal mine rocks. Due to their sudden and transient vibration and great destructive characteristics, these phenomena often cause serious casualties and resource waste, which seriously restrict the national economic development of China [
3].
In order to understand the mechanism of coal rock dynamic disasters such as rock bursts, researchers have recently carried out a large number of experimental studies on the dynamic and static mechanical properties of coal. Xue [
4] carried out orthogonal experiments of triaxial stress with CH
4 seepage, and a complete stress–strain relationship and the corresponding evolution of volumetric strain and permeability were obtained. Cai [
5] carried out multistage uniaxial compression creep tests on lean and raw coal samples and found that in the multistage creep process, the coal samples were first hardened, then weakened, and finally failed due to crack growth. Li’s [
6] tests on gas seepage in raw coal under three paths were carried out with a seepage tester under triaxial stress conditions. It was found that the permeability was subjected to the dual influence of stress and damage accumulation.
Currently, split Hopkinson pressure bar (SHPB) technology is widely applied in the investigation of the dynamic mechanical properties of materials [
7,
8,
9]. Zhao [
7] used an SHPB system to measure the semi-circular bending of incision and investigated the crack propagation fractal characteristics of coal seams under impact loads. His results showed that the existence of bedding had a significant impact on crack propagation. Feng [
8] used SHPB to carry out dynamic load tests on coal samples and analyzed their dynamic and energy consumption characteristics. Li [
9] used SHPB to study the impact failure of coal at impact velocities of 4.174–17.652 m/s and investigated the variation of different mechanical parameters such as stress, strain, incident energy, and dissipated energy.
Due to the limitations of experimental methods and equipment, the existing experimental findings on coal impact damage are seriously insufficient, and it is impossible to accurately determine stress and strain changes inside coal rock samples at the impact moment [
4,
5,
6,
7,
8,
9,
10]. However, through numerical simulations, the deformation and stress changes of coal during coal and gas outbursts could be visualized [
11,
12,
13,
14], and dynamic load tests carried out under limited laboratory conditions were supplemented and improved. The Holmquist–Johnson–Cook (HJC) constitutive model is a concrete constitutive model based on large strain, a high strain rate, and high pressure that was proposed by Holmquist [
15]. This constitutive model has been successfully applied to the numerical simulation of dynamic impact damage of concrete, rock, and other materials [
16,
17,
18,
19]. Due to the similarity of the mechanical properties and dynamic failure processes of coal and rock, the HJC constitutive model could be used to numerically simulate the impact damage of coal.
Considering the similar mechanical properties of coal rock, ordinary rock, and concrete materials, Xie [
20] used the HJC constitutive model to test coal samples. He also used finite element software LS-DYNA (one of the most commonly used explicit simulation software for the numerical simulation of explosion and shock) numerical simulation to demonstrate the SHPB process of coal impact failure at different impact velocities and found that simulation results were consistent with experimental measurements. Li and Wang [
21,
22] employed the HJC constitutive model to numerically simulate a SHPB experiment and passive confining pressure test of coal using LS-DYNA. The stress waveform of coal rock samples during the impact test, the oscillation of stress waves, and the damage of the test specimen were reproduced, and it was found that simulation results complied well with experimental findings.
Many researchers have provided HJC constitutive model parameters for various concretes, but to the best of our knowledge, no parameter values have been proposed for coal. In the numerical simulation of coal, basic parameters can be directly obtained, and the remaining parameters are generally considered to be the same as concrete model parameters, which decreases the accuracy of numerical simulation results. Therefore, it is essential to understand the mechanism of coal/rock dynamic disasters by studying the dynamic mechanical parameters of coal to propose a systematic method to determine HJC constitutive model parameters for coal outbursts.
In this paper, the parameters of the HJC constitutive model for briquette are studied using experimental and numerical simulation methods. HJC constitutive model parameters for briquette were obtained through a series of experiments. SHPB experiments were carried out and the impact damage of coal was numerically simulated using ANSYS/LS-DYNA software. Numerical simulation results and experimental findings were analyzed to verify the reliability of the HJC constitutive model parameters for briquette. The validated HJC constitutive model parameters were applied to the numerical simulation of the impact damage of tunnel face, and the failure process of coal seam in the roadway was visually displayed. The research findings are of great significance for improving and exploring the mechanism of coal-rock dynamic disasters.
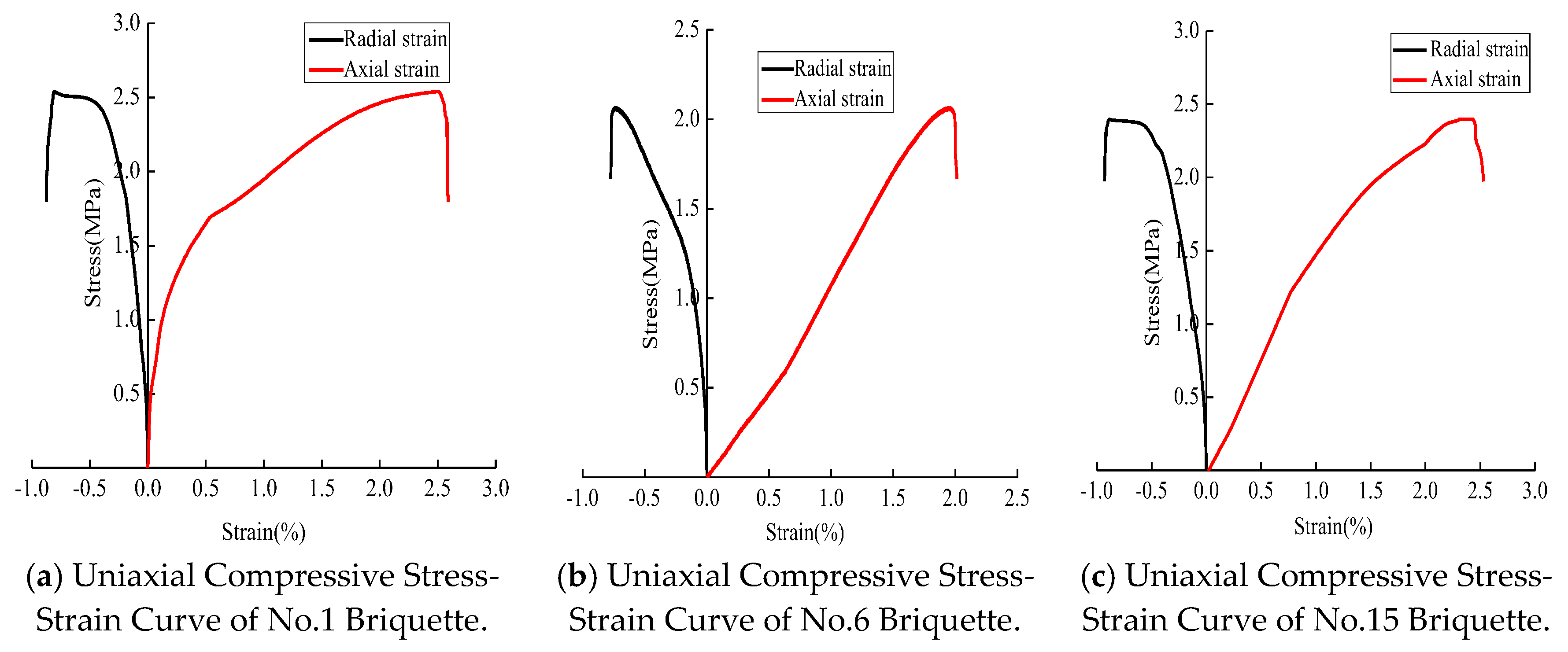
3. Coal Sample Preparation
The coal samples used in this research were obtained from Yongcheng Cheji Coal Mine, Henan Province, China, which is an outburst coal seam. The coal samples were high-quality anthracite with ultra-low sulfur, ultra-low phosphorus, medium ash, and high calorific values. The coal moisture M
ad was 0.81%, ash content A
d was 11.6%, and total volatile V
daf was 9.07%. A large-volume coal mass was crushed using a heavy hammer, and the obtained pieces were placed in a ball mill to be pulverized. The pulverized coal sample with particle diameter of 0.25 mm or below was screened out [
25]. To achieve the strength required for the experiment, 1000 g pulverized coal and 200 g coal tar were uniformly mixed to prepare coal samples. Standard cylindrical coal samples with a diameter of 50 mm and length of 100 mm as well as disc-shaped coal samples with a diameter of 50 mm and thickness of 25 mm were obtained by pouring the prepared pulverized coal into separate molds and pressing them under a pressure of 250 KN on a WAW-type electro-hydraulic servo press device (Jinan Tianchen Testing Machine Manufacturing Co., Ltd., Licheng District, Jinan City, Shandong Province, China). A total of 22 cylindrical and 4 disc-shaped coal samples were prepared (
Figure 1), and the basic parameters of the briquettes were assumed to be as summarized in
Table 2 and
Table 3.
As shown in
Figure 2, a compression-mirror analysis was conducted on press-formed briquette samples using a KYKY-EM6200 tungsten filament scanning electron microscope.
The strength of a briquette sample is closely related to its microstructure. If the gel content of the briquette sample is high, crystal development is enhanced, crystal distribution is more uniform, and briquette sample strength is higher [
26]. The microstructure of the prepared briquette can be visually evaluated using scanning electron microscopy, as shown in
Figure 3. It can be seen that the microstructure of coal samples had changed from granular to lamellar, and irregularly shaped crystals and gels were evenly distributed throughout the layered structure, indicating that the prepared briquette samples were well cemented, with high uniformity and strength. A large number of on-site experiments have shown that most prominent dangerous coal seams contain soft delamination with severe structural damage [
27]. The structural strength of briquette samples conformed to soft stratification properties with high uniformity.