Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin
Abstract
1. Introduction
- To introduce temperature dependency into the published kinetic model of batch enzymatic amoxicillin synthesis;
- To understand the attainable performances and inherent trade-offs (via isothermal operation) of varying batch times and operating temperatures;
- To optimise dynamic temperature profiles toward optimal process performance for varying product quality constraints.
2. Dynamic Modelling and Optimisation
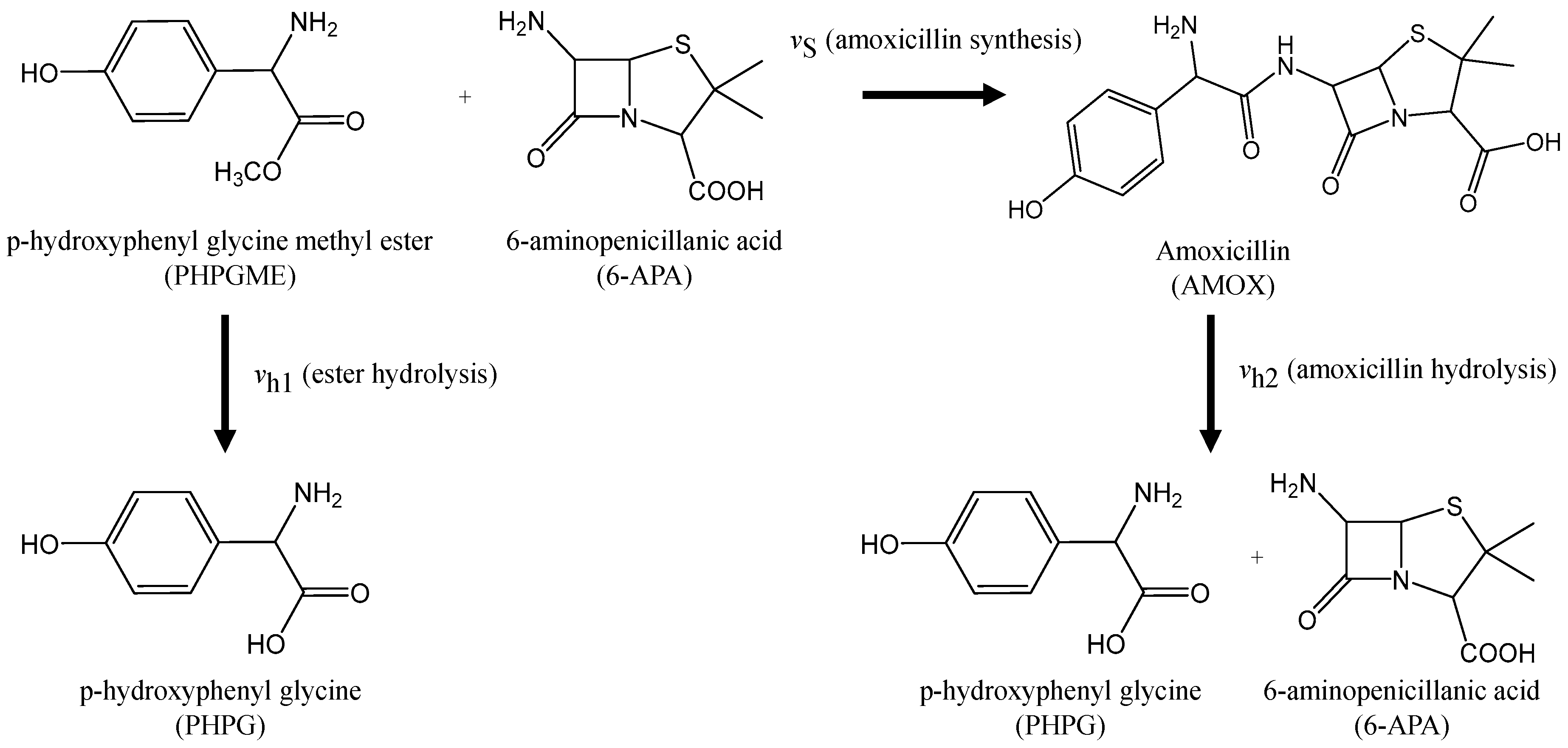
2.1. Amoxicillin Synthesis Pathway and Kinetic Model
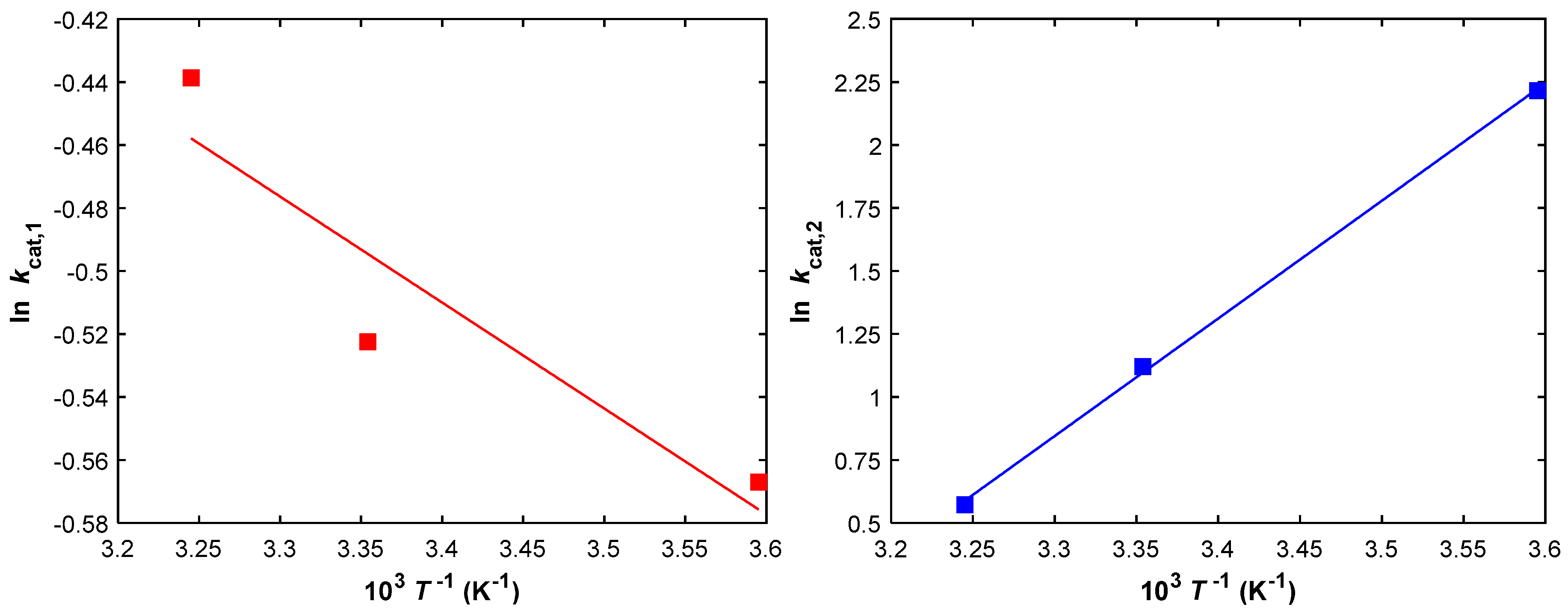
2.2. Kinetic Parameter Estimation
2.3. Dynamic Simulation and Optimisation
2.3.1. Design Space Investigation and Simulation
2.3.2. Dynamic Optimisation
3. Results and Discussion
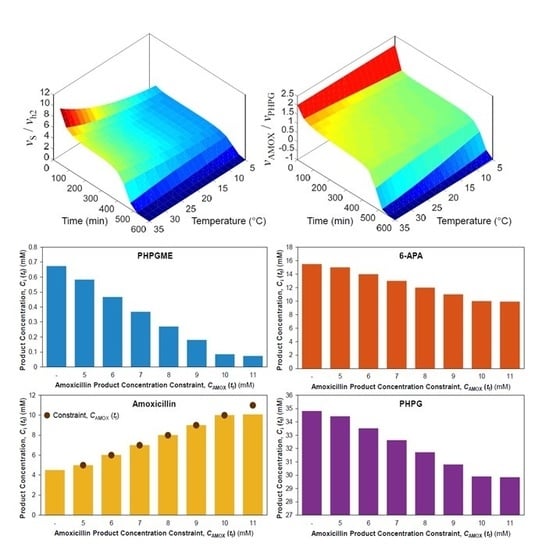
3.1. Dynamic Simulation
3.2. Non-Isothermal Simulation
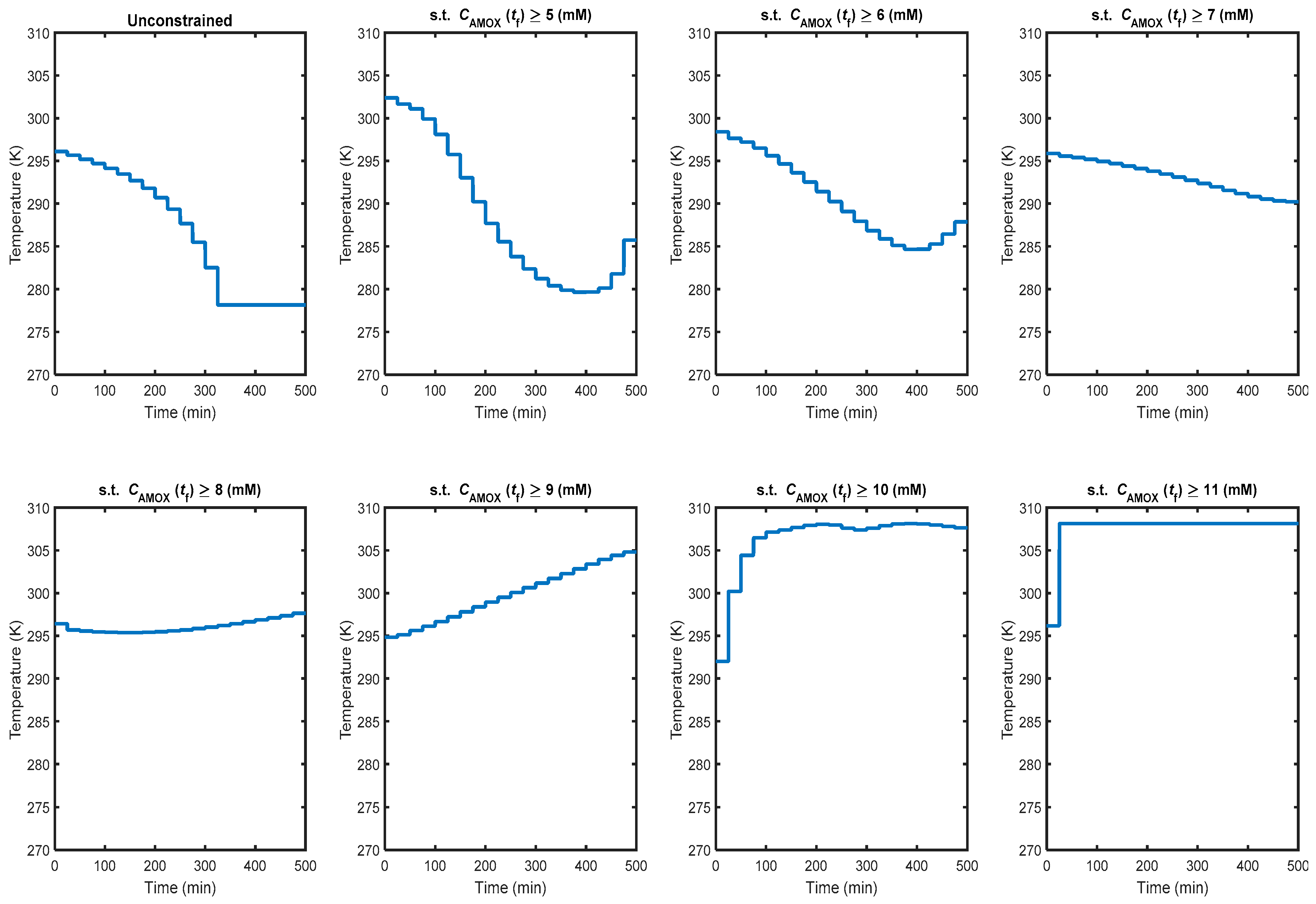
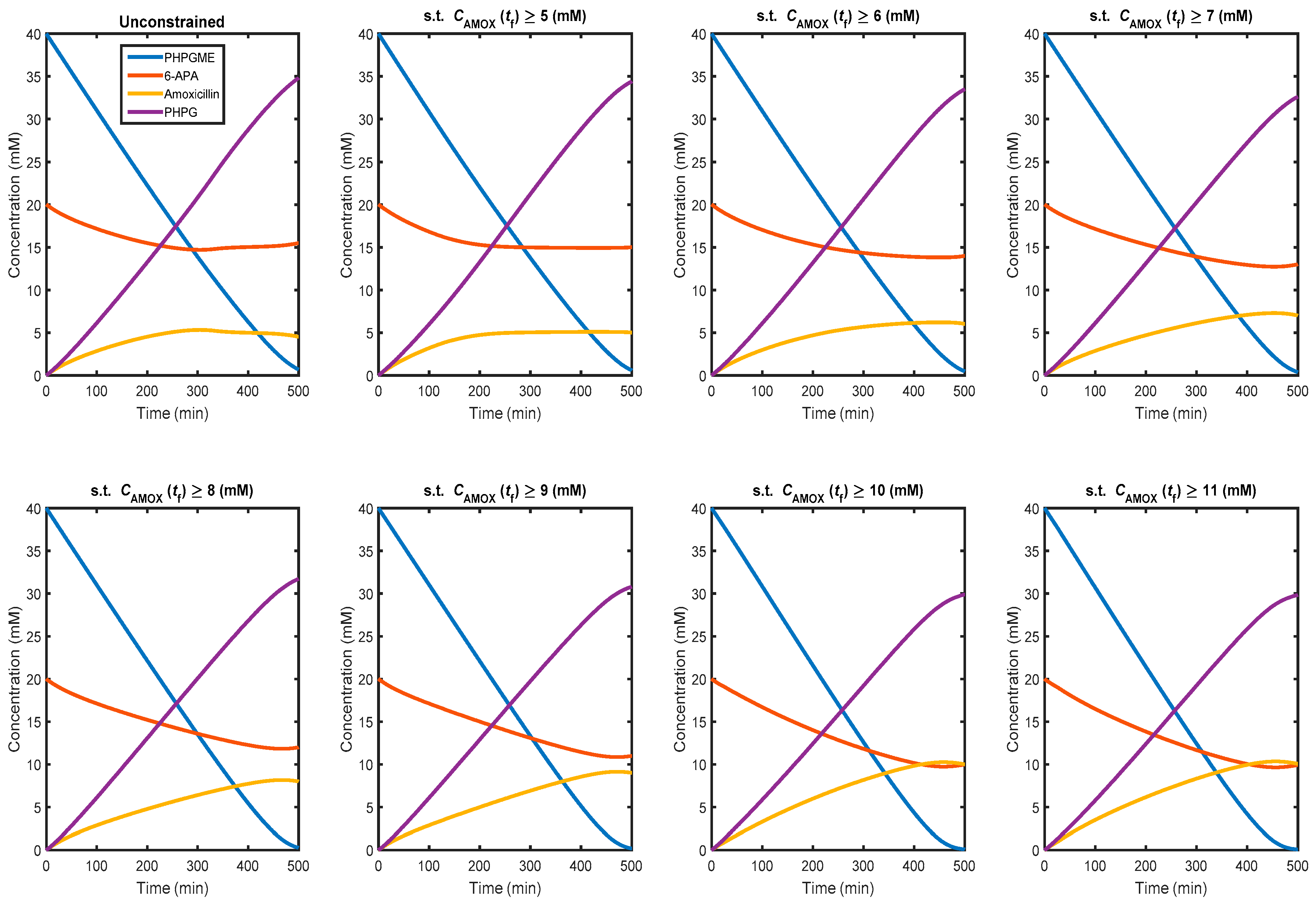
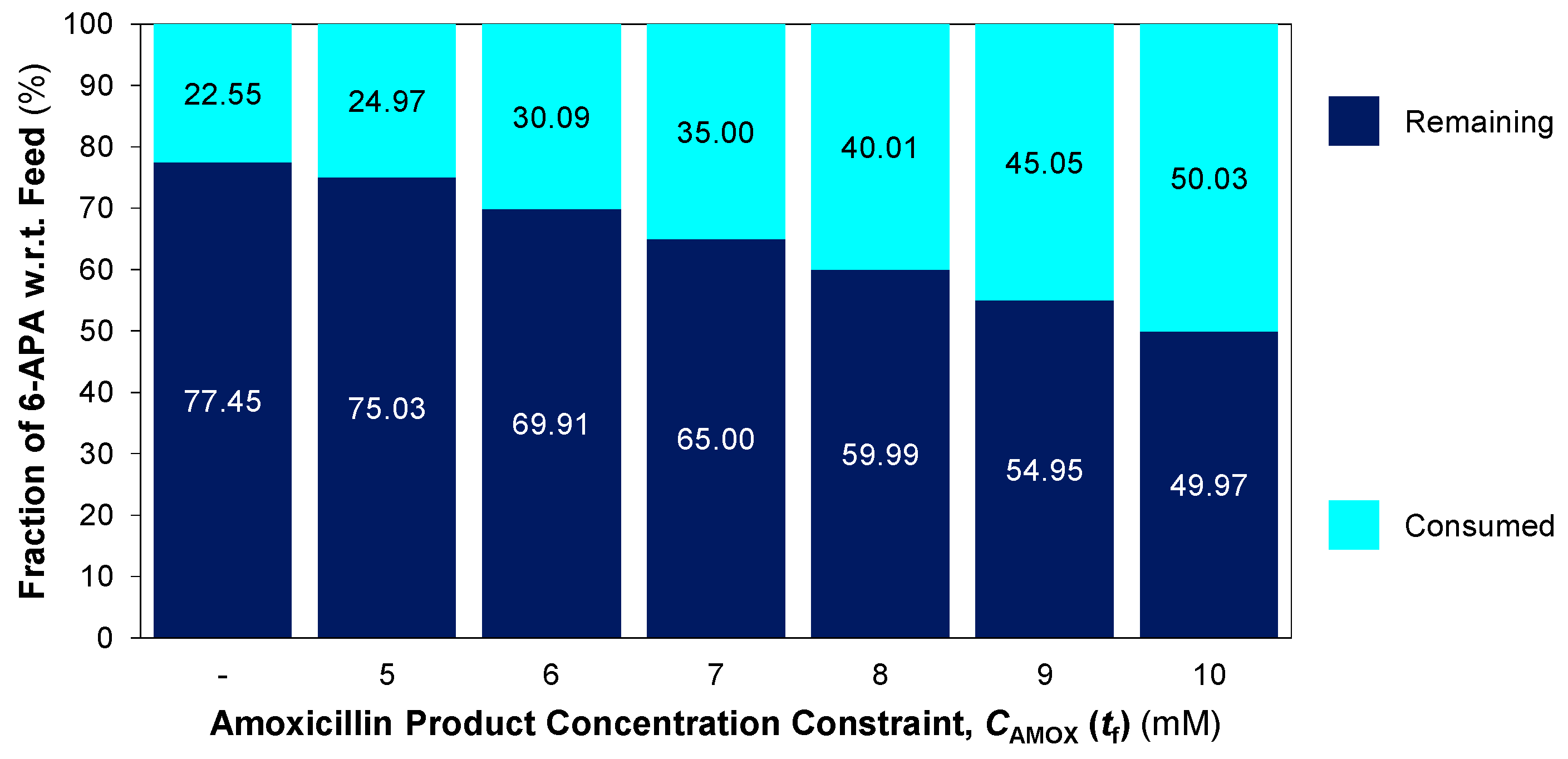
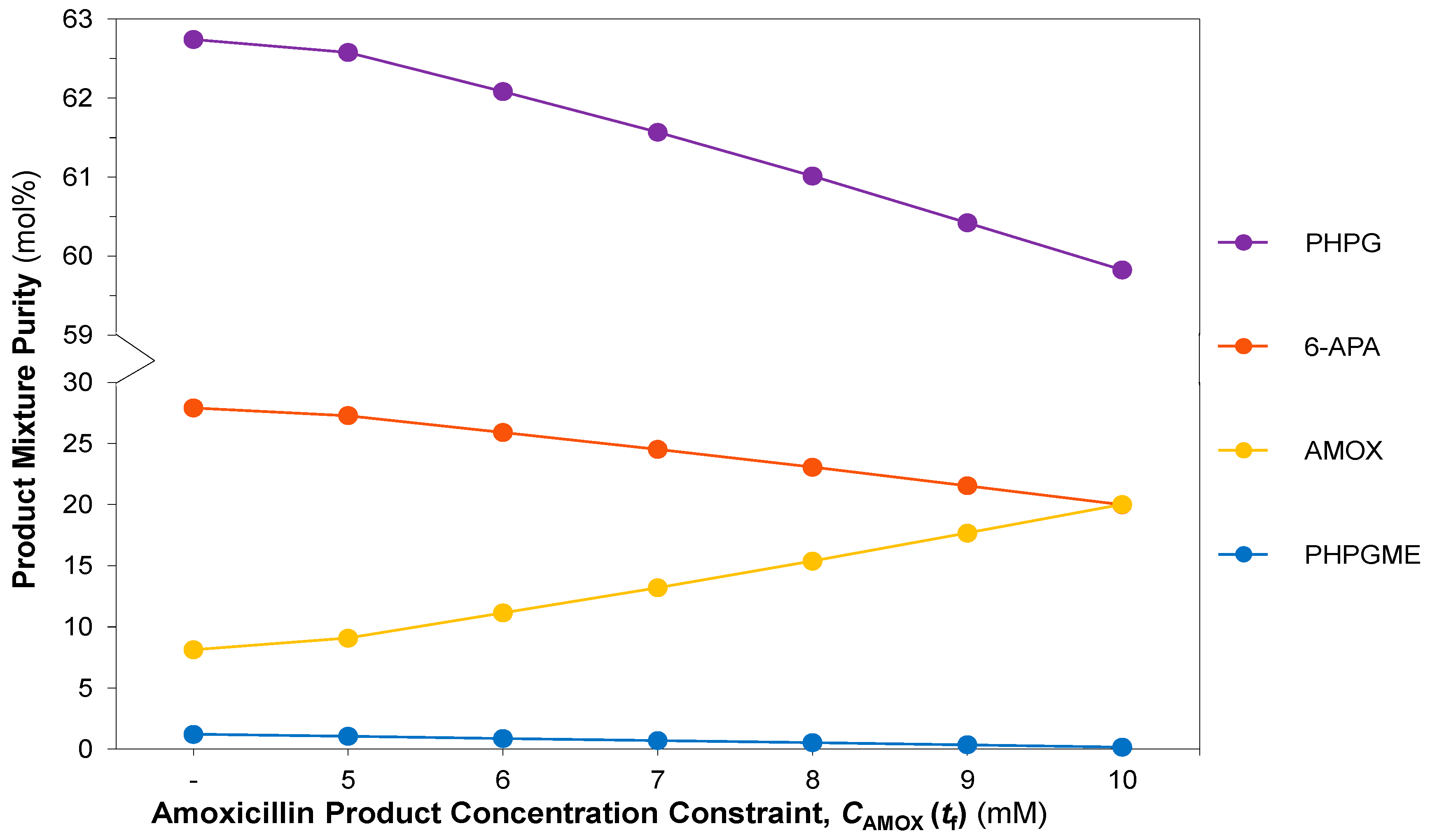
3.3. Non-Isothermal Dynamic Optimisation
4. Conclusions
- The first implementation of dynamic temperature profile optimisation in order to meet specific product quality constraints and minimise feedstock consumption in β-lactam antibiotic production.
Author Contributions
Funding
Conflicts of Interest
References
- Zaffiri, L.; Gardner, J.; Toledo-Pereyra, L.H. History of antibiotics. from salvarsan to cephalosporins. J. Investig. Surg. 2012, 25, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Balkhi, B.; Araujo-Lama, L.; Seoane-Vazquez, E.; Rodriguez-Monguio, R.; Szeinbach, S.L.; Fox, E.R. Shortages of systemic antibiotics in the USA: how long can we wait? J. Pharm. Heal. Serv. Res. 2013, 4, 13–17. [Google Scholar] [CrossRef]
- Pulcini, C.; Beovic, B.; Béraud, G.; Carlet, J.; Cars, O.; Howard, P.; Levy-Hara, G.; Li, G.; Nathwani, D.; Roblot, F.; et al. Ensuring universal access to old antibiotics: a critical but neglected priority. Clin. Microbiol. Infect. 2017, 23, 590–592. [Google Scholar] [CrossRef] [PubMed]
- Russell, M.G.; Jamison, T.F. Seven-step continuous flow synthesis of linezolid without intermediate purification. Angew. Chemie Int. Ed. 2019. [Google Scholar] [CrossRef]
- Lin, H.; Dai, C.; Jamison, T.F.; Jensen, K.F. A rapid total synthesis of ciprofloxacin hydrochloride in continuous flow. Angew. Chemie Int. Ed. 2017, 56, 8870–8873. [Google Scholar] [CrossRef] [PubMed]
- Giordano, R.C.; Ribeiro, M.P.A.; Giordano, R.L.C. Kinetics of β-lactam antibiotics synthesis by penicillin G acylase (PGA) from the viewpoint of the industrial enzymatic reactor optimization. Biotechnol. Adv. 2006, 24, 27–41. [Google Scholar] [CrossRef] [PubMed]
- Food and Drug Administration (FDA). Sales of antibacterial drugs in kilograms. 2010; 4–6. [Google Scholar]
- Food and Drug Administration (FDA). Sales of antibacterial drugs in kilograms. 2012; 5–8. [Google Scholar]
- Hamed, R.B.; Gomez-Castellanos, J.R.; Henry, L.; Ducho, C.; McDonough, M.A.; Schofield, C.J. The enzymes of β-lactam biosynthesis. Nat. Prod. Rep. 2013, 30, 21–107. [Google Scholar] [CrossRef]
- Elander, R.P. Industrial production of β-lactam antibiotics. Appl. Microbiol. Biotechnol. 2003, 61, 385–392. [Google Scholar] [CrossRef]
- Laxminarayan, R. The state of the world’s antibiotics in 2018. 3 July 2018. [Google Scholar]
- Gerogiorgis, D.I.; Jolliffe, H.G. Continuous pharmaceutical process engineering and economics investigating technical efficiency, environmental impact and economic viability. Chem. Today 2015, 33, 29–32. [Google Scholar]
- Diab, S.; Gerogiorgis, D.I. Process modelling, simulation and technoeconomic evaluation of crystallisation antisolvents for the continuous pharmaceutical manufacturing of rufinamide. Comput. Chem. Eng. 2018, 111, 102–114. [Google Scholar] [CrossRef]
- Rodman, A.D.; Gerogiorgis, D.I. An investigation of initialisation strategies for dynamic temperature optimisation in beer fermentation. Comput. Chem. Eng. 2019, 124, 43–61. [Google Scholar] [CrossRef]
- Rodman, A.D.; Gerogiorgis, D.I. Dynamic optimization of beer fermentation: sensitivity analysis of attainable performance vs. product flavour constraints. Comput. Chem. Eng. 2017, 106, 582–595. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Rousseau, R.W.; Grover, M.A. Continuous reactive crystallization of β-lactam antibiotics catalyzed by penicillin G acylase. part I: model development. Comput. Chem. Eng. 2019, 123, 331–343. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Grover, M.A.; Rousseau, R.W. Continuous reactive crystallization of β-lactam antibiotics catalyzed by penicillin G acylase. part II: case study on ampicillin and product purity. Comput. Chem. Eng. 2019, 126, 332–341. [Google Scholar] [CrossRef]
- Encarnación-Gómez, L.G.; Bommarius, A.S.; Rousseau, R.W. Crystallization kinetics of ampicillin using online monitoring tools and robust parameter estimation. Ind. Eng. Chem. Res. 2016, 55, 2153–2162. [Google Scholar] [CrossRef]
- McDonald, M.A.; Bommarius, A.S.; Rousseau, R.W. Enzymatic reactive crystallization for improving ampicillin synthesis. Chem. Eng. Sci. 2017, 165, 81–88. [Google Scholar] [CrossRef]
- Gonçalves, L.R.B.; Fernández-Lafuente, R.; Guisán, J.M.; Giordano, R.L.C. The role of 6-aminopenicillanic acid on the kinetics of amoxicillin enzymatic synthesis catalyzed by penicillin G acylase immobilized onto glyoxyl-agarose. Enzyme Microb. Technol. 2002, 31, 464–471. [Google Scholar] [CrossRef]
- UK Department of Health. Antimicrobial resistance empirical and statistical evidence-base. 2016. [Google Scholar]
- Alemzadeh, I.; Borghei, G.; Va, L.; Roostaazad, R. Enzymatic synthesis of amoxicillin with immobilized penicillin G acylase. Trans. C Chem. Chem. Eng. 2010, 17, 106–113. [Google Scholar]
- Schroën, C.G.P.H.; Van Roon, J.L.; Beefink, H.H.; Tramper, J.; Boom, R.M. Membrane applications for antibiotics production. Desalination 2009, 236, 78–84. [Google Scholar] [CrossRef]
- Fodi, T.; Didaskalou, C.; Kupai, J.; Balogh, G.T.; Huszthy, P.; Szekely, G. Nanofiltration-enabled in situ solvent and reagent recycle for sustainable continuous-flow synthesis. ChemSusChem 2017, 10, 3435–3444. [Google Scholar] [CrossRef] [PubMed]
- Pereira, S.C.; Castral, T.C.; Ribeiro, M.P.A.; Giordano, R.L.C.; Giordano, R.C. Green route for amoxicillin production through the integration with the recycle of the by-product (p-hydroxyphenylglycine). In Proceedings of the Brazilian Congress of Chemical Engineering, São Paulo, Spain, 7–12 June 2015; Blücher, E., Ed.; pp. 1823–1830. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Cuthrell, J.E.; Biegler, L.T. On the optimization of differential-algebraic process systems. AIChE J. 1987, 33, 1257–1270. [Google Scholar] [CrossRef]
- Logsdon, J.S.; Biegler, L.T. Accurate solution of differential-algebraic optimization problems. Ind. Eng. Chem. Res. 1989, 28, 1628–1639. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Čižniar, M.; Fikar, M.; Latifi, M.A. MATLAB dynamic optimisation code DynOpt. User’s guide, technical report. KIRP FCHPT STU Bratislava 2005. [Google Scholar]
- Hicks, M.B.; Farrell, W.; Aurigemma, C.; Lehmann, L.; Weisel, L.; Nadeau, K.; Lee, H.; Moraff, C.; Wong, M.; Huang, Y.; et al. Making the move towards modernized greener separations: introduction of the analytical method greenness score (AMGS) calculator. Green Chem. 2019, 21, 1816–1826. [Google Scholar] [CrossRef]
- Sheldon, R.A. Fundamentals of green chemistry: Efficiency in reaction design. Chem. Soc. Rev. 2012, 41, 1437–1451. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.G.T.C.; Machado, A.A.S.C. Greenness of chemical reactions—limitations of mass metrics. Green Chem. Lett. Rev. 2013, 6, 1–18. [Google Scholar] [CrossRef]
- Jolliffe, H.G.; Gerogiorgis, D.I. Plantwide Design and Economic Evaluation of Two Continuous Pharmaceutical Manufacturing (CPM) Cases: Ibuprofen and Artemisinin. Comput. Aided Chem. Eng. 2015, 37, 2213–2218. [Google Scholar]
- Li, J.; Lai, T.C.; Trout, B.L.; Myerson, A.S. Continuous crystallization of cyclosporine: the effect of operating conditions on yield and purity. Cryst. Growth Des. 2017, 17, 1000–1007. [Google Scholar] [CrossRef]
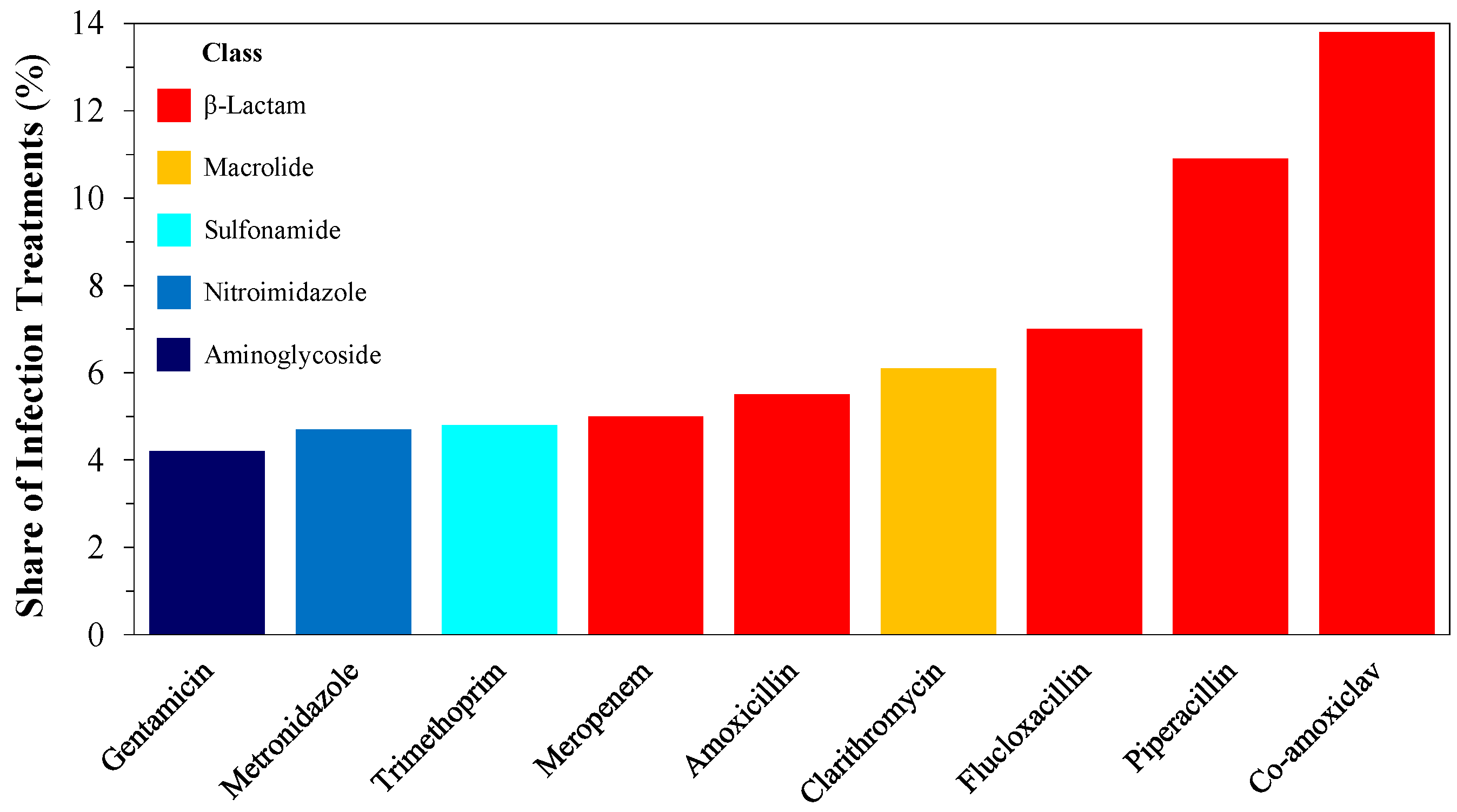
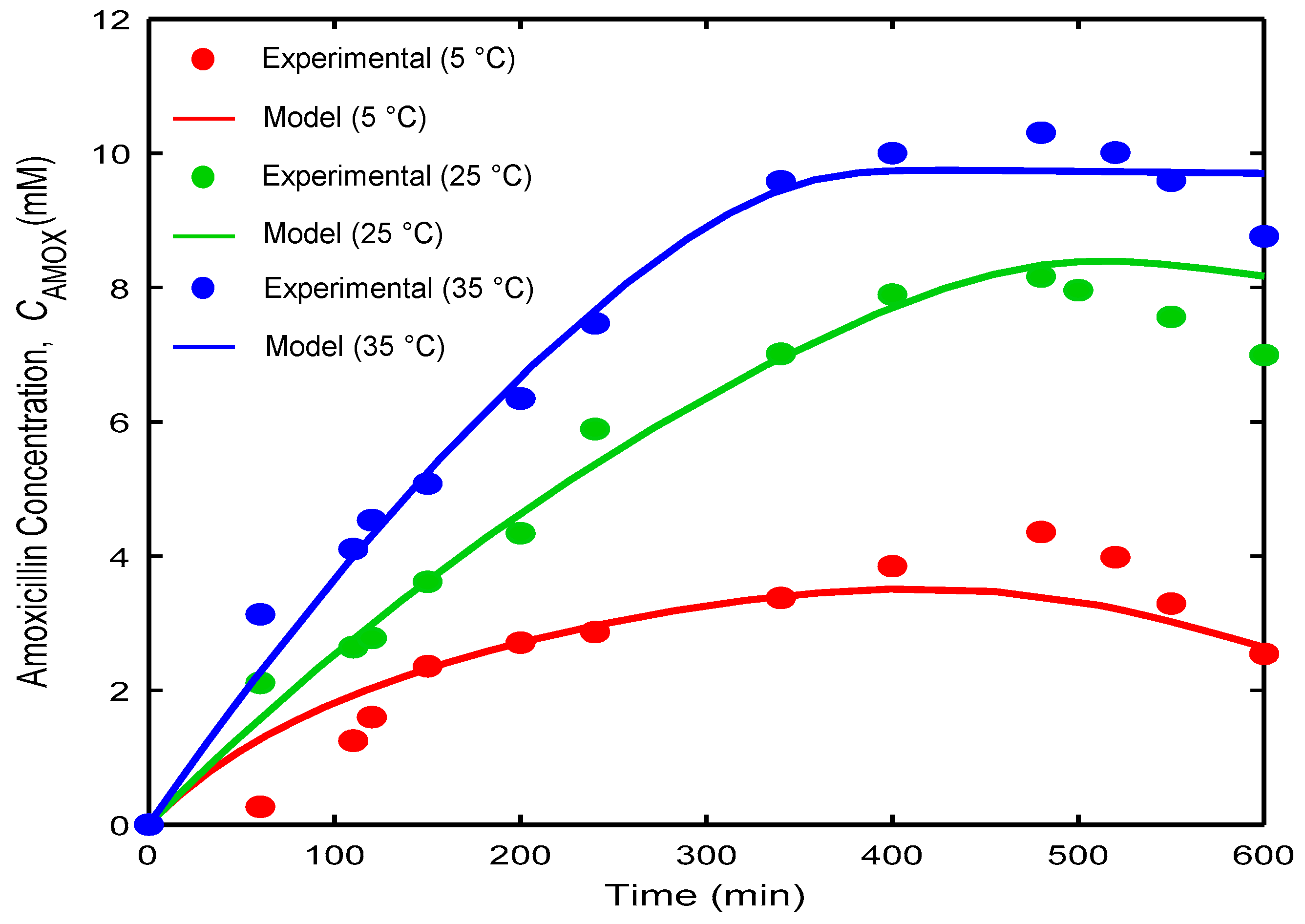
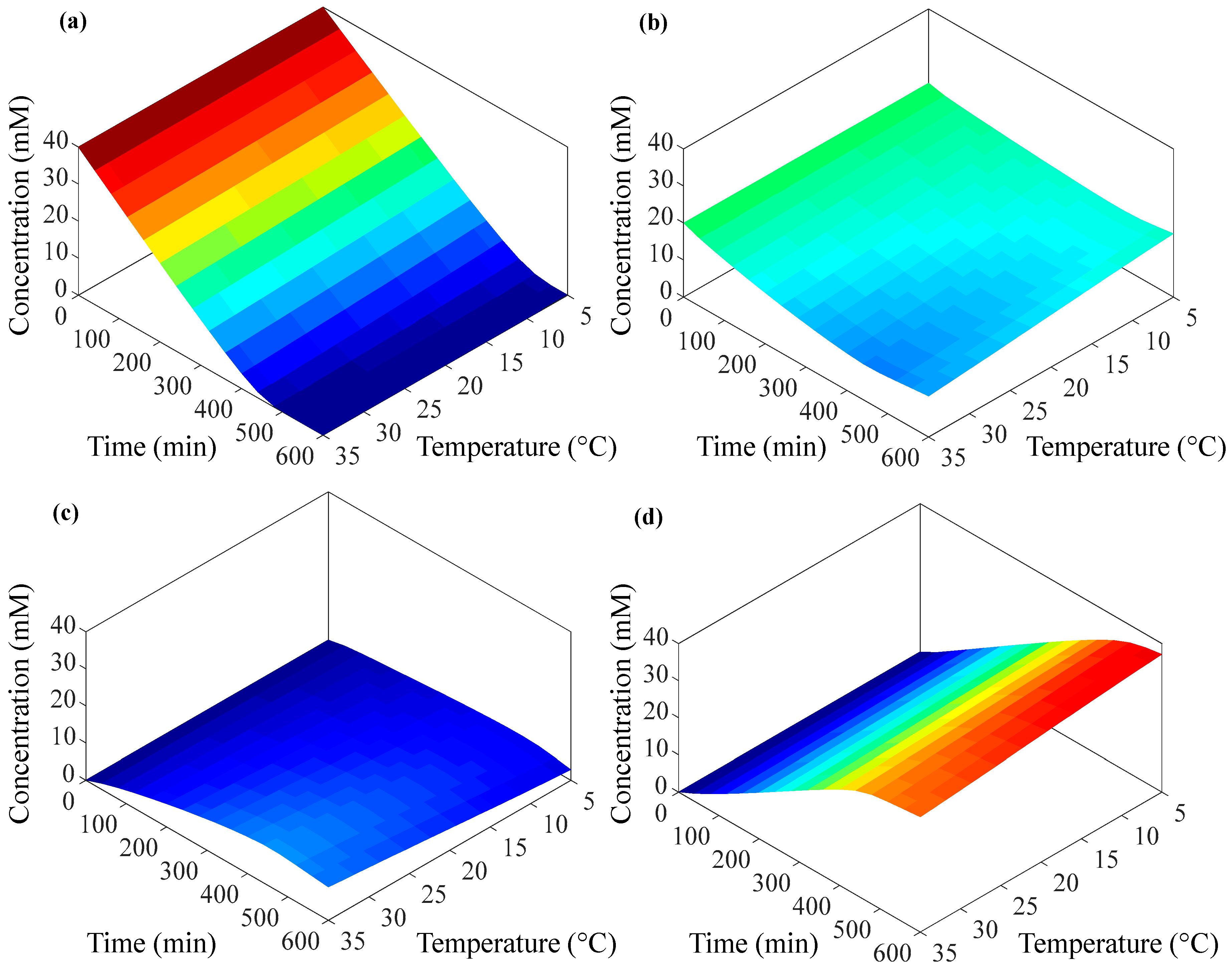
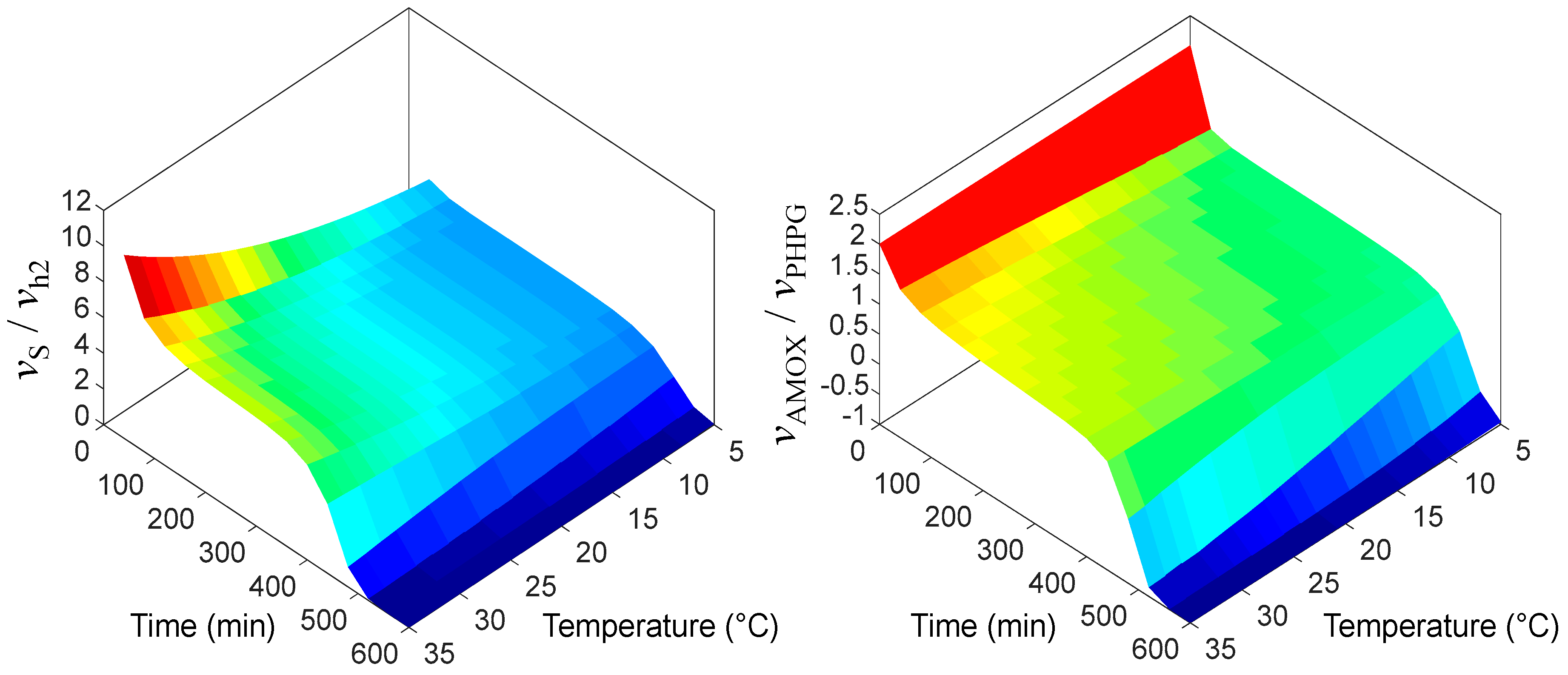
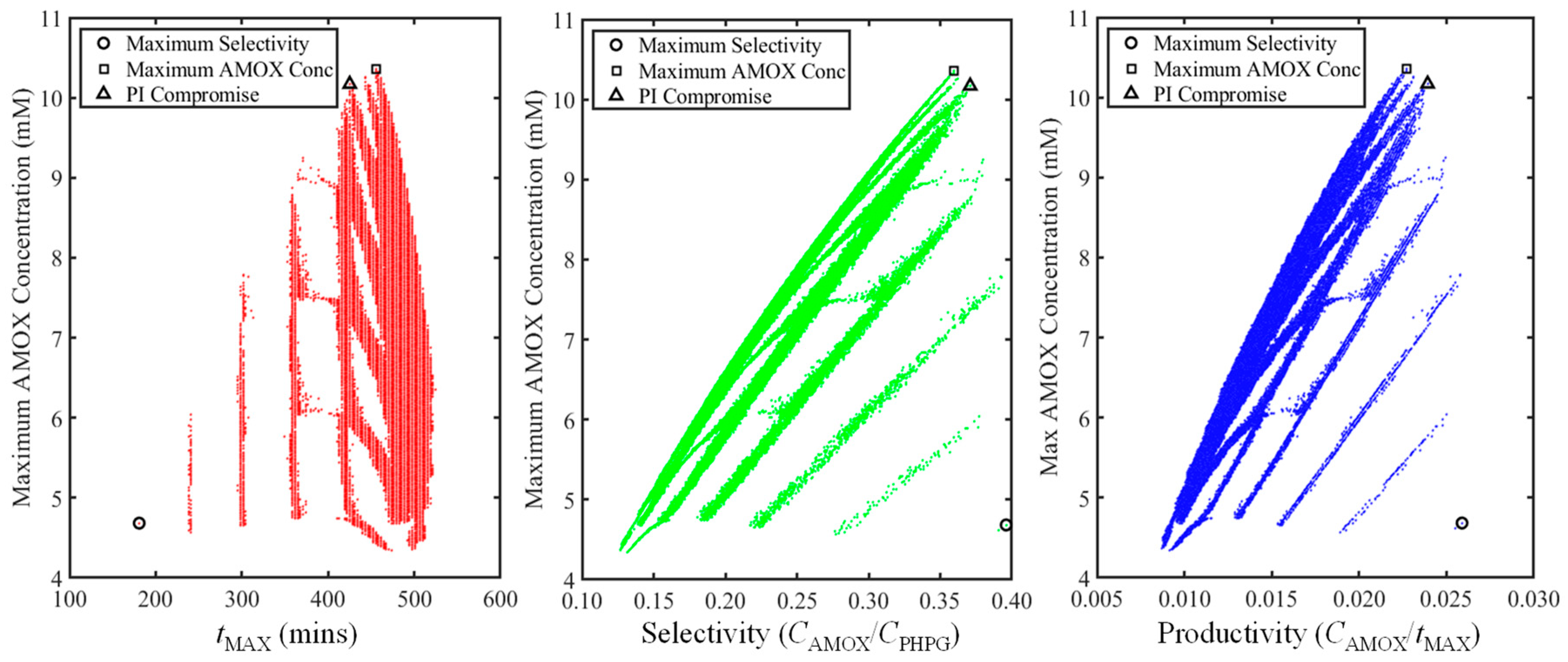



| Subclass | Antibiotic | Spectrum | Generation | Application | CAS # | MW | Sales [7,8] | Price |
|---|---|---|---|---|---|---|---|---|
| (g mol−1) | (tonnes) | (103 GBP kg−1) | ||||||
| Penicillin | Penicillin V | Narrow | 1st | Laryngitis, bronchitis, pneumonia, skin infections | 87-08-1 | 350.39 | 126.29 | 82.584 |
| Oxacillin | Narrow | 2nd | Staphylococci infections | 7240-38-2 | 401.44 | 2.87 | 293.334 | |
| Nafcillin | Narrow | 2nd | Staphylococci infections | 985-16-0 | 414.48 | 8.48 | 27.206 | |
| Dicloxacillin | Narrow | 2nd | Bronchitis, pneumonia, staphylococci infections | 3116-76-5 | 470.33 | 7.35 | 71.100 | |
| Ampicillin | Broad | 3rd | UTIs, pneumonia, gonorrhoea, meningitis, abdominal infections | 69-53-4 | 349.41 | 42.35 | 11.358 | |
| Amoxicillin | Broad | 3rd | Tonsillitis, bronchitis, pneumonia, gonorrhoea, sinus infections, UTIs | 26787-78-0 | 365.40 | 1,122.41 | 37.057 | |
| Ticarcillin | Broad | 4th | UTIs, bone + joint infections, stomach infections, skin infections | 34787-01-4 | 384.43 | 2.92 | 46.487 | |
| Piperacillin | Broad | 4th | UTIs, bone + joint infections, stomach infections, skin infections | 66258-76-2 | 517.56 | 140.51 | 60.854 | |
| Cephalosporin | Cephalexin | n/a | 1st | UTIs, upper respiratory tract infections, ear infections, skin infections | 15686-71-2 | 347.39 | 321.90 | 63.152 |
| Cefadroxil | n/a | 1st | UTIs, staphylococci infections, skin infections | 66592-87-8 | 363.39 | 11.75 | 83.638 | |
| Cefazolin | n/a | 1st | Respiratory tract infections, UTIs, skin infections, | 25953-19-9 | 454.51 | 39.39 | 5.930 | |
| Cefdinir | n/a | 2nd | Bronchitis, pneumonia, skin infections, sinus infections | 91832-40-5 | 395.42 | 41.77 | 59.457 | |
| Cefaclor | n/a | 2nd | UTIs, respiratory tract infections, sinus infections | 53994-73-3 | 367.81 | 2.95 | 33.487 | |
| Cefprozil | n/a | 2nd | Ear infections, skin infections | 92665-29-7 | 389.43 | 11.12 | 33.813 | |
| Cefoxitin | n/a | 2nd | UTIs, skin infections, pneumonia, bronchitis, tonsillitis, ear infections | 35607-66-0 | 427.45 | 4.30 | 156.519 | |
| Cefixime | n/a | 3rd | Sinus infections, bronchitis, pneumonia | 79350-37-1 | 453.45 | 1.73 | 59.919 | |
| Cefotaxime | n/a | 3rd | UTIs, pneumonia, abdominal infections, bone + joint infections | 63527-52-6 | 455.47 | 2.57 | 251.725 | |
| Ceftriaxone | n/a | 3rd | Lower respiratory tract infections, UTIs, skin infections | 104376-79-6 | 554.58 | 29.90 | 212.500 | |
| Monobactam | Aztreonam | n/a | n/a | Pneumonia | 1-5-7 | 435.43 | 3.72 | 39.492 |
| Compound | Abbreviation | Type | CAS # | MW (g mol−1) |
|---|---|---|---|---|
| p-hydroxyphenyl glycine methyl ester | PHPGME | Feed | 127369-30-6 | 180.18 |
| 6-aminopenicillanic acid | 6-APA | Feed/Side product | 551-16-6 | 216.26 |
| amoxicillin | AMOX | Product | 26787-78-0 | 365.40 |
| p-hydroxyphenyl glycine methyl ester | PHPG | Side product | 37784-25-1 | 167.16 |
| Parameter | T = 5 °C | T = 25 °C | T = 35 °C | |
|---|---|---|---|---|
| T-dependent | kcat,1 (IU g−1 min−1) | 0.57 | 0.59 | 0.64 |
| kcat,2 (IU g−1 min−1) | 9.16 | 3.07 | 1.77 | |
| Fixed | KM1 (mM) | 0.20 | 0.20 | 0.20 |
| KM2 (mM) | 27.47 | 27.47 | 27.47 | |
| Xmax (–) | 0.96 | 0.96 | 0.96 | |
| kE (mM) | 16.03 | 16.03 | 16.03 | |
| kPHPGME (mM) | 2672.04 | 2672.04 | 2672.04 | |
| kAMOX (mM) | 4.59 | 4.59 | 4.59 | |
| kPHPG (mM) | 4.51 | 4.51 | 4.51 | |
| k6-APA (mM) | 4550.28 | 4550.28 | 4550.28 |
| Parameter | kcat,1 | kcat,2 |
|---|---|---|
| k0 (IU g−1 min−1) | 1.89 | 4.74 × 10−7 |
| Ea (J mol−1) | 2.80 × 103 | −3.88 × 104 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuthbertson, A.B.; Rodman, A.D.; Diab, S.; Gerogiorgis, D.I. Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin. Processes 2019, 7, 318. https://doi.org/10.3390/pr7060318
Cuthbertson AB, Rodman AD, Diab S, Gerogiorgis DI. Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin. Processes. 2019; 7(6):318. https://doi.org/10.3390/pr7060318
Chicago/Turabian StyleCuthbertson, Andrew B., Alistair D. Rodman, Samir Diab, and Dimitrios I. Gerogiorgis. 2019. "Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin" Processes 7, no. 6: 318. https://doi.org/10.3390/pr7060318
APA StyleCuthbertson, A. B., Rodman, A. D., Diab, S., & Gerogiorgis, D. I. (2019). Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin. Processes, 7(6), 318. https://doi.org/10.3390/pr7060318