Design and Implementation of the Off-Line Robust Model Predictive Control for Solid Oxide Fuel Cells †
Abstract
1. Introduction
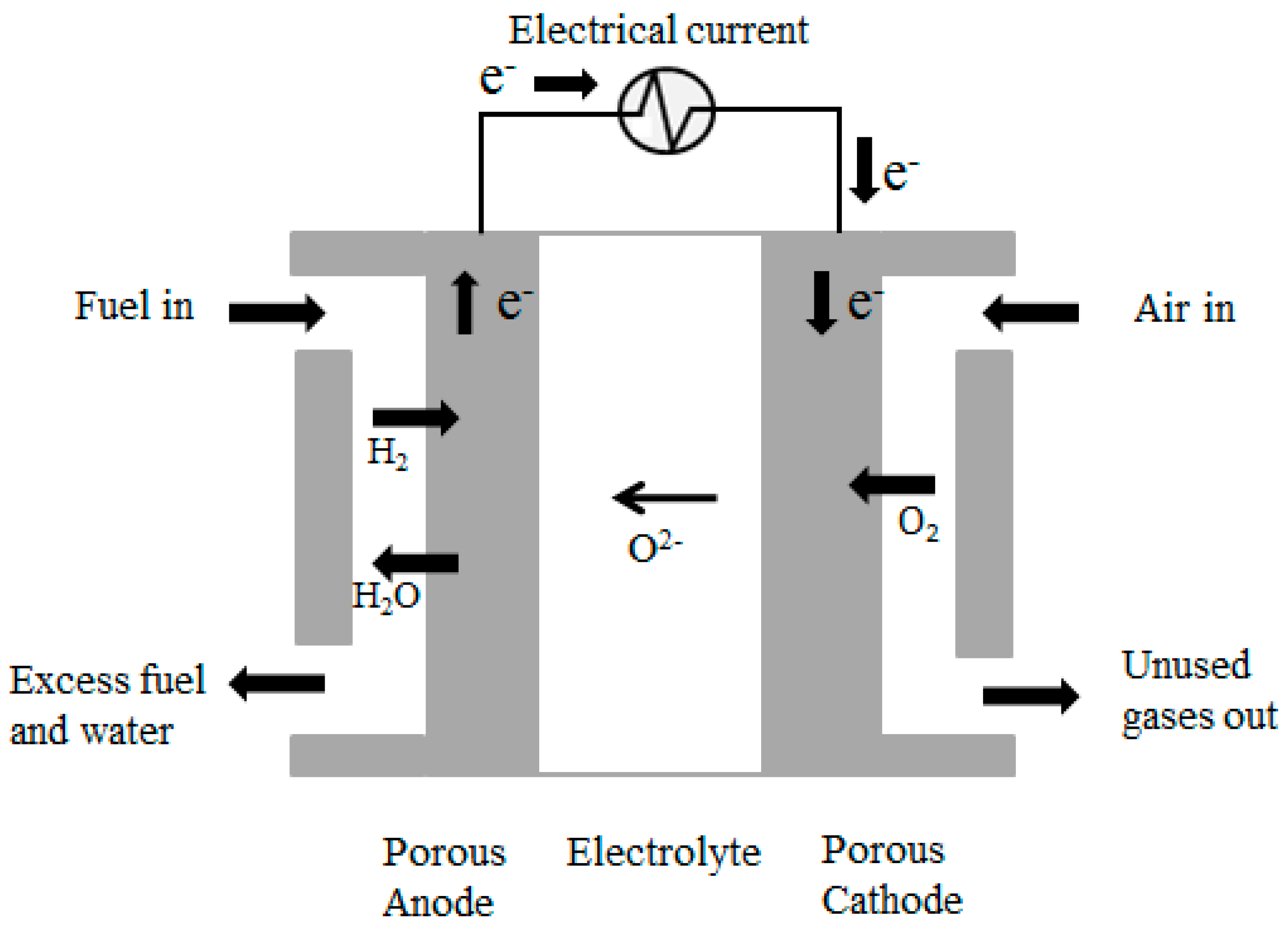
2. SOFC Model
2.1. Mass and Energy Balances
2.2. Electrochemical Model
3. Robust Model Predictive Control
3.1. Robust MPC Algorithm
3.2. Off-Line Robust MPC Algorithm Using Ellipsoidal Invariant Sets
4. SOFC Operation
5. Results and Discussion
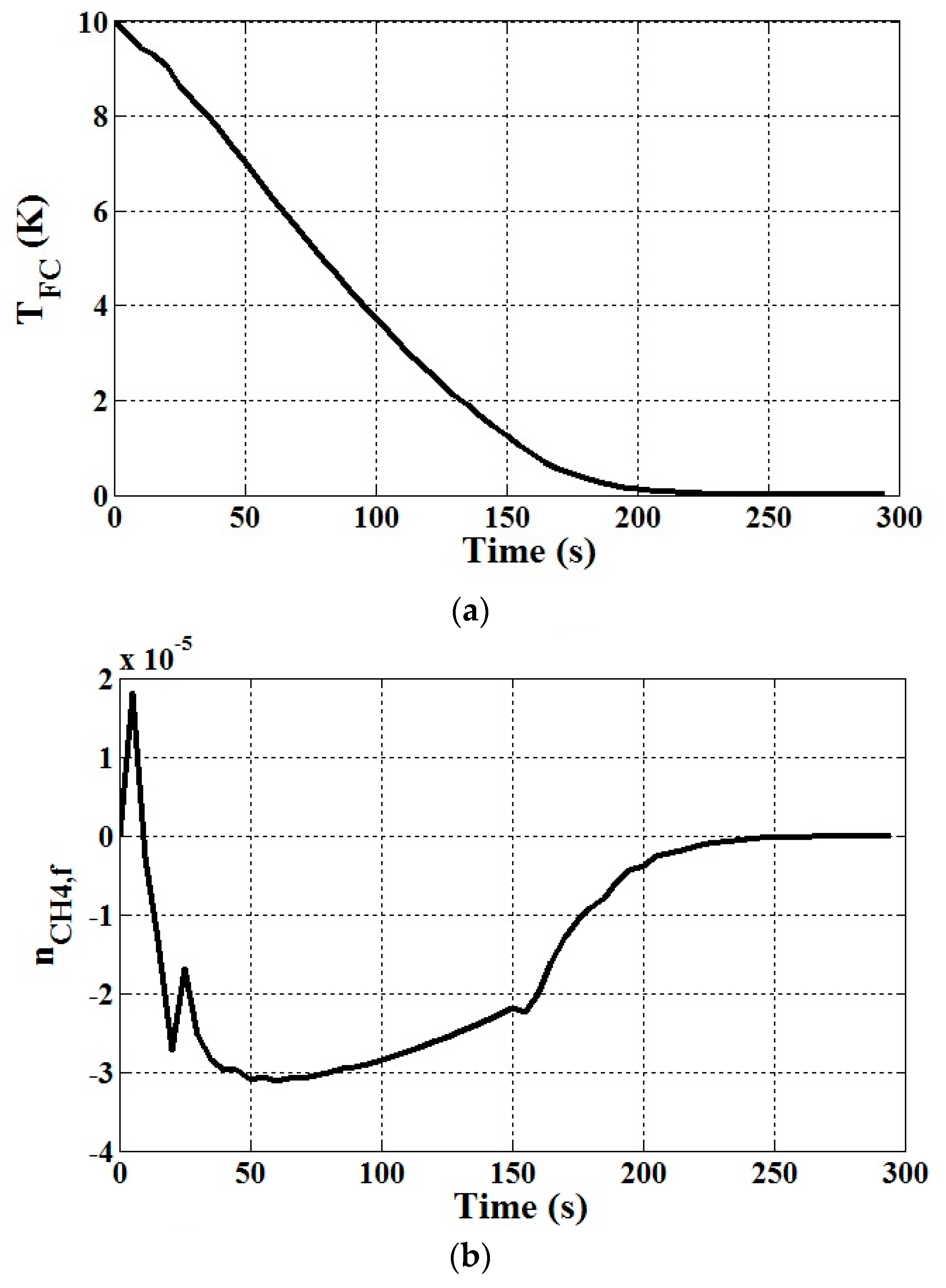
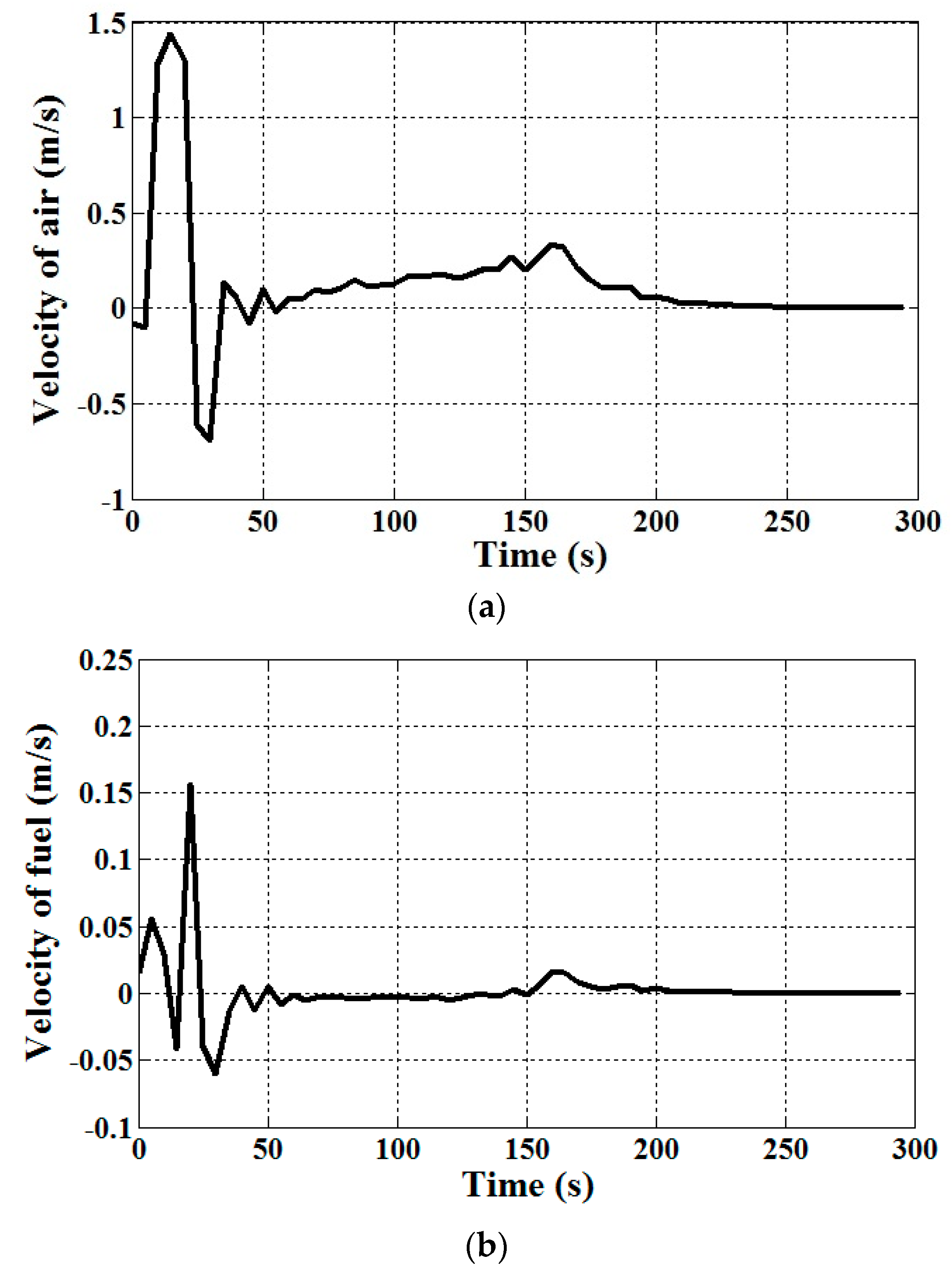
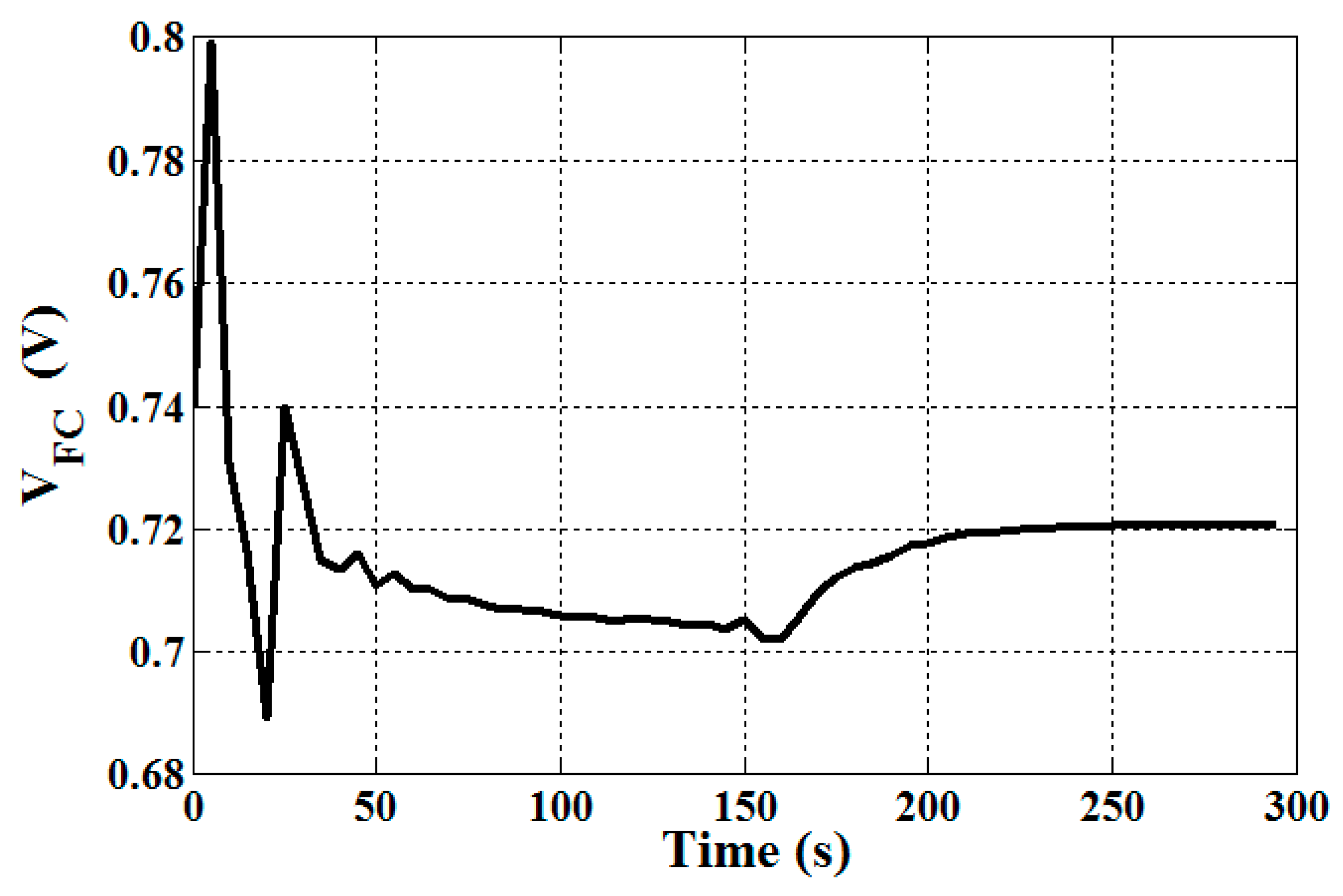
5.1. Dynamics of SOFC
5.2. Control of SOFC
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saedea, D.; Authayanun, S.; Patcharavorachot, Y.; Arpornwichanop, A. Effect of anode-cathode exhaust gas recirculation on energy recuperation in a solid oxide fuel cell-gas turbine hybrid power system. Energy 2016, 94, 218–232. [Google Scholar]
- Atawi, I.E.; Kassem, A.M.; Zaid, S.A. Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System. Processes 2019, 7, 85. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, C.; Jia, L.; Wang, Z.; Li, Y. Recent progress on solid oxide fuel cell: Lowering temperature and utilizing non-hydrogen fuels. Int. J. Hydrog. Energy 2013, 38, 16498–16517. [Google Scholar] [CrossRef]
- Palomba, V.; Ferraro, M.; Frazzica, A.; Vasta, S.; Sergi, F.; Antonucci, V. Experimental and numerical analysis of a SOFC-CHP system with adsorption and hybrid chillers for telecommunication applications. Appl. Energy 2018, 216, 620–633. [Google Scholar] [CrossRef]
- Fuqiang, W.; Lin, J.; Ziming, C.; Huaxu, L.; Jianyu, T. Combination of thermodynamic analysis and regression analysis for steam and dry methane reforming. Int. J. Hydrog. Energy 2019, 44, 15795–15810. [Google Scholar] [CrossRef]
- Liao, C.H.; Horng, R.F. Experimental study of syngas production from methane dry reforming with heat recovery strategy. Int. J. Hydrog. Energy 2017, 42, 25213–25224. [Google Scholar] [CrossRef]
- Lo Faro, M.; Trocino, S.; Zignani, S.C.; Italiano, C.; Vita, A.; Arico, A.S. Study of a solid oxide fuel cell fed with n-dodecane reformate. Part II: Effect of the reformate composition. Int. J. Hydrog. Energy 2017, 42, 1751–1757. [Google Scholar] [CrossRef]
- Mustapha, N.A.; Sharuddin, S.S.; Zainudin, M.H.M.; Ramli, N.; Shirai, Y.; Maeda, T. Inhibition of methane production by the palm oil industrial waste phospholine gum in a mimic enteric fermentation. J. Clean. Prod. 2017, 165, 621–629. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Corigliano, O.; Lo Faro, M.; Frontera, P.; Antonucci, P.; Zignani, S.C.; Trocino, S.; Mirandola, F.A.; Aricò, A.S.; Fragiacomo, P. Thermoelectric characterization of an intermediate temperature solid oxide fuel cell system directly fed by dry biogas. Energy Convers. Manag. 2016, 127, 90–102. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Fragiacomo, P. Electrical and thermal analysis of an intermediate temperature IIR- SOFC system fed by biogas. Energy Sci. Eng. 2018, 6, 60–72. [Google Scholar] [CrossRef]
- Triphob, N.; Wongsakulphasatch, S.; Kiatkittipong, W.; Charinpanitkul, T.; Praserthdam, P.; Assabumrungrat, S. Integrated methane decomposition and solid oxide fuel cell for efficient electrical power generation and carbon capture. Chem. Eng. Res. Des. 2012, 90, 2223–2234. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Tanveer, W.H.; Sayed, E.T.; Assad, M.; Allagui, A.; Cha, S.W. On the technical challenges affecting the performance of direct internal reforming biogas solid oxide fuel cells. Renew. Sustain. Energy Rev. 2019, 101, 361–375. [Google Scholar] [CrossRef]
- Anderson, T.; Vijay, P.; Tade, M.O. An adaptable steady state Aspen Hysys model for the methane fuelled solid oxide fuel cell. Chem. Eng. Res. Des. 2014, 92, 295–307. [Google Scholar] [CrossRef]
- Kupecki, J.; Papurello, D.; Lanzini, A.; Naumovich, Y.; Motylinski, K.; Blesznowski, M.; Santarelli, M. Numerical model of planar anode supported solid oxide fuel cell fed with fuel containing H2S operated in direct internal reforming mode (DIR-SOFC). Appl. Energy 2018, 230, 1573–1584. [Google Scholar] [CrossRef]
- Pret, M.G.; Ferrero, D.; Lanzini, A.; Santarelli, M. Thermal design, modeling and validation of a steam-reforming reactor for fuel cell applications. Chem. Eng. Res. Des. 2015, 104, 503–512. [Google Scholar] [CrossRef]
- Vijay, P.; Hosseini, S.; Tade, M.O. A novel concept for improved thermal management of the planar SOFC. Chem. Eng. Res. Des. 2013, 91, 560–572. [Google Scholar] [CrossRef]
- Vijay, P.; Tade, M.O. An adaptive non-linear observer for the estimation of temperature distribution in the planar solid oxide fuel cell. J. Process Control 2013, 23, 429–443. [Google Scholar] [CrossRef]
- Lu, X.; Li, T.; Bertei, A.; Cho, J.I.S.; Heenan, T.M.M.; Rabuni, M.F.; Li, K.; Brett, D.J.L.; Shearing, P.R. The application of hierarchical structures in energy devices: New insights into the design of solid oxide fuel cells with enhanced mass transport. Energy Environ. Sci. 2018, 11, 2390–2403. [Google Scholar] [CrossRef]
- Chaisantikulwat, A.; Diaz-Goano, C.; Meadows, E.S. Dynamic modeling and control of planar anode-supported solid oxide fuel cell. Comput. Chem. Eng. 2008, 32, 2365–2381. [Google Scholar] [CrossRef]
- Madani, O.; Das, T. Feedforward based transient control in solid oxide fuel cells. Control Eng. Pract. 2016, 56, 86–91. [Google Scholar] [CrossRef]
- Lotfi, N.; Zomorodi, H.; Landers, R.G. Active disturbance rejection control for voltage stabilization in open-cathode fuel cells through temperature regulation. Control Eng. Pract. 2016, 56, 92–100. [Google Scholar] [CrossRef]
- Li, Y.H.; Choi, S.S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Conver. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Aguiar, P.; Adjiman, C.S.; Brandon, N.P. Anode-supported intermediate-temperature direct internal reforming solid oxide fuel cell. II: Model-based dynamic performance and control. J. Power Sources 2005, 147, 136–147. [Google Scholar] [CrossRef]
- Stiller, C.; Thorud, B.; Bolland, O.; Kandepu, R.; Imsland, L. Control strategy for a solid oxide fuel cell and gas turbine hybrid system. J. Power Sources 2006, 158, 303–315. [Google Scholar] [CrossRef]
- Zhang, X.W.; Chan, S.H.; Ho, H.K.; Li, J.; Feng, Z. Nonlinear model predictive control based on the moving horizon state estimation for the solid oxide fuel cell. Int. J. Hydrog. Energy 2008, 33, 2355–2366. [Google Scholar] [CrossRef]
- Gutierrez, G.; Ricardez-Sandoval, L.A.; Budman, H.; Prada, C. An MPC-based control structure selection approach for simultaneous process and control design. Comput. Chem. Eng. 2014, 70, 11–21. [Google Scholar] [CrossRef]
- Wu, F. LMI-based robust model predictive control and its application to an industrial CSTR problem. J. Process Control 2001, 11, 649–659. [Google Scholar] [CrossRef]
- Tahir, F.; Jaimoukha, I.M. Robust feedback model predictive control of constrained uncertain systems. J. Process Control 2013, 23, 189–200. [Google Scholar] [CrossRef]
- Kothare, M.V.; Balakrishnan, V.; Morari, M. Robust constrained model predictive control using linear matrix inequalities. Automatica 1996, 32, 1361–1379. [Google Scholar] [CrossRef]
- Bahakim, S.S.; Ricardez-Sandoval, L.A. Simultaneous design and MPC-based control for dynamic systems under uncertainty: A stochastic approach. Comput. Chem. Eng. 2014, 63, 66–81. [Google Scholar] [CrossRef]
- Manthanwar, A.M.; Sakizlis, V.; Pistikopoulos, E.N. Robust parametric predictive control design for polytopically uncertain systems. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 3994–3999. [Google Scholar]
- Bumroongsri, P.; Kheawhom, S. An off-line robust MPC algorithm for uncertain polytopic discrete-time systems using polyhedral invariant sets. J. Process Control 2012, 22, 975–983. [Google Scholar] [CrossRef]
- Pannocchia, G. Robust model predictive control with guaranteed setpoint tracking. J. Process Control 2004, 14, 927–937. [Google Scholar] [CrossRef]
- Kouramas, K.; Varbanov, P.S.; Georgiadis, M.C.; Klemes, J.J.; Pistikopoulos, E.N. Explicit/multi-parametric model predictive control of a solid oxide fuel cell. In Proceedings of the 21st European Symposium on Computer Aided Chemical Engineering (ESCAPE21), Halkidiki, Greece, 29 May–1 June 2011; pp. 773–777. [Google Scholar]
- Wan, Z.; Kothare, M.V. Robust output feedback model predictive control using off-line linear matrix inequalities. J. Process Control 2002, 12, 763–774. [Google Scholar] [CrossRef]
- Pirkandi, J.; Ghassemi, M.; Hamedi, M.H.; Mohammadi, R. Electrochemical and thermodynamic modeling of a CHP system using tubular solid oxide fuel cell (SOFC-CHP). J. Clean. Prod. 2012, 29–30, 151–162. [Google Scholar] [CrossRef]
- Yang, Y.; Du, X.; Yang, L.; Huang, Y.; Xian, H. Investigation of methane steam reforming in planar porous support of solid oxide fuel cell. Appl. Therm. Eng. 2009, 29, 1106–1113. [Google Scholar] [CrossRef]
- Achenbach, E.; Riensche, E. Methane/steam reforming kinetics for solid oxide fuel cells. J. Power Sources 1994, 52, 283–288. [Google Scholar] [CrossRef]
- Xi, H.; Varigonda, S.; Jing, B. Dynamic modeling of a solid oxide fuel cell system for control design. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 423–428. [Google Scholar]
- Murshed, A.M.; Huang, B.; Nandakumar, K. Control relevant modeling of planar solid oxide fuel cell system. J. Power Sources 2007, 163, 830–835. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Micro-scale modeling of oxide fuel cells with micro-structurally graded electrodes. J. Power Sources 2007, 168, 369–378. [Google Scholar] [CrossRef]
- Patcharavorachot, Y.; Arpornwichanop, A.; Chuachuensuk, A. Electrochemical study of a planar solid oxide fuel cell: Role of support structures. J. Power Sources 2008, 177, 254–261. [Google Scholar] [CrossRef]
- Liu, R.W. Convergent systems. IEEE Trans. Autom. Control 1968, 13, 384–391. [Google Scholar]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM Studies in Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Georgis, D.; Jogwar, S.S.; Almansoori, A.S.; Daoutidis, P. Design and control of energy integrated SOFC systems for in situ hydrogen production and power generation. Comput. Chem. Eng. 2011, 35, 1691–1704. [Google Scholar] [CrossRef]
- Sturm, J.F. Using Sedumi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the IEEE International Symposium on Robotics and Automation, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]


| Reactions | No. | Reaction Equations | Reaction Rates | ∆H (kJ mol−1) |
|---|---|---|---|---|
| Steam reforming | (i) | 206.10 | ||
| Water-gas shift | (ii) | −41.15 | ||
| Hydrogen oxidation | (iii) | |||
| Oxygen reduction | (iv) | |||
| Overall redox reaction | (v) | −241.83 |
| Model Parameters | ||
| Anode effective diffusivity coefficient (Deff,anode) | 3.66 × 10–5 | m2 s−1 |
| Cathode effective diffusivity coefficient (Deff,cathode) | 1.37 × 10–5 | m2 s−1 |
| Electronic conductivity of anode (σanode) | 9.5 × 107/TFC exp(−1150/TFC) | Ω−1 m−2 |
| Electronic conductivity of cathode (σcathode) | 4.2 × 107/TFC exp(−1200/TFC) | Ω−1 m−2 |
| Ionic conductivity of electrolyte (σelectrolyte) | 33.4 × 103 exp(−10,300/TFC) | Ω−1 m−2 |
| Anode thickness (τanode) | 500 | μm |
| Cathode thickness (τcathode) | 50 | μm |
| Electrolyte thickness (τelectrolyte) | 20 | μm |
| Fuel channel height (hf) | 1 | mm |
| Air channel height (ha) | 1 | mm |
| Cell length (L) | 0.4 | m |
| Cell width (W) | 0.1 | m |
| Operating conditions | ||
| Pressure (P) | 1 | bar |
| Fuel inlet temperature (Tf0) | 1023 | K |
| Air inlet temperature (Ta0) | 1023 | K |
| Fuel utilization factor (Ufuel) | 70% | |
| Air ratio (λair) | 8.5 | |
| Fuel feed | S/C = 2, 10% pre-reforming | |
| Air feed | 21% O2, 79% N2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatrattanawet, N.; Kheawhom, S.; Chen, Y.-S.; Arpornwichanop, A. Design and Implementation of the Off-Line Robust Model Predictive Control for Solid Oxide Fuel Cells. Processes 2019, 7, 918. https://doi.org/10.3390/pr7120918
Chatrattanawet N, Kheawhom S, Chen Y-S, Arpornwichanop A. Design and Implementation of the Off-Line Robust Model Predictive Control for Solid Oxide Fuel Cells. Processes. 2019; 7(12):918. https://doi.org/10.3390/pr7120918
Chicago/Turabian StyleChatrattanawet, Narissara, Soorathep Kheawhom, Yong-Song Chen, and Amornchai Arpornwichanop. 2019. "Design and Implementation of the Off-Line Robust Model Predictive Control for Solid Oxide Fuel Cells" Processes 7, no. 12: 918. https://doi.org/10.3390/pr7120918
APA StyleChatrattanawet, N., Kheawhom, S., Chen, Y.-S., & Arpornwichanop, A. (2019). Design and Implementation of the Off-Line Robust Model Predictive Control for Solid Oxide Fuel Cells. Processes, 7(12), 918. https://doi.org/10.3390/pr7120918









