Model Study on Burden Distribution in COREX Melter Gasifier
Abstract
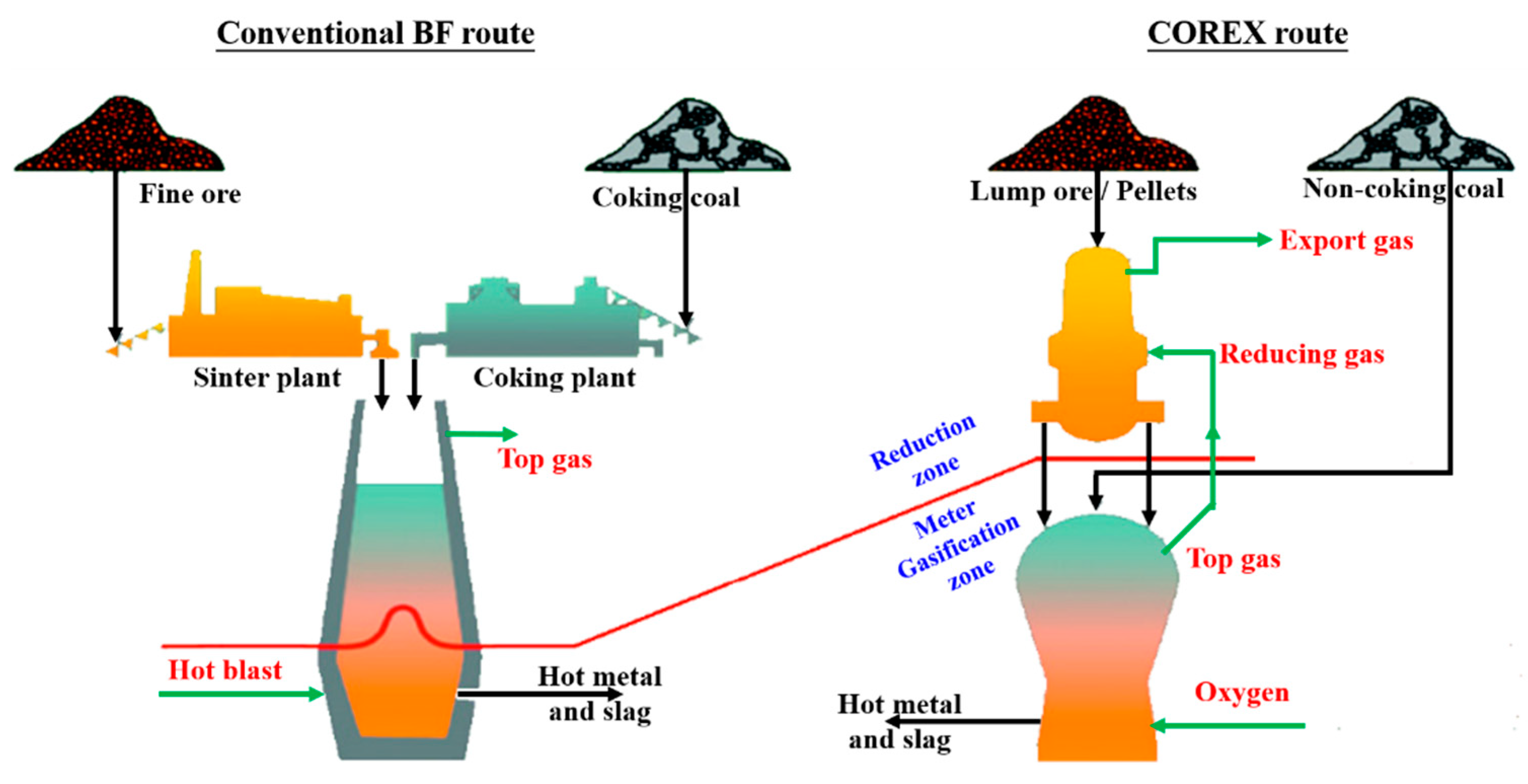
:1. Introduction
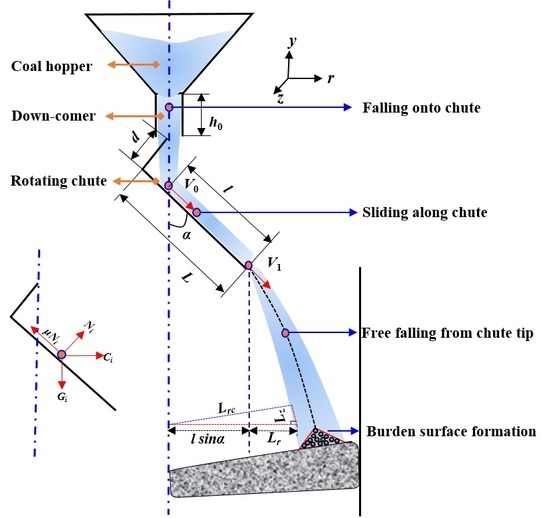
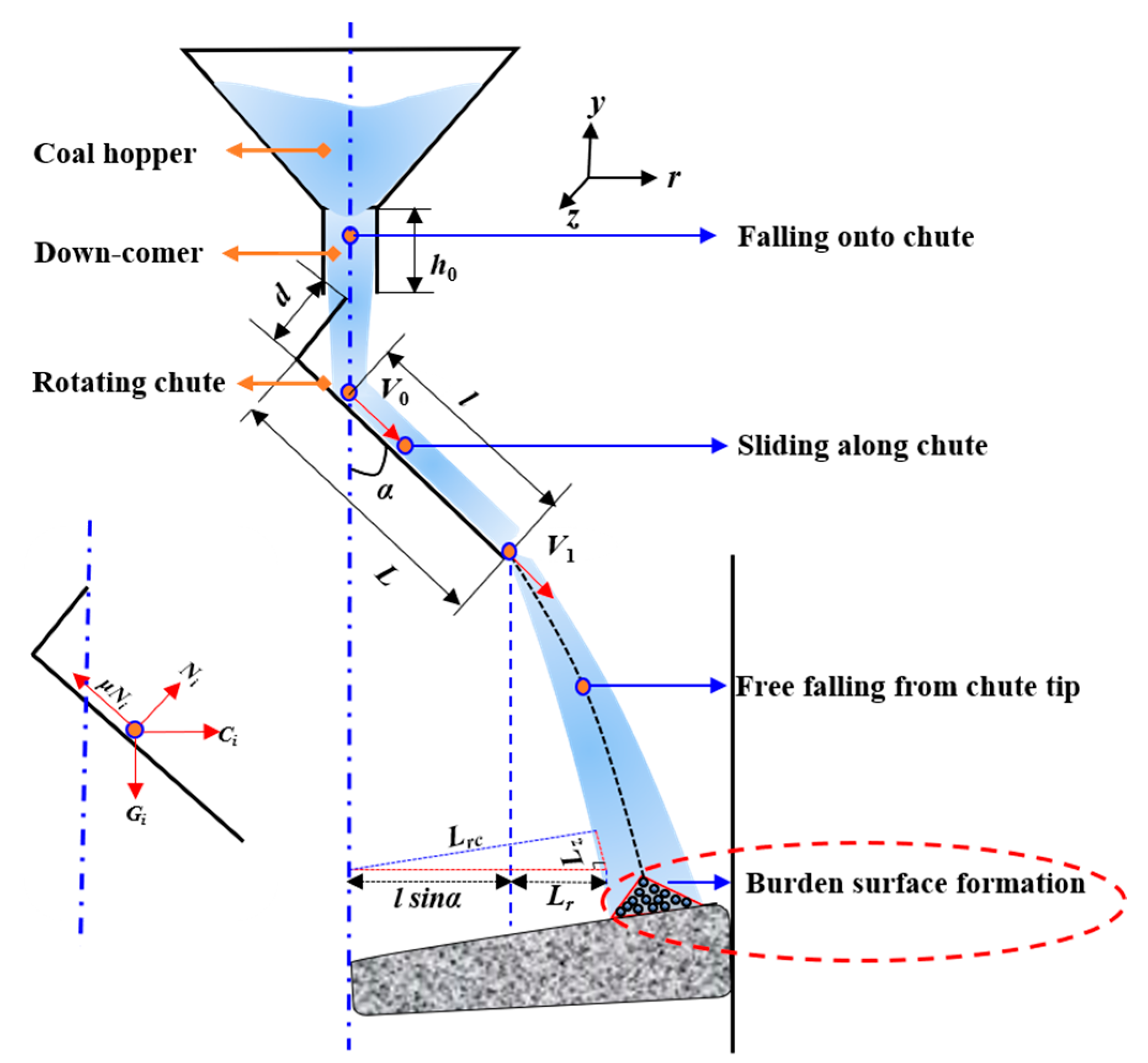
2. Mathematical Model
2.1. The Coal-Gimbal Distributor
2.2. The DRI-Flap Distributor
2.3. Formulation of Mathematical Model
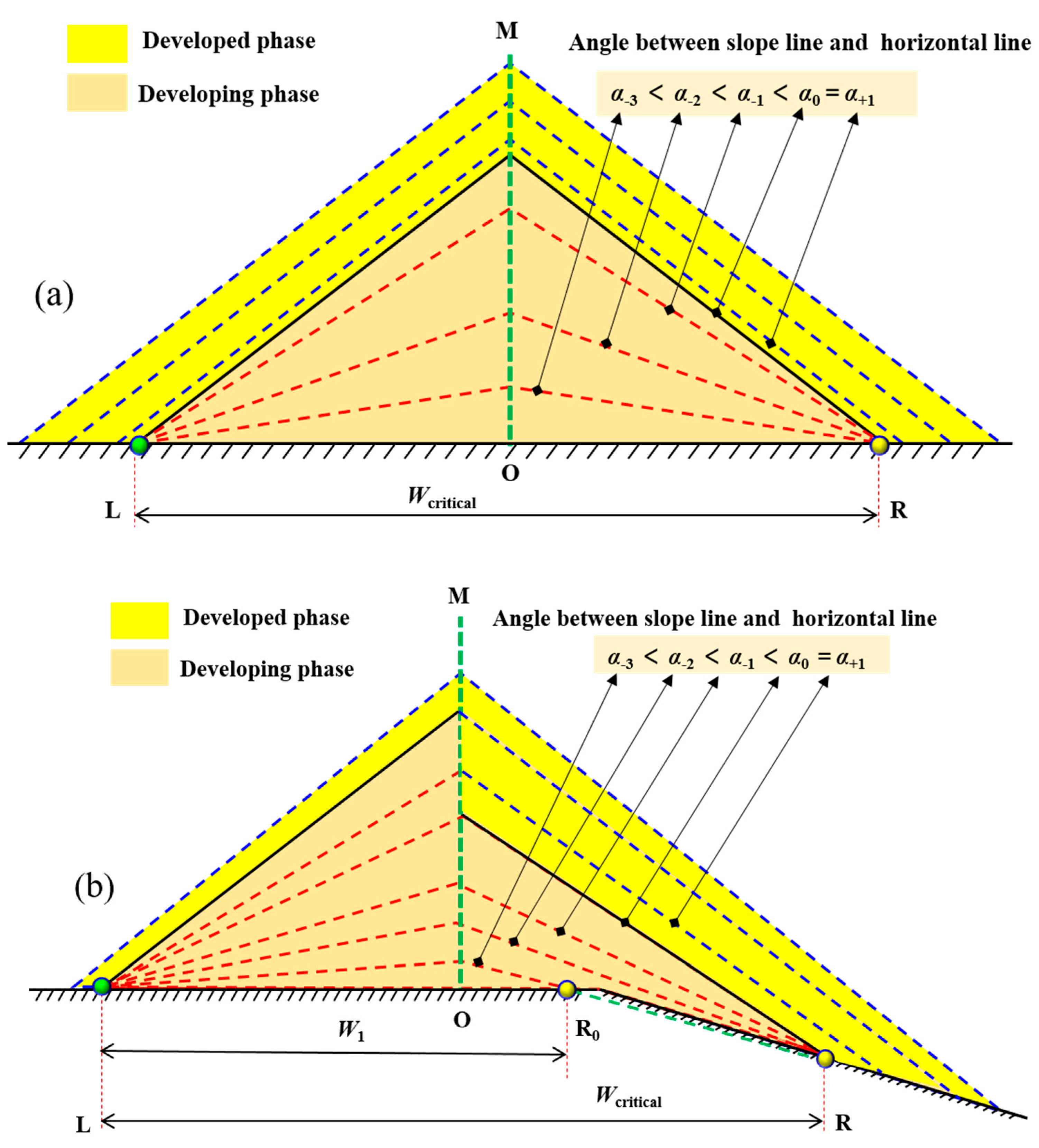
2.4. Result of Stable Initial Burden Profile
2.5. Growing Mechanism of Burden Surface
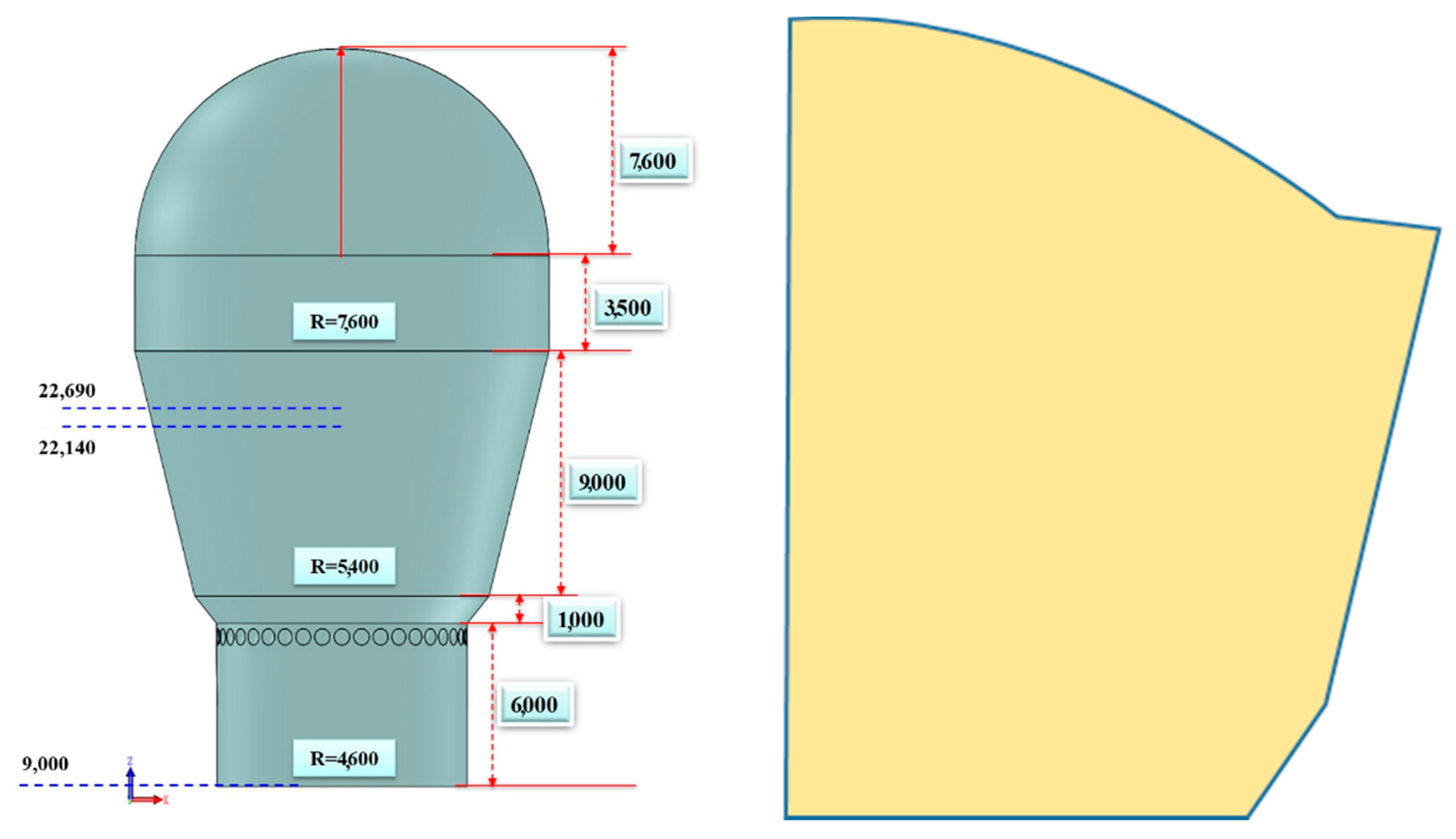
3. Results
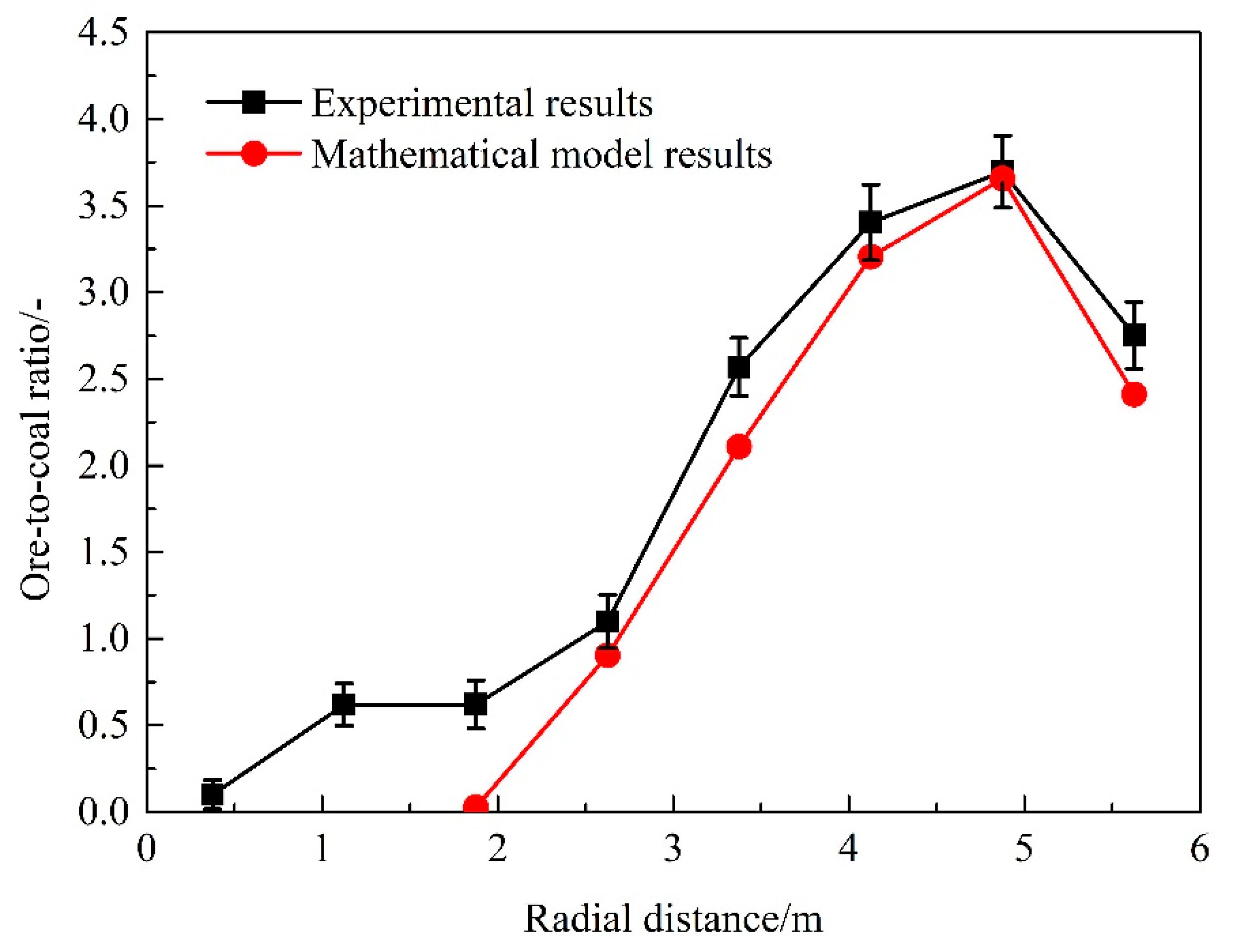
3.1. Verification of the Model
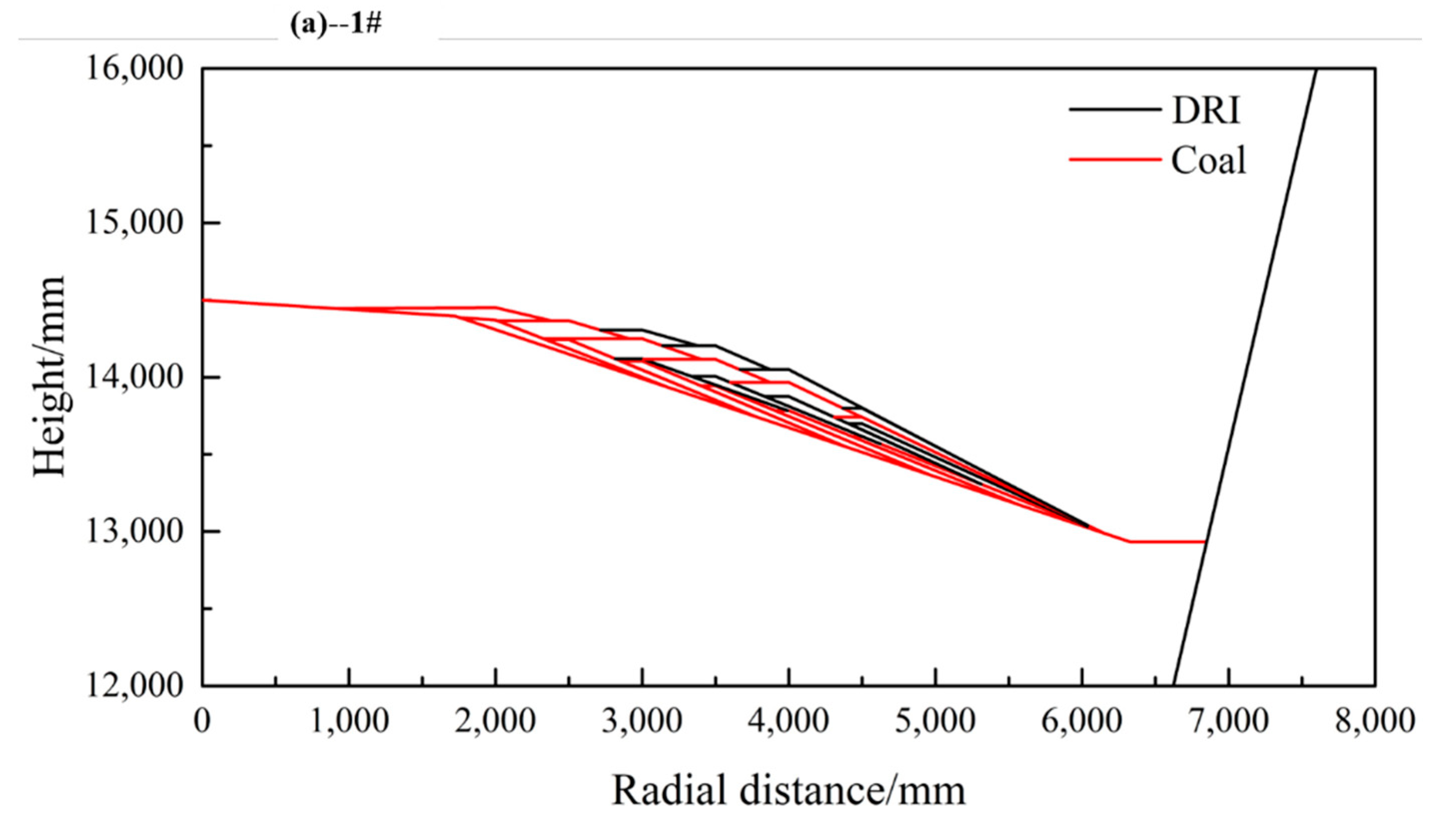
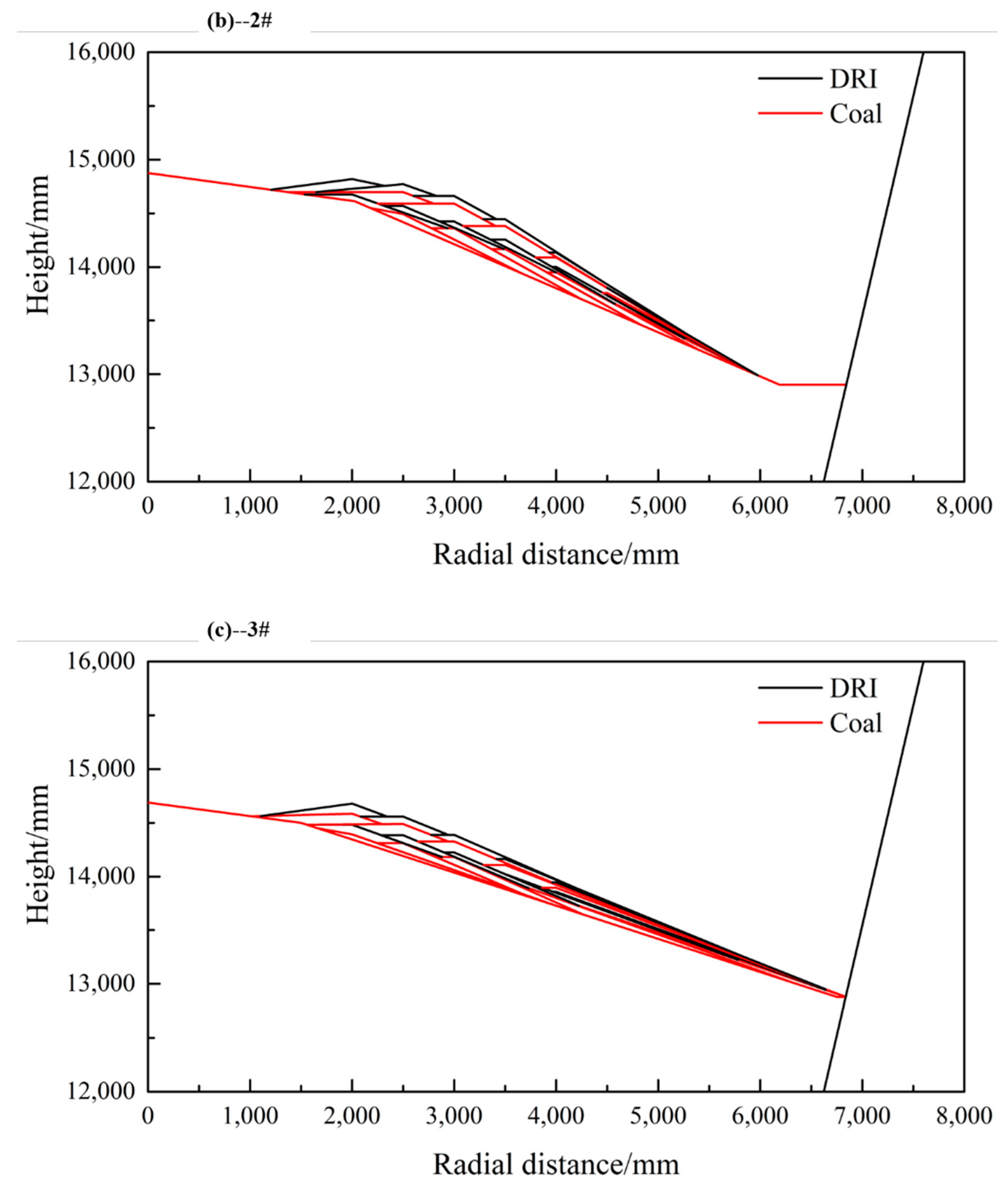
3.2. Application of the Model
4. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hasanbeigi, A.; Arens, M.; Price, L. Alternative emerging ironmaking technologies for energy-efficiency and carbon dioxide emissions reduction: A technical review. Renew. Sustain. Energy Rev. 2014, 33, 645–658. [Google Scholar] [CrossRef]
- Srishilan, C.; Shukla, A.K. Static thermochemical model of COREX melter gasifier. Metall. Mater. Trans. B 2018, 49, 388–398. [Google Scholar] [CrossRef]
- Song, J.Y.; Jiang, Z.Y.; Bao, C.; Xu, A.J. Comparison of Energy Consumption and CO2 Emission for Three Steel Production Routes—Integrated Steel Plant Equipped with Blast Furnace, Oxygen Blast Furnace or COREX. Metals 2019, 9, 364. [Google Scholar] [CrossRef]
- Xu, J.; Wu, S.L.; Kou, M.Y.; Zhang, L.H.; Yu, X.B. Circumferential burden distribution behaviors at bell-less top blast furnace with parallel type hoppers. Appl. Math. Model. 2011, 35, 1439–1455. [Google Scholar] [CrossRef]
- Ren, T.Z.; Jin, X.; Ben, H.Y.; Yu, C.Z. Burden distribution for bell-less top with two parallel hoppers. J. Iron Steel Res. Int. 2006, 13, 14–17. [Google Scholar] [CrossRef]
- Du, P.Y.; Cheng, S.S.; Teng, Z.J. Research of snakelike deviation in the burden distribution of a parallel-hopper bell-less top. J. Univ. Sci. Technol. Beijing 2011, 33, 479–485. (In Chinese) [Google Scholar]
- Shi, L.; Zhao, G.; Li, M.; Ma, X. A model for burden distribution and gas flow distribution of bell-less top blast furnace with parallel hoppers. Appl. Math. Model. 2016, 40, 10254–10273. [Google Scholar] [CrossRef]
- Park, J.I.; Jung, H.J.; Jo, M.K.; Oh, H.S.; Han, J.W. Mathematical modeling of the burden distribution in the blast furnace shaft. Met. Mater. Int. 2011, 17, 485–496. [Google Scholar] [CrossRef]
- Guo, H.W.; Zhang, J.L.; Chen, L.K.; Che, Y.M.; Yang, T.Y. Simulation of charging system in bell-less BF. Chin. J. Process. Eng. 2009, 9, 415–419. (In Chinese) [Google Scholar]
- Chen, L.S.; Luo, Z.G.; You, Y.; Zou, Z.S. Effects of Flap Angles on the Charging Procedure of Flap Distributors. J. Northeast. Univ. Nat. Sci. 2013, 34, 971–974. (In Chinese) [Google Scholar]
- You, Y.; Luo, Z.G.; Hou, Q.F.; Li, H.F.; Zhou, H.; Chen, R.; Zou, Z.S. Experimental Study of Burden Distribution in the COREX Melter Gasifier. Steel Res. Int. 2017, 88, 1700025. [Google Scholar] [CrossRef]
- Luo, Z.G.; You, Y.; Li, H.F.; Zhou, H.; Zou, Z.S. Experimental study on charging process in the COREX Melter Gasifier. Metall. Mater. Trans. B 2018, 49, 1740–1749. [Google Scholar] [CrossRef]
- Li, H.F.; You, Y.; Zou, Z.S.; Cai, J.J. Numerical simulation on the charging process of new DRI-Flap distributor. J. Northeast. Univ. Nat. Sci. 2016, 37, 800–804. (In Chinese) [Google Scholar]
- You, Y.; Luo, Z.G.; Li, H.F.; Zou, Z.S.; Yang, R.Y. Effects of the shape and inclination angle of DRI-flaps on DRI distribution in COREX Melter Gasifiers. Powder Technol. 2018, 339, 854–862. [Google Scholar] [CrossRef]
- Li, H.F.; You, Y.; Zhou, H.; Luo, Z.G.; Zou, Z.S. Study on burden pile profile prediction model for COREX-3000 Melter Gasifier. J. Chongqing Univ. 2015, 38, 39–44. (In Chinese) [Google Scholar]
- Zhang, H.M. CFD-DEM Modeling of Multiphase Flow in a FINEX Melter Gasifier. Ph.D. Thesis, University New South Wales, Sydney, Australia, 2015; pp. 95–144. [Google Scholar]
- Saxén, H.; Hinnelä, J. Model for Burden Distribution Tracking in the Blast Furnace. Miner. Process. Extr. Metall. Rev. 2004, 25, 1–27. [Google Scholar] [CrossRef]
- Mitra, T.; Saxén, H. Model for Fast Evaluation of Charging Programs in the Blast Furnace. Metall. Mater. Trans. B 2014, 45, 2382–2394. [Google Scholar] [CrossRef]
- Li, H.F.; Saxén, H.; Liu, W.Q.; Shao, L.; Zou, Z.S. Model-based analysis of factors affecting the burden layer structure in the blast furnace shaft. Metals 2019, 9, 1003. [Google Scholar] [CrossRef]
- You, Y.; Luo, Z.G.; Zou, Z.S.; Yang, R.Y. Numerical study on mixed charging process and gas-solid flow in COREX Melter Gasifier. Powder Technol. 2019. [Google Scholar] [CrossRef]




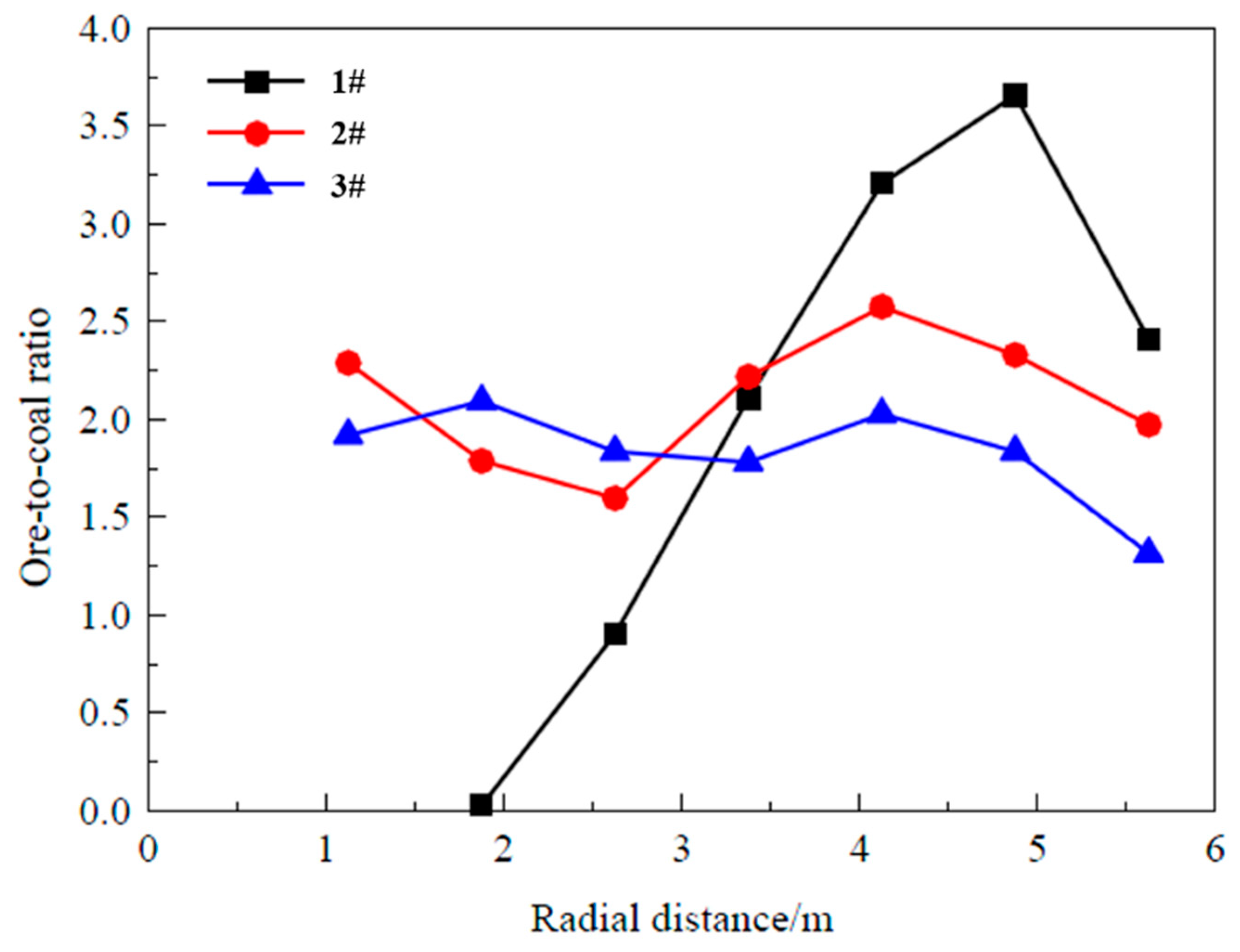
| Parameters | R0.5 | R1.0 | R1.5 | R2.0 | R2.5 | R3.0 | R3.5 | R4.0 | R4.5 | R5.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| Wcoal | - | 220 | 240 | 265 | 280 | 300 | 320 | 350 | 365 | - |
| Lcoal | - | 37 | 94 | 151 | 208 | 264 | 320 | 376 | 431 | - |
| Rcoal | - | 257 | 334 | 412 | 490 | 567 | 644 | 721 | 797 | - |
| WDRI | - | - | - | 300 | - | 330 | - | 350 | - | 370 |
| LDRI | - | - | - | 134 | - | 237 | - | 389 | - | 563 |
| RDRI | - | - | - | 437 | - | 563 | - | 738 | - | 935 |
| Rings | R0.5 | R1.0 | R1.5 | R2.0 | R2.5 | R3.0 | R3.5 | R4.0 | R4.5 | R5.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | |||||||||||
| Relative thickness of coal | - | - | - | 0.5 | 0.6 | 0.7 | 0.6 | 0.6 | 0.5 | - | |
| Volume of coal/m3 | - | - | - | 0.639 | 0.958 | 1.341 | 1.341 | 1.533 | 1.437 | - | |
| Relative thickness of DRI | - | - | - | - | - | 0.5 | 0.8 | 1 | 1 | - | |
| Volume of DRI/m3 | - | - | - | - | - | 0.504 | 0.941 | 1.344 | 1.512 | ||
| Parameters | R0.5 | R1.0 | R1.5 | R2.0 | R2.5 | R3.0 | R3.5 | R4.0 | R4.5 | R5.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| Lcoal | 0.00 | 276.98 | 704.83 | 1131.57 | 1556.92 | 1980.52 | 2401.81 | 2819.98 | 3233.79 | 3641.21 |
| Rcoal | 1490.65 | 1923.88 | 2507.98 | 3090.97 | 3672.58 | 4252.43 | 4829.96 | 5404.39 | 5974.45 | 6538.12 |
| LDRI | 0.00 | 0.00 | 0.00 | 1003.81 | 1373.31 | 1777.01 | 2285.95 | 2916.84 | 3588.18 | 4224.70 |
| RDRI | 2013.75 | 2100.00 | 2186.25 | 3276.31 | 3732.06 | 4222.01 | 4817.20 | 5534.34 | 6291.93 | 7014.70 |
| Case NO. | Materials Type | Relative Thickness (–) at Different Rings Locations (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R1.0 | R1.5 | R2.0 | R2.5 | R3.0 | R3.5 | R4.0 | R4.5 | R5.0 | ||
| 1# | Coal | - | - | 0.5 | 0.6 | 0.7 | 0.6 | 0.6 | 0.5 | - |
| DRI | - | - | - | - | 0.5 | 0.8 | 1.0 | 1.0 | - | |
| 2# | Coal | - | - | - | 0.5 | 0.8 | 0.7 | 0.6 | 0.15 | - |
| DRI | - | - | 1.0 | 0.8 | 0.8 | 0.7 | 0.6 | 0.2 | - | |
| 3# | Coal | - | - | 0.7 | 0.7 | 0.8 | 0.9 | 0.8 | - | - |
| DRI | - | - | 1.0 | 0.8 | 0.8 | 0.8 | 0.75 | - | - | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zou, Z.; Luo, Z.; Shao, L.; Liu, W. Model Study on Burden Distribution in COREX Melter Gasifier. Processes 2019, 7, 892. https://doi.org/10.3390/pr7120892
Li H, Zou Z, Luo Z, Shao L, Liu W. Model Study on Burden Distribution in COREX Melter Gasifier. Processes. 2019; 7(12):892. https://doi.org/10.3390/pr7120892
Chicago/Turabian StyleLi, Haifeng, Zongshu Zou, Zhiguo Luo, Lei Shao, and Wenhui Liu. 2019. "Model Study on Burden Distribution in COREX Melter Gasifier" Processes 7, no. 12: 892. https://doi.org/10.3390/pr7120892
APA StyleLi, H., Zou, Z., Luo, Z., Shao, L., & Liu, W. (2019). Model Study on Burden Distribution in COREX Melter Gasifier. Processes, 7(12), 892. https://doi.org/10.3390/pr7120892