Abstract
The objective of this article is to investigate the impacts of thermo-diffusion effect on unsteady axisymmetric Casson flow over a time-dependent radially stretching sheet with a multi-slip parameter and the force of chemical reaction. We employed an established similarity transformation to this non-linear partial differential system to convert it into a system of ordinary differential equations. The numerical results are attained for this system by using KELLER-BOX implicit finite difference scheme. It has great reliability and accuracy even a very short time period for computational simulation. The impacts of influential flow parameters on fluid flow are sketched through graphs and the numerical results are thoroughly argued. The temperature, velocity and wall concentration control parameters are analyzed. (i) It is witnessed that chemical reaction is not favorable to enhance the velocity profile. (ii) Multi-slip parameters vary inversely with velocity profile. (iii) The fluid concentration in its boundary layer decreases with the increase of heavier species, the parameter of the reaction rate and the exponent of power law for fluids having Prandtl number = 10.0, 15.0, 20.0 and 25.0. Moreover, the skin-friction-coefficient factor and Nusselt-number are compared with the published work. A strong numerical solution agreement is being observed.
1. Introduction
The knowledge of non-Newtonian fluids has great importance for their characteristics and remarkable applications in industrial, medical products, and procedures to the researcher. These all non-Newtonian type fluids have non-linear relation between stress and strain, whereas Newtonian fluid model has a linear relations mode. Investigations of flow field and individualities in these fluids are completely different as compare to Newtonian fluids. The Casson fluid model is popular for good explanation of non-Newtonian fluids and their behavior, especially flow curves for blood. It is recordable convincing fluid model because of important useful implications in our daily life as in bio medical field and polymer processing. For practical purposes, it provides a convenient means for evaluating the two characteristics; Cason viscosity and the apparent yield stress. A great number of investigations have described about this chemical fields. In species research of mass and heat transformations with chemical reactions are of extensive importance in specially hydrometallurgical and chemical at the industrial level. Last past few decades, a basic “Penetration Theory” “Highie 1935” had been extensively practically applied to the time dependent diffusional problems without and with chemical reactions. As long we ascertain all about the results with chemical reactions were found for the case of mid-infinite bodies of fluids, even though physically absorptions into a determinate based film were measured. Several interesting phenomena were considered for analysis of mass transformations liminal with forced convection and chemical reactions [1]. For the work about vapor-deposition chemically fundamental results are obtained [2]. In diffusion model the chemical effect on browning motion was carried out by [3]. Some of the others investigation was studied by [4,5,6,7].
Until now, in the absence of Soret and Dufour impacts, all the above studies have been conducted. In a flowing fluid, heat and mass transfer occurring simultaneously results in a complicated relationship between the fluxes and the fluid’s flowing existence. Energy diffusion can be produced not only by gradients of temperature, but also by gradients of composition. The temperature gradients that result in Soret (thermo-diffusion) effect can create mass fluxes. At the other hand, the effect of the energy fluxes causedby the gradients of composition is called Dufour (diffusion-thermo). Such fluxes play an important role when there is a density difference in the flow regime.
The fluids of the boundary layer flow due to stretching /shrinking surfaces is a significant kind of flow occurring in engineering and chemical industries flow processes. These include paper production, liquid metal, glass fiber, and polymer sheet synthesis. The manufacture of non-newtonian fluids, including lubricants, physiological liquids, paints, colloidal liquids, biological liquids, biopolymer, and foodstuff, plays an important role in our daily lives. Bagh et al. [8] examined the influence of multiple slip-on non-newtonian fluids and they described that the velocity profile decline due to increasing in the hydrodynamic slip. Raza [9] analyzed the Casson fluid flow over a sheet and examined the radiation effects on temperature. Ashraf and coauthors [10] have investigated the micro-polar fluid flow toward a shrinking surface and also studied the radiation effects on thermal conductivity. Daniel et al. [11] studied the numerical solution of mixed convection magnetohydrodynamic flow over a sheet. Dhanai et al. [12] Several Magneto-hydro-dynamics (MHD) heat transfer fluid solutions were achieved with viscous dissipation. The study of the unsteady axisymmetric flow of non-Newtonian fluid over a radially stretch sheet has considered by Shahzad et al. [13]. They also studied the radiation effects on the thermal boundary layer. Ashraf et al. [14] examined the magnetohydrodynamic flow and heat transfer in a micro-polar fluid using a stretchable disk. Azeem et al. [15] analyzed the heat transfer of an axisymmetric viscous fluid over a nonlinear radially stretching sheet.
The study of free convection flow is important in the electronics cooling process and heat exchangers etc. Chen [16] examined the laminar mixed convection flow over a continuously stretching sheet. Numerous researchers have been occupied with investigating the mixed convection flow of non-Newtonian fluids [17,18,19]. Bhargava et al. [20] have analyzed the free convection flow of magnetohydrodynamic micro-polar fluid. Elahi et al. [21] described the numerical solution of mixed convection heat transfer over a stretching sheet. Asmat et al. [22] studied the effect of thermal radiation on velocity and temperature over a stretching porous sheet. Hayat et al. [23] considered on magnetohydrodynamic the flow of non-Newtonian nano-fluid flow with the convective condition. They investigated the slip effects in the MHD flow of non-Newtonian by a stretching surface. They also found radiation effects on velocity, temperature and concentration profile.
Baag et al. [24] have studied the stagnation point on magnetohydrodynamic non-newtonian fluid subject to the chemical reaction and heat source. Singh [25] examined the effects of viscous on free convection non-newtonian fluid in the presence of chemical reaction. Mabood et al. [26] discussed steady non-Newtonian fluid with a chemical reaction through a porous medium. Hayat et al. [27] are discussed non-Newtonian fluid with chemical aspects and they investigated a numerical solution. Seth et al. [28] examined chemically reacting nanofluid over a permeable vertical plate.
Motivated by the above-mentioned studies in literature and a wide range of their applications, the thermo-diffusion and multi-slip effects on an axisymmetric Casson flow over a time-dependent radially stretching sheet in the presence of chemical reaction is presented which has not been discussed yet. The focal point of the current study is to extend the recently published work of Azeem et al. [13]. The governing nonlinear PDEs are transformed into a set of highly nonlinear ODEs with the aid of suitable similarity transformations and the nonlinear coupled ODEs are solved numerically with most popular Keller-Box technique. The effects of magnetic parameter M, Dufour parameter , Schmidt number parameter , chemical reaction parameter , Soret parameter , Prandtl number , slip parameters (), suction/injuction parameter S, Unsteadiness parameter , thermal buoyancy , and Casson parameter on the fluid velocity, temperature, and concentration functions are examined in detail. Additionally, a comparison is made for the skin friction coefficient and Nusselt number. Good agreement is established which further authenticates the validity of our results.
2. Mathematical Formulation
Let us consider a steady magnetohydrodynamic flow of incompressible viscous flow with thermo-diffusion are included over a radially stretching sheet, the sheet is placed at , and is examined in the presence of chemical reaction effects. The flow of conducting fluid is assumed to be linear along the radial direction , where a is a dimensional constant. Where is the wall temperature, is the ambient temperature respectively. (see Figure 1). It is supposed that the variable magnetic field intensity acts along z-direction normal to the sheet. Under the above conditions, the governing equations of continuity, momentum conservation, and conservation can be expressed as (see [13,29]):
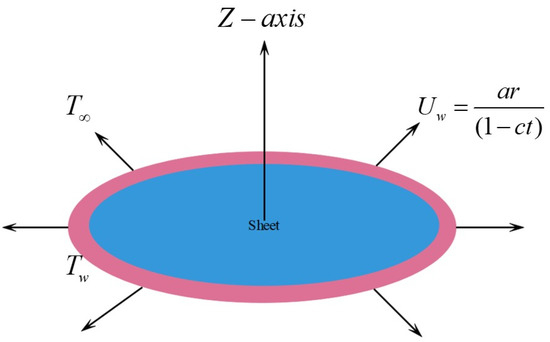
Figure 1.
Thermo-diffusion flow diagram.
The velocity vector of flow is , where u and v are component of velocity towards r and z directions respectively. , , , , D, , , and are electrical conductivity, kinetic viscosity, the viscosity of fluid, solutal, Soret, Dufour diffusities, and chemical reaction respectively, The corresponding boundary conditions are (see [13,29]):
where is the velocity slip, is the velocity slip factor, is the thermal slip, is the temperature slip factor, and denotes the suction/injection of mass transfer rate at the surface. Here a > 0, b > 0, and c > 0 are constant having dimension 1/time (t), where t stand for the time such that product ct < 1 (see [29]).
The Equations (1)–(4), We consider the similarity transformations stated as (see [29]):
In view of Equation (7), the system of partial differential Equations (2)–(5) transform into the following system of coupled and non-linear ODE’s:
and the transformed boundary conditions Equations (5) and (6) are:
where primes represent differentiation w.r.t the variable . The parameters in Equations (8)–(10) are described as:
, , , , , ,
where M is magnetic parameter, is define as the Prandtl number, is the Dufour parameter, is the Soret parameter, is determine as the Schmidt number, and is the chemical reaction term.
The interested physical quantities are coefficient of skin-friction , local nusselt number , and Sherwood number defined as:
whereas the skin-friction coefficient , the heat and mass transformation from the sheet and are follow:
The dimension free variables explained in Equation (7) and these quantities becomes as:
where is the local Reynolds number based on the radially stretching velocity .
3. Results and Discussion
The main goal of the proposed study was to define the role of mass transformation factor, heat transformation factor, chemical reaction and thermal radiation factors in the time-dependent axisymmetric boundary layer MHD flow of Casson fluid if multiple-slip, and thermo-diffusion effects are employed over a stretching surface.
The control model Equations (8)–(10) with boundary conditions Equations (11) and (12) were solved numerically by Keller-Box finite difference method. The values of the velocity, temperature, and concentration profiles are analyzed in the current section using the numerical technique. We have graphically discussed the influence of these profiles on various parameters such as Casson, magnetic, Prandtl number, Dufour parameter, Soret number, chemical reaction, Schidmt number, unsteadiness, buoyancy, hydrodynamic, suction/injection parameter, and thermal slips. In order to validate the numerical method in Table 1, presents the comparison of our work that of Azeem et al. [29] and an excellent correlation is achieved which shows the authenticity of numerical solutions.

Table 1.
Present results are Compared with [29] of and for various values of , S and .
Figure 2a,b depict the influence of Casson parameter at velocity, temprature and concentration profile. The velocity profile decreases with an increase in Casson fluid parameter () but opposite behavior is observed in Figure 2a,b for the temperature and concentration functions. Figure 3a,b shows the influence of the magnetic parameter M on the free dimension velocity, temperature, and concentration profiles, It is noticed that the velocity distribution decline due to increment in the magnetic field. It is clearly seen in Figure 3a increase in the value of M slow down the movementum and hence a decline in radial velocity. Temperature, and concentration profiles are observed increases near to the boundary wall. The escalation in the values of magnetic causes increment in thermal and solutal boundary thickness. Physically, the magnetic parameter produced Lorentz force which slows down the motion of the fluid.
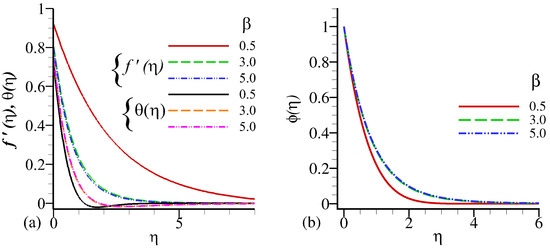
Figure 2.
Influence of on velocity profile , temperature profile , and concentration profile against .
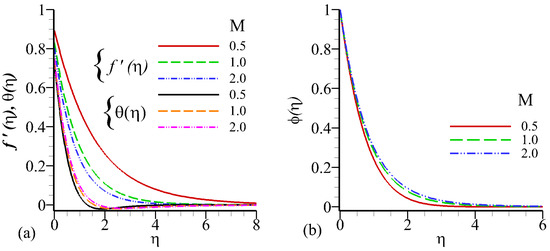
Figure 3.
Influence of M on velocity profile , temperature profile , and concentration profile against .
In Figure 4a,b the influence of dimensionless unsteady parameter () on the velocity, temperature and concentration profiles is shown. It is found that the velocity, temperature, and concentration profiles decline as an increasing values of the unsteady parameter () whereas the temperature profile is an increasing function near the boundary.
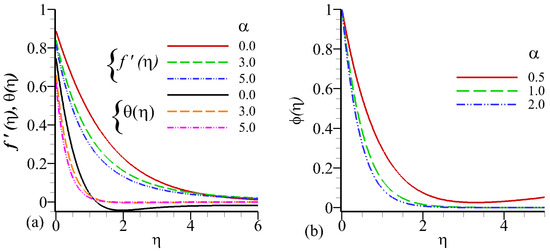
Figure 4.
Influence of on velocity profile , temperature profile , and concentration profile against .
Figure 5a,b illustrates the profiles of dimension-less velocity, temperature, and concentration for different values of buoyancy (). It is observed that velocity increases whereas the concentration profile and temperature decreased with increasing values of buoyancy () (see Figure 5a,b. The extra force is added in fluid due to buoyant that’s why the velocity profile enhance.
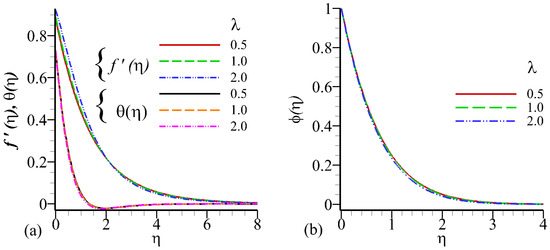
Figure 5.
Influence of on velocity profile , temperature profile , and concentration profile against .
Figure 6a,b depicts radial velocity and temperature profiles in which the boundary layer thickness is reduced near the wall with the rise in Prandtl number . Prandtl number effect on concentration profile slightly differs form radially stretching velocity, and temperature profiles as we can see in Figure 6b, which shows that it is slow rising effect away to the boundary and decreases closed to the boundary layer with rising in Prandtl number. Casson fluids include in the present investigation it has determined with great viscosity therefore, the Prandtl number is used to increase the rate of cooling in conducting flows.This is due to the fact that number is defined as the ratio between momentum and thermal diffusivity. In present investigation number is very suitable for cooling purposed.
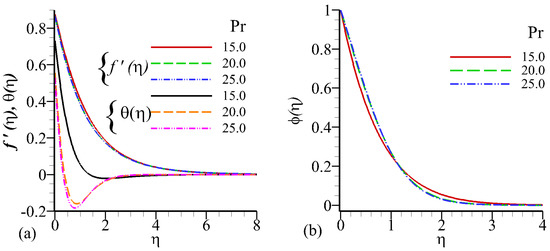
Figure 6.
Influence of on velocity profile , temperature profile , and concentration profile against .
Similar behavior of Figure 6a,b is observed in Figure 7a,b for Dufour parameter as the profiles of velocity, temperature, and Concentration. It is also noticed from Figure 7a,b that the increase in the Soret parameter decreases the radially stretching velocity and temperature profile, while the temperature profile decreases faster than the radial velocity near to the boundary layer. Figure 7b elucidates that the amassed value of the Soret parameter is enhancing in boundary layer thickness with the slip effect parameter effect which is increasing the concentration profile away from the boundary-wall.
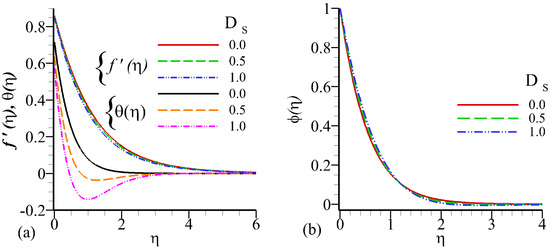
Figure 7.
Influence of on velocity profile , temperature profile , and concentration profile against .
Figure 8a,b exhibits the influence of Schmidt number on velocity and temperature profiles. Schmidt number is the ratio of momentum and mass diffusivity and is utilized to characterize fluid flows for momentum and mass diffusion convection process. The rise in values of Sc reduces the radially stretching velocity and temperature profiles at a slow rate. The same effect is observed in Figure 8b which shows that increase in Schmidt number has a decreasing effect in concentration profile.
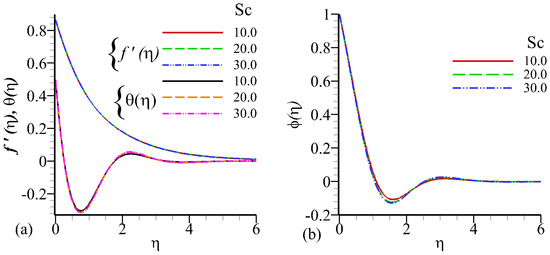
Figure 8.
Influence of on velocity profile , temperature profile , and concentration profile against .
The Soret effect is where the temperature gradient separates light and heavy molecules. This effect is usually important when there are more than one chemical species in a very large temperature gradient, such as CVD problems and chemical reactors. Figure 9a,b shows the Soret effect of the velocity, temperature, and concentration profiles on a radially stretching sheet. The greater value of Soret parameter results in an increase of velocity, temperature, and concentration profiles away to the boundary wall but closed to the wall little opposite effects can be seen.
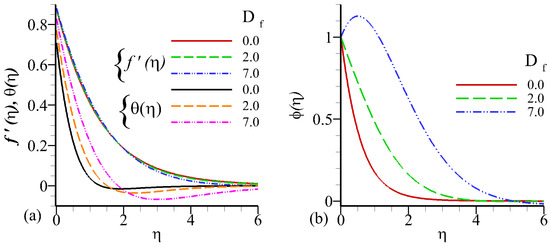
Figure 9.
Influence of on velocity profile , temperature profile , and concentration profile against .
A chemical reaction is a mechanism leading to the chemical change of one collection of chemicals into another. Figure 10a,b elucidates the impacts of chemical reaction in the fluid. It is depicted from the graph that increasing values of chemical reaction creates some reaction in the fluid flow and slow down the radially stretching velocity, temperature, and concentration profiles of the fluid. Increasing the temperature profile closed to the wall also show that the boosting the value of chemical reaction that the effect is diminutions the concentration profile away to the wall but closed to the wall it little growing effect find-out.
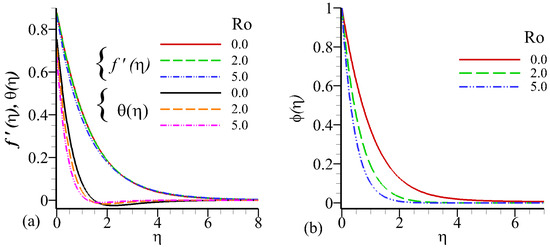
Figure 10.
Influence of on velocity profile , temperature profile , and concentration profile against .
A parallel crossposting trend is perceived in the velocity, temperature and concentration distribution functions for the increment of Dufour parameter but the opposite behavior is observed in the thermal boundary layer near the boundary. Figure 11 and Figure 12 demonstrate the influence of hydrodynamic and thermal slip on the velocity, temperature, and concentration profiles. It is clear from the Figure 11a that, the consultant radially velocity decreases as the hydrodynamic slip increases but the inverse trend is seen in the temperature and concentration functions (see Figure 11a,b). It is obvious that the velocity, temperature and concentration profiles decrease by increasing the thermal slip value. As the thermal slip parameter value increases, the thermal limit layer thickness decreases even when a small amount of heat is transferred from the surface to the liquid. The velocity, temperature, and concentration boundary layer shrink due to enhancement in thermal slip which is cleary seen in the Figure 12a,b.
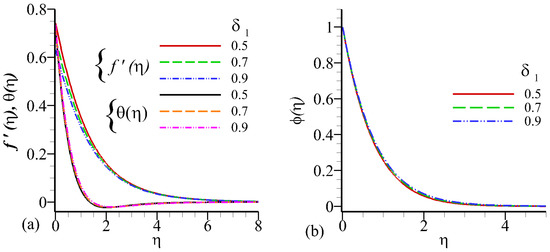
Figure 11.
Influence of on velocity profile , temperature profile , and concentration profile against .
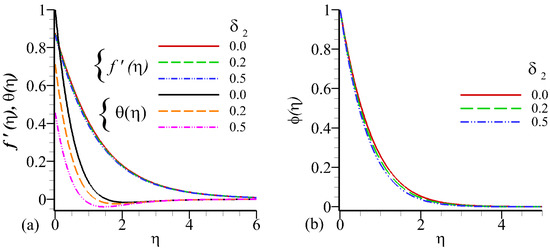
Figure 12.
Influence of on velocity profile , temperature profile , and concentration profile against .
The Figure 13a,b and Figure 14a,b depicts the behavior of suction/injection on fluid velocity, temperature, and concentration profile.The boundary layer of velocity is observed decreasing effect when we enhance in the value of suction parameter but inverse behavior is seen for velocity, temperature, and concentration profiles when we increase in the values of injection parameter . Figure 15a–c and Figure 16a–c. described the influence of several parameters on the shear stresses, the heat, and mass transfer rates, Figure 15a and Figure 16a illustrate the influence of several parameters on the skin friction factor, that indicate that friction increases with Chemical reaction, and suction parameter, are enhanced. In results weaker matrix resistance factors to thermo-diffusion flow behaviours in an acceleration leading to increased shearing at the sheet surface and enhance the magnitudes of skin friction factor. Figure 15b and Figure 16b indicates that the variation effect on heat transfer rates for different parameter. The amount of heat transfer rises as, the Chemical reaction, and suction parameter both are increased. In thermo-diffusion flow, a more inertial impact, obviously aggravates heat diffusion from the radial sheet to the fluid. Figure 15c and Figure 16c show the influence of different parameters on increases in Sherwood number i.e., Chemical reaction, and suction parameter both are enhancing the magnitude of Sherwood number.
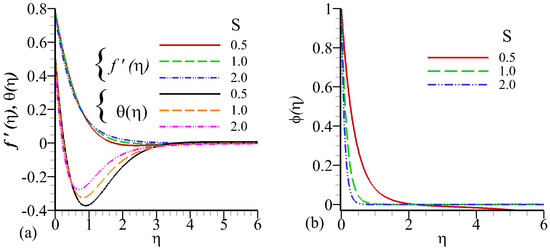
Figure 13.
Influence of S on velocity profile , temperature profile , and concentration profile against .
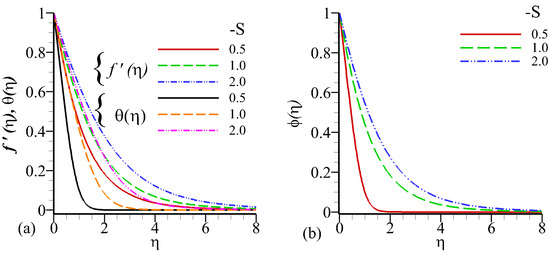
Figure 14.
Influence of on velocity profile , temperature profile , and concentration profile against .
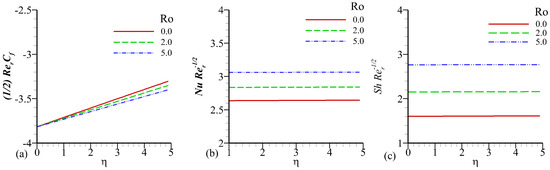
Figure 15.
Influence of S on , , and .
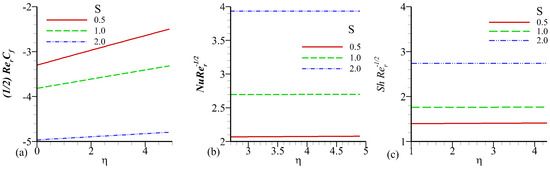
Figure 16.
Influence of S on , , and .
In Table 2 we analysis the variation of physical parameters M, , , , and , on skin friction co-efficient , Nusselt number , and Sherwood number .

Table 2.
Influence of some parameters on , , and when .
The following results are concluded from the Table 2. (i) The Skin-friction coefficient is increasing while reducing the local Nusselt and Sherwood numbers through improvement in the increment of Magnetic parameter. (ii) The increment in thermal buoyancy parameter , cause decreasing the Skin-friction coefficient while increasing the factor of Nusselt number, and Sherwood number. (iii) With the increasing unsteadiness parameter , the Skin-friction, local Nusselt, and Sherwood numbers are also increasing. (iv) The Skin-friction coefficient is increasing with the increment in Prandtl number also increasing the local Nusselt number but opposite trend is observed for Sherwood number. (v) The Skin-friction coefficient and Sherwood number are decreasing with the increasing Casson parameter and increment in the local Nusselt number.
4. Conclusions
The thermo-diffusion and multi-slip effects on an axisymmetric Casson fluid flow over a time-dependent radially stretching sheet with in the presence of chemical reaction is presented. The governing nonlinear PDEs are transformed into a set of highly nonlinear ODEs with the aid of suitable similarity transformations which are solved numerically by utilizing the Keller-Box technique. The computations have been performed for velocity, temperature, and solutal functions for various values of physical parameters. The key conclusions of this work are as follows:
- The velocity profiles are observed to be decreased with increasing values of the Casson, unsteadiness, magnetic, Prandtl number, Dufour, Soret number, chemical, Schmidt number and slips parameters, but the effect of increasing buoyancy parameter values and injection parameters is the opposite.
- Increments in unsteadiness, magnetic field, buoyancy, Prandtl number, Soret, thermal slip, Dufour, and chemical parameters decline the fluid temperature. However, the opposite effect is observed with increasing values of Schmidt number, magnetic, Casson, suction/injection, and hydrodynamic slip parameters.
- The concentration profle are found to be reduced with increasing values of the unsteadiness, buoyancy, Soret, Schmidt number, thermal slip, Prandtl number, chemical reaction, and suction parameters. But the concentration profile are enhanced by increment in the magnetic field, Casson, Prandtl number, Dufour, injection, and hydrodynamic slip parameters.
- The obtained results are presented in graphical and tabular formats. An excellent agreement of our numerical results is obtained with the existing literature which assists with the authenticity of proposed study.
- Destructive chemical reactions are favorable in order to enhance the mass transfer rate.
Author Contributions
F.F. and S.M.I. modeled the problem and wrote the manuscript. B.A. thoroughly checked the mathematical modeling. S.H. checked English corrections. F.F. solved the problem using “Fortran” software. F.F., S.H. and S.M.I. writing—review and editing. F.F., S.M.I. and S.H. contributed to the results and discussions. All authors finalized the manuscript after its internal evaluation.
Funding
This research received no external funding.
Acknowledgments
We are grateful to the Chinese government scholarship council (CSC) for the scholarship award. Also, thankful to Yong Xu for his continued guidance throughout the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goddard, J.; ACRIVOS, A. An analysis of laminar forced-convection mass transfer with homogeneous chemical reaction. Q. J. Mech. Appl. Math. 1967, 20, 471–497. [Google Scholar] [CrossRef]
- Kong, J.; Cassell, A.M.; Dai, H. Chemical vapor deposition of methane for single-walled carbon nanotubes. Chem. Phys. Lett. 1998, 292, 567–574. [Google Scholar] [CrossRef]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Nayak, B.; Mishra, S.; Krishna, G.G. Chemical reaction effect of an axisymmetric flow over radially stretched sheet. Propuls. Power Res. 2019, 8, 79–84. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, R.; Sheikholeslami, M.; Chamkha, A.J. Irreversibility analysis of the three dimensional flow of carbon nanotubes due to nonlinear thermal radiation and quartic chemical reactions. J. Mol. Liq. 2019, 274, 379–392. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Mishra, S.; Abbas, T.; Rashidi, M.M. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput. Appl. 2018, 30, 1237–1249. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial. J. Mol. Liq. 2018, 259, 274–283. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite Element Simulation of Multiple Slip Effects on MHD Unsteady Maxwell Nanofluid Flow over a Permeable Stretching Sheet with Radiation and Thermo-Diffusion in the Presence of Chemical Reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef]
- Raza, J. Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propuls. Power Res. 2019, 8, 138–146. [Google Scholar] [CrossRef]
- Ashraf, M.; Bashir, S. Numerical simulation of MHD stagnation point flow and heat transfer of a micropolar fluid towards a heated shrinking sheet. Int. J. Numer. Methods Fluids 2012, 69, 384–398. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Daniel, S.K. Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alex. Eng. J. 2015, 54, 705–712. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. Critical values in slip flow and heat transfer analysis of non-Newtonian nanofluid utilizing heat source/sink and variable magnetic field: Multiple solutions. J. Taiwan Inst. Chem. Eng. 2016, 58, 155–164. [Google Scholar] [CrossRef]
- Shahzad, A.; Ali, R.; Hussain, M.; Kamran, M. Unsteady axisymmetric flow and heat transfer over time-dependent radially stretching sheet. Alex. Eng. J. 2017, 56, 35–41. [Google Scholar] [CrossRef]
- Ashraf, M.; Batool, K. MHD flow and heat transfer of a micropolar fluid over a stretchable disk. J. Theor. Appl. Mech. 2013, 51, 25–38. [Google Scholar]
- Shahzad, A.; Ahmed, J.; Khan, M. On heat transfer analysis of axisymmetric flow of viscous fluid over a nonlinear radially stretching sheet. Alex. Eng. J. 2016, 55, 2423–2429. [Google Scholar] [CrossRef]
- Chen, C.H. Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transf. 1998, 33, 471–476. [Google Scholar] [CrossRef]
- Thumma, T.; Beg, O.A.; Kadir, A. Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a non-linear inclined stretching/shrinking sheet. J. Mol. Liq. 2017, 232, 159–173. [Google Scholar] [CrossRef]
- Seth, G.; Sarkar, S. MHD natural convection heat and mass transfer flow past a time dependent moving vertical plate with ramped temperature in a rotating medium with Hall effects, radiation and chemical reaction. J. Mech. 2015, 31, 91–104. [Google Scholar] [CrossRef]
- Takhar, H.S.; Agarwal, R.; Bhargava, R.; Jain, S. Mixed convection flow of a micropolar fluid over a stretching sheet. Heat Mass Transf. 1998, 34, 213–219. [Google Scholar] [CrossRef]
- Bhargava, R.; Rana, P. Finite element solution to mixed convection in MHD flow of micropolar fluid along a moving vertical cylinder with variable conductivity. Int. J. Appl. Math. Mech. 2011, 7, 29–51. [Google Scholar]
- Ellahi, R.; Zeeshan, A.; Shehzad, N.; Alamri, S.Z. Structural impact of Kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: Application of cooling process. J. Mol. Liq. 2018, 264, 607–615. [Google Scholar] [CrossRef]
- Ara, A.; Khan, N.A.; Khan, H.; Sultan, F. Radiation effect on boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet. Ain Shams Eng. J. 2014, 5, 1337–1342. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A.; Shehzad, S. Magnetohydrodynamic flow of burgers fluid with heat source and power law heat flux. Chin. J. Phys. 2017, 55, 318–330. [Google Scholar] [CrossRef]
- Baag, S.; Mishra, S.; Dash, G.; Acharya, M. Numerical investigation on MHD micropolar fluid flow toward a stagnation point on a vertical surface with heat source and chemical reaction. J. King Saud Univ.-Eng. Sci. 2017, 29, 75–83. [Google Scholar] [CrossRef]
- Singh, K.; Kumar, M. Effect of viscous dissipation on double stratified MHD free convection in micropolar fluid flow in porous media with chemical reaction, heat generation and ohmic heating. Chem. Process Eng. Res. 2015, 31, 75–80. [Google Scholar]
- Mabood, F.; Shateyi, S.; Rashidi, M.; Momoniat, E.; Freidoonimehr, N. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 742–749. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Mathematical modeling of non-Newtonian fluid with chemical aspects: A new formulation and results by numerical technique. Colloids Surf. A Physicochem. Eng. Asp. 2017, 518, 263–272. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.; Athira, P. Radiated flow of chemically reacting nanoliquid with an induced magnetic field across a permeable vertical plate. Results Phys. 2017, 7, 2375–2383. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S. Multiple Slip Effects on MHD Unsteady Flow Heat and Mass Transfer Impinging on Permeable Stretching Sheet with Radiation. Model. Simul. Eng. 2019, 2019. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).