Abstract
Liquid–liquid equilibria (LLE) characterization is a task requiring considerable work and appreciable financial resources. Notable savings in time and effort can be achieved when the experimental plans use the methods of the optimal design of experiments that maximize the information obtained. To achieve this goal, a systematic optimization formulation based on Semidefinite Programming is proposed for finding optimal experimental designs for LLE studies carried out at constant pressure and temperature. The non-random two-liquid (NRTL) model is employed to represent species equilibria in both phases. This model, combined with mass balance relationships, provides a means of computing the sensitivities of the measurements to the parameters. To design the experiment, these sensitivities are calculated for a grid of candidate experiments in which initial mixture compositions are varied. The optimal design is found by maximizing criteria based on the Fisher Information Matrix (FIM). Three optimality criteria (D-, A- and E-optimal) are exemplified. The approach is demonstrated for two ternary systems where different sets of parameters are to be estimated.
1. Motivation
This paper addresses the design of locally optimal experimental plans for liquid–liquid equilibria (LLE) characterization. For a systematic handling of the problem, we propose semidefinite programming (SDP) formulations combined with the Model-based Optimal Designs of Experiments (M-bODE) using thermodynamic models for forecasting the equilibria. The innovations of the paper are twofold: (i) presenting a systematic approach based on mathematical programming strategies to handle the optimal design of experiments for LLE characterization; and (ii) addressing the difficulties in model-based optimal designs of experiments for models described by implicit nonlinear algebraic equations including the factors, the measurements and the parameters to be estimated. Typically, the statistics community focuses on M-bODE for models described by explicit algebraic equations where the measurements are related to the experimental factors and the parameters. The generalization to implicit nonlinear models was, as far as we know, not previously considered. The novelty lies in the computation of the parametric sensitivities which, for the LLE problem, require solving a linear system of equations.
Liquid–liquid extraction is an important separation unit operation that finds application in a variety of areas of the chemical process industries, including those for petrochemicals, food, and pharmaceuticals. Accurate phase equilibrium data are important for the design and optimization of industrial plants for extraction processes. Moreover, ternary systems equilibrium data are essential for the proper understanding of the solvent extraction process and so for solvent selection. Typically, characterizing the LLE for ternary mixtures requires complex experimental plans to obtain data for subsequently fitting thermodynamic models able to simulate and optimize unit operations []. Several methods can be used to obtain LLE data [] but in most cases the task requires considerable resources, both human and economic. The building of adequate mathematical models from LLE data typically involves:
- (i)
- choosing the appropriate thermodynamic model according to the nature of the mixture and the region of operation;
- (ii)
- defining the methodology to estimate parameters that are able to describe well the experimental data;
- (iii)
- iterative computation of LLE and stability analysis to prevent spurious phase predictions;
- (iv)
- refinement of existing models, by planning further experiments; and
- (v)
- designing experiments prior to the laboratory experiments.
While Items (i)–(iii) are extensively studied in literature, Items (iv)–(v) are scarcely tackled in the context of chemical thermodynamics. The main reasons are that the models are of large complexity and include highly nonlinear terms. This study contributes to filling the gap detected.
The approach proposed herein requires an approximated knowledge of the binary interaction parameters (BIPs), which can be obtained from data in the literature for similar components to those in the mixture of interest or estimated from group contribution methods, such as UNIFAC. In addition, a prior knowledge is required of the number of immiscible pairs of components in the ternary system, i.e., its type. Using this information, the method is capable of calculating a locally optimal experimental design. The experimental results either will confirm the estimates of the initial BIPS, or will update their values. In the latter case, the method finds another optimal experimental design, now based on the updated BIPs. The method is thus: (i) used for parameter confirmation; or (ii) included in a sequential procedure where the parameters are iteratively refined.
M-bODE generates efficient plans of experiments for parameter estimation and has currently gained importance due to the necessity of judiciously choosing the most informative experiments, given the budgetary constraints on resources. M-bODE thus allows important cost savings in scientific studies by determining the most efficient designs for accurate inference [].
It is a matter of surprise that M-bODE is not reported for generating experimental plans for LLE characterization. The exception is the work of Dechambre et al. [], who proposed a strategy combining the discretization of the initial mixture space with an algorithm similar those of the classic exchange methods [,,].
Among the classic approaches, various numerical algorithms based on exchange methods [,,] have been developed for the construction of optimal experimental designs. These algorithms are iterative, requiring a starting design and a stopping criterion in the search for the optimal solution. They iteratively replace current design points by one or more points that may be either new or already in the support of the current design. The rule for selecting the point or points for generating the next design vary depending on the type of algorithm and the design criterion. The numerical efficiency of these Wynn–Fedorov schemes has been improved by several authors, including Wu [], Wu and Wynn [], Pronzato [] and Harman and Pronzato []. They were reviewed and compared by Meyer and Nachtsheim [] and Pronzato [], among others. Another approach to finding continuous optimal designs is based on Multiplicative algorithms, which have found broad application due to their simplicity []. The basic algorithm was proposed by Titterington [] and later exploited by Pázman [], Fellman [], Pukelsheim and Torsney [], Torsney and Mandal [], Mandal and Torsney [], Dette et al. [], Torsney and Martín-Martín [], Yu [], and Yu []. Recently, cocktail algorithms, which rely on both exchange and multiplicative algorithms, have been proposed []. Another algorithm falling in the same class was proposed by Yang et al. [] where the iterative procedure includes a Newton method-based solver for determining the weights given a set of support points and an optimization step where the dispersion function is maximized by choosing the set of support points. All these approaches find the optimal discrete set of design points constructed from the original continuous design space.
We also discretize the initial mixture domain to produce a set of candidate one-point experiments, but instead propose a mathematical programming (MP) based approach to determine the relative weights of individual one-point experiments (most weights will be zero). Mathematical programming approaches have been successfully applied to solve many design problems. Some examples are Linear Programming [,], Second Order Conic Programming [,], Semidefinite Programming (SDP) [,,], Semi-Infinite Programming (SIP) [,], Nonlinear Programming (NLP) [,], NLP combined with stochastic procedures such as genetic algorithms [,], and global optimization techniques [,]. They are particularly efficient for approximate (also called continuous) optimal designs, characterized by a continuous representation of the weights of each constituent one-point experiment in the plan; the design problem has convex properties and the quality of the optimum can be checked with a General Equivalence Theorem (GET). Moreover, the resulting optimization problem can be solved efficiently using state-of-the-art solvers that guarantee global optimality, especially when the optimization problem belongs to a convex programming class.
It is important to emphasize that most of the MP-based formulations listed above are for explicit models where by “explicit models” we refer to functional forms that explicitly relate the response variables and the control factors. Contrarily, in this study, we address implicit models which are functionals of nonlinear type relating the responses, control factors and parameters; a classic example is the LLE thermodynamic model []. As far as we know, the use of classic approaches to handle implicit models is not reported in the literature because of the additional complexity of computing the parametric sensitivity. In practice, MP-based approaches are more suitable for this class of models since the construction of the FIM can be embedded in the formulation for finding the optimal design. MP-based approaches are also advantageous in finding constrained optimal designs, where additional constraints on the distribution of weights are explicitly included in the formulation. Finally, the mathematical programming problems falling into convex formulations (as is the case of SDP formulations), guarantee the global optimality of the obtained design for the chosen discrete set of candidate points. The classic algorithms lack such a proof.
A disadvantage of MP-based methods is that the size of the optimization problem increases almost exponentially with the number of candidate points. The solvers may take larger computational times than those required by classic algorithms and may even not converge for problems of large dimension. However, the current SDP solvers based on interior point methods can efficiently handle problems with 1 × 104 constraints [].
Paper Organization and Nomenclature
Section 2 presents the mathematical representation of the LLE model, the background required for applying the methods of optimal experimental design and the fundamentals of SDP. Section 3 formulates the optimal design of experiments for an SDP solution, covering the details of: (i) FIM construction; and (ii) computational implementation. Section 4 applies the proposed formulations to systems of Type 1, which are the most common in liquid–liquid extraction processes; for the classification of LLE systems topology, see Treybal []. Two different classes of ternary system of Type 1 are considered for demonstration purposes: (i) Class I, where Components 2 and 3 are completely miscible but Components 1 and 2 and 1 and 3 are both partially miscible; and (ii) Class II, where Components 1 and 3 and 2 and 3 are completely miscible but Components 1 and 2 are only partially miscible ([], p. 8.163).
We use bold face lowercase letters to represent vectors, bold face capital letters for continuous domains, blackboard bold capital letters for discrete domains, and capital letters for matrices. Finite sets containing elements are compactly represented by . The symbol “” is used to indicate the vector/matrix transpose operation, stands for the trace of a matrix and for the cardinality of a discrete set.
2. Background
This section provides the background material required by the mathematical formulation for obtaining approximate optimal designs for LLE characterization. First, we introduce the model used to describe the LLE for ternary systems (Section 2.1). Next, the basic theory of model-based optimal designs of experiments is provided (Section 2.2), and Section 2.3 introduces the fundamentals of SDP.
2.1. Liquid–Liquid Equilibria: Mathematical Representation
We first present the model relating the compositions of each component of a ternary mixture in each phase. The LLE characterization studies are performed at constant pressure and temperature. Let be the set of components in the mixture, and the set of phases into which the original mixture separates. Consequently, , such that and . The set of candidate experiments is formed by a finite number () of vectors , i.e., . The compositions of the components in each phase are denoted by where the first subscript identifies the phase, , and the second is for the component, . Similarly, in each phase and ignoring any measurement errors, the component fractions sum to 1, i.e., and .
The LLE model includes mass balances and the equilibrium conditions relating the compositions of the components in both phases. Here, we assume the equilibrium of chemical potentials which translate into iso-fugacity relations. The activity coefficient, here denoted by , is determined using the Non-random Two-liquid (NRTL) model [], but without loss of generalization other models such as the Universal Quasichemical (UNIQUAC) model [] and the UNIQUAC Functional-group Activity Coefficients (UNIFAC) model [] can be used. The vector of parameters in the model, , includes the dimensionless pair of interaction parameters, , in turn related to the interaction energy parameters, and the non-randomness parameters, . Consequently, in this study, we have . For ternary systems, is a matrix containing the interactions between all the pairs of components in the mixture. Since the interaction energy of each species with itself is null, corresponding to for , the complete set of parameters to be estimated from the proposed experimental plan includes six pairs of interaction parameters, . Similarly, is a symmetric matrix, where the elements on the diagonal are 0, and . For ternary systems, the number of additional parameters is three. However, in some of the experimental plans, we assume fixed having a value in the interval (see Rappel et al. [] among others) and focus only on the determination of the parameters . Summing up, if the experimental plan aims at finding only the pairs of interaction parameters, includes six s, i.e., . Otherwise, if the goal is estimation of the pair interaction parameters and the pairs of non-randomness parameters, includes six s and three s, i.e., . The calculation of designs for both cases is demonstrated in Section 4.
The LLE model is compactly written in the form where is a set of nonlinear algebraic equations:
Equation (1a) represents the iso-fugacity constraints for all the components, Equation (1b) is for the summation of the component fractions in each phase after separation, and Equation (1c) is the mass balance for the second component obtained by applying the lever rule. Alternatively, Equation (1c) can be replaced by the mass balance for the third component, corresponding to . The activity coefficients , are modeled by the NRTL model presented in Appendix A. For compactness, represents the vector of compositions of the components in the pth phase. Note that: (i) the link between the equilibrium composition and that of the initial mixture is Equation (1c) but the equilibrium can only be fully characterized after solving all equations in Equation (1) together; and (ii) by assumption .
Typically, an experiment to characterize LLE requires choosing an initial mixture, , providing a separation in two phases is obtained, and measuring at least the composition of two components in each phase, e.g., Components 1 and 2. The measurement errors of all four variables are assumed independent and identically distributed with mean zero and constant variance.
2.2. Optimal Design of Experiments
The regression models addressed herein are described by and have a four-variate response with two independent variables (covariates) used to set the initial mixture composition, e.g., and . The remaining fraction is dependent on the first two so that . The mean response at is
where and solve Equation (1) for a given . Here, where is a compact domain containing the parameters values and is the expectation operator with respect to the error distribution.
Because the model is nonlinear, the FIM is dependent on the values of to be estimated from the experimental design. Here, we address locally optimal designs [] where the model parameters are taken from previous studies or experiments and they are then treated as known in the FIM construction. We note that this framework is particularly useful when a good estimate is available and the study serves to confirm parameter estimates or is a step of a sequential design (see Atkinson et al. []).
In this study, we focus on approximate designs, , which allocate a weight to ith candidate experiment , with . The weights can also be interpreted as the relative effort put on initial mixtures , and many of them may be null in the optimal design if the additional information provided by the corresponding mixtures is low (or none). In practice, approximate designs are implemented by taking roughly replicates at mixture after rounding to an integer subject to the constraint where k stands for the number of support point of the optimal design. Advantages of working with continuous designs are many, and there is a unified framework for finding optimal continuous designs for M-bODE problems when the design criterion is a convex function on the set of all approximate designs []. In particular, the optimal design problem can be formulated into a mathematical optimization program with convex properties and equivalence theorems are available to check the optimality of a design. In many algorithms for finding optimal designs, the number k of support points has to be specified by the experimenter, with comparisons between designs for different k leading to the optimal value. However, in our formulation, the optimal value of k is part of the output of the algorithm and is found solving the problem using SDP. Rounding procedures for exact designs can be found in the work of Pukelsheim and Rieder [].
We identify the set of all feasible approximate designs in as the -dimensional simplex in the space of weights satisfying . An optimal experimental design is represented by a k-tuple
where k candidate one-point designs have . Here, the first three lines are for the compositions in the initial mixture and the fourth for the weight of this candidate experiment. The corresponding equilibrium compositions in both phases are stored in a -tuple
where each column contains the compositions in each phase after separation for each one-point design forming the optimal design. The second subscript of y is to identify the support point while the first is for phase.
The performance of the design is measured by a convex functional of its FIM. The elements of the normalized FIM obtained after adjusting for the sample size are the negatives of the expectation of the second-order derivatives with respect to the parameters of the log-likelihood of Equation (2) for component j in phase p given the set of candidate treatments , denoted as . This matrix is proportional to
where is the FIM from the design considering a single measurement—the composition of jth component in phase p, i.e., . is the corresponding elemental FIM from point . The global FIM including all four responses is obtained summing up the FIMs weighted by the variance–covariance matrix for the corresponding pair of observations [,], i.e.,
Here, we assume that the measurements are independent, which implies that the variance–covariance matrix is diagonal. Additionally, by assumption, all the measurements have the same error variance, which yields an equally weighted sum in Equation (4), i.e., .
When errors are normally and independently distributed, the volume of the confidence region for the model parameters is inversely proportional to . Consequently, maximizing the determinant of the FIM, by choice of a design leads to the most accurate estimates for the parameters. If the interest is in finding the approximate D-optimal design, the optimization problem is
Other design criteria optimize the FIM in different ways. For example, if the formulation is used to find A-optimal designs, the optimization problem is
and, if the objective is finding E-optimal designs, the optimization problem is
where stands for the minimum eigenvalue of •. To check the optimality of the designs found, we use the equivalence theorems [,]. The scaled sensitivity function, , for a point is given by
where is the vector of sensitivities at , and is the eigenvector of corresponding to . The sensitivity function in Equation (8) is limited from above by 0, and achieves the maximum at the support points.
2.3. Semidefinite Programming
In this paper, semidefinite programming is employed to solve the optimal design problems for D-, A- and E-optimality criteria over a given discrete domain . In this section, we introduce the fundamentals of this class of mathematical programs.
Let be the space of symmetric positive semidefinite matrices, and the space of symmetric matrices. A convex set is semidefinite representable (SDr) if , interpreted as the projection on to a higher dimensional set , can be described by Linear Matrix Inequalities (LMIs). That is, is SDr if and only if there exists some symmetric matrices such that []
Here, ⪰ is the semidefinite operator, i.e., , where is the Frobenius inner product operator, is a point of the original set , and is a point of the incremental dimensional subspace.
In turn, a convex (or concave) function is SDr if and only if the epigraph of , , or the hypograph, , respectively, are SDr and can be casted by LMIs [,]. The optimal values, , of SDr functions are then formulated as semidefinite programs of the form
In our design context, is a vector of known constants that depends on the design problem, and matrices contain local FIMs and other matrices produced by the reformulation of the functions into LMIs. The decision variables in vector are the weights , of the optimal design and other auxiliary variables required. The problem of calculating a design for a pre-specified set of candidate experiments of points , is solved with the formulation in Equation (10) complemented by the linear constraints on : (i) ; and (ii) , where is a unitary column vector with lines. The problem in Equation (10) is the classic SDP problem which includes LMIs representing conic constraints.
Ben-Tal and Nemirovski [] provided a list of SDr functions useful for solving continuous optimal design problems with SDP formulations (see Boyd and Vandenberghe [], Section 7.3). Recently, Sagnol [] showed that each criterion in the Kiefer class of optimality criteria defined by
is SDr for all rational values of and general SDP formulations exist for them. This result also applies to the case when ; the problems in Equations (5)–(7) fall into this class. Practically, the problem of finding optimal approximate plans of experiments for the most common (convex) criteria can be formulated as a semidefinite programming problem falling into the general representation (9) (see Vandenberghe and Boyd [] and Duarte and Wong [] among others).
3. SDP Formulations for Finding Optimal Design of Experiments
This section presents the formulations for finding approximate optimal designs via SDP. First, we introduce the approach used for calculating the FIM (see Section 3.1). In Section 3.2, we introduce the SDP formulations for finding approximate D-, A- and E-optimal designs for the LLE model, and Section 3.3 covers implementation aspects.
3.1. FIM Construction
This section describes the procedure used to construct the global FIM for a candidate initial mixture . We recall the model in Equation (1) is formed by six algebraic equations with general form where . The model derivation with respect to the parameters leads to
where denotes the sensitivity of the measurement to parameter with defined in Section 2.1. The resulting set of linear algebraic Equation (12) can be cast as
where F is the matrix formed by terms , and b is a column vector of size containing the terms . Consequently, the solution of Equation (13) is obtained inverting F, i.e.,
3.2. SDP Formulations for D-, A- and E-Optimal Designs
This section presents the formulations for finding optimal designs via SDP. The D-optimality criterion is addressed first. Next, the formulations for A- and E-optimal design problems are introduced.
Here, we recall the approximate D-optimal design problem in Equation (5), and use the formulation proposed by Vandenberghe and Boyd [] to handle the problem. That is, given the LLE model, the set of local parameters, the set of candidate experiments (already generated), the elemental FIMs for each candidate experiment and the total number of experiments , the formulation for finding approximate D-optimal designs on may be formulated as follows:
where Equation (16a) is the objective function, Equation (16b) assures the semidefinite positiveness of the global FIM, Equation (16c) is for the global FIM equality, Equation (16d) generates the FIMs for each measurement, Equation (16e) represents the semidefinite positiveness of , and Equation (16f) guarantees that the weights sum to 1. Here, is a matrix of zeros. Similarly, the formulation for the A-optimality criterion introduced in Equation (6), is as follows:
where the difference is solely in the objective function. Finally, for the E-optimal design problem presented in Equation (7), the formulation is
3.3. Implementation Aspects
In this section, we detail the computational implementation of the procedure for finding optimal designs for LLE experiments.
The nonlinear algebraic equations in Equation (1) are solved for each candidate mixture using a Newton–Krylov–Armijo algorithm. The solver uses the Krylov method for computing Newton inexact directions and the Armijo rule to globalize the Newton method (see Kelley []). The relative and absolute tolerances used in the solver are 1 × 10−7 and 1 × 10−8, respectively.
The set of candidate experiments is constructed using an equidistributed grid in both coordinates and . An equal step is used for both and all the points satisfy the condition . Finally, is computed as .
Both derivatives in Equation (12) ( and ) are determined via automatic differentiation using ADiMat code [].
To handle the SDP problems in Equations (16)–(18), there are user-friendly interfaces, such as cvx [] or Picos [], that automatically transform the semidefinite constraints in Equations (16b) and (16e) and the objective functions into a series of LMIs before passing them to SDP solvers such as SeDuMi [] or Mosek []. This is possible when is SDr, which is true for our design criteria. In our work, we solved all SDP problems using the cvx environment combined with the solver Mosek that uses an efficient interior point algorithm [].
To check the optimality of the designs found, we compute the scaled sensitivity function for every initial mixture using Equation (8). From this set of values, we extract the maximum, that, practically, corresponds to a support point. The values of the scaled sensitivity function of the other support points, here denoted as , are also used for comparison and we require that , where is the minimum threshold allowed and was set to −0.02. The rational for choosing the value of is that we require approximate designs with at least 98% efficiency.
All computations in this paper were carried using on an Intel Core i7 machine (Intel Corporation, Santa Clara, CA, USA) running 64 bits Windows 10 operating system with . The relative and absolute tolerances used to solve the SDP problems were set to 1 × 10−5 in all problems.
4. Results
In this section, we apply the formulations of Section 3.2 to find locally D-, A- and E-optimal designs for LLE characterization. We consider three examples to demonstrate the approach: In the first two examples, the set of parameters to be estimated from the experiments is only the vector of dimensionless binary interaction parameters, i.e., , which is six parameters. We consider two ternary systems to demonstrate that the strategy can be applied to Type 1 systems of Class I (Section 4.1) and Class II (Section 4.2). Finally, we present an example where the non-random binary interaction parameters are also included in the set of parameters to be estimated, i.e., , thus there are nine parameters (see Section 4.3).
A generalization of the method for systems of Type 2 (with delamination in two binary subsystems) and of Type 3 (with delamination in all three binary subsystems) requires the adaptation of the strategy to the specificities of the system. However, the strategy to follow is similar and involves: (i) experiments of mutual solubility of immiscible pairs of components; (ii) determination of binodal points by successively adding the third component; and (iii) the determination of the tie-lines where the LLE is characterized at different compositions of the ternary mixture. The proposed method can be similarly used to assist the laboratory work in Step (iii) with Steps (i) and (ii) used to generate prior knowledge.
In all examples, the initial grid of mixtures result from equistributing the points with a constant interval in the composition domain . In all examples, we use ; the complete set of candidate experiments is populated with 66 mixtures. Naturally, other step sizes can be used. Typically, the CPU time required by the SDP solver increases as the grid becomes finer, but the solver can efficiently tackle problems including thousands of LMIs.
All designs presented in following paragraphs were submitted to optimality checking employing the approach described in Section 3.3. All of them guarantee scaled sensitivity values at the support points below 2%, which allows inferring they are nearly optimal for practical implementation.
4.1. Example 1—Ternary System of Type 1, Class I; Including Dimensionless BIPs
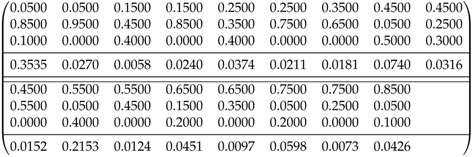
First, let us consider that only includes the dimensionless binary interaction parameters and the ternary system is of Type 1 (Class I). Here, we consider the system formed by water (1), toluene (2) and aniline (3), compactly represented by WAT-TOL-ANL []. The matrices and are, respectively,
Our goal is to find the optimal design to estimate the six dimensionless binary interaction parameters in considering fixed. The optimal designs are listed in Table 1, while Table 2 lists the expected compositions in both equilibrium phases. In Table 1, the columns of the matrices forming the optimal design () correspond to support points (which have ); the first three lines in each column specify the composition of the initial mixture () and the fourth is for the weights. In Table 2, each column reports the composition in separating phases after reaching the equilibrium. The first three lines of each column are for the composition of Phase 1, and the lines below are for the composition of Phase 2.

Table 1.
Optimal experimental designs for ternary system WAT-TOL-ANL (initial mixtures).

Table 2.
Optimal experimental designs for ternary system WAT-TOL-ANL (compositions in equilibrium phases).
The results show that: (i) the D-optimal design has five support points and the other criteria require designs with six support points; and (ii) the CPU time required by all problems is relatively low. We note that each support point provides four measurements, thus, for D-optimal design, we end with a set of 20 measurements to fit a model with six parameters.
Figure 1 shows sets of tie lines connecting the two phases in equilibrium for any mixture on the line, the amounts of the equilibrium phases depending on distances along the line. The complete set of tie-lines connecting the phases in equilibrium that contain the initial 66 mixtures is displayed in Figure 1a. Figure 1b shows the tie-lines for the locally D-optimal design presented in Table 1. We note that the mixtures for this design are located at extreme conditions, some with little ANL and near the critical point where the mixtures are homogeneous. The support points of the designs found for all the optimality criteria are similar; contrarily, the weights are significantly different, which is a trend observed for all the other examples.
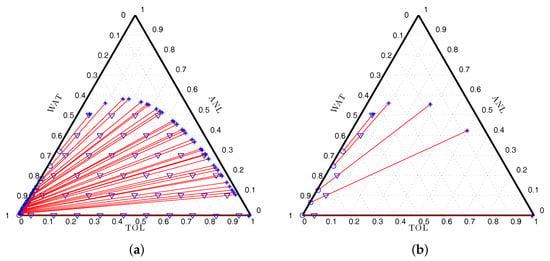
Figure 1.
D-optimal design of experiments for system WAT-TOL-ANL: (a) candidate initial mixtures and corresponding tie-lines; and (b) tie-lines corresponding to D-optimal design (symbols: o, Phase 1 composition; *, Phase 2 composition; ∇, initial mixture composition; tie lines in red).
4.2. Example 2—Ternary System of Type 1, Class II; Including Dimensionless BIPs
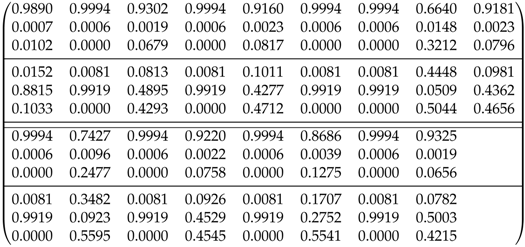
Now, we consider ternary systems of Type 1 (Class II) and only includes the dimensionless binary interaction parameters. The ternary system is formed by water (1), trichloroethylene (2) and acetone (3), represented by WAT-TCE–KET []. The matrices and are:
The optimal designs obtained are listed in Table 3 and the corresponding composition of the phases in equilibrium is in Table 4. Here, we note the D-optimal design has seven support points, the A-optimality criterion produces a design with four points and the E-optimal design is formed by nine support points. Figure 2a presents the initial set of candidate mixtures and corresponding tie-lines while Figure 2b shows the tie-lines for the set of mixtures forming the D-optimal design (Table 3).

Table 3.
Optimal experimental designs for ternary system WAT-TCE–KET (initial mixtures).

Table 4.
Optimal experimental designs for ternary system WAT-TCE–KET (compositions in equilibrium phases).
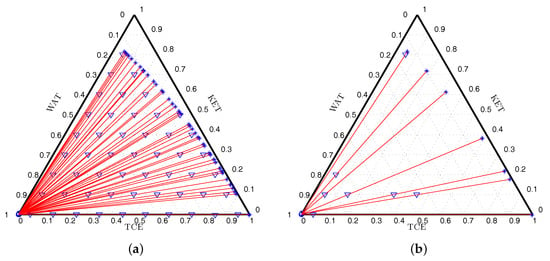
Figure 2.
D-optimal designs for system WAT-TCE–KET: (a) candidate initial mixtures and corresponding tie-lines; and (b) tie-lines corresponding to D-optimal design (symbols: o, Phase 1 composition; *, Phase 2 composition; ∇, initial mixture composition; tie lines in red).
4.3. Example 3—Ternary System of Type 1, Class I; Including Dimensionless and Non-Random BIPs
Here, we assume a ternary system of Type 1 (Class I) and includes the dimensionless binary interaction parameters and the binary interaction non-randomness parameters. The support points of the optimal designs for this problem are shown in Table 5; we note that the D-optimality criterion requires a design with 7 initial mixtures, A-optimality requires 9 and E-optimality needs 17, some of them having reduced relative importance (presented in two lines). Typically, all the designs have more support points than those in Table 1, determined for the same system, when the aim was to estimate only the elements of matrix . That the number of initial mixtures would increase was expected since the number of free parameters is larger. However, the computation time is similar to that of Example 1 as the number of candidate initial mixtures used is the same, which, in turn, yield SDP problems of equal size. The main difference is that the dimension of the FIM increases from six to nine. Table 6 shows the equilibrium compositions for designs in Table 5.

Table 5.
Optimal designs for ternary system WAT-TOL-ANL and including nine parameters (initial mixtures).

Table 6.
Optimal designs for ternary system WAT-TOL-ANL and including nine parameters (compositions in equilibrium phases).
5. Conclusions
We present SDP formulations for finding approximate D-, A- and E-optimal experimental designs for characterizing LLE in ternary systems. We consider the NRTL for describing the activity coefficient and derive M-bODE for estimating the dimensionless pairs of interaction parameters (six parameters) as well as the non-randomness pairs (three parameters). The strategy requires discretizing the space of initial mixtures and generating a finite set of candidate experiments. Then, the composition of the separating phases is determined for each candidate point, and the sensitivity of the measurements (the composition of two of the components of the mixture in each phase) obtained after applying automatic differentiation. Afterwards, the sensitivity is used to construct local FIMs and the SDP problem representing the approximate optimal design is solved using an interior point-based solver. The solution is described by the set of relative experimental effort at each initial candidate point—many initial points are not included in the optimal experiments. We apply the strategy to systems of Type 1 falling in Classes I and II, and consider different cases where: (i) only the interaction parameters are to be estimated; and (ii) the interaction and the non-randomness parameters are both to be estimated. One development which, in the interests of brevity, we do not discuss here, is that the approximate designs can be used to compute related exact optimal designs for a previously given number of experiments using classic rounding algorithms. The SDP formulation used here can be extended to other thermodynamic models. Our problems using an initial set of 66 candidate mixtures require mild computational times.
Author Contributions
Conceptualization, B.P.M.D. and J.F.O.G.; methodology, B.P.M.D. and A.C.A.; software, B.P.M.D.; validation, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; formal analysis, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; investigation, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; resources, B.P.M.D.; data curation, B.P.M.D.; writing–original draft preparation, B.P.M.D.; writing–review and editing, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; visualization, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; supervision, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; project administration, B.P.M.D., A.C.A., J.F.O.G. and N.M.C.O.; funding acquisition, B.P.M.D., and N.M.C.O.
Funding
This research received no external funding. The article processing charges were funded by Centro de Investigação em Engenharia dos Processos Químicos e dos Produtos da Floresta (CIEPQPF).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. NRTL Model
In this section, we present the NRTL model for activity coefficients []. The activity model is
References
- Aspentech, Inc. Aspen Physical Property System; V9; Aspentech, Inc.: Bedford, MA, USA, 2016. [Google Scholar]
- Muhlbauer, A. Phase Equilibria: Measurement & Computation; Series in Chemical and Mechanical Engineering; Taylor & Francis: Abingdon, UK, 1997. [Google Scholar]
- Fedorov, V.V.; Leonov, S.L. Optimal Design for Nonlinear Response Models; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Dechambre, D.; Wolff, L.; Pauls, C.; Bardow, A. Optimal experimental design for the characterization of liquid-liquid equilibria. Ind. Eng. Chem. Res. 2014, 53, 19620–19627. [Google Scholar] [CrossRef]
- Fedorov, V.V. Theory of Optimal Experiments; Academic Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Mitchell, T.J. An algorithm for the construction of D-optimal experimental designs. Technometrics 1974, 16, 203–210. [Google Scholar]
- Wynn, H.P. Results in the theory and construction of D-optimum experimental designs. J. R. Stat. Soc.-Ser. B 1972, 34, 133–147. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Miller, F.L., Jr. Use of Design Repair to Construct Designs for Special Linear Models; Technical Report 130-131; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1970. [Google Scholar]
- Wynn, H.P. The sequential generation of D-optimum experimental designs. Ann. Math. Statist. 1970, 41, 1655–1664. [Google Scholar] [CrossRef]
- Wu, C.F. Some algorithmic aspects of the theory of optimal designs. Ann. Statist. 1978, 6, 1286–1301. [Google Scholar] [CrossRef]
- Wu, C.F.; Wynn, H.P. The convergence of general step-length algorithms for regular optimum design criteria. Ann. Statist. 1978, 6, 1273–1285. [Google Scholar] [CrossRef]
- Pronzato, L. Removing non-optimal support points in D-optimum design algorithms. Stat. Probab. Lett. 2003, 63, 223–228. [Google Scholar] [CrossRef]
- Harman, R.; Pronzato, L. Improvements on removing non-optimal support points in D-optimum design algorithms. Stat. Probab. Lett. 2007, 77, 90–94. [Google Scholar] [CrossRef]
- Meyer, R.K.; Nachtsheim, C.J. The coordinate-exchange algorithm for constructing exact optimal experimental designs. Technometrics 1995, 37, 60–69. [Google Scholar] [CrossRef]
- Pronzato, L. Optimal experimental design and some related control problems. Automatica 2008, 44, 303–325. [Google Scholar] [CrossRef]
- Mandal, A.; Wong, W.K.; Yu, Y. Algorithmic searches for optimal designs. In Handbook of Design and Analysis of Experiments; CRC Press: New York, NY, USA, 2015; Chapter 21; pp. 755–786. [Google Scholar]
- Titterington, D.M. Algorithms for computing D-optimal design on finite design spaces. Proc. Conf. Inf. Sci. Syst. 1976, 3, 213–216. [Google Scholar]
- Pázman, A. Foundations of Optimum Experimental Design; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Fellman, J. An empirical study of a class of iterative searches for optimal designs. J. Statist. Plann. Inference 1989, 21, 85–92. [Google Scholar] [CrossRef]
- Pukelsheim, F.; Torsney, B. Optimal weights for experimental designs on linearly independent support points. Ann. Statist. 1991, 19, 1614–1625. [Google Scholar] [CrossRef]
- Torsney, B.; Mandal, S. Two classes of multiplicative algorithms for constructing optimizing distributions. Comput. Stat. Data Anal. 2006, 51, 1591–1601. [Google Scholar] [CrossRef]
- Mandal, S.; Torsney, B. Construction of optimal designs using a clustering approach. J. Stat. Plan. Inference 2006, 136, 1120–1134. [Google Scholar] [CrossRef]
- Dette, H.; Pepelyshev, A.; Zhigljavsky, A.A. Improving updating rules in multiplicative algorithms for computing D-optimal designs. Comput. Stat. Data Anal. 2008, 53, 312–320. [Google Scholar] [CrossRef]
- Torsney, B.; Martín-Martín, R. Multiplicative algorithms for computing optimum designs. J. Stat. Plan. Inference 2009, 139, 3947–3961. [Google Scholar] [CrossRef]
- Yu, Y. Strict monotonicity and convergence rate of Titterington’s algorithm for computing D-optimal designs. Comput. Stat. Data Anal. 2010, 54, 1419–1425. [Google Scholar] [CrossRef]
- Yu, Y. Monotonic convergence of a general algorithm for computing optimal designs. Ann. Statist. 2010, 38, 1593–1606. [Google Scholar] [CrossRef]
- Yu, Y. D-optimal designs via a cocktail algorithm. Stat. Comput. 2010, 21, 475–481. [Google Scholar] [CrossRef]
- Yang, M.; Biedermann, S.; Tang, E. On optimal designs for nonlinear models: A general and efficient algorithm. J. Am. Stat. Assoc. 2013, 108, 1411–1420. [Google Scholar] [CrossRef]
- Gaivoronski, A. Linearization methods for optimization of functionals which depend on probability measures. In Stochastic Programming 84 Part II; Prékopa, A., Wets, R.J.B., Eds.; Mathematical Programming Studies Book Series; Springer: Berlin/Heidelberg, Germany, 1986; Volume 28, pp. 157–181. [Google Scholar]
- Harman, R.; Jurík, T. Computing c-optimal experimental designs using the Simplex method of linear programming. Comput. Stat. Data Anal. 2008, 53, 247–254. [Google Scholar] [CrossRef]
- Sagnol, G. Computing optimal designs of multiresponse experiments reduces to second-order cone programming. J. Stat. Plan. Inference 2011, 141, 1684–1708. [Google Scholar] [CrossRef]
- Sagnol, G.; Harman, R. Computing exact D-optimal designs by mixed integer second order cone programming. Ann. Stat. 2015, 43, 2198–2224. [Google Scholar] [CrossRef]
- Vandenberghe, L.; Boyd, S. Applications of semidefinite programming. Appl. Numer. Math. 1999, 29, 283–299. [Google Scholar] [CrossRef]
- Papp, D. Optimal designs for rational function regression. J. Am. Stat. Assoc. 2012, 107, 400–411. [Google Scholar] [CrossRef]
- Duarte, B.P.M.; Wong, W.K. Finding Bayesian optimal designs for nonlinear models: A semidefinite programming-based approach. Int. Stat. Rev. 2015, 83, 239–262. [Google Scholar] [CrossRef] [PubMed]
- Duarte, B.P.M.; Wong, W.K. A semi-infinite programming based algorithm for finding minimax optimal designs for nonlinear models. Stat. Comput. 2014, 24, 1063–1080. [Google Scholar] [CrossRef]
- Duarte, B.P.M.; Wong, W.K.; Atkinson, A.C. A Semi-Infinite Programming based algorithm for determining T-optimum designs for model discrimination. J. Multivar. Anal. 2015, 135, 11–24. [Google Scholar] [CrossRef] [PubMed]
- Chaloner, K.; Larntz, K. Optimal Bayesian design applied to logistic regression experiments. J. Stat. Plan. Inference 1989, 59, 191–208. [Google Scholar] [CrossRef]
- Molchanov, I.; Zuyev, S. Steepest descent algorithm in a space of measures. Stat. Comput. 2002, 12, 115–123. [Google Scholar] [CrossRef]
- Heredia-Langner, A.; Montgomery, D.C.; Carlyle, W.M.; Borror, C.M. Model-robust optimal designs: A Genetic Algorithm approach. J. Qual. Technol. 2004, 36, 263–279. [Google Scholar] [CrossRef]
- Zhang, Y. Bayesian D-Optimal Design for Generalized Linear Models. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2006. [Google Scholar]
- Boer, E.; Hendrix, E. Global optimization problems in optimal design of experiments in regression models. J. Glob. Optim. 2000, 18, 385–398. [Google Scholar] [CrossRef]
- Duarte, B.P.M.; Wong, W.K.; Oliveira, N.M.C. Model-based optimal design of experiments—Semidefinite and nonlinear programming formulations. Chemom. Intell. Lab. Syst. 2016, 151, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Englezos, P.; Kalogerakis, N.; Bishnoi, P. Simultaneous regression of binary VLE and VLLE data. Fluid Phase Equilibria 1990, 61, 1–15. [Google Scholar] [CrossRef]
- Treybal, R.E. Liquid Extraction, 2nd ed.; MacGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Rappel, R.; Góis, L.M.N.; Mattedi, S. Liquid–liquid equilibria data for systems containing aromatic + nonaromatic + sulfolane at 308.15 and 323.15 K. Fluid Phase Equilibria 2002, 202, 263–276. [Google Scholar] [CrossRef]
- Chernoff, H. Locally optimal designs for estimating parameters. Ann. Math. Stat. 1953, 24, 586–602. [Google Scholar] [CrossRef]
- Atkinson, A.C.; Donev, A.N.; Tobias, R.D. Optimum Experimental Designs, with SAS; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Fedorov, V.V. Convex design theory. Math. Operationsforsch. Statist. Ser. Statist. 1980, 11, 403–413. [Google Scholar]
- Pukelsheim, F.; Rieder, S. Efficient rounding of approximate designs. Biometrika 1992, 79, 763–770. [Google Scholar] [CrossRef]
- Draper, N.R.; Hunter, W.G. Design of experiments for parameter estimation in multiresponse situations. Biometrika 1966, 53, 525–533. [Google Scholar] [CrossRef]
- Wong, W.K.; Yin, Y.; Zhou, J. Optimal designs for multi-response nonlinear regression models with several factors via Semidefinite Programming. J. Comput. Graph. Stat. 2019, 28, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, J.; Wolfowitz, J. The equivalence of two extremum problem. Can. J. Math. 1960, 12, 363–366. [Google Scholar] [CrossRef]
- Helton, J.W.; Vinnikov, V. Linear matrix inequality representation of sets. Comm. Pure Appl. Math. 2007, 60, 654–674. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A.S. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; University Press: Cambridge, UK, 2004. [Google Scholar]
- Sagnol, G. On the semidefinite representation of real functions applied to symmetric matrices. Linear Algebra Appl. 2013, 439, 2829–2843. [Google Scholar] [CrossRef]
- Shahmohammadi, A.; McAuley, K.B. Sequential model-based A-optimal design of experiments when the Fisher Information Matrix is noninvertible. Ind. Eng. Chem. Res. 2019, 58, 1244–1261. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Linear and Nonlinear Equations; Frontiers in Applied Mathematics series; Number 16; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Bischof, C.H.; Bücker, H.M.; Lang, B.; Rasch, A.; Vehreschild, A. Combining Source Transformation and Operator Overloading Techniques to Compute Derivatives for Matlab Programs. In Proceedings of the Second IEEE International Workshop on Source Code Analysis and Manipulation (SCAM 2002), Montreal, QC, Canada, 1 October 2002; IEEE Computer Society: Los Alamitos, CA, USA, 2002; pp. 65–72. [Google Scholar]
- Grant, M.; Boyd, S.; Ye, Y. cvx Users Guide for cvx, version 1.22; CVX Research, Inc.: Austin, TX, USA, 2012. [Google Scholar]
- Sagnol, G. PICOS, a Python Interface to Conic Optimization Solvers; Technical Report 12-48; ZIB: Berlin, Germany, 2012. [Google Scholar]
- Sturm, J. Using SeDuMi 1.02, a Matlab toolbox for optimization oversymmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Andersen, E.; Jensen, B.; Jensen, J.; Sandvik, R.; Worsøe, U. MOSEK, version 6; Technical Report TR–2009–3; MOSEK: Copenhagen, Denmark, 2009. [Google Scholar]
- Ye, Y. Interior Point Algorithms: Theory and Analysis; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).