1. Introduction
Extremum-seeking control (ESC) has grown to become the leading approach to solve real-time optimization problems [
1]. Following the seminal work of Krstic and coworkers ([
2,
3,
4,
5,
6,
7]), this general and practically relevant control approach is equipped with an established and well understood theoretical framework, as highlighted in the proof of Krstic and Wang [
2]. The standard perturbation ESC algorithm has been generalized in various forms to handle output and input constraints. ESC in the presence of constraints has been investigated in various form in the literature. Constrained ESC was first considered in [
8] where a trajectory tracking approach was used to address the constrained ESC problem for a class of nonlinear systems with parametric uncertainties. In this approach, a barrier function or interior-point method was used to enforce constraints and feasibility of the closed-loop trajectories. A similar model-free extremum-seeking approach was presented in [
9]. A Lagrangian, saddle-point, ESC technique is proposed in [
10], and a similar approach is proposed in [
11] to handle a class of stochastic control systems. In [
12], a Shahshahani gradient approach was proposed. This techniques allows one to handle ESC problems subject to linear constraints by a simple reformulation of the gradient descent dynamics. In contrast to Lagrangian-based techniques, the main advantage of the Shahshahani gradient and barrier function approaches is the ability to preserve feasibility throughout the optimization.
For ESC in the presence of input constraints, a variety of techniques have been proposed. In [
13] and [
14], a projection algorithm is used to solve ESC problems subject to constraints in the decision variables. In [
15], a comprehensive study of anti-windup mechanisms for standard ESC is presented. The approach draws a parallel between penalty (barrier) function methods and an anti-windup mechanism. A proof of convergence of the ESC in the presence of constraints is provided. In [
16], a simplistic windup algorithm for a standard ESC technique is implemented experimentally for the real-time optimization of airside economizers.
The vast majority of existing results on ESC have focussed on continuous-time systems, as is the case for the existing approaches for ESC in the presence of constraints. Although discrete-time systems can be treated in an essentially similar fashion, the application of gradient descent in a discrete-time setting requires some care. A discrete-time version of the standard ESC loop was studied in [
4,
6] where convergence results similar to continuous time systems are obtained. A similar algorithm was also proposed in [
17] for the tuning of PID controllers in unknown dynamical systems using ESC. Discrete-time ESC subject to stochastic perturbations is studied in [
18]. The use of approximate parameterizations of the unknown cost function using quadratic functions was recently proposed in [
19]. An alternative ESC-like method was proposed in [
20]. In this study, a trajectory-based technique is used to analyze the properties of nonlinear optimization algorithms as dynamical systems. It is shown that properties of the nonlinear-optimization algorithms are suitable to assess the convergence of certain classes of ESC applied in a sampled-data approach. This method was recently studied in the context of global sampling methods in [
21] where trajectory-based properties of nonlinear optimization methods are used to establish robust convergence. The main objective with the trajectory-based techniques is to analyze the properties of optimization algorithms assuming that they can converge to the true optimum using only the measurement of the objective function and possibly the constraints.
This paper proposes an extremum-seeking controller (ESC) design for a class of discrete-time nonlinear control systems subject to input constraints. Two actuation scenarios are considered. In the first scenario, we consider the ESC in the presence of saturated inputs. The proposed method generalizes the discrete-time proportional-integral ESC proposed in [
22] to incorporate a new discrete-time anti-windup mechanism for ESC. One contribution of this study is the development of a saturation bias estimation mechanism that can be used to remove the impact of dither on or near the saturation level. This mechanism ensures that violation of the constraints due to the dither signal are removed without the introduction of a gradient estimation bias. Moreover, it allows the system to remain responsive to changes in the system despite operating on or very close to the saturation level. An amplitude update routine is also proposed as a discrete-time generalization of the method proposed in [
23]. The amplitude update is coupled with the saturation bias estimation algorithm to account for the inherent bias associated with systems operated at or near saturation conditions.
In the second scenario, we adapt the application of the anti-reset windup strategy and the saturation bias estimation routine to handle systems with quantized actuators. We focus on ESC design for systems with “on/off” actuators. Since the excitation signal is limited to the on or off position, the application of the saturation bias estimation is able to remove the impact of the dither to allow the ESC system to converge to the correct position. Such actuators have not been treated in the literature.
The paper is organized as follows. A description of the ESC problem along with the key assumptions are given in
Section 2. The proportional-integral ESC controller are presented in
Section 3. The anti-windup mechanism and amplitude adjustment mechanism are described in
Section 4. The design of ESC for quantized actuators are presented in
Section 5. Simulation examples are presented in
Section 6 followed by brief conclusions and proposed future work are in
Section 7.
2. Problem Description
We consider a class of nonlinear systems of the form:
where
is the vector of state variables at time
k,
is the input variable at time
k taking values in
and
is the objective function at step
k, to be minimized. It is assumed that
and
are smooth vector valued functions and that
is a unknown smooth function.
The objective is to stabilize the system at the equilibrium conditions,
and
, that achieves the minimum value of
subject to saturation of the input. The input variable,
, is required to lie in the interval
. At equilibrium, the state variables are given by the map
that solves the following equation:
The corresponding equilibrium cost function is given by:
The steady-state optimization problem is to find the minimizer of subject to . The set represents a neighbourhood of the equilibrium .
The steady-state cost function, , meets the following assumptions.
Assumption 1. The nonlinear system is such that. Assumption 2. The cost is such that
where β is a strictly positive constant.
Following [
22], we write the cost dynamics as:
where
,
and
for
.
The following assumptions are required to ensure the stability of the closed-loop system.
Assumption 3. There exists a function that solves the identity: This assumption states that the feedback:
is well defined.
The following stabilizability condition for the nonlinear system subject to input saturation is also required.
Assumption 4. There exists a positive definite function that satisfies the following inequalities:with positive constants and . For all there exists a positive constant such that:with positive constant and and 4. Input Constrained ESC
In this section, we present the main contribution of this study. The proposed technique incorporates three mechanisms for the solution of ESC problems in the presence of input constraints. The first mechanism consists of a standard anti-windup mechanism that exploits the proportional integral formulation of the ESC considered. The second mechanism proposes a dither bias estimation routine that eliminates the presence of biases introduced when the dither signal input pushes the input to its saturation limit. The third mechanism is a dither amplitude update that is used to remove the dither signal when the system has converged to its optimal value, or its optimal saturation limit.
4.1. Anti-Windup Mechanism
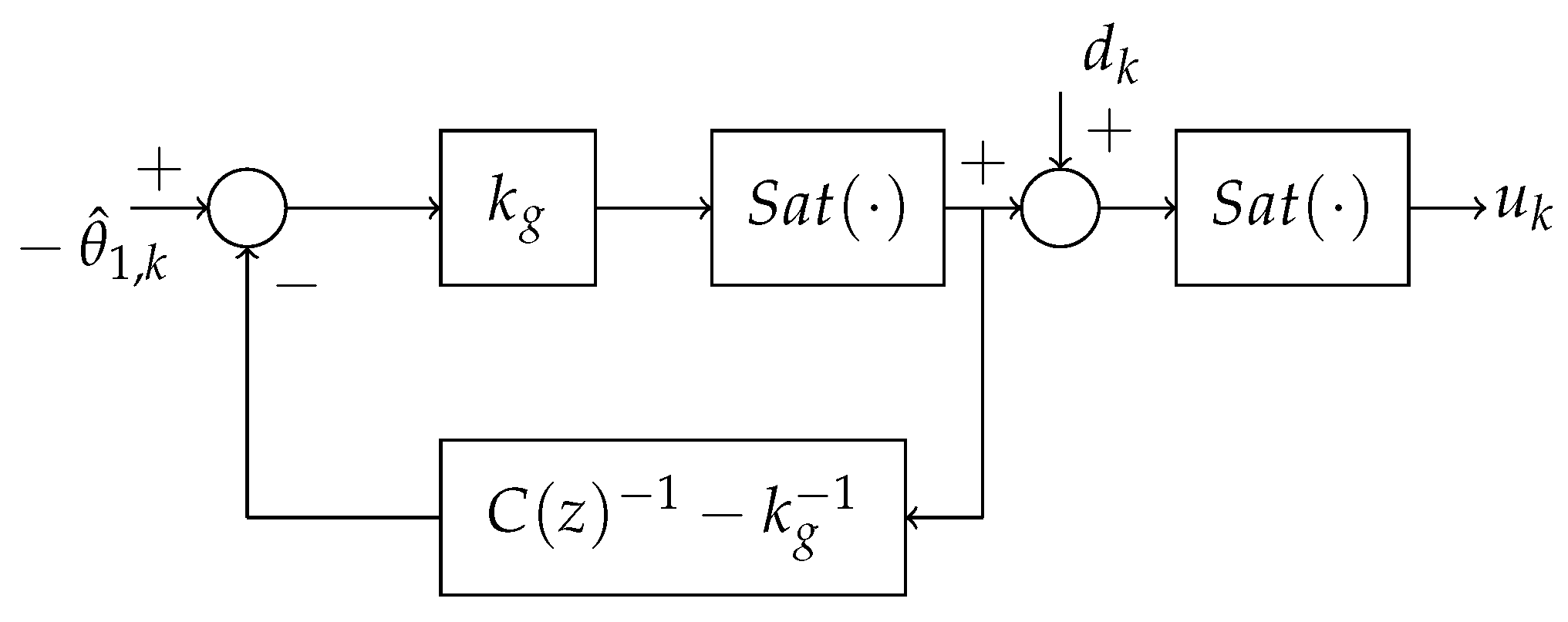
In this paper, we propose the use of an anti-windup mechanism for the proportional integral ESC controller (
5). A block diagram of the mechanism is shown in
Figure 1.
In
Figure 1,
represents the discrete-time transfer function of the proportional-integral controller
The mechanism places the dither addition after the anti-windup loop but before the final saturation. This mechanism guarantees that the dither signal is not removed when the system operates at the saturation limits. It also guarantees that the dithered input does not violate the input constraints.
The operator Sat
denotes the saturation function:
The proposed dynamics of the anti-windup mechanism is given by:
The anti windup loop is such that, in the absence of saturation, the control law reduces to the proportional integral law and the control law becomes:
Please note that the Sat remains in the control loop to ensure that the added dither signal does not cause input constraint violation.
One of the difficulties associated with such an approach is that the saturation creates a bias in the dither signal. This is problematic in cases where the optimum input lies close to or on the saturation limit. This bias in the dither signal can lead to a bias in the estimation of the parameters. As result, the value of the parameter does not converge to zero even when the true value vanishes.
It is, therefore, imperative to provide a mechanism to introduce the dither signal that prevents the estimation bias. We consider two mechanisms in this study.
4.2. Saturation Bias Estimation
Let us consider the case in which the optimum occurs on the upper saturation level
. At the optimum, the control signal for the ESC is given by
The filter (or regressor) vector yields:
One of the key properties of the dither signal is that
. In the absence of input saturation, the average regressor is such that
In the presence of a bias in the dither signal, the regressor vector does not average to the correct value. As a result, the parameter estimation of is subject to a bias, and the system would converge to an erroneous optimum state and input.
In this section, we design an update mechanism that accounts for this saturation bias. This is achieve by introducing a signal
in the control,
, which is such that the average input is unbiased. That is, for a fixed value of the input
, the following property is achieved:
We first define the variable
The bias estimation update proposed in this study is given by:
Proposition 1. The saturation bias estimate update (10) is such that: For , For , or ,
Proof. For Statement 1, the conclusion is straightforward.
The proof of Statement 2 is as follows. To establish the property (
9), we first compute the average in the case where the value of the input is at one its saturation limits. Let us consider the case where the input is at its upper limit,
. From a set of
N samples of the input, assume that there are
samples at which Sat
with the remaining
samples for which Sat
. Let
,
denote the indices of the samples that are not saturated. As a result, we can decompose the averaged quantity as follows:
Thus if one considers the update (
10). Following the above argument, we average both sides by summing over
N samples. Let us consider the situation where the input is at its upper saturation limit
and decompose the overall average into
saturated values and
inputs whose perturbed value is not saturated. This yields
This gives the following recursion of sums:
For every sample from the set of points that are saturated at step
k, it follows that
. As a result, we can write
Defining the variable
we obtain the following recursion:
As a result, we see that the average
approaches the negative value of the mean dither
. As a result, the bias (
9) is completely removed by the saturation bias update (
10). This completes the proof of Statement 2. □
In cases where the optimum lies on or close to a saturation, the update (
10) would lead to an effective removal of the dither signal. However, in fact, the dither is not removed. It is simply compensated for by the bias estimate
. If a disturbances affects the system, moving the optimum inside the saturation, then the dither signal would resume and the ESC would operate in a normal way. As a result, the dither would not be effectively removed.
4.3. Dither Amplitude Update
In this study, we consider a dither signal of the form: where can be taken to be a zero-mean Gaussian variable or simply for some frequency . The amplitude of the dither signal is obtained using an amplitude update.
Let the upper or lower limit if
be denoted generically by
. We first define the signal:
The proposed amplitude update is given by:
where
,
,
and
are tuning parameters. This mechanism confers two actions to adjust the amplitude of the dither signal.
The term
decreases the amplitude when the gradient estimate decreases or when the system has reached an equilibrium corresponding to a saturation input level. In [
23], a similar amplitude update is proposed. The proposed method complements that approach in two ways. First, we adjust for the situation in which the input has stabilized on a saturation level. In this case, the estimated value of
cannot reach 0. As a result, the approach of [
23] using only
would yield a larger value of the amplitude. If the optimization does not lead to a saturated value of the input, the update acts as the update of [
23] and reduces the amplitude to a suitable lower level.
Second, the proposed method assigns a minimum value of the amplitude
. As the proof of stability of the PI-ESC algorithm demonstrates [
22], the practical stability of the unknown optimum requires a persistent dither signal with
for all
k. In practice, setting
would prevent the system from responding to possible changes in the changes that may arise from changing conditions. This property of the ESC system was recognized in [
23], which required a fixed lower bound for the amplitude. However, the choice of this lower bound can be conservative. The second term in the update (
11),
, aims to increase the amplitude
when the smallest eigenvalue of the matrix
decreases. This update guarantees a minimum amount of excitation in the system in order to respond to possible process changes.
The action of the amplitude update can be summarized as follows.
Proposition 2. For , the update (11) is such that is bounded and approaches in a region of an unconstrained optimum or on a saturation level of the input . The combination of the anti-windup (
Figure 1) and the amplitude update (
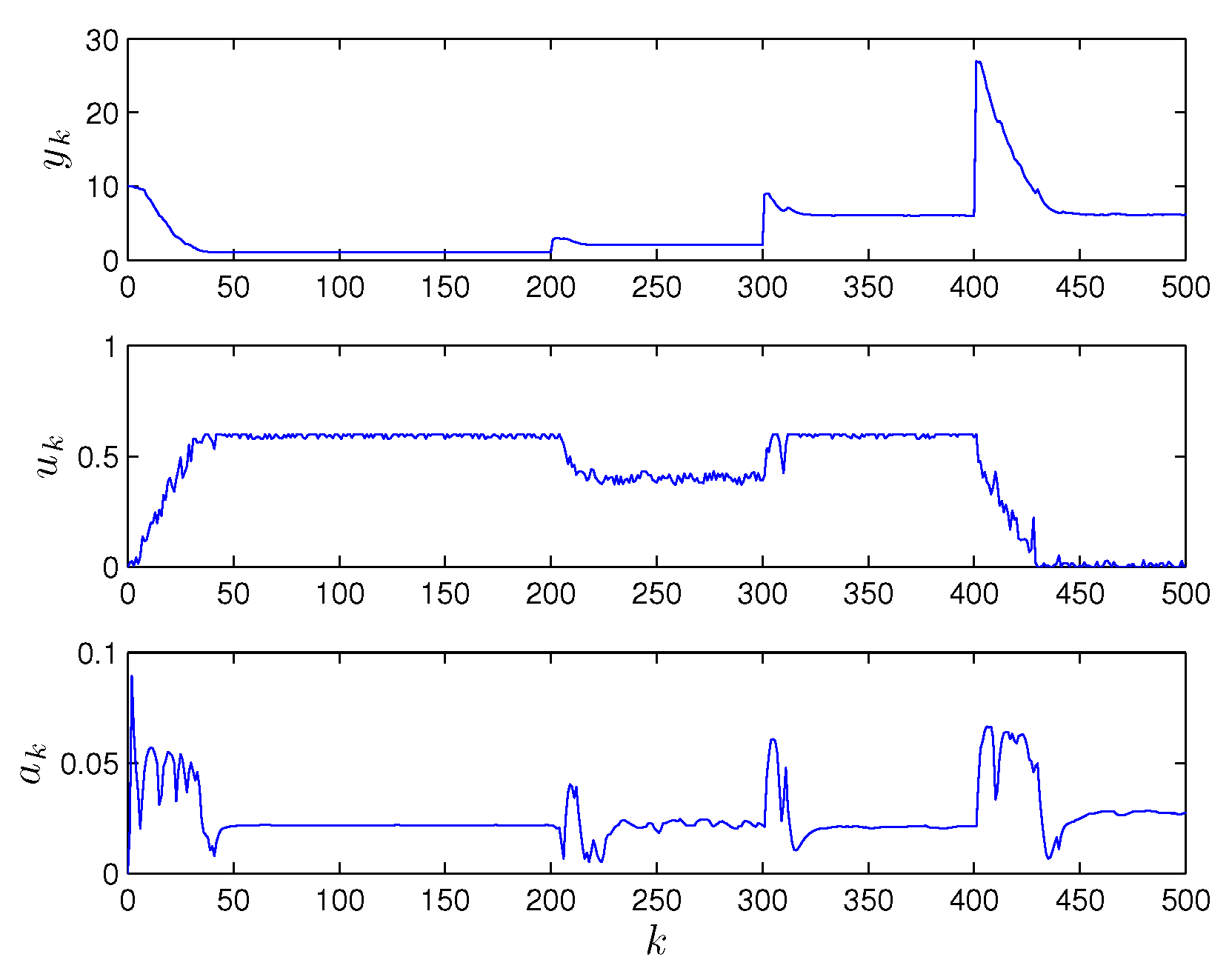
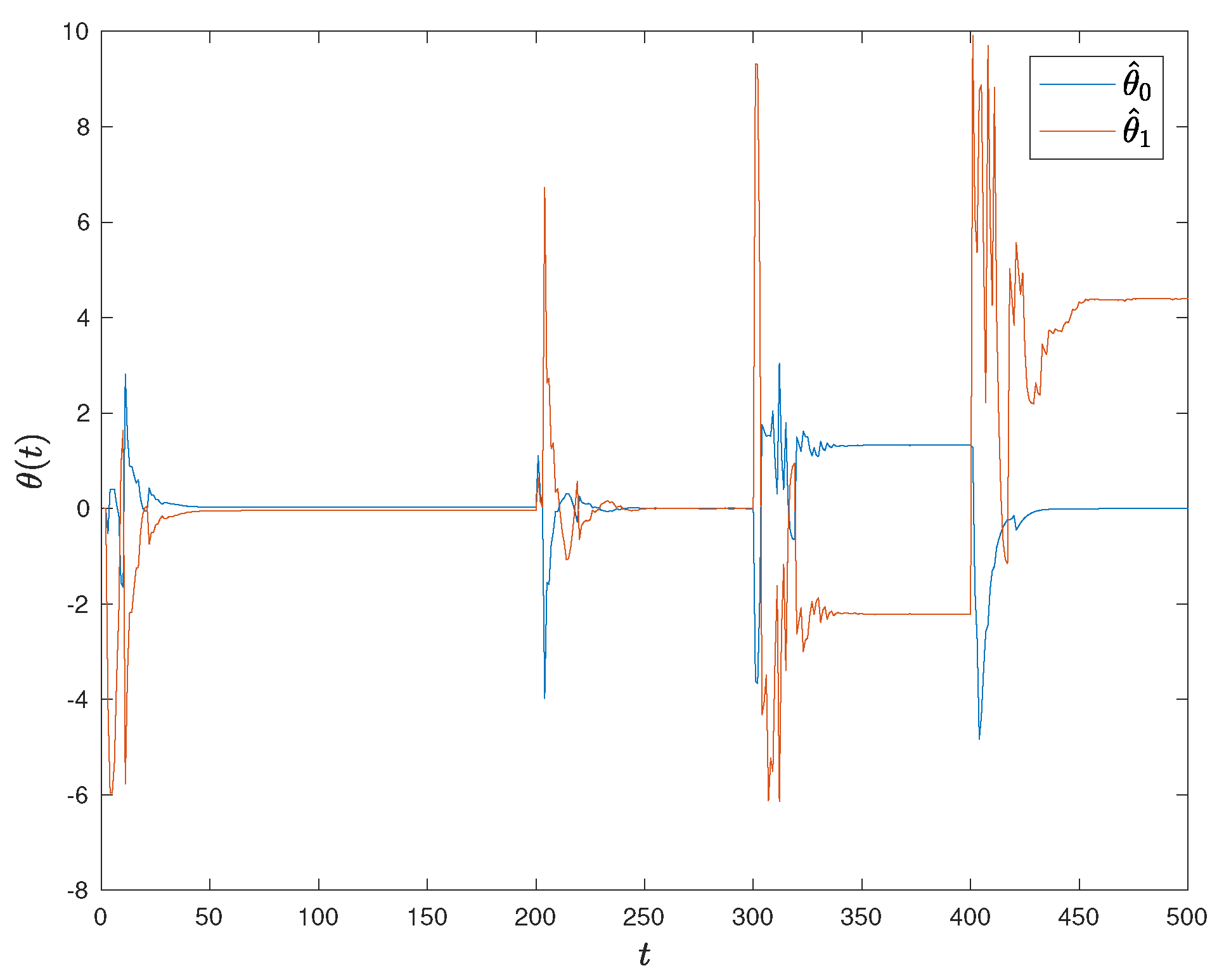
11) provides an effective mechanism to minimize the bias of the system arising from the saturation. It also removes the need for the tuning of the amplitude. We demonstrate this in simulations in the next section.
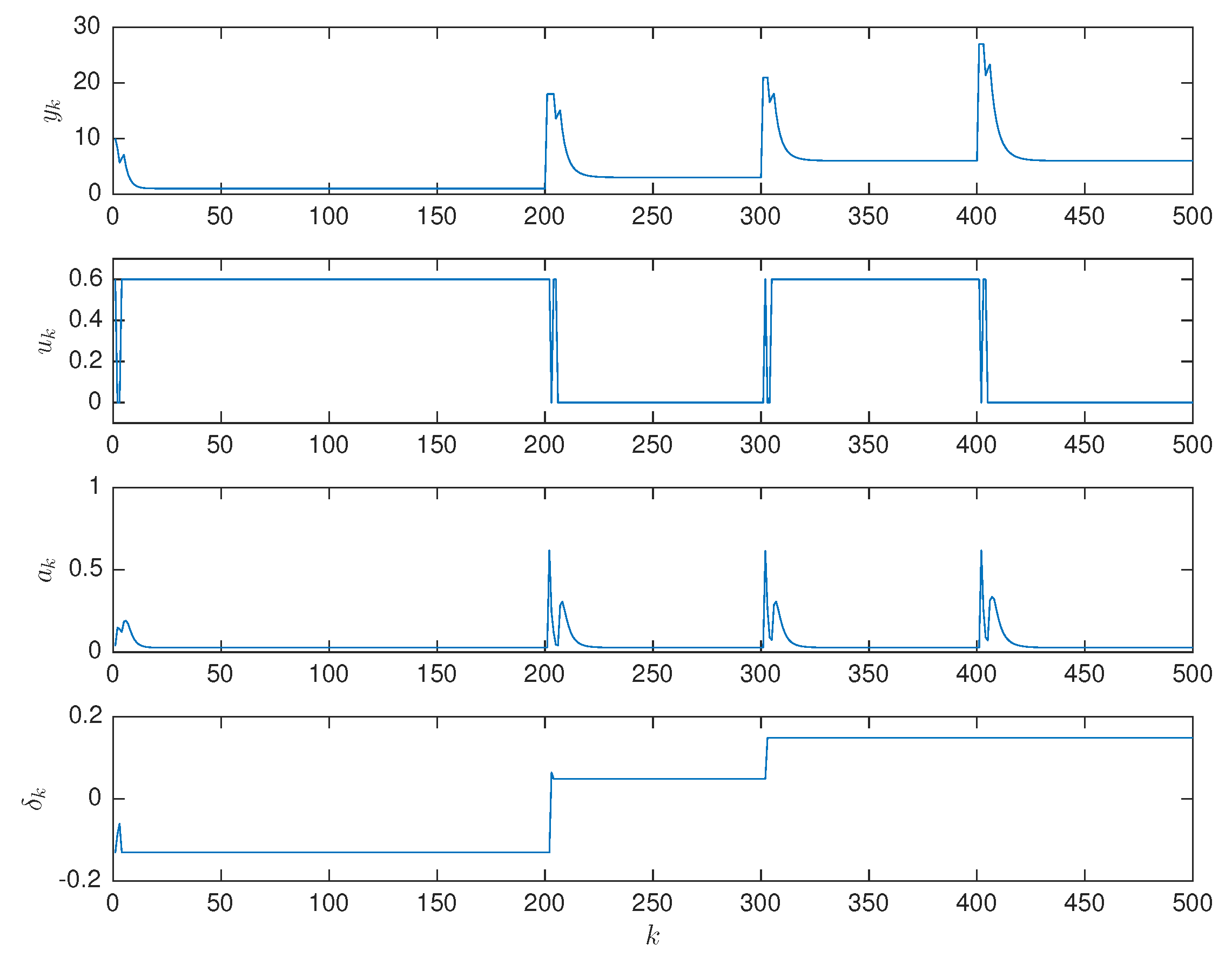
5. ESC for Systems with Quantized Actuators
The three mechanisms proposed in the previous section can be easily adapted to a situation where the actuators of the system are limited to quantized (or on-off) input settings. In this case, we consider an actuator whose on-off action can be implemented using a hysteresis mechanism of the form:
where
is a small positive constant. The function
implements the discrete actuator using a hysteresis mechanism.
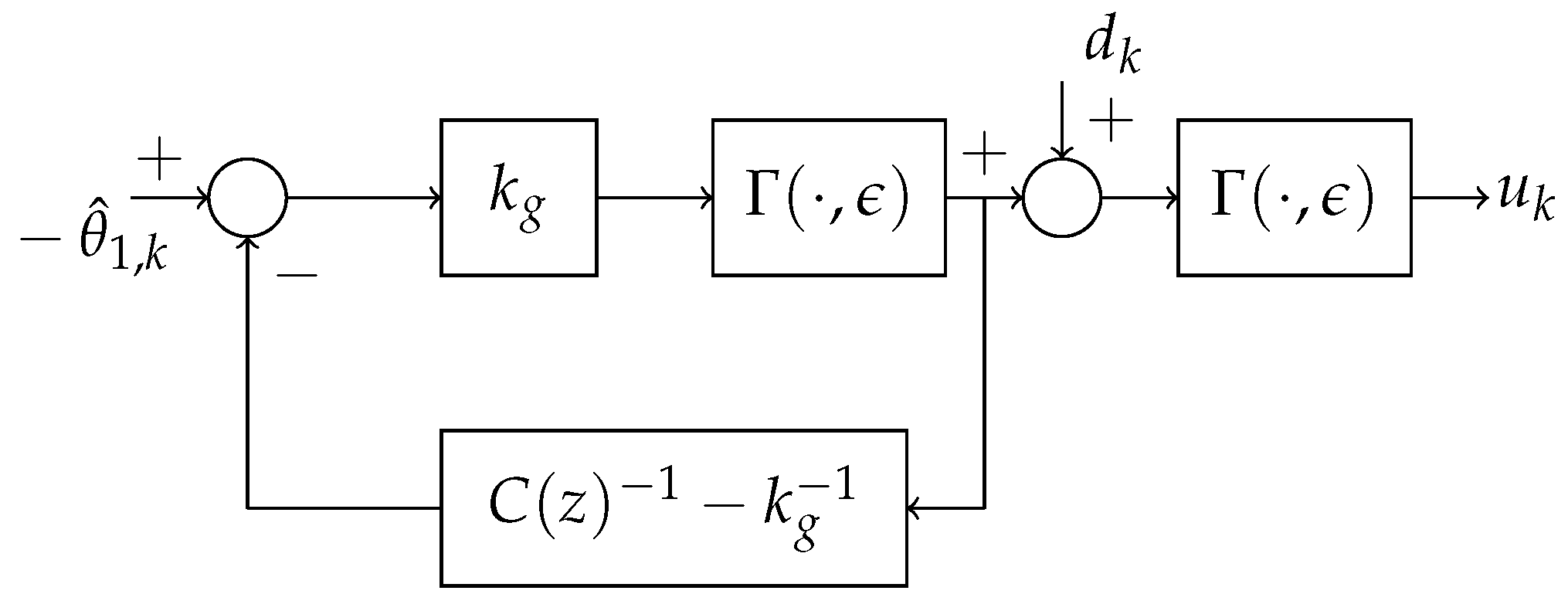
In this study, we propose a quantized actuator ESC using the mechanism depicted in
Figure 2.
As above, we consider the anti-windup ESC given by:
Since the ESC only provides quantized control action
or
, we must consider a saturation bias estimation to eliminate the bias and remove the b presented in
Section 4.3. The reason for this is that the update (
14) yields the required property of the saturation bias as the system reaches the limits. The proposed bias update is given by:
where
The amplitude of the dither signal is implemented as in
Section 4.3.