A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems
Abstract
1. Introduction
- (1)
- The PID tuning formula is analytically derived in terms of the relative delay margin for FOPDT systems.
- (2)
- The stability regions for and based on a given derivative gain () and the process model are analyzed.
- (3)
- The desired delay robustness-constrained optimization (DRO) for the PID controller is formulated and a set of recommended parameters is offered for the ease of use.
- (4)
- Illustrative examples are carried out and results verify the superiority of the proposed DRO design for the PID controller.
2. Problem Formulation
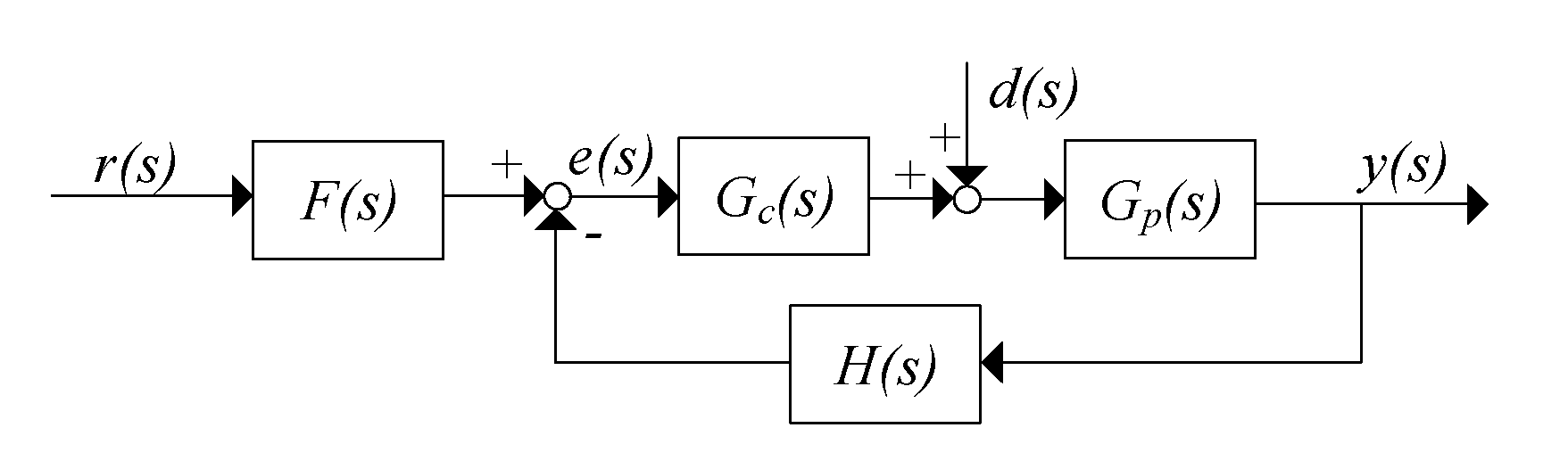
2.1. The Basic Control Structure
2.2. Problem Formulation
- (1)
- The maximum sensitivity function, , is defined in the closed-loop form and this results in some difficulties in analysis. Besides, is the maximum value of the sensitivity function over the whole frequency range. On the contrary, the delay margin is an open-loop measure with the information in a single point.
- (2)
- As is well known, there is a fundamental limit on for the processes with time delay, i.e., [8]. Note that the qualitative inequality is extended for a quantitative purpose.
- (3)
- The delay margin is dimensionless and can reflect the influence of the time delay on the variation in the delay time. Besides, the delay margin can be used to optimize parameters of the PID controller directly and easily as shown in next section. However, is often used to test the robustness of the closed-loop system with designed parameters.
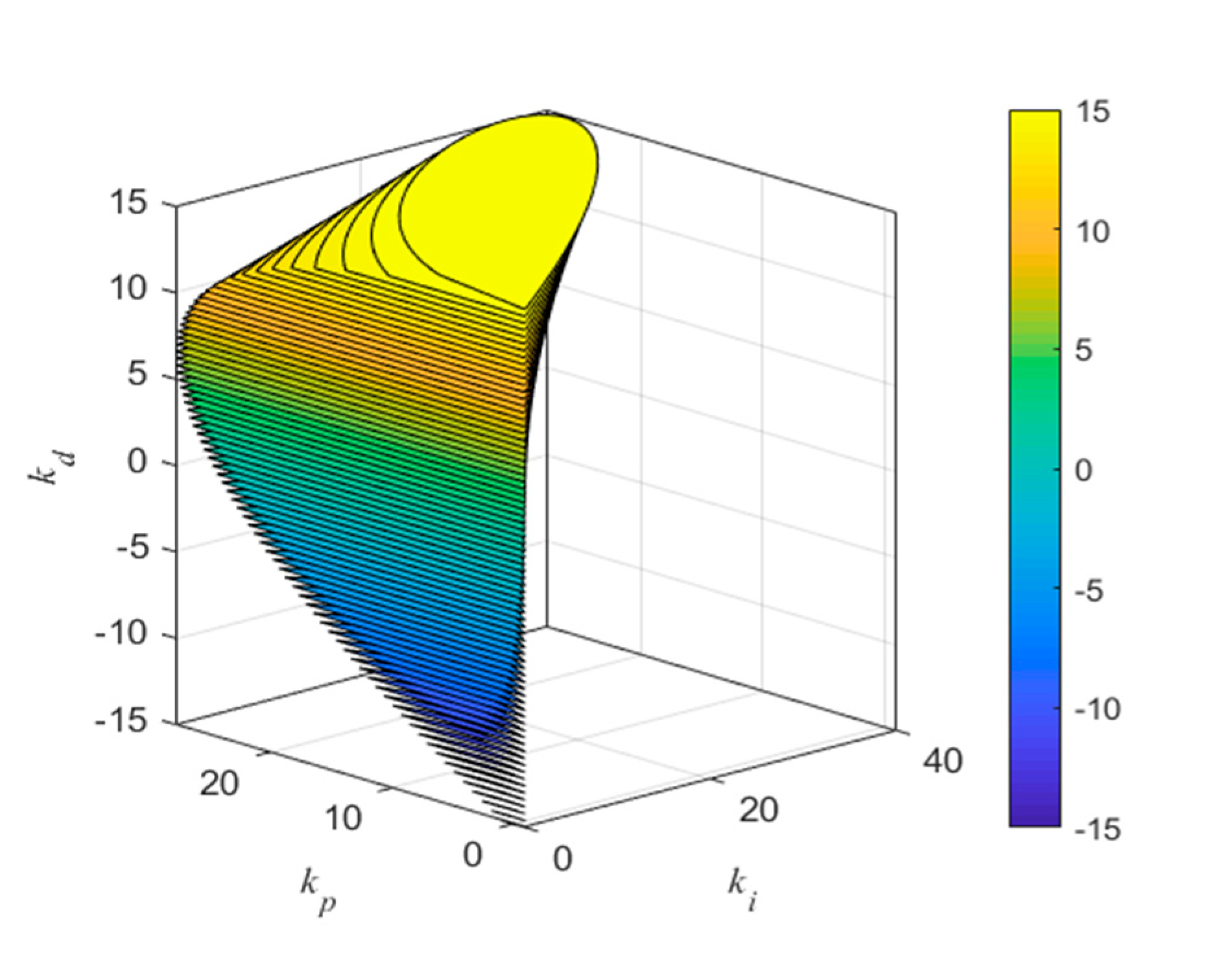
3. Stability Regions Based on the Relative Delay Margin
4. PID Tuning with Constraints on Relative Delay Margin
- (1)
- The approximate FOPDT model (, , and ) is obtained by various approximation methods.
- (2)
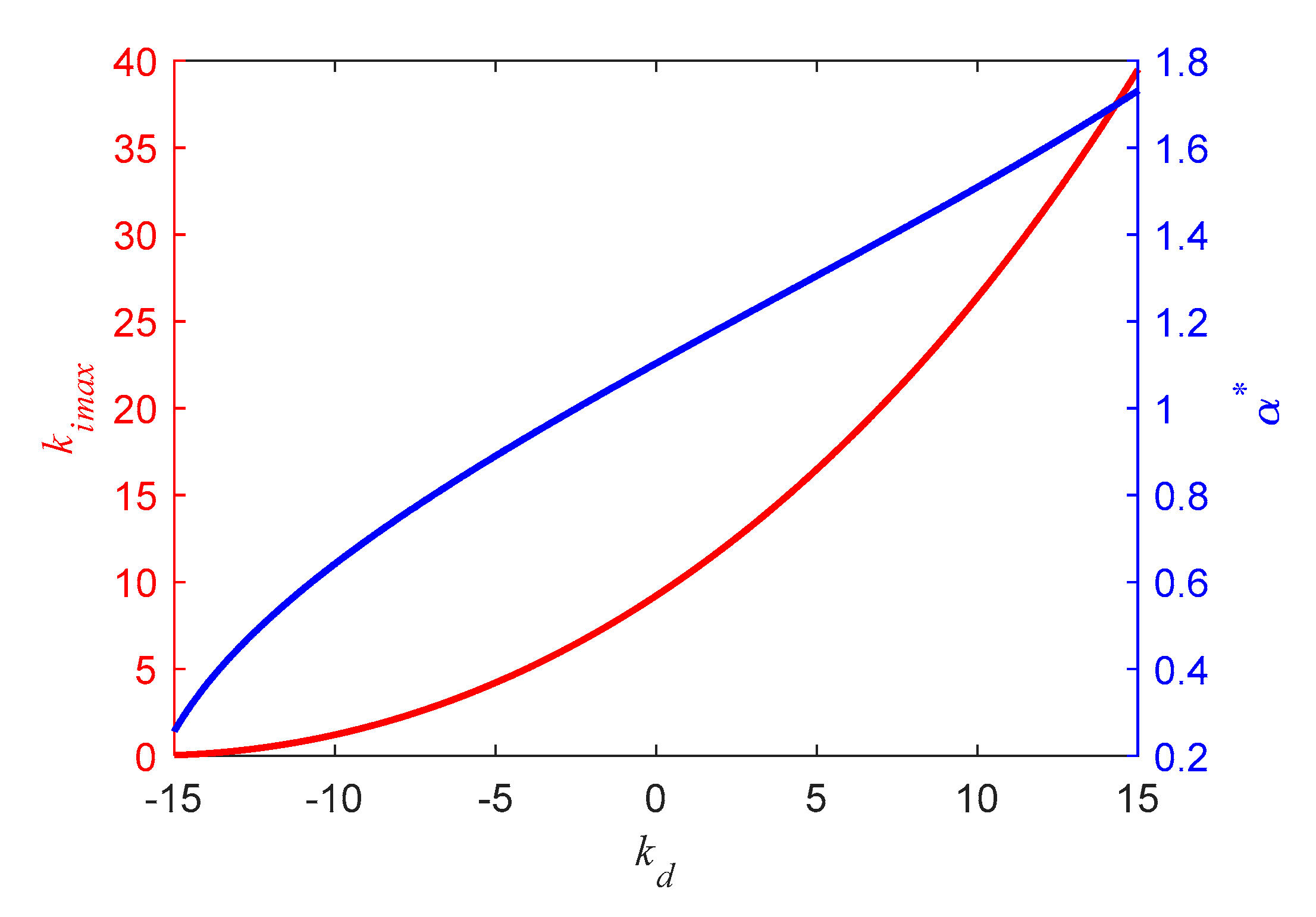
- The derivative gain can be given by Equation (36) and a desired robustness level is also given. can be obtained by solving Equation (35).
- (3)
- and are calculated by Equation (16). Adjust the prefilter parameters ( and ) manually to obtain the satisfactory tracking performance.
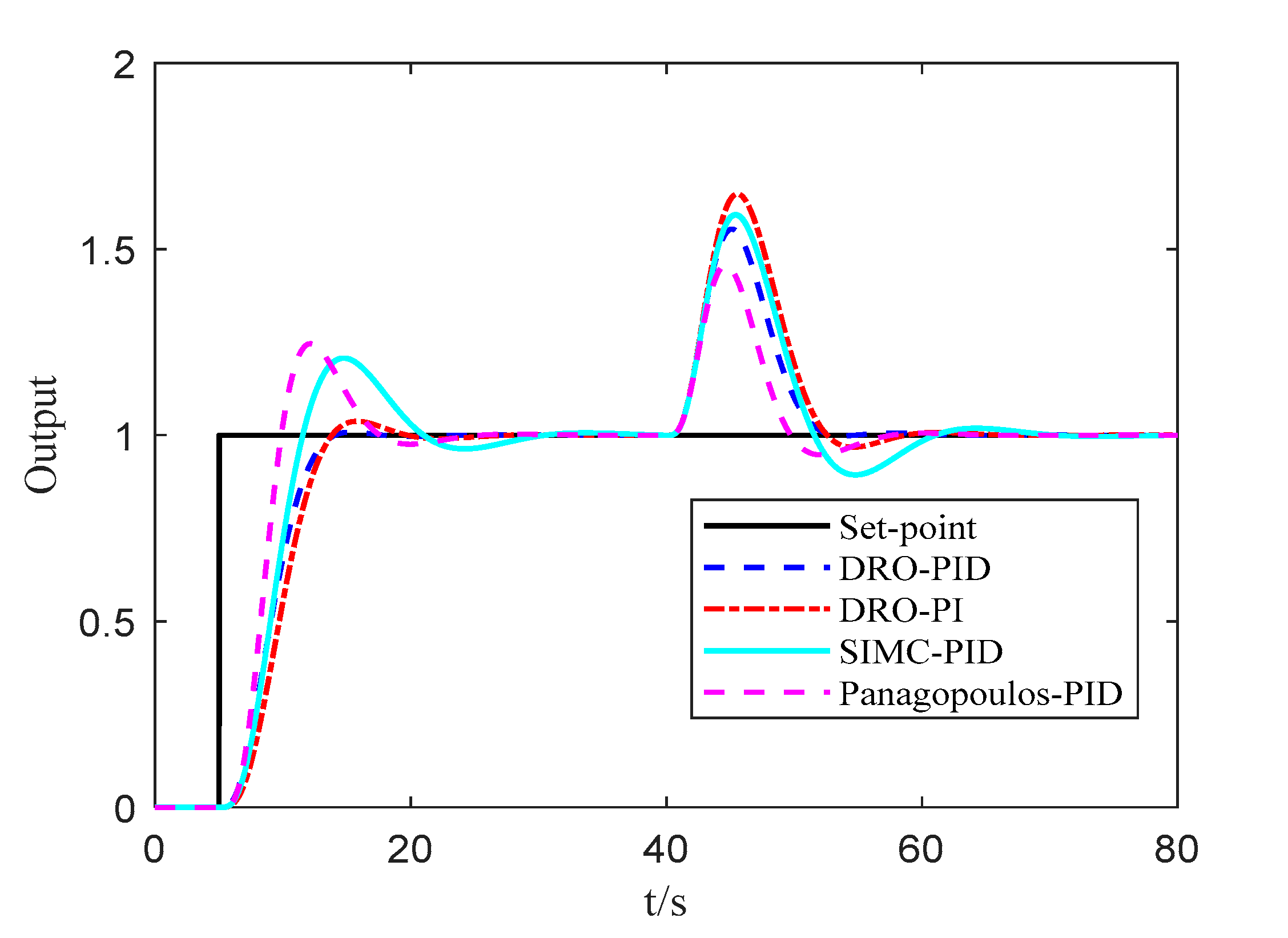
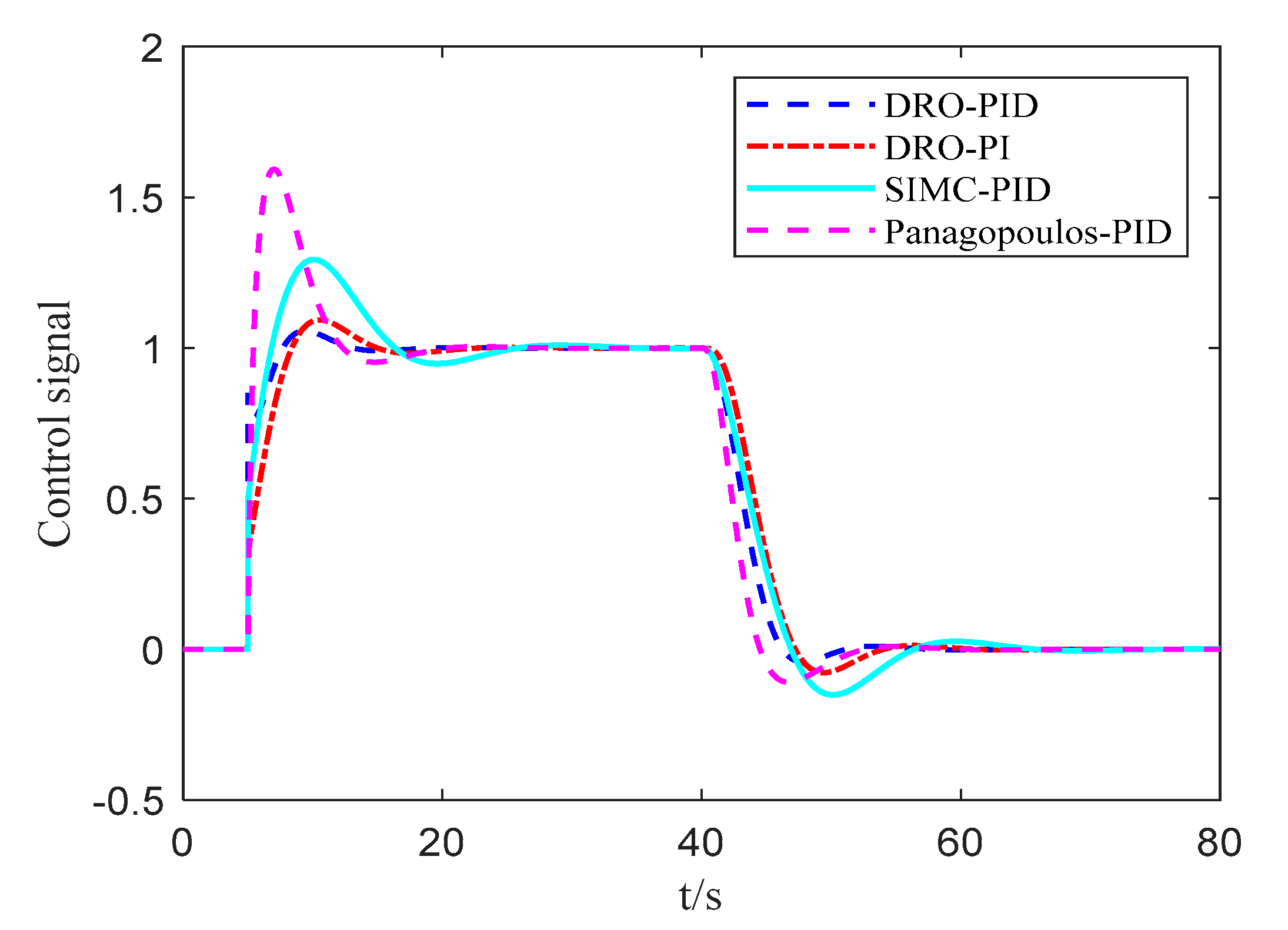
5. Illustrative Examples
5.1. Example 1
5.2. Example 2
5.3. Example 3
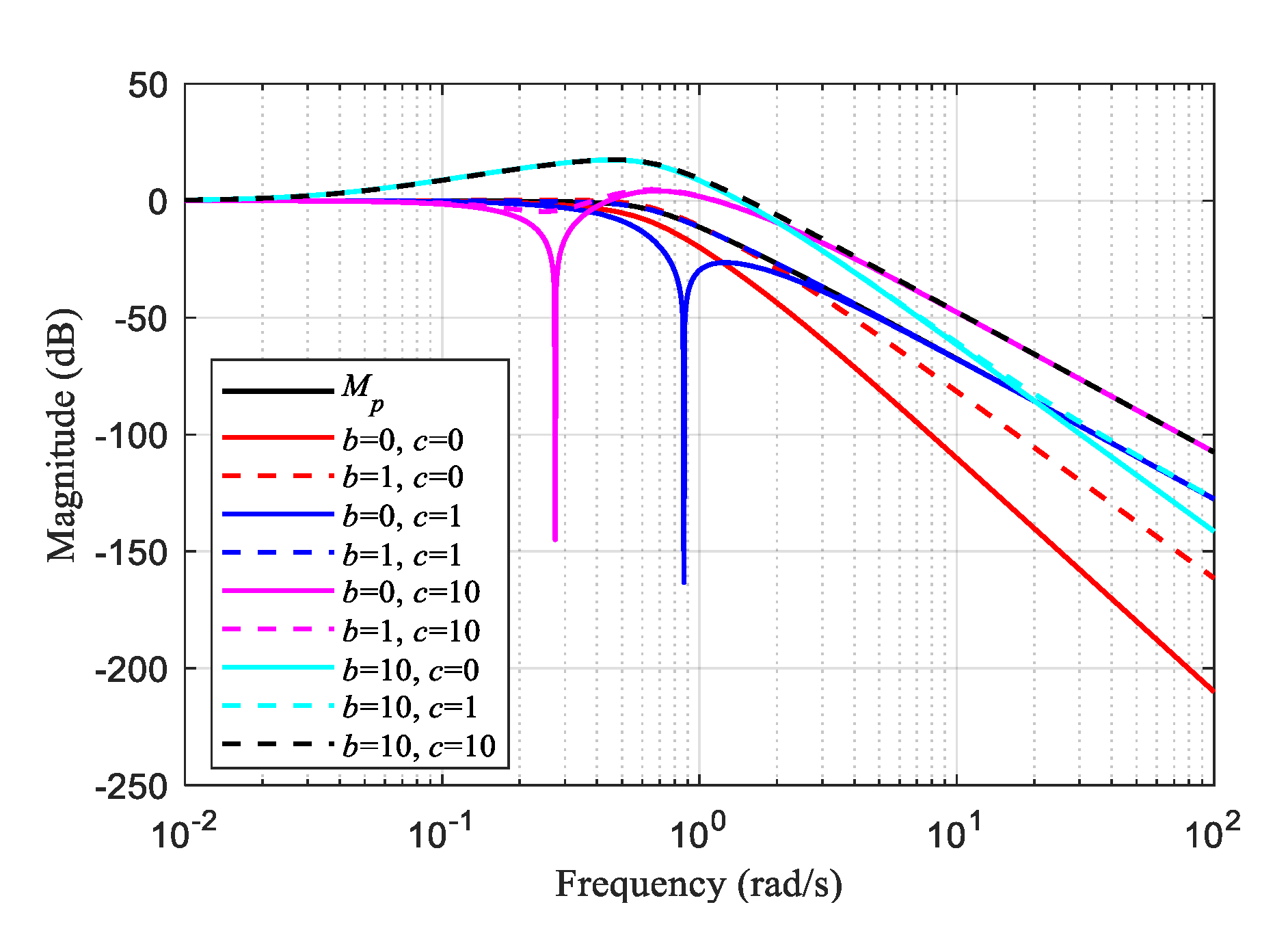
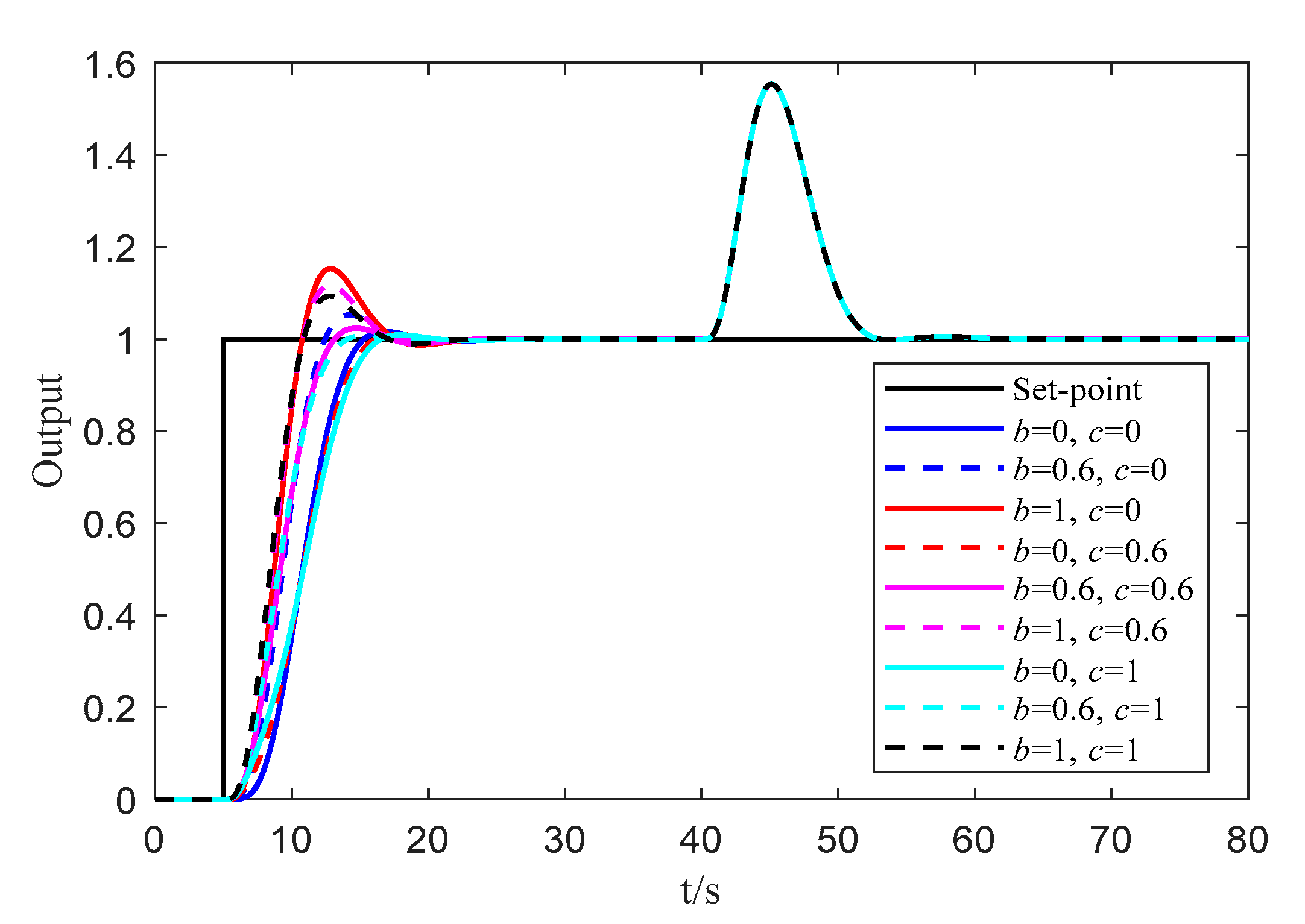
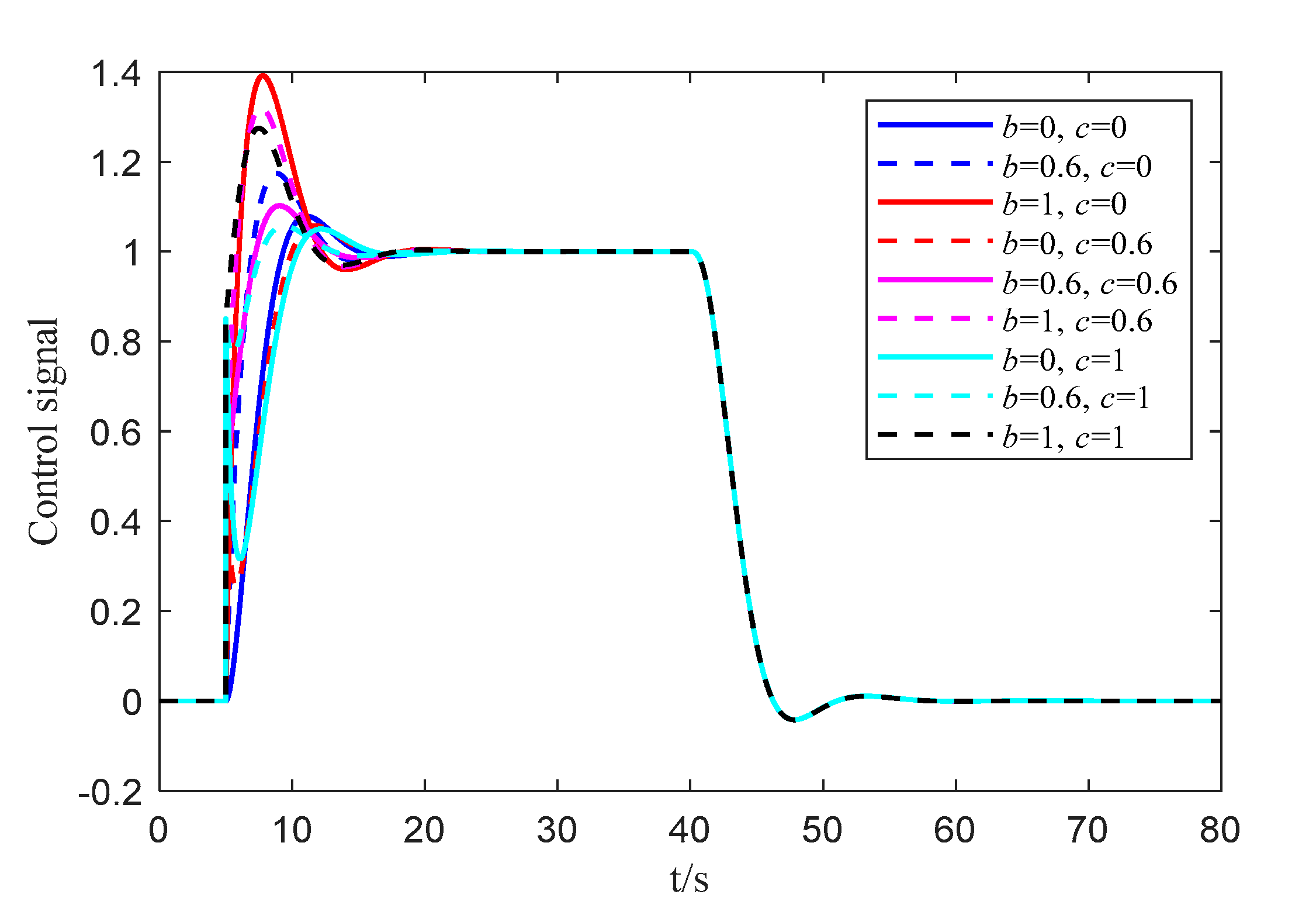
5.4. Discussion about the Implementation of the Derivative
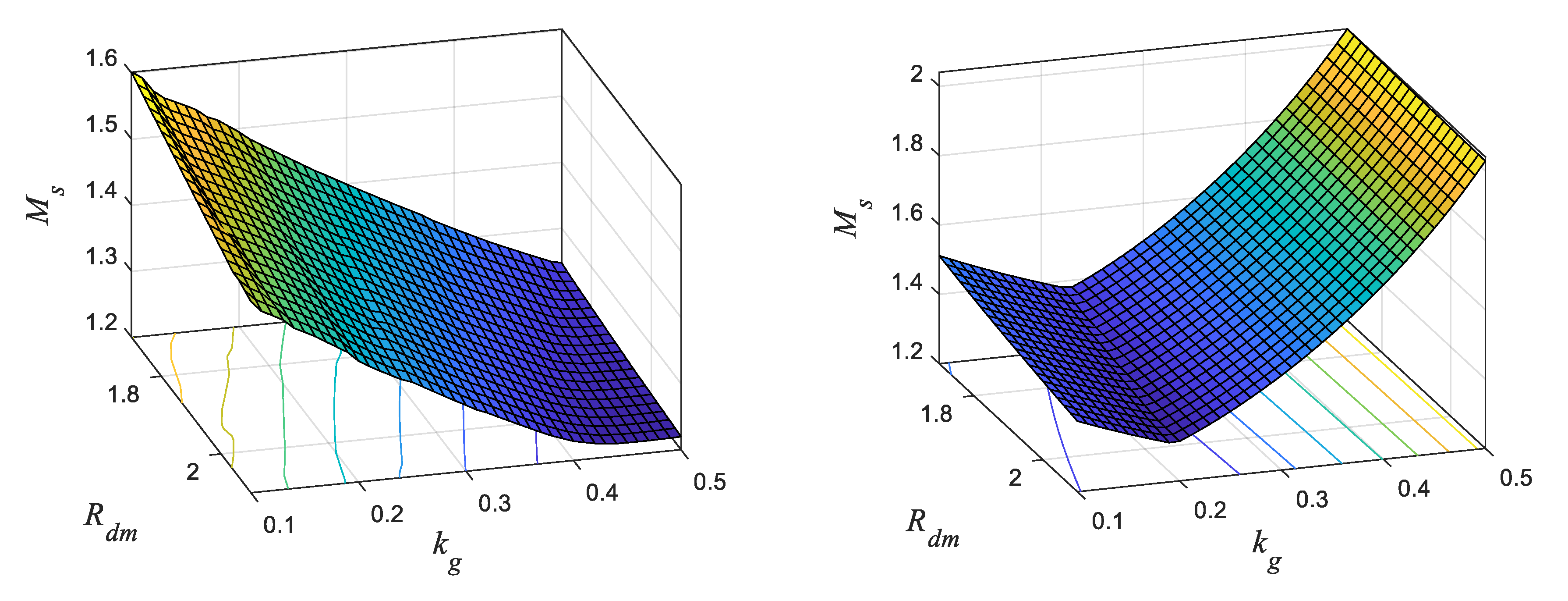
5.5. Discussion about the Relationship between and
6. Conclusions
- (1)
- The PID tuning formula is analytically derived in terms of the relative delay margin for first order plus dead-time systems.
- (2)
- A theorem about the ranges of and is given and the proof is also offered.
- (3)
- The design method based on the delay robustness-constrained optimization for the proportional-integral-derivative controller is given and a set of recommended parameters is offered for the ease of use.
- (4)
- Illustrative examples are carried out and results verify the superiority of the proposed proportional-integral-derivative controller design method.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| The gain margin | |
| The maximum sensitivity function | |
| The gain crossover frequency | |
| The integral gain of the PID controller | |
| The transfer function of the controlled plant | |
| The set-point prefilter | |
| The process gain | |
| The delay time | |
| The derivative time of the PID controller | |
| The process output | |
| The set-point weighting factor | |
| The Laplace transforms of the output | |
| The Laplace transforms of the input disturbance | |
| The transfer function from the input disturbance to the output | |
| The open loop transfer function | |
| The Laplacian operator | |
| The normalized time delay | |
| TV | The total variation of control signal |
| The approximate FOPDT model | |
| The phase margin | |
| The relative delay margin | |
| The proportional gain of the PID controller | |
| The derivative gain of the PID controller | |
| The transfer function of the PID controller | |
| The feedback controller on the feedback path | |
| The time constant | |
| The integral time of the PID controller | |
| The reference signal | |
| The input disturbance | |
| The set-point weighting factor | |
| The Laplace transforms of the reference | |
| The transfer function from the reference to the output | |
| IE | The integral of the error |
| The dimensionless parameter, | |
| IAE | The integrated absolute error |
| The settling time | |
| N | The filter coefficient and |
Appendix A
Appendix B
- (1)
- The approximate FOPDT model (, , and ) is obtained by various approximation methods and in Equation (A12) can be obtained
- (2)
- and a desired robustness level are fixed. can be obtained by solving Equation (A26).
- (3)
- and are calculated by Equation (A20). The values of , , and can be obtained. Adjust the prefilter parameters ( and ) manually to obtain the satisfactory tracking performance.
Appendix C
References
- Åström, K.J.; Panganamala, R.K. Control: A perspective. Automatica 2014, 50, 3–43. [Google Scholar] [CrossRef]
- Wu, Z.L.; Li, D.H.; Xue, Y.; Chen, Y.Q. Gain Scheduling Design Based on Active Disturbance Rejection Control for Thermal Power Plant under Full Operating Conditions. Energy 2019, 185, 744–762. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Li, H.; Shi, P.; Yao, D.; Wu, L. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 2016, 64, 133–142. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, L. PID controller design for second order nonlinear uncertain systems. Sci. China Inf. Sci. 2017, 60, 022201. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Åström, K.J.; Tore, H. Advanced PID Control; The Instrumentation, Systems, and Automation Society Press: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Åström, K.J.; Hägglund, T. Automatic tuning of simple regulators with specifications on phase and amplitude margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 4. [Google Scholar]
- Åström, K.J.; Panagopoulos, H.; Hägglund, T. Design of PI controllers based on non-convex optimization. Automatica 1998, 34, 585–601. [Google Scholar] [CrossRef]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules; Imperial College Press: London, UK, 2009. [Google Scholar]
- Hägglund, T.; Åström, K.J. Revisiting the Ziegler-Nichols tuning rules for PI control. Asian J. Control 2002, 4, 364–380. [Google Scholar] [CrossRef]
- Wang, X.; Yan, X.; Li, D.; Sun, L. An Approach for Setting Parameters for Two-Degree-of-Freedom PID Controllers. Algorithms 2018, 11, 48. [Google Scholar] [CrossRef]
- Sundaramoorthy, S.; Ramasamy, M. Tuning Optimal Proportional–Integral–Derivative Controllers for Desired Closed-Loop Response Using the Method of Moments. Ind. Eng. Chem. Res. 2014, 53, 17403–17418. [Google Scholar] [CrossRef]
- Srivastava, S.; Pandit, V.S. A 2-Dof LQR based PID controller for integrating processes considering robustness/performance tradeoff. ISA Trans. 2017, 71, 426–439. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.F.; Li, D.H. Decentralized PID controllers based on probabilistic robustness. J. Dyn. Syst. Meas. Control 2011, 133, 061015. [Google Scholar] [CrossRef]
- Begum, K.G.; Rao, A.S.; Radhakrishnan, T.K. Enhanced IMC based PID controller design for non-minimum phase (NMP) integrating processes with time delays. ISA Trans. 2017, 68, 223–234. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Du, W. Design of PID controller based on a self-adaptive state-space predictive functional control using extremal optimization method. J. Frankl. Inst. 2018, 355, 2197–2220. [Google Scholar] [CrossRef]
- Wang, Y.; Rajamani, R.; Zemouche, A. A quadratic matrix inequality based PID controller design for LPV systems. Syst. Control Lett. 2019, 126, 67–76. [Google Scholar] [CrossRef]
- Verma, B.; Padhy, P.K. Indirect IMC-PID controller design. IET Control Theory Appl. 2018, 13, 297–305. [Google Scholar] [CrossRef]
- Wcislik, M.; Laskawski, M. Tuning methods of the PI and PID controllers parameters. U.S. Patent Application No. EP 2 715 458 B1, 20 March 2014. [Google Scholar]
- Laskawski, M.; Wcislik, M. Sampling rate impact on the tuning of PID controller parameters. Int. J. Electron. Telecommun. 2016, 62, 43–48. [Google Scholar] [CrossRef][Green Version]
- Laskawski, M.; Wcislik, M. Influence of sampling on the tuning of PID controller parameter. In Proceedings of the 13th IFAC and IEEE Conference on Programmable Devices and Embedded Systems PDES 2015, Cracow, Poland, 3–15 May 2015; pp. 441–446. [Google Scholar]
- Li, D.H.; Gao, F.; Xue, Y.; Lu, C. Optimization of decentralized PI/PID controllers based on genetic algorithm. Asian J. Control 2007, 9, 306–316. [Google Scholar] [CrossRef]
- Killingsworth, N.J.; Krstic, M. PID tuning using extremum seeking: Online, model-free performance optimization. IEEE Control Syst. Mag. 2006, 26, 70–79. [Google Scholar]
- Wu, Z.L.; Li, D.H.; Wang, L. Control of the superheated steam temperature: A comparison study between PID and fractional order PID controller. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 10521–10526. [Google Scholar]
- Han, J.; Wang, P.; Yang, X. Tuning of PID controller based on fruit fly optimization algorithm. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 409–413. [Google Scholar]
- Fang, J.A.; Zheng, D.; Ren, Z. Computation of stabilizing PI and PID controllers by using Kronecker summation method. Energy Convers. Manag. 2009, 50, 1821–1827. [Google Scholar] [CrossRef]
- Mercader, P.; Åström, K.J.; Banos, A.; Hägglund, T. Robust PID design based on QFT and convex–concave optimization. IEEE Trans. Control Syst. Technol. 2017, 25, 441–452. [Google Scholar] [CrossRef]
- Hohenbichler, N. All stabilizing PID controllers for time delay systems. Automatica 2009, 45, 2678–2684. [Google Scholar] [CrossRef]
- Ma, D.; Chen, J. Delay margin of low-order systems achievable by PID controllers. IEEE Trans. Autom. Control 2018, 64, 1958–1973. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D. An improved coordinated control technology for coal-fired boiler-turbine plant based on flexible steam extraction system. Appl. Therm. Eng. 2017, 125, 1047–1060. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.H.; Lee, K.Y. Optimal disturbance rejection for PI controller with constraints on relative delay margin. ISA Trans. 2016, 63, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, M.; Jin, Q.B.; Liu, Y. Design of DOB-Based Control System in the Presence of Uncertain Delays for Low-Order Processes. IEEE Trans. Control Syst. Technol. 2018. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Hu, K.; Lee, K.Y.; Pan, F. On tuning and practical implementation of active disturbance rejection controller: A case study from a regenerative heater in a 1000 MW power plant. Ind. Eng. Chem. Res. 2016, 55, 6686–6695. [Google Scholar] [CrossRef]
- Åström, K.J.; Panagopoulos, H.; Hägglund, T. Design of PID controllers based on constrained optimization. IEEE Proc. Control Theory Appl. 2002, 149, 32–40. [Google Scholar]
- Jin, Q.B.; Liu, Q.; Wang, Q.; Li, S.N.; Wang, Z. IMC–PID design: Analytical optimization for performance/robustness tradeoff tuning for servo/regulation mode. Asian J. Control 2014, 16, 1252–1261. [Google Scholar] [CrossRef]
- Garrido, J.; Ruz, M.; Morilla, F.; Vázquez, F. Interactive Tool for Frequency Domain Tuning of PID Controllers. Processes 2018, 6, 197. [Google Scholar] [CrossRef]
- Wang, L. From Plant Data to Process Control: Ideas for Process Identification and PID Design; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Laskawski, M.; Wcislik, M. New optimal settings of PI and PID controllers for the first-order inertia and dead time plant. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Ostrava, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Srivastava, S.; Pandit, V.S. A PI/PID controller for time delay systems with desired closed loop time response and guaranteed gain and phase margins. J. Process Control 2016, 37, 70–77. [Google Scholar] [CrossRef]
- Silva, G.J.; Datta, A.; Bhattacharyya, S.P. New results on the synthesis of PID controllers. IEEE Trans. Autom. Control 2002, 47, 241–252. [Google Scholar] [CrossRef]
- Xue, D.Y. Computer Aided Control Systems Design Using MATLAB Language; Tsinghua University: Beijing, China, 2006. [Google Scholar]
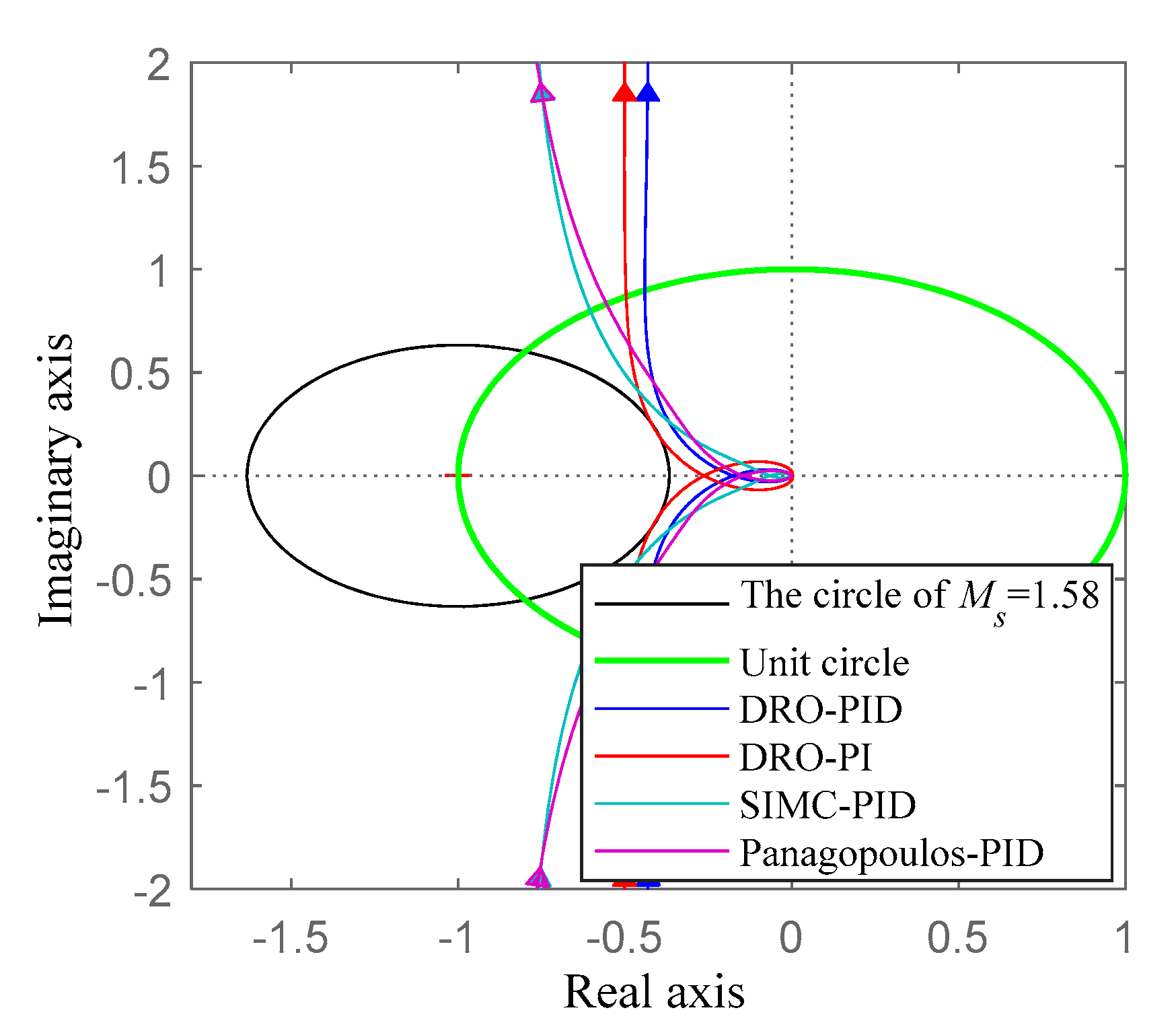
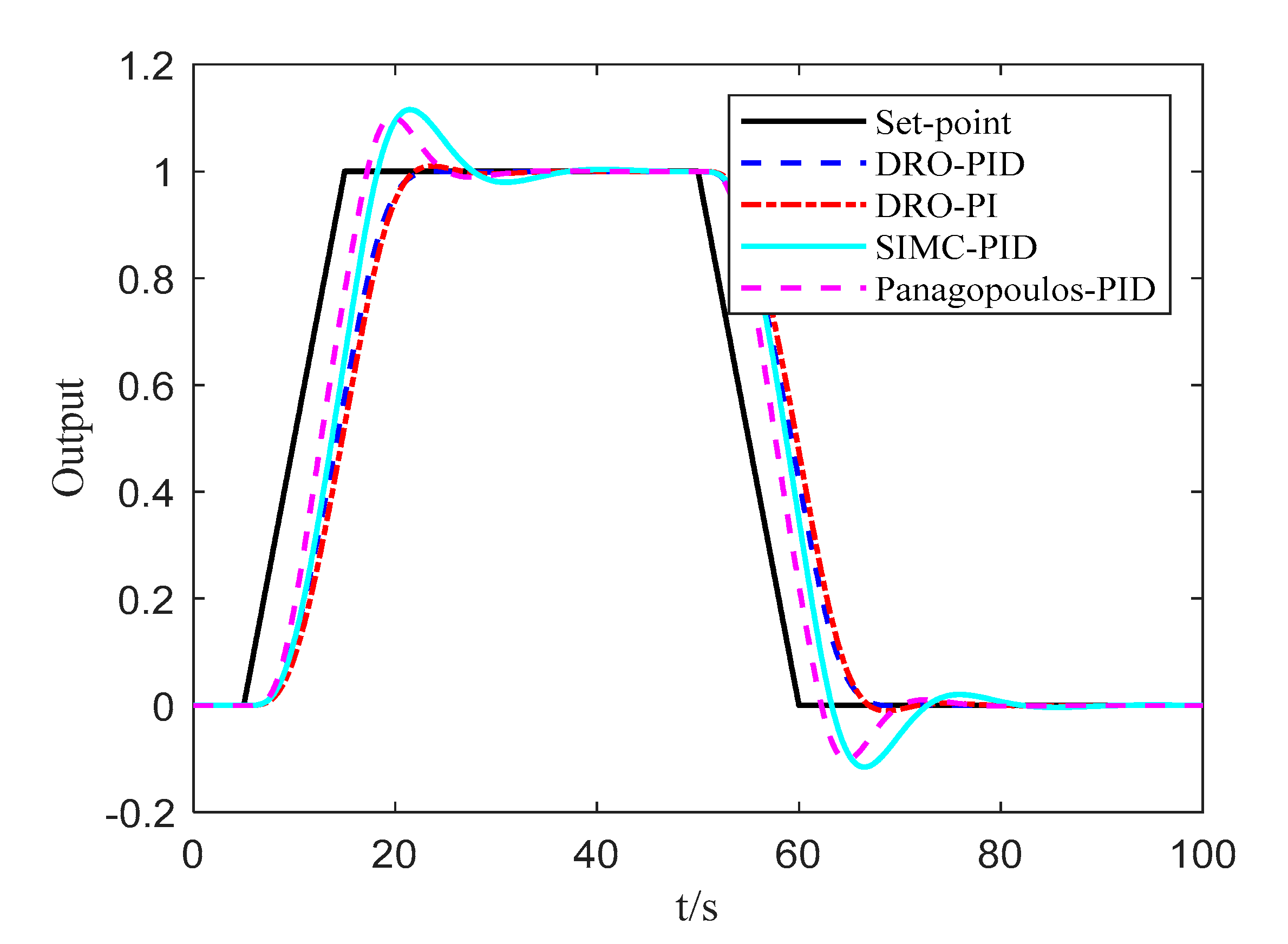
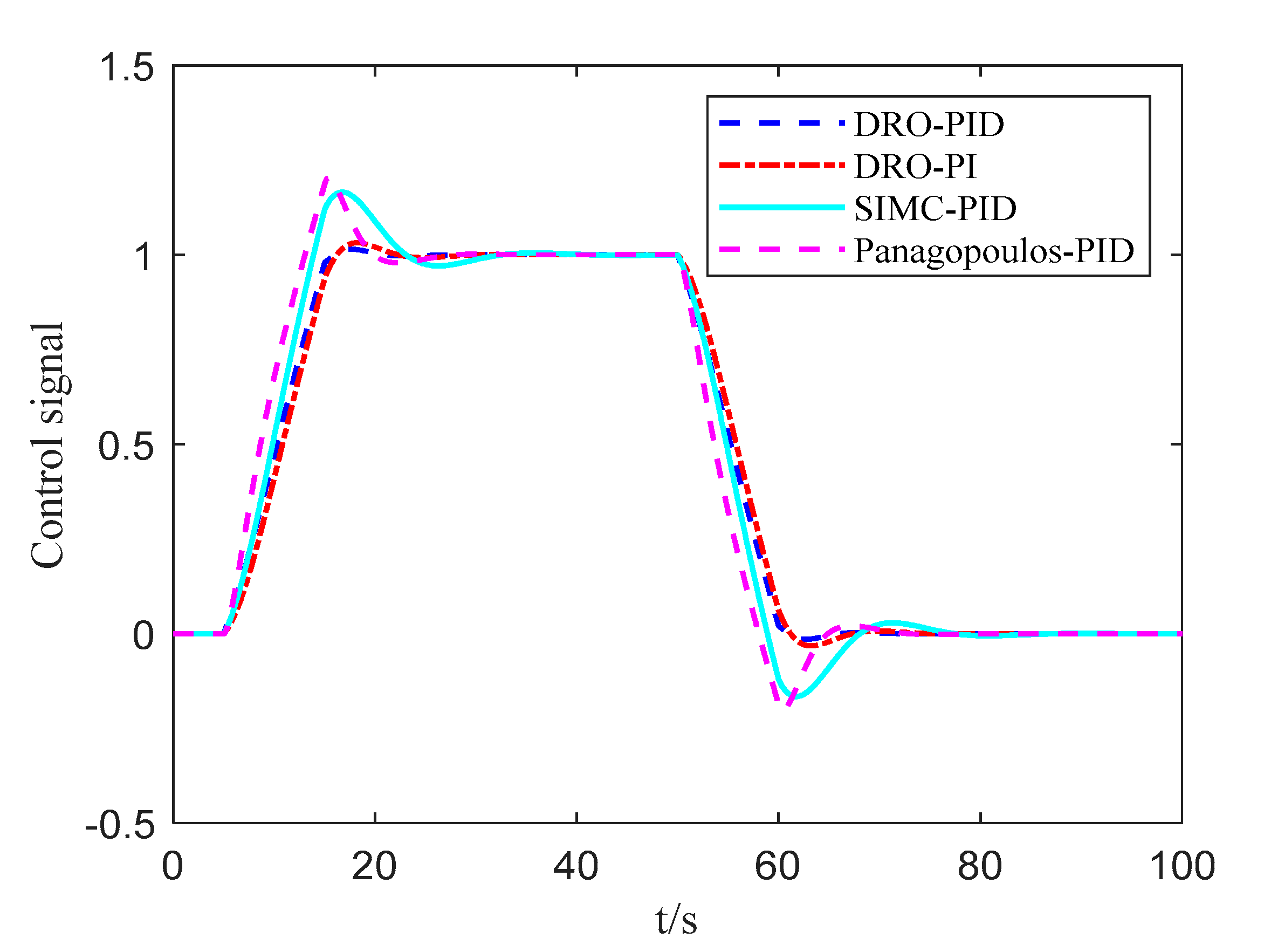
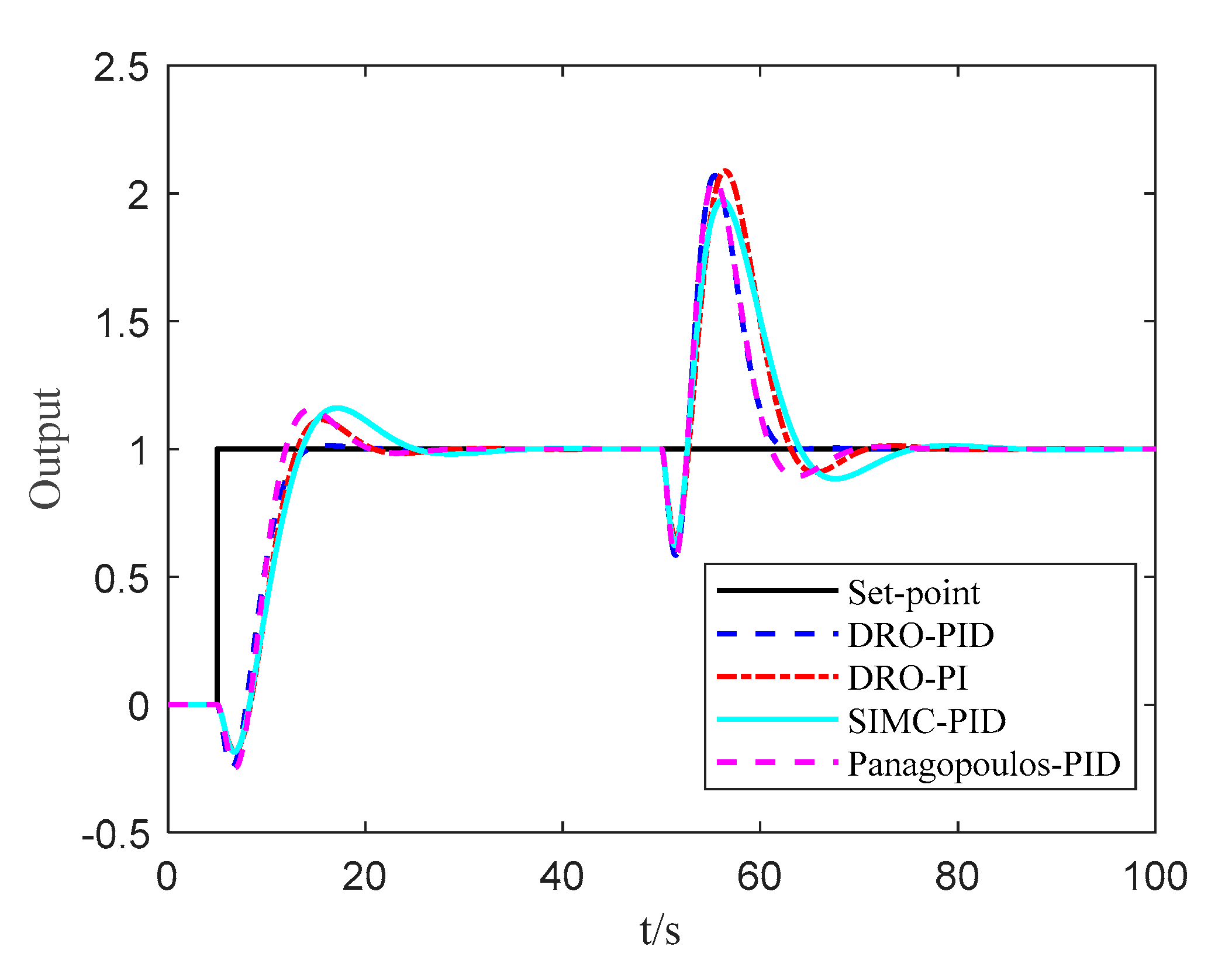
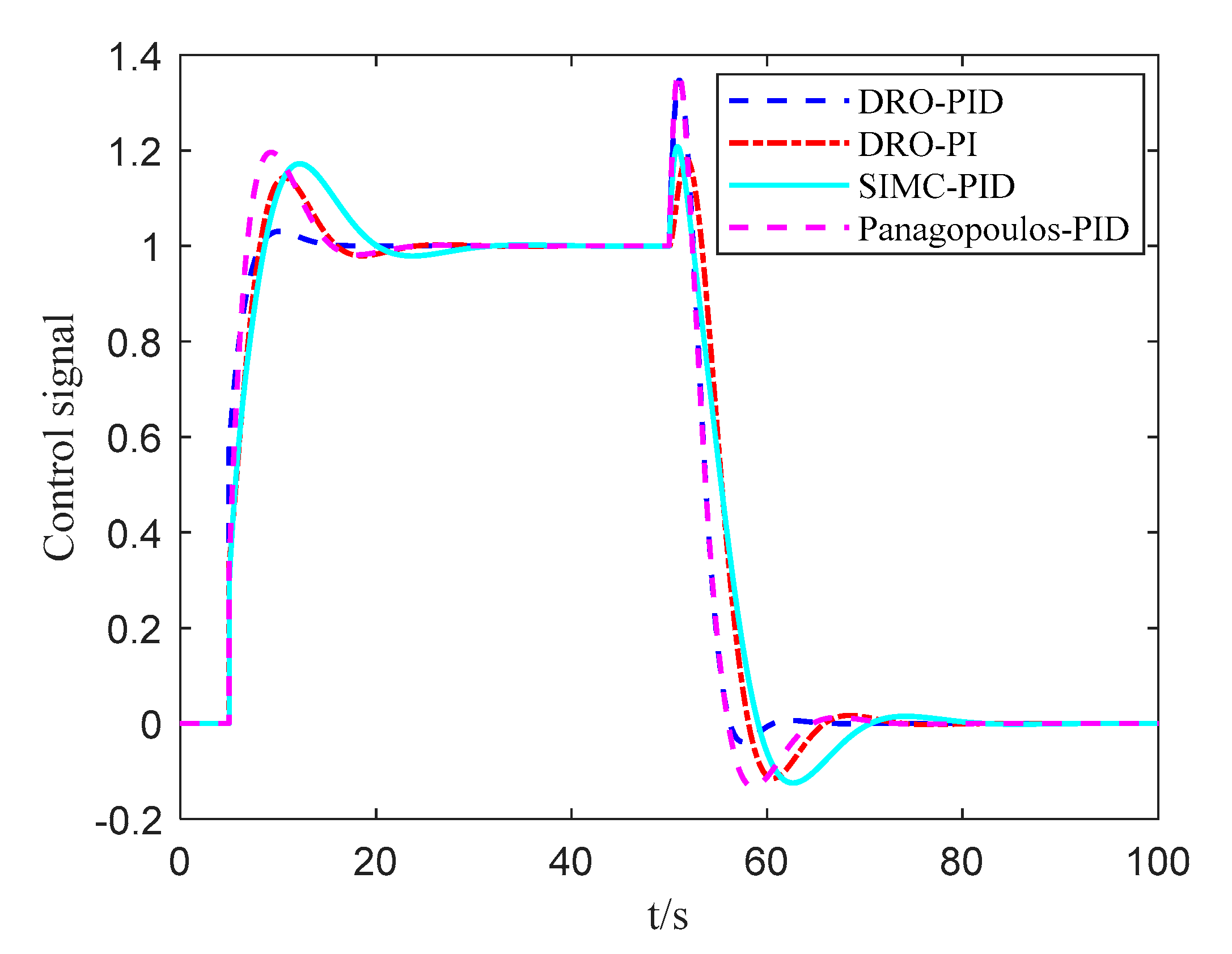
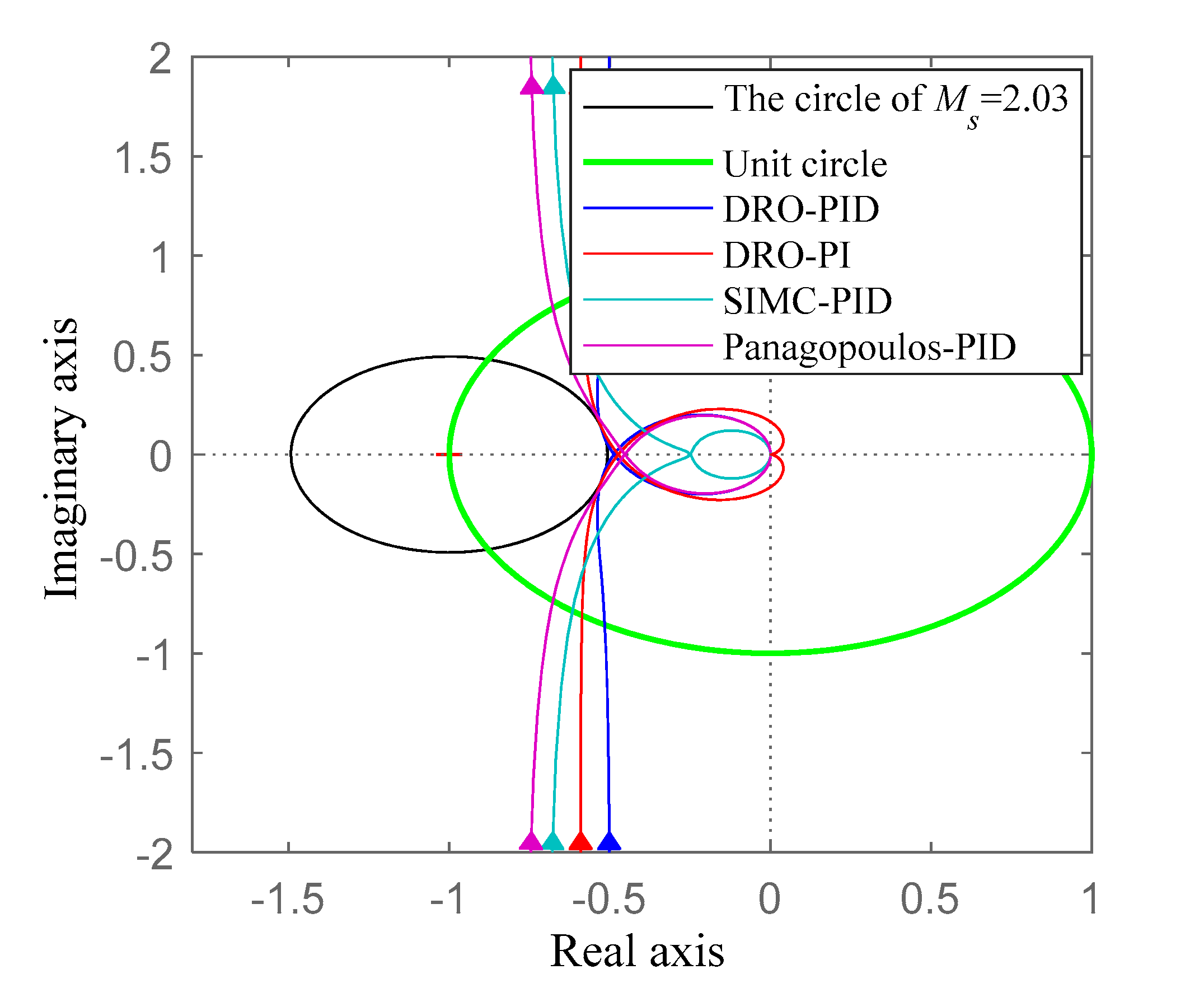
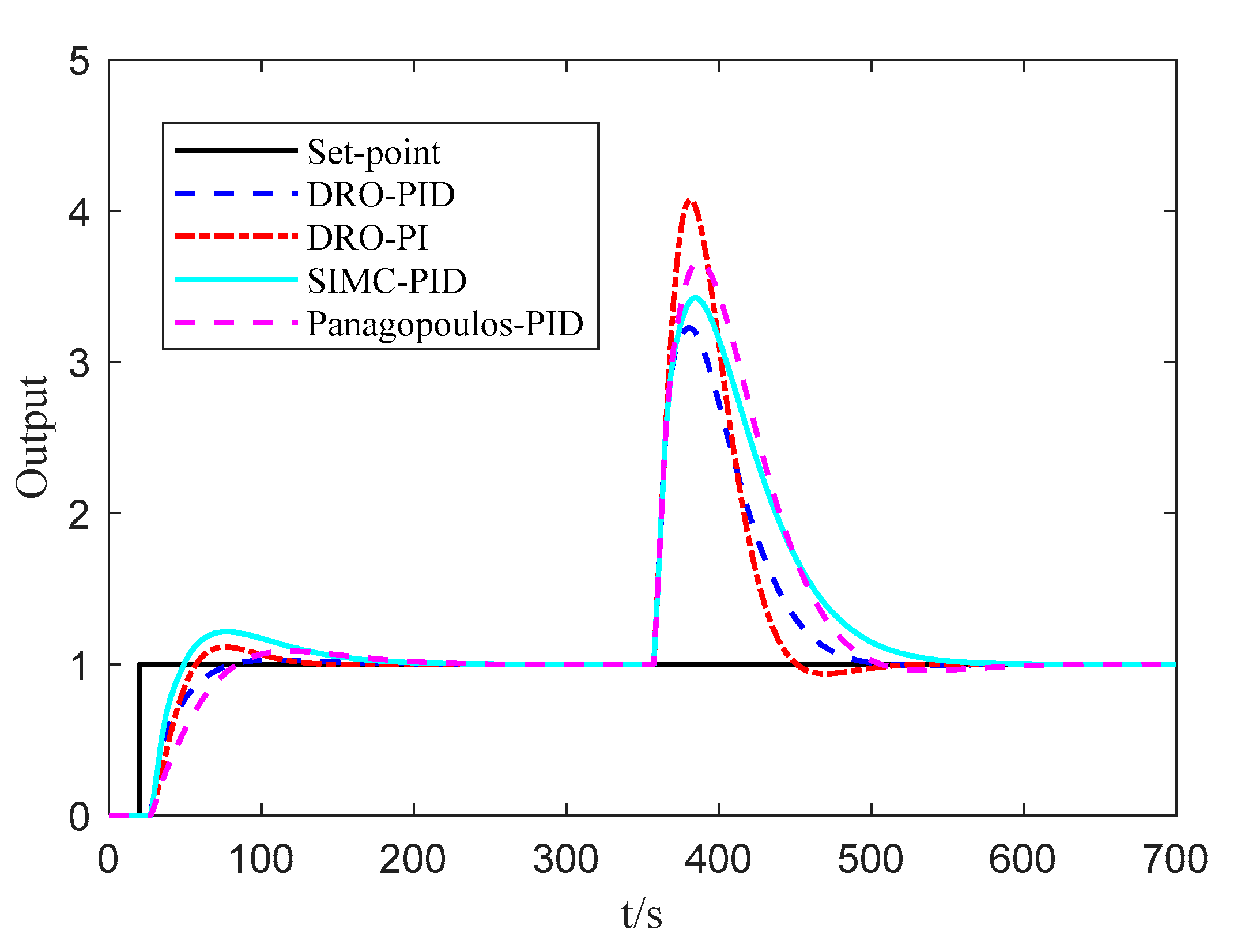
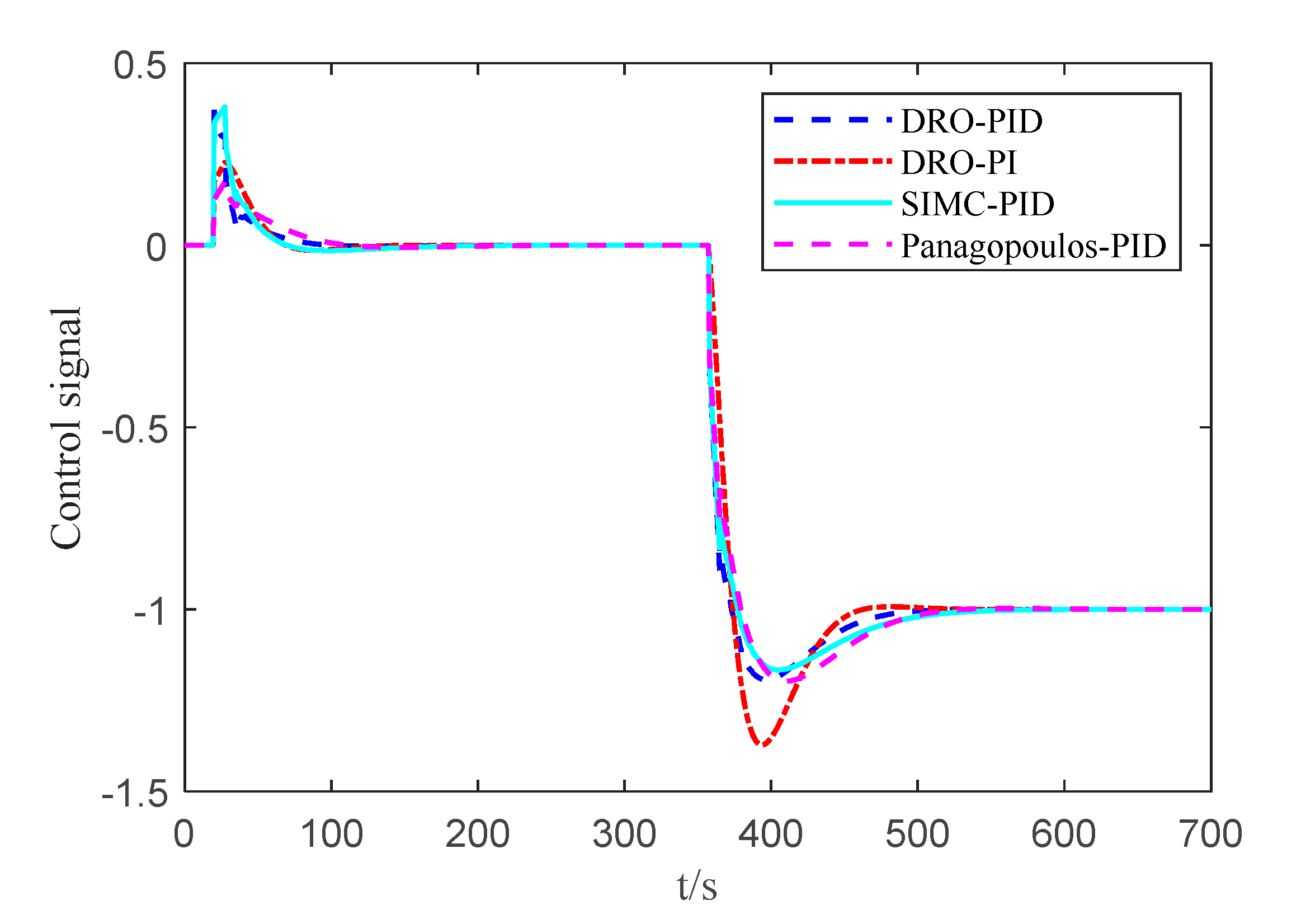
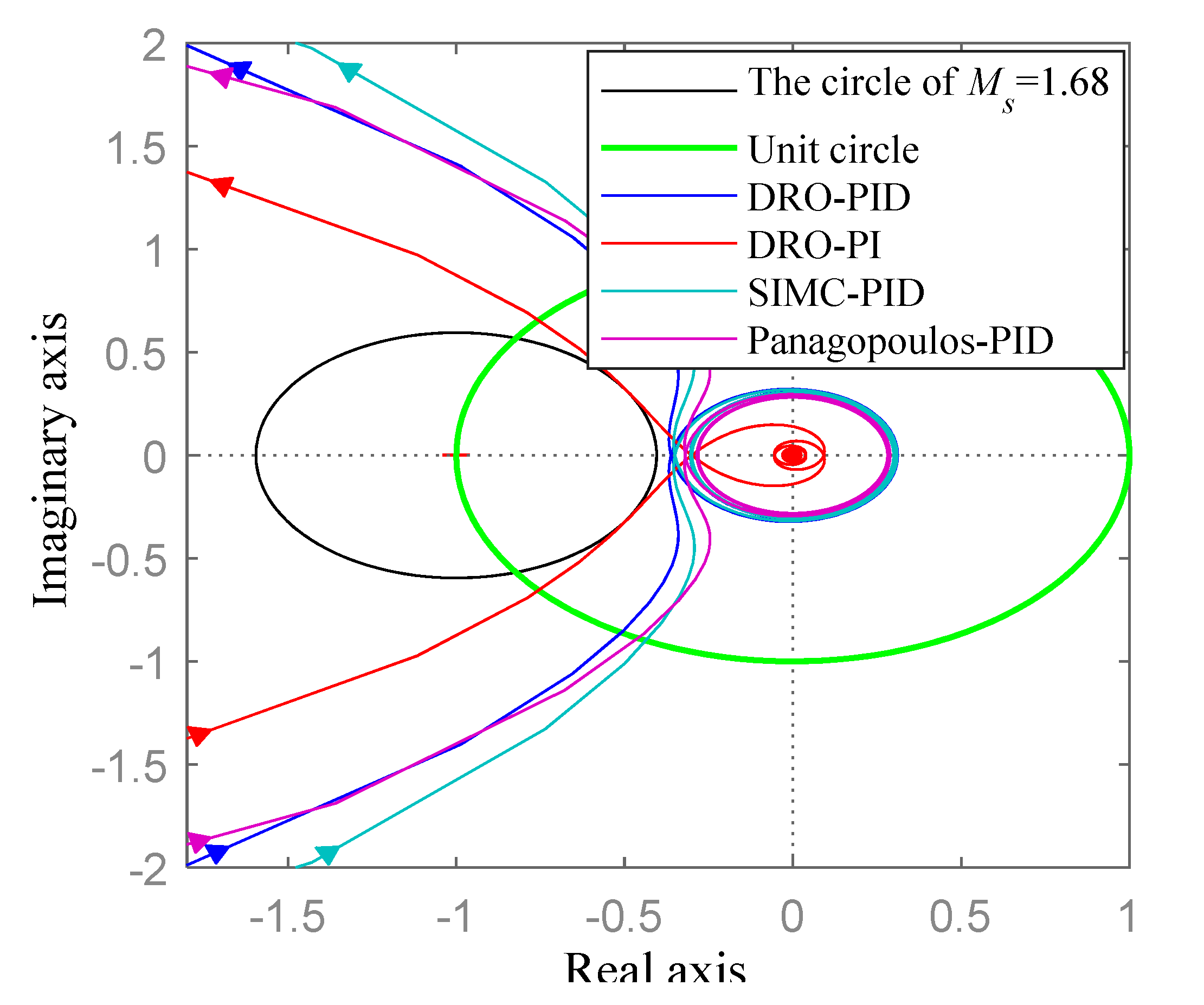
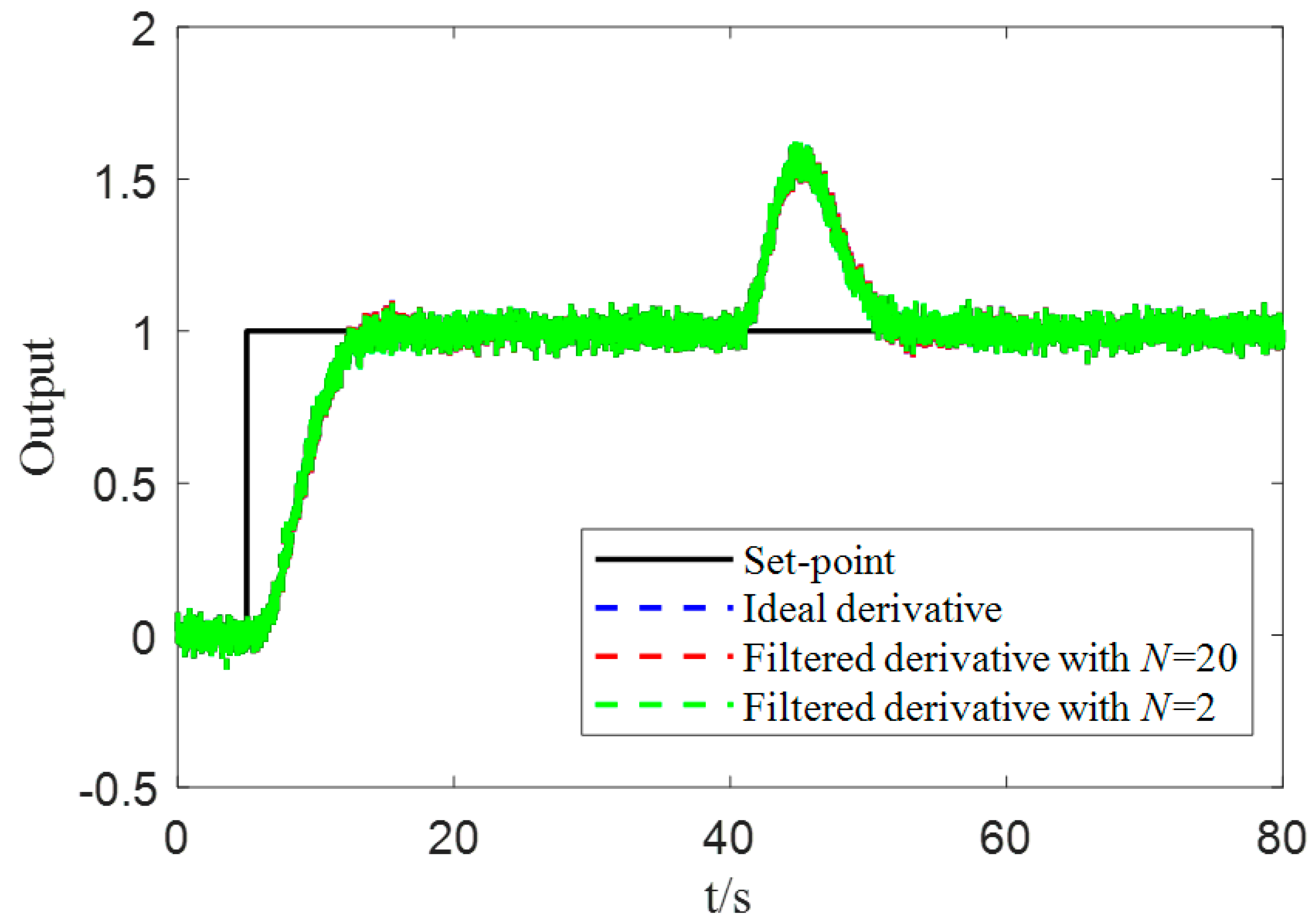
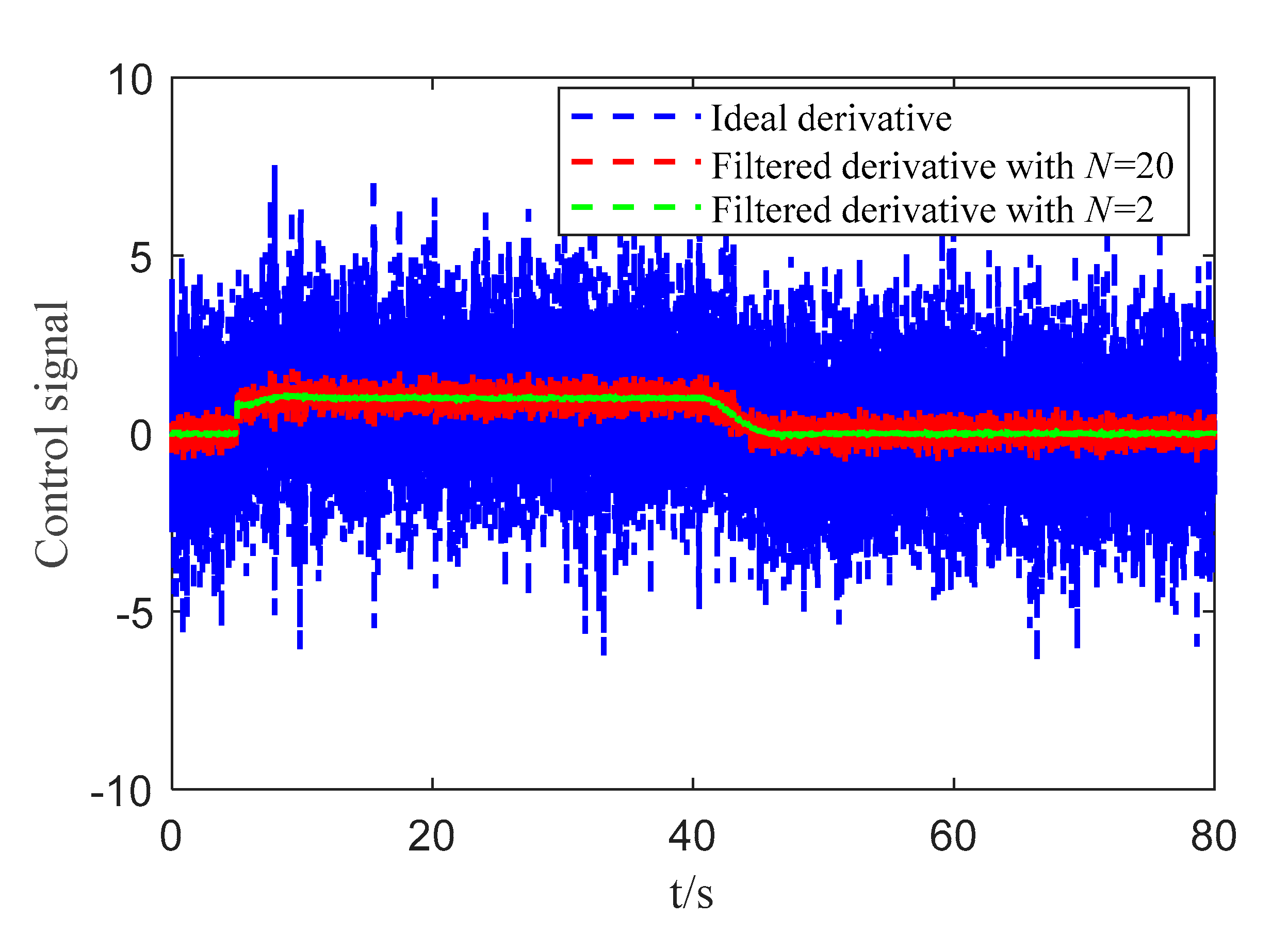
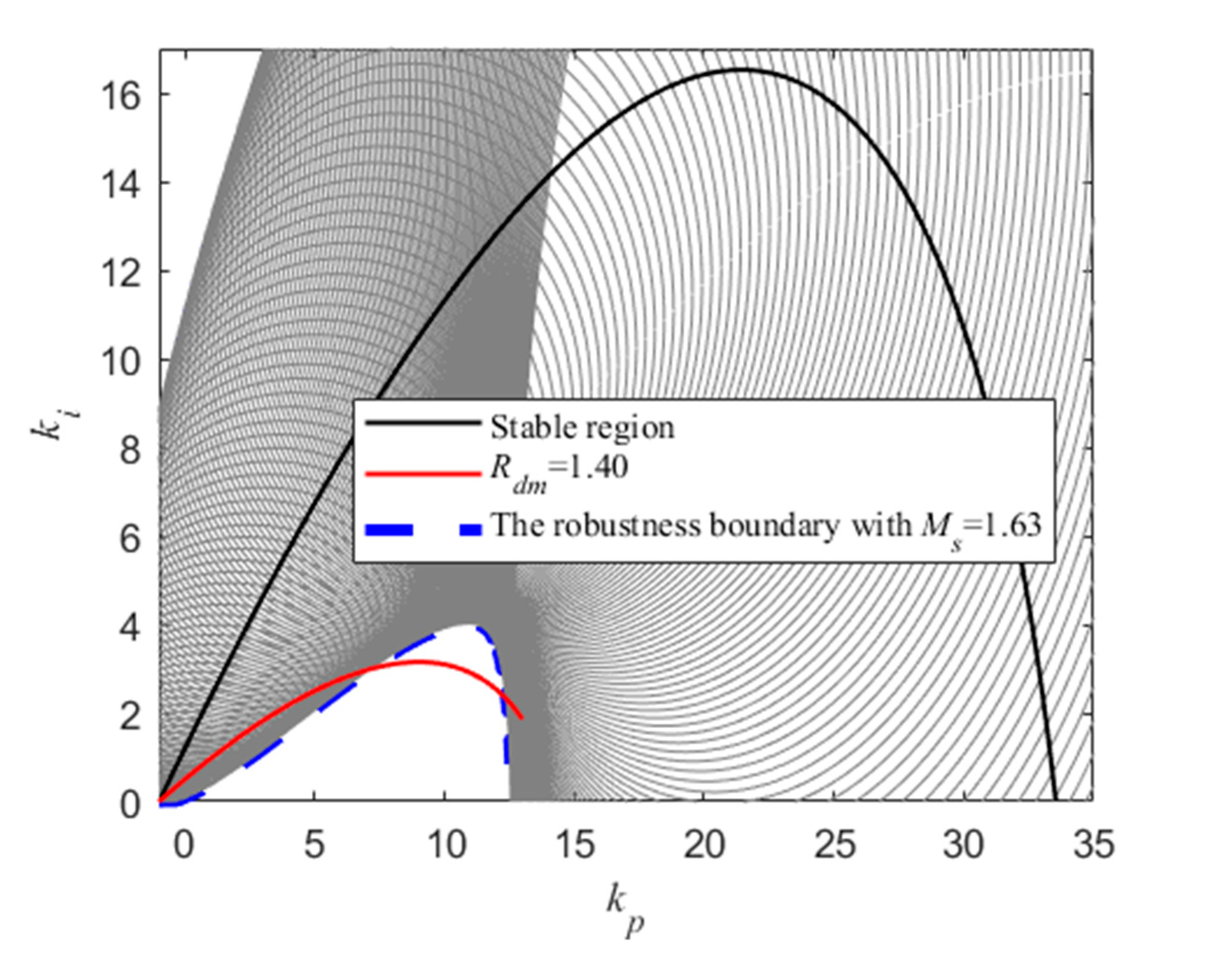
| Parameters | ||||
|---|---|---|---|---|
| 1.00 | 1.05 | 1.13 | 1.15 | |
| 0.53 | 0.55 | 0.57 | 0.61 | |
| 0.6 | 0.6 | 0.6 | 0.6 | |
| 1 | 1 | 1 | 1 | |
| 0.3 | 0.2 | 0.2 | 0.2 |
| Controllers | Parameters of Different Controllers |
|---|---|
| DRO-PID | , *, , , . |
| DRO-PI | *, , . [34] |
| SIMC-PID | , *, , , . [6] |
| Panagopoulos-PID | *, , , . [37] |
| Controllers | IAEsp | TVsp | IAEud | TVud | ||
|---|---|---|---|---|---|---|
| DRO-PID | 8.24 | 4.26 | 1.29 | 3.15 | 1.11 | 1.45 |
| DRO-PI | 12.83 | 4.96 | 1.23 | 4.10 | 1.18 | 1.58 |
| SIMC-PID | 22.38 | 5.39 | 1.71 | 4.22 | 1.36 | 1.48 |
| Panagopoulos-PID | 16.38 | 4.36 | 2.29 | 2.43 | 1.24 | 1.40 |
| Controllers | IAEsp | TVsp | |
|---|---|---|---|
| DRO-PID | 15.95 | 8.43 | 2.07 |
| DRO-PI | 15.95 | 9.49 | 2.16 |
| SIMC-PID | 26.47 | 8.66 | 2.80 |
| Panagopoulos-PID | 18.75 | 6.27 | 2.90 |
| Controllers | Parameters of Different Controllers |
|---|---|
| DRO-PID | , *, , , . |
| DRO-PI | *, , . [34] |
| SIMC-PID | , *, , , . [6] |
| Panagopoulos-PID | *, , , . [37] |
| Controllers | IAEsp | TVsp | IAEud | TVud | ||
|---|---|---|---|---|---|---|
| DRO-PID | 8.49 | 5.48 | 1.06 | 5.63 | 1.78 | 2.01 |
| DRO-PI | 14.81 | 6.44 | 1.33 | 7.36 | 1.63 | 2.02 |
| SIMC-PID | 18.76 | 7.14 | 1.39 | 7.71 | 1.70 | 1.73 |
| Panagopoulos-PID | 14.41 | 6.16 | 1.43 | 6.15 | 2.02 | 2.00 |
| Controllers | Parameters of Different Controllers |
|---|---|
| DRO-PID | , *, , , . |
| DRO-PI | *, , . [34] |
| SIMC-PID | , *, , , . [6] |
| Panagopoulos-PID | *, , , . [37] |
| Controllers | IAEsp | TVsp | IAEud | TVud | ||
|---|---|---|---|---|---|---|
| DRO-PID | 117.49 | 23.04 | 0.83 | 128.06 | 1.58 | 1.58 |
| DRO-PI | 100.31 | 25.04 | 0.49 | 138.65 | 1.76 | 1.68 |
| SIMC-PID | 160.29 | 31.29 | 0.85 | 175.27 | 1.52 | 1.54 |
| Panagopoulos-PID | 175.71 | 35.88 | 0.38 | 184.39 | 1.57 | 1.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Li, D.; Xue, Y. A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems. Processes 2019, 7, 713. https://doi.org/10.3390/pr7100713
Wu Z, Li D, Xue Y. A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems. Processes. 2019; 7(10):713. https://doi.org/10.3390/pr7100713
Chicago/Turabian StyleWu, Zhenlong, Donghai Li, and Yali Xue. 2019. "A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems" Processes 7, no. 10: 713. https://doi.org/10.3390/pr7100713
APA StyleWu, Z., Li, D., & Xue, Y. (2019). A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems. Processes, 7(10), 713. https://doi.org/10.3390/pr7100713




