Abstract
This paper deals with a sustainable personnel scheduling problem of personnel working in a large-scale natural gas combined-cycle power plant in Turkey. The proposed model focuses on employee complaints due to unfair work schedules and the results of balanced assignments based on power plant interruptions. Eighty personnel work in three shifts at this natural gas combined-cycle power plant. The model is solved with respect to some of the workers’ skills, and there are 20 criteria regarding skills. The analytic network process method is used to get the weights of workers’ skills, which are calculated and included in the model. Goal programming is used in this paper. Our proposed model gives cost minimization and fair work schedules for the power plant. Compared with the literature, the number and set of criteria are unique in terms of personnel competency in the energy sector. Minimizing cost and imbalanced assignments was achieved by the proposed model for the first time without considering the sector.
1. Introduction
The personnel scheduling problem (PSP) is known as the process of creating an optimized model for work allocation. Many different PSP models have been improved and have evolved in different ways, such as with GP, due to the advantages of many shifts and numerous employees. However, although this problem directly affects social and commercial life, work on the PSP is still lacking for energy-related work situations [1,2,3]. It is very important that electricity generation is continuously maintained in a natural gas combined-cycle power plant (NGCCPP). Shutdown of generation due to shift schedules is a big problem for NGCCPPs. There are several jobs that help personnel generate electricity in power plants: process monitoring, maintenance, and repair work. These tasks have complex structure and require specialization and intensive use of the labor force. When we talk about a sustainable energy supply, NGCCPPs come to mind, because they are efficient, economical, environmentally friendly, reliable, and they never stop. Therefore, controlling electricity generation, labor, materials, and maintenance processes is an indispensable requirement in power plants. It is a difficult process to operate facilities in accordance with operating rules and in line with objectives such as balancing work distribution, maximizing employee performance, assigning appropriate employees to appropriate jobs, etc. With the help of technological developments, power plants are controlled and operated by supervisory control and data acquisition (SCADA) systems, distributed to remote-control centers from the central system by power plant personnel. The SCADA system is a combination of data acquisition and telemetry. It performs the functions of collecting and sending data from the center, conducting analysis, and then displaying the data on an operator screen. The SCADA system monitors and controls field equipment at the same time. System operators, from a central control point to a wide geographical area, monitor pipe systems, water networks, valves, cutters, disconnectors, electrical machines, motors, and electronics; remotely switch electrohydraulic and electropneumatic valves on and off; change setpoints; and view alarms and temperature. The system provides the advantages of reliable, safe, and economical performance of measuring and collecting information on moisture, frequency, weight, number, and elements. SCADA includes features such as motion, sizing, flashing and filling, discharging, and ease of use that attract the attention of operators by using the kernel software that is included in its structure [4].
SCADA systems are currently used in power plants in Turkey and other countries around the world, such as Canada, Russia, China, and India [4]. In power plants where this system is not available, personnel do the work themselves to fulfill the requirements of the system. Although there are no SCADA systems at power stations, technologically old power plants continue to be used in Turkey. This system is expensive to install and requires a certain number of personnel. Instead, deploying personnel without installing the system is an alternative. The number of power plants operated this way is higher than the number of power plants operated with SCADA. Operator errors by shift personnel (fatigue, lack of concentration, inexperience, lack of fair work distribution, etc.) are more likely to occur in these power plants than in SCADA-controlled plants. Therefore, these facilities may make errors due to lack of motivation. As a result, long-term shutdowns cause loss of energy and revenue. Interruption of the sustainable energy supply can cause major power outages. Therefore, in order to ensure a sustainable energy supply, fair and efficient personnel scheduling models implemented in NGCCPPs are very important.
Our paper suggests a new model application for the PSP that is related to the solutions of personnel scheduling studies. In the literature, other PSPs have not been investigated in energy sector applications [1,2,3]. When the world’s electricity generation distribution data are examined, coal is the most common source of electricity generation, and natural gas is the second most common [5]. Looking at the countries that have the largest share of electricity generation—such as the United States, China, India, and Germany—coal is mainly used. Natural gas in Russia, nuclear energy in France, and renewable energy sources in Canada are the most common sources of electricity generation. Over the last 10 years, natural gas has been the main source of electricity generation in Turkey, and this ranking has not changed; 39% of electric energy in the last 10 years has been generated with natural gas, and its share in Turkey’s energy mix is 25.14% as of the first quarter of 2019 [5].
There are scarce resources for natural gas in Turkey but, NGCCPPs are most commonly used because of the high capacity, low setup time and installation costs, and low environmental impact. There are significant advantages in the short term. Compared to fossil fuels, natural gas has the advantages of time saving, high efficiency, ease of use, fast maintenance, economic, and long life. The purpose of studying large-scale NGCCPP staff in Turkey is fair scheduling according to people’s abilities. The advantages of natural gas and the high rate of Turkey’s NGCCPP total power generation mean personnel at power plants are very important. Previous studies show that personnel scheduling of this size in the energy sector (30-day assignment for 80 people) has not been studied before. Sustainability in personnel scheduling, and thus continuity of the energy supply, are the main foundations of this study. Problems stemming from personnel appointment threaten the sustainability of the energy supply. A staffing system based on a specific basis supports sustainable human resources policies. The planning of personnel in such critical power plants needs to be done much more precisely and without error. In this study, 20 criteria were evaluated for personnel. These evaluations were calculated by using the ANP method. The number of criteria that were determined and evaluated using the ANP method is comprehensive enough to reflect the truth in terms of determining the adequacy of personnel working in the power plant. Thanks to this method, schedules can be made that take into account the capabilities of each staff member. In the literature on the energy sector, work on personnel scheduling with the number of employees at this level and taking into account a range of skills criteria is unique. Minimizing costs and unbalanced assignments was achieved by the proposed model for the first time without considering the sector. The large number of personnel differentiates this from other studies in terms of the size of the problem. Finally, as a result of the model’s solution, stopping points and cost due to unbalanced assignment are decreased by 62.5%.
Preparing staff schedules manually is very inefficient and time-consuming. Therefore, a methodical approach is needed to create useful schedules in a short period of time. Currently, NGCCPP staff scheduling is done manually. This paper addresses the issue of creating a sustainable mathematical model for NGCCPP personnel. The PSP describes the nature of the industry and the organizational policies and conditions that determine the daily preferences of workers according to newly defined constraints. This study helps to create suitable monthly personnel schedules that maximize employee satisfaction. Thus, shutdowns are reduced from 44 h to 14 h, leading to fewer personnel mistakes, cost reduction is achieved, and the goal of a sustainable energy supply is reached in this power plant. In addition, this study eliminates shortcomings of multi-objective scheduling based on cost minimization for 80 personnel. This is done for the first time with workers at NGCCPPs in the literature on PSPs. The application in this study was carried out at an NGCCPP that has a different structure than other power plants. The proposed model can only be used at other power plants with some restriction changes following the successful implementation at this power plant. The necessary data were taken by the experts from the power plant. The proposed mathematical model solutions were checked carefully. The criteria considered in the ANP are comprehensive, reflecting the truth in terms of determining the competence of personnel working at the power plant.
Our research is structured as follows: after a detailed introduction, Section 2 presents information from the literature about PSPs. In Section 3, the perspective and practice of the study are given. Section 4 includes a discussion of the calculation results and finalization of the study. The large number of personnel considered differentiates this study from other studies in terms of the size of the problem. Finally, as a result of the solution of the model, stops caused by unbalanced assignment and their costs are decreased by 92.5%.
2. Personnel Scheduling Problem
Personnel scheduling deals with adjustments in workloads and schedules, and assignments of personnel to shifts in order to meet requirements that change over time. In recent years, PSPs have been frequently studied. The PSP is a branch of scheduling problems, which are very important for service personnel such as phone operators, hospital workers, police officers, and transportation workers. In these sectors, operations are often sustained and changeable, and personnel needs do not change over time. Labor union rules, equipment requirements, etc., generally involve scheduling rules. These scheduling rules are shaped by some legal restrictions. The resulting problems tend to be difficult to unify. One of the most important factors in studying this problem is the economic dimension. For most companies, the cost of workers is at the top of the cost items. It can be possible to reduce this cost by rescheduling existing personnel. Current PSPs differ from the problem structures of Dantzig [6] and Eddie [7] in the 1950s. The scheduling mentioned in that period consisted of meeting staff needs or the number of workers required. However, today staff requests and satisfactory scheduling decisions are made. When creating schedules, firms propose a number of methods, such as part-time recruitment or flexible working hours, in order to meet the wishes and preferences of workers (working on a particular shift, working with a specific person, having a specific day off, etc.). A scheduling policy, or ‘schedulability’, is defined as sustainable if any task system determined to be schedulable remains so if it behaves ‘better’ than mandated by its system specifications [8]. A formal definition of sustainability is provided in the literature and the concept has been subjected to systematic analysis in the context of uniprocessor scheduling of periodic and sporadic task systems [8]. Therefore, we can call our study a sustainable personnel scheduling study. Also, our study is different from other studies in terms of cost reduction and job assignment by considering personnel skills.
PSPs were first solved by mathematical models in the literature. However, it is seen that computer-aided solutions have been proposed in recent studies. In 1987, Min studied one of the first PSPs [9]. The author applied the 0–1 GP method to prepare schedules for library staff. The model used in the study can be used to solve many problems in real life.
Some studies integrate machines and PSP. PSP studies are also popular in scheduling studies [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. The research process of this study began with the investigation of personnel scheduling review articles [1,2,3]. In literature reviews related to personnel scheduling, the problems do not have a general model structure like other scheduling problems, because the model structure of each personnel scheduling task is unique [1,2,3]. Instead, it was stated that it would make more sense to classify personnel scheduling according to certain criteria [1,2,3]. For example, the constraint requiring the application of labor law in theory is a reflection of the model in reality. These and other constraints make staff scheduling models unique. General personnel scheduling model structures were examined, and each one was found to be different from the others. The authors chose to classify them, as it seems difficult to reduce the model structures in personnel scheduling. According to the latest classification structure in the literature, there are four main topics [3]:
- Permanent Centered Planning, (police station, hospital scheduling, etc.)
- Alternating Centered Planning, (call center, fast food center, post office, warehouse or distribution center scheduling)
- Mobility Centered Planning (transportation-airline and railway scheduling)
- Project Centered Planning (studies where specific work is divided into projects)
It has been determined that the working trend related to PSPs is to develop methods with heuristic solutions and use hybrid algorithms [10,11,12,17,45,49,60,62]. In addition, specific personnel scheduling models are available in the literature; for example, models based on flexible demand, models in which the workplace is changed, and models with restricted task changes. Personnel scheduling is a very important issue for work efficiency. The environment in which the scheduling is performed is often unstable, where personnel requirements fluctuate over time. The process typically includes equipment requirements, trade union rules, and so on. Various restrictions need to be considered. The resulting problems tend to be difficult to solve because they contain more types of combinations [8].
The structure of the PSP can be divided into several categories. The general solution method uses integer programming. This method includes a large class of PSP solutions. In addition, there is a special class of integer programming problems known as cyclic personnel problems. This type of problem can be looked at from the class and combinatorial point of view [7].
After this point, the subject given in the review articles is examined in the paper. The complete reference list has been checked and completed in the relevant articles. Then, classification methods were investigated in these articles. Many databases were searched for personnel scheduling in energy-related studies. In the literature, there are many classification studies in PSPs [52]. The personnel scheduling literature shows several research methods that combine a solution or evaluation technique with an analytical approach [50]. Mathematical programming optimization categories—such as integer, goal, linear, or dynamic programming—are classified in many studies. Queuing, constraint programming, and simulation are other solution techniques [15,16,51,52].
A PSP is a type of problem that takes a long time to solve. There are some example solutions for large-scale scheduling problems in the literature [52]. The literature review shows that there are few PSP studies in the energy sector [10,11,52]. PSPs can be complicated by many shifts, employees, and capabilities, especially due to complex constraints and solution alternatives [51].
Personnel scheduling is studied in the literature in the fields of health, education, security, and production. Related studies are shown in Table 1. Those studies are the most related to our paper. As shown in Table 1, solution methods and application areas are investigated. Generally, GP [15,21,38,40,43,44,50,51,52], heuristic methods [10,11,12,16,17,24,25,45,49], and integer programming [13,14,19,20,23,24,27,28] are the most used techniques for solving PSPs. Some papers that are salient and used models most like the mathematical model structure in our study were selected and are explained in detail below.

Table 1.
Related studies about personnel scheduling.
Blöchliger [1] conducted a descriptive study on how to set up the models of PSPs. Employee, time, work, cost, and decision variables, which are the elements of the PSP, were examined from a general perspective. At the same time, recommendations were made on how to create constraints and an objective function in the study.
Ernst et al. [2] examined personnel scheduling practices, methods, and models in the literature, showing that personnel scheduling is a frequently studied problem, and it has been reported that studies on this subject continue. Considering the studies examined above, it appears that each study needs different constraints. In other words, the results obtained in each study are different from each other. This makes it impossible to compare the performance of different methods.
Bergh et al. [3] conducted a bibliographic study on staff scheduling problems. They reviewed the research articles beforehand and classified the articles they examined in accordance with this classification. This study is enlightening with regard to the status of whole staff scheduling studies. Another study about personnel scheduling was conducted by Bard et al. [13], on a tour scheduling problem of a postal service in the United States. This problem was expressed with the help of an integer linear programming model including two types of workers, full-time and part-time. They complied with the constraints in labor contracts. According to their results, measurable savings were achieved with the help of a mathematical model.
Labor balancing and regulation problem models were studied by Corominas et al. [14], Azaies and Al-Sharif [15], Güneş et al. [16], Yunes et al. [17], Topaloğlu [18], Trilling et al. [19], Lezaun et al. [20], and Chu [21]. A study by Lezaun et al. [22] is about the labor force of railway drivers. Corominas et al. [23], Thompson and Pullman [24], Sinreich and Jabali [25], and Horn et al. [26] solved the problem of staff shift scheduling using a linear programming model and simulation tools. Çetin et al. [27], Sungur [28], and De Matta and Peters [29] solved the PSP using integer programming.
Tsai and Li [30], Rönnberg and Larsson [32], and Öztürkoğlu and Çalışan [42] studied the nurse scheduling problem and solved the assignment problem of nurses in the health sector. Lezaun et al. [31] studied a shift scheduling problem for railway workers. Zolfaghari et al. [33] and Kassa and Tizazu [39] discussed the staff scheduling problem. Fırat and Hurkens [34] conducted staff scheduling with mixed integer programming. Bağ et al. [35], Hung-Tso et al. [36], Bektur and Hasgül [38], and Louly [40] used the GP method to solve the PSP. Li et al. [37] performed staff scheduling using intuitive methods together with GP.
Alfieri et al. [46] presented an implicit column generation solution approach to find a suitable solution for pricing. The authors used a dynamic programming approach based on an intuitive algorithm. They tested the results for the timeline of the intercity train series of the largest passenger train operator in the Netherlands.
In the model proposed by Alsheddy and Tsang [47], an automatic mechanism that controls the cost of violating employee demands maintains fairness. The model was applied to solve a workforce planning problem that involved the planning of a highly skilled workforce according to geographically dispersed tasks. The results of this model demonstrated that an organization effectively provides the empowerment of employees.
Asensio-Cuesta et al. [48] used a multicriteria genetic algorithm to form work rotation schedules, taking into account the most appropriate personnel tasks. The algorithm provides the best available competence among workers and the qualifications required to perform tasks. The design of rotation programs is based not only on ergonomic criteria, but also on product quality and employee satisfaction. The model includes the competency of workers as a criterion for the best solutions.
Ásgeirsson [49] took partial scheduling of requests from employees and worked on an algorithm that established a timeline meeting most of the employees’ requests, ensuring that no rules and regulations were violated. The algorithm is based on independent modules that can be executed in any order, and each module attempts to emulate some operations received by a personnel manager. The purpose is to create a transparent and fair system that creates high-quality timelines. At the same time, this algorithm is a system by which employees can obtain explanations and justifications for every change made to meet demands. The algorithm simulates the actions of staff managers. In this way, it is easily understood by managers and easier to explain any decisions to employees by using the detailed logs of any action. After presenting the algorithm, the authors applied the results to four real-world companies and organizations and showed that it can achieve good results with a simple module-based heuristic and can create fair and applicable programs that encourage employees to participate in their own scheduling process.
Özder et al. [51] verified that proper deployment of cleaning personnel is a major problem in public institutions. By assigning cleaning personnel to the most appropriate duty areas, cleaning service can be provided in the best possible way, so they studied the problem of assigning cleaning personnel to the most appropriate places to clean. They chose to apply the study to a 58-room university hospital that operates 24 h a day. They used a GP model to establish the problem and solved the PSP for 70 cleaning personnel for a month. The ILOG CPLEX Optimization program was used to solve the mathematical model. The mathematical model showed that the intended goals were achieved, and better results were obtained from the existing schedule.
To the best of our knowledge, there are a few energy-related personnel scheduling studies in the literature [10,11,12,50,52,61,62,63,64,65,66]. Personnel scheduling studies have been reported in energy-related journals, but studies on this subject are quite rare [9]. As Jorne et al. [3] explained, there are not many studies in the literature regarding personnel scheduling in the energy sector [9]. Personnel scheduling in the energy sector is a virgin area and is waiting to be discovered. However, the main purpose of electricity generation power plants is to realize sustainable energy supply. Sustainable electricity generation should be uninterrupted, economical, efficient, and environmentally friendly. The impact of staff working for this comprehensive goal is high [52]. In this context, this study focused on PSPin a large-scale NGCCPP. The details of the energy-related studies presented in Table 1 are as follows.
Eitzen et al. [10] carried out a study to assign staff who have skills in many areas to specialized areas in a power plant. They investigated Ernst et al.’s [2] study and proposed a multi-skilled rostering problem and a number of solution strategies for the set covering approach and compared the results. Another energy-related study is by Lilly et al. [10]. They said that the main costs of power plants are labor costs. They proposed a model to reduce maintenance labor costs to a minimum in order to perform maintenance operations at an electricity generation company in Nigeria.
Yaoyuenyong and Nanthavani [12] created a schedule for the least number of workers to meet the required workforce. They created a mathematical model and explained two heuristics and one exact algorithm. Based on their computational experiment, a hybrid procedure consisting of the above-mentioned algorithms was found to be very efficient at solving this workforce scheduling problem to optimality.
Shuib and Kamarudin [50] studied the scheduling problem of workers in Malaysia’s largest power plant. The model in this work optimizes the workers’ working preferences during the day shift. The shift scheduling used the GP model to determine the optimal scheduling for the problem. This work focuses on three aspects: shift scheduling, permission scheduling, and scheduling according to demand. The study involves scheduling 43 people for three shifts (morning, evening, and night) over 28 days in a certain part of the power plant.
Özder et al. [52] studied an NGCCPP’s PSP using GP and ANP techniques. They verified nine criteria for personnel skills and calculated skill weights with the help of ANP method. Their study deals with fair scheduling, and they did not include cost minimization in their mathematical models. Our study differs from this study in terms of the number of evaluation criteria for calculating the skill weights and cost minimization.
Liu et al. [60] are dealt with modeling, planning, and management of energy systems for isolated areas. They have provided a comprehensive literature review to identify, classify, evaluate, and analyze the performance of different methodologies and models for energy systems. The authors also provided some forecasting techniques of energy demand and renewable energy resources, energy models, application of hybrid renewable energy systems, and management for energy planning.
Koltsaklis et al. [61], presented a generic optimization framework to address the problem of the optimal design and operational scheduling of energy microgrids. They used mixed-integer linear programming technique for solving the energy planning and scheduling problem. They measured the efficiency and applicability of their proposed model with using three case studies. Their proposed model provides a systematic and analytical methodological framework for detailed planning and scheduling for energy microgrids.
Hemmati et al. [62] presented an optimal planning and scheduling on energy storage systems for congestion management in electric power systems including renewable energy resources. They tried to find optimal capacity of electric power systems and used simulation techniques. According to their results, their scheduling can manage congestion of the network efficiently while dealing with wind and solar resources uncertainties.
Amiri et al. [63] studied energy hub scheduling in consideration of preventive maintenance policy. This study tries to determine the preventive maintenance cycles and the best strategy to allocate hub energy capacity under different demand scenarios, while the goals are to minimize costs and to maximize the reliability of the system. They used integer linear programming and gave sensitivity analysis to provide the effect of parameters.
Ma et al. [64] proposed a model to design multi energy systems, which can obtain both the optimal structure configuration and energy management strategies. They gave a generic optimal planning framework. Author compared three different energy system schemes for demonstrating the effectiveness and advantages of their proposed optimal planning model.
Deshmukh and Deshmukh [65] proposed a new approach to micro-level energy planning. They tried to find optimal energy resource allocation by using multi-objective goal programming approach. Their results are much better than the previous energy plans.
Jinturkar and Deshmukh [66] studied the energy planning model. They developed mixed integer goal programming model for rural cooking and heating energy planning in a region of India. They tried to minimize cost, minimize emissions, maximize social acceptance, and maximize use of local resources. They achieved a better solution for decision making in rural energy planning.
According to a review of personnel scheduling papers, most of them consider a realistic workload, and they deal with creating suitable schedules for personnel. Very rarely, PSPs are integrated with other programming problems such as machine scheduling and operating room scheduling. In addition, they rarely integrate all decisions of the PSP, such as workload distribution, job placement, recruitment dismissal, training skills, and considering days off or shift preferences. This is a main area of future research; it is the main objective to include all these decisions in a single PSP. The parts that differentiate our study from other studies and contribute to the literature can be listed as follows:
- Application area and applicability: The field of application is very rare in PSPs.
- Solution method: We proposed a combined ANP-GP model. In addition, this study addresses cost minimization as well as fair work distribution.
- Application results: We give an overview of the results of the PSP. Most of the studies give experimental results.
3. Methodology
PSPs can be solved by methods such as linear programming, GP, integer programming, mixed integer programming, dynamic programming, and genetic algorithms [53]. Two methods are used in this study, ANP and GP. These techniques are described below.
3.1. Analytic Network Process
ANP is a more general approach to the analytic hierarchy process (AHP). This method developed by Thomas L. Saaty [54] is one of the most frequently used decision-making methods. ANP is easy to use and can be used in all areas because it is a common method of use. The present problems cannot be explained by showing a hierarchical structure in the structuring of problem-solving problems. The reason for the problem is that the problem has been a link between higher-level formations and lower-level phenomena. For this reason, instead of determining criteria according to the alternative in hierarchical order, alternative determination according to the criteria is made even more attractive [55].
ANP is a method that considers the relationship between the factors and the relationships between the factors in the decision problem. There are a few factors that make up the key point of ANP. These factors are interaction, bonding and feedback. The biggest difference of ANP from other methods is that it takes feedback and the factors are considered by the ties between each other. This method takes into account the positive and negative aspects of alternatives while evaluating alternatives. Since its first appearance, ANP has maintained its place as an important method in multi-criteria decision-making problems. ANP consists of two parts in general. The first is a form of network structure, which is called the control hierarchy, that is, the interaction of criteria or sub-criteria. The second is the network structure representation that illustrates the state of the effect between clusters and factors [56].
The path followed in the implementation of the ANP method can be expressed as follows [57]:
- First Step—The decision problem determination
- Second Step—Relationship determination among the criteria
- Third Step—Making bilateral comparisons between criteria
- Fourth Step—Check if the comparison matrices are consistent
- Fifth Step—Creation of super matrices in sequence
- Sixth Step—Determination and selection of the best alternative
3.2. Goal Programming
When it comes to multi-objective programming model, GP comes to mind. In multi-objective programming models based on optimization thinking, the aim is to determine a solution vector that simultaneously fills the contradictory objectives according to the restrictive set. GP is the oldest branch of multi-objective optimization [67]. It has been used to solve many problems. The general aim of GP is to minimize the deviations from the target values of two or more objectives whose values are determined precisely. The original objectives are expressed in linear equations with target values and two auxiliary variables [67].
Although it is similar to linear programming as a mathematical model, it involves the provision of multiple objectives at the same time. The objectives of the decision-maker in accordance with the priority structure or by weighting tries to optimize. In the GP model, it is tried to determine a solution that the decision maker finds satisfactory. For this reason, it can be said that GP is based on a notion of satisfaction rather than an optimization idea. GP is based on minimization of deviations from target values [58]. In doing so, the goals and their weights and priorities are also considered. One of the most important benefits of the goal program is that it can work with different evaluation principles and different units.
A general GP model can be given in the following format [67]:
g = 1 … e s = 1 … y g: goal numbers s: decision variable numbers
4. Application
Our study is done on the biggest NGCCPP in Turkey. This shift scheduling model is applied to a large-scale facility. The study examines the ANP-GP hybrid model for 30 days and 80 personnel. The study was performed by combining the methods mentioned in the literature for the first time. In terms of the field of application and the magnitude of the problem, the model and methods used are unique. The application steps of the study are given in Figure 1.
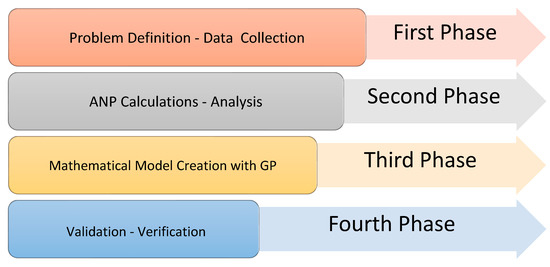
Figure 1.
Schematic representation of the study.
Our study consists of four stages. The first stage is defining the problem, collecting the data, and deciding on the methods for application. The second stage involves the ANP calculation process and analysis of the mathematical model. Model validation and verification make up the fourth stage. In the beginning, all data were taken from the experts and technical managers at the selected NGCCPP.
There are 80 personnel (P1 to P80) at this NGCCPP, and they were divided into four categories. The power plant runs in three 8 h shifts (k): morning (S1), evening (S2), and night (S3). The scheduling horizon is 30 days (j). There are four seniority level for personnel at the power plant. These are:
- First Seniority—Shift Supervisors (SS) (P1 to P4—4 Shift Supervisors)
- Second Seniority—Foremen (F) (P5 to P16—12 Foremen)
- Third Seniority—Experts (E) (P17 to P40—24 Experts)
- Fourth Seniority—Assistants (A) (P41 to P80—40 Assistants).
4.1. Determining Workers’ Skill Weights with ANP
Some studies in the literature used the ANP method for ability or skill comparisons [35,51,52]. Due to the nature of the current problem and criteria, it was considered appropriate to use the ANP technique.
ANP takes into account the relationships and ties between factors in the decision-making process. A number of factors make up the key points of ANP: interaction, bonding, and feedback. The main difference between ANP and other methods is that it takes feedback and applies the factors taking into account the ties between them. This method takes into consideration and reveals the positive and negative aspects of alternatives while evaluating the alternatives. ANP uses a control network or hierarchy to evaluate different criteria. In this way, factors such as benefits, opportunities, costs, and risks can be analyzed. On the other hand, depending on the control factors, ANP can be said to process data from different senses in a similar way as the integration process. The hierarchical structure is results-oriented and only deals with alternatives. It does not contain internal or external dependence. Interactions between factors are not taken into account. However, they do not exist in the network structure. Inter-cluster interactions are considered. It is known that the criteria that are expected to be weighed do not constitute a hierarchical structure by themselves. Therefore, the ANP method is thought to be an effective way to determine these ability weights.
The experience of a team of 12 power plant engineers was used in determining the criteria. These engineers have 10 to 15 years of experience in general rules of power plant operation; their areas of education were electrical-electronics, mechanical, chemical and industrial engineering. The criteria were composed of vital criteria for power plant operation. There are situations where electricity generation in a power plant should be controlled and intervened when necessary. Failure to follow this may result in problems that stop electricity generation. Each worker on the natural gas combined-cycle line has the ability to intervene in these situations. Therefore, including the capabilities of each staff member in the model is critical. Given this importance, staff capability values for PSP work affect the course of the solution. Therefore, calculating and including these values in the model provides more realistic results. In this paper, 20 skill criteria were determined with the help of power plant experts based on personnel ranking studies, and the values of these criteria were calculated by the ANP method and integrated into the GP model. These criteria are about the capacity and capability of personnel. Personnel qualifications of the criteria determined in the NGCCPP fully meet real-life conditions. In addition, this level of sectoral work has not been done before. This PSP is solved by running the ANP algorithm. The ANP method was selected because there are some interactions between criteria. Due to the requirements of the ANP technique, a network structure was established among the criteria. For each criterion, an individual evaluation was applied to the personnel. The personnel evaluation system data, which measure the effectiveness of the personnel, were used to assess these evaluations. Previous error statistics were also used. Support was received from the human resources department of the power plant. After the criteria were determined in this way, the scores of each worker for the 20 criteria were determined by the power plant experts based on personnel ranking studies. Four of the criteria scores (C15, C16, C17, and C19) were prepared according to the results documented when the workers were hired. The values of the remaining 16 criteria scores were calculated. According to the results, the steps of the ANP method had begun to be applied. The skill weight of each worker was calculated according to the 20 criteria, shown in Table 2.

Table 2.
Criteria about personnel skills (C1, C2, …, C20).
The consistency ratio is an important issue in ANP calculations. That means that the matrices are consistent, and the results are meaningful and convenient. The ratios of the binary comparison matrices were prepared with the power plant experts. With the help of the 20 criteria, each employee’s weight score was found after all ANP calculations. All ANP weights scores of personnel are given in Table 3.

Table 3.
ANP weights () of the workers (P1, P2, P3, … P80).
The calculation was made based on personnel classification in this mathematical model. For each classification level, mean values were calculated separately in order to incorporate the ability basics into the model. Individual skill weight values and seniority levels were used in calculating these average values (according to four seniority levels that were gathered in ANP calculations). Therefore, the skill weights are included in the mathematical model. The average skill weight values of personnel are given in Table 4 for SS, F, E, and A.

Table 4.
Seniority-based ANP weights () of the workers.
Table 3 values were used in the mathematical model as goal constraints.
4.2. Proposed Goal Programming Model
Although there is one objective function of this study, it has a multi-objective structure. There are two main objective sets in the study: to seek fair appointment without disregarding seniority levels and skills of personnel, and to minimize the costs of overtime and unbalanced appointments. In addition, these costs lead to increases in other cost items as well as generation downtime. GP, which is the algorithm used, by its nature includes multiple objectives in a single objective function. Each objective is added to the model as a separate constraint and efforts are made to minimize deviations from the objectives. Usually, a set of methods in which multiple goals are performed in order of priority are used in GP [67]. There are three solution algorithms in GP: weighting, equal weighting, and prioritization [67]. All three are based on transforming multiple goals into one goal. In the model created in the GP in this study, the goals are assumed to have equal weight.
4.2.1. Model Notations
Restrictions and constraints intended to be complied with in the operation are designed as operating requirements. It is essential to operate the electricity generation power plant in a way to ensure energy supply security. These constraints, established to meet the four sustainable electricity generation conditions, were confirmed by long observations by 12 engineers specializing in the field which are mentioned before. These include the minimum constraints that must be observed for the NGCCPP to function properly (e.g., constraint 1). The obligation to comply with certain constraints stems from labor laws (e.g., constraint 6). The long-term observations of the power plant experts were used to identify constraints that would allow the power plant to function properly. Ensuring that these constraints are met is vital for the power plant. Our mathematical model includes the following constraints:
Constraint 1: A certain number of workers are required for each day and each shift, and assignments are done according to seniority level (total 20 people for 3 shifts): 1 shift supervisor with at least seniority level 1, 3 foremen with at least seniority level 2, 6 experts with at least seniority level 3, and 10 assistants with at least seniority level 4.
Constraint 2: Anyone who works any night shift should not work the morning and evening shifts the next day.
Constraint 3: Anyone who works the evening shift should not work the morning shift the next day.
Constraint 4: Everyone should take at least one day off a week.
Constraint 5: No one should work on their day off.
Constraint 6: No one can work more than six evening shifts consecutively (this restriction is included because it is specified in the labor law).
Constraint 7: The total cost due to personnel wages should be minimized (on weekends, all personnel wages rise according to seniority apart from the regular day wages).
Wage details according to seniority level are shown in Figure 2.
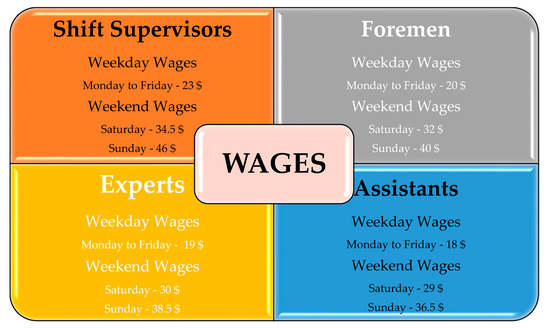
Figure 2.
The wage details.
The formulation of the mathematical model is given as follows: , , , and decision variables are used; , , and are the indices for 80 personnel, 30 days, and 3 shifts, respectively; means worker i is assigned to work on day in shift ; and means worker i is assigned day j as a day off. The model has some cost limits, which are determined in such a way that the maximum number of personnel required to be assigned in a shift does not exceed the seniority level. The cost limits from to indicate seniority levels. These numbers are calculated based on the number of personnel to be appointed in a shift and the current cost value given in Figure 2. For example, is calculated like this: shift supervisor for 22 weekdays, 4 Saturdays, and 4 Sundays in a month; 22 × $23 + 4 × 34, $5 + 4 × $46 = $827. The model formulation is as follows.
4.2.2. Model Parameters
Index for personnel: i = 1, 2, ..., l
Index for day: j = 1, 2, ..., m
k: Shift index, k = 1, 2, ..., n
Index for Goal: g = 1, 2, …, 8
Personnel: l = 80
Day: m = 30
Shift: n = 3
Skills weights of each personnel: ti, i = 1, 2, ..., l
cj: The cost variable of the shift supervisors, j = 1, 2, ..., m
dj: The cost variable of the foremen, j = 1, 2, ..., m
ej: The cost variable of the experts, j = 1, 2, ..., m
fj: The cost variable of the assistants, j = 1, 2, ..., m
C1: Cost lower limit value of the shift supervisors, C1 = 827 $
C2: Cost lower limit value of the foremen, C2 = 2176 $
C3: Cost lower limit value of the experts, C3 = 4235 $
C4: Cost lower limit value of the assistants, C4 = 6680 $
4.2.3. Decision Variables
4.2.4. Constraints
Constraint 1: j = 1, 2, ..., m k = 1, 2, …, n
Constraint 2: i = 1, 2, 3, …, l j = 1, 2, ..., m − 1
Constraint 3: i = 1, 2, 3, …, l j = 1, 2, ..., m − 1
Constraint 4: i = 1, 2, ..., l j = 1, 2, ..., 24
Constraint 5: i = 1, 2, 3, …, l j = 1, 2, ..., m
Constraint 6: i = 1, 2, 3, ..., l j = 1, 2, ..., m − 5
Constraint 7: j = 1, 2, ..., m k = 1, 2, …, n
4.2.5. Goal Constraints: j = 1, 2, 3, …, m k = 1, 2, …, n
1. Goal: Shift Supervisors’ constraint for skill-based assignment
2. Goal: Foremen constraint for skill-based assignment
3. Goal: Experts’ constraint for skill-based assignment
4. Goal: Assistants’ constraint for skill-based assignment
5. Goal: Shift Supervisors’ constraint for cost minimization
6. Goal: Foremen constraint for cost minimization
7. Goal: Experts’ constraint for cost minimization
8. Goal: Assistants’ constraint for cost minimization
4.2.6. Objective Function
4.3. Analysis of Results
The proposed model was written in ILOG CPLEX Studio IDE version 12.8 and solved. The computation of the results contained 9600 decision variables, 9880 constraints, and 720 goal constraints. The model was solved in 5.12 s. Deviation rates were calculated to examine the results in detail. According to the results, a positive deviation of 0.02% was observed from the second goal, and a negative deviation of 0.04% was observed from the fourth goal. There was no deviation from other goals. As can be seen here, the deviation rates are very low, and the model yielded positive and efficient results. The assignment table is shown in Figure 3, where 0 means the worker does not work on this day and shift, and 1 means the worker works on this day and shift. Shift 1 is morning, shift 2 is evening, and shift 3 is night. The right side of the figure shows the total workload of each person.

Figure 3.
The final schedule.
The current schedules used in the power plant are done manually by shift supervisors every week. Shift supervisors make appointments based on subjective factors such as work intensity, employee experience, readiness, and motivation of employees. This process is unprofessional. In addition, it is not systematic. Therefore, unbalanced job assignments cause major problems, such as general motivation and generation downtimes.
In this study, manual personnel scheduling is intended to be modeled with GP. The current total workloads of staff members in a month are given in Table 5. As can be seen from the existing workloads, it is understood that there is a problem in their distribution. Since the scheduling does not follow rules and standards, there is injustice. In order to prevent losses caused by errors in the work plans of shift personnel, in this study, restrictions such as balancing the working days for shift personnel are established by considering legal obligations and the working principles of power plant management and improvements such as appointing personnel to shifts in a balanced and fair manner. The proposed GP model was obtained as a result of the solution.

Table 5.
Workloads of each personnel with manual scheduling.
This study first examines the behavior of the model developed on real data obtained from a NGCCPP. Then, the model and results created according to the size of the problem are presented. The actual data obtained from the power plant were used to examine the behavior of the developed model. At this stage, first, problem details are given and then the application and calculation results are provided. In order to show that the developed model can produce solutions for PSPs, real data were used first.
According to these data, fair work distribution is obtained as a result of the solution of the skill-based mathematical model developed within the constraints and aims reflecting the realities of the power plant. After all; 40 staff work for 22 days and 40 staff work for 23 days.
After this study, it has been seen that the four main characteristics of sustainable electricity generation supply should be provided: energy must be uninterrupted, environmentally friendly, efficient, and economical. As a result of this scheduling, personnel-related postures were eliminated, environmentally friendly generation was started, personnel utilization efficiency increased, and the excess costs of wages and downtime decreased. Justice in the work plans was achieved and arbitrary appointments were terminated.
The significant economic losses associated with shutdowns caused by power plants, and the satisfactory results obtained from the personnel scheduling and the rarely used PSP in the energy sector are presented in the literature. In particular, the application of this study at the power plant and the positive results indicate that this study is different from other studies.
5. Results and Discussion
This study shows that the proposed model needs to adapt the personnel assignments because it provides fairness and cost minimization of shift assignments. Thus, personnel satisfaction will increase with the proposed schedule. The model was applied at the power plant for one year. Afterwards, face-to-face interviews were conducted with the scheduled personnel and the results of the annual operating report were examined. In these analyses, it was found that there was a full improvement in satisfaction compared to the previous year’s schedule. All staff are satisfied that the assignment is fair allocation. Assignment in each shift according to their abilities has created an atmosphere of trust in all personnel. The fair distribution of jobs among all 80 staff had a positive impact. These statements are also confirmed by improvements in the achieved sustainable electricity generation aim. For example, the reduction in generation shutdowns and the reduction in costs confirm the results. Workloads of personnel are given in Table 5. When schedules are done manually, workloads are irregular and unstable.
Personnel workloads after scheduling with the mathematical model can be seen in Table 6. All hard constraints and many of the soft constraints are satisfied. Worker preferences are not ignored.

Table 6.
Workloads of each personnel after scheduling is done with mathematical model.
Comparative results can be seen in Table 7. As seen from the results, in the new proposed schedule, all constraints are provided. Four preferences that were not provided in the previous schedule are as follows: a staff member working the evening shift one day worked the morning shift the next day; a staff member worked more than six days on the evening shift; in all, a balanced assignment requirement was not provided; and some people at some seniority levels were overworked. All of these scheduling preferences are provided in the newly applied schedule. Observed results show that fair schedules were provided without ignoring the skills of the personnel. This result is especially effective with respect to cost minimization. Also, staff wages are much higher on weekends. Therefore, overtime assignments on weekends were prevented with this model. With the previous manual schedule, 4 of 17 constraints were not available; 40 of the 80 personnel worked 22 days, and 40 worked 23 days in a month. It is a good achievement considering assignment fairness.

Table 7.
Computational result.
This study makes great a contribution to reducing costs with PSPs. It is more appropriate to explain the calculation of power plant capacity in this regard. Due to the unbalanced assignment of workloads in the previous manual shift scheduling, the large number of daily personnel causes higher wage costs; $40,190.50 was the wage cost with manual scheduling, and this was reduced to $34,245.50. Therefore, a 15% cost improvement was achieved with the help of our proposed mathematical model.
This study shows that staff motivation has a great impact on the power plant. Personnel scheduling in the NGCCPP is quite comprehensive. For this reason, it was found that manual scheduling had bad results, because while scheduling, some special features such as expertise and preventing overtime should not be ignored. The main purpose of this model, which includes these features, is to ensure the security of a sustainable energy supply. Previously unbalanced work distribution was eliminated, downtimes were reduced, and energy supply security was ensured.
6. Conclusions
Personnel scheduling is an important area of study in operations research, which has a positive effect on performance in terms of increasing employee motivation by producing a fair and balanced work plan. In addition, electrical energy, which is the output of billions of dollars of investment and complex generation and maintenance repair processes and even a few hours of shutdown, has important economic and social impacts, and is an indispensable consumption point of today’s political, socioeconomic, and diplomatic aspects. In view of this, it is necessary to employ qualified personnel to maintain performance at the highest levels.
NGCCPPs are labor units where labor, an expensive resource, is used intensively. The primary aim in such enterprises is to ensure maximum employee satisfaction with minimum operating and labor costs. To meet this goal, companies must use various techniques. Shift scheduling models can be considered as useful tools in this respect. NGCCPPs are the leaders in energy supply as of the end of the first quarter of 2019 despite the limited resource availability, because they have many advantages. The main purpose of NGCCPPs is to supply interrupted electricity, and the most important aspect of this comprehensive goal is that it is uninterrupted. NGCCPPs can be stopped because of factors such as bad fuel quality, network failure, atmospheric conditions, and lack of water. These shutdowns happen in currently operating NGCCPPs without considering maintenance and operation instructions. NGCCPPs are managed from main control rooms or by interfering with equipment spread over the power plant in the absence of a SCADA system.
The personnel at the power plant were previously scheduled randomly, arbitrarily, and without regard to their working abilities. Therefore, the attention level of the operators was significantly reduced, the situation of completing job requirements decreased, and employee motivation fell. For these reasons, power plant failure interrupted generation for 44 h because of operator errors. This loss meant millions of kWh of energy, which equals a large monetary loss. Within the scope of this study, the personnel schedule created by the proposed model maximizes operator motivation on the basis of fair business distribution and capabilities. Operator-centered shutdowns were measured by the power plant experts for 48 h and 36 min before scheduling. After this study was applied, an improvement of 62.5% was achieved and this rate decreased to 18 h and 4 min. It is estimated that the power plant generates approximately 1599 MW of electricity per hour and sells it for $30/MW (20 h 32 min × 1599 MW × $30 = $1007.37), so this study can prevent millions of dollars in losses.
The model is solved in a reasonable time using the IBM ILOG Optimization Tool. The proposed mathematical model markedly reduced the time to create a monthly schedule based on the already used schedule. By using the proposed model, it was shown that optimum results can be achieved that maximize days off and work preferences. This model can be applied to other power plants with small changes. Because of that, we can say that the model is sustainable for personnel schedules.
In this study, in order to prevent losses due to mistakes made in the preparation of a work plan for personnel, the constraints that balance the working days for shift staff are formed by considering the legal requirements and working principles that the power plant owner must comply with. Improvements, such as assigning personnel to shifts in a balanced and equitable manner, were realized with the solution of the GP model. There can be significant economic losses from the poor condition of personnel in power plants. Based on the satisfactory results obtained from personnel scheduling in this study and the rarely used PSP in the energy sector, new models can be proposed in the future for both shift personnel and maintenance and repair personnel. In addition, the study area discussed in this study can be evaluated from different perspectives with all personnel qualifications, using analytical methods such as other multicriteria decision-making or statistical methods.
In recent years, despite the significant increase in the efficiency of algorithms to solve integer programming problems, they cannot be applied frequently to solve medium and large practical problems due to memory restrictions. Besides, it is difficult to gather results after a long time period. Therefore, it can be assumed that the proposed model will provide complete or approximate solutions with short calculation periods for the application of production schedules of future workers in electricity generating power plants. Other recommendations for future implementation include reducing the number of decision variables and constraints, which could help to make future studies more practical; or researchers could create a user-friendly interface to use the mathematical model and information based on users’ solutions to quickly resolve PSPs.
Author Contributions
The analyses were carried out by E.H.Ö. and E.Ö. This paper was written by E.H.Ö., T.E. and E.Ö. supervised the conducted research, reviewed, and revised the paper. E.Ö. reviewed, revised, and improved the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blöchliger, I. Modeling staff scheduling problems. A tutorial. Eur. J. Oper. Res. 2004, 158, 533–542. [Google Scholar] [CrossRef]
- Ernst, A.T.; Jiang, H.; Krishnamoorthy, M.; Sier, D. Staff scheduling and rostering: A review of applications, methods and models. Eur. J. Oper. Res. 2004, 153, 3–27. [Google Scholar] [CrossRef]
- Bergh, J.V.; Beliën, J.; Bruecker, P.; Demeulemeester, E.; Boeck, L. Personnel Scheduling: A Literature Review. Eur. J. Oper. Res. 2013, 226, 367–385. [Google Scholar] [CrossRef]
- Özcan, E.; Varli, E.; Eren, T. Shift Personnel Scheduling in Hydroelectric Power Plants with Goal Programming Approach. J. Inf. Technol. 2017, 10, 363–370. [Google Scholar]
- Electricity Generation Company of Turkey. Yearly Activity Report; EUAS: Ankara, Turkey, 2019. [Google Scholar]
- Edie, L.C. Traffic delays at toll booths. Oper. Res. 1954, 2, 107–138. [Google Scholar] [CrossRef]
- Dantzig, B.G. Letter to the Editor—A Comment on Edie’s Traffic Delays at Toll Booths. Oper. Res. 1954, 2, 339–341. [Google Scholar] [CrossRef]
- Burns, A.; Baruah, S. Sustainability in Real-time Scheduling. J. Comput. Sci. Eng. 2008, 2, 74–97. [Google Scholar] [CrossRef][Green Version]
- Min, H. A disaggregate zero-one goal programming model for the flexible staff scheduling problem. Socio-Econ. Plan. Sci. 1987, 21, 271–282. [Google Scholar] [CrossRef]
- Eitzen, G.; Panton, D.; Mills, G. Multi-Skilled Workforce Optimization. Ann. Oper. Res. 2004, 127, 359–372. [Google Scholar] [CrossRef]
- Lilly, M.T.; Emovon, I.; Ogaji, S.O.T.; Probert, S.D. Four-Day Service-Staff Workweek in order to Complete Maintenance Operations More Effectively in a Nigerian Power Generating Station. Appl. Energy 2007, 84, 1044–1055. [Google Scholar] [CrossRef]
- Yaoyuenyong, K.; Nanthavanij, S. Energy-based Workforce Scheduling Problem: Mathematical model and Solution Algorithms. Sci. Asia 2005, 31, 383–393. [Google Scholar] [CrossRef]
- Bard, J.F.; Binici, C.; De Silva, A.H. Staff scheduling at the United States Postal Service. Comput. Oper. Res. 2003, 30, 745–771. [Google Scholar] [CrossRef]
- Corominas, A.; Lusa, A.; Pastor, R. Planning annualised hours with a finite set of weekly working hours and joint holidays. Ann. Oper. Res. 2004, 128, 217–233. [Google Scholar] [CrossRef]
- Azaiez, M.N.; Al-Sharif, S.S. A 0–1 goal programming model for nurse scheduling. Comput. Oper. Res. 2005, 32, 491–507. [Google Scholar] [CrossRef]
- Güneş, A.; Kahvecioğlu, A.; Tuncel, H. Askeri nöbet çizelgelerinin genetik algoritma kullanılarak en iyilenmesi. In Proceedings of the Elektrik-Elektronik-Bilgisayar Mühendisliği 11’inci Ulusal Kongresi ve Fuarı, İstanbul, Turkey, 22 September 2005; pp. 470–474. [Google Scholar]
- Yunes, T.H.; Moura, A.V.; De Souza, C.C. Hybrid column generation approaches for urban transit crew management problems. Transp. Sci. 2005, 39, 273–288. [Google Scholar] [CrossRef]
- Topaloğlu, S. A multi-objective programming model for scheduling emergency medicine residents. Comput. Ind. Eng. 2006, 51, 375–388. [Google Scholar] [CrossRef]
- Trilling, L.; Guinet, A.; Le Magny, D. Nurse Scheduling Using Integer Linear Programming and Constraint Programming, 12th IFAC International Symposium; Elsevier: Amsterdam, The Netherlands, 2006; Volume 3, pp. 651–656. [Google Scholar]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Crew rostering problem in a public transport company. J. Oper. Res. Soc. 2006, 57, 1173–1179. [Google Scholar] [CrossRef]
- Chu, S.C.K. Generating, scheduling and rostering of shift crew-duties: Applications at the Hong Kong International Airport. Eur. J. Oper. Res. 2007, 177, 1764–1778. [Google Scholar] [CrossRef]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Rostering in a rail passenger carrier. J. Sched. 2007, 10, 245–254. [Google Scholar] [CrossRef]
- Corominas, A.; Lusa, A.; Pastor, R. Using a MILP model to establish a framework for an annualised hours agreement. Eur. J. Oper. Res. 2007, 177, 1495–1506. [Google Scholar] [CrossRef]
- Thompson, G.M.; Pullman, M.E. Scheduling workforce relief breaks in advance versus in real-time. Eur. J. Oper. Res. 2007, 181, 139–155. [Google Scholar] [CrossRef]
- Sinreich, D.; Jabali, O. Staggered work shifts: A way to downsize and restructure an emergency department workforce yet maintain current operational performance. Health Care Manag. Sci. 2007, 10, 293–308. [Google Scholar] [CrossRef] [PubMed]
- Horn, M.; Jiang, H.; Kilby, P. Scheduling patrol boats and crews for the Royal Australian Navy. J. Oper. Res. Soc. 2007, 58, 1284–1293. [Google Scholar] [CrossRef]
- Çetin, E.İ.; Kuruüzüm, A.; Irmak, S. Ekip Çizelgeleme Probleminin Küme Bölme Modeli ile Çözümü. Havacılık Ve Uzay Teknol. Derg. 2008, 3, 47–54. [Google Scholar]
- Sungur, B. Bir güzellik salonunun tur çizelgeleme problemi için karma tamsayılı hedef programlama modelinin geliştirilmesi. İstanbul Üniversitesi İşletme Fakültesi Derg. 2008, 37, 49–64. [Google Scholar]
- De Matta, R.; Peters, E. Developing work schedules for an inter-city transit system with multiple driver types and fleet types. Eur. J. Oper. Res. 2009, 192, 852–865. [Google Scholar] [CrossRef]
- Tsai, C.C.; Li, S.H.A. A two-stage modeling with genetic algorithms for the nurse scheduling problem. Expert Syst. Appl. 2009, 36, 9506–9512. [Google Scholar] [CrossRef]
- Lezaun, M.; Perez, G.; De La Maza, E.S. Staff rostering for the station personnel of a railway company. J. Oper. Res. Soc. 2010, 61, 1104–1111. [Google Scholar] [CrossRef]
- Rönnberg, E.; Larsson, T. Automating the self-scheduling process of nurses in Swedish healthcare: A pilot study. Health Care Manag. Sci. 2010, 13, 35–53. [Google Scholar] [CrossRef]
- Zolfaghari, S.; Quan, V.; El-Bouri, A.; Khashayardoust, M. Application of a genetic algorithm to staff scheduling in retail sector. Int. J. Ind. Syst. Eng. 2010, 5, 20–47. [Google Scholar] [CrossRef]
- Fırat, M.; Hurkens, C.A.J. An improved MIP-based approach for a multi-skill workforce scheduling problem. J. Sched. 2011, 15, 363–380. [Google Scholar] [CrossRef]
- Bağ, N.; Özdemir, M.; Eren, T. 0-1 Hedef Programlama ve ANP Yöntemi ile Hemşire Çizelgeleme Problemi Çözümü. Int. J. Eng. Res. Dev. 2012, 1, 2–6. [Google Scholar]
- Hung-Tso, L.; Yen-Ting, C.; Tsung-Yu, C.; Yi-Chun, L. Crew rostering with multiple goals: An empirical study. Comput. Ind. Eng. 2012, 63, 483–493. [Google Scholar]
- Li, J.; Burke, E.K.; Curtois, T.; Petrovic, S.; Rong, Q. The falling tide algorithm: A new multi-objective approach for complex workforce scheduling. Omega 2012, 40, 283–293. [Google Scholar] [CrossRef]
- Bektur, G.; Hasgül, S. Kıdem seviyelerine göre işgücü çizelgeleme problemi: Hizmet sektöründe bir uygulama. Afyon Kocatepe Üniversitesi İktisadi Ve İdari Ve Bilimler Fakültesi Derg. 2013, 15, 385–402. [Google Scholar]
- Kassa, B.A.; Tizazu, A.E. Personnel Scheduling Using an Integer Programming Model—An Application at Avanti Blue-Nile Hotels. SpringerPlus 2013, 2, 333. [Google Scholar] [CrossRef]
- Louly, M.A. A goal programming model for staff scheduling at a telecommunications center. J. Math. Model. Algorithms Oper. Res. 2013, 12, 167–178. [Google Scholar] [CrossRef]
- Labidi, M.; Mrad, M.; Gharbi, A.; Louly, M.A. Scheduling IT Staff at a Bank: A Mathematical Programming Approach. Sci. World J. 2014. [Google Scholar] [CrossRef]
- Öztürkoğlu, Y.; Çalışkan, F. Hemşire Çizelgelemesinde Esnek Vardiya Planlaması ve Hastane Uygulaması. Dokuz Eylül Üniversitesi Sos. Bilimler Enstitüsü Derg. 2014, 16, 115–133. [Google Scholar] [CrossRef][Green Version]
- Todovic, D.; Makajic-Nikolic, D.; Kostic-Stankovic, M.; Martic, M. Police officer scheduling using goal programming. Polic. Int. J. Police Strateg. Manag. 2015, 38, 295–313. [Google Scholar] [CrossRef]
- Kaçmaz, Ö.; Alakaş, H.M.; Eren, T. Shift Scheduling with the Goal Programming Method: A Case Study in the Glass Industry. Mathematics 2019, 7, 561. [Google Scholar] [CrossRef]
- Castillo, I.; Joro, T.; Li, Y.Y. Workforce Scheduling with Multiple Objectives. Eur. J. Oper. Res. 2009, 196, 162–170. [Google Scholar] [CrossRef]
- Alfieri, A.; Kroon, L.; Van den Velde, S. Personnel scheduling in a complex logistic system: A railway application case. J. Intell. Manuf. 2007, 18, 223–232. [Google Scholar] [CrossRef]
- Alsheddy, A.; Tsang, E.P.K. Empowerment scheduling for a field workforce. J. Sched. 2011, 14, 639–654. [Google Scholar] [CrossRef]
- Asensio-Cuesta, S.; Diego-Mas, J.A.; Canos-Daros, L.; Andres-Romano, C. A genetic algorithm for the design of job rotation schedules considering ergonomic and competence criteria. Int. J. Adv. Manuf. Technol. 2012, 60, 1161–1174. [Google Scholar] [CrossRef]
- Ásgeirsson, E. Bridging the gap between self-schedules and feasible schedules in staff scheduling. Ann. Oper. Res. 2014, 218, 51–69. [Google Scholar] [CrossRef]
- Shuib, A.; Kamarudin, F.I. Solving shift scheduling problem with days-off preference for power station workers using binary integer goal programming model. Ann. Oper. Res. 2019, 272, 355–372. [Google Scholar] [CrossRef]
- Özder, E.H.; Varlı, E.; Eren, T. A Model Suggestion for Cleaning Staff Scheduling Problem with Goal Programming Approach. Black Sea J. Sci. 2017, 7, 114–127. [Google Scholar] [CrossRef]
- Özder, E.H.; Özcan, E.; Eren, T. Staff Task-Based Shift Scheduling Solution with an ANP and Goal Programming Method in a Natural Gas Combined-cycle Power Plant. Mathematics 2019, 7, 192. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with The Analytical Hierarchy Process; RWS Publications: Pittsburg, PA, USA, 1994; pp. 69–84. [Google Scholar]
- Saaty, T.L. Fundamentals of The Analytic Network Process. In Proceedings of the 5th International Symposium on the Analytic Hierarchy Process, Kobe, Japan, 12–14 August 1999; pp. 12–14. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback the Analytic Network Process, 2nd ed.; RWS Publications: Pittsburg, PA, USA, 2001. [Google Scholar]
- Gür, Ş.; Eren, T. Scheduling and Planning in Service Systems with Goal Programming: Literature Review. Mathematics 2018, 6, 265. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Raylı Sistem Projeleri Kararında Ahs-Hp ve Aas-Hp Kombinasyonu. Gazi Mühendislik Bilimleri Derg. 2017, 3, 1–13. [Google Scholar]
- Hamurcu, M.; Gür, Ş.; Özder, E.H.; Eren, T. A Multicriteria Decision Making for Monorail Projects with Analytic Network Process and 0–1 Goal Programming. Int. J. Adv. Electron. Comput. Sci. 2016, 3, 8–12. [Google Scholar]
- Özcan, E.C.; Ünlüsoy, S.; Eren, T. A combined goal programming–AHP approach supported with TOPSIS for maintenance strategy selection in hydroelectric power plants. Renew. Sustain. Energy Rev. 2017, 78, 1410–1423. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, S.; Zhu, Y.; Wang, D.; Liu, J. Modeling, planning, application and management of energy systems for isolated areas: A review. Renew. Sustain. Energy Rev. 2018, 82, 460–470. [Google Scholar] [CrossRef]
- Koltsaklis, N.E.; Giannakakis, M.; Georgiadis, M.C. Optimal energy planning and scheduling of microgrids. Chem. Eng. Res. Des. 2018, 131, 318–332. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H.; Jirdehi, M.A. Stochastic planning and scheduling of energy storage systems for congestion management in electric power systems including renewable energy resources. Energy 2017, 133, 380–387. [Google Scholar] [CrossRef]
- Amiri, S.; Honarvar, M.; Sadegheih, A. Providing an integrated Model for Planning and Scheduling Energy Hubs and preventive maintenance. Energy 2018, 163, 1093–1114. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Lee, W.J.; Yan, H.; Li, D. The optimal structure planning and energy management strategies of smart multi energy systems. Energy 2018, 160, 122–141. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Deshmukh, M.K. A new approach to micro-level energy planning—A case of northern parts of Rajasthan, India. Renew. Sustain. Energy Rev. 2009, 13, 634–642. [Google Scholar] [CrossRef]
- Jinturkar, A.M.; Deshmukh, S.S. A fuzzy mixed integer goal programming approach for cooking and heating energy planning in rural India. Expert Syst. Appl. 2011, 38, 11377–11381. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Goal programming and multiple objective optimizations. Eur. J. Oper. Res. 1977, 1, 39–54. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).