Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes
Abstract
1. Introduction
2. Preliminaries and Notations
3. Main Results
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
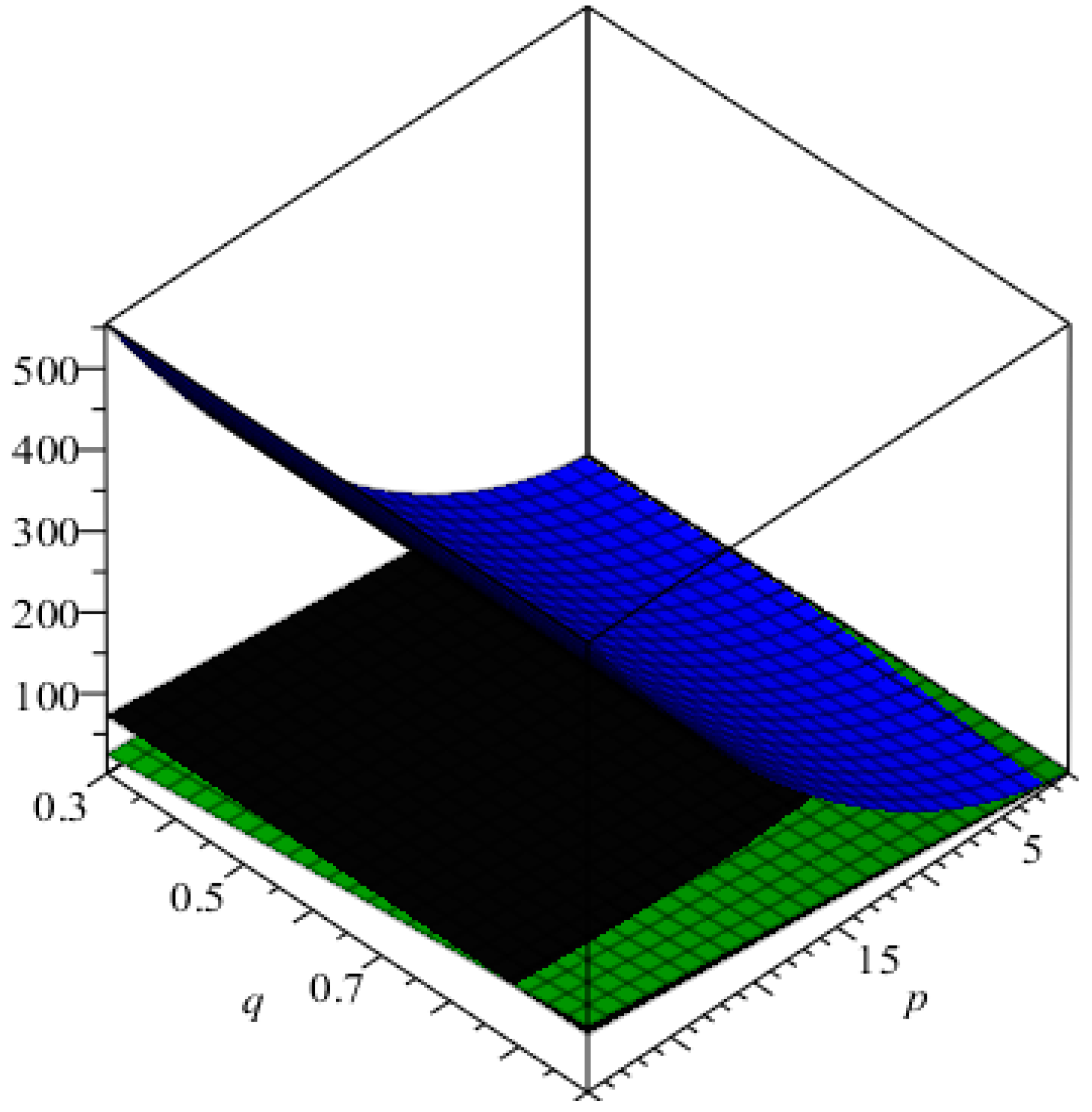
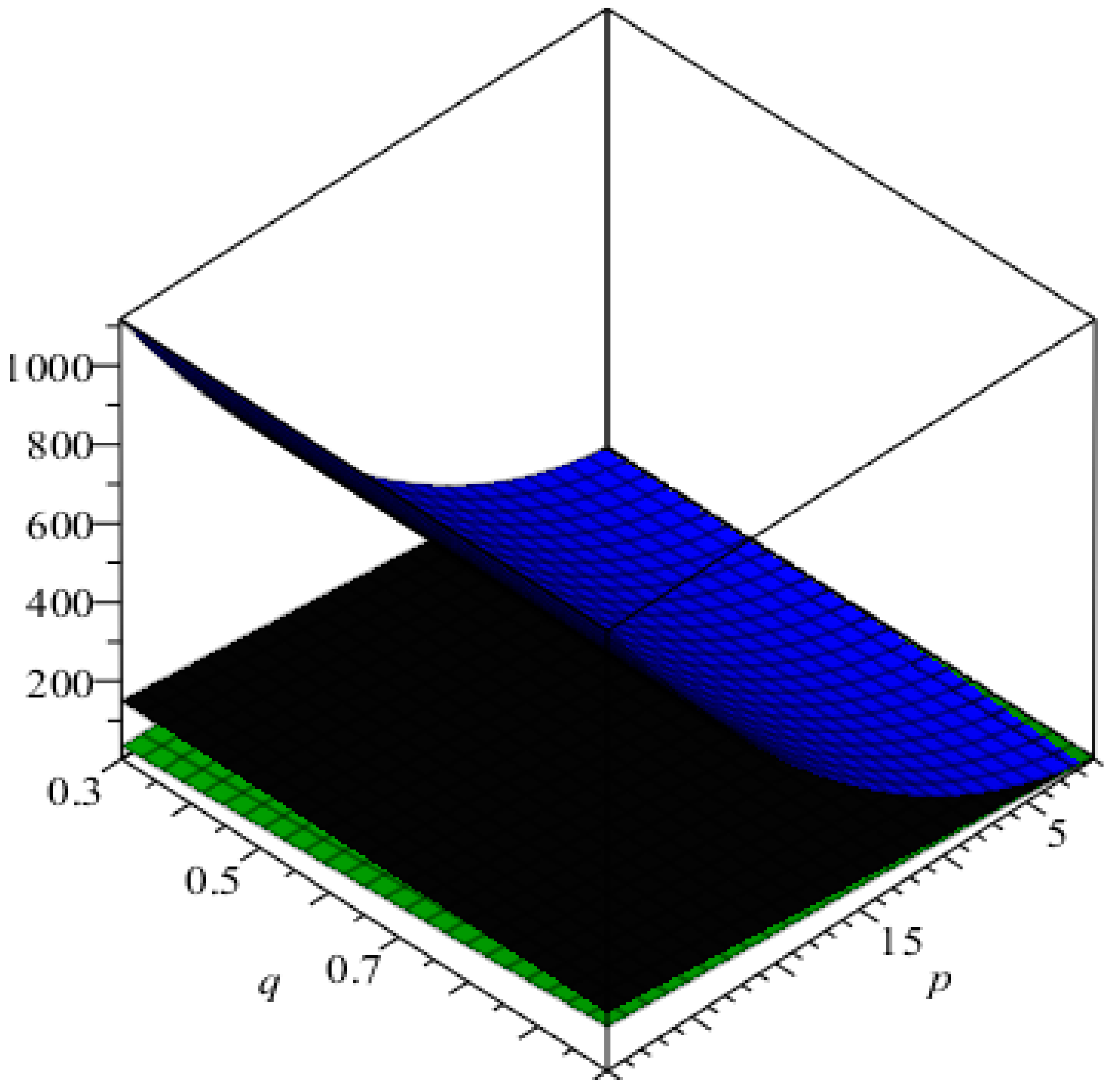
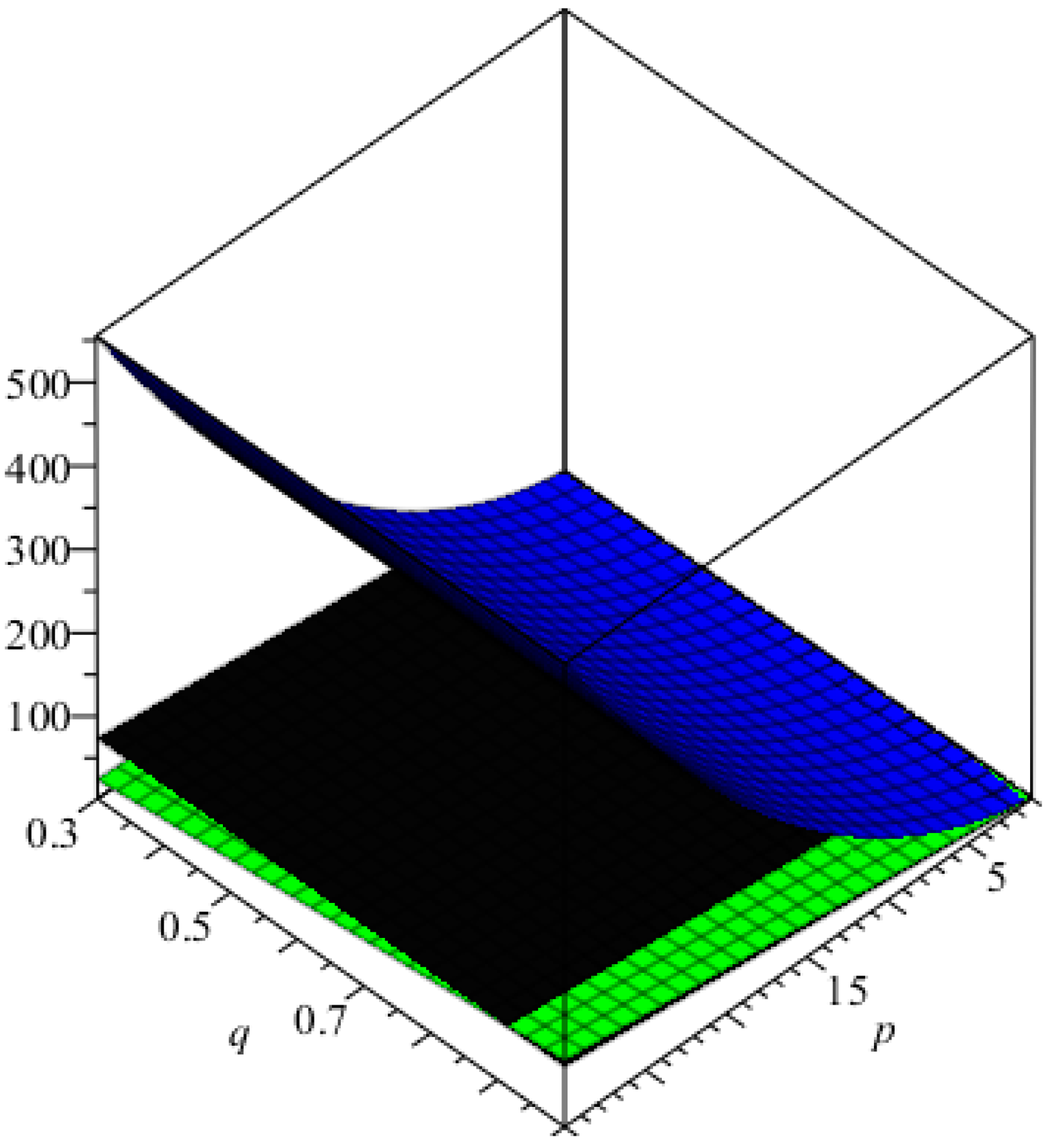
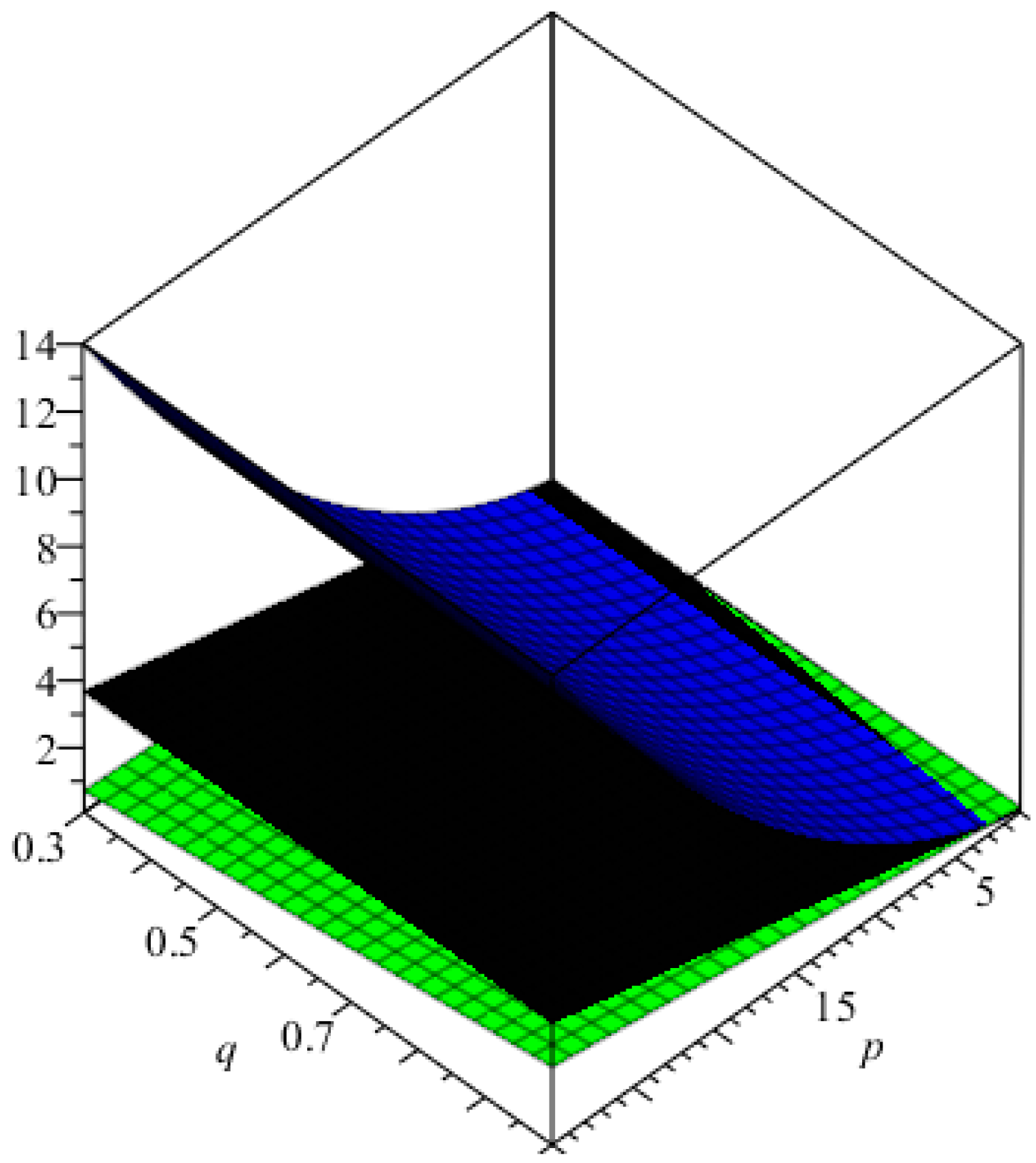
4. Conclusions, Graphical Analysis and Discussions
Author Contributions
Funding
Conflicts of Interest
References
- Rucker, G.; Rucker, C. On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer: New York, NY, USA, 1986. [Google Scholar]
- Randic, M. On the characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. Atomic bond connectivity and the energetic of branched alkanes. Chem. Phys. Lett. 2008, 463, 422–425. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom–bond connectivity index: Modeling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37, 849–855. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Chemistry and Drug Research; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure Activity Analysis; Wiley: New York, NY, USA, 1986. [Google Scholar]
- ISO. TS 12901-2 Nanotechnologies—Occupational Risk Management Applied to Engineered Nanomaterials—Part 2: Use of the Control Banding Approach; The International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Warheit, D.B. Hazard and risk assessment strategies for nanoparticle exposures: How far have we come in the past 10 years? F1000Research 2018, 7, 376. [Google Scholar] [CrossRef] [PubMed]
- Morgeneyer, M.; Aguerre-Chariol, O.; Bressot, C. Stem imaging to characterize nanoparticle emissions and help to design nanosafer paints. Chem. Eng. Res. Des. 2018, 136, 663–674. [Google Scholar] [CrossRef]
- Salmatonidis, A.; Viana, M.; Pérez, N.; Alastuey, A.; de la Fuente, G.F.; Angurel, L.A.; Sanfélix, V.; Monfort, E. Nanoparticle formation and emission during laser ablation of ceramic tiles. J. Aerosol Sci. 2018, 126, 152–168. [Google Scholar] [CrossRef]
- Bressot, C.; Shandilya, N.; Jayabalan, T.; Fayet, G.; Voetz, M.; Meunier, L.; Le Bihan, O.; Aguerre-Chariol, O.; Morgeneyer, M. Exposure assessment of nanomaterials at production sites by a short time sampling (sts) approach strategy and first results of measurement campaigns. Process Saf. Environ. Prot. 2018, 116, 324–332. [Google Scholar] [CrossRef]
- Morgeneyer, M.; Ramirez, A.; Smith, S.M.; Tweedie, R.; Heng, J.; Maass, S.; Bressot, C. Particle technology as a uniform discipline? Towards a holistic approach to particles, their creation, characterization, handling and processing! Chem. Eng. Res. Des. 2019, 146, 162–165. [Google Scholar] [CrossRef]
- Reti, T.; Sharfdini, R.; Dregelyi-Kiss, A.; Hagobin, H. Graph irregularity indices used as molecular discriptors in QSPR studies. MATCH Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Estrada, E. Randic index, irregularity and complex biomolecular networks. Acta Chim. Slov. 2010, 57, 597–603. [Google Scholar] [PubMed]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Von Collatz, L.; Sinogowitz, U. Spektren Endlicher Grafen. In Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg; Springer-Verlag: Hamberg, Germany, 1957; Volume 21, pp. 63–77. [Google Scholar]
- Dorogovtsev, S.N.; Mendes, J.F.F. Evolution of networks with aging of sites. Phys. Rev. E 2000, 62, 1842–1845. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Redner, S.; Leyvraz, F. Connectivity of growing random networks. Phys. Rev. Lett. 2000, 85, 4629–4632. [Google Scholar] [CrossRef]
- West, D.B. An Introduction to Graph Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–61. [Google Scholar]
- Bell, F.K. A note on the irregularity of graphs. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef]
- Albertson, M.O. The irregularity of a graph. Ars Comb. 1997, 46, 219–225. [Google Scholar]
- Gutman, I. Irregularity of molecular graphs. Kragujev. J. Sci. 2016, 38, 71–78. [Google Scholar] [CrossRef]
- Dimitrov, D.; Reti, T. Graphs with equal irregularity indices. Acta Polytech. Hung. 2014, 11, 41–57. [Google Scholar]
- Bezugly, V.J.; Kunstmann Stok, G.B.; Frauenheim, T.; Niehaus, T.; Cuniberti, G. Highly conductive boron nanotubes: Transport properties, work functions, and structural stabilities. ACS Nano 2011, 5, 4997–5005. [Google Scholar] [CrossRef] [PubMed]
- Manuel, P. Computational aspects of carbon and boron nanotubes. Molecules 2010, 15, 8709–8722. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Ding, Y.; Ni, J. Ab initio prediction of stable boron sheets and boron nanotubes: Structure, stability, and electronic properties. Phys. Rev. B 2008, 77, 041402. [Google Scholar] [CrossRef]
- Sun, M.L.; Slanina, Z.; Lee, S.L. Square/hexagon route towards the boron-nitrogen clusters. Chem. Phys. Lett. 1995, 233, 279–283. [Google Scholar] [CrossRef]
- Slanina, Z.; Sun, M.L.; Lee, S.L. AM1 stability prediction: B36N24 > B36P24 > Al36N24 > Al36P24. J. Mol. Struct. 1995, 334, 229–233. [Google Scholar] [CrossRef]
- Slanina, Z.; Sun, M.L.; Lee, S.L. Computations of boron and boron-nitrogen cages. Nan. Mater. 1997, 8, 623–635. [Google Scholar] [CrossRef]
- Lau, K.C.; Pandey, R. Stability and Electronic Properties of Atomistically Engineered 2D Boron Sheets. Phys. Chem. C 2007, 111, 2906–2912. [Google Scholar] [CrossRef]
- Rehman, M.U.; Sardar, R.; Raza, A. Computing topological indices of Hex Board and its line graph. Open J. Math. Sci. 2017, 1, 62–71. [Google Scholar] [CrossRef]
- Riaz, M.; Gao, W.; Baig, A.Q. M-Polynomials and degree-based Topological Indices of Some Families of Convex Polytopes. Open J. Math. Sci. 2018, 2, 18–28. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-Polynomials and topological indices of V-Phenylenic Nanotubes and Nanotori. Sci. Rep. 2017, 7, 8756. [Google Scholar] [CrossRef] [PubMed]
- Kwun, Y.C.; Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. Computational Analysis of topological indices of two Boron Nanotubes. Sci. Rep. 2018, 8, 14843. [Google Scholar] [CrossRef] [PubMed]
- Hussain, Z.; Munir, M.; Rafique, S.; Kang, S.M. Topological Characterizations and Index-Analysis of New Degree-Based Descriptors of Honeycomb Networks. Symmetry 2018, 10, 478. [Google Scholar] [CrossRef]
- Chartrand, G.; Erdos, P.; Oellermann, O. How to define an irregular graph. Coll. Math. J. 1988, 19, 36–42. [Google Scholar] [CrossRef]
- Majcher, Z.; Michael, J. Highly irregular graphs with extreme numbers of edges. Discr. Math. 1997, 164, 237–242. [Google Scholar] [CrossRef]
- Behzad, M.; Chartrand, G. No graph is perfect. Am. Math. Mon. 1947, 74, 962–963. [Google Scholar] [CrossRef]
- Horoldagva, B.; Buyantogtokh, L.; Dorjsembe, S.; Gutman, I. Maximum size of maximally irregular graphs. Match Commun. Math. Comput. Chem. 2016, 76, 81–98. [Google Scholar]
- Liu, F.; Zhang, Z.; Meng, J. The size of maximally irregular graphs and maximally irregular triangle–free graphs. Graphs Comb. 2014, 30, 699–705. [Google Scholar] [CrossRef]
- Collatz, L.; Sinogowitz, U. Spektren endlicher Graphen. Abh. Math. Sem. Univ. Hambg. 1957, 21, 63–77. [Google Scholar]
- Abdo, H.; Brandt, S.; Dimitrov, D. The total irregularity of a graph. Discr. Math. Theor. Comput. Sci. 2014, 16, 201–206. [Google Scholar]
- Vukičević, D.; Graovac, A. Valence connectivities versus Randić, Zagreb and modified Zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat. Chem. Acta 2004, 77, 501–508. [Google Scholar]
- Abdo, H.; Dimitrov, D. The total irregularity of graphs under graph operations. Miskolc Math. Notes 2014, 15, 3–17. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D. The irregularity of graphs under graph operations. Discuss. Math. Graph Theory 2014, 34, 263–278. [Google Scholar] [CrossRef]
- Gutman, I. Topological Indices and Irregularity Measures. J. Bull. 2018, 8, 469–475. [Google Scholar]
- Zahid, I.; Aslam, A.; Ishaq, M.; Aamir, M. Characteristic study of irregularity measures of some Nanotubes. Can. J. Phys. 2019. [Google Scholar] [CrossRef]
- Gao, W.; Aamir, M.; Iqbal, Z.; Ishaq, M.; Aslam, A. On Irregularity Measures of Some Dendrimers Structures. Mathematics 2019, 7, 271. [Google Scholar] [CrossRef]
- Gao, W.; Abdo, H.; Dimitrov, D. On the irregularity of some molecular structures. Can. J. Chem. 2017, 95, 174–183. [Google Scholar] [CrossRef]
- Hussain, Z.; Rafique, S.; Munir, M.; Athar, M.; Chaudhary, M.; Ahmad, H.; Min Kang, S. Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems. Processes 2019, 7, 413. [Google Scholar] [CrossRef]
- Hussain, Z.; Munir, M.; Rafique, S.; Hussnain, T.; Ahmad, H.; Chel Kwun, Y.; Min Kang, S. Imbalance-Based Irregularity Molecular Descriptors of Nanostar Dendrimers. Processes 2019, 7, 517. [Google Scholar] [CrossRef]
- Liu, J.B.; Wang, C.; Wang, S.; Wei, B. Zagreb Indices and Multiplicative Zagreb Indices of Eulerian Graphs. Bull. Malays. Math. Sci. Soc. 2019, 42, 67–78. [Google Scholar] [CrossRef]







| Number of Indices | |
|---|---|
| (3,5) | 6q |
| (4,4) | 2pq − q |
| (4,5) | 6q (2p − 1) |
| (5,5) | 4pq |
| Irregularity Indices | p = 1, q = 1 | p = 2, q = 2 | p =3, q = 3 | p = 4, q = 4 | p = 5, q = 5 |
|---|---|---|---|---|---|
| 7.40 | 22.20 | 44.40 | 74 | 111 | |
| 18 | 60 | 126 | 216 | 330 | |
| 4.41 | 14.17 | 29.28 | 49.75 | 75.58 | |
| 5.50 | 17 | 34.50 | 58 | 87.50 | |
| 2.89 | 11.15 | 24.78 | 43.77 | 68.12 | |
| 30 | 84 | 162 | 264 | 390 | |
| 4.34 | 14 | 29 | 49.34 | 75 | |
| 10.76 | 38.14 | 82.16 | 142.82 | 220.109 | |
| 0.94 | 2.033 | 3.299 | 4.74 | 6.34 | |
| 0.24 | 0.62 | 1.14 | 1.82 | 2.65 | |
| 1.86 | 5.055 | 9.59 | 15.46 | 22.67 | |
| 7.40 | 22.20 | 44.40 | 74 | 111 |
| Number of Indices | |
|---|---|
| (4,4) | |
| (4,5) | |
| (4,6) | |
| (5,5) | |
| (5,6) | |
| (6,6) |
| Irregularity Indices | p = 1, q = 1 | p = 2, q = 2 | p = 3, q = 3 | p = 4, q = 4 | p = 5, q = 5 |
|---|---|---|---|---|---|
| 5.33 | 12.87 | 22.60 | 34.53 | 48.67 | |
| 13 | 32 | 57 | 88 | 125 | |
| 2.6329646 | 6.3598584 | 11.1806814 | 17.0954336 | 24.1041150 | |
| 3.10 | 7.40 | 12.90 | 19.60 | 27.50 | |
| 2.627930 | 6.351306 | 11.170128 | 17.084396 | 24.094110 | |
| 21 | 48 | 81 | 120 | 165 | |
| 2.59 | 6.27 | 11.04 | 16.90 | 23.86 | |
| 7.8601835 | 19.87924 | 36.0571905 | 56.3940140 | 80.8897175 | |
| 0.0438011 | 0.0967118 | 0.1587321 | 0.2298620 | 0.3101015 | |
| 0.106514 | 0.23792 | 0.39423 | 0.57543 | 0.78153 | |
| 1.46734 | 4.0301 | 7.6883 | 12.4420 | 18.2911 | |
| 5.33 | 12.87 | 22.60 | 34.53 | 48.67 |
| Number of Indices | |
|---|---|
| (4,4) | |
| (4,6) | |
| (6,6) |
| Irregularity Indices | p = 1, q = 1 | p = 2, q = 2 | p =3, q = 3 | p = 4, q = 4 | p = 5, q = 5 |
|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | |
| 12 | 24 | 36 | 48 | 60 | |
| 2.44 | 4.87 | 7.30 | 9.75 | 12.17 | |
| 3 | 6 | 9 | 12 | 15 | |
| 2.45 | 4.90 | 7.35 | 9.80 | 12.25 | |
| 24 | 48 | 72 | 96 | 120 | |
| 2.4 | 4.8 | 7.2 | 9.6 | 12 | |
| 6.59 | 13.18 | 19.78 | 26.37 | 32.98 | |
| 0.05051 | 0.10102 | 0.15153 | 0.20204 | 0.2526 | |
| 0.123 | 0.245 | 0.3674 | 0.489 | 0.612 | |
| 1.2122 | 2.4244 | 3.6368 | 4.8490 | 6.0612 | |
| 5 | 10 | 15 | 20 | 25 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Munir, M.; Rafique, S.; Ahmad, H.; Liu, J.-B. Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes. Processes 2019, 7, 678. https://doi.org/10.3390/pr7100678
Yang B, Munir M, Rafique S, Ahmad H, Liu J-B. Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes. Processes. 2019; 7(10):678. https://doi.org/10.3390/pr7100678
Chicago/Turabian StyleYang, Bin, Mobeen Munir, Shazia Rafique, Haseeb Ahmad, and Jia-Bao Liu. 2019. "Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes" Processes 7, no. 10: 678. https://doi.org/10.3390/pr7100678
APA StyleYang, B., Munir, M., Rafique, S., Ahmad, H., & Liu, J.-B. (2019). Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes. Processes, 7(10), 678. https://doi.org/10.3390/pr7100678






