1. Introduction
Reactive transport models have been commonly used to simulate the fate and transport of contaminants in both laboratory and field-scale problems. The accuracy and reliability of these models would strongly depend on the values of model parameters, which are commonly estimated from controlled laboratory and/or field experiments. These experiments are often conducted by isolating certain reaction steps to fully understand the complex biogeochemical interactions occurring in the subsurface. The experimental data obtained from the laboratory experiments are then used to formulate a general bio-kinetic or geochemical models that can describe contaminant transformation processes. Once the process model is formulated, several unknown parameters in the overall model are usually estimated by a trial and error process to minimize the sum-squared errors between the experimental data and the model fitted data [
1,
2,
3,
4]. The trial-and-error process, however, could become inefficient as the number of unknown parameters in the model increases. Therefore, some type of numerical inverse routine is employed (e.g., CXTFIT [
5]) to automatically estimate these unknown model parameters. Unfortunately, several of these inverse methods can converge to a local minimum and their overall performance depends on the robustness of the search algorithm and the choice of the initial parameters supplied by the user [
5]. Doherty and Hunt [
6] developed a robust parameter estimator, PEST, for solving highly parameterized groundwater problems using regularized inversion schemes. Baginska et al. [
7] applied the Annualized Agricultural Nonpoint Source Model (AnnAGNPS) for the prediction of export of nitrogen and phosphorous in Currency Creek of the Sydney Region. In addition, they have also used PEST to determine the sensitivity and importance of the key parameters of the model. Yabusaki et al. [
8] used PEST by coupling with BIOGEOCHEM to automate the calibration procedure in understanding the transport and bioreduction of uranium. Groundwater reactive transport problems are nonlinear with respect to their parameters due to the presence of advection, dispersion, and coupled reaction process. These could create complex objective functions with multiple local minima. Therefore, the parameter estimation models that use gradient-based algorithms perform poorly because they stop at the local minimum [
9]. Genetic algorithms use a random search method that preserves the local minimum and continues searching for the global minimum. These algorithms have been employed in parameter estimation of batch as well as column reactive transport experiments [
10,
11].
Genetic algorithms (GAs) are a branch of evolutionary algorithms developed based on the concept of natural selection and the rearrangement of genetic material [
12]. In the field of groundwater hydrology, the GAs have been used in the optimization of the pumping problem and for the estimation of system parameters in heterogeneous aquifers [
13]. Wang [
14] studied the usefulness of GAs for calibrating rainfall-runoff models with nine parameters and found that the GA was able to attain the global minimum for a hypothetical catchment. Wang and Zheng [
15] have coupled MODFLOW and MT3D with a GA routine to find the optimal pumping and injection rates for a remediation process. They applied the model to a 3D field problem and demonstrated the superiority of their GA solution to an existing solution obtained using a trial-and-error approach. Mulligan and Brown [
16] used a GA to optimize the water quality model parameters and found that it was a useful calibration tool to estimate the least-squares parameters by accumulating useful information about the response surface. Reed et al. [
17] studied GAs to find a theoretical relationship for population size and the number of generations required for convergence in groundwater well monitoring design applications. Giacobbo et al. [
18] investigated the feasibility of using GAs for estimating groundwater contaminant transport parameters for a three-layered one-dimensional saturated flow and transport problem. Singh et al. [
19] presented an interactive GA to solve an inverse problem that estimated the conductivity of a heterogeneous hypothetical aquifer whose value was known a priori. Béranger et al. [
20] coupled a GA with an analytical, one-dimensional, multicomponent, reactive transport model to estimate the first-order decay coefficients and enrichment factors. Singh et al. [
21] developed a novel interactive framework, called the ‘Interactive MultiObjective Genetic Algorithm’ (IMOGA), to solve the groundwater inverse problem considering different sources of quantitative data and qualitative expert knowledge. Massoudieh, Mathew, and Ginn [
10] used a GA to minimize the error between measured and modeled breakthrough data for reactive transport involving Cd, tributyltin and estimated the equilibrium constants. Lee and Heber [
22] combined a GA with biofiltration models to estimate unknown model parameters, and the model was subsequently used to predict ethylene removal efficiencies. Madsen and Perry [
23] coupled a simple GA with MODFLOW to optimize the net groundwater flow into a river by optimizing the following four input parameters: recharge rate, river conductance, and water levels at two general head boundaries. Kontos and Katsifarakis [
24] used genetic algorithms to manage polluted aquifers but they have used a simplified 2D reactive transport model and have also adopted instantaneous dispersion to account for inaccuracies in results generated due to their assumptions.
GAs are computationally intensive routines because they search through a large set of solutions to find the optimal solution. This process can take a substantial amount of time if it is not optimized. Parallel computing techniques can be used to improve the efficiency of GAs by exploiting the concurrency of calculations performed in genetic algorithms. Depending on their architecture, the computers capable of running parallel codes can be classified as either distributed memory computers or shared memory computers [
25]. Most of the earlier work on parallel computing efforts focused on distributed memory computers, where several computers are connected using a fast network to reduce the communication time between the processors to implement parallel genetic algorithms [
26,
27,
28,
29]. In the field of groundwater, McKinney and Lin [
30] used parallel genetic algorithms to solve three groundwater management problems involving maximization of pumping from an aquifer, the minimization of cost for a water supply problem, and minimization of cost for an aquifer remediation problem. They observed that the genetic algorithms performed efficiently to obtain globally optimal solutions and the speedup of the parallel genetic algorithm was almost linear. Tsai et al. [
31] developed a production well management model for water resource management in semi-arid areas by integrating a large-scale pressurized water distribution system management model, EPANET, and a three-dimensional groundwater model, MODFLOW, under a unified optimization framework. They used a 64-processor cluster to run the computer code in a parallel mode.
The speedup on distributed memory computers can be hindered by the communication time between the processors because each processor has its own local memory, which is not available to the other processors; hence, the programmer must manually sync the variables after each generation. However, in shared memory computers, all the processors have access to the same memory and the synchronization step can be avoided [
32]. Sarma and Adeli [
33] used parallel fuzzy genetic algorithms for optimizing steel structures using two different schemes. The authors also presented two bilevel parallel genetic algorithms that combine message passing interface (MPI) and OpenMP programming languages for optimization. They observed almost linear speedup for 16 processors. Fredrickson et al. [
34] evaluated the performance of the parallel genetic algorithm (PGA) using OpenMP constructs, kernels, and application benchmarks on large-scale symmetric multiprocessing (SMP) systems using a 72 node Sun Fire 15k SMP node. They reported the basic timings, scalability, and run times for different parallel regions.
GAs are robust algorithms that have been proven to be suitable for solving different types of parameter estimation problems using an appropriate encoding method. The process by which a population is coded into a suitable form that enables genetic recombination is called encoding. The early studies of GA in reactive transport problems are limited by their usage of binary encoding, especially when the parameters of different magnitudes are present [
10,
13]. Also, most of these algorithms have been optimized to solve a single problem and their ability to run different kinds of reactive transport problems has not been explored. Moreover, none of these studies considered optimizing the implementation of parallel GAs for multicore personal computers that use shared memory architecture.
Shared memory, multicore PCs have become common computational platforms in recent years with the introduction of Intel and AMD multicore processors in desktop and laptop computers. These multicore systems are powerful processors that can be used to improve the efficiency of current GA algorithms by implementing them using shared memory and a parallel computing language such as OpenMP FORTRAN. Based on our literature review, we found that only a limited amount of information is available in the hydrogeology literature in analyzing problems in an OpenMP platform to optimally use a GA for estimating model parameters in multicomponent reactive transport models. The objective of this study is to develop a general parallel genetic algorithm (PGA) that can estimate both transport and kinetic parameters in reactive transport models. We coupled the FORTRAN version of the one-dimensional multispecies reactive transport model, RT1D [
35] with the genetic algorithm for parameter estimation. The performance of the PGA was compared using four different benchmark problems and the speedup for the PGA using four threads on a desktop computer is also presented.
4. Summary and Conclusions
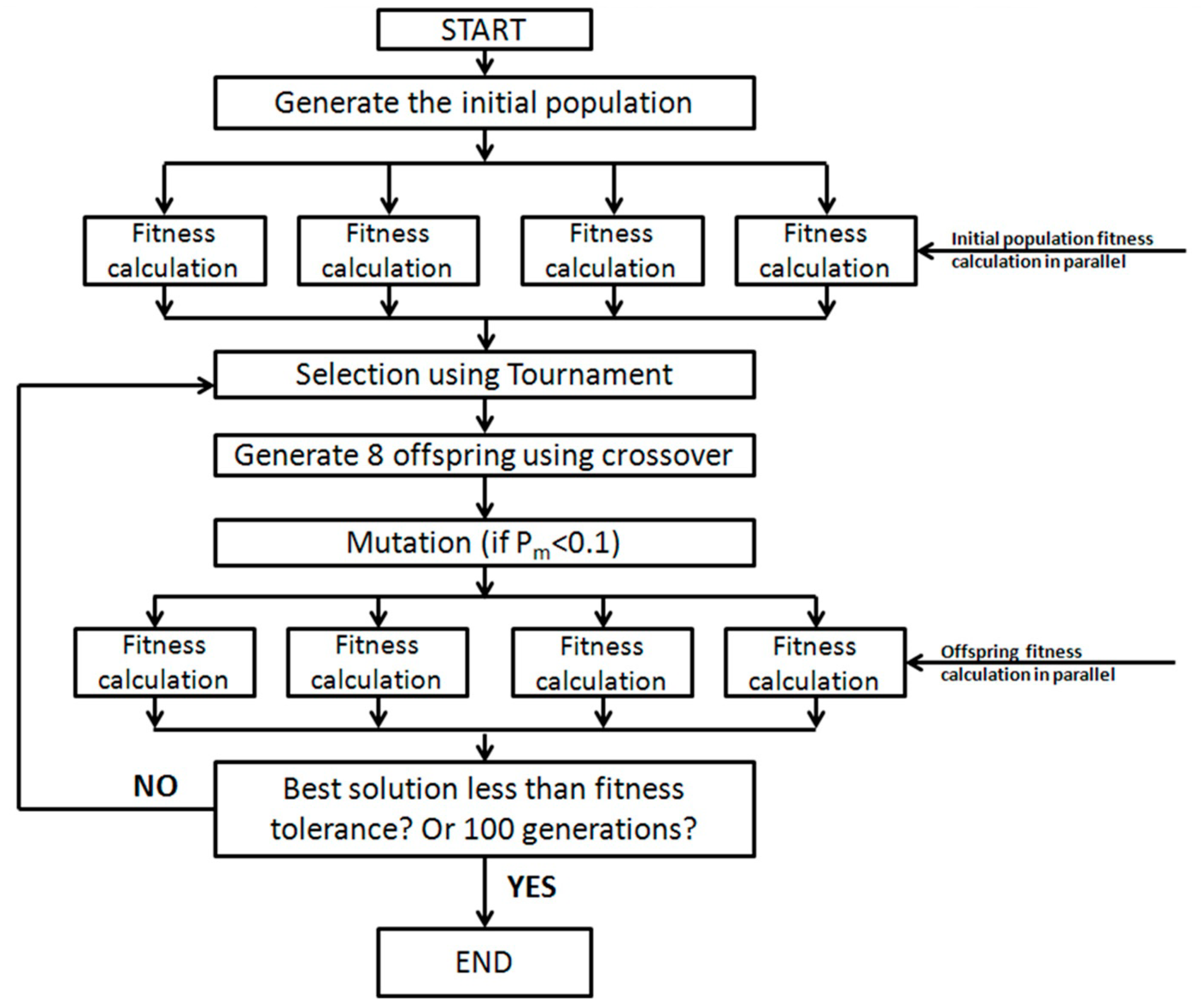
In this study, we coupled a PGA with a one-dimensional multicomponent reactive transport model, RT1D, to develop a parameter estimation tool. PGA can directly use the existing forward model with randomly generated initial population to converge to the best fit parameter. The presence of randomness in the initial population and their ability to preserve the best solutions enables them to search through a vast population to find the global minimum. In addition, the algorithm can also be parallelized since the fitness calculations can be performed simultaneously on separate processors. This allows for a significant reduction in program runtime where the fitness calculations are computationally intensive.
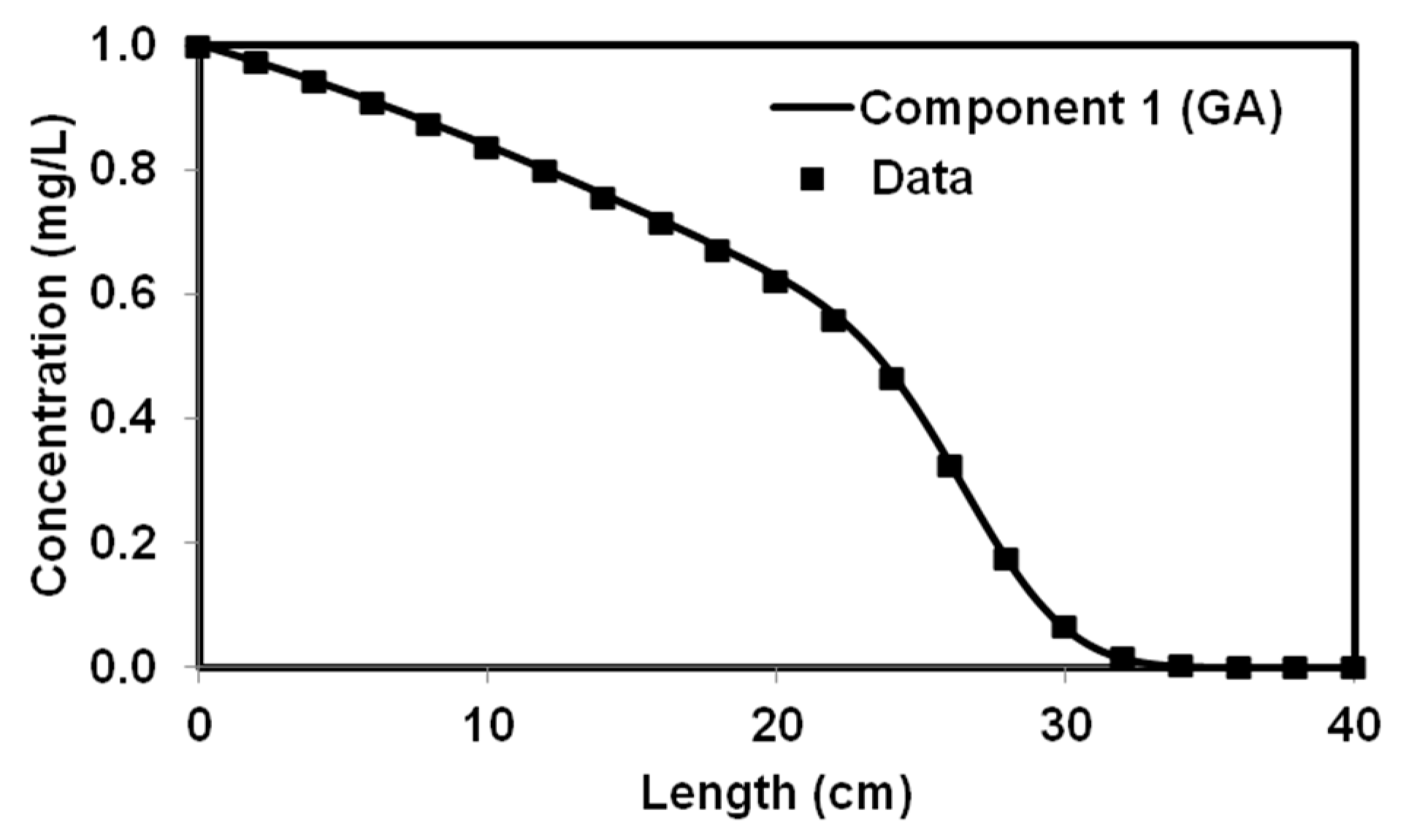
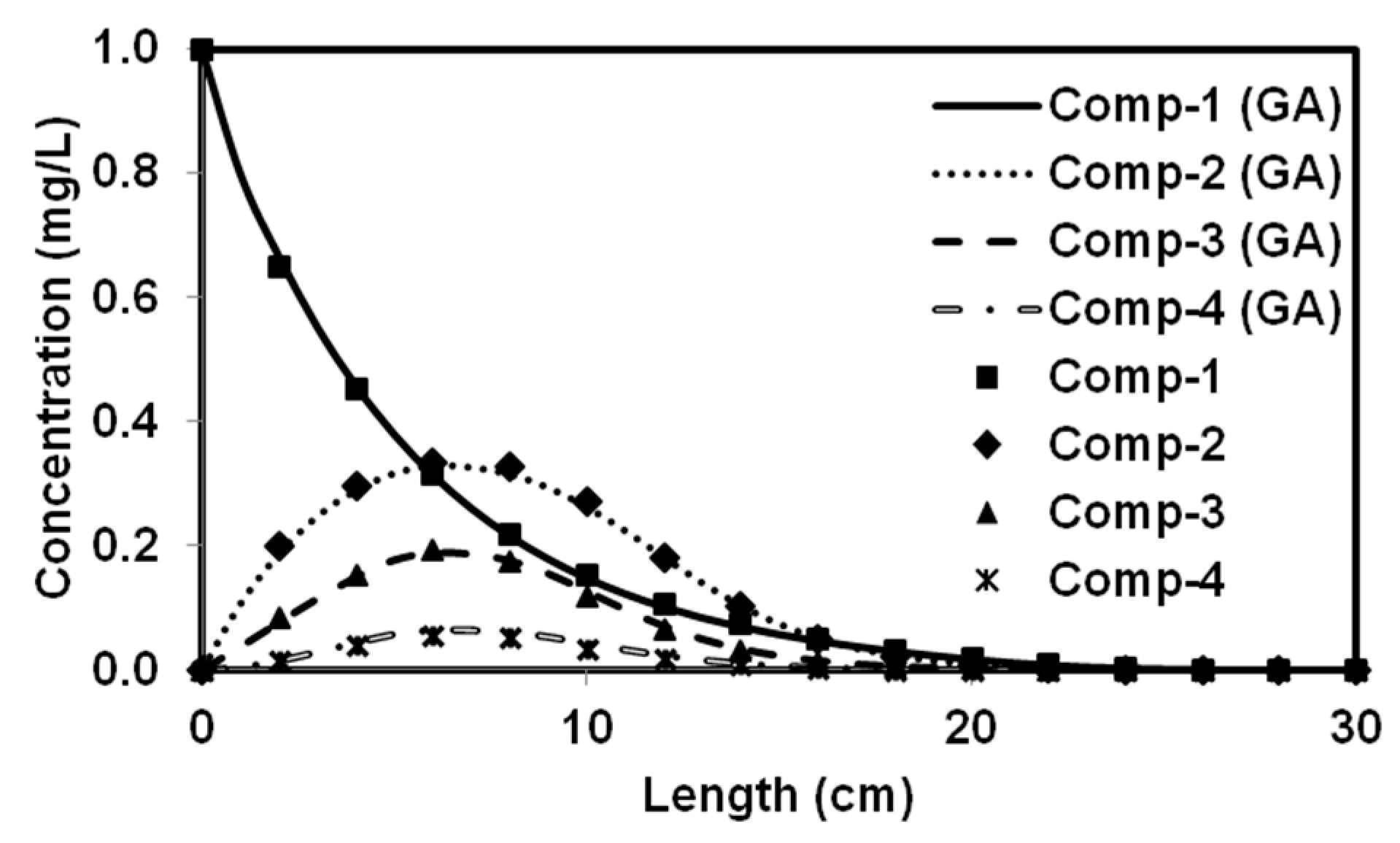
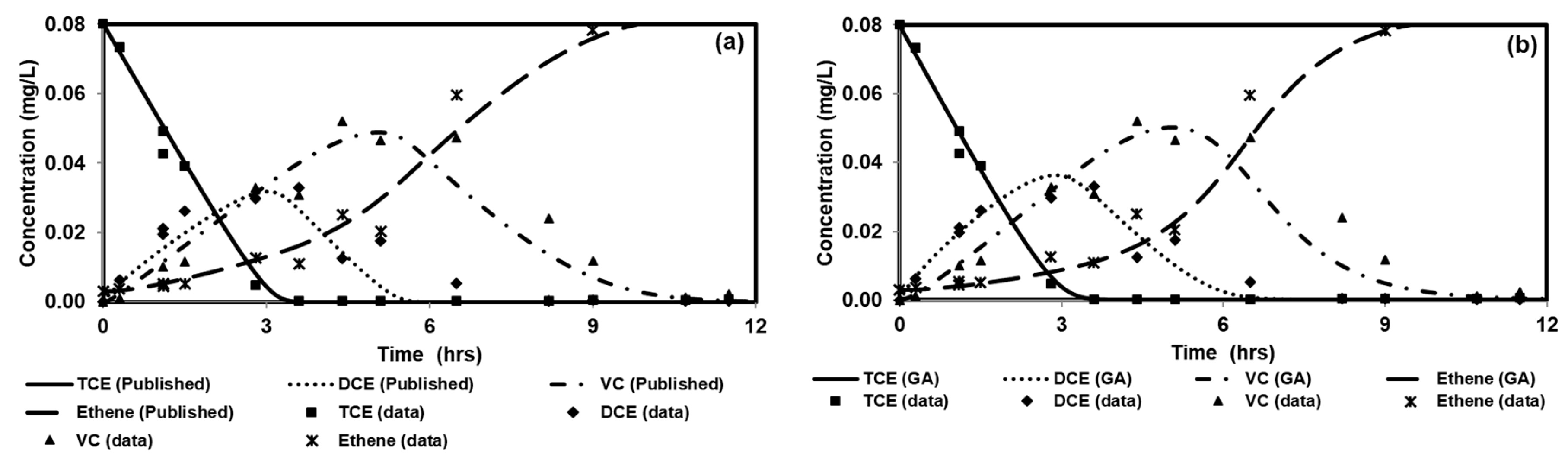
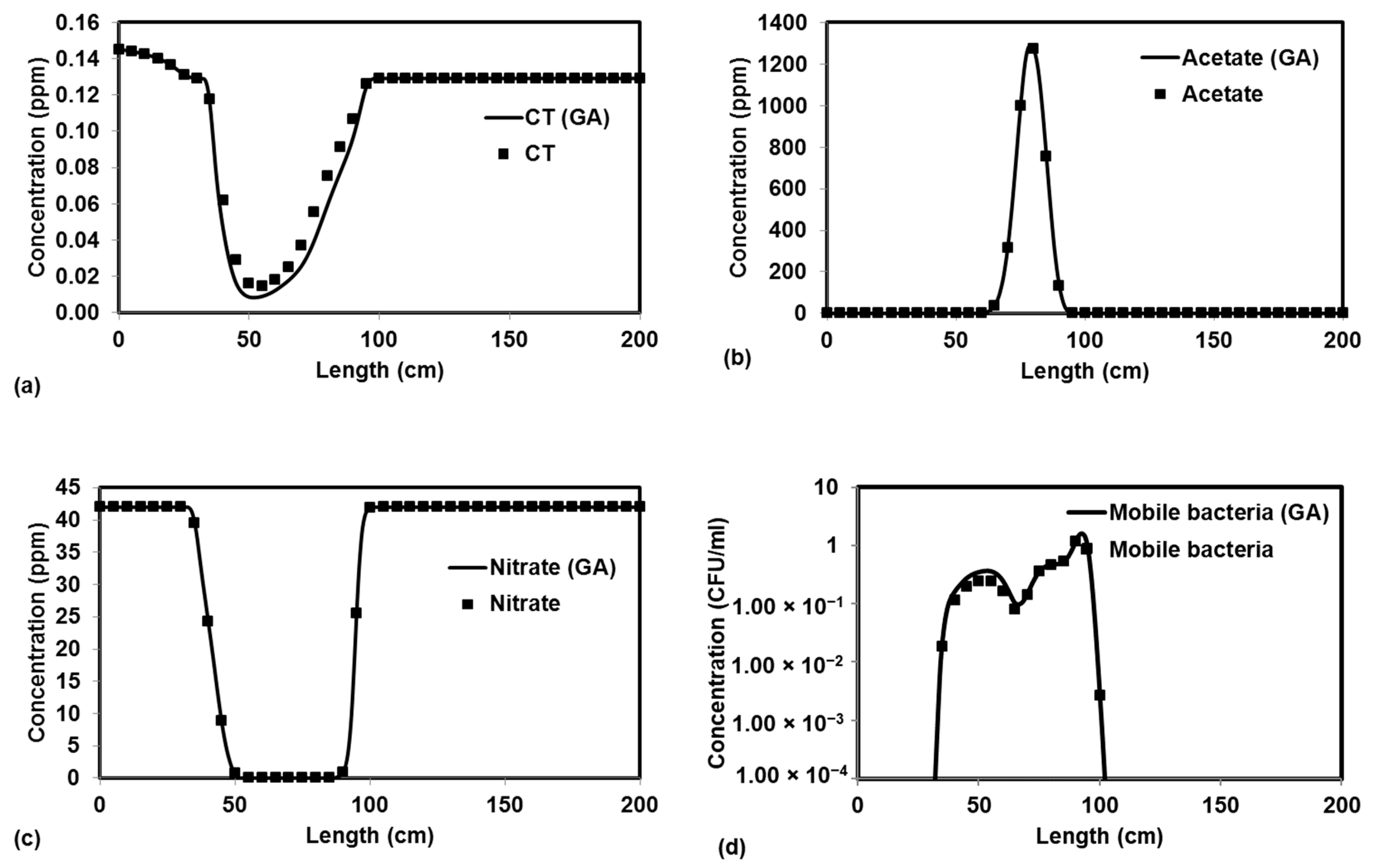
We tested the performance of a parallel version of PGA by solving four benchmark problems that simulated both batch and reactive-transport scenarios. The benchmark problems chosen to test the performance of the algorithm have analytical solutions and published numerical solutions. The PGA algorithm was able to reproduce the model parameters with minimum error for both analytical benchmark problems. Furthermore, the simulation results from these parameters were able to match the original experimental or analytical/numerical data well. For benchmark problems 3 and 4, the PGA was provided with the experimental data as the input and we were able to fit the data well in both cases. Particularly, for benchmark problem 3 where the trial-and-error method was used, we were able to show better fitness than the original model. The PGA presented in this study was versatile and did not require any problem-specific modifications except for the kinetic equations which were solved by the one-dimensional reactive transport model, RT1D.
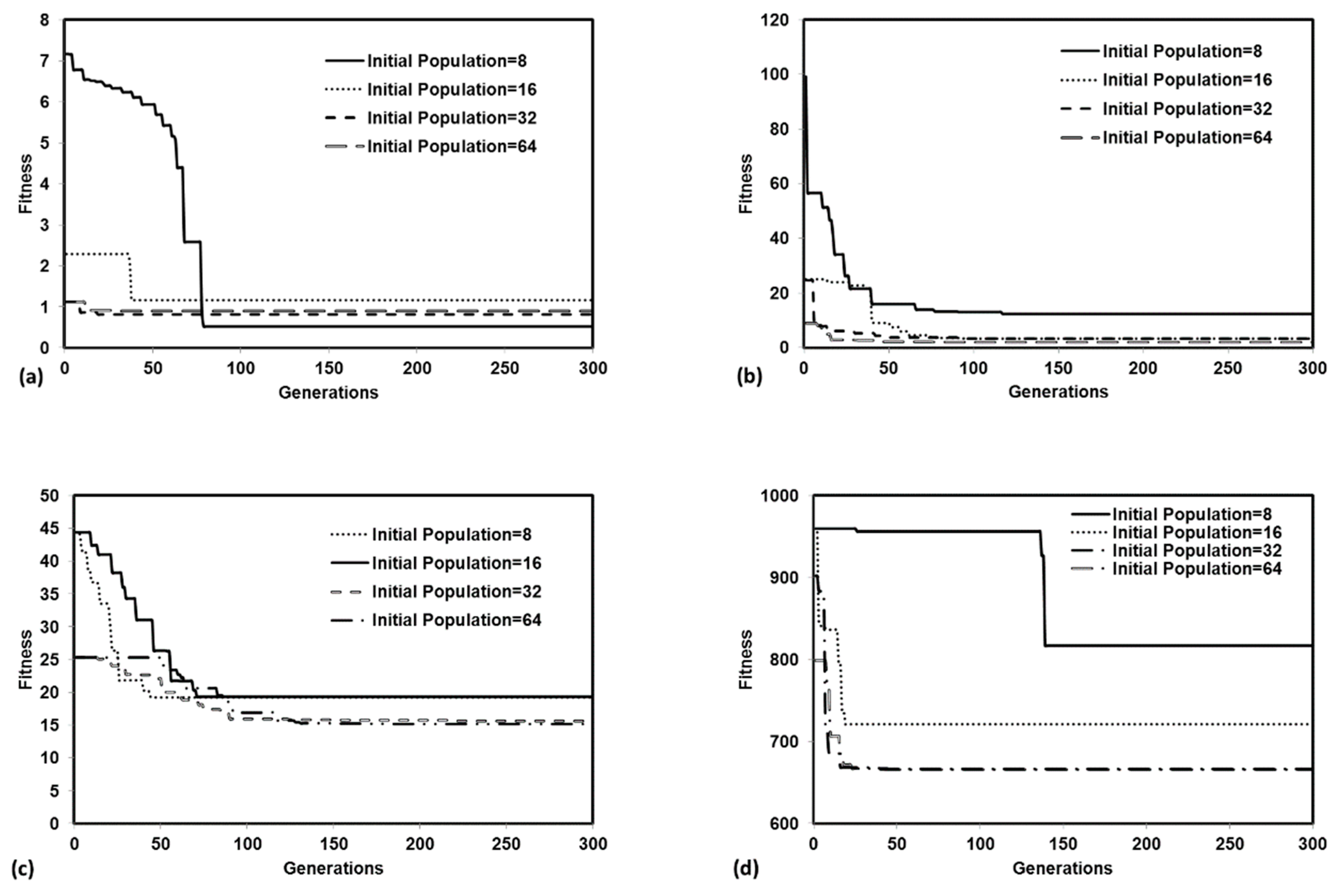
Sensitivity studies show that our model is sensitive to the initial bounds for each parameter when the difference in the order of magnitudes for the lower and higher bounds was too large. For the benchmark problems tested in the study, the lower and higher bounds were at least one order of magnitude higher. The observed trends in the sensitivity studies were still within the margin of error for two orders of magnitude but were particularly worse when the difference in the order of magnitudes was three times (scenario 4). In most real cases, the user should have access to the order of magnitude for the unknown parameters from the literature. This could potentially be a limitation if the unknown parameter does not have published values. However, the model can be calibrated by starting with a larger bound and can be refined with multiple iterations. The user should, however, be careful not to overconstrain the problem and ensure that the upper and lower parameter bounds are adequately large to generate enough initial solutions to avoid convergence to a local optimum. Parameter estimation techniques are used to minimize the objective function and present solutions. Doherty and Hunt [
6] discuss the importance of user expertise in determining the feasibility of solutions as well as constraining the optimization problem. If more parameters are estimated than the valid dimension, it is possible that we increase the number of feasible solutions. The uncertainty of parameters in groundwater reactive transport problems is further discussed in Shi et al. [
9].
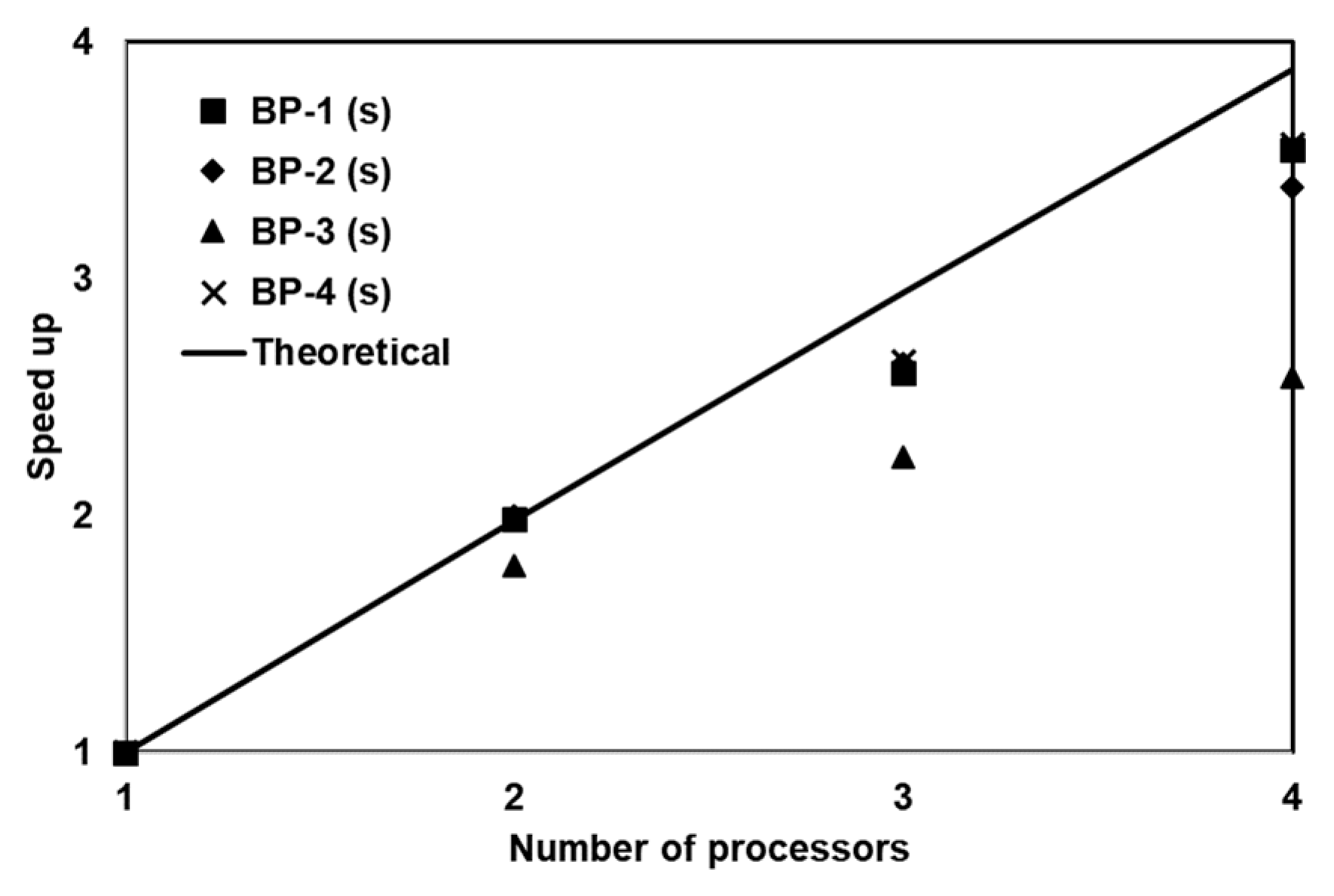
The PGA was optimized to run in the parallel mode using the OpenMP framework available within the Intel FORTRAN v9.0 compiler on a shared memory system. The speedup was quantified for four benchmark problems and the results indicate close to linear speedup for three benchmark problems. The fourth benchmark (designated as Problem 3) was a much simpler problem that required very little computational effort and hence the parallel computing steps did not reduce the overall computational time. These results show that the use of PGA was more appropriate for solving computationally intensive reactive transport problems. The overall computational gain obtained using this hardware was significant. Since most modern desktop PCs are now equipped with multicore processors, the methods used in this study can be easily adapted to take advantage of these platforms. The proposed optimization framework, which was used for estimating unknown kinetic and transport parameters in our multicomponent reactive transport problems, is a generic procedure that can be adapted to solve a variety of water quality problems. In addition, these benchmark problems can be used by other researchers to compare their optimization algorithms.