Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization
Abstract
1. Introduction
2. Integrating CFD-Based Compartmental Model with Surrogate Based Optimization
2.1. CFD-Based Compartmental Model
2.1.1. A Brief Review of Compartmental Model
2.1.2. Compartmental Model Development
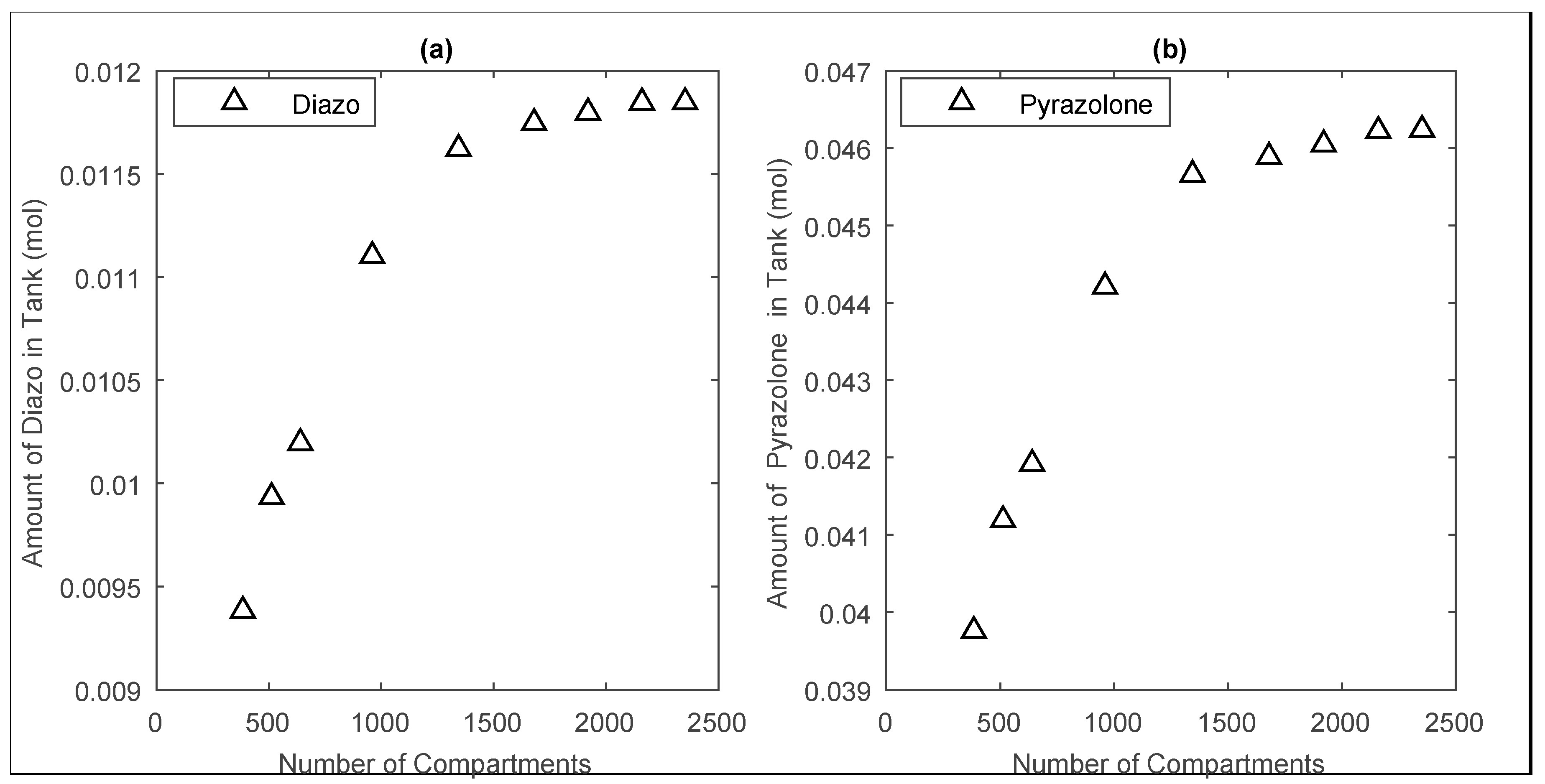
2.1.3. Grid Independence
2.2. Surrogate-Based Optimization
2.2.1. A Brief Review of Surrogate-Based Optimization
2.2.2. Problem Formulation
3. Case Study
3.1. Reactor Setup
3.2. Chemical Kinetics
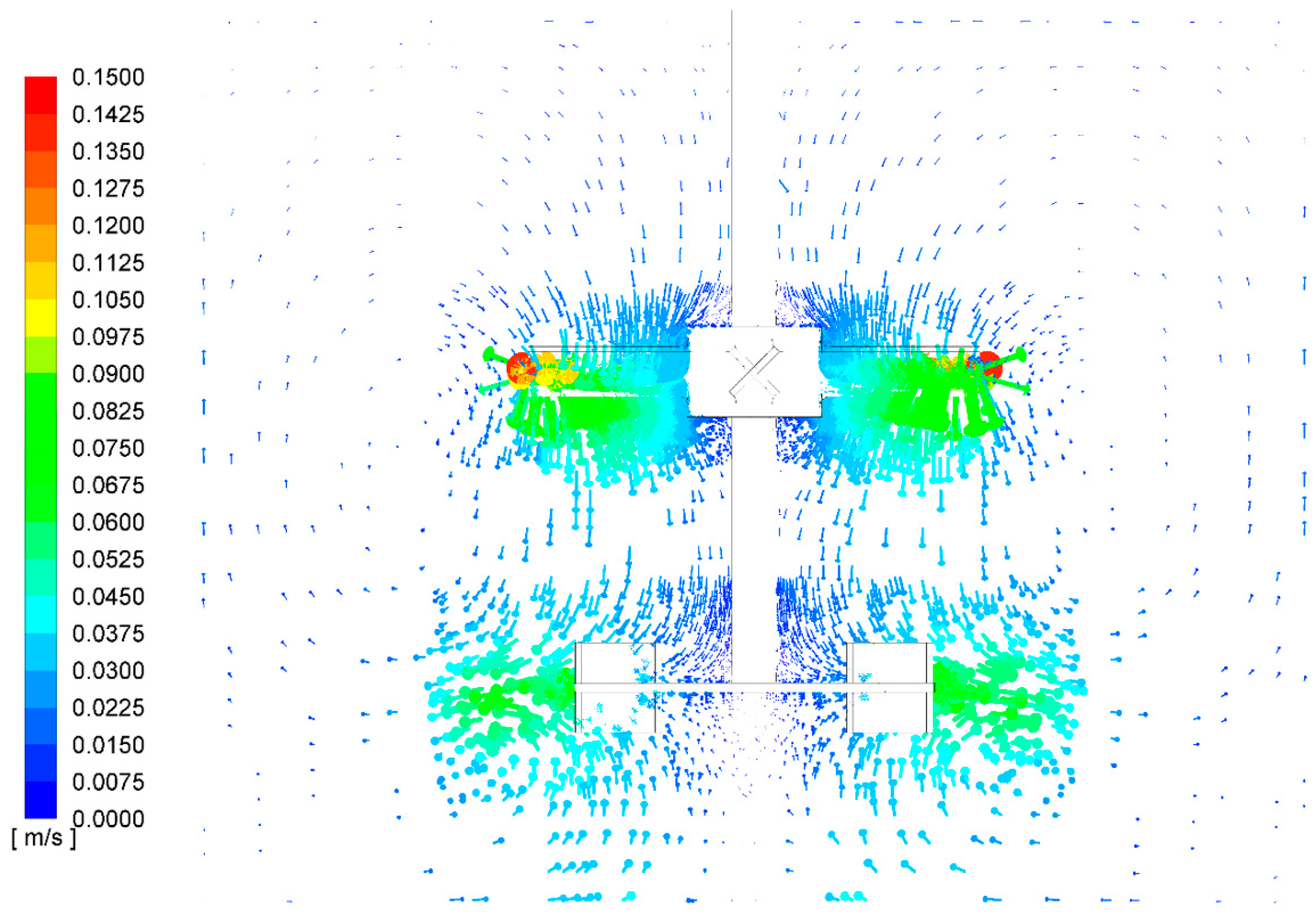
3.3. Flow Field Simulation
3.4. Compartmental Modeling and Grid Independence Test
3.5. Optimization and Results
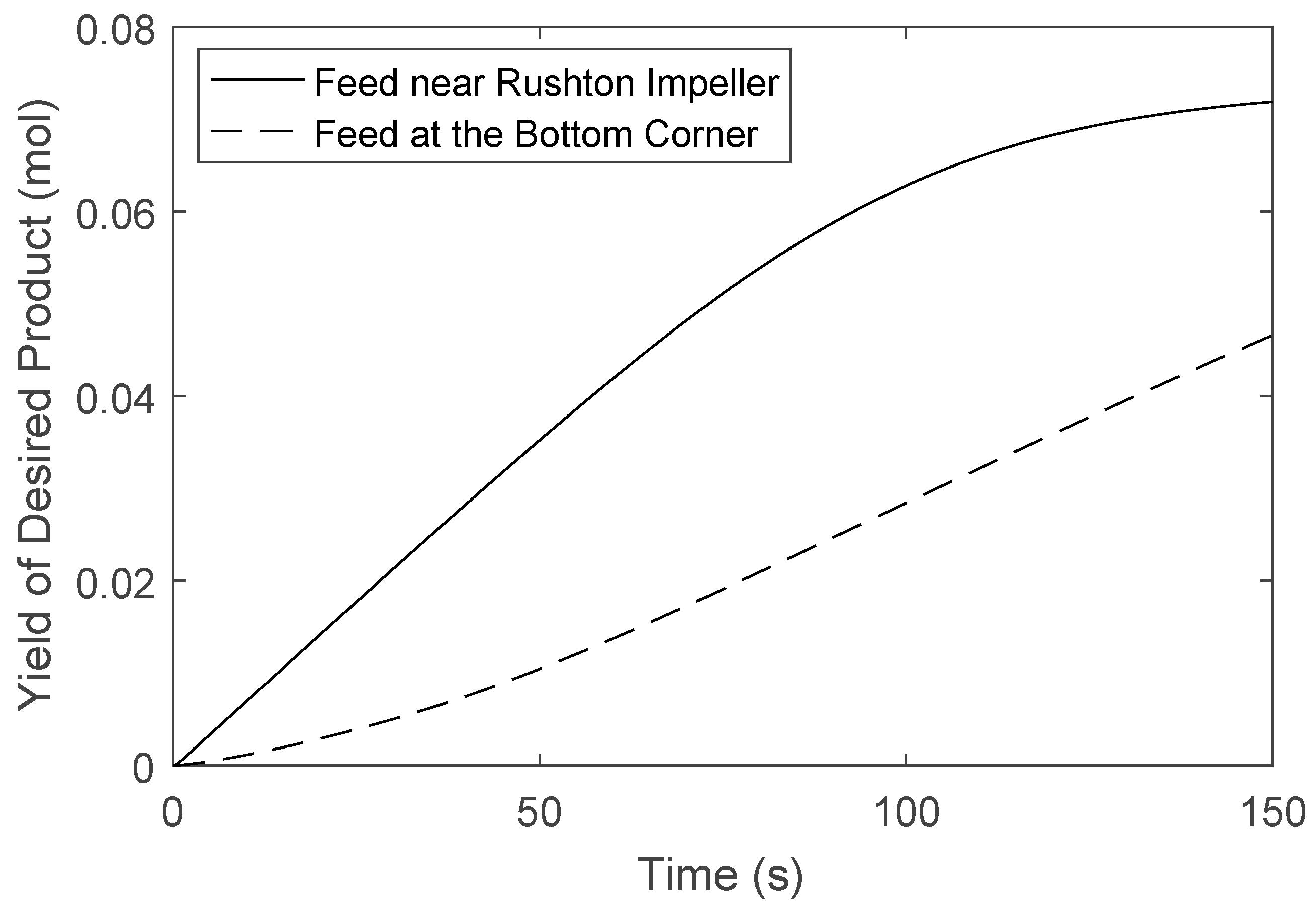
3.5.1. Optimal Location of Feeding
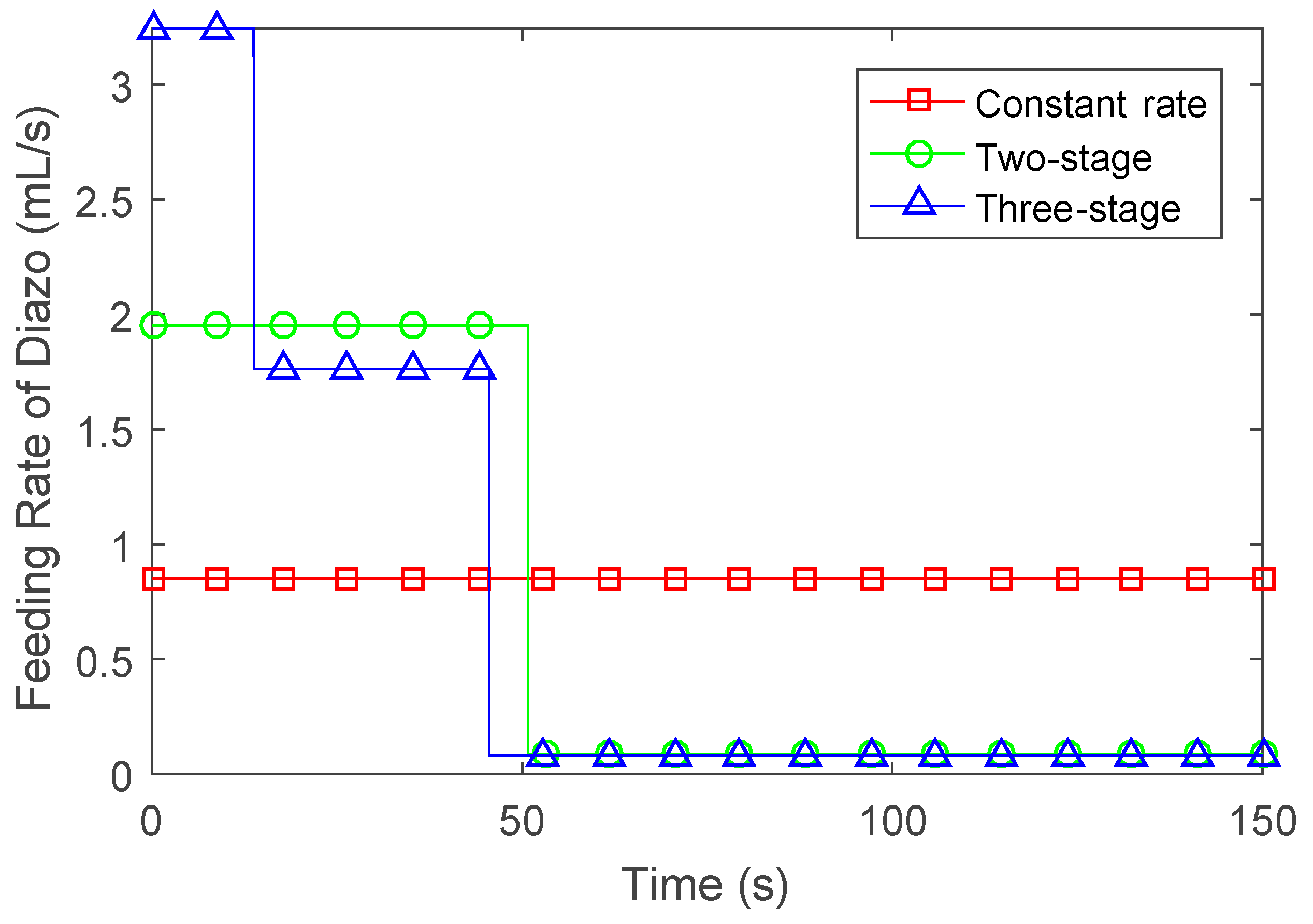
3.5.2. Optimal Rate of Feeding
3.5.3. Traditional Process Design with Perfect-Mixing Assumptions
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CPP | Critical process parameters |
| CFD | Computational fluid dynamics |
| QbD | Quality by design |
| RTD | Residence time distribution |
| GA | Genetic algorithm |
| RBF | Radial basis function |
| CMC | Chemistry, manufacturing, and controls |
| ANN | Artificial neural network |
| RANS | Reynolds averaged Navier-Stocks |
| MRF | Multi-reference frame |
| API | Active pharmaceutical ingredient |
| SBO | Surrogate-based opitmization |
| List of Symbols: | |
| c | Concentration |
| N | Mass flux |
| D | Diffusivity |
| R | Source |
| V | Volume |
| S | Surface area |
| Q | Mass flow rate |
| Da | Damköhler number |
| Pe | Péclet number |
| k | Reaction rate constant |
| L | Characteristic length |
| u | Characteristic velocity |
| P | Price |
| y | Yield |
| Ns | Number of feeding stages |
| Nc | Number of compartments |
| t | Duration |
| f | Feed rate |
| Subscripts: | |
| i | ith species |
| j | jth compartment |
| m | mth stage of operation |
References
- Plutschack, M.B.; Pieber, B.; Gilmore, K.; Seeberger, P.H. The Hitchhiker’s Guide to Flow Chemistry(II). Chem. Rev. 2017, 117, 11796–11893. [Google Scholar] [CrossRef]
- Gobert, S.R.L.; Kuhn, S.; Braeken, L.; Thomassen, L.C.J. Characterization of Milli- and Microflow Reactors: Mixing Efficiency and Residence Time Distribution. Org. Process. Res. Dev. 2017, 21, 531–542. [Google Scholar] [CrossRef]
- Fogler, H.S. Essentials of Chemical Reaction Engineering; Pearson Education: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Gresch, M.; Brugger, R.; Meyer, A.; Gujer, W. Compartmental Models for Continuous Flow Reactors Derived from CFD Simulations. Environ. Sci. Technol. 2009, 43, 2381–2387. [Google Scholar] [CrossRef]
- Nienow, A.W. On impeller circulation and mixing effectiveness in the turbulent flow regime. Chem. Eng. Sci. 1997, 52, 2557–2565. [Google Scholar] [CrossRef]
- Rosseburg, A.; Fitschen, J.; Wutz, J.; Wucherpfennig, T.; Schluter, M. Hydrodynamic inhomogeneities in large scale stirred tanks–Influence on mixing time. Chem. Eng. Sci. 2018, 188, 208–220. [Google Scholar] [CrossRef]
- Levesque, F.; Bogus, N.J.; Spencer, G.; Grigorov, P.; McMullen, J.P.; Thaisrivongs, D.A.; Davies, I.W.; Naber, J.R. Advancing Flow Chemistry Portability: A Simplified Approach to Scaling Up Flow Chemistry. Org. Process. Res. Dev. 2018, 22, 1015–1021. [Google Scholar] [CrossRef]
- Aubin, J.; Ferrando, M.; Jiricny, V. Current methods for characterising mixing and flow in microchannels. Chem. Eng. Sci. 2010, 65, 2065–2093. [Google Scholar] [CrossRef]
- Commenge, J.M.; Falk, L. Villermaux-Dushman protocol for experimental characterization of micromixers. Chem. Eng. Process. 2011, 50, 979–990. [Google Scholar] [CrossRef]
- Reckamp, J.M.; Bindels, A.; Duffield, S.; Liu, Y.C.; Bradford, E.; Ricci, E.; Susanne, F.; Rutter, A. Mixing Performance Evaluation for Commercially Available Micromixers Using Villermaux-Dushman Reaction Scheme with the Interaction by Exchange with the Mean Model. Org. Process. Res. Dev. 2017, 21, 816–820. [Google Scholar] [CrossRef]
- Cheng, D.; Feng, X.; Cheng, J.C.; Yang, C. Numerical simulation of macro-mixing in liquid-liquid stirred tanks. Chem. Eng. Sci. 2013, 101, 272–282. [Google Scholar] [CrossRef]
- Liu, L.; Barigou, M. Experimentally Validated Computational Fluid Dynamics Simulations of Multicomponent Hydrodynamics and Phase Distribution in Agitated High Solid Fraction Binary Suspensions. Ind. Eng. Chem. Res. 2014, 53, 895–908. [Google Scholar] [CrossRef]
- Reinecke, S.F.; Deutschmann, A.; Jobst, K.; Hampel, U. Macro-mixing characterisation of a stirred model fermenter of non-Newtonian liquid by flow following sensor particles and ERT. Chem. Eng. Res. Des. 2017, 118, 1–11. [Google Scholar] [CrossRef]
- Warmeling, H.; Behr, A.; Vorholt, A.J. Jet loop reactors as a versatile reactor set up—Intensifying catalytic reactions: A review. Chem. Eng. Sci. 2016, 149, 229–248. [Google Scholar] [CrossRef]
- Farzan, P.; Ierapetritou, M.G. Integrated modeling to capture the interaction of physiology and fluid dynamics in biopharmaceutical bioreactors. Comput. Chem. Eng. 2017, 97, 271–282. [Google Scholar] [CrossRef]
- Foli, K.; Okabe, T.; Olhofer, M.; Jin, Y.C.; Sendhoff, B. Optimization of micro heat exchanger: CFD, analytical approach and multi-objective evolutionary algorithms. Int. J. Heat Mass Transf. 2006, 49, 1090–1099. [Google Scholar] [CrossRef]
- Uebel, K.; Rößger, P.; Prüfert, U.; Richter, A.; Meyer, B. CFD-based multi-objective optimization of a quench reactor design. Fuel Process. Technol. 2016, 149, 290–304. [Google Scholar] [CrossRef]
- Chen, M.; Wang, J.; Zhao, S.; Xu, C.; Feng, L. Optimization of Dual-Impeller Configurations in a Gas–Liquid Stirred Tank Based on Computational Fluid Dynamics and Multiobjective Evolutionary Algorithm. Ind. Eng. Chem. Res. 2016, 55, 9054–9063. [Google Scholar] [CrossRef]
- Na, J.; Kshetrimayum, K.S.; Lee, U.; Han, C. Multi-objective optimization of microchannel reactor for Fischer-Tropsch synthesis using computational fluid dynamics and genetic algorithm. Chem. Eng. J. 2017, 313, 1521–1534. [Google Scholar] [CrossRef]
- De-Sheng, Z.; Jian, C.; Wei-Dong, S.H.I.; Lei, S.H.I.; Lin-Lin, G. Optimization of hydrofoil for tidal current turbine based on particle swarm optimization and computational fluid dynamic ethod. Thermal Sci. 2016, 20, 907–912. [Google Scholar]
- Sierra-Pallares, J.; del Valle, J.G.; Paniagua, J.M.; Garcia, J.; Mendez-Bueno, C.; Castro, F. Shape optimization of a long-tapered R134a ejector mixing chamber. Energy 2018, 165, 422–438. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of cyclone separators with eccentric vortex finders using large eddy simulation and artificial neural network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Jung, I.; Kshetrimayum, K.S.; Park, S.; Na, J.; Lee, Y.; An, J.; Park, S.; Lee, C.-J.; Han, C. Computational Fluid Dynamics Based Optimal Design of Guiding Channel Geometry in U-Type Coolant Layer Manifold of Large-Scale Microchannel Fischer–Tropsch Reactor. Ind. Eng. Chem. Res. 2016, 55, 505–515. [Google Scholar] [CrossRef]
- Park, S.; Na, J.; Kim, M.; Lee, J.M. Multi-objective Bayesian optimization of chemical reactor design using computational fluid dynamics. Comput. Chem. Eng. 2018, 119, 25–37. [Google Scholar] [CrossRef]
- Rößger, P.; Richter, A. Performance of different optimization concepts for reactive flow systems based on combined CFD and response surface methods. Comput. Chem. Eng. 2018, 108, 232–239. [Google Scholar] [CrossRef]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.-T. Learning from Dat; AMLBook: New York, NY, USA, 2012; Volume 4. [Google Scholar]
- Kapsoulis, D.; Tsiakas, K.; Trompoukis, X.; Asouti, V.; Giannakoglou, K. A PCA-assisted hybrid algorithm combining EAs and adjoint methods for CFD-based optimization. Appl. Soft. Comput. 2018, 73, 520–529. [Google Scholar] [CrossRef]
- Muller, J.; Shoemaker, C.A.; Piche, R. SO-MI: A surrogate model algorithm for computationally expensive nonlinear mixed-integer black-box global optimization problems. Comput. Oper. Res. 2013, 40, 1383–1400. [Google Scholar] [CrossRef]
- Boltersdorf, U.; Deerberg, G.; SCHLÜTER, S. Computational study of the effects of process parameters on the product distribution for mixing sensitive reactions and on distribution of gas in stirred tank reactors. Recent Res. Dev. Chem. Eng. 2000, 4, 15–43. [Google Scholar]
- Guha, D.; Dudukovic, M.P.; Ramachandran, P.A.; Mehta, S.; Alvare, J. CFD-based compartmental modeling of single phase stirred-tank reactors. AlChE J. 2006, 52, 1836–1846. [Google Scholar] [CrossRef]
- Nørregaard, A.; Bach, C.; Krühne, U.; Borgbjerg, U.; Gernaey, K.V. Hypothesis-driven compartment model for stirred bioreactors utilizing computational fluid dynamics and multiple pH sensors. Chem. Eng. J. 2019, 356, 161–169. [Google Scholar] [CrossRef]
- Zhao, W.; Buffo, A.; Alopaeus, V.; Han, B.; Louhi-Kultanen, M. Application of the compartmental model to the gas-liquid precipitation of CO2-Ca(OH)2 aqueous system in a stirred tank. AlChE J. 2017, 63, 378–386. [Google Scholar] [CrossRef]
- Bezzo, F.; Macchietto, S.; Pantelides, C.C. A general methodology for hybrid multizonal/CFD models. Comput. Chem. Eng. 2004, 28, 501–511. [Google Scholar] [CrossRef]
- Vrabel, P.; van der Lans, R.; Cui, Y.Q.; Luyben, K. Compartment model approach: Mixing in large scale aerated reactors with multiple impellers. Chem. Eng. Res. Des. 1999, 77, 291–302. [Google Scholar] [CrossRef]
- Du, J.; Johansen, T.A. Integrated Multilinear Model Predictive Control of Nonlinear Systems Based on Gap Metric. Ind. Eng. Chem. Res. 2015, 54, 6002–6011. [Google Scholar] [CrossRef]
- Srilatha, C.; Morab, V.V.; Mundada, T.P.; Patwardhan, A.W. Relation between hydrodynamics and drop size distributions in pump–mix mixer. Chem. Eng. Sci. 2010, 65, 3409–3426. [Google Scholar] [CrossRef]
- Bezzo, F.; Macchietto, S. A general methodology for hybrid multizonal/CFD models—Part II. Automatic zoning. Comput. Chem. Eng. 2004, 28, 513–525. [Google Scholar] [CrossRef]
- Nienow, A.W.; Drain, S.M.; Boyes, A.P.; Mann, R.; El-Hamouz, A.M.; Carpenter, K.J. A new pair of reactions to characterize imperfect macro-mixing and partial segregation in a stirred semi-batch reactor. Chem. Eng. Sci. 1992, 47, 2825–2830. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Introduction to Derivative-Free Optimization; Siam: Philadelphia, PA, USA, 2009. [Google Scholar]
- Boukouvala, F.; Misener, R.; Floudas, C.A. Global optimization advances in Mixed-Integer Nonlinear Programming, MINLP, and Constrained Derivative-Free Optimization, CDFO. Eur. J. Oper. Res. 2016, 252, 701–727. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Improved strategies for radial basis function methods for global optimization. J. Glob. Optim. 2007, 37, 113–135. [Google Scholar] [CrossRef]
- Oeuvray, R.; Bierlaire, M. BOOSTERS: A derivative-free algorithm based on radial basis functions. Int. J. Model. Simul. 2009, 29, 26–36. [Google Scholar] [CrossRef]
- Wild, S.M.; Shoemaker, C.A. Global Convergence of Radial Basis Function Trust-Region Algorithms for Derivative-Free Optimization. SIAM Rev. 2013, 55, 349–371. [Google Scholar] [CrossRef]
- Regis, R.G.; Wild, S.M. CONORBIT: constrained optimization by radial basis function interpolation in trust regions. Optim. Meth. Softw. 2017, 32, 552–580. [Google Scholar] [CrossRef]
- Wang, Z.L.; Ierapetritou, M. A novel feasibility analysis method for black-box processes using a radial basis function adaptive sampling approach. AlChE J. 2017, 63, 532–550. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Boukouvala, F.; Ierapetritou, M.G. Derivative-free optimization for expensive constrained problems using a novel expected improvement objective function. AlChE J. 2014, 60, 2462–2474. [Google Scholar] [CrossRef]
- Regis, R.G. Trust regions in Kriging-based optimization with expected improvement. Eng. Optim. 2016, 48, 1037–1059. [Google Scholar] [CrossRef]
- Beykal, B.; Boukouvala, F.; Floudas, C.A.; Sorek, N.; Zalavadia, H.; Gildin, E. Global optimization of grey-box computational systems using surrogate functions and application to highly constrained oil-field operations. Comput. Chem. Eng. 2018, 114, 99–110. [Google Scholar] [CrossRef]
- Wang, Z.L.; Ierapetritou, M. Constrained optimization of black-box stochastic systems using a novel feasibility enhanced Kriging-based method. Comput. Chem. Eng. 2018, 118, 210–223. [Google Scholar] [CrossRef]
- Fernandes, F.A.N. Optimization of Fischer-Tropsch synthesis using neural networks. Chem. Eng. Technol. 2006, 29, 449–453. [Google Scholar] [CrossRef]
- Henao, C.A.; Maravelias, C.T. Surrogate-Based Superstructure Optimization Framework. AlChE J. 2011, 57, 1216–1232. [Google Scholar] [CrossRef]
- Sen, O.; Gaul, N.J.; Choi, K.K.; Jacobs, G.; Udaykumar, H.S. Evaluation of multifidelity surrogate modeling techniques to construct closure laws for drag in shock-particle interactions. J. Comput. Phys. 2018, 371, 434–451. [Google Scholar] [CrossRef]
- Müller, J. MISO: mixed-integer surrogate optimization framework. Optim. Eng. 2015, 17, 177–203. [Google Scholar] [CrossRef]
- Zhang, W.P.; Wang, X.; Feng, X.; Yang, C.; Mao, Z.S. Investigation of Mixing Performance in Passive Micromixers. Ind. Eng. Chem. Res. 2016, 55, 10036–10043. [Google Scholar] [CrossRef]
- Lin, X.Y.; Wang, K.; Zhang, J.S.; Luo, G.S. Liquid-liquid mixing enhancement rules by microbubbles in three typical micro-mixers. Chem. Eng. Sci. 2015, 127, 60–71. [Google Scholar] [CrossRef]
- Fluent, A. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]

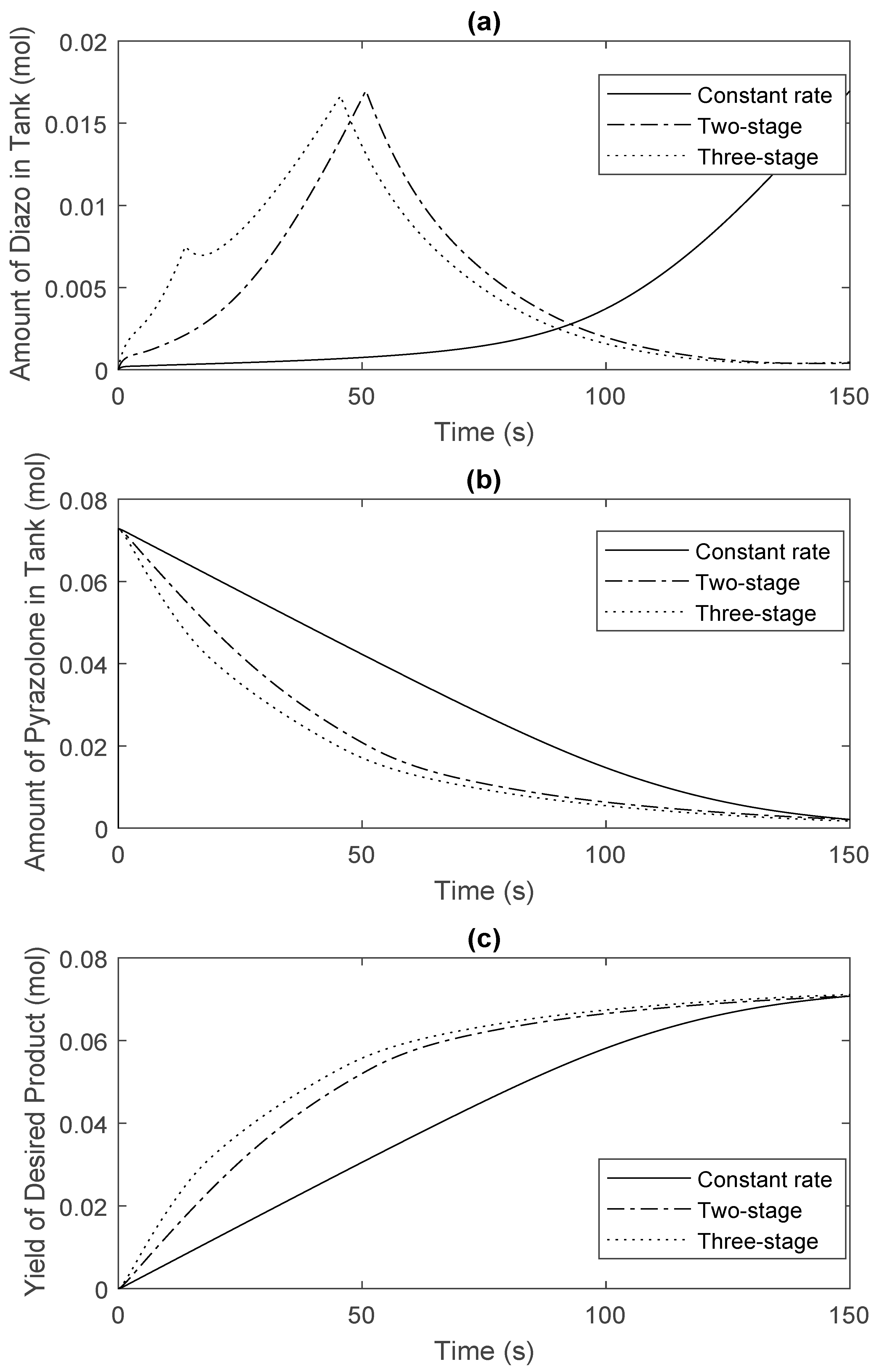
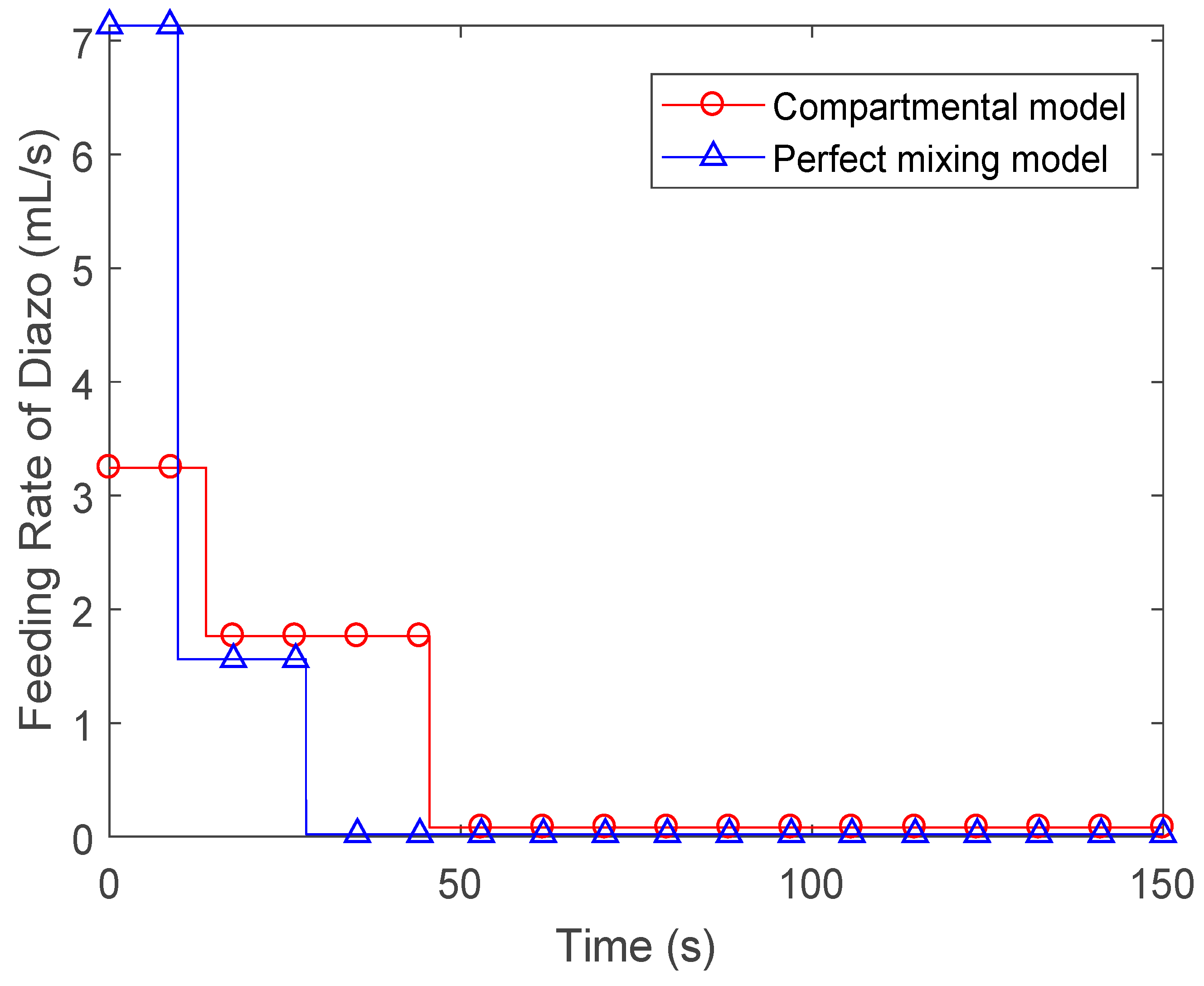
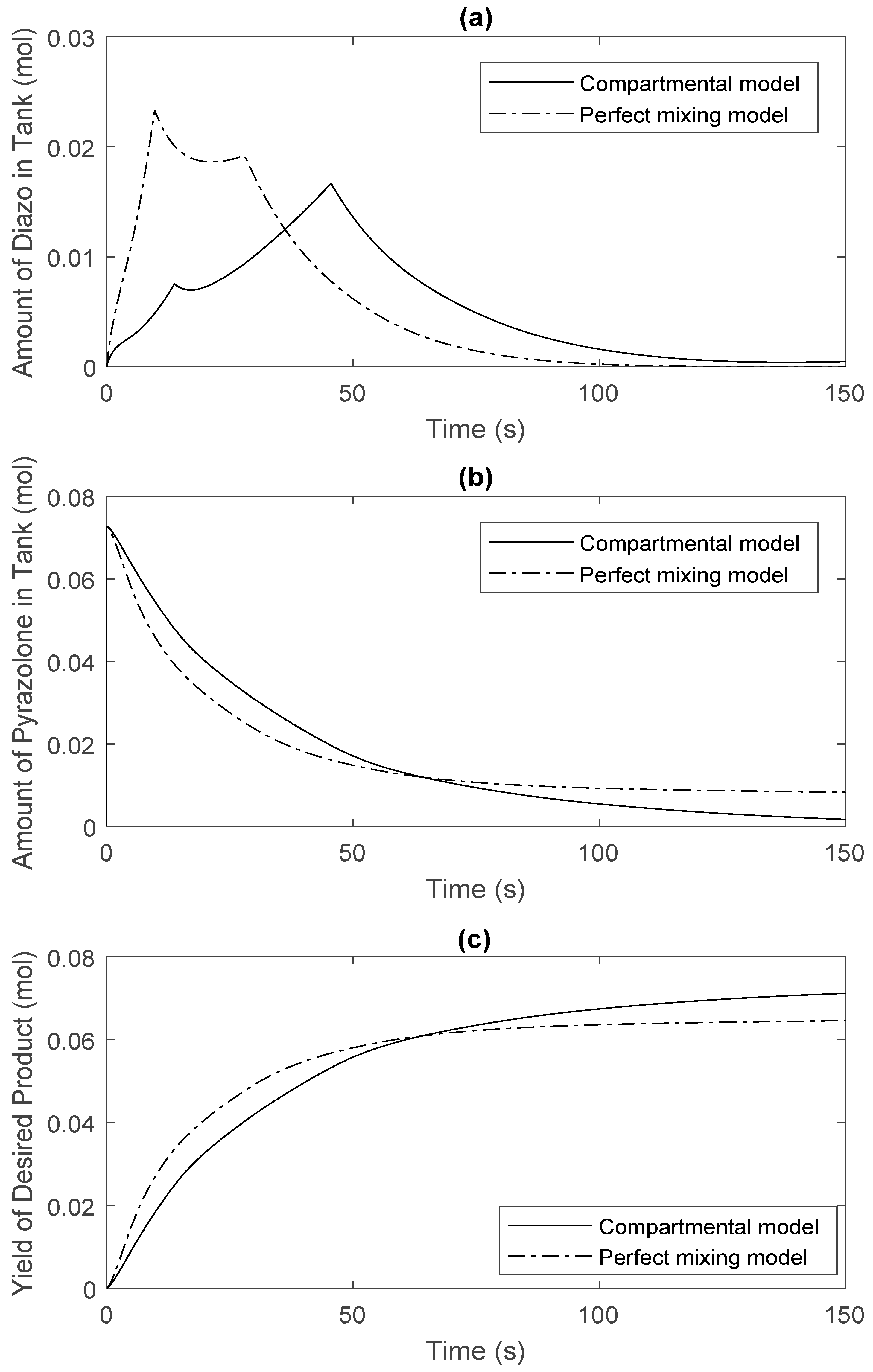
| Reagent Injection Policy | Optimal Injection Location | |
|---|---|---|
| Height (m) | Radial Position (m) | |
| Constant Rate Feeding | 0.1–0.13 | 0.22–0.25 |
| Two-stage Dynamic Feeding | 0.1–0.13 | 0.22–0.25 |
| Three-stage Dynamic Feeding | 0.1–0.13 | 0.22–0.25 |
| Reagent Injection Policy | Optimal Process Productivity ($) |
|---|---|
| Constant Rate Feeding | 6162.90 |
| Two-stage Dynamic Feeding | 6410.43 |
| Three-stage Dynamic Feeding | 6411.76 |
| Methodology | Simulated Process Productivity ($) |
|---|---|
| Perfect-mixing Model | 6162.90 |
| CFD-based Compartmental Model | 6410.43 |
| Methodology | Computational Expense for One Simulation (s) |
|---|---|
| Dynamic CFD simulation | 104 |
| CFD-based Compartmental Model | 70 |
| Methodology | Simulated Process Productivity ($) |
|---|---|
| Perfect-mixing Model | 5713.18 |
| Compartmental Model (constant rate) | 6126.90 |
| Compartmental Model (dynamic rate) | 6411.76 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Kiang, S.; Farzan, P.; Ierapetritou, M. Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization. Processes 2019, 7, 9. https://doi.org/10.3390/pr7010009
Yang S, Kiang S, Farzan P, Ierapetritou M. Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization. Processes. 2019; 7(1):9. https://doi.org/10.3390/pr7010009
Chicago/Turabian StyleYang, Shu, San Kiang, Parham Farzan, and Marianthi Ierapetritou. 2019. "Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization" Processes 7, no. 1: 9. https://doi.org/10.3390/pr7010009
APA StyleYang, S., Kiang, S., Farzan, P., & Ierapetritou, M. (2019). Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization. Processes, 7(1), 9. https://doi.org/10.3390/pr7010009





