2.1. Brief Introduction into the GSPT
Here, we give a brief overview on the topic of GSPT. In general, a slow-fast system is of the form
where
,
,
,
with
and
. We denote by
x and
y the state space variables and by
p the system parameters, while the small parameter
represents the ratio of time scales. Moreover, the functions
and
are assumed to be sufficiently smooth, typically
. The space variables
x are called fast variables, while the space variables
y are called slow variables. Moreover,
denotes the slow time scale and the fast time scale
t is given by
. If we rescale the system (
5) in time—switching from the slow time scale to the fast one—we arrive at
In general, solutions of slow-fast systems frequently exhibit slow and fast epochs characterised by the speed at which the solution advances. If
tends to zero, the trajectories of (
5) converge during the slow epochs to the solution of the slow flow/slow subsystem or reduced system
while during fast epochs the trajectories of (
6) converge to the fast subsystem or layer problem
The fast subsystem describes the evolution of the fast variables
for fixed
, while the slow subsystem describes the evolution of the slow variables
. The phase space of the slow flow (reduced problem) is the critical manifold
, which is defined by
A subset
is called normally hyperbolic if the
matrix
of the first partial derivatives with respect to the fast variables
x, i.e., the Jacobian of
F with respect to
x, has no eigenvalues with zero real part for all
. Moreover, we call a normally hyperbolic subset
attracting if all eigenvalues of
have negative real parts, while we call a normally hyperbolic subset
repelling if all eigenvalues of
have positive real parts. If
is normally hyperbolic and neither attracting nor repelling, it is of saddle type. Usually, the interesting dynamics are localised around these non-hyperbolic regions. There may be isolated points in
, i.e., folded singularities, satisfying
and
, where the trajectories of the slow flow switch from incoming to outgoing. Away from fold points the implicit function theorem implies that
is locally the graph of a function
. Then, the reduced system (
7) can be expressed as
, where
. However, it is more convenient to write the slow flow in terms of the fast variables
x and we can keep the differential-algebraic equations structure of (
7). To this aim we determine the total (time) derivative of
. This yields
and we can write the slow flow (
7) as the restriction to
of the vector field
This vector field blows up if
F is singular and the slow flow is not defined on
, i.e., the set of folded singularities, before desingularisation. Therefore, we consider the desingularised reduced system, which is given by
restricted to
, where we rescaled the time by
. Moreover, ordinary singularities satisfy
are equilibria of the desingularised reduced system (
10), the reduced system (
9) and can be equilibria of the original system (
5). Against it folded singularities are in general no equilibria of the reduced system (
9) and of the original system (
5). Notice that in the reduced system (
9) folded singularities are special points, since both sides of the first equation vanish simultaneously. This means that there is potentially a cancellation of a simple zero, i.e.,
is finite and non-zero at a folded singularity. This allows trajectories to cross the fold in finite time. Such solutions are called singular canards and their persistence under small perturbations gives rise to complex dynamics. If
, the Jacobian of (
10) evaluated at the folded singularities has
zero eigenvalues and two remaining eigenvalues
. Moreover, the folded singularities are classified as follows
Here, we have to highlight that folded saddles, folded nodes and folded foci are also known as canard points, see [
22]. Even more, for sufficiently small values of the perturbation parameter
it is possible to calculate the maximal number of small oscillations of a MMO pattern, see [
23,
24]. For instance, if
and
are the eigenvalues of the linearisation of the desingularised system at a folded node and
with
, then the maximal number of small oscillations in the MMO (in a neighbourhood of the folded node) is given by
i.e., the greatest integer less than or equal to
, provided
.
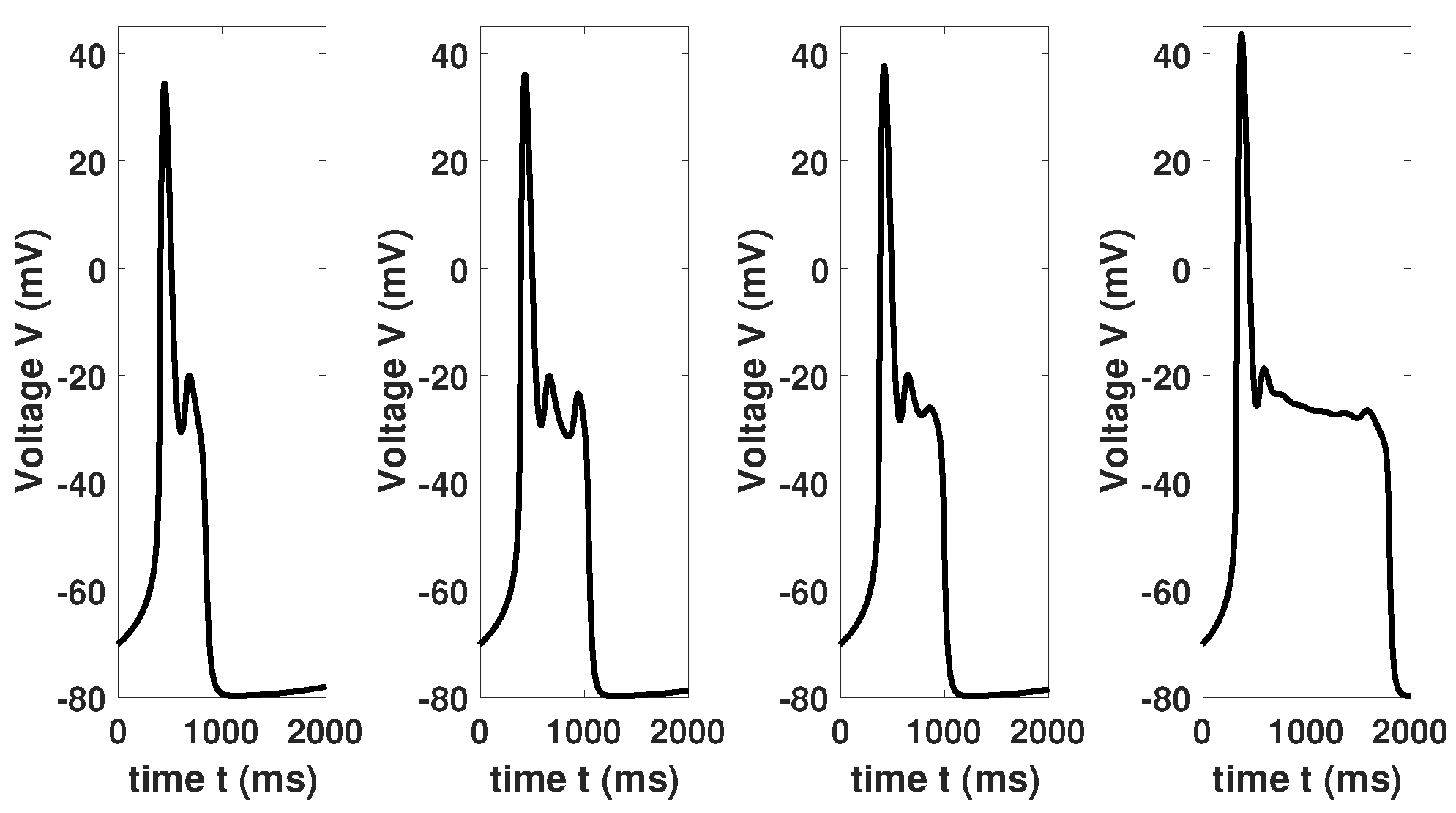
2.2. The Study of EADs as MMOs
After this short introduction into the topic of GSPT, we will go on with the investigation of the dynamics of our multiple time scale problem. To this aim we first have to derive a suitable model to be able to apply this theory. To determine the different time scales we use a certain type of time scale separation argument, cf. [
25]. Thus, we introduce a new (dimensionless) time variable
satisfying
, where
is a reference time. Choosing
and rewriting (
1)–(
3), we get:
where we divided the first equation by
and defined
and
to derive the dimensionless singular perturbation parameters
,
and
. Using the setting from above we have that
with
, which implies that the system exhibits three different time scales, where
d and
V are the fastest variables and
x the slowest one. First of all, we have to notice that there are several system parameters, which have a huge influence on the time scale separation and the time scales, i.e.,
,
,
,
,
and
, cf. (
13). Our next step is to derive the critical manifold
. This yields
We want to highlight that the critical manifold
is the same in both cases (
V and
d are of the same time scale, or
V is the fast variable and
in the 3D system). Since the critical manifold
is the same in both cases and
implying that
one can show that the desingularised slow flow of (
13) restricted to
is also the same as the one of the three dimensional system with
. Moreover, for
we have the following slow subsystem:
and similarly the fast subsystem
From (
10), using
we can derive immediately the desingularised slow flow:
restricted to
, where
. Remember that system (
17) is the desingularised version of
restricted to
. An ordinary singularity of (
17) is given if
, while a fold point
is a folded singularity of (
17) if
This yields explicit expressions for
and
depending on
, i.e.,
and
At this stage we see that the shape of the critical manifold is not depending on
or the choice of
and
, but the location of the folded singularities and their stability. Moreover, notice that the Jacobian of (
17) has at least one zero eigenvalue. Furthermore, varying the ratio
changes the desingularised slow flow (
17). Notice that for
we have an one dimensional slow flow, where
f is determined by the critical manifold and
x is constant. Therefore, it does not make sense to consider both limits
and
simultaneously. However, varying
may compensate the effect of an enhanced calcium current, cf. [
15]. Moreover, the critical manifold
as well as the desingularised slow flow are depending on
and
, cf. (
14) and (
17). Hence, varying
and/or
has an influence on (
14) and (
17). Furthermore,
and
have only an influence on the time scale separation argument and after passing to the singular limit
our discussion is independent on
and
.
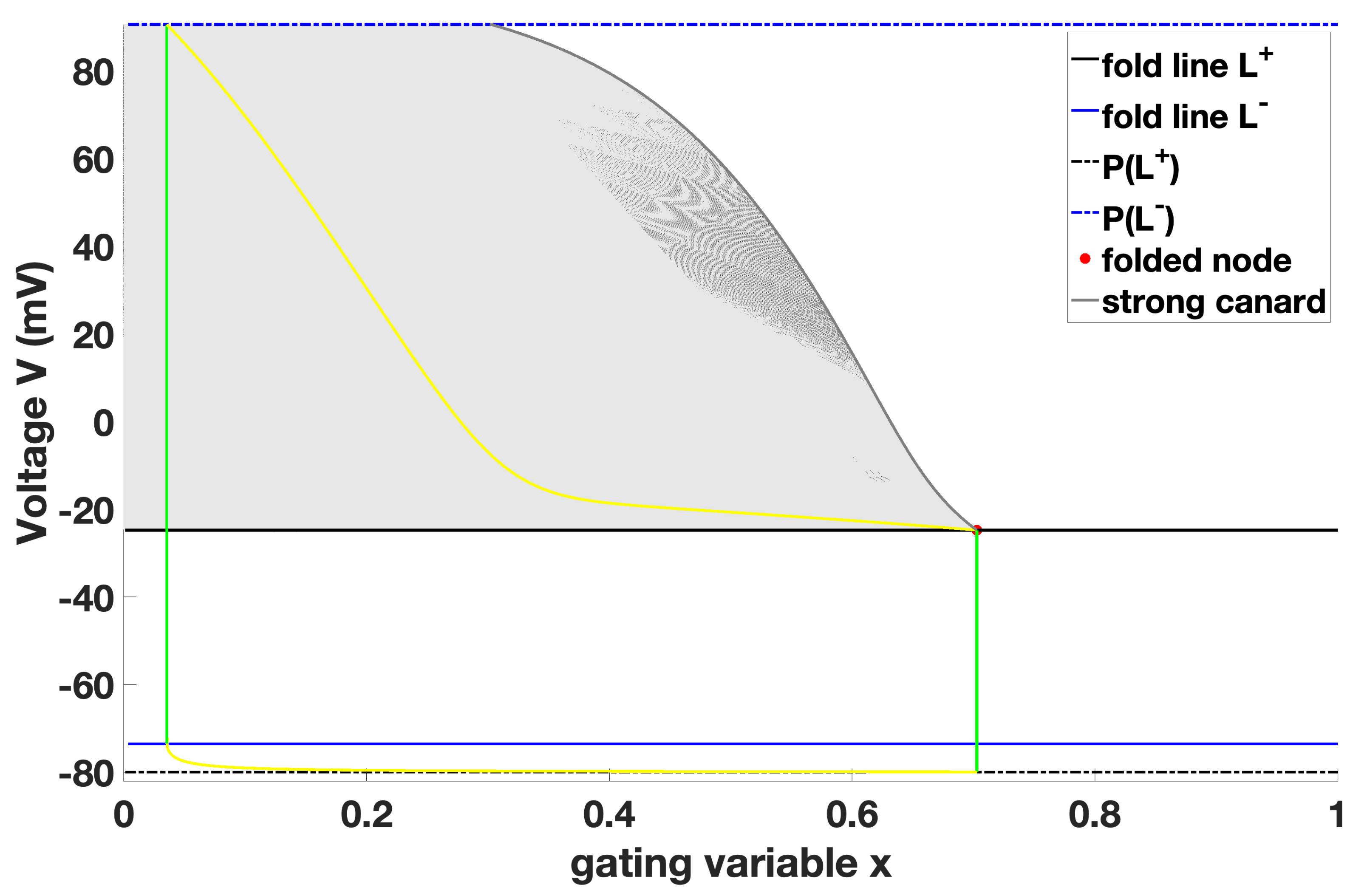
In the following, we consider
. Computing the critical manifold
(
14) together with two fold lines
, the folded node
with eigenvalues
and
, an ordinary singularity
and the singular orbit, we gain
Figure 2. Notice that for
and
satisfying the ratio
the folded node will be the same—similarly if
. The critical manifold is divided into two attracting sheets
and one repelling sheet
, where
lies between the two fold lines
. The fold lines are nondegenerate since
or
or both is satisfied. Moreover, we have an ordinary singularity on
. Notice that spiking, bursting and plateauing are only possible provided that the ordinary singularity is unstable, i.e. the ordinary singularity lies on the repelling manifold
, cf. [
26]. The singular or relaxation orbit consists of four distinct segments, i.e., two slow orbit
and two fast orbit
segments. Notice that in general, singular periodic orbits which are filtered into the folded node on
are singular representations of MMOs. The aim of GSPT is now to combine information from the reduced and layer problems in order to understand the dynamics of the cell model (
1), particularly the oscillatory behaviour. Thus, we use the reduced and the layer flows to construct singular periodic orbits, which—according to GSPT [
26,
27]—will perturb to nearby periodic orbits of the full system (
1) for sufficiently small perturbations.
The singular orbit is constructed as follows. From lower fold line
there is a rapid evolution
described by (
16) towards the upper attracting manifold
. Once the trajectory reaches
the reduced flow
takes over until the trajectory reaches the upper fold line
. Then, at the fold line the reduced flow is singular and there is a finite time blow-up of the solution. The layer problem (
16) becomes the appropriate descriptor and there is a fast down-jump to the lower attracting manifold. Here, the reduced system (
15) describes the slow motions along the critical manifold until the trajectory once again hits the fold line. The GSPT guarantees that this singular orbit will persist as a nearby periodic relaxation oscillation corresponding to a spiking solution of (
1). A folded node occurs in generic slow-fast systems with two (or more) slow variables [
22,
24,
27]. Moreover, a folded node allows for an entire sector of trajectories to pass from the upper attracting branch
of the critical manifold to the repelling branch
and to follow that repelling branch for an
time on the slow time scale. Notice that solutions of the reduced problem (
18) passing through a canard point from an attracting manifold
to a repelling manifold
are called singular canards. The sector of canard solutions (the singular funnel, cf.
Figure 3) is bounded by the fold line
and by the strong canard
, which is the unique trajectory tangential to the strong eigendirection of the folded node, cf. [
26]. Two singular canards are related to the eigendirections of the folded node, i.e., the weak and strong canards. They correspond to the smallest and largest (in absolute value) eigenvalues respectively.
There are two major requirements that the singularly perturbed system has to satisfy to guarantee the existence of canard-induced MMOs, see [
28] and cf. also [
23], i.e.,
- (a)
The reduced flow (desingularised slow flow) has to possess a folded node.
- (b)
There is a singular periodic orbit formed by the slow and fast segments of the reduced and layer problems (slow and fast subsystem) which starts with a fast fiber segment at the folded node. This guarantees that the global return of such singular periodic orbit is within the singular funnel of the folded node.
Both conditions are satisfied in our situation. This implies that the MMOs are canard-induced and we have canard-induced EADs. Moreover, if
, then
, cf. (
12). Please also note that that system (
13) exhibits several types of folded singularities mentioned in (
11) for different values of conductance
. If we increase
the folded node will travel on the fold line
to the “right”, which means that the values of
f and
x at the folded node become bigger. Moreover, the ordinary singularity will travel also towards the folded node until both point collide. Then, the folded node becomes a folded saddle. If the folded node travels to the “left”, then it will become a folded focus for smaller values of
. Furthermore, we have a two dimensional fast subsystem, but then this system exhibits only limit point bifurcations and no Andronov-Hopf bifurcations. Hence, there are no Hopf-induced EADs induced by an enhanced calcium current. Thus, we have shown that system (
13) exhibits only canard-induced EADs via an enhanced calcium current. Finally, we want to highlight also that system (
13) exhibits Hopf-induced EADs provided we consider a fixed singular perturbation parameter
and
. In this case we have a three dimensional fast subsystem with one bifurcation parameter
x, but the occurring EADs are then related to a reduced potassium current [
1].
2.3. The Study of EADs Using Bifurcation Analysis
In
Section 2.2 we established that EADs related to an enhanced calcium current are canard-induced. Here, we did simultaneous the discussion for
and all
, provided
. In addition, from (
12) we know that
if
. Regarding our setting for the relaxation time constant
ms and the membrane capacity
we see that
and thus,
is not satisfied. Moreover, for a setting like
ms and
one diverges more from the condition
, since
. However, the system still exhibits MMOs or EADs but does not satisfy (
12), since the condition
is barely to fulfil.
Our next step is the study of system (
1) using bifurcation analysis. In general, a bifurcation of a dynamical system is a qualitative change in its dynamics produced by varying parameters. Since we investigate the occurrence of EADs induced by an enhancement in the calcium current
, we will choose the conductance
as bifurcation parameter to be able to simulate the decreasing or mainly the increasing of the calcium current. Moreover, we will use our observation from above to analyse the behaviour of system (
1). First of all, determining the equilibrium curve of system (
1), which is basically the equilibria of this system for different values of
, yields two stable branches and one unstable branch for all parameter settings. Depending on the parameter setting the equilibrium curve loses or wins stability via a sub- or supercritical Andronov-Hopf bifurcation, cf. also [
15]. An Andronov-Hopf bifurcation is characterised by a pair of purely imaginary eigenvalues, where the equilibrium changes stability and a unique limit cycle bifurcates from it, i.e., it is the birth of a limit cycle. The distinction into sub- or supercritical means that an unstable or stable limit cycle, respectively, bifurcates. For the standard setting
ms system (
1)–(
4) exhibits two supercritical Andronov-Hopf bifurcations (black dots), cf.
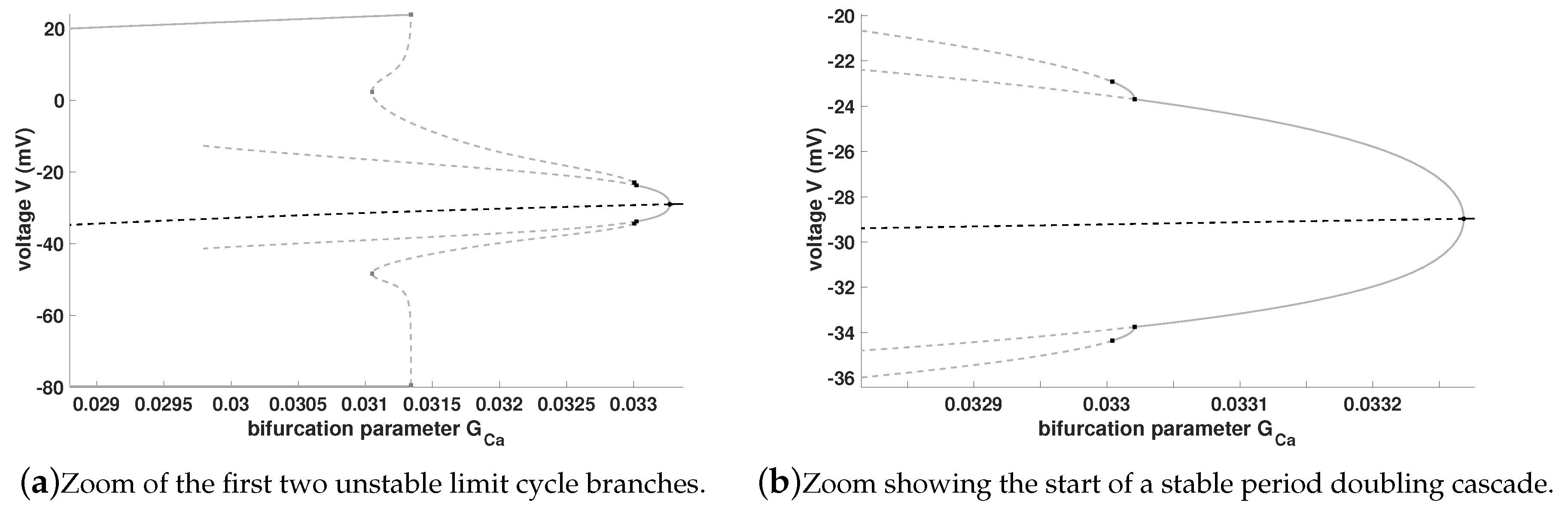
Figure 4.
From the first Andronov-Hopf bifurcation (
) a stable limit cycle branch bifurcates which becomes unstable via a limit point of cycle (
) before it wins again stability via a period doubling bifurcation. There is also a second stable limit cycle branch bifurcating from the second Andronov-Hopf bifurcation (
) which becomes unstable via a period doubling bifurcation (connection of both limit cycle branches), cf. also
Figure 5b.
This unstable limit cycle branch has of course influence on the system (
1) but it does not yields automatically EADs, it also may correspond to an AP. Notice that the limit cycle branches are determined via a continuation algorithm included in MATCONT. The region between the first Andronov-Hopf bifurcation and the first limit point of cycle (
) indicates the region, where no EADs occur, cf. [
15]. EADs appear after the first limit point of cycle. In
Figure 5a the transient from AP to EADs via the limit point of cycle bifurcation is highlighted, while
Figure 5b shows the beginning of a stable period doubling cascade. In Figure 9 we see that this transient might be also via a period doubling bifurcation. Moreover, in
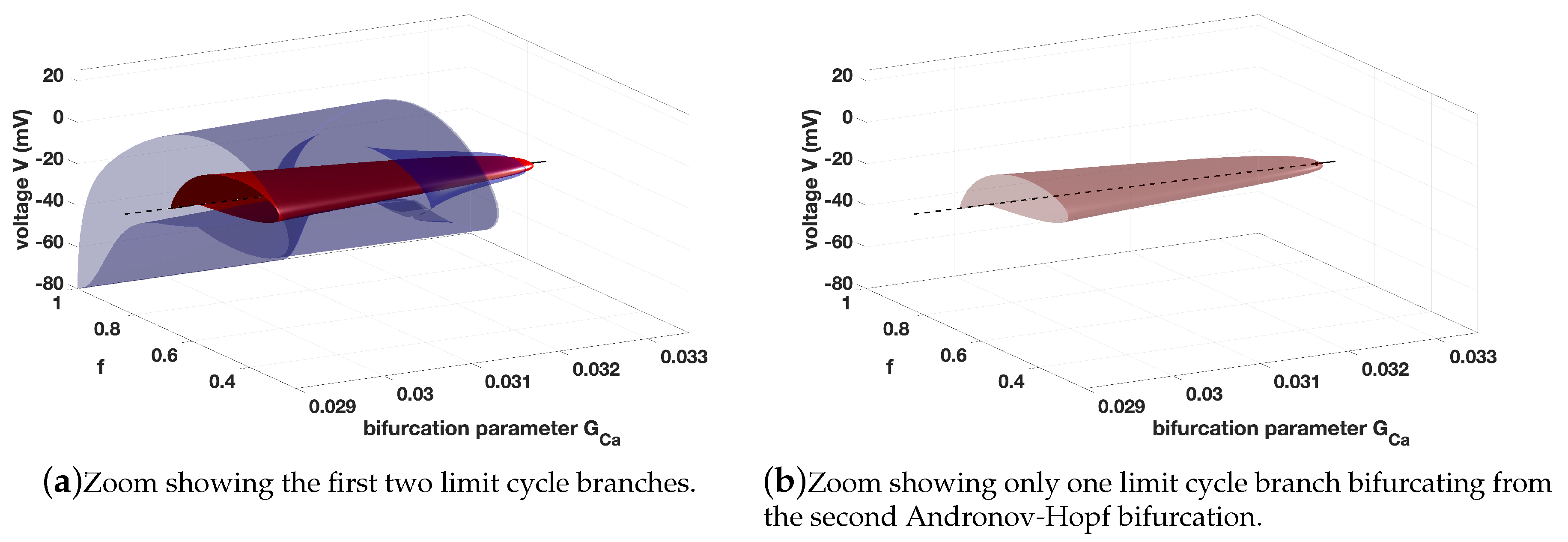
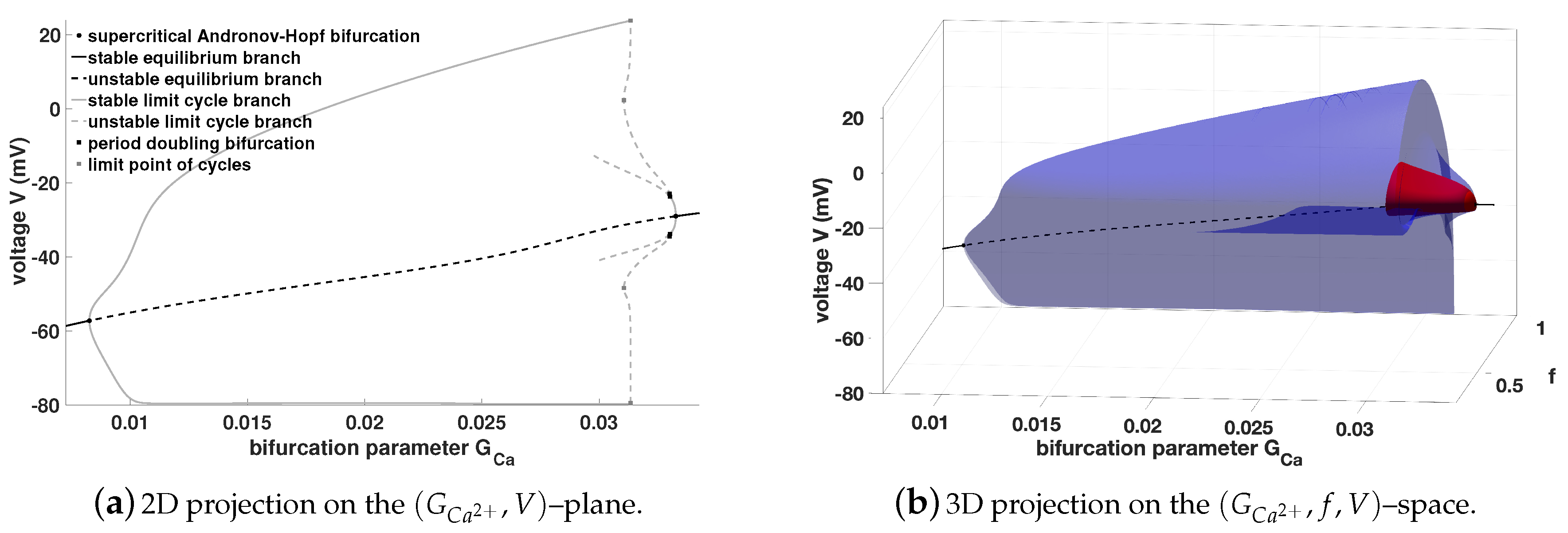
Figure 6 we illustrate the limit cycle branches in 3D.
For a better understanding we included in
Figure 7 also two trajectories, one represents a normal AP, while the other shows an EAD.
Notice that we have a four dimensional phase space plus a further dimension for the parameter. Therefore, we have a five dimensional object which we can only plot in 2D or 3D as a projection on a 2D plane or 3D space. This makes the visualisation slightly difficult and it becomes more difficult if the dimension of the system increases. Nevertheless, one gets a good description of the behaviour of the considered system using the bifurcation theory. From the 2D and 3D projection in
Figure 4,
Figure 5 and
Figure 6 one might get the impression that the limit cycle starting from the second Andronov-Hopf bifurcation is not completed, but this limit cycle terminates at the unstable equilibrium branch, cf. the projection on the
–space in
Figure 8a. In
Figure 8b we show for comparison the corresponding bifurcation diagram with
and
instead of with
and
, cf.
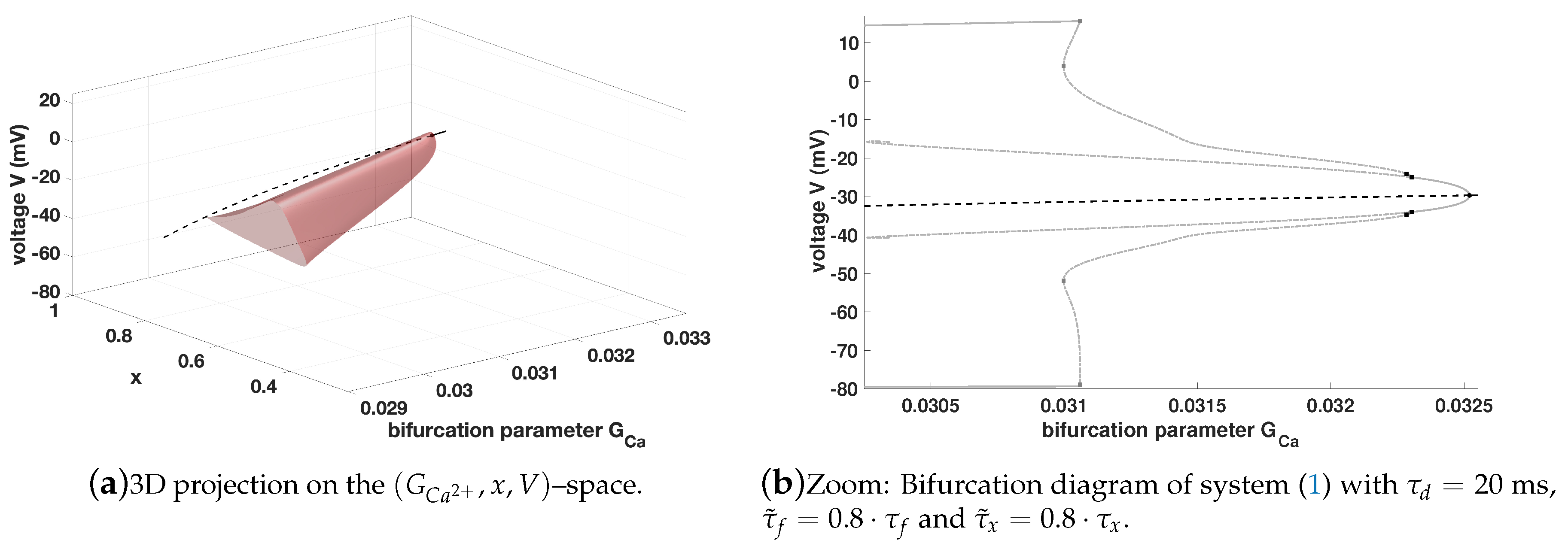
Figure 5b. Here, one sees that the behaviour is different compared to the standard setting, while in the discussion of the GSPT this change has no influence. Thus, it is important to use both approaches for the investigation of such phenomena.
Finally, if we consider the bifurcation diagram of (
1)–(
3) with
ms and
instead of
ms and
, we see again the importance to consider all these parameters, cf.
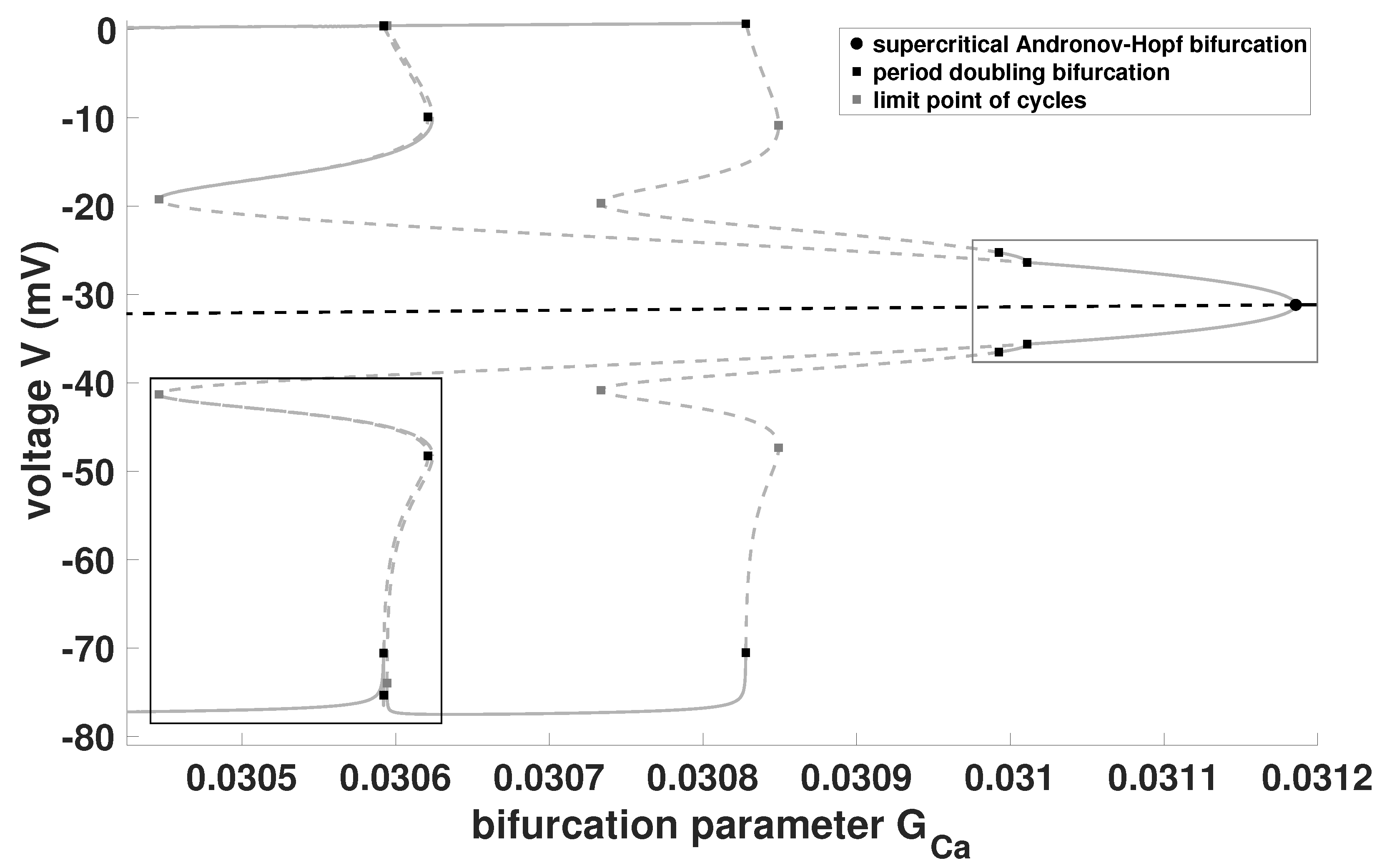
Figure 9.
In
Figure 9 and
Figure 10a we see that the system (
1) may exhibit different type of MMOs and critical transient regions depending on the choice of the system parameters. Even more, it also shows that
in combination with
does not yield MMOs, cf.
Figure 9. The reason for this is that the condition
is not suitable satisfied. Notice that there is no explicit condition how small
has to be, only it has to be much smaller than 1. Nevertheless,
Figure 9 shows the system (
1) exhibits MMOs, but for smaller values of
. For a more suitable visualisation of
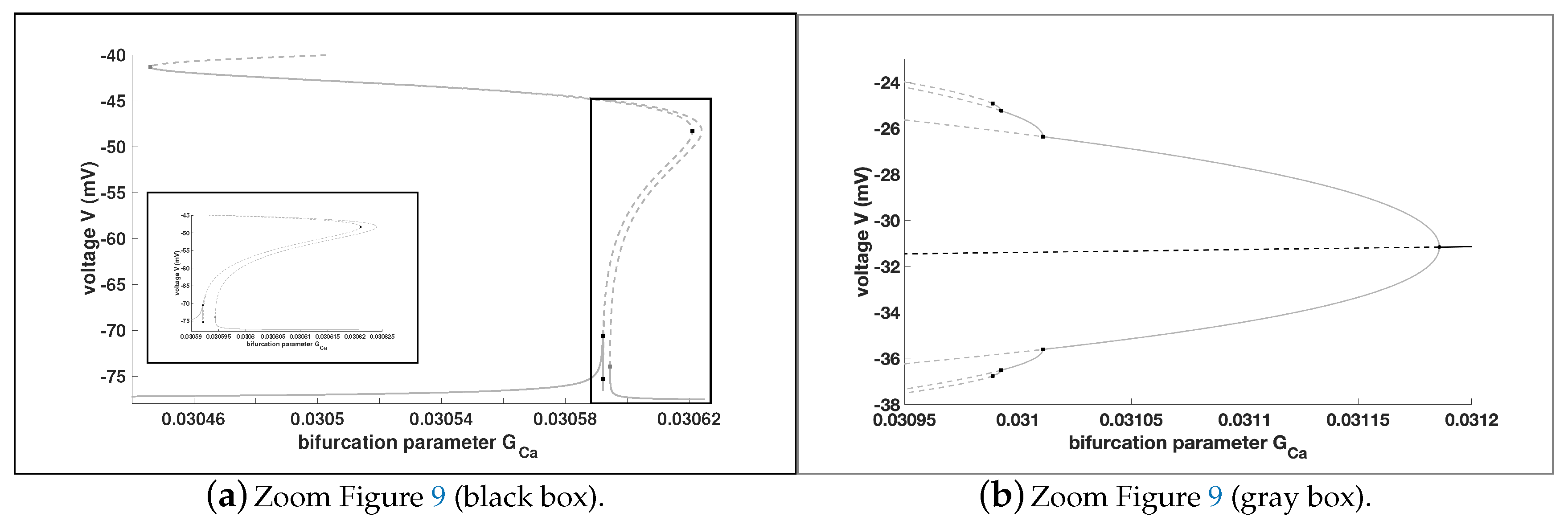
Figure 9, we present in
Figure 10 two zooms of
Figure 9. Notice that the system exhibits for this setting two supercritical Andronov-Hopf bifurcations. From the supercritical Andronov-Hopf bifurcation shown in
Figure 10b a stable period doubling cascade bifurcates, which is a route to chaos, cf. [
29].
Furthermore, we have shown that the GSPT gives information about the nature of the oscillatory behaviour and even more, one can use the GSPT to determine the important system parameters yielding these oscillations. However, we saw that it is not sufficient to consider only one parameter to analyse the complete dynamics of a dynamical system. Here, we have seen the high relevance for the investigation of MMOs in combination with bifurcation analysis to derive a more detailed understanding of EADs, which one can use to prevent them. In [
15] some approaches to control the effect of an enhanced calcium current are established and for this aim a further system parameter is highly interesting, e.g., increasing of
may smooth out this effect yielding EADs. Moreover, these observations, i.e., the system exhibits several time scales and MMOs as in
Figure 1, motivate the investigation of system (
13) in the sense of the geometric singular perturbation theory.