A New Pseudo Steady-State Constant for a Vertical Well with Finite-Conductivity Fracture
Abstract
:1. Introduction
- (1)
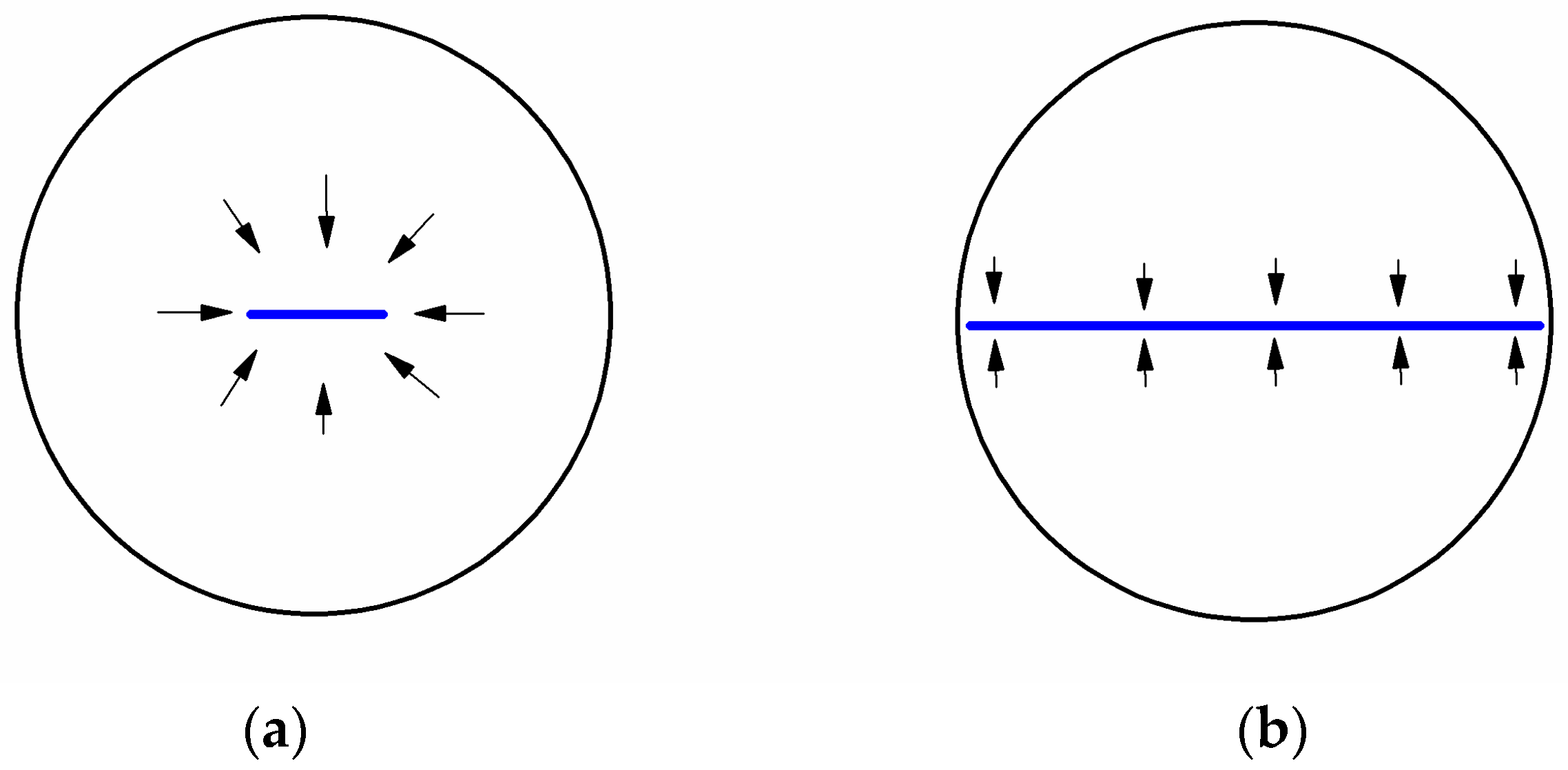
- The assumption of elliptical flow is an approximate model of the circular boundary [29]. For a fractured well, the real pressure front should be a circle instead of an ellipse during the late-time flow regime.
- (2)
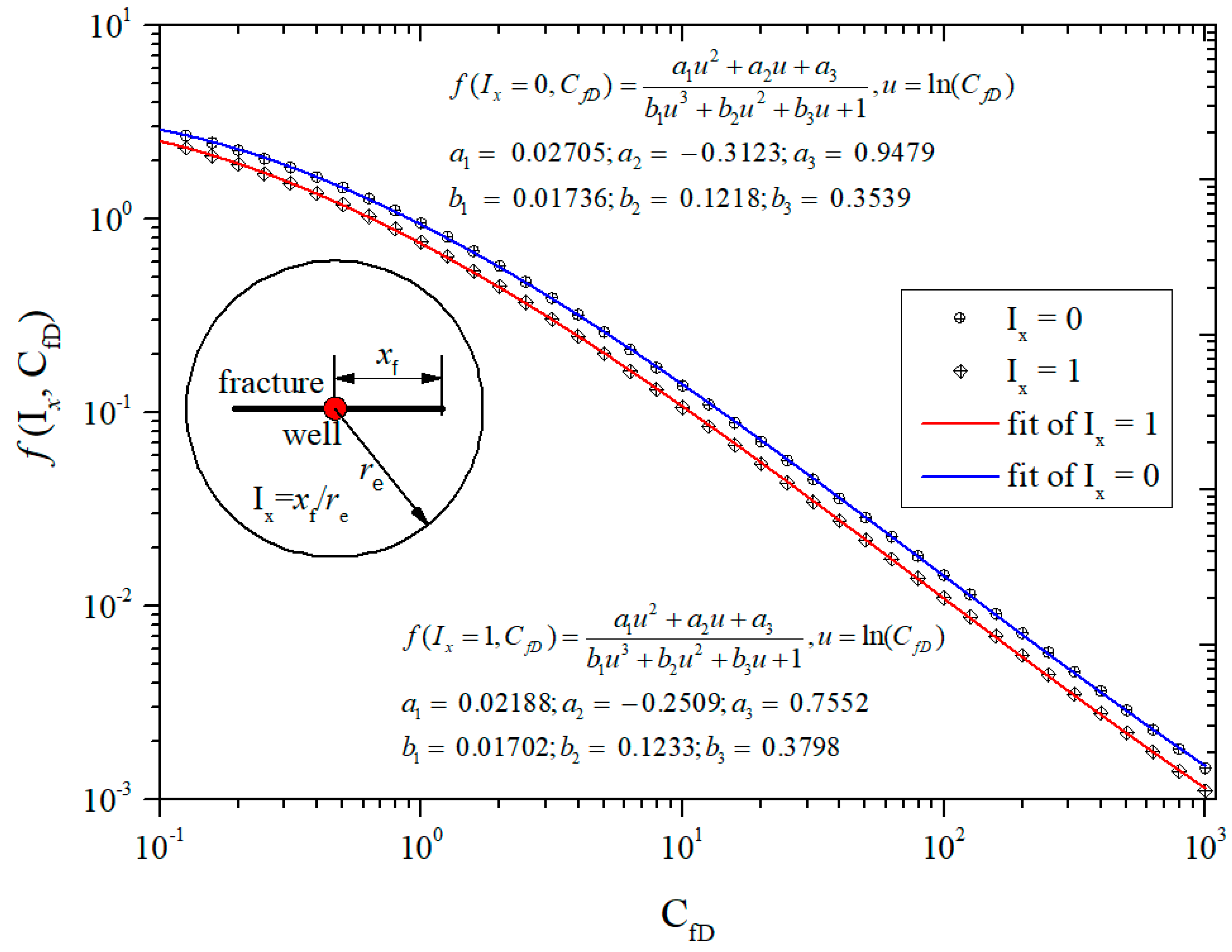
- When CfD trends to infinity, i.e., the infinite-conductivity fracture, Equations (4), (6), and (7) cannot meet the following condition, meaning the limit of conductivity-influence function f(CfD) should be zero.
- (3)
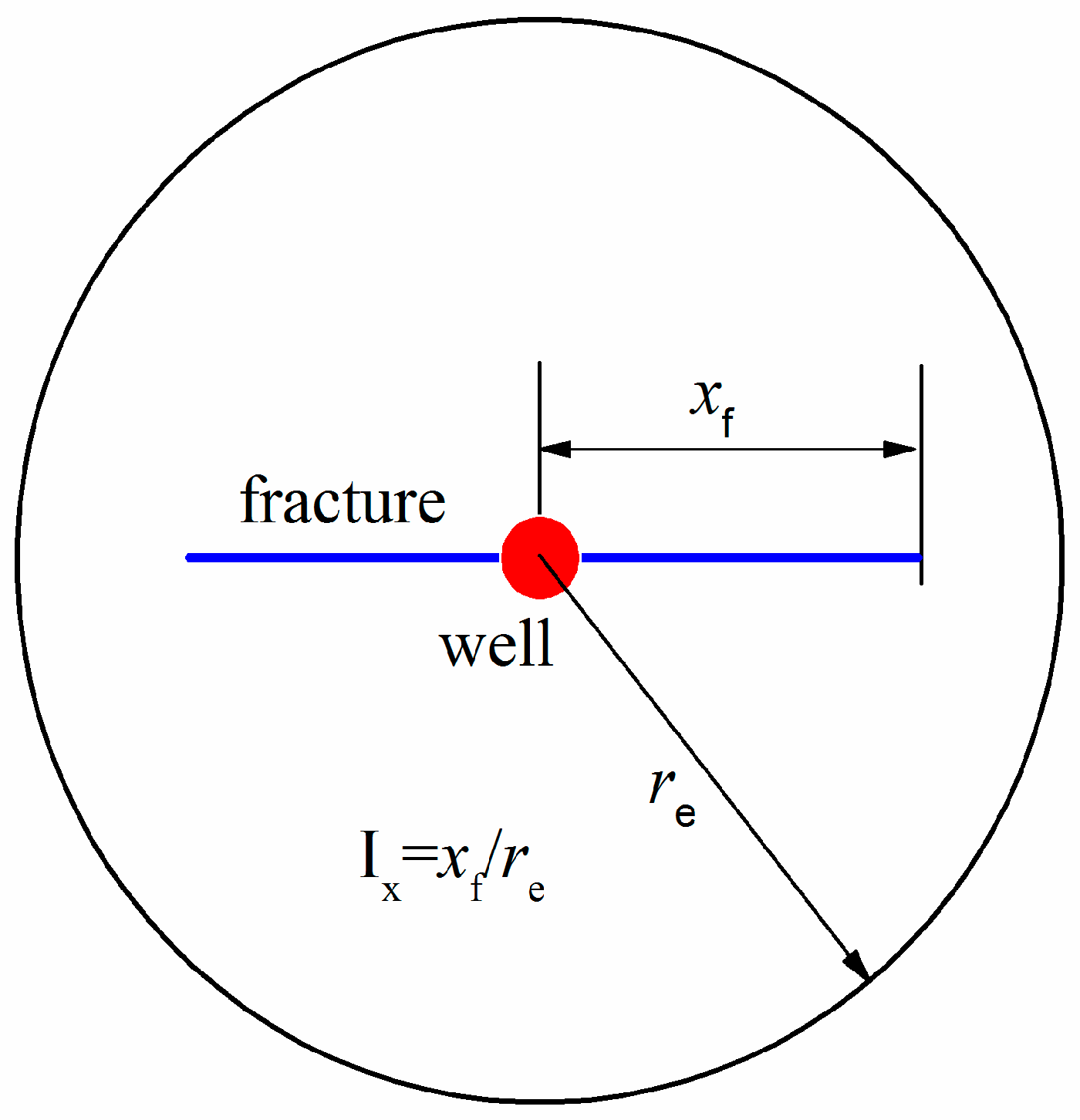
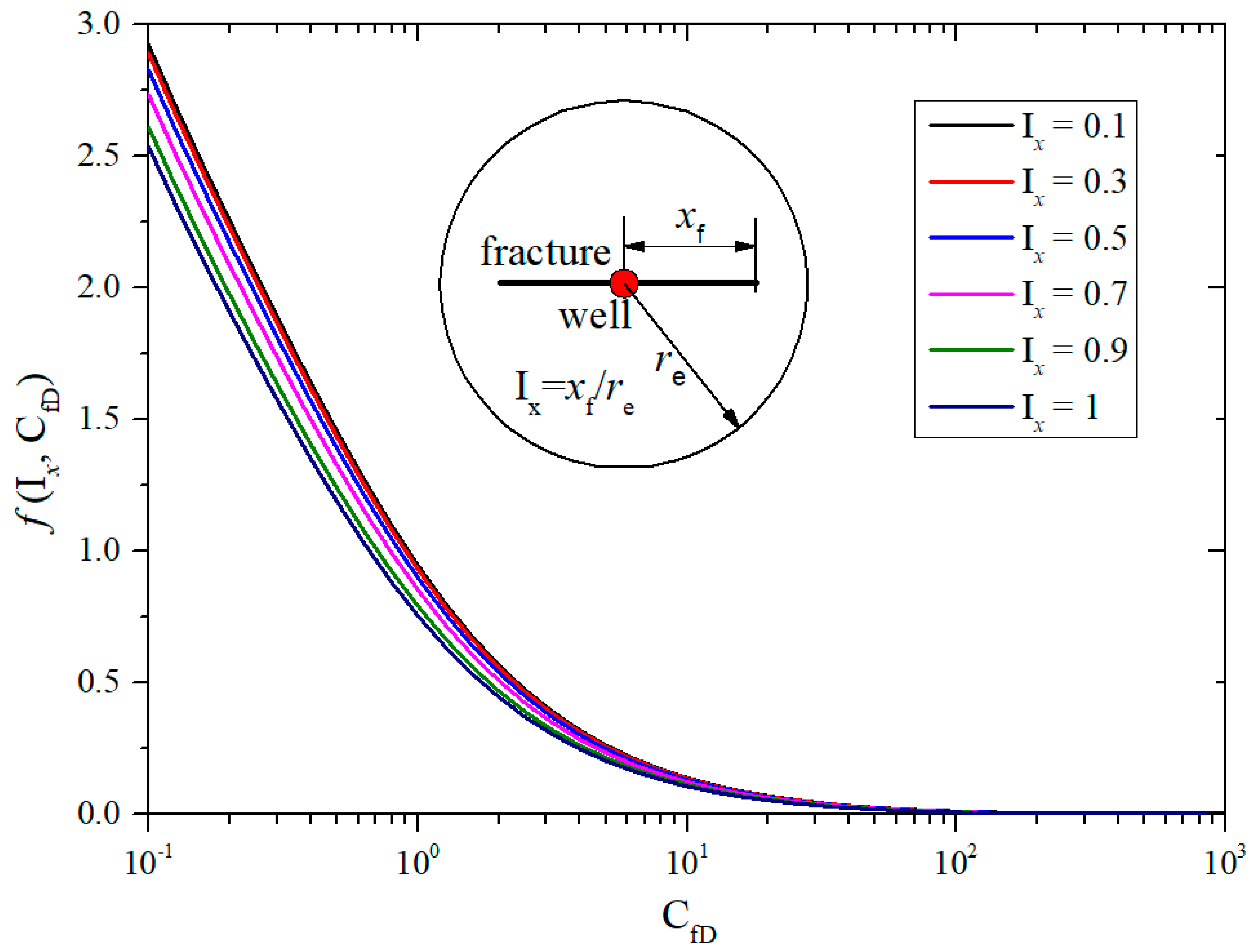
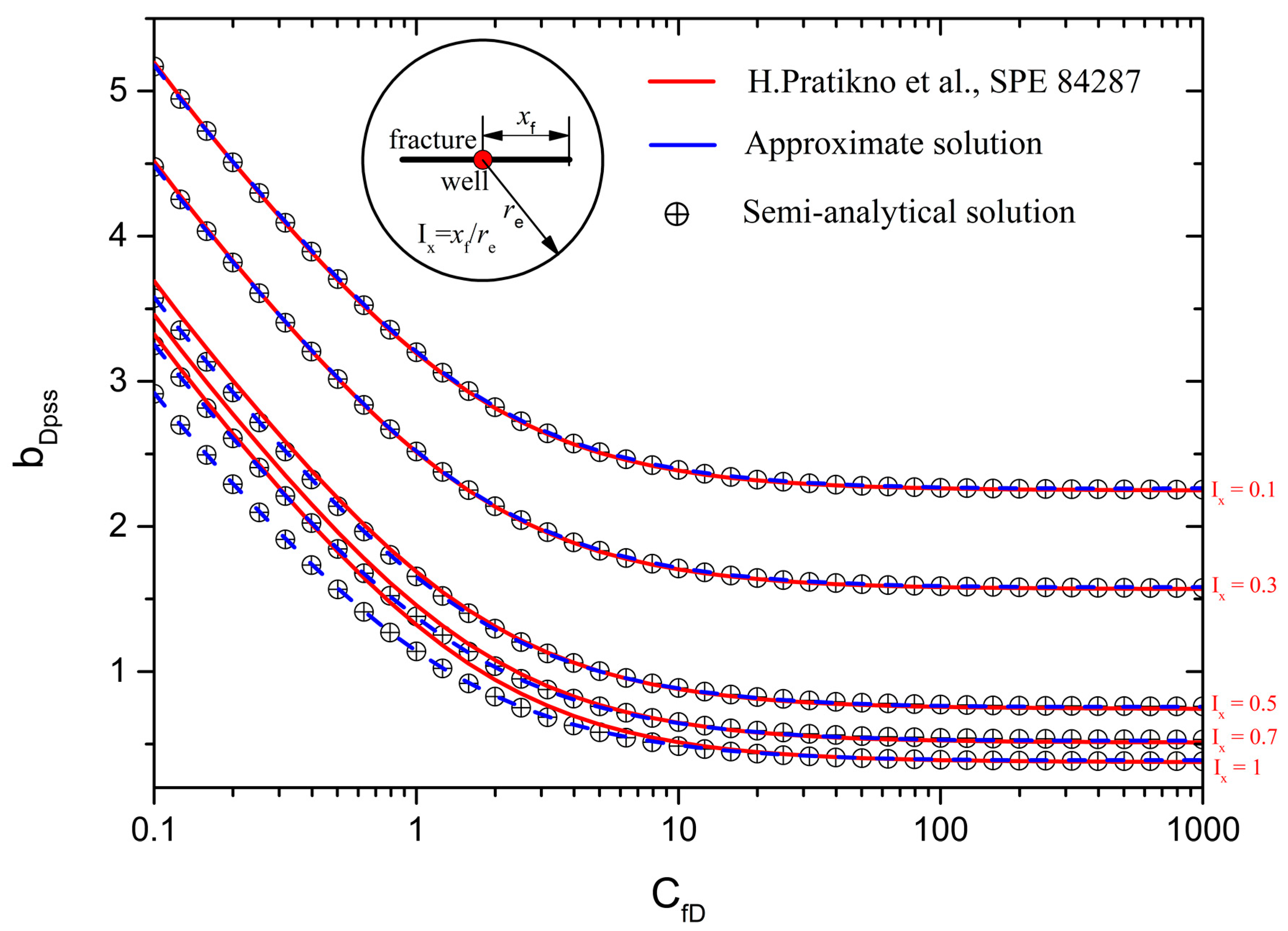
- For the existing approximate models [20,21,23], the conductivity-influence function f(CfD) is only relative to the fracture conductivity. For different penetration fracture ratios Ix, the distributions in the flow field around the fracture are different, which affects the value of conductivity-influence function (Figure 2). Thus, CIF is not only a function of conductivity, but also related to penetration ratio.
2. Mathematical Model
2.1. Basic Assumptions
2.2. Semi-Analytical Model for bDpss Calculation
2.2.1. Flow Model of the Reservoir
2.2.2. Flow Model of the Fracture
2.2.3. Semi-Analytical Solution for bDpss
2.3. Conductivity-Influence Function (CIF)
2.4. New Approximate Solution of Pseudo Steady-State Constant bDpss
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wasantha, P.L.P.; Konietzky, H. Fault reactivation and reservoir modification during hydraulic stimulation of naturally-fractured reservoirs. J. Nat. Gas Sci. Eng. 2016, 34, 908–916. [Google Scholar] [CrossRef]
- Ghaderi, S.M.; Clarkson, C.R. Estimation of fracture height growth in layered tight/shale gas reservoirs using flowback gas rates and compositions—Part I: Model development. J. Nat. Gas Sci. Eng. 2016, 36, 1018–1030. [Google Scholar] [CrossRef]
- Taheri-Shakib, J.; Ghaderi, A.; Hosseini, S.; Hashemi, A. Debonding and coalescence in the interaction between hydraulic and natural fracture: Accounting for the effect of leak-off. J. Nat. Gas Sci. Eng. 2016, 36, 454–462. [Google Scholar] [CrossRef]
- Li, B.; Liu, R.; Jiang, Y. Influences of hydraulic gradient, surface roughness, intersecting angle, and scale effect on nonlinear flow behavior at single fracture intersections. J. Hydrol. 2016, 538, 440–453. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections. Adv. Water Res. 2016, 88, 53–65. [Google Scholar] [CrossRef]
- Haeri, F.; Izadi, M.; Zeidouni, M. Unconventional multi-fractured analytical solution using dual porosity model. J. Nat. Gas Sci. Eng. 2017, 45, 230–242. [Google Scholar] [CrossRef]
- Al-Rbeawi, S. Analysis of pressure behaviors and flow regimes of naturally and hydraulically fractured unconventional gas reservoirs using multi-linear flow regimes approach. J. Nat. Gas Sci. Eng. 2017, 45, 637–658. [Google Scholar] [CrossRef]
- Oyedokun, O.; Schubert, J. A quick and energy consistent analytical method for predicting hydraulic fracture propagation through heterogeneous layered media and formations with natural fractures: The use of an effective fracture toughness. J. Nat. Gas Sci. Eng. 2017, 44, 351–364. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramsey, H.J., Jr.; Raghavan, R. Unsteady Pressure Distribution Created by a Well with a Single Infinite-Conductivity Vertical Fracture. SPE J. 1974, 14, 347–360. [Google Scholar] [CrossRef]
- Ozkan, E. Performance of Horizontal Wells. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 1988. [Google Scholar]
- Ozkan, E.; Raghavan, R. Some new solutions to solve problems in well test analysis: I. Computational considerations and applications. SPE Form. Eval. 1991, 6, 359–368. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Goode, P.A.; Wilkinson, D.J.; Thambynayagam, R.K.M. Pressure-transient behavior of horizontal wells with and without gas cap or aquifer. SPE Form. Eval. 1991, 6, 86–94. [Google Scholar] [CrossRef]
- Hagoort, J. The productivity of a well with a vertical infinite-conductivity fracture in a rectangular closed reservoir. SPE J. 2009, 14, 715–720. [Google Scholar] [CrossRef]
- Cinco-Ley, H.; Samaniego, V.F.; Dominguez, A.N. Transient Pressure Behavior for a Well with a Finite-Conductivity Vertical Fracture. SPE J. 1978, 18, 253–264. [Google Scholar] [CrossRef]
- Cinco-Ley, H.; Meng, H.Z. Pressure transient of wells with finite conductivity vertical fractures in double porosity reservoirs. Presented at the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. [Google Scholar]
- Lee, S.T.; Brockenbrouth, J.R. A new approximate analytic solution for finite conductivity vertical fractures. Presented at the SPE annual technical conference and exhibition, San Francisco, CA, USA, 5–8 October 1986. [Google Scholar]
- Blasingame, T.A.; Poe, B.D. Semianalytic solutions for a well with a single finite-conductivity vertical fracture. Presesnted at the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. [Google Scholar]
- Luo, W.; Tang, C. A semi-analytical solution of a vertical fractured well with varying conductivity under non-darcy-flow condition. SPE J. 2015, 20, 1028–1040. [Google Scholar] [CrossRef]
- Pratikno, H.; Rushing, J.A.; Blasingame, T.A. Decline Curve Analysis Using Type Curves—Fractured Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, Denver, Colorado, 5–8 October 2003. [Google Scholar]
- Amini, S.; Liik, D.; Blasingame, T.A. Evaluation of the Elliptical Flow Period for Hydraulically-Fracture Wells in Tight Gas Sands-Theoretical Aspects and Practical Considerations. Presented at the SPE Hydraulic Fracturing Technology Conference, College Station, TX, USA, 29–31 January 2007. [Google Scholar]
- Hagoort, J. Semisteady-State Productivity of a Well in a Rectangular Reservoir Producing at Constant Rate or Constant Pressure. SPE Res. Eval. Eng. 2011, 14, 677–686. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.D.; Ding, X.M.; Chen, L. Rate Decline Curves Analysis of a Vertical Fractured Well with Fracture Face Damage. J. Energy Resour. Technol. 2012, 134, 032803. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, K.P. Productivity-Index Optimization for Hydraulically Fractured Vertical Wells in a Circular Reservoir: A Comparative Study with Analytical Solutions. SPE J. 2016, 21, 2208–2219. [Google Scholar] [CrossRef]
- Fetkovich, M.J. Decline Curve Analysis Using Type Curves. J. Pet. Technol. 1980, 32, 1065–1077. [Google Scholar] [CrossRef]
- Fetkovich, M.J.; Vienot, M.E.; Bradley, M.D.; Kiesow, U.G. Decline Curve Analysis Using Type Curves—Case Histories. SPE Form. Eval. 1987, 2, 637–656. [Google Scholar] [CrossRef]
- Doublet, L.E.; Blasingame, T.A. Decline Curve Analysis Using Type Curves: Water Influx/Waterflood Cases. Presented at the 1995 Annual SPE Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar]
- Agarwal, R.G.; Gardner, D.C.; Kleinsteiber, S.W.; Fussell, D.D. Analyzing Well Production Data Using Combined-Type-Curve and Decline-Curve Analysis Concepts. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Houston, TX, USA, 3–6 October 1999; pp. 478–486. [Google Scholar]
- Prats, M.; Hazebroek, P.; Strickler, W.R. Effect of vertical fractures on reservoir behavior--compressible-fluid case. SPE J. 1962, 2, 87–94. [Google Scholar] [CrossRef]
- Luo, W.; Wang, X.; Tang, C.; Feng, Y.; Shi, E. Productivity of multiple fractures in a closed rectangular reservoir. J. Pet. Sci. Eng. 2017, 157, 232–247. [Google Scholar] [CrossRef]
| CfD | Ix | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.05 | 0.01 | 0.05 | 0.1 | 0.3 | 0.5 | 0.8 | 1 | |
| 0.1 | 2.924955 | 2.923983 | 2.924917 | 2.923983 | 2.921063 | 2.889918 | 2.82763 | 2.675801 | 2.535652 |
| 0.125893 | 2.694126 | 2.693183 | 2.694089 | 2.693183 | 2.690353 | 2.660159 | 2.599771 | 2.452575 | 2.316702 |
| 0.158489 | 2.473614 | 2.472703 | 2.473578 | 2.472703 | 2.46997 | 2.440814 | 2.382503 | 2.240371 | 2.109172 |
| 0.199526 | 2.259775 | 2.258901 | 2.25974 | 2.258901 | 2.256277 | 2.228293 | 2.172325 | 2.035904 | 1.909976 |
| 0.251189 | 2.050804 | 2.049971 | 2.050771 | 2.049971 | 2.047474 | 2.02083 | 1.967543 | 1.837656 | 1.71776 |
| 0.316228 | 1.846441 | 1.845657 | 1.84641 | 1.845657 | 1.843302 | 1.818188 | 1.767959 | 1.645526 | 1.532512 |
| 0.398107 | 1.647651 | 1.64692 | 1.647622 | 1.64692 | 1.644726 | 1.621328 | 1.574532 | 1.460467 | 1.355176 |
| 0.501187 | 1.456232 | 1.45556 | 1.456206 | 1.45556 | 1.453543 | 1.432024 | 1.388986 | 1.284082 | 1.187247 |
| 0.630957 | 1.274395 | 1.273785 | 1.274371 | 1.273785 | 1.271955 | 1.252433 | 1.213389 | 1.118219 | 1.03037 |
| 0.794328 | 1.104337 | 1.103791 | 1.104315 | 1.103791 | 1.102154 | 1.084688 | 1.049755 | 0.964606 | 0.886007 |
| 1 | 0.9479 | 0.947418 | 0.947881 | 0.947418 | 0.945973 | 0.930557 | 0.899725 | 0.824572 | 0.7552 |
| 1.258925 | 0.806339 | 0.805919 | 0.806322 | 0.805919 | 0.80466 | 0.791229 | 0.764366 | 0.698889 | 0.638448 |
| 1.584893 | 0.680231 | 0.67987 | 0.680217 | 0.67987 | 0.678786 | 0.667223 | 0.644099 | 0.587732 | 0.535701 |
| 1.995262 | 0.569498 | 0.56919 | 0.569486 | 0.56919 | 0.568267 | 0.558422 | 0.538731 | 0.490735 | 0.446431 |
| 2.511886 | 0.473515 | 0.473256 | 0.473505 | 0.473256 | 0.472478 | 0.464176 | 0.447573 | 0.407101 | 0.369743 |
| 3.162278 | 0.391259 | 0.391042 | 0.39125 | 0.391042 | 0.390391 | 0.383452 | 0.369573 | 0.335742 | 0.304514 |
| 3.981072 | 0.321455 | 0.321276 | 0.321448 | 0.321276 | 0.320736 | 0.314979 | 0.303467 | 0.275404 | 0.2495 |
| 5.011872 | 0.262718 | 0.26257 | 0.262712 | 0.26257 | 0.262125 | 0.257382 | 0.247898 | 0.224778 | 0.203437 |
| 6.309573 | 0.213648 | 0.213526 | 0.213643 | 0.213526 | 0.213162 | 0.209279 | 0.201513 | 0.182584 | 0.16511 |
| 7.943282 | 0.17291 | 0.172811 | 0.172906 | 0.172811 | 0.172514 | 0.169353 | 0.16303 | 0.147618 | 0.133391 |
| 10 | 0.139273 | 0.139193 | 0.13927 | 0.139193 | 0.138953 | 0.136392 | 0.131272 | 0.118789 | 0.107268 |
| 12.58925 | 0.111637 | 0.111572 | 0.111634 | 0.111572 | 0.111379 | 0.109316 | 0.105189 | 0.095131 | 0.085847 |
| 15.84893 | 0.089036 | 0.088984 | 0.089034 | 0.088984 | 0.088829 | 0.087175 | 0.083866 | 0.075802 | 0.068357 |
| 19.95262 | 0.070637 | 0.070596 | 0.070636 | 0.070596 | 0.070472 | 0.069152 | 0.066513 | 0.060078 | 0.054139 |
| 25.11886 | 0.055731 | 0.055698 | 0.05573 | 0.055698 | 0.0556 | 0.054552 | 0.052457 | 0.047349 | 0.042633 |
| 31.62278 | 0.043716 | 0.043691 | 0.043715 | 0.043691 | 0.043613 | 0.042785 | 0.04113 | 0.037096 | 0.033371 |
| 39.81072 | 0.034091 | 0.03407 | 0.03409 | 0.03407 | 0.034009 | 0.033359 | 0.032058 | 0.028887 | 0.02596 |
| 50.11872 | 0.026434 | 0.026418 | 0.026433 | 0.026418 | 0.02637 | 0.025861 | 0.024844 | 0.022363 | 0.020074 |
| 63.09573 | 0.020396 | 0.020383 | 0.020395 | 0.020383 | 0.020346 | 0.01995 | 0.019157 | 0.017225 | 0.015441 |
| 79.43282 | 0.015687 | 0.015677 | 0.015687 | 0.015677 | 0.015648 | 0.015341 | 0.014725 | 0.013223 | 0.011838 |
| 100 | 0.012068 | 0.012061 | 0.012068 | 0.012061 | 0.012038 | 0.011799 | 0.011321 | 0.010155 | 0.009078 |
| 125.8925 | 0.009341 | 0.009335 | 0.009341 | 0.009335 | 0.009318 | 0.009131 | 0.008758 | 0.007849 | 0.007009 |
| 158.4893 | 0.007342 | 0.007337 | 0.007342 | 0.007337 | 0.007324 | 0.007177 | 0.006883 | 0.006166 | 0.005504 |
| 199.5262 | 0.005936 | 0.005933 | 0.005936 | 0.005933 | 0.005922 | 0.005803 | 0.005567 | 0.004991 | 0.004459 |
| 251.1886 | 0.005012 | 0.005009 | 0.005012 | 0.005009 | 0.005 | 0.004902 | 0.004706 | 0.004228 | 0.003786 |
| 316.2278 | 0.004479 | 0.004476 | 0.004478 | 0.004476 | 0.004468 | 0.004383 | 0.004213 | 0.003799 | 0.003417 |
| 398.1072 | 0.004259 | 0.004257 | 0.004259 | 0.004257 | 0.00425 | 0.004172 | 0.004017 | 0.003639 | 0.00329 |
| 501.1872 | 0.004292 | 0.004289 | 0.004292 | 0.004289 | 0.004283 | 0.004208 | 0.004059 | 0.003695 | 0.003359 |
| 630.9573 | 0.004525 | 0.004523 | 0.004525 | 0.004523 | 0.004516 | 0.00444 | 0.00429 | 0.003923 | 0.003584 |
| 794.3282 | 0.004917 | 0.004914 | 0.004916 | 0.004914 | 0.004907 | 0.004828 | 0.00467 | 0.004285 | 0.00393 |
| 1000 | 0.005431 | 0.005429 | 0.005431 | 0.005429 | 0.005421 | 0.005336 | 0.005167 | 0.004753 | 0.004372 |
| Semi-Analytical Solutions (This Study) | H.Pratikno et al. Solutions (2003) SPE 84287 | Approximate Solutions (This Study) | Relative Error between H.Pratikno et al. Solutions and Semi-Analytical Solutions, % | Relative Error between Semi-Analytical Solutions and Approximate Solutions, % | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CfD | Ix = 0.1 | Ix = 0.5 | Ix = 1 | Ix = 0.1 | Ix = 0.5 | Ix = 1 | Ix = 0.1 | Ix = 0.5 | Ix = 1 | Ix = 0.1 | Ix = 0.5 | Ix = 1 | Ix = 0.1 | Ix = 0.5 | Ix = 1 |
| 0.1000 | 5.1692 | 3.5727 | 2.9135 | 5.1960 | 3.6909 | 3.3237 | 5.1787 | 3.5801 | 2.9210 | 0.52 | 3.31 | 14.08 | 0.18 | 0.21 | 0.26 |
| 0.1259 | 4.9454 | 3.3517 | 2.7003 | 4.9595 | 3.4544 | 3.0872 | 4.9480 | 3.3523 | 2.7020 | 0.29 | 3.06 | 14.33 | 0.05 | 0.02 | 0.06 |
| 0.1585 | 4.7252 | 3.1350 | 2.4928 | 4.7319 | 3.2268 | 2.8596 | 4.7276 | 3.1350 | 2.4945 | 0.14 | 2.93 | 14.72 | 0.05 | 0.00 | 0.07 |
| 0.1995 | 4.5091 | 2.9230 | 2.2915 | 4.5115 | 3.0064 | 2.6392 | 4.5139 | 2.9248 | 2.2953 | 0.05 | 2.85 | 15.18 | 0.11 | 0.06 | 0.17 |
| 0.2512 | 4.2979 | 2.7163 | 2.0972 | 4.2976 | 2.7924 | 2.4253 | 4.3051 | 2.7201 | 2.1031 | 0.01 | 2.80 | 15.64 | 0.17 | 0.14 | 0.28 |
| 0.3162 | 4.0924 | 2.5160 | 1.9111 | 4.0902 | 2.5850 | 2.2179 | 4.1009 | 2.5205 | 1.9179 | 0.05 | 2.74 | 16.05 | 0.21 | 0.18 | 0.35 |
| 0.3981 | 3.8940 | 2.3234 | 1.7340 | 3.8902 | 2.3851 | 2.0179 | 3.9024 | 2.3270 | 1.7405 | 0.10 | 2.66 | 16.37 | 0.22 | 0.16 | 0.37 |
| 0.5012 | 3.7040 | 2.1396 | 1.5672 | 3.6989 | 2.1938 | 1.8267 | 3.7112 | 2.1415 | 1.5726 | 0.14 | 2.53 | 16.55 | 0.19 | 0.09 | 0.34 |
| 0.6310 | 3.5242 | 1.9663 | 1.4118 | 3.5181 | 2.0130 | 1.6458 | 3.5296 | 1.9659 | 1.4157 | 0.17 | 2.37 | 16.57 | 0.15 | 0.02 | 0.27 |
| 0.7943 | 3.3560 | 1.8048 | 1.2687 | 3.3493 | 1.8442 | 1.4770 | 3.3598 | 1.8023 | 1.2713 | 0.20 | 2.18 | 16.42 | 0.11 | 0.14 | 0.21 |
| 1.0000 | 3.2008 | 1.6563 | 1.1386 | 3.1939 | 1.6888 | 1.3216 | 3.2036 | 1.6522 | 1.1405 | 0.21 | 1.96 | 16.08 | 0.09 | 0.25 | 0.17 |
| 1.2589 | 3.0597 | 1.5217 | 1.0218 | 3.0530 | 1.5479 | 1.1807 | 3.0623 | 1.5169 | 1.0238 | 0.22 | 1.72 | 15.55 | 0.09 | 0.32 | 0.19 |
| 1.5849 | 2.9333 | 1.4015 | 0.9186 | 2.9271 | 1.4220 | 1.0548 | 2.9364 | 1.3966 | 0.9210 | 0.21 | 1.46 | 14.83 | 0.10 | 0.35 | 0.27 |
| 1.9953 | 2.8219 | 1.2957 | 0.8285 | 2.8162 | 1.3111 | 0.9439 | 2.8259 | 1.2912 | 0.8318 | 0.20 | 1.18 | 13.94 | 0.14 | 0.35 | 0.40 |
| 2.5119 | 2.7249 | 1.2039 | 0.7508 | 2.7198 | 1.2147 | 0.8475 | 2.7301 | 1.2001 | 0.7551 | 0.19 | 0.89 | 12.89 | 0.19 | 0.32 | 0.57 |
| 3.1623 | 2.6418 | 1.1253 | 0.6847 | 2.6371 | 1.1320 | 0.7648 | 2.6480 | 1.1221 | 0.6899 | 0.18 | 0.60 | 11.71 | 0.24 | 0.29 | 0.75 |
| 3.9811 | 2.5713 | 1.0587 | 0.6290 | 2.5671 | 1.0620 | 0.6948 | 2.5784 | 1.0560 | 0.6348 | 0.16 | 0.31 | 10.47 | 0.28 | 0.26 | 0.93 |
| 5.0119 | 2.5121 | 1.0030 | 0.5825 | 2.5068 | 1.0017 | 0.6345 | 2.5198 | 1.0004 | 0.5888 | 0.21 | 0.12 | 8.93 | 0.30 | 0.26 | 1.06 |
| 6.3096 | 2.4630 | 0.9567 | 0.5441 | 2.4585 | 0.9534 | 0.5862 | 2.4708 | 0.9540 | 0.5505 | 0.18 | 0.35 | 7.73 | 0.31 | 0.28 | 1.15 |
| 7.9433 | 2.4225 | 0.9186 | 0.5126 | 2.4180 | 0.9129 | 0.5457 | 2.4301 | 0.9155 | 0.5187 | 0.19 | 0.62 | 6.46 | 0.31 | 0.33 | 1.19 |
| 10.0000 | 2.3894 | 0.8874 | 0.4868 | 2.3847 | 0.8796 | 0.5124 | 2.3966 | 0.8838 | 0.4926 | 0.20 | 0.88 | 5.26 | 0.30 | 0.41 | 1.18 |
| 12.5893 | 2.3625 | 0.8620 | 0.4659 | 2.3576 | 0.8525 | 0.4853 | 2.3690 | 0.8577 | 0.4712 | 0.20 | 1.11 | 4.17 | 0.28 | 0.51 | 1.12 |
| 15.8489 | 2.3406 | 0.8415 | 0.4490 | 2.3356 | 0.8305 | 0.4633 | 2.3465 | 0.8364 | 0.4537 | 0.21 | 1.31 | 3.19 | 0.25 | 0.61 | 1.04 |
| 19.9526 | 2.3230 | 0.8249 | 0.4354 | 2.3179 | 0.8128 | 0.4456 | 2.3281 | 0.8190 | 0.4395 | 0.22 | 1.47 | 2.35 | 0.22 | 0.72 | 0.93 |
| 25.1189 | 2.3088 | 0.8116 | 0.4244 | 2.3037 | 0.7985 | 0.4314 | 2.3132 | 0.8050 | 0.4280 | 0.22 | 1.61 | 1.64 | 0.19 | 0.83 | 0.83 |
| 31.6228 | 2.2974 | 0.8009 | 0.4157 | 2.2923 | 0.7872 | 0.4200 | 2.3012 | 0.7936 | 0.4187 | 0.22 | 1.72 | 1.04 | 0.17 | 0.92 | 0.73 |
| 39.8107 | 2.2883 | 0.7924 | 0.4086 | 2.2832 | 0.7781 | 0.4109 | 2.2916 | 0.7846 | 0.4113 | 0.22 | 1.80 | 0.56 | 0.15 | 0.99 | 0.65 |
| 50.1187 | 2.2810 | 0.7855 | 0.4030 | 2.2760 | 0.7709 | 0.4037 | 2.2840 | 0.7774 | 0.4054 | 0.22 | 1.86 | 0.18 | 0.13 | 1.05 | 0.59 |
| 63.0957 | 2.2752 | 0.7801 | 0.3986 | 2.2703 | 0.7652 | 0.3980 | 2.2780 | 0.7717 | 0.4008 | 0.21 | 1.90 | 0.13 | 0.12 | 1.09 | 0.56 |
| 79.4328 | 2.2705 | 0.7757 | 0.3950 | 2.2658 | 0.7607 | 0.3935 | 2.2733 | 0.7672 | 0.3972 | 0.21 | 1.93 | 0.36 | 0.12 | 1.10 | 0.55 |
| 100.0000 | 2.2668 | 0.7722 | 0.3921 | 2.2623 | 0.7572 | 0.3900 | 2.2697 | 0.7638 | 0.3944 | 0.20 | 1.95 | 0.55 | 0.12 | 1.10 | 0.58 |
| 125.8925 | 2.2639 | 0.7695 | 0.3899 | 2.2595 | 0.7543 | 0.3872 | 2.2670 | 0.7613 | 0.3924 | 0.20 | 1.96 | 0.69 | 0.13 | 1.08 | 0.63 |
| 158.4893 | 2.2616 | 0.7673 | 0.3881 | 2.2573 | 0.7521 | 0.3850 | 2.2650 | 0.7594 | 0.3908 | 0.19 | 1.97 | 0.80 | 0.15 | 1.04 | 0.71 |
| 199.5262 | 2.2597 | 0.7655 | 0.3866 | 2.2555 | 0.7504 | 0.3832 | 2.2636 | 0.7581 | 0.3898 | 0.19 | 1.98 | 0.89 | 0.17 | 0.98 | 0.81 |
| 251.1886 | 2.2582 | 0.7641 | 0.3855 | 2.2541 | 0.7489 | 0.3818 | 2.2626 | 0.7572 | 0.3891 | 0.18 | 1.99 | 0.97 | 0.20 | 0.91 | 0.93 |
| 316.2278 | 2.2570 | 0.7630 | 0.3846 | 2.2529 | 0.7478 | 0.3806 | 2.2621 | 0.7567 | 0.3888 | 0.18 | 2.00 | 1.04 | 0.22 | 0.83 | 1.07 |
| 398.1072 | 2.2561 | 0.7621 | 0.3839 | 2.2519 | 0.7468 | 0.3796 | 2.2619 | 0.7565 | 0.3886 | 0.19 | 2.01 | 1.11 | 0.26 | 0.74 | 1.23 |
| 501.1872 | 2.2553 | 0.7614 | 0.3833 | 2.2511 | 0.7459 | 0.3788 | 2.2619 | 0.7566 | 0.3887 | 0.19 | 2.03 | 1.18 | 0.29 | 0.64 | 1.39 |
| 630.9573 | 2.2547 | 0.7609 | 0.3828 | 2.2503 | 0.7452 | 0.3780 | 2.2621 | 0.7568 | 0.3889 | 0.20 | 2.06 | 1.26 | 0.33 | 0.54 | 1.56 |
| 794.3282 | 2.2543 | 0.7604 | 0.3825 | 2.2496 | 0.7445 | 0.3774 | 2.2625 | 0.7572 | 0.3893 | 0.21 | 2.09 | 1.34 | 0.37 | 0.43 | 1.74 |
| 1000 | 2.2539 | 0.7601 | 0.3822 | 2.2490 | 0.7439 | 0.3767 | 2.2631 | 0.7577 | 0.3897 | 0.22 | 2.13 | 1.44 | 0.40 | 0.32 | 1.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Lu, B.; Wu, M.; Luo, W. A New Pseudo Steady-State Constant for a Vertical Well with Finite-Conductivity Fracture. Processes 2018, 6, 93. https://doi.org/10.3390/pr6070093
Cui Y, Lu B, Wu M, Luo W. A New Pseudo Steady-State Constant for a Vertical Well with Finite-Conductivity Fracture. Processes. 2018; 6(7):93. https://doi.org/10.3390/pr6070093
Chicago/Turabian StyleCui, Yudong, Bin Lu, Mingtao Wu, and Wanjing Luo. 2018. "A New Pseudo Steady-State Constant for a Vertical Well with Finite-Conductivity Fracture" Processes 6, no. 7: 93. https://doi.org/10.3390/pr6070093
APA StyleCui, Y., Lu, B., Wu, M., & Luo, W. (2018). A New Pseudo Steady-State Constant for a Vertical Well with Finite-Conductivity Fracture. Processes, 6(7), 93. https://doi.org/10.3390/pr6070093





