Abstract
This work presents a mathematical model for the simultaneous optimisation of water and energy usage in hydraulic fracturing using a continuous time scheduling formulation. The recycling/reuse of fracturing water is achieved through the purification of flowback wastewater using thermally driven membrane distillation (MD). A detailed design model for this technology is incorporated within the water network superstructure in order to allow for the simultaneous optimisation of water, operation, capital cost, and energy used. The study also examines the feasibility of utilising the co-produced gas that is traditionally flared as a potential source of energy for MD. The application of the model results in a 22.42% reduction in freshwater consumption and 23.24% savings in the total cost of freshwater. The membrane thermal energy consumption is in the order of 244 × 103 kJ/m3 of water, which is found to be less than the range of thermal consumption values reported for membrane distillation in the literature. Although the obtained results are not generally applicable to all shale gas plays, the proposed framework and supporting models aid in understanding the potential impact of using scheduling and optimisation techniques to address flowback wastewater management.
1. Introduction
The “shale revolution” has triggered a dramatic change in oil and natural gas production globally. From 2007 to 2015, the US witnessed an increase in the amount of shale gas produced from 2 to 15 trillion cubic feet per year [1], with estimates of continued growth to support monetisation projects [2]. The process by which shale gas production is carried out, known as hydraulic fracturing, is associated with several environmental challenges, i.e., water usage and wastewater discharge as well as flaring of co-produced gas. Water management decisions within shale gas production can be grouped into two main categories, i.e., the usage of water in the process of hydraulic fracturing and managing the effluent generated from drilling and production. The production of shale gas typically requires 7000 to 18,000 m3 of water to fracture and drill a typical well [3,4,5]. A main challenge associated with water usage in hydraulic fracturing is the relatively short time within which the large volume of fracturing fluid is needed [4]. Another issue of contention that has impeded the ongoing progress in shale gas production processes is water contamination. Two categories of wastewater are generated: flowback water and produced water. Flowback water is the wastewater that returns to the surface within the first few weeks after hydraulic fracturing, and is characterised by a high flowrate and volume generated in the range between 10% and 40% of the initial injected fluid [4]. The contaminants found in flowback water include total suspended solids (TSS), metals, organics, and total dissolved solids (TDS), with the TDS value ranging between 20,000 mg/L and 300,000 mg/L depending on the shale formation and how long the water remains underground [3,4]. Produced water, on the other hand, is the wastewater generated in the production stages. It is made up of the formation water and the injected fracturing fluid generally characterised by high salinity. In selecting appropriate options for the effective management of the high volume of the generated flowback water, several factors have to be considered. These include environmental regulation, the amount and types of contaminants in the wastewater, and economics factors. Thus, water consumption in shale gas production is a serious matter, making water resource management an important operational and environmental issue [6]. The increase in the cost of freshwater and the disposal of generated wastewater, limitations in providing fresh water for fracturing, and the concerns about the negative environmental impact of shale gas wastewater have spurred the interest in identifying cost-effective technologies that can reduce the usage of fresh water and the discharge of wastewater in shale gas production [7].
The proper management of water resources requires wastewater treatment for reuse and/or recycling, which can be accomplished by the use of water treatment units, categorised as membrane or non-membrane processes. Flowback water reuse in hydraulic fracturing demands low salinity, as high salinity can lead to formation damage, affect the performance of some friction reducers, and damage the drilling equipment [8]. The choice of the treatment technology depends on the level of purity required, the mobility, and the economics of the process. The membrane-based process for water treatment is energy intensive; therefore, minimising energy is also of great importance. In this study, we considered membrane distillation (MD) as the membrane technology of interest. MD has emerged as a promising technology in wastewater treatment, gaining a high level of interest in industries especially where high purity separation is of great importance. It is capable of treating wastewater from oil and gas effectively [8]. In MD, the feed is pre-heated to a temperature below the boiling point, which ranges between 323 and 363 K in the case of water treatment application. The water vapour then travels through a hydrophobic, microporous membrane. The vapour is condensed on the permeate side using the stored permeate and collected as pure liquid. The driving force in membrane distillation is the chemical potential difference across the membrane, which depends on the difference between the vapour pressure of the feed and the permeate sides. There are various benefits associated with the use of MD in the areas of water recycling and/or reuse as well as desalination, particularly in shale exploration [8,9]. These include:
- Low-level heating and the ability to operate with moderate temperature and pressure; this is a very crucial factor in shale exploration due to the availability of wasted energy from flaring which can be used as an energy source for MD.
- The ability to treat a highly concentrated feed, which is the case with water, generated from hydraulic fracturing.
- Compact size and modular nature: MD is characterised with a small footprint due to the high surface area to volume ratio of the membrane. It can also be easily adjusted to the required capacity by the removal or addition of MD modules, which allow for easy movement from one well pad to another. All of these factors make MD a candidate desalination technology in this study.
Several authors have developed various optimisation strategies for water management in shale gas production. Yang et al. [4] developed a mixed integer linear programming (MILP) model, which later extended to a mixed integer nonlinear programming (MINLP) model [10] for the investment and scheduling of optimal water management in shale gas production using a discrete time formulation. The linear and nonlinear models dealt with short-term and longer-term operations, respectively. Gao and You [11] approached a similar issue by developing a mixed integer linear fractional programming (MILFP) that focuses on the minimisation of freshwater use in hydraulic fracturing per unit of profit but assumed a fixed schedule for the well pad fracturing. Gao and You [12] also developed a stochastic mixed integer linear fractional programming (SMILFP) model for the optimisation of the levelized cost of energy produced from shale gas. Elsayed et al. [8] proposed an optimisation method based on multi-period formulation for the treatment of shale gas flowback water, which takes into account the fluctuation in the contaminant concentration and flowrate using membrane distillation. Bartholomew and Mauter [13] developed a multi-objective MILP model which is formulated to determine the water management approach that reduces both financial, human health, and environment cost associated with shale gas water management. Lira-Barragán et al. [14] developed an optimisation framework to deal with the uncertainties associated with the management of water in shale gas production. However, most of these studies have either adopted the discrete time scheduling formulation for the well pad fracturing or assumed a fixed schedule. A limitation of discretising the time horizon is the explosive binary dimension that could lead to higher computational time and suboptimal solution. Assuming a fixed schedule is a huge drawback, as this has a great effect on the overall profit. In addition, most of the research conducted in this area has represented the wastewater treatment unit as a “black box” which does not give the true cost representation of the project or uses “short cut” regenerator model [15] due to the complexity of the regenerator design.
Flaring is the burning of natural gas that cannot be refined or sold. Flaring is carried out frequently in most industrial plants, especially in managing unusual or irregular occurrences. Flaring in most industries is carried out to decrease hazard in the course of distress in an industrial operation, to get rid of associated gases, or to safely manage process start-up and shutdown [16]. In order to minimise flaring in industries, legislative acts should be implemented so that industries will take necessary precautions. Another way of achieving this is by the recovery and efficient utilisation of flaring streams [17]. In the context of shale exploration, flaring is common in areas where oil and gas are co-produced with no sufficient infrastructure for gathering the gas. Because of this drawback, the producer either choses to build the pipeline or gathering facilities, flare the gas, or find a useful way of utilising the gas on site [18]. Although facts about the rate of flaring after well completion is yet to be published, information from the literature suggests that the time at which gas is mostly flared coincides with the time when a substantial volume of flowback water is recovered. According to Glaizer et al. [18], flaring of gas is mostly done in the first 10 producing days after initial completion or recompletion of a well. For example, 15,041 wells were completed in Texas in 2012, which led to the flaring of 1.36 billion m3 (48 billion ft3) of natural gas. The estimated rate of flare based on these figures can be set at 9600 m3 per well per day, though variation might occur based on a particular well [18]. In general, flaring is found to be a waste of resources globally, resulting in serious environmental problems such as air, thermal, and light pollution [19]. Studies available in the literature for the utilisation of the co-produced gas that is flared after well completion is either focused on onsite atmospheric water harvesting [19] using the captured gas or using it as a source of heat [18] for heat-based regenerators. However, it needs to be mentioned that the work by Glazer et al. [18] was conducted based on analytical framework and not in the context of mathematical optimisation.
This paper focuses on the synthesis and optimisation of an integrated water and membrane network that simultaneously optimises water and energy consumption in hydraulic fracturing using continuous time mathematical formulation for scheduling. The membrane technology considered is membrane distillation (MD). A detailed design of MD is incorporated to determine the optimal operating conditions for efficient energy use. The rest of the paper is structured as follows. Section 2 gives the general problem statement and its assumption. Section 3 provides detailed information about the superstructure for the total network. The model formulation is presented in Section 4, while in Section 5 a case study is examined to demonstrate the model applicability. Finally, the conclusions are given in Section 6.
2. Problem Statement
The problem statement in this work can be stated as follows.
Given the following:
- Number of freshwater sources (interruptible and uninterruptible);
- Set of well pads S to be fractured with a known volume of water required for fracturing and a maximum allowable contaminant concentration in the fracturing fluid;
- Total number of frac stages for each well pad;
- Earliest fracturing date for each well pad;
- Set of wastewater injection wells D;
- Volume of water required per stage;
- Minimum and maximum number of stages that can be fractured per day;
- Time horizon of interest;
- Network of regenerator;
- Gas storage facility;
- Historical stream data for the interruptible source,
Determine the optimal configuration of the total network that gives:
- Optimal fracturing schedule of the well pads;
- Minimum freshwater intake and wastewater generation;
- Optimal operation and design conditions of the regenerator such as the number of membrane modules and the energy consumption;
- Feasibility of using captured flared gas as an energy source for the regenerator.
The assumptions made in the model formulation are as follows:
- The wells in each well pad are aggregated [4];
- Each well pad is connected to exactly one of the impoundment through piping [4];
- The number of fracturing stages that could be fractured per day is kept constant at 4 instead of allowing it to be variable between 2 and 4 stages [4];
- The flowback water from the fractured well pad is assumed to be 25% [10] of the initial water used;
- The capacity of the wastewater tank and fracturing tank on each well pad varies depending on its water requirement;
- The water treatment unit is located onsite and can be moved from one well pad to the other;
- The historical flowrate data for the interruptible water source from each calendar year is treated as a scenario, and each year is treated with equal probability [4].
3. Superstructure Representation
Based on the problem statement, the superstructure in Figure 1 is developed. In the superstructure, two types of freshwater sources are considered (interruptible and uninterruptible sources) [4]. An uninterruptible source is a big water body with guaranteed water availability throughout the year, but the mode of transportation is trucking. The interruptible source is a nearby source that requires piping but with uncertain water availability all year round. These two sources are considered because water management decisions are primarily influenced by transportation costs [4]. In order to complete a typical well pad, roughly 4000–6500 one-way truck trips are needed. Hence, due to the high cost of trucking and other environmental impacts related to drawing water from uninterruptible sources, operators are encouraged to draw water from sources that are close by through piping [4]. The water from any of these sources can be stored in any impoundment t prior to its usage. S represents a set of well pads to be fractured in which the fracking fluid is blended using freshwater from the impoundment and the recycled water from the fracturing tank. The maximum concentration of TDS into the well pads is kept at an upper limit of 50,000 ppm [10,13]. The flowback water generated from the fractured well pad in the first two weeks after fracturing is assumed to be 25% of the initial water used [10]. This flowback water can be sent to regenerator R for treatment or any injection well D for disposal. The flowback water sent to regenerator R is treated before it is sent to the fracturing tank for reuse in the next well pad. The product of a particular well pad after stimulation can be either oil and gas or gas only, depending on the geological formation of the shale play. For a well pad that produces oil and gas, the co-produced gas can be captured and stored in the gas storage facility from where it is supplied to the regenerator R as fuel, which in turn produces the heat energy needed by the regenerator while the oil is sent to the market. In the case of a gas-producing well, part of the gas can be diverted into the gas storage facility for wastewater treatment while the rest can be sent to the market.
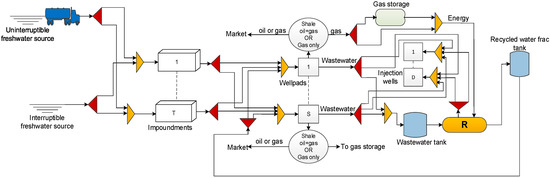
Figure 1.
Superstructure representation of the water network.
The mode of operation of the regenerator is as stated below:
- The transfer of water from the wastewater tank to the regenerator R is conducted provided that there is a well pad to be fractured. Whenever the regenerator starts operation, it operates continuously until the wastewater tank becomes empty.
- The regenerator only operates if there is a well pad to be fractured, otherwise it remains inactive.
- The performance of the regenerator is specified based on a variable removal ratio.
4. Model Formulation
The mathematical model presented in this section is based on the superstructure given in Figure 1. The problem is formulated as a mixed integer nonlinear programming (MINLP) model, which is divided into two sections developed inside the same structure to simultaneously optimise water and energy. The first section focuses on mass balance and scheduling while the second is based on the detailed membrane distillation model. The scheduling framework adopted here is based on the state task network (STN) and unequal discretisation of the time horizon, which involves time point n occurring at an unknown time. A time point is a precise moment within a given horizon when an event occurs (e.g., start of task, end of task, transfer of materials, etc.). It is generally used to track inventory levels and model the occurrence of tasks in batch and semi-batch processes. Among the important decision variables are the 0–1 variables which indicate if a well pad is fractured or if water is transferred to storage and if regeneration takes place. The following three sets of binary variables are used:
is assigned a value of 1 if well pad s is stimulated at time point n.
is assigned a value of 1 if the transfer of water takes place from well pad s to storage at time point n.
is assigned a value of 1 if the transfer of water from storage to the regenerator takes place at time point n.
In order to explain the model, the constraints characterising the optimisation formulation are described.
4.1. Mass Balance Constraint
It is important to state the mass balances around each well pad, the impoundment, the wastewater storage tank, the fracturing tank, the injection well, and the regenerator.
4.1.1. Mass Balance around Well Pad s
The mass balance around a well pad is conducted in accordance with Figure 2. The total volume of water required to fracture well pad s at time point n, , is given by Equation (1), where is the amount of water required to fracture well pad s and is the binary variable that indicates if well pad s is fractured at time point n. This water requirement is supplied with freshwater from the impoundment and/or reused water from the fracturing tank , which is obtained by Equation (2). Equation (3) specifies that only freshwater is to be used at the first time point.
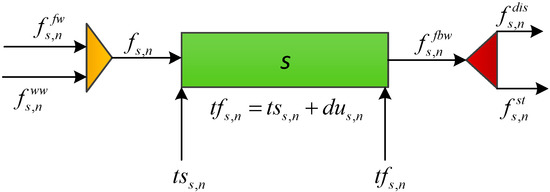
Figure 2.
Mass balance representation around a well pad.
The flowback water generated in the first two weeks after fracturing is assumed to be 25% of the initial water used and is given by Equation (4). Equation (5) gives the TDS concentration in the wastewater where is the flowback water concentration of well pad s. The value used is between the average value in the first two weeks after fracturing and the highest value that can be found in typical flowback water, as reported in literature. Equation (6) states that the flowback water after well pad fracturing could be discarded as effluent or sent to the wastewater storage tank where is the volume of wasewater sent to storage and is the volume of wastewater sent to disposal from well pad s at time point n.
The mass balance around the impoundment is conducted in accordance with Figure 3, as given in Equations (7) and (8). Equation (7) describes the total water use from impoundment t at time point n given the piping connection TPs,t between impoundment t and well pad s. The volume of impoundment t at time point n for a given scenario year is described by Equation (8). The equation states that the volume of freshwater stored in the impoundment consists of the volume stored at the previous time point and the difference between the amount of water entering the impoundment through trucking and piping and the total water leaving the impoundment to well pads. is a continuous variable which specifies the amount of water supplied through piping from an interruptible source to the corresponding impoundment at time point n and is the amount of water supplied through trucking.
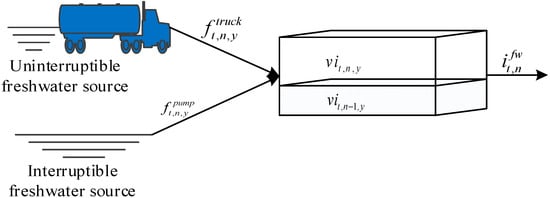
Figure 3.
Mass balance representation around the impoundment.
Equation (9) states that the total volume of water disposed at time point n is the sum of the flowback water sent to disposal from well pad s and the concentrate from the regenerator . This total amount of water can be disposed into any injection well , as given in Equation (10), while Equation (11) states that the throughput into each injection well should not exceed the maximum it can take. is a continous variable indicating the throughput of an injection well d at time point n, and is the parameter indicating the maximum capacity of the injection well.
Equation (12) gives the expected production from well pad s at time point n, where is a parameter indicating the gas production of well pad s.
4.1.2. Mass Balance around the Wastewater Storage Tank and the Fracturing Tank
The mass and contaminant balances around the wastewater storage tank and the fracturing tank are conducted in accordance with Figure 4. Part of the assumption made in this study is that all of the flowback water sent to storage from well pad s fractured at a previous time point is the quantity that is treated by the regenerator at time point n, as stated in Equation (13). This indicates that the volume of the wastewater tank on each well pad becomes zero at the end of each time point. The concentration of water sent to the treatment unit is given by Equation (14), where is the contaminant concentration in the treatment unit at time point n.
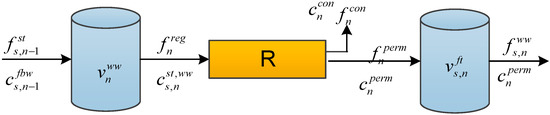
Figure 4.
Mass balance representation around the storage tank, regenerator, and fracturing tank.
The capacity of the treatment wastewater tank at time point n is bounded by the volume of flowback water to be treated at time point n, as given in Equation (15). Equations (16)–(18) ensure that the maximum capacity of the tank is not exceeded, where and are parameters that indicate the maximum and minimum capacity of the wastewater storage tank, respectively. Equation (19) ensures that no water is stored in the storage tank at the end of the time horizon.
The capacity of the fracturing tank on well pad s depends on the volume of wastewater required at the well pad, as defined in Equation (20).
4.1.3. Mass Balance around the Regenerator
Equation (21) states that the total volume of water into the regenerator at time point n is the sum of the amount collected as permeate and the amount sent to disposal as concentrate . The contaminant balance around the regenerator is given in Equation (22), where represents the outlet concentration of contaminants from the regenerator and is the contaminant concentration removed from the water by the regenerator at time point n. Equation (23) states that the inlet contaminant concentration into the regenerator should not exceed the maximum it can take, where is the maximum inlet concentration into the regenerator. The performance of the regenerator is a function of the removal ratio (RR) of contaminants, as stated in Equation (24). The quantity of water to be collected as permeate and concentrate depends on the recovery ratio (LR), as stated in Equations (25) and (26), respectively.
The amount of wastewater reused at any time point is supplied through the permeate stream from the regenerator, as given in Equation (27). Equation (28) ensures that the maximum allowable concentration in the well pad is not exceeded, where is the maximum inlet contaminant concentration in well pad s.
4.2. Scheduling Model
The scheduling part of the model captures the time dimension related to the process. These are categorised into three parts, namely:
- well pad scheduling,
- wastewater storage tank scheduling, and
- regenerator scheduling.
4.2.1. Well Pad Scheduling
Equation (29) is the allocation constraint that specifies that each well pad s has to be fractured exactly once at a given time point n in the time horizon.
Equation (30) states that no task can start at the end of the time horizon.
The duration of each well pad is calculated by Equation (31), where is the time required to fracture well pad s. Equations (32) and (33) give the finish time of each well pad expressed with big-M constraints, which are only active if well pad s is stimulated at time point n, where is the start time of fracturing well pad s at time point n.
Equation (34) states that the time at which the fracturing of well pad s begins, , is equal to the time at which time point n occurs , i.e., the start time of each well pad must coincide with a time point.
Equation (35) gives the sequence-dependent change over time between well pad s and . It states that the start time of well pad s’ at time point n must be equal to or greater than the finish time of well pad s at a previous time point plus the crew transition time between well pad s and s’. Equation (36) states that the time at which time point n occurs must correspond with the availability time of well pad s.
4.2.2. Storage Tank Scheduling
Water usage in hydraulic fracturing and the water sent to the storage tank for treatment are linked by Equation (37). This equation states that water can only be transferred from well pad s to the wastewater tank for treatment if well pad fracturing takes place at that time point. Equations (38) and (39) ensure that the transfer time of water from a well pad into storage corresponds with the time when the fracturing task ends .
4.2.3. Regenerator Scheduling
Equation (40) relates the regeneration and fracturing task starting at time point n. It states that water regeneration can only take place at time point n if there is a well pad to be fractured at that time point. Equations (41) and (42) ensure that the time at which regeneration starts coincides with the time at which the fracturing task starts, at time point n. This is because all tasks starting at point n must start at the same time, although their finish times do not have to coincide. Equation (43) gives the duration of regeneration, where is the finish time of regeneration at time point n, is the total volume of water in the regenerator at time point n, and is the feed flowrate into the regenerator.
4.2.4. Tightening Constraint
Tightening formulations play an important role in finding good solutions for the original problem. Not adding a tightening constraint can lead to weak relaxation. Equation (44) imposes the requirement that the sum of the fracturing durations of all well pads should be less than or equal to the time horizon , while Equation (45) restricts the sum of the fracturing time of all well pads starting after to be smaller than the remaining time, where is the time at which time point n occurs.
4.3. Membrane Distillation (MD) Model
The detailed design model for the membrane distillation unit, which is based on the work of Elsayed et al. [9], is presented in this section. Various configurations of MD have been reported in the literature [9,20] with variation based on mode of vapour collection on the permeate side and the method of the driving force enhancement across the membrane. The focus of this study is on direct contact membrane distillation (DCMD), which is found to be the most commonly used configuration. Some of the merits associated with DCMD are ease of construction, operation, maintenance, and stability in operation [9]. Figure 5 illustrates a schematic representation of a typical direct contact membrane distillation unit. The flowback water is pre-heated to effect evaporation and the degree of pre-heating becomes an optimisation variable. The vapour passes through the membrane and condensation occurs on the permeate side using stored permeate, which is at relatively low temperature than the feed. Consideration must be given to both heat and mass transfer from the feed side to the permeate side of the membrane. Mass and heat transfer takes place across three sections [9,20]: mass transfer takes place in the boundary layer of the membrane on the feed side, across the membrane, and on the permeate side boundary layer. Heat transfer, on the other hand, takes place from the bulk of the feed to the interface of the membrane through a boundary layer via convection, across the membrane via conduction and latent heat associated with the vaporised flux, and through the boundary layer from the interface of the membrane to the bulk of the permeate via convection. In order to describe mass transfer through the membrane, a model such as Knudsen diffusion, molecular diffusion, or the incorporation of both have been established to yield quality results [20].
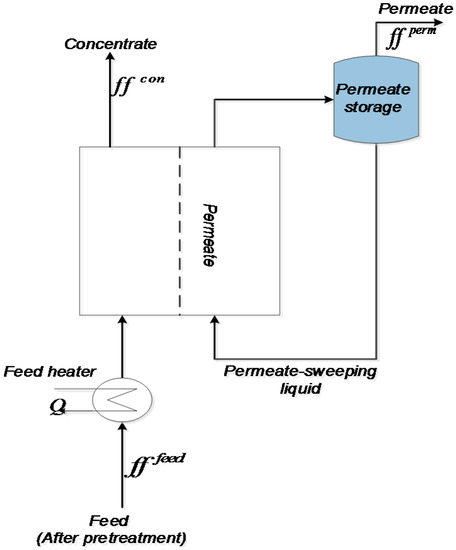
Figure 5.
Schematic representation of a typical direct contact membrane distillation.
The membrane distillation considered is a polyvinylidene fluoride flat sheet membrane used in DCMD. The details of this are given in Yun et al. [20].
The following assumptions are made for the constraints in the plant using a set of mathematical equations describing its operation:
Flowback water contains organics, oils, and total dissolved solids (TDS), mainly in the form of salts and other contaminants [21]. It is assumed that the flowback water is pre-treated to remove oils, organics, and other necessary contaminants. Membrane distillation is used to remove TDS, as this is the main contaminant of interest for water reuse/recycling in hydraulic fracturing.
The separation efficiency of the MD modules depends on temperature. This is because the permeate flux is also temperature-dependent.
The driving force for the water flux across the membrane, , is the difference in pressure of the water vapour and is defined in Equation (46):
where is the membrane permeability, is the water vapour pressure of the feed, is the water vapour pressure of the permeate, is the activity coefficient of water in the feed, and is the mole fraction of water in the feed.
The Antoine equation [21] is used to estimate the water vapor pressure of the feed and the permeate which depends on the temperature as given in Equations (47) and (48), where and are the temperature of the feed and the permeate on the membrane, respectively.
The activity coefficient is dependent on the concentration and on the assumption of NaCl as the primary solute. Equation (49) [22] can be used to estimate the activity coefficient, where is the molar concentration of NaCl in the feed.
Sodium chloride is chosen as the basis of calculation because it is reported to be the dominant species with regards to the concentration in the flowback/produced water [23,24,25]. It makes up over 50% of the total dissolved solids.
The permeability of the membrane depends on the membrane temperature , which differs based on the kind of diffusion. The permeability of membranes in which molecular diffusion occurs is calculated through Equation (50) as proposed by Elsayed et al. [9], where is the temperature-independent base value of membrane permeability.
The membrane temperature is the mean value of the bulk temperature of the feed, , and of the permeate, [26]. Therefore, the average temperature in the MD module can be determined by the expression given in Equation (51).
Mass and salt balance around the MD unit is conducted in accordance with Figure 3, as given in Equations (52)–(54):
where is the total flowrate into MD, and are the permeate and concentrate flowrate, and is the density of the water. The amount of water collected as permeate highly depends on the energy supplied to the unit. Therefore, the heat required by the feed is given in Equation (55):
where , , , are the specific heat capacity of the feed stream, temperature of the feed in the bulk, and temperature of the feed water into MD, respectively. Only a portion of the heat supplied to the unit is used to vaporise the permeate. This portion is the efficiency factor . Thus, Equation (56) gives the heat balance for the MD unit [9], where is the latent heat of vaporisation for water.
The thermal efficiency of MD, , can be measured using experimental data or a semi-empirical formula [9], as indicated in Equation (57). In this equation, is the membrane thermal conductivity and is the membrane thickness.
The thermal conductivity of a particular membrane can be determined using Equation (58), which is correlated based on the data of Khayet and Matsuura [27].
Equation (59), as proposed by Elsayed et al. [9], can be used to determine water vaporisation in the feed side of the membrane.
The transfer of heat through the boundary layers on the two sides of the membrane results in a temperature gradient between the bulk solutions and the surface of the membrane known as temperature polarisation, . This occurrence may lead to a significant reduction in the driving force; therefore, it is necessary to consider the temperature gradient across the membrane. Based on this, the temperature polarisation coefficient [28] may be used to calculate the membrane temperature profile as given in Equation (60).
In order to estimate the temperature polarisation coefficient of a particular membrane, experimental data or correlations may be used [27,29]. A linear behaviour as a function of the temperature, as provided by Khayet and Matsuura [27], is given in Equation (61).
In accordance with the experimental observation, two other simple assumptions are suggested [9,26]. The first assumption is that for MD with laminar flows of the feed and the sweeping liquid, the absolute value of the temperature difference between the bulk and the membrane on each side of the membrane is nearly the same, as given in Equation (62).
The second assumption is that the membrane temperature is the mean value of the bulk temperature of the feed and permeate, as specified in Equation (51) above. The liquid recovery, LR, is the fraction of the feed in the regenerator that is recovered as permeate. The fraction of water recovery by the MD unit is given by Equation (63).
The removal ratio, RR, is the mass load of contaminants in the concentrate stream of the regenerator as a fraction of the feed. It is assumed to be a variable in this work and is defined as given in Equation (64).
In order to determine the area of the membrane required, , the permeate flow rate is divided by the water flux as given in Equation (65).
The regeneration network takes into account the capital and the operational cost involved in the operation of the unit. These are incorporated in the overall objective function in order for the energy consumed as well as the cost associated with regeneration to be optimised together with water utilisation. The annual fixed cost of the MD network, , as proposed by Elsayed et al. [9], is given by Equation (66).
The annual operating cost excluding heating, , as proposed by Elsayed et al. [9], is given by Equation (67), where is the ratio of recycled reject to raw feed.
The annual heating cost, , is given by Equation (68), where is the annual operating time, is the heat requred by the feed into MD, and is a parameter indicating the cost of heating.
4.4. Additional Constraints
The thermal energy consumption per unit of water treated, , is given by Equation (69). Equation (70) gives the total energy required for treatment at any time point, . The volume of natural gas needed per time point, , is given in Equation (71), where is the energy density.
4.5. Objective Function
The objective is to maximise profit, which comprises of the following terms: (1) revenue from gas production, (2) freshwater transportation cost, (3) wastewater treatment cost, (4) disposal cost, (5) wastewater storage cost, and (6) pumping cost to treatment facility, as given in Equation (72).
Equations (1)–(71) constitute the full set of constraints for the optimisation program. In the aforementioned formulation, the following is the list of the decision variables for optimisation:
- : Total area of membranes (m2), defined by Equation (65).
- : Water pumped from an interruptible source at time point n in scenario year y (m3), defined by Equation (8).
- : Water trucked from an uninterruptible source at time point n in scenario year y (m3), defined by Equation (8).
- : Freshwater required to fracture well pad s at time point n (m3), defined by Equation (2).
- : Wastewater required to fracture well pad s at time point n (m3), defined by Equation (2).
- : Total flowback water to be treated at time point n (m3), defined by Equations (15).
- : Total flowrate into MD (m3/day), defined by Equation (43).
- : Total freshwater required from impoundment t for fracturing at time point n (m3), defined by Equation (7).
- : Water flux across the membrane (kg/(m2·s)), defined by Equation (46).
- : Water vapour pressure of the feed in MD (pa), defined by Equation (47).
- : Water vapour pressure of the permeate in MD (pa), defined by Equation (48).
- : Heat required by the feed into MD (kJ/day), defined by Equation (55).
- : Regenerator removal ratio, defined by Equation (64).
- : Temperature of the feed on the membrane (K), defined by Equation (60).
- : Temperature of the permeate on the membrane (K), defined by Equation (60).
- : Membrane average temperature (K), defined by Equation (51).
- : Temperature of the feed in the bulk (K), defined by Equation (55).
- : Temperature of permeate in the bulk (K), defined by Equation (51).
- : Volume of impoundment t at time point n in scenario year y (m3), defined by Equation (8).
- : Activity coefficient of water in the feed for membrane distillation, defined by Equation (49).
5. Case Study
In order to demonstrate the applicability of the proposed model, an example taken from Yang et al. [4] is considered. This case study represents the typical Marcellus Shale play. The example considered 14 well pads, a time horizon of 540 days, one uninterruptible freshwater source, and two interruptible sources connected to impoundments, as illustrated in Table 1. Thirty years of historical data were provided for the two interruptible sources. The selected membrane distillation is a polyvinylidene fluoride used in direct-contact membrane distillation. The details of this membrane module are given in Yun et al. [20] and Elsayed et al. [9]. The permeability of the membrane is a function of the membrane temperature, which varies depending on the type of diffusion. This is calculated based on molecular diffusion through Equation (50). In order to ensure a complete analysis of the model, three different scenarios are considered. Scenario 1 is the base case which is the water integration without regeneration. Scenario 2 is the case where black box model is used; i.e., water minimisation only and a linear cost function is used to estimate the cost associated with regeneration. Scenario 3 considers water integration involving a detailed regenerator where water and energy are optimised simultaneously.

Table 1.
Well pad data [4].
The parameters and the cost coefficients are given in Table 2 while the information regarding the average flowback water and total dissolved solids (TDS) profile for a given well pad in the first 14–20 days after well pad fracturing, and the expected gas production for each well pad are obtained from Yang et al. [4].

Table 2.
Parameters and cost coefficients.
The resulting model was implemented in GAMS and solved using the general purpose global optimisation solver (BARON), which uses a branch-and-reduce algorithm to obtain a solution. Although BARON is not always guaranteed to converge to the global optimum, it has a proven track record in solving non-convex MINLP problems. The performance of BARON and statistics in solving a wide variety of test problems have been reported in the literature [30,31,32]. The solution comparison and the computational statistics between the three scenarios are given in Table 3 and Table 4, respectively. The total volume of water required for the 14 well pads is found to be 818,800 m3. The results encourage the use of freshwater from interruptible sources, which is achieved through piping, thereby reducing the high cost and environmental issues that are associated with trucking. It should be noted that Scenario 1, which involved the use of freshwater only, does not take into account the extra cost associated with the water network such as the cost of treatment and storage. Thus, no comparison with regard to profit is conducted between the three scenarios, as shown in Table 3. The total revenue for both Scenarios 2 and 3 is found to be $261.24 million and the total profit for Scenario 3 is found to be 0.6% higher than the profit obtained in Scenario 2. This is mainly due to the fact that the costs of wastewater disposal and treatment cost are higher in Scenario 2 compared to Scenario 3.

Table 3.
Solution comparison.

Table 4.
Computational statistics.
The fracturing schedules for the three scenarios are presented in Figure 6, Figure 7 and Figure 8. As can be seen from these figures, the schedules involved different timing and sequences. As the schedule in Figure 6 only consider freshwater usage, the well pads fracturing followed each other depending on the availability of each well pad and also on the water availability in the impoundment. The gap between S7 and S8 in Figure 6 is due to the fact that S7 is available from day 1 while S8 only becomes available after day 273. In Figure 7 and Figure 8, it is observed that well pad 6 is fractured last in both schedules. This is because well pad 6 has the least number of stages, which implies that it will require the lowest volume of water for fracturing, thereby reducing the volume of wastewater to be disposed in the last time point. The gaps between S8 and S9 in Figure 6, S5 and S4 in Figure 7, and S3 and S5 in Figure 8 may be attributed to what is referred to as a frac holiday, which depends mainly on water availability for fracturing. According to the literature [4], fracturing idle time (holiday) is a flexible period when the fracturing crew takes time off, usually due to low water availability. Figure 7 and Figure 8 show that the tightness in the fracturing schedule of each group of well pads which is much more profound in Figure 8, improve the effectiveness of flowback water reuse.
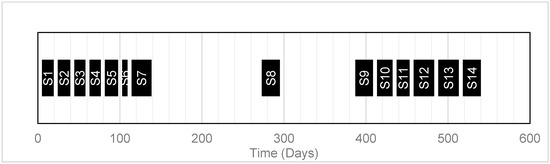
Figure 6.
Fracturing schedule (base case).
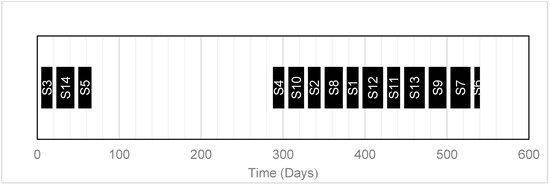
Figure 7.
Fracturing schedule (Scenario 2).
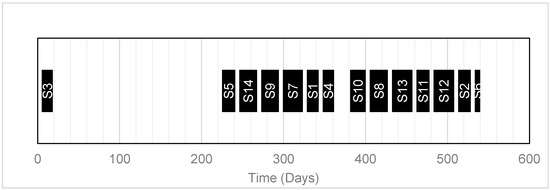
Figure 8.
Fracturing schedule (Scenario 3).
As a result of effective flowback water reuse, a saving of 183,534.65 m3 of freshwater is achieved out of the total volume of 818,800 m3 required for the 14 well pads. The saving is found to be 21.23% higher than those of a previous study in literature [4] that uses discrete time formulation. In Scenario 2, 96.7% of the flowback water is sent to the regenerator (R) and the remaining 3.3% is sent to the injection well to be disposed, while in Scenario 3, 99.4% of the flowback water is sent to the regenerator (R) while the remaining 0.6% is disposed.
In order to calculate the cost and energy associated with wastewater regeneration, cost analyses based on the black box model, standalone model, and detailed model were performed. The costs of regeneration were found to be $11.2 million, $9.8 million, and $10.5 million, respectively. The results show that the deviation of the cost function (black box model) from the actual cost of regeneration (standalone model) is 12.7%. The result obtained in Scenario 3 shows that the optimised cost of regeneration is 6.6% higher than the cost of MD standalone model. This is because optimising the temperature of the feed into MD results in a reduction of the water flux, thereby increasing the membrane area required which in turn leads to an increase in the fixed cost of the membrane. When water minimisation alone is considered, the membrane operates at the maximum feed temperature of 363 K which leads to the maximisation of the water flux across the membrane, hence the membrane area and the fixed cost are minimised. However, this does not necessarily indicate that the membrane performance is optimal, which is in agreement with the work of Elsayed et al. [9]. The design specifications for the optimal design of the MD regenerator are given in Table 5. The optimal feed temperature was found to be 354 K and the membrane area required was 186.67 × 103 m2. The permeate flux, thermal efficiency, thermal energy required, and the removal ratio are also given in Table 5. The model prediction of 0.013 kg/(m2 s) fow Much Water Does U.S [9], as well as the experimental data of 0.0125 kg/(m2 s) at 351 K reported by Yun et al. [20].

Table 5.
Design specification for MD.
The simultaneous optimisation of both energy and water within the water network results in a 12.7% reduction in the amount of energy required by the regenerator based on the throughput per day. The amount of energy required is reduced from 699 × 106 kJ (equivalent to 18,250 m3 of natural gas) to 610 × 106 kJ (equivalent to 15,926 m3 of natural gas). The value of energy consumed by the regenerator is 244 × 103 kJ/m3 of distillate, which is found to be less than the range of thermal energy reported in the literature for membrane distillation. The range of thermal energy required by membrane distillation is between 120 and 1700 kWh/m3, equivalent to between 432 × 103 kJ/m3 and 6.12 × 106 kJ/m3 [23,33]. The average volume of flared gas per unit time based on literature [18] is used in this study and this is compared to the energy requirement of the regenerator. Gas that would otherwise be flared is used as the source of heat for the regenerator, thereby, making the heating cost in the objective function to become zero.
6. Conclusions and Recommendations for Future Work
This work explores simultaneous water and energy optimisation in shale play using continuous time formulation with the incorporation of a detailed MD model within the water network. The goal is to balance the trade-off between water acquisition from interruptible and uninterruptible water sources. It was shown that water acquisition from interruptible sources through piping can lead to a reduction in both the freshwater cost and the high environmental impact associated with trucking water from uninterruptible sources. The results also demonstrated that for the considered case study, membrane distillation is capable of handling wastewater from hydraulic fracturing effectively, so that 99.4% of the flowback water generated is treated and reused. The efficient reuse of wastewater leads to a 22.42% reduction in the amount of freshwater required. The importance of simultaneously optimising the fracturing schedule with water and energy management was demonstrated. The approach indicates that optimising energy and water simultaneously results in a significant reduction in the amount of thermal energy required for regeneration. It is difficult to find the specific amount/volume of gas flared per well pad in the literature. However, based on the average data gathered from the literature, the amount of gas that is flared in most shale play is sufficient to provide the energy needed for regeneration. Considering the uncertainties associated with shale gas exploration in terms of water usage for hydraulic fracturing, flowback water generation, the cost associated with water management, and the price of oil and gas, future work will address the uncertainties associated with the process and the possible impact of such uncertainties on the overall project. Future work can also consider multiple desalination technologies and the integration of fossil energy with renewable sources to reduce the carbon footprint of the resulting network [34,35]. Hence, sustainability-based objective functions can be used to optimise the system design [36,37].
Author Contributions
Conceptualisation, D.O., T.M., R.M., D.S., and M.E.-H.; Data curation, D.O. and T.M.; Formal analysis, D.O., T.M., R.M., and D.S.; Funding acquisition, T.M.; Investigation, D.O. and T.M.; Methodology, D.O., T.M., and M.E.-H.; Resources, T.M.; Software, D.O., T.M., R.M., D.S., and M.E.-H.; Supervision, T.M. and M.E.-H.; Validation, D.O., T.M., R.M., D.S., and M.E.-H.; Visualisation, D.O., T.M., R.M., D.S., and M.E.-H.; Writing–original draft, D.O.; Writing−review and editing, D.O., T.M., R.M., D.S., and M.E.-H.
Funding
This research was funded by the National Research Foundation (NRF), South Africa.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Sets | |
| {d | d = injection well} | |
| {n | n = time point} | |
| {s | s = well pad} | |
| {t | t = an interruptible source and its corresponding impoundment} | |
| Match between well pad s and source t | |
| {y | y = historical river flowrate data year} | |
| Parameters | |
| Availability time of well pad s, day | |
| Annual operating time, h | |
| Temperature independent base value for the permeability, kg/m2.s.pa.K1.334 | |
| Specific heat capacity of the feed stream, KJ/(kg K) | |
| Maximum inlet concentration in the treatment unit, mg/L t | |
| Concentration of the feed water in MD, mg/L | |
| Maximum inlet concentration in well pad s, mg/L | |
| Flowback water concentration in well pad s, mg/L | |
| Crew transition time between well pads, day | |
| Maximum capacity of injection well d, m3 | |
| Distance from well pad s to a treatment facility, km | |
| Time horizon of interest, day | |
| Liquid recovery for the regenerator | |
| Number of historical year, year | |
| Freshwater pumping cost, $/m3 | |
| Freshwater trucking cost, $/m3 | |
| Wastewater pumping cost, $/m3/km | |
| Cost of wastewater disposal, $/m3 | |
| Cost of wastewater storage, $/m3 | |
| Cost of heating, $/(109 J) | |
| Gas production of well pad s, m3 | |
| Unit price of natural gas, $/m3 | |
| Availability date of well pad s, day | |
| Time required fracturing well pad s, day | |
| Temperature of feed water in the treatment unit, K | |
| Ratio of recycled reject to raw feed | |
| Maximum capacity of storage, m3 | |
| Minimum capacity of storage, m3 | |
| Amount of water required to fracture well pad s, m3 | |
| Molar concentration of NaCl in the feed | |
| Membrane thickness, mm | |
| Energy density, kJ/ m3 | |
| Density of water, kg/ m3 | |
| Binary variables | |
| Defines the beginning of stimulating each well pad s at time point n | |
| Transfer of water from well pad to storage at time point n | |
| Transfer of water from storage to the regenerator at time point n | |
| Continuous variables | |
| Required membrane area, m2 | |
| Annualised fixed capital cost for the regenerator, $/year | |
| Annualised heating cost for the regenerator, $/year | |
| Annualised operating cost for the regenerator, $/year | |
| Membrane permeability, kg/(m2 pa) | |
| Flowback water concentration of well pad s at time point n, mg/L | |
| Contaminant concentration in the treatment unit at time point n, mg/L | |
| Outlet concentration of contaminant from the regenerator at time point n, mg/L | |
| Contaminant concentration removed from the water by the regenerator at time point n, mg/L | |
| Permeate concentration from MD, mg/L | |
| Retentate concentration from MD, mg/L | |
| Duration of well pad s at time point n, day | |
| Thermal energy consumption per unit of water treated, kJ/m3 | |
| Thermal energy required at time point n, kJ | |
| Total water required to fracture well pad s at time point n, m3 | |
| Water pumped from interruptible source at time point n in scenario year y, m3 | |
| Water trucked from uninterruptible source at time point n in scenario year y, m3 | |
| Freshwater required to fracture well pad s at time point n, m3 | |
| Wastewater required to fracture well pad s at time point n, m3 | |
| Flowback water from well pad s at time point n, m3 | |
| Flowback water sent to storage tank from well pad s at time point n, m3 | |
| Flowback water sent to disposal from well pad s at time point n, m3 | |
| Total flowback water to be treated at time point n, m3 | |
| Amount of water collected as permeate from the regenerator at time point n, m3 | |
| Amount of retentate from the regenerator at time point n, m3 | |
| Total water sent to disposal at time point n, m3 | |
| Throughput of an injection well d at time point n, m3 | |
| Total flowrate into MD, m3/day | |
| Total flowrate into MD, kg/day | |
| Permeate flowrate from MD, kg/day | |
| Retentate flowrate from MD, kg/day | |
| Total freshwater required from impoundment t for fracturing at time point n, m3 | |
| Water flux across the membrane, kg/(m2·s) | |
| Membrane thermal conductivity, kW/(m·K) | |
| Expected gas production of well pad s at time point n, m3 | |
| Water vapour pressure of the feed in MD, pa | |
| Water vapour pressure of the permeate in MD, pa | |
| Heat required by the feed into MD, kJ/day | |
| Regenerator removal ratio | |
| Start time of well pad s at time point n, day | |
| Finish time of well pad s at time point n, day | |
| Time that corresponds to time point n, day | |
| Start time of regeneration at time point n, day | |
| Duration of regeneration at time point n, day | |
| Time at which water is transferred from well pad s to storage tank at time point n, day | |
| Temperature of the feed on the membrane, K | |
| Temperature of the permeate on the membrane, K | |
| Membrane average temperature, K | |
| Temperature of the feed in the bulk, K | |
| Temperature of permeate in the bulk, K | |
| Volume of impoundment t at time point n in scenario year y, m3 | |
| Capacity of wastewater tank at time point n, m3 | |
| Capacity of fracturing tank on well pad s at time point n, m3 | |
| Volume of natural gas needed to produce the required energy at time point n, m3 | |
| Mole fraction of water in the feed | |
| Activity coefficient of water in the feed for membrane distillation | |
| Overall thermal efficiency of the regenerator | |
| Latent heat of vaporisation for water, kJ/kg | |
| Temperature polarisation coefficient | |
| Superscript | |
| con | Concentrate |
| cons | Consumption |
| dis | Disposal |
| feed | Feed |
| ft | Fracturing tank |
| fw | Freshwater |
| fbw | Flowback water |
| gas | Gas |
| ht | Heating |
| max | Maximum |
| min | Minimum |
| nat | Natural gas |
| pump | Pumping |
| perm | Permeate |
| reg | Regenerator |
| st | Storage |
| total | Total |
| truck | Trucking |
| vap | Vapour |
| ww | Wastewater |
| Subscript | |
| bp | Permeate bulk |
| bf | Feed bulk |
| m | Membrane |
| mp | Membrane permeate |
| mf | Membrane feed |
| wf | Feed water |
| wp | Permeate water |
References
- Al-Douri, A.; Sengupta, D.; El-Halwagi, M.M. Shale Gas Monetization—A review of downstream processing of chemical and fuels. J. Nat. Gas. Eng. 2017, 45, 436–455. [Google Scholar] [CrossRef]
- Zhang, C.; El-Halwagi, M.M. Estimate the capital cost of shale-gas monetization projects. Chem. Eng. Prog. 2017, 113, 28–32. [Google Scholar]
- Arthur, J.D.; Bohm, B.; Layne, M. Hydraulic fracturing considerations for natural gas wells of the Marcellus Shale. In Proceedings of the Ground Water Protection Council 2008 Annual Forum, Cincinnati, OH, USA, 21–24 September 2008; pp. 1–16. [Google Scholar]
- Yang, L.; Grossmann, I.E.; Manno, J. Optimization models for shale gas water management. AIChE J. 2014, 60, 3490–3501. [Google Scholar] [CrossRef]
- Vengosh, A. How Much Water Does U.S. Fracking Really Use? 2015. Available online: https://today.duke.edu/2015/09/frackfoot (accessed on 25 May 2018).
- Hasaneen, R.; El-Halwagi, M.M. Integrated process and microeconomic analyses to enable effective environmental policy for shale gas in the United States. Clean Technol. Environ. Policy 2017, 19, 1775–1789. [Google Scholar] [CrossRef]
- Petrakis, S. Reduce cooling water consumption: New closed loop cooling method improves process cooling tower operations. Hydrocarb. Process. 2008, 87, 95–98. [Google Scholar]
- Elsayed, N.A.; Barrufet, M.A.; Eljack, F.T.; El-Halwagi, M.M. Optimal design of thermal membrane distillation systems for the treatment of shale gas flowback water. Int. J. Membr. Sci. 2015, 2, 1–9. [Google Scholar]
- Elsayed, N.A.; Barrufet, M.A.; El-Halwagi, M.M. Integration of thermal membrane distillation networks with processing facilities. Ind. Eng. Chem. Res. 2013, 53, 5284–5298. [Google Scholar] [CrossRef]
- Yang, L.; Grossmann, I.E.; Mauter, M.S.; Dilmore, R.M. Investment optimization model for freshwater acquisition and wastewater handling in shale gas production. AIChE J. 2015, 61, 1770–1782. [Google Scholar] [CrossRef]
- Gao, J.; You, F. Optimal design and operations of supply chain networks for water management in shale gas production: MILFP model and algorithm for the water-enegy nexus. AIChE J. 2015, 61, 1184–1208. [Google Scholar] [CrossRef]
- Gao, J.; You, F. Deciphering and handling uncertainty in shale gas supply chain design and optimization: Novel modelling framework and computational efficient solution algorithm. AIChE J. 2015, 61, 3739–3760. [Google Scholar] [CrossRef]
- Bartholomew, T.V.; Mauter, M.S. Multiobjective optimization model for minimizing cost and environmental impact in shale gas water and wastewater management. ACS Sustain. Chem. Eng. 2016, 4, 3728–3735. [Google Scholar] [CrossRef]
- Lira-Barragán, L.; Ponce-Ortega, J.M.; Guillén-Gosálbez, G.; El-Halwagi, M.M. Optimal Water Management under Uncertainty for Shale Gas Production. Ind. Eng. Chem. Res. 2016, 55, 1322–1335. [Google Scholar] [CrossRef]
- Yang, L.; Salcedo-Diaz, R.; Grossmann, I.E. Water network optimization with wastewater regeneration models. Ind. Eng. Chem. Res. 2014, 53, 17680–17695. [Google Scholar] [CrossRef]
- Kamrava, S.; Gabriel, K.J.; El-Halwagi, M.M.; Eljack, F.T. Managing abnormal operation through process integration and cogeneration systems. Clean Techn. Environ. Policy 2015, 17, 119–128. [Google Scholar] [CrossRef]
- Kazi, M.K.; Eljack, F.; Elsayed, N.A.; El-Halwagi, M.M. Integration of energy and wastewater treatment alternatives with process facilities to manage industrial flares during normal and abnormal operations: A multi-objective extendible optimization framework. Ind. Eng. Chem. Res. 2016, 55, 2020–2034. [Google Scholar] [CrossRef]
- Glazer, Y.R.; Kjellsson, J.B.; Sanders, K.T.; Webber, M.E. Potential for using energy from flared gas for on-site hydraulic fracturing wastewater treatment in Texas. Environ. Sci. Technol. Lett. 2014, 1, 300–304. [Google Scholar] [CrossRef]
- Wikramanayake, E.; Bahadur, V. Flared natural gas-based onsite atmospheric water harvesting (AWH) for oilfield operations. Environ. Res. Lett. 2016, 11, 1748–9326. [Google Scholar] [CrossRef]
- Yun, Y.; Ma, R.; Zhang, W.; Fane, A.G.; Li, J. Direct contact membrane distillation mechanism for high concentration NaCl solutions. Desalination 2006, 188, 251–262. [Google Scholar] [CrossRef]
- Gregory, K.B.; Vidic, R.D.; Dzombak, D.A. Water management challenges associated with the production of shale gas by hydraulic fracturing. Elements 2011, 7, 181–186. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation: Review. J. Membr. Sci. 1997, 124, 9–25. [Google Scholar] [CrossRef]
- Camacho, L.M.; Dume´e, L.; Zhang, J.; Li, J.D.; Duke, M.; Gomez, J.; Gray, S. Advances in membrane distillation for water desalination and purification applications. Water 2013, 5, 94–196. [Google Scholar] [CrossRef]
- Estrada, J.M.; Bhamidimarri, R. A review of the issues and treatment options for wastewater from shale gas extraction by hydraulic fracturing. Fuel 2016, 182, 292–303. [Google Scholar] [CrossRef]
- Engle, M.A.; Rowan, E.L. Geochemical evolution of produced waters from hydraulic fracturing of the Marcellus Shale, northern Appalachian Basin: A multivariate compositional data analysis approach. Int. J. Coal Geol. 2014, 126, 45–56. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. Sustainable Design through Process Integration: Fundamentals and Applications to Industrial Pollution Prevention, Resource Conservation, and Profitability Enhancement; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Khayet, M.; Matsuura, T. Membrane Dstillation: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in seawater desalination: thermal efficiency, sensitivity study and cost estimation. J. Memb. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- MINLPLib. Available online: http://www.minlplib.org (accessed on 19 June 2018).
- Nohra, C.J.; Sahinidis, N.V. Global optimization of nonconvex problems with convex-transformable intermediates. J. Glob. Optim. 2018, 1–22. [Google Scholar] [CrossRef]
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. Math. Program. 2005, 103, 225–249. [Google Scholar] [CrossRef]
- Suarez, F.; Urtubia, R. Tackling the water-energy nexus: an assessment of membrane distillation driven by salt-gradient solar ponds. Clean Technol. Environ. Policy 2016, 18, 1–16. [Google Scholar] [CrossRef]
- Al-Aboosi, F.Y.; El-Halwagi, M.M. An integrated approach to water-energy nexus in shale gas production. Processes 2018, 6, 52. [Google Scholar] [CrossRef]
- Baaqeel, H.; El-Halwagi, M.M. Optimal multi-scale capacity planning in seawater desalination systems. Processes 2018, 6, 68. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. A return on investment metric for incorporating sustainability in process integration and improvement projects. Clean Technol. Environ. Policy 2017, 19, 611–617. [Google Scholar] [CrossRef]
- Guillen-Cuevas, K.; Ortiz-Espinoza, A.P.; Ozinan, E.; Jiménez-Gutiérrez, A.; Kazantzis, N.K.; El-Halwagi, M.M. Incorporation of safety and sustainability in conceptual design via a return on investment metric. ACS Sustain. Chem. Eng. 2018, 6, 1411–1416. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).