A Framework for the Development of Integrated and Computationally Feasible Models of Large-Scale Mammalian Cell Bioreactors
Abstract
1. Introduction
1.1. The Importance of Reliable Unit Operation Models
1.2. Bioreactor
1.3. Existing Culture Models and Their Need for Improvement
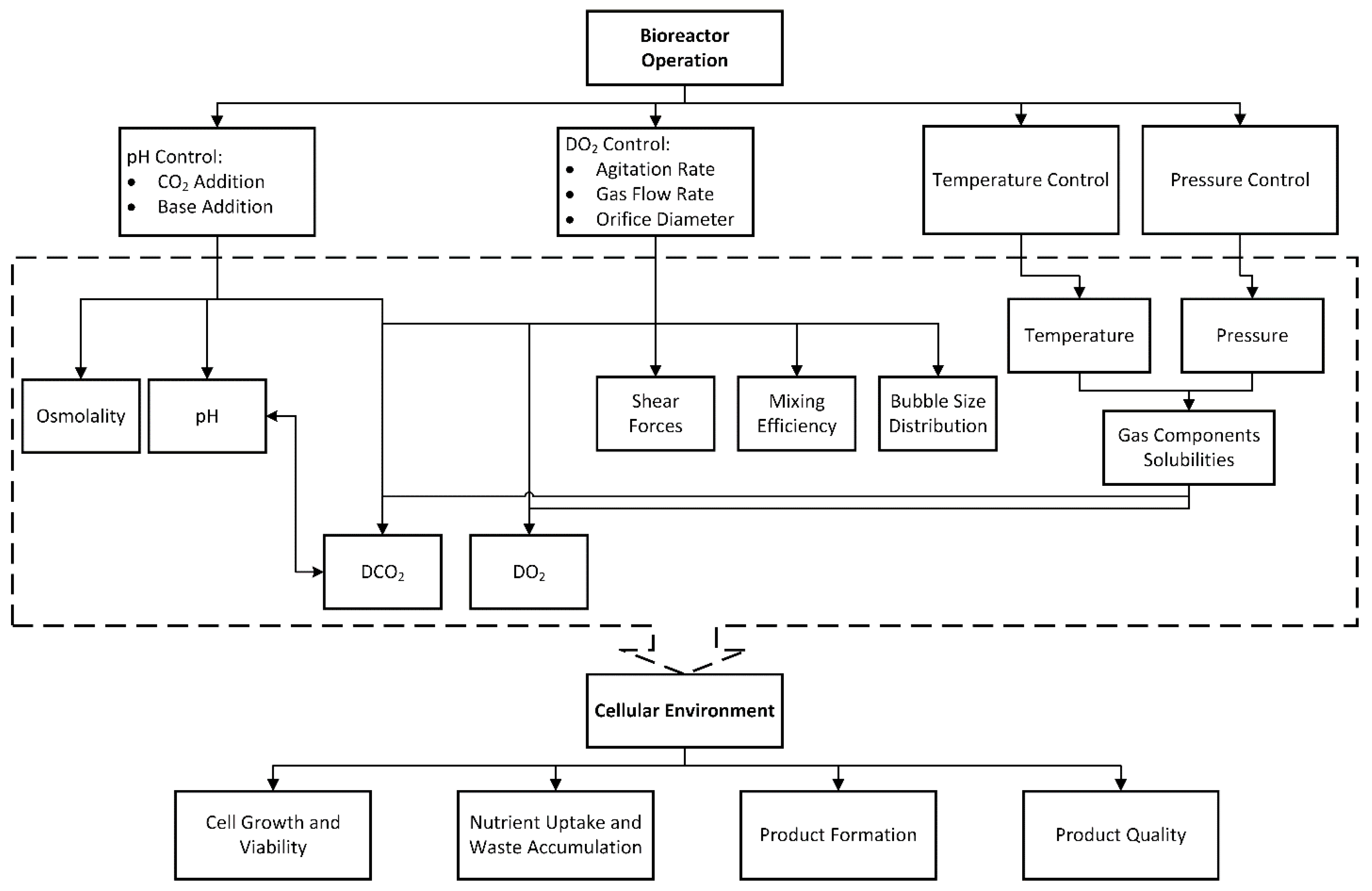
2. Development of a Dynamic, Integrated, and Computationally Feasible Bioreactor Model
2.1. Development of CFD Simulations
2.2. Development of the Integrated Model
2.3. Coupling the Model with Nonlinear Solvers
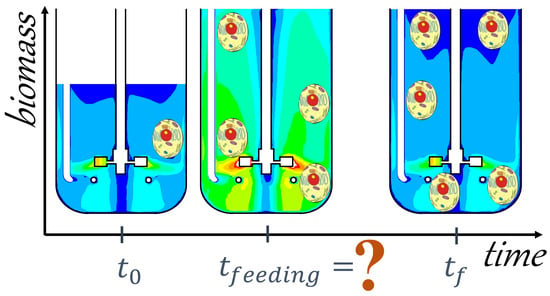
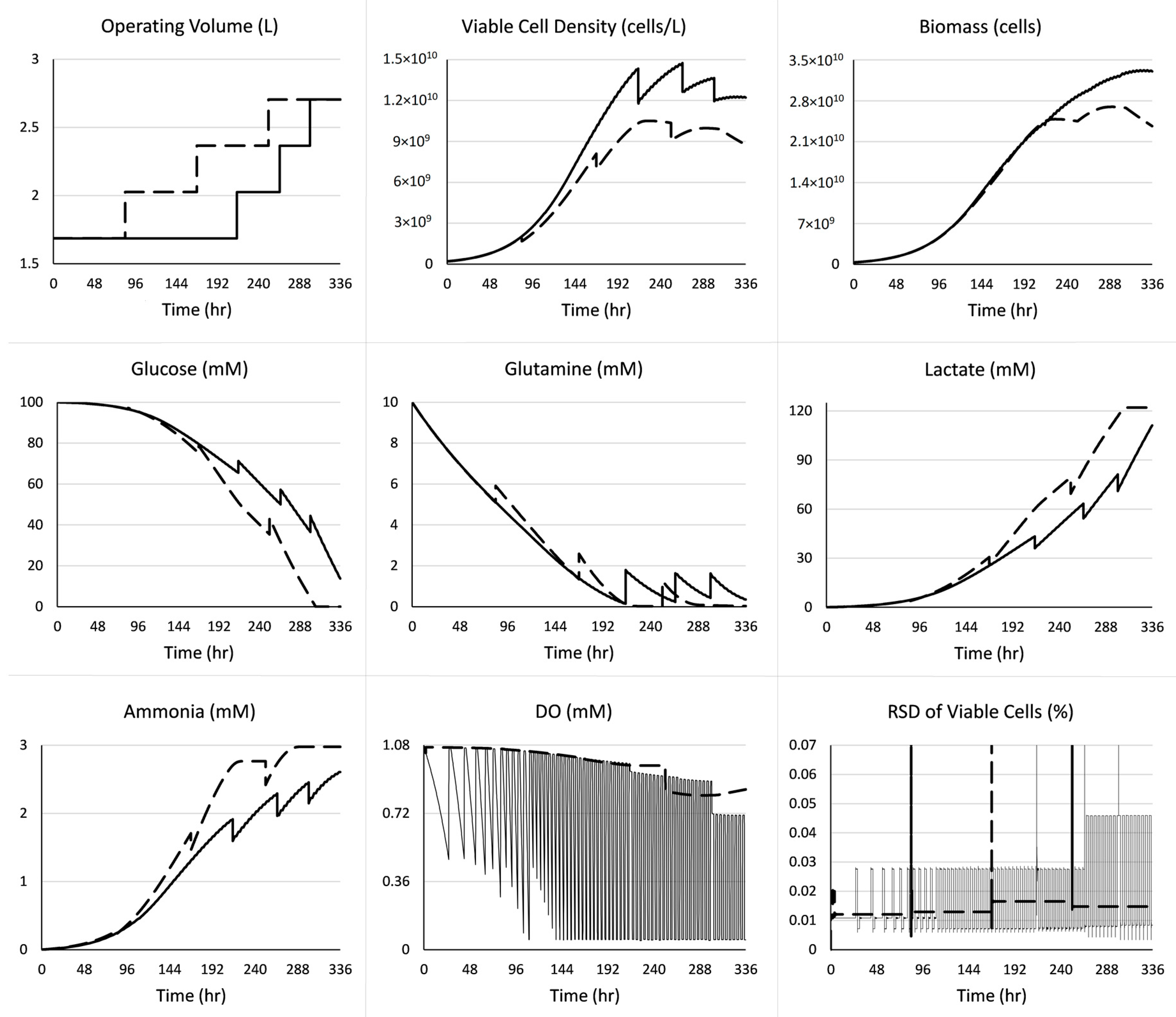
3. Case Study
4. Conclusions and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moorkens, E.; Meuwissen, N.; Huys, I.; Declerck, P.; Vulto, A.G.; Simoens, S. The Market of Biopharmaceutical Medicines: A Snapshot of a Diverse Industrial Landscape. Front. Pharmacol. 2017, 8, 314. [Google Scholar] [CrossRef] [PubMed]
- Davidson, A.; Farid, S.S. Innovation in Biopharmaceutical Manufacture. BioProcess Int. 2014, 12, 12–19. [Google Scholar]
- Rader, R.A.; Langer, E.S. 30 years of upstream productivity improvements. BioProcess Int. 2015, 13, 10–15. [Google Scholar]
- Farid, S.S. Process economics of industrial monoclonal antibody manufacture. J. Chromatogr. B-Anal. Technol. Biomed. Life Sci. 2007, 848, 8–18. [Google Scholar] [CrossRef] [PubMed]
- Terry, C.; Lesser, N. Balancing the R&D Equation; Deloitte Center for Health Solutions: London, UK, 2017. [Google Scholar]
- Gyurjyan, G.; Thaker, S.; Westhues, K.; Zwaanstra, C. Rethinking Pharma Productivity; McKinsey & Company: New York, NY, USA, 2017. [Google Scholar]
- Varma, V.A.; Reklaitis, G.V.; Blau, G.E.; Pekny, J.F. Enterprise-wide modeling & optimization—An overview of emerging research challenges and opportunities. Comput. Chem. Eng. 2007, 31, 692–711. [Google Scholar]
- Grossmann, I.E. Advances in mathematical programming models for enterprise-wide optimization. Comput. Chem. Eng. 2012, 47, 2–18. [Google Scholar] [CrossRef]
- Lara, A.R.; Galindo, E.; Ramírez, O.T.; Palomares, L.A. Living with heterogeneities in bioreactors. Mol. Biotechnol. 2006, 34, 355–381. [Google Scholar] [CrossRef]
- Xie, L.; Zhou, W.; Robinson, D. Protein production by large-scale mammalian cell culture. New Compr. Biochem. 2003, 38, 605–623. [Google Scholar]
- Spier, R.E. Encyclopedia of Cell Technology. In Wiley Biotechnology Encyclopedias; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Panda, T. Bioreactors: Analysis and Design; Tata McGraw-Hill Education Private Limited: New York, NY, USA, 2011. [Google Scholar]
- Ho, C.S.; Wang, D.I.C. Animal Cell Bioreactors; Biotechnology Series; Davies, J.E., Ed.; Butterworth-Heinemann: Oxford, UK, 1991. [Google Scholar]
- Mandenius, C.-F.; Titchener-Hooker, N.J. Measurement, Monitoring, Modelling and Control of Bioprocesses. In Advances in Biochemical Engineering/Biotechnology; Springer: Berlin, Germany, 2013. [Google Scholar]
- Meyer, H.-P.; Schmidhalter, D. Industrial Scale Suspension Culture of Living Cells; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Shuler, M.L.; Kargi, F. Bioprocess Engineering, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Prokop, A. Implications of Cell Biology in Animal Cell Biotechnology. In Animal Cell Bioreactors; Ho, C.S., Wang, D.I.C., Eds.; Butterworth-Heinemann: Oxford, UK, 1991. [Google Scholar]
- Pigou, M.; Morchain, J. Investigating the interactions between physical and biological heterogeneities in bioreactors using compartment, population balance and metabolic models. Chem. Eng. Sci. 2015, 126, 267–282. [Google Scholar] [CrossRef]
- Meshram, M.; Naderi, S.; McConkey, B.; Ingalls, B.; Scharer, J.; Budman, H. Modeling the coupled extracellular and intracellular environments in mammalian cell culture. Metab. Eng. 2013, 19, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Sidoli, F.R.; Asprey, S.P.; Mantalaris, A. A Coupled Single Cell-Population-Balance Model for Mammalian Cell Cultures. Ind. Eng. Chem. Res. 2006, 45, 5801–5811. [Google Scholar] [CrossRef]
- Mantzaris, N.V.; Daoutidis, P. Cell population balance modeling and control in continuous bioreactors. J. Process Control 2004, 14, 775–784. [Google Scholar] [CrossRef]
- Mantzaris, N.V. Stochastic and deterministic simulations of heterogeneous cell population dynamics. J. Theor. Biol. 2006, 241, 690–706. [Google Scholar] [CrossRef] [PubMed]
- Dorka, P.; Fischer, C.; Budman, H.; Scharer, J.M. Metabolic flux-based modeling of mAb production during batch and fed-batch operations. Bioprocess Biosyst. Eng. 2009, 32, 183–196. [Google Scholar] [CrossRef] [PubMed]
- Fadda, S.; Cincotti, A.; Cao, G. A novel population balance model to investigate the kinetics of in vitro cell proliferation: Part I. model development. Biotechnol. Bioeng. 2012, 109, 772–781. [Google Scholar] [CrossRef] [PubMed]
- Jandt, U.; Platas Barradas, O.; Pörtner, R.; Zeng, A.P. Synchronized Mammalian Cell Culture: Part II—Population Ensemble Modeling and Analysis for Development of Reproducible Processes. Biotechnol. Prog. 2015, 31, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Craven, S.; Whelan, J.; Glennon, B. Glucose concentration control of a fed-batch mammalian cell bioprocess using a nonlinear model predictive controller. J. Process Control 2014, 24, 344–357. [Google Scholar] [CrossRef]
- Sbarciog, M.; Coutinho, D.; Wouwer, A.V. A simple output-feedback strategy for the control of perfused mammalian cell cultures. Control Eng. Pract. 2014, 32, 123–135. [Google Scholar] [CrossRef]
- Amribt, Z.; Niu, H.X.; Bogaerts, P. Macroscopic modelling of overflow metabolism and model based optimization of hybridoma cell fed-batch cultures. Biochem. Eng. J. 2013, 70, 196–209. [Google Scholar] [CrossRef]
- Mantzaris, N.V.; Liou, J.J.; Daoutidis, P.; Srienc, F. Numerical solution of a mass structured cell population balance model in an environment of changing substrate concentration. J. Biotechnol. 1999, 71, 157–174. [Google Scholar] [CrossRef]
- Farzan, P.; Mistry, B.; Ierapetritou, M.G. Review of the Important Challenges and Opportunities related to Modeling of Mammalian Cell Bioreactors. AIChE J. 2017, 63, 398–408. [Google Scholar] [CrossRef]
- Rocha, I. Model-Based Strategies for Computer-Aided Operation of Recombinant E. coli Fermentation; Universidade do Minho: Braga, Portugal, 2003. [Google Scholar]
- Lopez-Meza, J.; Araíz-Hernández, D.; Carrillo-Cocom, L.M.; López-Pacheco, F.; del Refugio Rocha-Pizaña, M.; Alvarez, M.M. Using simple models to describe the kinetics of growth, glucose consumption, and monoclonal antibody formation in naive and infliximab producer CHO cells. Cytotechnology 2016, 68, 1287–1300. [Google Scholar] [CrossRef] [PubMed]
- Cachaza, E.M.; Díaz, M.E.; Montes, F.J.; Galán, M.A. Simultaneous Computational Fluid Dynamics (CFD) simulation of the hydrodynamics and mass transfer in a partially aerated bubble column. Ind. Eng. Chem. Res. 2009, 48, 8685–8696. [Google Scholar] [CrossRef]
- Wang, H.N.; Jia, X.; Wang, X.; Zhou, Z.; Wen, J.; Zhang, J. CFD modeling of hydrodynamic characteristics of a gas-liquid two-phase stirred tank. Appl. Math. Model. 2014, 38, 63–92. [Google Scholar] [CrossRef]
- Azargoshasb, H.; Mousavi, S.M.; Amani, T.; Jafari, A.; Nosrati, M. Three-phase CFD simulation coupled with population balance equations of anaerobic syntrophic acidogenesis and methanogenesis reactions in a continouos stirred bioreactor. J. Ind. Eng. Chem. 2015, 27, 207–217. [Google Scholar] [CrossRef]
- Kerdouss, F.; Bannari, A.; Proulx, P.; Bannari, R.; Skrga, M.; Labrecque, Y. Two-phase mass transfer coefficient prediction in stirred vessel with a CFD model. Comput. Chem. Eng. 2008, 32, 1943–1955. [Google Scholar] [CrossRef]
- Micale, G.; Montante, G.; Grisafi, F.; Brucato, A.; Godfrey, J. CFD simulation of particle distribution in stirred vessels. Chem. Eng. Res. Des. 2000, 78, 435–444. [Google Scholar] [CrossRef]
- Farzan, P.; Ierapetritou, M.G. Integrated Modeling to Capture the Interaction of Physiology and Fluid Dynamics in Biopharmaceutical Bioreactors. Comput. Chem. Eng. 2017, 97, 271–282. [Google Scholar] [CrossRef]
- Bezzo, F.; Macchietto, S.; Pantelides, C.C. A general methodology for hybrid multizonal/CFD models: Part I. Theoretical framework. Comput. Chem. Eng. 2004, 28, 501–511. [Google Scholar] [CrossRef]
- Delafosse, A.; Collignon, M.L.; Calvo, S.; Delvigne, F.; Crine, M.; Thonart, P.; Toye, D. CFD-based compartment model for description of mixing in bioreactors. Chem. Eng. Sci. 2014, 106, 76–85. [Google Scholar] [CrossRef]
- Kagoshima, M.; Mann, R. Development of a networks-of-zones fluid mixing model for an unbaffled stirred vessel used for precipitation. Chem. Eng. Sci. 2006, 61, 2852–2863. [Google Scholar] [CrossRef]
- Vrabel, P.; Van der Lans, R.G.J.M.; Cui, Y.Q.; Luyben, K.C.A. Compartment model approach: Mixing in large scale aerated reactors with multiple impellers. Chem. Eng. Res. Des. 1999, 77, 291–302. [Google Scholar] [CrossRef]
- Bashiri, H.; Heniche, M.; Bertrand, F.; Chaouki, J. Compartmental modelling of turbulent fluid flow for the scale-up of stirred tanks. Can. J. Chem. Eng. 2014, 92, 1070–1081. [Google Scholar] [CrossRef]
- Vrabel, P.; van der Lans, R.G.; Luyben, K.C.A.; Boon, L.; Nienow, A.W. Mixing in large-scale vessels stirred with multiple radial or radial and axial up-pumping impellers: Modelling and measurements. Chem. Eng. Sci. 2000, 55, 5881–5896. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: Berlin, Germany, 2011. [Google Scholar]
- ANSYS Inc. ANSYS Fluent Theory Guide, Release 15.0 ed.; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Schmalzriedt, S.; Jenne, M.; Mauch, K.; Reuss, M. Integration of physiology and fluid dynamics. In Process Integration in Biochemical Engineering; Springer: Berlin, Germany, 2003; pp. 19–68. [Google Scholar]
- ANSYS Inc. ANSYS Fluent User’s Guide, Release 15.0 ed.; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Adams, R.L.P. Cell Culture for Biochemists; Elsevier: New York, NY, USA, 1990. [Google Scholar]
- Kaiser, S.C.; Löffelholz, C.; Werner, S.; Eibl, D. CFD for Characterizing Standard and Single-use Stirred Cell Culture Bioreactors. In Computational Fluid Dynamics Technologies and Applications; Minin, I.V., Minin, O.V., Eds.; InTech: Vienna, Austria, 2011; pp. 97–122. [Google Scholar]
- Chalmers, J. Animal cell culture, effects of agitation and aeration on cell adaption. In Encyclopedia of Cell Technology; Spier, R.E., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Sarkar, J.; Shekhawat, L.K.; Loomba, V.; Rathore, A.S. CFD of mixing of multi-phase flow in a bioreactor using population balance model. Biotechnol. Prog. 2016, 32, 613–628. [Google Scholar] [CrossRef] [PubMed]
- Alves, S.S.; Maia, C.I.; Vasconcelos, J.M.T.; Serralheiro, A.J. Bubble size in aerated stirred tanks. Chem. Eng. J. 2002, 89, 109–117. [Google Scholar] [CrossRef]
- Chatterjee, A. An introduction to the proper orthogonal decomposition. Curr. Sci. 2000, 78, 808–817. [Google Scholar]
- Chen, H.; Reuss, D.L.; Sick, V. On the use and interpretation of proper orthogonal decomposition of in-cylinder engine flows. Meas. Sci. Technol. 2012, 23, 085302. [Google Scholar] [CrossRef]
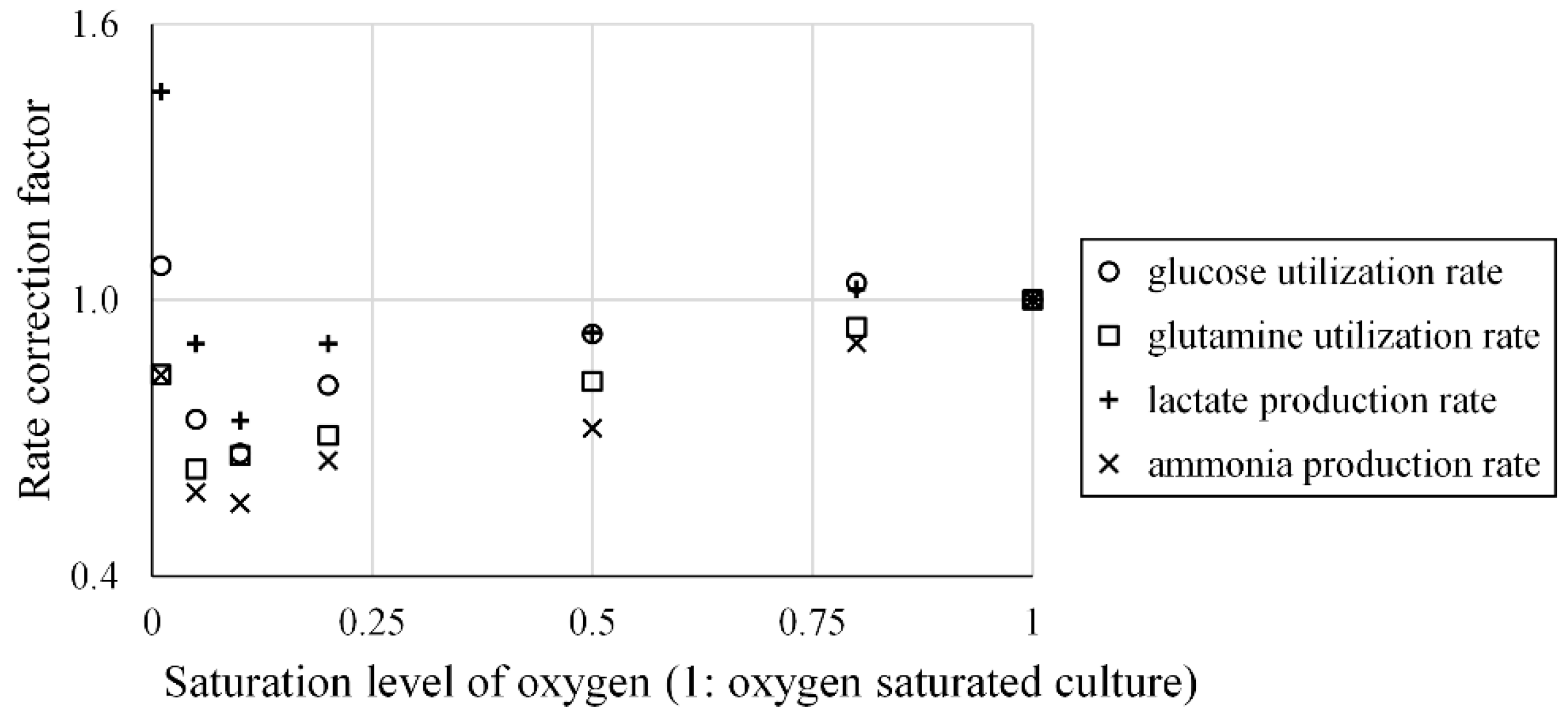
- Xiu, Z.-L.; Deckwer, W.-D.; Zeng, A.-P. Estimation of rates of oxygen uptake and carbon dioxide evolution of animal cell culture using material and energy balances. Cytotechnology 1999, 29, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, S.S.; Gu, X.J. Strategies for improved dCO(2) removal in large-scale fed-batch cultures. Biotechnol. Prog. 2003, 19, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Kolev, N.I. Solubility of O2, N2, H2 and CO2 in water. In Multiphase Flow Dynamics 4 Turbulence, Gas Adsorption and Release, Diesel Fuel Properties; Kolev, N.I., Ed.; Springer: Berlin, Germany, 2012; pp. 209–239. [Google Scholar]
- Ozturk, S.S.; Palsson, B.O. Growth, metabolic, and antibody-production kinetics of hybridoma cell-culture: 2. Effects of serum concentration, dissolved-oxygen concentration, and medium PH in a batch reactor. Biotechnol. Prog. 1991, 7, 481–494. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.Z.; Bishop, N.; Leister, K.; Li, Z.J. Modeling Kinetics of a Large-Scale Fed-Batch CHO Cell Culture by Markov Chain Monte Carlo Method. Biotechnol. Prog. 2010, 26, 208–219. [Google Scholar] [CrossRef] [PubMed]
- Biegler, L.T.; Lang, Y.D.; Lin, W.J. Multi-scale optimization for process systems engineering. Comput. Chem. Eng. 2014, 60, 17–30. [Google Scholar] [CrossRef]
- Bryson, J.A.E.; Ho, Y.-C. Applied Optimal Control: Optimization, Estimation and Control; CRC Press: Boca Raton, FL, USA, 1975. [Google Scholar]
- Flores-Tlacuahuac, A.; Moreno, S.T.; Biegler, L.T. Global optimization of highly nonlinear dynamic systems. Ind. Eng. Chem. Res. 2008, 47, 2643–2655. [Google Scholar] [CrossRef]
- Mahadevan, R.; Doyle, F.J. On-line optimization of recombinant product in a fed-batch bioreactor. Biotechnol. Prog. 2003, 19, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Banga, J.R.; Balsa-Canto, E.; Moles, C.G.; Alonso, A.A. Dynamic Optimization of Bioreactors: A Review. Proc. Ind. Natl. Sci. Acad. 2003, 69, 257–265. [Google Scholar]
- Cuthrell, J.E.; Biegler, L.T. Simultaneous-Optimization and Solution Methods for Batch Reactor Control Profiles. Comput. Chem. Eng. 1989, 13, 49–62. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Shishavan, R.A.; Powell, K.M.; Edgar, T.F. Nonlinear modeling, estimation and predictive control in APMonitor. Comput. Chem. Eng. 2014, 70, 133–148. [Google Scholar] [CrossRef]
- Constantinides, A.; Mostoufi, N. Numerical Methods for Chemical Engineers with MATLAB Applications; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Farzan, P. A framework for development of integrated and computationally feasible models of large-scale mammalian cell bioreactors. In Chemical and Biochemical Engineering; Rutgers, The State University of New Jersey: New Brunswick, NJ, USA, 2018. [Google Scholar]
- Zhao, Y.; Amemiya, Y.; Hung, Y. Efficient Gaussian Process Modeling using Experimental Design-Based Subagging. In Proceedings of the Conference on Experimental Design and Analysis (CEDA), Taipei, Taiwan, 15–17 December 2016; Institute of Statistical Science, Academia Sinica: Taipei, Taiwan, 2016. [Google Scholar]
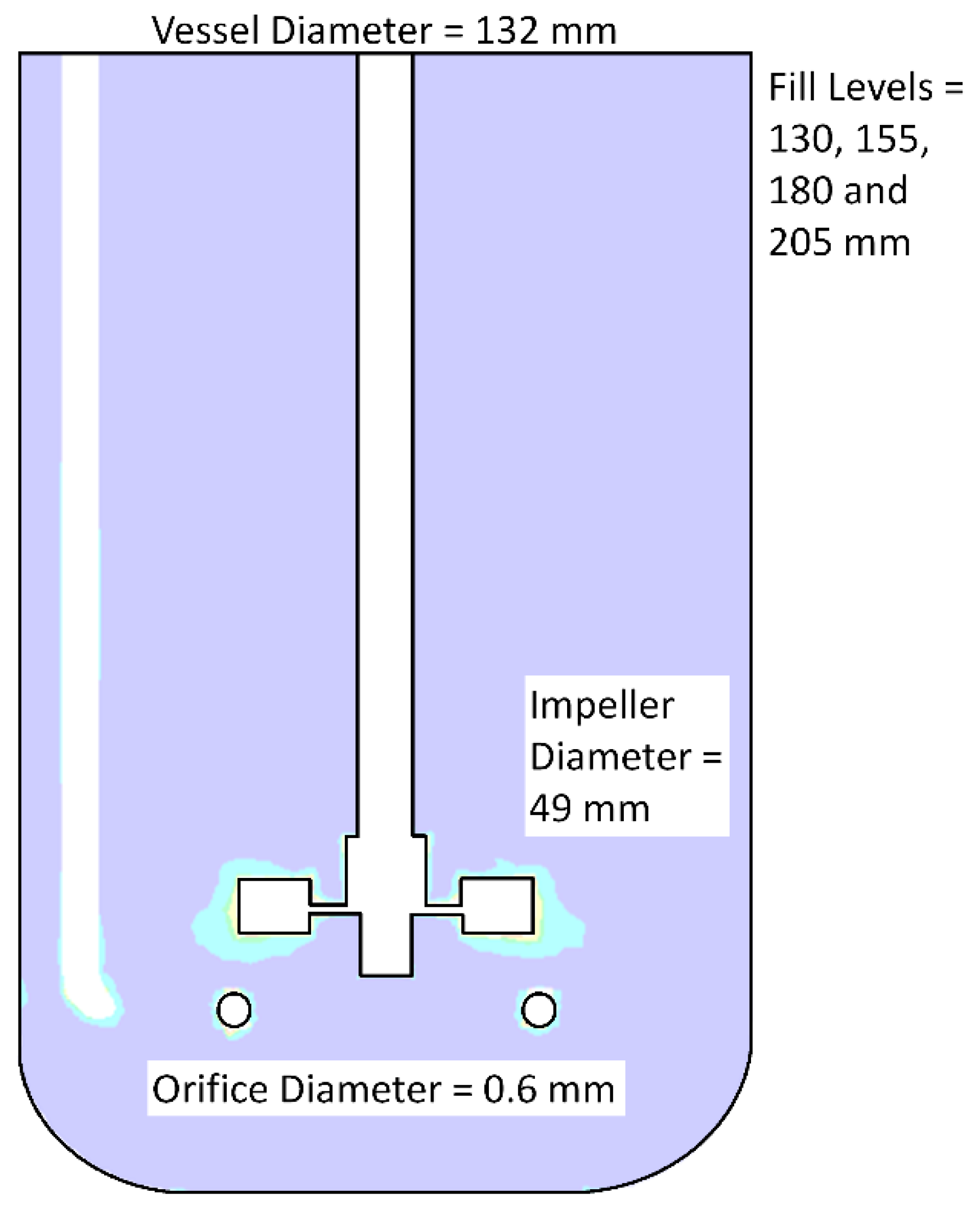
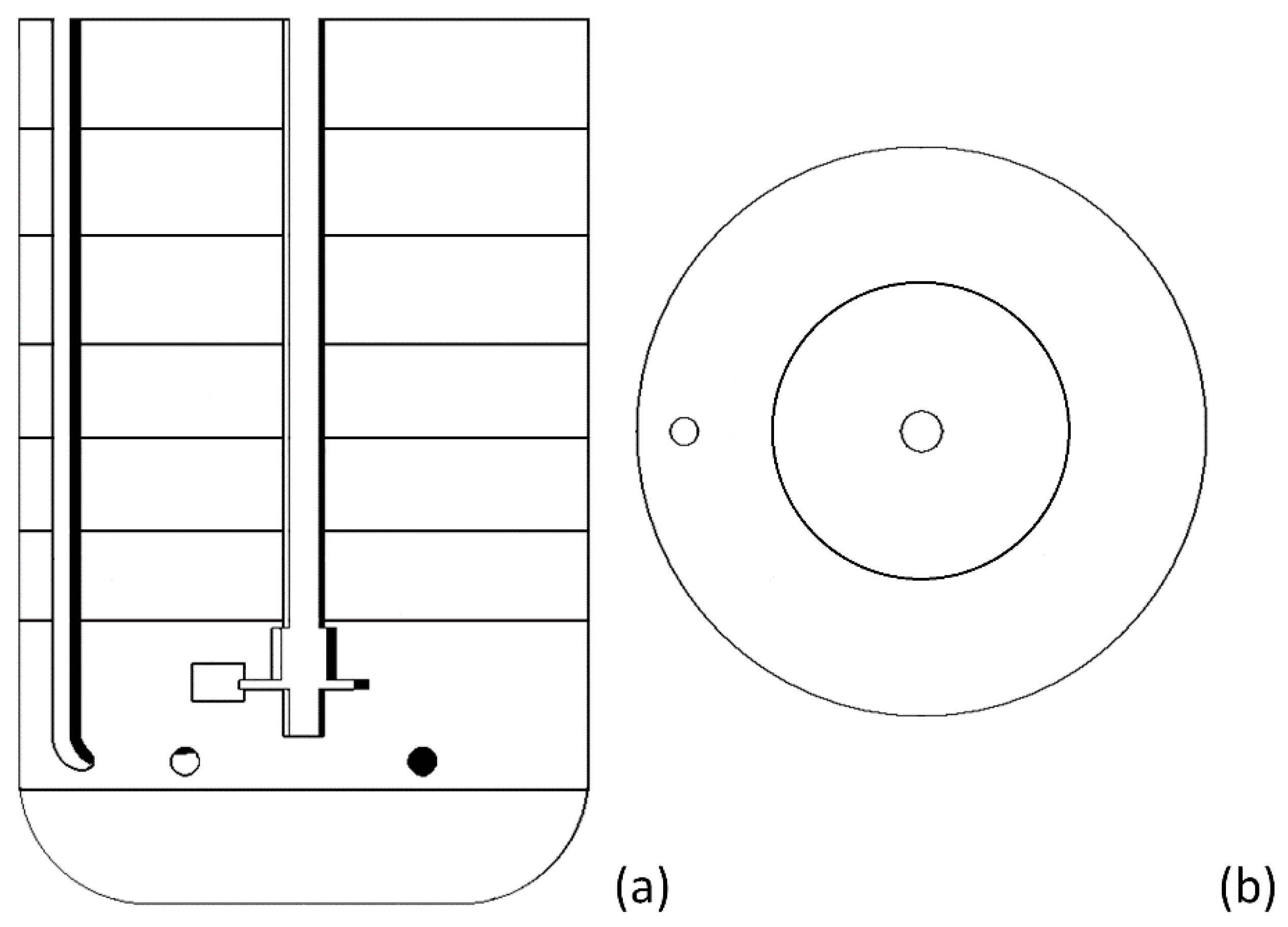
| No Aeration | Aerated System | |||||
|---|---|---|---|---|---|---|
| Fill Level (mm) | Impeller Rotation Speed (RPM) | Power Input (W%·m−3) | Fill Level (mm) | Impeller Rotation Speed (RPM) | Power Input (W%·m−3) | Volumetric Mass Transfer (h−1) |
| 130 | 150 | 3.8 | 130 | 150 | 3.5 | 12.8 |
| 225 | 11.0 | 225 | 11.1 | 16.6 | ||
| 300 | 24.5 | 300 | 26.5 | 14.9 | ||
| 155 | 150 | 3.2 | 155 | 150 | 3.1 | 10.9 |
| 225 | 9.5 | 225 | 9.7 | 11.3 | ||
| 300 | 21.6 | 300 | 23.6 | 16.1 | ||
| 180 | 150 | 2.7 | 180 | 150 | 2.4 | 14.4 |
| 225 | 8.4 | 225 | 7.9 | 14.8 | ||
| 300 | 19.2 | 300 | 19.6 | 20.4 | ||
| 205 | 150 | 2.3 | 205 | 150 | 2.7 | 11.9 |
| 225 | 7.0 | 225 | 6.5 | 9.6 | ||
| 300 | 16.1 | 300 | 15.5 | 13.7 | ||
| Parameter | Value | Unit |
|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farzan, P.; Ierapetritou, M.G. A Framework for the Development of Integrated and Computationally Feasible Models of Large-Scale Mammalian Cell Bioreactors. Processes 2018, 6, 82. https://doi.org/10.3390/pr6070082
Farzan P, Ierapetritou MG. A Framework for the Development of Integrated and Computationally Feasible Models of Large-Scale Mammalian Cell Bioreactors. Processes. 2018; 6(7):82. https://doi.org/10.3390/pr6070082
Chicago/Turabian StyleFarzan, Parham, and Marianthi G. Ierapetritou. 2018. "A Framework for the Development of Integrated and Computationally Feasible Models of Large-Scale Mammalian Cell Bioreactors" Processes 6, no. 7: 82. https://doi.org/10.3390/pr6070082
APA StyleFarzan, P., & Ierapetritou, M. G. (2018). A Framework for the Development of Integrated and Computationally Feasible Models of Large-Scale Mammalian Cell Bioreactors. Processes, 6(7), 82. https://doi.org/10.3390/pr6070082