1. Introduction
The issue of operating centrifugal pumps with gas-liquid two-phase mixtures has been addressed by many researchers [
1,
2,
3,
4,
5,
6,
7], as the gas will strongly affect the pump’s operability and reduce the lifetime of the system. One of the main conclusions observed in the studied literature relates to the complexity of the operation under two-phase conditions, particularly detecting when the air content becomes dangerous for the pump. A second one refers to the necessity of using experimental work for assessing the performance of a specific type of pump [
6,
7] to determine the equipment state when air entrapment takes place. From a process standpoint, this can be defined as non-standard, since the working parameters will deviate from the standard or expected parameters. A third conclusion refers to the difficulty of finding a general analytical model that explains the changes of the pump characteristic curve [
3,
6].
The development in materials and pump construction have led to an increased life time and better reliability of the products. The pump application may limit the access of personnel for a thorough visual pump inspection, so that under these conditions, the use of non-intrusive sensors can replace humans for detecting pump failure. Sometimes, air entrapment does not necessarily lead to a major failure, hence the pump may work under two-phase flow until a replacement/solution is found. However, as the pump characteristic is changing, the control system needs to know how to adjust the pumping parameters accordingly, so that the pump runs under safe conditions.
This paper shows the concept of how the pump characteristic curves transform from the normal state to the conditions of circulating a two-phase mixture. Several papers have shown and demonstrated the ability of vibrations measurement as an effective solution to identify improper machine state (such as valve opening or pump vibrations) [
8,
9,
10,
11,
12,
13,
14] and therefore is studied in conjunction with changes of the pump characteristic curve [
4]. Data acquisition of vibration and sound is directly related to large data volumes that must be transferred, stored, and processed, and therefore this technology became available with current developments in computing power. Being able to look back at the pump vibration history brings us to the actual sciences of data analytics and its processing. Nevertheless, the processing requires reference information generated through experimental investigations for calibration and validation purposes, which is the aim of this work.
Xu et al. [
15] show a good synthesis of visual methods used to investigate various types of flow, particularly two-phase mixtures. The importance of optical monitoring is that it allows experiments without any direct contact with the monitored process. However, when investigating real machineries, such as pumps, it is not possible to use transparent sections for optical monitoring, because of material limitations. Therefore, our experimental design was developed around two other investigation techniques: vibration analysis and sound processing. Both technologies imply large data volumes generation, and real-time processing and analysis.
Numerous experiments on mixed gas-liquid flow were performed on centrifugal pumps. These studied to what extent the increase in the amount of gas in the liquid results in a decrease in pump performance at the same flow rate, decreasing the pumping head and efficiency. Turpin et al. published a classic study of the problem of two-phase flow in centrifugal pumps [
16]. Several types of submersible multistage (5 to 8 stages) centrifugal pumps (electric submersible pumps, or ESP) were studied with a fluid mixture consisting of air-water and diesel fuel-carbon dioxide (CO
2). In this study, the mixture head
was calculated with the relation:
and the density of the mixture
was established with the relationship:
with
density of water,
density of air,
volumetric flow rate of water,
volumetric flow rate of air at the average pressure between inlet and outlet pressure. The efficiency of the pump was calculated from the ratio of the output hydraulic power to the input electric motor power:
The volumetric gas fraction (
) was calculated with as (see Section 6 for nomenclature):
It has been found that the pump head is reduced as the volume of gas in the mixture increases, and the limit for the air volumetric fraction in the air-water mixture was 0.11, at which the pumping height was about 50% of the pumping height for single phase water flow. At this fraction, the head began to oscillate between two values within a time frame of 1–2 s. The limit for CO2 in the CO2-diesel fuel mixture was 0.40, at which point the pumping height was about 90% of the height when only pumping diesel fuel.
The influence of the pressure at the pump inlet on the two-phase mixture flow through the pump was studied as well. It was found that a pressure increase at the pump inlet from 3.5 barg to 6.9 barg and then to 27.5 barg resulted in a better behavior of the pump’s characteristic (close to the liquid characteristic) and even entertained the possibility of operating at higher volumetric fraction of gas (up to 0.5). A relationship between the heads
(liquid only) and
(liquid-gas mixture), was sought:
In this relation, the function
has different mathematical expressions depending on the type of pump on which the experiments were made. An important factor,
, was defined:
which allows to determine the conditions of validity of relationship (5), which is valid (there is a connection between the two heads
) for
. Moreover,
must have acceptable values compared to
(the head produced by mixture flow is still a substantial part of the liquid-only head).
Of course, there are some valuable studies previously published that capture the essential findings of Turpin et al. [
16] Mikielewicz [
17] used a semi-empirical method to compare the performance of a liquid-only centrifugal pump with a pump carrying gas and liquid phases. A parameter named head-loss ratio is used, which is the apparent loss of head in two-phase flow divided by the loss of head in single-phase flow. The density of the mixture
is expressed as:
and alternatively, the mixture head prediction can also be expressed by multiplying the single-phase head with the mixture-water density ratio, a relationship which can be used as a correction model for the pump characteristic curve:
Minemura et al. [
18] introduced an analytical model to predict the performances of a centrifugal pump under air-water flow conditions. The two-phase model is solved numerically in the case of a radial flow pump and predicts the head and shaft power of the centrifugal pump. The precision is within ±20% of the rated flow capacity (resulted from comparison with experimental results).
With technology advancements, the two-phase centrifugal pump studies began to include computer simulations using finite element methods. Fu et al. [
19] presented a 3D model of a centrifugal pump in 2016. The elements of a centrifugal pump assembly were modeled in a drafting software and was imported into a finite element method (FEM) program. The boundary conditions were dictated by the pump inlet pressure and mass flow at the pump outlet. A FEM analysis was performed for various volumetric gas fractions, and monitoring points along current lines were analyzed. The results, verified by experimental tests, indicate a slight decrease in the pumping height at low volumes of gas. At large volumes of gas, the pumping height suddenly decreases. Increasing the suction pressure results in a better behavior (head reduction is lower at the same flow as the suction pressure increases). The limits of 0.1 for the volume fraction of the gas for minor influences over the pump characteristic and 0.15 for the gas volumetric fraction for unstable behavior are indicated.
Computational fluid dynamics (CFD) multiphase models are a common method of investigating centrifugal pumps. Medvitz et al. [
20] indicate the possibilities of cavitation detection and analysis of pump performance near cavitation. The reduction of the head in the case of two-phase flow is included into a model based on the forces acting on bubbles within centrifugal impellers [
6,
21,
22]. Computational Fluid Dynamics (CFD) is a very powerful instrument in the analysis of two phase flow, an aspect proven by the very good agreement with the experimental results.
Minggao et al. [
23] demonstrated that operating at parameters other than designed, especially at low flow rates, leads to an increase in vibration energy. Decreasing the centrifugal pump performance means wasted energy, and the vibration level of the pump is an indicator. A close connection between the flow aspect and the vibration energy can be found in [
2].
Zhang et al. [
24] show that the vibration signals can be used to monitor fully developed cavitation in centrifugal pumps. In this way, the cavitation detection method by determining the decrease of pumping height by 3% is replaced with a vibration analysis.
More complex methods have also been developed, using neural networks to analyze centrifugal pump vibration under different conditions [
25,
26], resulting in promising results in associating the vibration frequency with a certain defect and abnormal pump operation. As an alternative method, the noise measurement is correlated with the operation of the centrifugal pump, enabling the determination of conditions when cavitation occurs in a centrifugal pump by using sound analysis [
8,
10,
11,
12,
13,
14,
27,
28,
29]. Alfayeza et al. [
27] used an application of acoustic emission to detect incipient cavitation. However, it has been found that in the case of cavitation detection, the technique is only use5ul at the incipient cavity. At developed cavity, there is a phenomenon of noise attenuation.
The sound detection technology used for this project is rather simple, but strong developments have been made in the area of robotics or unmanned aerial vehicles (UAV) [
10]. According to Hoshiba et al. [
10], there are five main challenges that need to be developed in order to better adapt sound technique as a remote sensing technology:
If the first three challenges are mainly based on the hardware quality and performance, the last two challenges will require a large amount of real time data analyzing and a complex network of acquisition and interpretation software. Kim et al. [
14] show the possibility of using a single microphone combined with a small profile monaural structure to locate the source of the sound.
Neumann et al. [
30] studied gas accumulation in centrifugal pumps under steady-state two-phase flow conditions for gas flow rates up to 5% by using high-resolution gamma-ray computed tomography and a synchronized CT scanning technique within the impeller region. This approach allowed the analysis of the inlet flow conditions and gas fraction distributions and gas holdup within the impeller region on the pump performance, showing that inlet flow conditions dominate pump performance characteristic and, for the first time, a visualization of thin gas films at the impeller pressure side.
Controlling the operating parameters of submersible oil extraction pumps (ESP), which depends on the amount of gas dissolved in oil, is also a very important practical problem [
17,
26,
31,
32]. Mikielewicz et al. [
17] indicated how to determine the conditions in which pump instability occurs when increasing the amount of gas. A technique based on neural networks (as in the cavitation case) was developed to determine the safe operating region.
2. Materials and Methods
The stand used in this work is formed by a centrifugal pump (main parameters are presented in
Table 1), driven by an alternative current motor (nominal speed 2950 RPM, engine power of 5.5 kW), an air compressor, a separator tank and a water tank (see
Figure 1). The pump used for the experiment is designed for clean, corrosive or non-corrosive fluids with gas (sea water, hot water, overheated water, acid and base solutions, gas and liquids mixture), and is produced by Aversa Manufacturing. The engine speed at the compressor (direct current motor) can be adjusted by changing the intensity of the current supply with a rheostat. A speed measuring gauge is mounted on the motor shaft (both at pump engine and compressor engine through a PCE-DT 65 tachometer. The pump is linked with the motor through a mechanical coupling to compensate misalignments. The pump flow rate is controlled with the discharge valve, while the pump flow is measured using a turbine flow meter (FTB 1318 Omega, 45–855 L/min). The hydrostatic head created by the centrifugal pump is determined by the pressure difference between the pressure gauges mounted on the suction and discharge of the pump (see relationship 1). Water enters the pump through the suction vane. The air is added to the water in the mixture head for homogenization. The air pressure and flow rate are measured after leaving the air tank through the air regulator (see
Figure 1). The mixture is then transferred by the pump through the discharge vane into the separator and then the water goes into the water tank. The water flow rate is measured before entering the mixture head, while pressure is monitored before and after exiting the pump through pressure gauges. The pump rotational speed is measured through a sensor mounted on the electric motor shaft that is directly driving the pump. As shown in
Figure 2, the noise receiver is mounted on an isolated surface outside of the pump setup.
All experiments have been performed with the centrifugal pump operating with water (used as reference) and an air-water mixture. The air-water mixture is generated by adding air, which is provided by a reciprocating compressor into the mixing head (EC 5H1, manufactured by Hidromecanica with the following parameters: 5.5 kW power, 160 L/min suction flow, 10 barg maximum discharge pressure). The air pressure of the intermediate vessel is adjusted with a pressure regulator so that the desired gas amount is introduced. The air flow of the compressor is measured by a flow meter (FTB 932-Omega, 0.75–5 cubic feet per minute). At the outlet pipe, the air-water mixture passes through a separator (here, the velocity of the mixture is increased and the pressure is reduced) which separates air at the top, and water without air is introduced again into the water tank.
The vibration level on the pump housing is measured with a vibration transducer (Brüel & Kjær Type 8341 accelerometer), which measures acceleration and calculates velocity (see Equation (9)) by using the root mean square (RMS) of the last 8 records (RMS vibration recorder). The measurements also involve the simultaneous recording of the pump shaft speed with an optical transducer, mounted next to the pump coupling. The results are stored in the vibrometer (Brüel & Kjær TYPE 2270).
where
v is the velocity,
a is the measured acceleration, and
f is the frequency.
Although the data acquisition system automatically computes the RMS velocity, conventionally, one would first plot the acquired velocity versus frequency, then sum the area below this curve for 8 consecutive records. Taking the square root of the sum will deliver the RMS of velocity.
As a secondary measurement, an omni-directional microphone is installed 1 m away from the pump (see
Figure 2), to record the environmental sound or the acoustic signature of the system, which can be used to detect changes in the standard working condition of the equipment (e.g., cavitation process). The microphone, connected to a Digital Audio Workstation, has a response bandwidth of 50–20 kHz and a sensitivity of −48 dB. The high-fidelity field microphone has been used to monitor changes in the amplitude and frequency of the sound generated by the pumping system at normal operating conditions and once air enters the flow loop. The sound was recorded in real-time through a Digital Audio Workstation (Ableton™) and processed by using the SPAN Plus plug-in created by Voxengo™. Through Fourier Transformation, this displays the recorded waveform as an amplitude versus frequency plot over the recorded time, allowing us to analyze changes in amplitude and frequency.
An overview of the pump, motor and sensors positioning is shown in
Figure 2. As mentioned, two methods of determining the vibration were used: a vibration velocity transducer (
Figure 2a) and a sound level meter (
Figure 2b). Both methods manage to capture changes in the equipment working condition, with a better accuracy achieved through the vibration velocity transducer, which is closer to the pump. For incompressible single-phase fluids at a known intake pressure and temperature, the pressure increment developed by a specific stage is a function of the flow rate and the density. For air-water mixtures, the pressure increment of the centrifugal pump stage is directly proportional to the mixture’s fluid density.
3. Results
The experiments were performed on the stand from
Figure 1. The parameters of the centrifugal pump used are listed in
Table 1, and
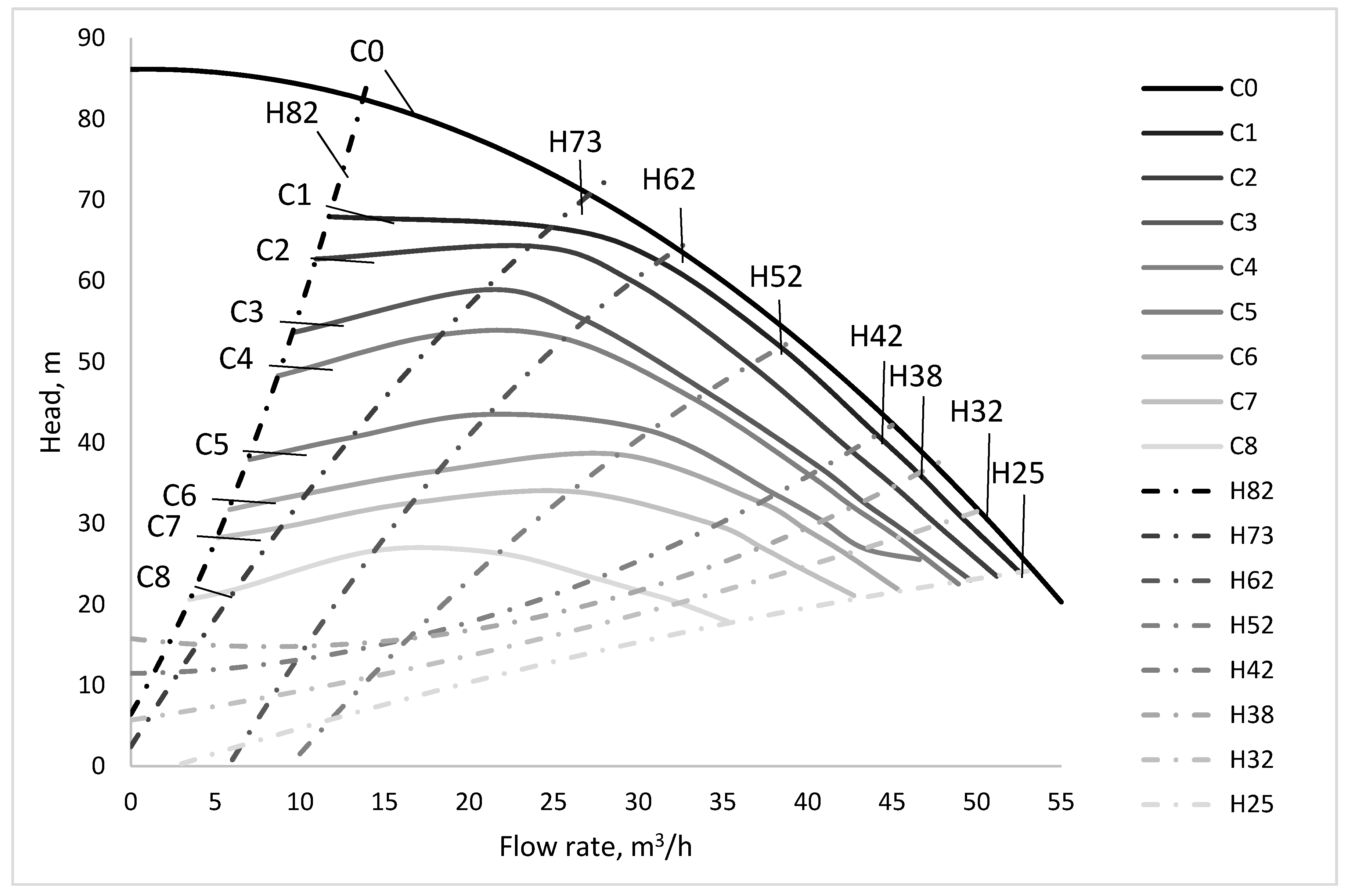
Table 2 gives an overview of the pump flow rates and water head in the handled scenarios. The characteristic curves of the centrifugal pump shown in
Figure 3 were obtained by measuring the following values:
Q—pump flow rate;
ρm—mixture density;
pd—pressure at the outlet of the pump;
ps—pressure at the pump inlet;
Qa—air flow rate.
To study the influence of the air/water ratio, different air flow rates have been mixed with water through the mixing head. The comparison with the normal situation of operation is shown in
Figure 3. The following flow rate values (
Qa) have been used: 1.28 m
3S/h; 1.60 m
3S/h; 1.92 m
3S/h; 2.24 m
3S/h; 2.56 m
3S/h; 2.88 m
3S/h; 3.2 m
3S/h; and respectively 3.52 m
3S/h.
The introduction of air into the water changes the pump characteristic curve, as shown in
Figure 3, and the hydraulic performance (flow rate, pump head, pump efficiency) is lower. If we follow a point on the initial characteristic curve, it can be noted that it moves to the left and down (curves noted with C in
Figure 3). Changes of a point (from pump characteristic curve) coordinated with the amount of air are accompanied by a modifying level of vibration and sound signature. These are compared with the H curve, representing the recorded vibrations to normal operation at different flow rates (see
Figure 4). For example, the transformation of a point of the pump characteristic curve (
Q = 14 m
3/h; H water = 82 m) in
Figure 3, is shown by the curve H82. By reading this curve from right to left, the switch from normal operation can be observed. Initially, the vibration velocities are close to the vibration values at normal operating conditions, shown in curve H. An increase in the amount of air amplifies the vibrations, which are strongest at the flow rate of 7.5 m
3/h. This aspect is also maintained in high pressure and low flow scenarios (see lines H73, H62, H52 in
Figure 4). The points on the pump characteristic curves H42, H38, H32, H25 (with low pressure and high flow) have initial speeds of vibration slightly higher than at normal operating conditions. The vibration level is almost unaffected by flow rate in the 22–55 m
3/h interval. With the reduction of flow, vibrations decrease rapidly as the amount of air becomes important into the mixture, acting as a dampener.
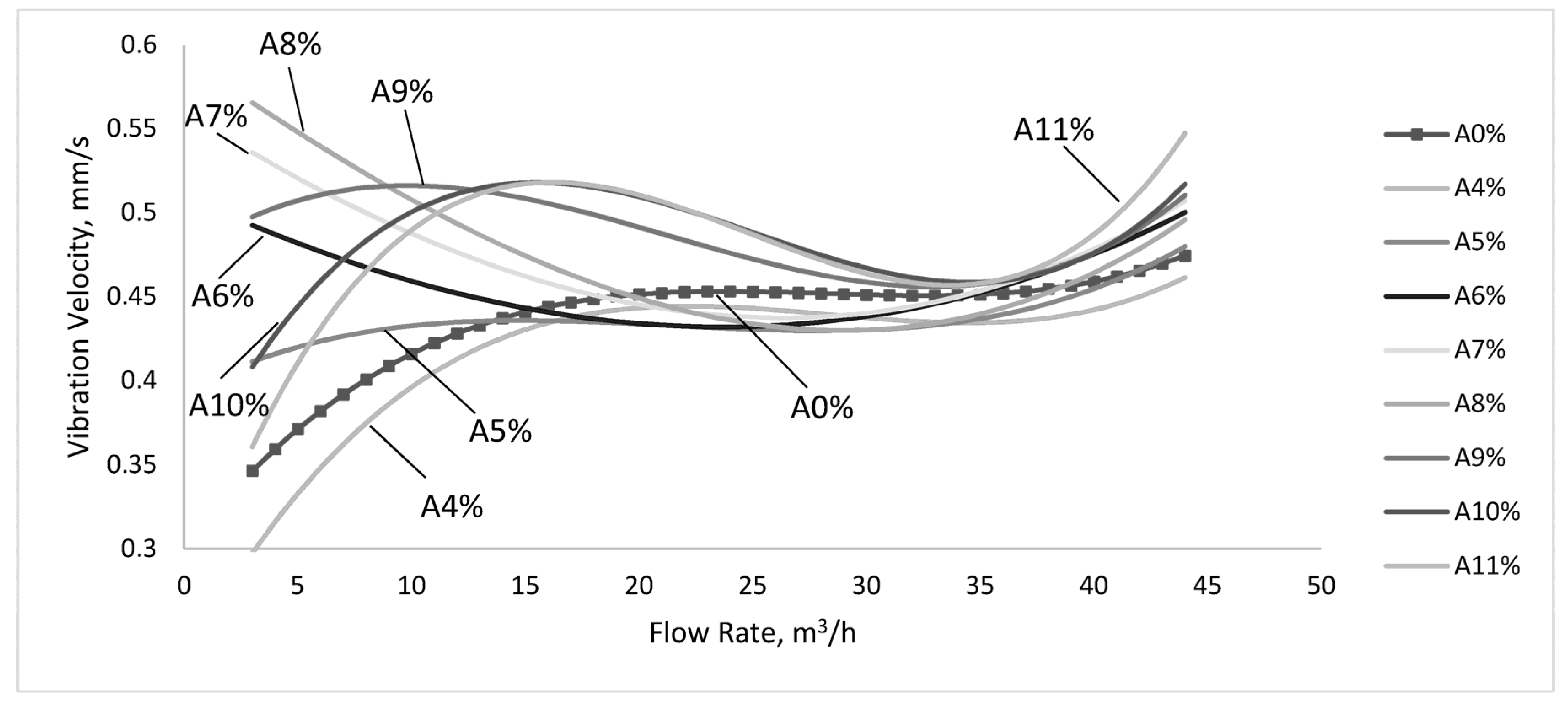
Figure 5 shows the vibration characteristics for normal operation A0% (no air introduced into the working fluid) and at the introduction of air (expressed as a percentage of the nominal flow of the pump). Influences are noticeable at an air flow rate of at least 4% of the nominal flow rate of the pump. The curves A4% and A5% have a shape similar to the normal operation conditions but the vibration velocity values are slightly lower (there is an exception for A5%, at rates up to 12 m
3/h, with higher values).
By increasing the flow rate of air (A6%, A7%, A8%), vibration is higher than in normal operation at low flow rates of up to 15–19 m3/h, after which the vibration velocities are constant and under normal operation values. However, the difference is small and we can say that air influx does not influence the pump operating condition. At flow rates above 38 m3/h, the vibration velocities are greater than those of normal operation. The situation is different for the introduction of large amounts of air A9%, A10% and A11%. In all these three cases, the recorded velocities exceeding the normal functioning values and their trend is accompanied by maximum and minimum values for certain flow rates. To conclude, the vibrations intensify with increasing air in the pump at levels above 5% of the nominal pump flow. The influence is strongest at low flow rates (up to 15 m3/h). As we approach the nominal flow rate, differences are reduced. At flow rates higher than 38 m3/h, the values corresponding to the normal operation are increasing again. All in all, the operation at the flow rates that differ from Qn (particularly under 0.6 of Qn and more than 1.2 of Qn), with an amount of air higher than 5% of Qn is characterized by velocities of vibration up to 60% larger, compared to values at normal operating conditions.
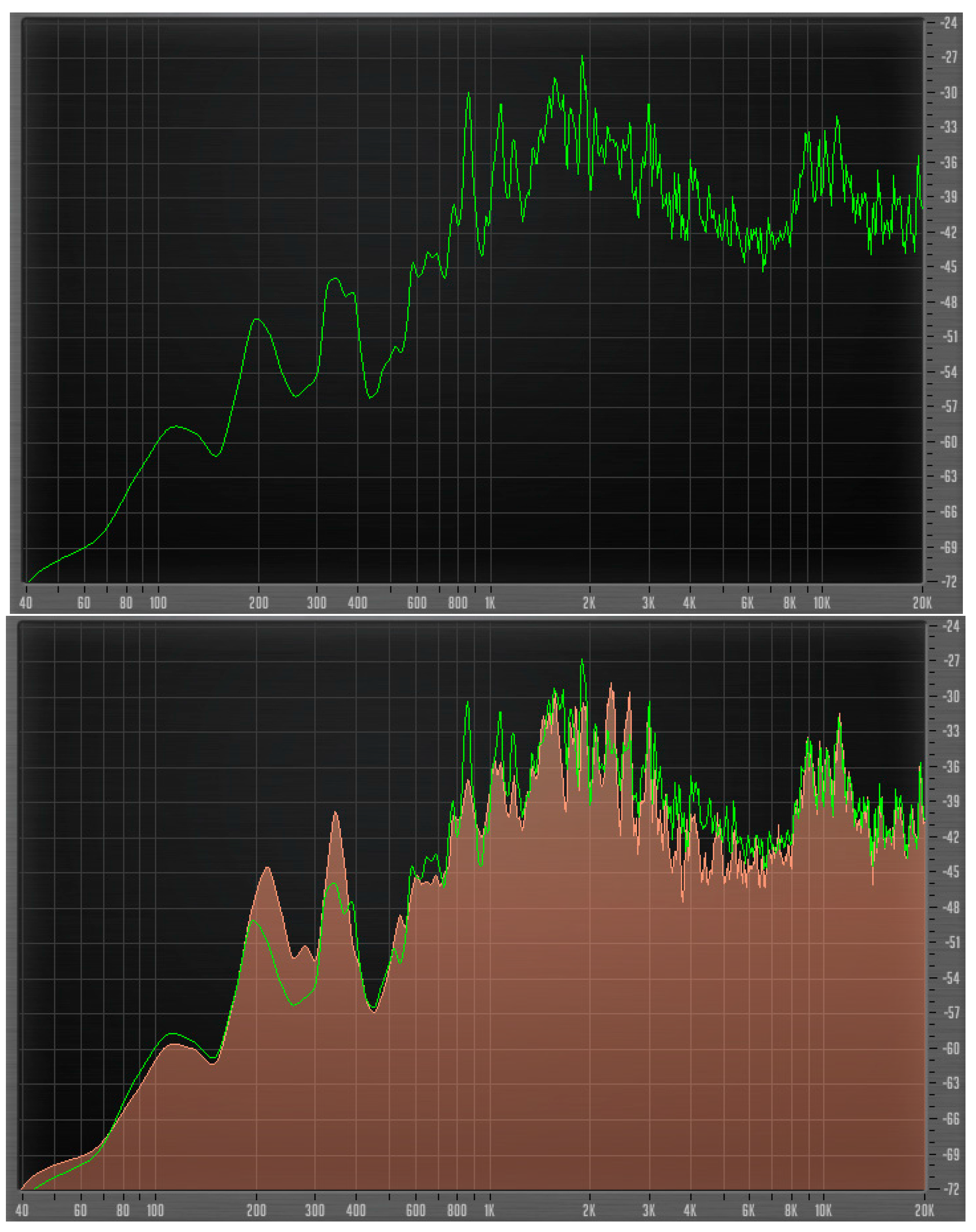
The recorded audio data can be displayed in real time or played back to follow changes in the amplitude-frequency domain. The two figures below present data extracted at approximately 3 minutes after operating the pumping system without and with air.
Figure 6 (top) shows the spectrum of the standard (without air) pump working condition (green line) at frequencies between 40 Hz and 20 kHz, whereas
Figure 6 (bottom) displays a second line (marked red), which shows the amplitude versus frequency plot after air enters the system.
We observe a decrease of the amplitudes of frequencies between 3120 and 8385 Hz and 580 to 1250 Hz, and an increase in amplitudes of frequencies spanning between 160 and 420 Hz once air enters the system. This approach, pinpointing changes in the initial operating condition of the equipment, might enable a further improving of predictive equipment methods through further analysis and experimental work, as also presented by [
8,
9]. As mentioned above, the air entrapment plays a shock absorbing (or dampening) role inside of the pump, leading to the frequency change observed. The air entering the pump will also show a high peak at around 200 Hz and 350 Hz, which could be considered as the signature of the cavitation phenomenon inside of the pump rotor.
One of the biggest challenges observed when employing this procedure is background noise isolation and the processing of large data volumes. Its main advantages are the lack of contact between measurement equipment and the pump (nonintrusive), its broad frequency spectrum, and the multitude of post-processing options (amplification, filtering, enhanced visualization), which are not as common in conventional vibration analysis [
8].
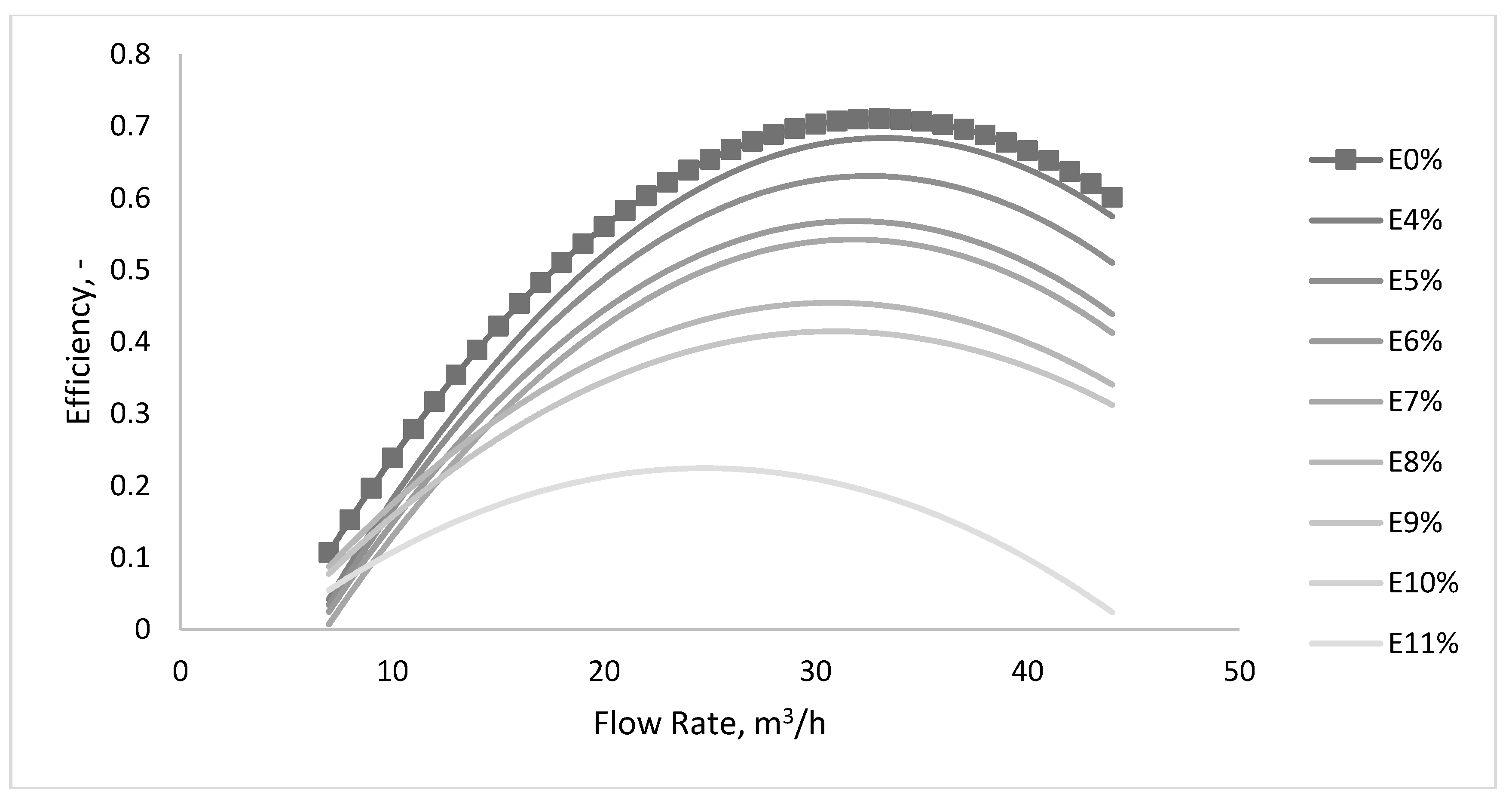
Figure 7 shows the efficiency curves corresponding to the normal operating conditions of the pump (e.g., without air intake and with air intake). The air flow rates for each curve are presented in
Table 2 and the pump nominal flow is 32 m
3/h. The pump efficiency decrease is proportional with the amount of air introduced into the system. Efficiency is declining rapidly when the amount of air is over 10%, so the pump stops having an active role in the pumping system. Functioning with an air-water mixture indicates energy losses related to the lack of control over the fluid, which exhibits an eddy movement between the blades. From the vibration viewpoint, pump malfunctioning is observed outside of the 0.6–1.2 Q
n range, where the two-phase mixture leads to stronger vibrations. It was observed that when the pump delivers near the nominal flow rate, vibrations are close to those of the normal functioning condition and therefore cannot be used as an indicator of a low efficiency. Hence, at these flow rates, the vibration measurement is not a measure of the capability of the pump.
5. Conclusions
The main conclusions drawn from the various measurements and their analysis relate to how air affects the pump characteristic curve, the application of analytical correction methods, and the vibration and sound analysis.
It was found that the introduction of air into the water changes the pump characteristic curve, leading to a lower hydraulic performance (flow, head, efficiency), as shown in
Figure 3 and
Figure 6. No model describing how the pump characteristic curves change with air inflow was found in the literature and it is therefore presented within this paper. Changes of a point’s coordinates from the pump characteristic curve with the amount of air are accompanied by modifying levels of vibration and a change in the acoustic signature of the pumping system. The operation at flow rates different from Q
n (in particular under 0.6 of Q
n and larger than 1.2 of Q
n), with more than 5% of Q
n air is characterized by velocities of vibration up to 60% higher compared to the values of normal operation. It can be observed that the analytical method of correction cannot be used in practice. Differences between the experimental curves corresponding air-water mixture and those determined by the method of correction are important, as shown in
Figure 8.
Through the experimental determination of vibration velocities at different two-phase flow conditions, a set of values showing standard functioning conditions and deviations from normal working parameters is presented, so that changes in vibration can correlate to efficiency changes. Moreover, acoustic measurements exhibit changes in their amplitude-frequency domain associated with air intake. Further experimental work is recommended to correlate air intake, pump characteristic curves, vibration, and acoustic signature, for the better evaluation of equipment condition and the improvement of predictive maintenance schedules.