Modeling and Simulation of Energy Systems: A Review
Abstract
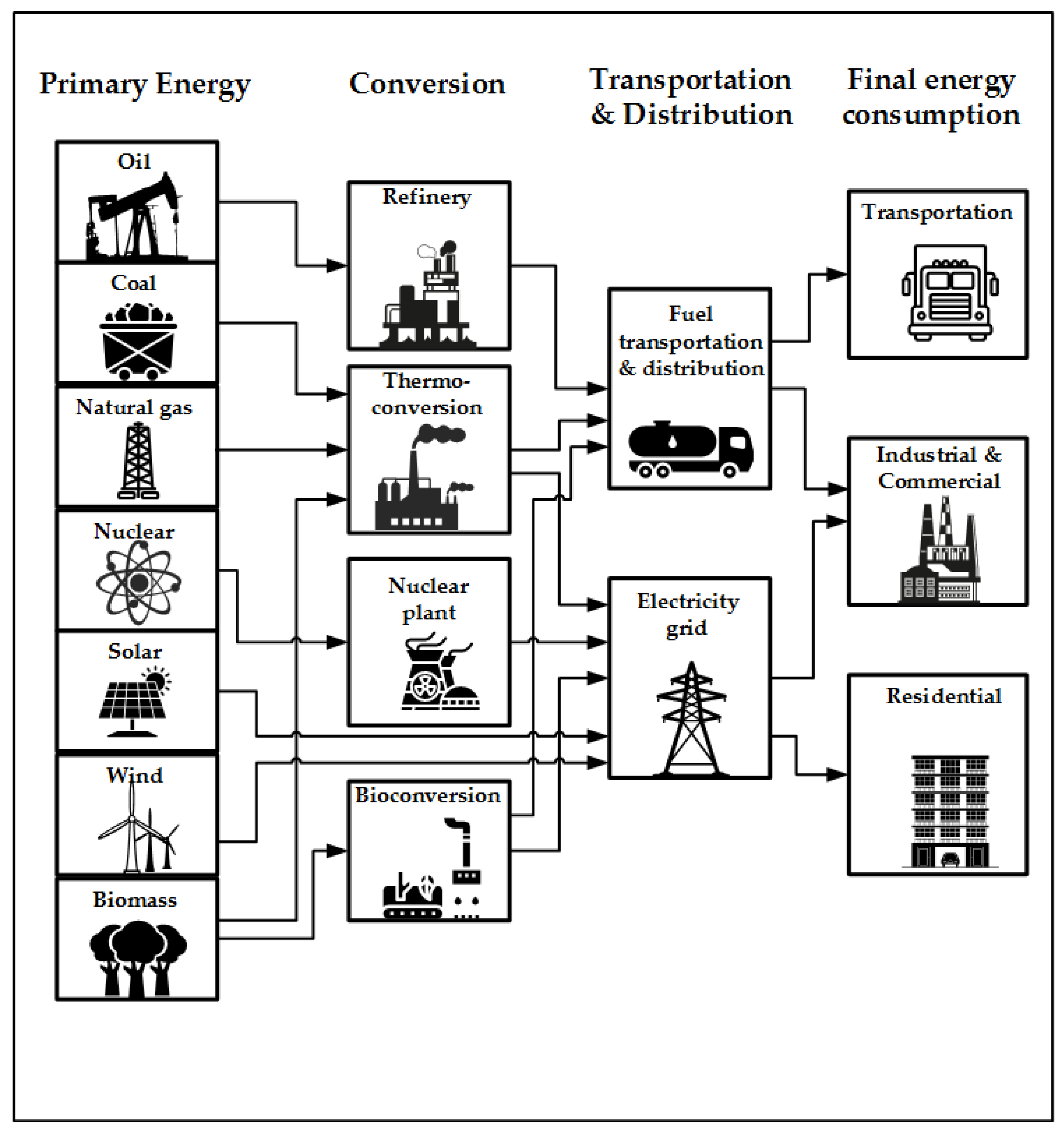
1. Introduction
- Emphasis on critical review papers of the different sub-fields within EE and PSE. These are denoted using blue in Table 1.
- Emphasis on the most impactful papers (measured by number of citations) or seminal works that presented novel approaches. These are denoted using red in Table 1.
- Emphasis on the modeling approach used rather than the application area.
- Emphasis on open access models or modeling tools to reflect the open source ethos of the Processes journal. These are denoted using black in Table 1.
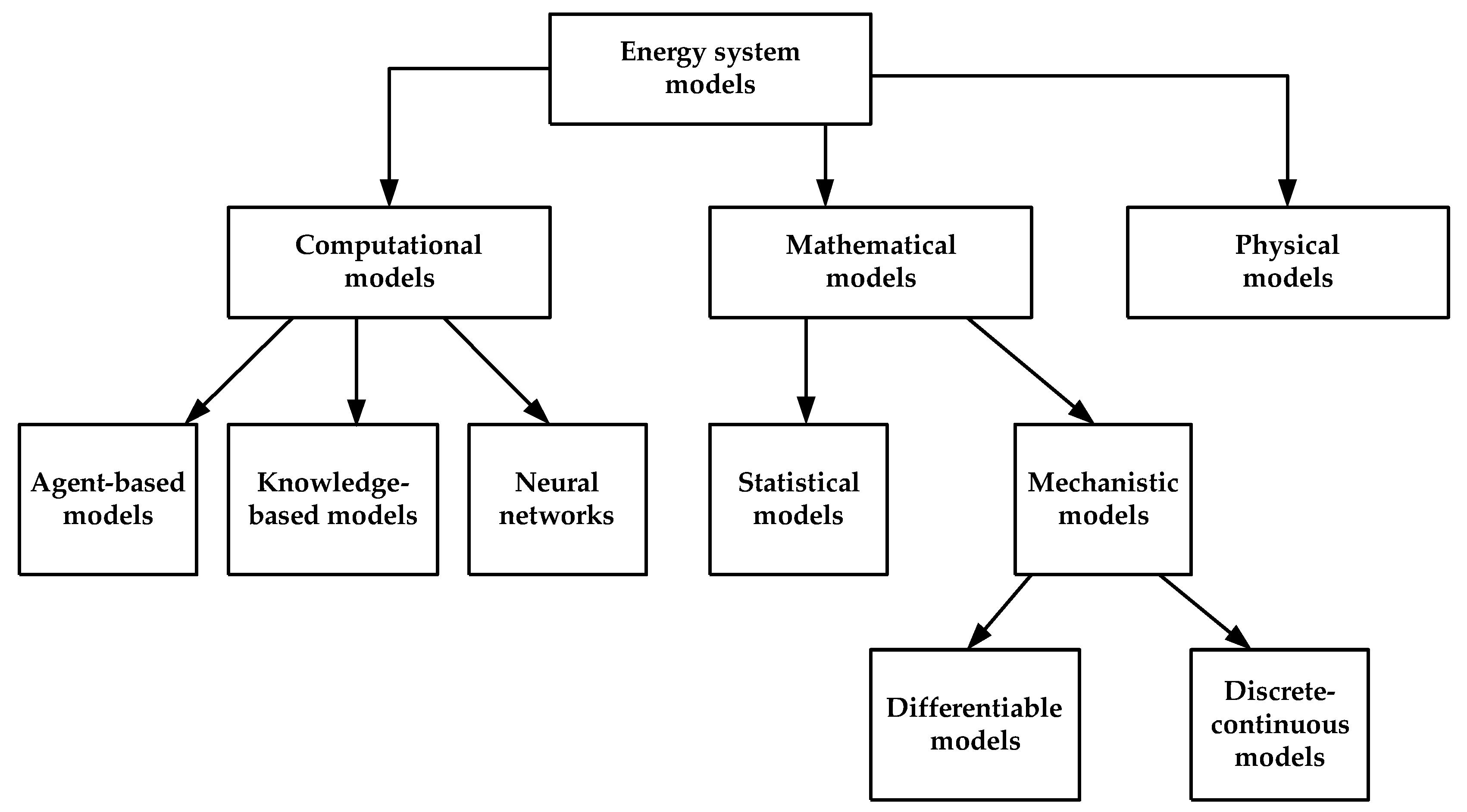
- First, we propose a categorization according to modeling approach namely into computational, mathematical, and physical approaches. With this categorization, we highlight certain novel hybrid approaches that combine aspects of the different groups proposed.
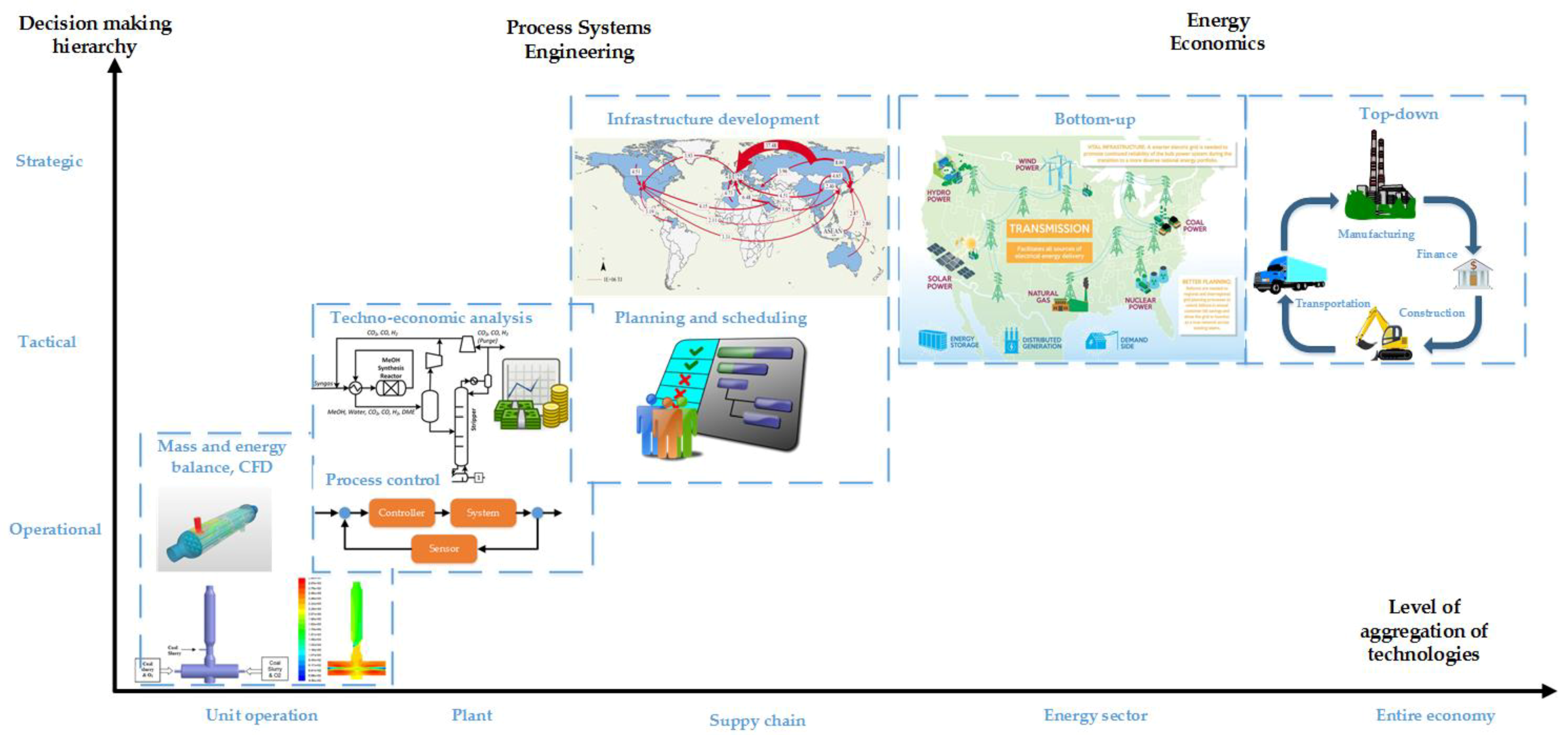
- Second, we propose a categorization according to field namely Process Systems Engineering (PSE) and Energy Economics (EE). We use the following criteria to illustrate the difference: the nature of variables, theoretical underpinnings, level of technological aggregation, spatial and temporal scales, and model purpose. With this categorization, we present the interaction between the PSE and EE fields and make the case for combining these two complementary approaches to get a more holistic picture of energy systems.
2. Categorization According to Modeling Approach
3. The PSE Approach to Energy System Modeling and Simulation
3.1. Multi-Scale Systems Engineering
3.1.1. Designing Novel Conversion Processes for Heterogeneous Feedstocks
3.1.2. Modeling and Optimal Design of Supply Chains for Distributed Energy Sources
3.2. Modeling Sustainability Criteria
3.2.1. Economic Criteria
3.2.2. Environmental Criteria
3.2.3. Social Criteria
4. The EE Approach to Energy System Modeling and Simulation
4.1. Demand and Supply Forecasting Models
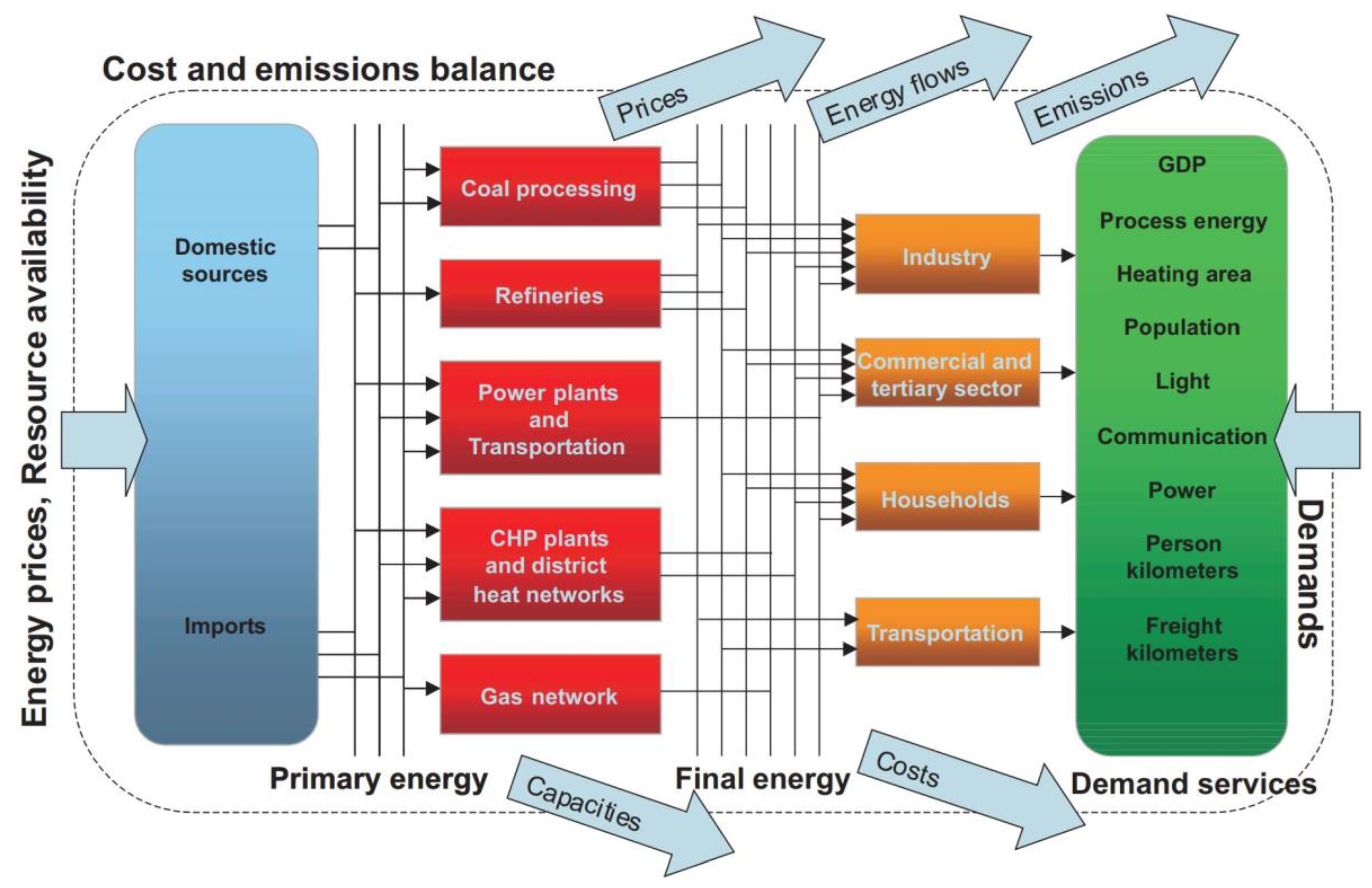
4.2. Bottom-Up Models
- Given a set of end users and forecasts for their demand over a certain (usually long term) time horizon, a set of candidate primary energy sources, and a set of corresponding conversion and distribution technologies; determine the optimal energy system configuration that minimizes overall costs (or maximizes overall efficiency) such that energy demand is satisfied by supply in each time period.
4.3. Top-Down Models
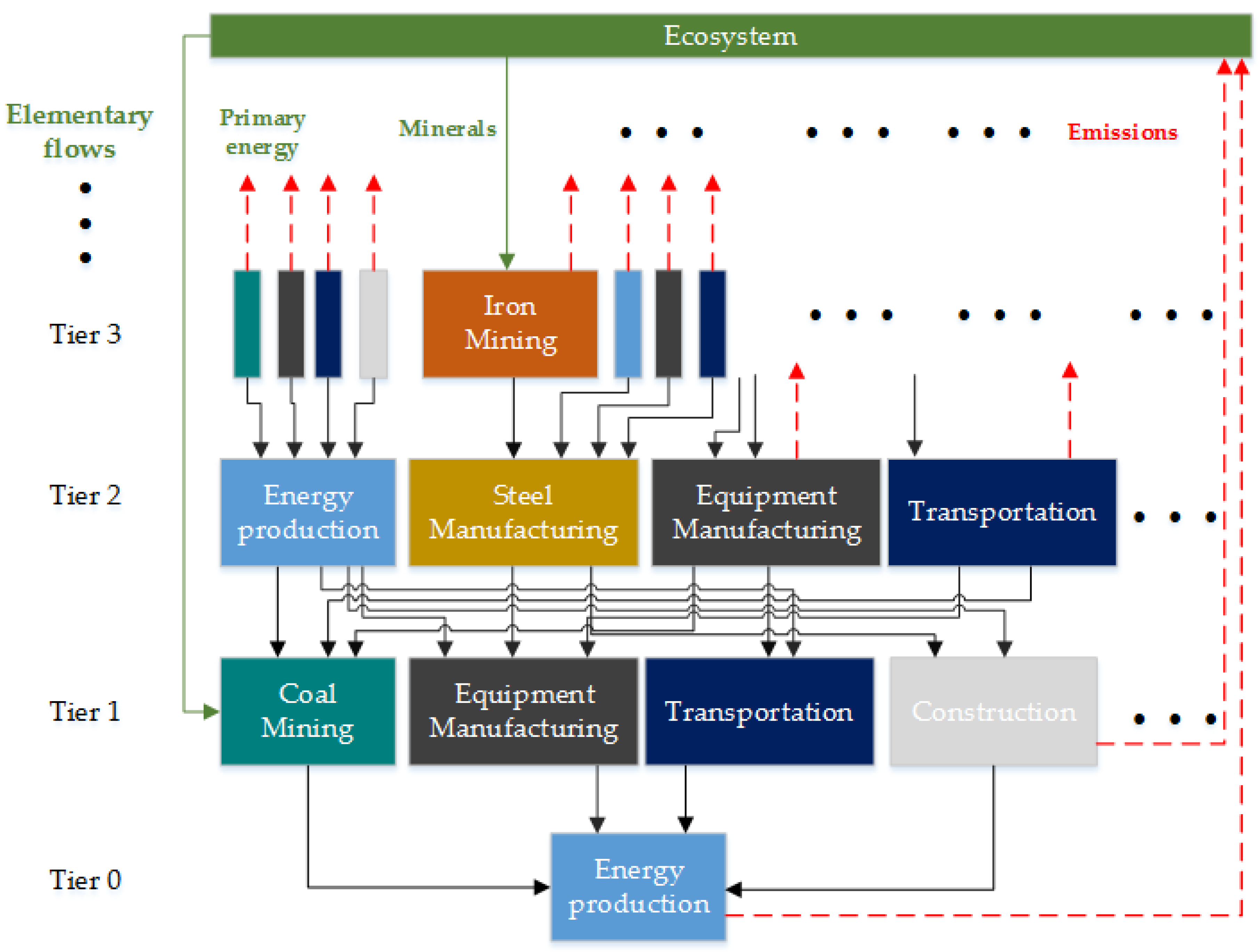
4.3.1. Input-Output (IO) Models
4.3.2. Input-Output LCA Models
4.3.3. Equilibrium Modeling
5. Combining PSE and EE Approaches
5.1. Optimal Design and Operation of Flexible Processes Using Demand and Price Forecasts
5.2. Sustainability Analysis and Process Design Using Hybrid Methods
5.3. Accounting for Feedback Effects of Breakthrough Technologies
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. World Energy Outlook; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Allwood, J.M.; Bosetti, V.; Dubash, N.K.; Gómez-Echeverri, L.; von Stechow, C. Glossary. In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Bruckner, T.; Bashmakov, I.A.; Mulugetta, Y.; Chum, H.; Navarro, A.D.; Edmonds, J.; Faaij, A.; Fungtammasan, B.; Garg, A.; Hertwich, E.; et al. Energy Systems. In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Grossmann, I.E.; Guillén-Gosálbez, G. Scope for the application of mathematical programming techniques in the synthesis and planning of sustainable processes. Comput. Chem. Eng. 2010, 34, 1365–1376. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C. Energy Economics: Concepts, Issues, Markets and Governance; Springer: London, UK, 2011; ISBN 978-0-85729-267-4. [Google Scholar]
- Foley, A.M.; Gallachóir, B.Ó.; Hur, J.; Baldick, R.; McKeogh, E.J. A strategic review of electricity systems models. Energy 2010, 35, 4522–4530. [Google Scholar] [CrossRef]
- Ventosa, M.; Baíllo, Á.; Ramos, A.; Rivier, M. Electricity market modeling trends. Energy Policy 2005, 33, 897–913. [Google Scholar] [CrossRef]
- Elia, J.A.; Baliban, R.C.; Floudas, C.A. Nationwide energy supply chain analysis for hybrid feedstock processes with significant CO2 emissions reduction. AIChE J. 2012, 58, 2142–2154. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Lang, Y.; Zitney, S.E.; Biegler, L.T. Optimization of IGCC processes with reduced order CFD models. Comput. Chem. Eng. 2011, 35, 1705–1717. [Google Scholar] [CrossRef]
- Adams, T.A., II; Thatho, T.; Feuvre Le, M.C.; Swartz, C.L.E. The Optimal Design of a Distillation System for the Flexible Polygeneration of Dimethyl Ether and Methanol under Uncertainty. Front. Energy Res. 2018, 6, 41. [Google Scholar] [CrossRef]
- Chen, G.Q.; Wu, X.F. Energy overview for globalized world economy: Source, supply chain and sink. Renew. Sustain. Energy Rev. 2017, 69, 735–749. [Google Scholar] [CrossRef]
- Biegler, L.T.; Grossmann, I.E.; Westerberg, A.W. Systematic Methods for Chemical Process Design; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997; ISBN 0-13-492422-3. Available online: https://www.osti.gov/biblio/293030-systematic-methods-chemical-process-design (accessed on 12 October 2018).
- Smith, R. Chemical Process: Design and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 9781118699096. [Google Scholar]
- Cameron, I.T.; Gani, R. Product and Process Modelling: A Case Study Approach; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Nishida, N.; Stephanopoulos, G.; Westerberg, A.W. A review of process synthesis. AIChE J. 1981, 27, 321–351. [Google Scholar] [CrossRef]
- Grossmann, I.E. Mixed-integer programming approach for the synthesis of integrated process flowsheets. Comput. Chem. Eng. 1985, 9, 463–482. [Google Scholar] [CrossRef]
- Gani, R.; Cameron, I.; Lucia, A.; Sin, G.; Georgiadis, M. Process Systems Engineering, 2. Modeling and Simulation. In Ullmann’s Encyclopedia of Industrial Chemistry; American Cancer Society: Atlanta, GA, USA, 2012; ISBN 978-3-527-30673-2. [Google Scholar]
- Marquardt, W. Trends in computer-aided process modeling. Comput. Chem. Eng. 1996, 20, 591–609. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Apap, R.M.; Calfa, B.A.; García-Herreros, P.; Zhang, Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty. Comput. Chem. Eng. 2016, 91, 3–14. [Google Scholar] [CrossRef]
- Barton, P.I.; Pantelides, C.C. Modeling of combined discrete/continuous processes. AIChE J. 1994, 40, 966–979. [Google Scholar] [CrossRef]
- Barton, P.I.; Lee, C.K. Modeling, simulation, sensitivity analysis, and optimization of hybrid systems. ACM Trans. Model. Comput. Simul. 2002, 12, 256–289. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport phenomena. Appl. Mech. Rev. 2002, 55, R1–R4. [Google Scholar] [CrossRef]
- Marquardt, W. Towards a Process Modeling Methodolgy. In Methods of Model Based Process Control; Springer: Dordrecht, The Netherlands, 1995; pp. 3–40. [Google Scholar]
- Watson, H.A.; Vikse, M.; Gundersen, T.; Barton, P.I. Reliable Flash Calculations: Part 2. Process flowsheeting with nonsmooth models and generalized derivatives. Ind. Eng. Chem. Res. 2017, 56, 14848–14864. [Google Scholar] [CrossRef]
- Psichogios, D.C.; Ungar, L.H. A hybrid neural network-first principles approach to process modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Thompson, M.L.; Kramer, M.A. Modeling chemical processes using prior knowledge and neural networks. AIChE J. 1994, 40, 1328–1340. [Google Scholar] [CrossRef]
- Hoseinzade, L.; Adams, T.A., II. Modeling and simulation of an integrated steam reforming and nuclear heat system. Int. J. Hydrogen Energy 2017, 42, 25048–25062. [Google Scholar] [CrossRef]
- Okeke, I.J.; Adams, T.A., II. Combining petroleum coke and natural gas for efficient liquid fuels production. Energy 2018, 163, 426–442. [Google Scholar] [CrossRef]
- Miller, D.C.; Agarwal, D.; Bhattacharyya, D.; Boverhof, J.; Chen, Y.; Eslick, J.; Leek, J.; Ma, J.; Mahapatra, P.; Ng, B.; et al. Innovative computational tools and models for the design, optimization and control of carbon capture processes. In Process Systems and Materials for CO2 Capture: Modelling, Design, Control and Integration; Papadopoulos, A.I., Seferlis, P., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2017; pp. 311–342. Available online: https://github.com/CCSI-Toolset/ (accessed on 12 October 2018).
- Yu, M.; Miller, D.C.; Biegler, L.T. Dynamic Reduced Order Models for Simulating Bubbling Fluidized Bed Adsorbers. Ind. Eng. Chem. Res. 2015, 54, 6959–6974. [Google Scholar] [CrossRef]
- Modekurti, S.; Bhattacharyya, D.; Zitney, S.E. Dynamic modeling and control studies of a two-stage bubbling fluidized bed adsorber-reactor for solid–sorbent CO2 capture. Ind. Eng. Chem. Res. 2013, 52, 10250–10260. [Google Scholar] [CrossRef]
- Garcia, D.J.; You, F. Supply chain design and optimization: Challenges and opportunities. Comput. Chem. Eng. 2015, 81, 153–170. [Google Scholar] [CrossRef]
- Shah, N. Process industry supply chains: Advances and challenges. Comput. Chem. Eng. 2005, 29, 1225–1235. [Google Scholar] [CrossRef]
- Papageorgiou, L.G. Supply chain optimisation for the process industries: Advances and opportunities. Comput. Chem. Eng. 2009, 33, 1931–1938. [Google Scholar] [CrossRef]
- Barbosa-Póvoa, A.P. Progresses and challenges in process industry supply chains optimization. Curr. Opin. Chem. Eng. 2012, 1, 446–452. [Google Scholar] [CrossRef]
- Nikolopoulou, A.; Ierapetritou, M.G. Optimal design of sustainable chemical processes and supply chains: A review. Comput. Chem. Eng. 2012, 44, 94–103. [Google Scholar] [CrossRef]
- Laínez, J.M.; Puigjaner, L. Prospective and perspective review in integrated supply chain modelling for the chemical process industry. Curr. Opin. Chem. Eng. 2012, 1, 430–445. [Google Scholar] [CrossRef]
- Min, H.; Zhou, G. Supply chain modeling: Past, present and future. Comput. Ind. Eng. 2002, 43, 231–249. [Google Scholar] [CrossRef]
- Niziolek, A.M.; Onel, O.; Tian, Y.; Floudas, C.A.; Pistikopoulos, E.N. Municipal solid waste to liquid transportation fuels—Part III: An optimization-based nationwide supply chain management framework. Comput. Chem. Eng. 2017, in press. [Google Scholar] [CrossRef]
- You, F.; Grossmann, I.E. Design of responsive supply chains under demand uncertainty. Comput. Chem. Eng. 2008, 32, 3090–3111. [Google Scholar] [CrossRef]
- You, F.; Grossmann, I.E. Mixed-integer nonlinear programming models and algorithms for large-scale supply chain design with stochastic inventory management. Ind. Eng. Chem. Res. 2008, 47, 7802–7817. [Google Scholar] [CrossRef]
- You, F.; Tao, L.; Graziano, D.J.; Snyder, S.W. Optimal design of sustainable cellulosic biofuel supply chains: Multiobjective optimization coupled with life cycle assessment and input–output analysis. AIChE J. 2012, 58, 1157–1180. [Google Scholar] [CrossRef]
- Liu, S.; Papageorgiou, L.G. Multiobjective optimisation of production, distribution and capacity planning of global supply chains in the process industry. Omega 2013, 41, 369–382. [Google Scholar] [CrossRef]
- Verderame, P.M.; Elia, J.A.; Li, J.; Floudas, C.A. Planning and Scheduling under Uncertainty: A Review Across Multiple Sectors. Ind. Eng. Chem. Res. 2010, 49, 3993–4017. [Google Scholar] [CrossRef]
- Maravelias, C.T.; Sung, C. Integration of production planning and scheduling: Overview, challenges and opportunities. Comput. Chem. Eng. 2009, 33, 1919–1930. [Google Scholar] [CrossRef]
- Floudas, C.A.; Lin, X. Continuous-time versus discrete-time approaches for scheduling of chemical processes: A review. Comput. Chem. Eng. 2004, 28, 2109–2129. [Google Scholar] [CrossRef]
- Li, Z.; Ierapetritou, M. Process scheduling under uncertainty: Review and challenges. Comput. Chem. Eng. 2008, 32, 715–727. [Google Scholar] [CrossRef]
- Méndez, C.A.; Cerdá, J.; Grossmann, I.E.; Harjunkoski, I.; Fahl, M. State-of-the-art review of optimization methods for short-term scheduling of batch processes. Comput. Chem. Eng. 2006, 30, 913–946. [Google Scholar] [CrossRef]
- Kallrath, J. Planning and scheduling in the process industry. OR Spectr. 2002, 24, 219–250. [Google Scholar] [CrossRef]
- Reklaitis, G.V. Overview of scheduling and planning of batch process operations. In Batch Processing Systems Engineering; Springer: Berlin/Heidelberg, Germany, 1996; pp. 660–705. [Google Scholar]
- Mitra, S.; Grossmann, I.E.; Pinto, J.M.; Arora, N. Optimal production planning under time-sensitive electricity prices for continuous power-intensive processes. Comput. Chem. Eng. 2012, 38, 171–184. [Google Scholar] [CrossRef]
- Mitra, S.; Sun, L.; Grossmann, I.E. Optimal scheduling of industrial combined heat and power plants under time-sensitive electricity prices. Energy 2013, 54, 194–211. [Google Scholar] [CrossRef]
- Birewar, D.B.; Grossmann, I.E. Simultaneous production planning and scheduling in multiproduct batch plants. Ind. Eng. Chem. Res. 1990, 29, 570–580. [Google Scholar] [CrossRef]
- Julka, N.; Srinivasan, R.; Karimi, I. Agent-based supply chain management—1: Framework. Comput. Chem. Eng. 2002, 26, 1755–1769. [Google Scholar] [CrossRef]
- Karimi, I.A.; McDonald, C.M. Planning and Scheduling of Parallel Semicontinuous Processes. 2. Short-Term Scheduling. Ind. Eng. Chem. Res. 1997, 36, 2701–2714. [Google Scholar] [CrossRef]
- McDonald, C.M.; Karimi, I.A. Planning and Scheduling of Parallel Semicontinuous Processes. 1. Production Planning. Ind. Eng. Chem. Res. 1997, 36, 2691–2700. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust process control. Chem. Eng. Res. Des. 1987, 65, 462–479. [Google Scholar]
- Luyben, W.L. Process Modeling, Simulation and Control for Chemical Engineers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989; ISBN 978-0-07-039159-8. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007; Volume 2, pp. 359–368. [Google Scholar]
- Hussain, M.A. Review of the applications of neural networks in chemical process control—Simulation and online implementation. Artif. Intell. Eng. 1999, 13, 55–68. [Google Scholar] [CrossRef]
- Bequette, B.W. Nonlinear control of chemical processes: A review. Ind. Eng. Chem. Res. 1991, 30, 1391–1413. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Skogestad, S. Plantwide control: The search for the self-optimizing control structure. J. Process Control 2000, 10, 487–507. [Google Scholar] [CrossRef]
- Skogestad, S. Control structure design for complete chemical plants. Comput. Chem. Eng. 2004, 28, 219–234. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Halemane, K.P.; Swaney, R.E. Optimization strategies for flexible chemical processes. Comput. Chem. Eng. 1983, 7, 439–462. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Morari, M. Operability, Resiliency, and Flexibility: Process Design Objectives for a Changing World. 1983. Available online: https://pdfs.semanticscholar.org/2b7c/85a9ff57ba9322910fc00128bca66ba0b544.pdf (accessed on 13 November 2018).
- Halemane, K.P.; Grossmann, I.E. Optimal process design under uncertainty. AIChE J. 1983, 29, 425–433. [Google Scholar] [CrossRef]
- Gonzalez-Salazar, M.A.; Kirsten, T.; Prchlik, L. Review of the operational flexibility and emissions of gas-and coal-fired power plants in a future with growing renewables. Renew. Sustain. Energy Rev. 2018, 82, 1497–1513. [Google Scholar] [CrossRef]
- Meerman, J.C.; Ramírez, A.; Turkenburg, W.C.; Faaij, A.P.C. Performance of simulated flexible integrated gasification polygeneration facilities. Part A: A technical-energetic assessment. Renew. Sustain. Energy Rev. 2011, 15, 2563–2587. [Google Scholar] [CrossRef]
- Liu, P.; Pistikopoulos, E.N.; Li, Z. A multi-objective optimization approach to polygeneration energy systems design. AIChE J. 2010, 56, 1218–1234. [Google Scholar] [CrossRef]
- Chen, Y.; Adams, T.A., II; Barton, P.I. Optimal Design and Operation of Flexible Energy Polygeneration Systems. Ind. Eng. Chem. Res. 2011, 50, 4553–4566. [Google Scholar] [CrossRef]
- Swaney, R.E.; Grossmann, I.E. An index for operational flexibility in chemical process design. Part I: Formulation and theory. AIChE J. 1985, 31, 621–630. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Floudas, C.A. Active constraint strategy for flexibility analysis in chemical processes. Comput. Chem. Eng. 1987, 11, 675–693. [Google Scholar] [CrossRef]
- Yunt, M.; Chachuat, B.; Mitsos, A.; Barton, P.I. Designing man-portable power generation systems for varying power demand. AIChE J. 2008, 54, 1254–1269. [Google Scholar] [CrossRef]
- Weijermars, R.; Taylor, P.; Bahn, O.; Das, S.R.; Wei, Y.-M. Review of models and actors in energy mix optimization-can leader visions and decisions align with optimum model strategies for our future energy systems? Energy Strateg. Rev. 2012, 1, 5–18. [Google Scholar] [CrossRef]
- Strantzali, E.; Aravossis, K. Decision making in renewable energy investments: A review. Renew. Sustain. Energy Rev. 2016, 55, 885–898. [Google Scholar] [CrossRef]
- Nakata, T.; Silva, D.; Rodionov, M. Application of energy system models for designing a low-carbon society. Prog. Energy Combust. Sci. 2011, 37, 462–502. [Google Scholar] [CrossRef]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Optimal planning and design of a renewable energy based supply system for microgrids. Renew. Energy 2012, 45, 7–15. [Google Scholar] [CrossRef]
- Manne, A.; Mendelsohn, R.; Richels, R. MERGE: A model for evaluating regional and global effects of GHG reduction policies. Energy Policy 1995, 23, 17–34. [Google Scholar] [CrossRef]
- Hennicke, P. Scenarios for a robust policy mix: The final report of the German study commission on sustainable energy supply. Energy Policy 2004, 32, 1673–1678. [Google Scholar] [CrossRef]
- Kydes, A.S. The Brookhaven Energy System Optimization Model: Its Variants and Uses. In Energy Policy Modeling: United States and Canadian Experiences; Springer: Dordrecht, The Netherlands, 1980; pp. 110–136. [Google Scholar]
- Naill, R.F. A system dynamics model for national energy policy planning. Syst. Dyn. Rev. 1992, 8, 1–19. [Google Scholar] [CrossRef]
- Jacobsson, S.; Lauber, V. The politics and policy of energy system transformation—Explaining the German diffusion of renewable energy technology. Energy Policy 2006, 34, 256–276. [Google Scholar] [CrossRef]
- Lund, H.; Mathiesen, B.V. Energy system analysis of 100% renewable energy systems—The case of Denmark in years 2030 and 2050. Energy 2009, 34, 524–531. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Kydes, A.S.; Whitman, P. The National Energy Modeling System: A Large-Scale Energy-Economic Equilibrium Model. Oper. Res. 2001, 49, 14–25. [Google Scholar] [CrossRef]
- Available online: https://openmod-initiative.org/ (accessed on 12 October 2018).
- Howells, M.; Rogner, H.; Strachan, N.; Heaps, C.; Huntington, H.; Kypreos, S.; Hughes, A.; Silveira, S.; DeCarolis, J.; Bazillian, M. OSeMOSYS: The open source energy modeling system: An introduction to its ethos, structure and development. Energy Policy 2011, 39, 5850–5870. [Google Scholar] [CrossRef]
- Howells, M.; Welsch, M. OSeMOSYS-The Open Source Energy Modelling System; International Energy Workshop: Stockholm, Sweden, 2010. [Google Scholar]
- Löffler, K.; Hainsch, K.; Burandt, T.; Oei, P.-Y.; Kemfert, C.; von Hirschhausen, C. Designing a Model for the Global Energy System—GENeSYS-MOD: An Application of the Open-Source Energy Modeling System (OSeMOSYS). Energies 2017, 10, 1468. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hirth, L.; Schlecht, I.; Schmid, E.; Wiese, F.; Brown, T.; Davis, C.; Gidden, M.; Heinrichs, H.; Heuberger, C.; et al. Opening the black box of energy modelling: Strategies and lessons learned. Energy Strateg. Rev. 2018, 19, 63–71. [Google Scholar] [CrossRef]
- Kannan, R.; Strachan, N. Modelling the UK residential energy sector under long-term decarbonisation scenarios: Comparison between energy systems and sectoral modelling approaches. Appl. Energy 2009, 86, 416–428. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Torriti, J. A review of time use models of residential electricity demand. Renew. Sustain. Energy Rev. 2014, 37, 265–272. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Timilsina, G.R. Energy Demand Models for Policy Formulation: A Comparative Study of Energy Demand Models; Policy Research Working Papers; The World Bank: Washington, DC, USA, 2009. [Google Scholar]
- Bhattacharyya, S.C.; Timilsina, G.R. A review of energy system models. Int. J. Energy Sect. Manag. 2010, 4, 494–518. [Google Scholar] [CrossRef]
- Craig, P.P.; Gadgil, A.; Koomey, J.G. What Can History Teach us? A Retrospective Examination of Long-Term Energy Forecasts for the United States. Annu. Rev. Energy Environ. 2002, 27, 83–118. [Google Scholar] [CrossRef]
- Werbos, P.J. 2.1. Econometric techniques: Theory versus practice. Energy 1990, 15, 213–236. [Google Scholar] [CrossRef]
- Huang, Y.; Bor, Y.J.; Peng, C.Y. The long-term forecast of Taiwan’s energy supply and demand: LEAP model application. Energy Policy 2011, 39, 6790–6803. [Google Scholar] [CrossRef]
- Ulbricht, R.; Fischer, U.; Lehner, W.; Donker, H. First steps towards a systematical optimized strategy for solar energy supply forecasting. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECMLPKDD 2013), Prague, Czech Republic, 23–27 September 2013; Volume 2327. [Google Scholar]
- Ekonomou, L. Greek long-term energy consumption prediction using artificial neural networks. Energy 2010, 35, 512–517. [Google Scholar] [CrossRef]
- Kankal, M.; Akpınar, A.; Kömürcü, M.İ.; Özşahin, T.Ş. Modeling and forecasting of Turkey’s energy consumption using socio-economic and demographic variables. Appl. Energy 2011, 88, 1927–1939. [Google Scholar] [CrossRef]
- Kandananond, K. Forecasting electricity demand in Thailand with an artificial neural network approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Hamzaçebi, C. Forecasting of Turkey’s net electricity energy consumption on sectoral bases. Energy Policy 2007, 35, 2009–2016. [Google Scholar] [CrossRef]
- Floudas, C.A.; Niziolek, A.M.; Onel, O.; Matthews, L.R. Multi-scale systems engineering for energy and the environment: Challenges and opportunities. AIChE J. 2016, 62, 602–623. [Google Scholar] [CrossRef]
- Hasan, M.F. Multi-scale Process Systems Engineering for Carbon Capture, Utilization, and Storage: A Review. In Process Systems and Materials for CO2 Capture: Modelling, Design, Control and Integration; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Biegler, L.T.; Lang, Y.; Lin, W. Multi-scale optimization for process systems engineering. Comput. Chem. Eng. 2014, 60, 17–30. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Shah, N. Multi-scale process and supply chain modelling: From lignocellulosic feedstock to process and products. Interface Focus 2011. [Google Scholar] [CrossRef] [PubMed]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Optimization framework for the simultaneous process synthesis, heat and power integration of a thermochemical hybrid biomass, coal, and natural gas facility. Comput. Chem. Eng. 2011, 35, 1647–1690. [Google Scholar] [CrossRef]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Simultaneous process synthesis, heat, power, and water integration of thermochemical hybrid biomass, coal, and natural gas facilities. Comput. Chem. Eng. 2012, 37, 297–327. [Google Scholar] [CrossRef]
- Niziolek, A.M.; Onel, O.; Hasan, M.M.F.; Floudas, C.A. Municipal solid waste to liquid transportation fuels—Part II: Process synthesis and global optimization strategies. Comput. Chem. Eng. 2015, 74, 184–203. [Google Scholar] [CrossRef]
- Ghouse, J.H.; Adams, T.A., II. A multi-scale dynamic two-dimensional heterogeneous model for catalytic steam methane reforming reactors. Int. J. Hydrogen Energy 2013, 38, 9984–9999. [Google Scholar] [CrossRef]
- Seepersad, D.; Ghouse, J.H.; Adams, T.A., II. Dynamic simulation and control of an integrated gasifier/reformer system. Part I: Agile case design and control. Chem. Eng. Res. Des. 2015, 100, 481–496. [Google Scholar] [CrossRef]
- Zitney, S.E. Process/equipment co-simulation for design and analysis of advanced energy systems. Comput. Chem. Eng. 2010, 34, 1532–1542. [Google Scholar] [CrossRef]
- Lang, Y.; Malacina, A.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Reduced order model based on principal component analysis for process simulation and optimization. Energy Fuels 2009, 23, 1695–1706. [Google Scholar] [CrossRef]
- Lang, Y.-D.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Advanced Process Engineering Co-Simulation Using CFD-Based Reduced Order Models; National Energy Technology Laboratory (NETL): Pittsburgh, PA, USA; Morgantown, WV, USA; Albany, OR, USA, 2007.
- Bakshi, B.R.; Fiksel, J. The quest for sustainability: Challenges for process systems engineering. AIChE J. 2003, 49, 1350–1358. [Google Scholar] [CrossRef]
- Bakshi, B.R. Methods and tools for sustainable process design. Curr. Opin. Chem. Eng. 2014, 6, 69–74. [Google Scholar] [CrossRef]
- Cano-Ruiz, J.A.; McRae, G.J. Environmentally Conscious Chemical Process Design. Annu. Rev. Energy Environ. 1998, 23, 499–536. [Google Scholar] [CrossRef]
- Fiksel, J. Designing Resilient, Sustainable Systems. Environ. Sci. Technol. 2003, 37, 5330–5339. [Google Scholar] [CrossRef] [PubMed]
- Pintarič, Z.N.; Kravanja, Z. Selection of the Economic Objective Function for the Optimization of Process Flow Sheets. Ind. Eng. Chem. Res. 2006, 45, 4222–4232. [Google Scholar] [CrossRef]
- Guinée, J.B. Handbook on life cycle assessment operational guide to the ISO standards. Int. J. Life Cycle Assess. 2002, 7, 311. [Google Scholar] [CrossRef]
- Matthews, H.S.; Hendrickson, C.T.; Matthews, D.H. Life Cycle Assessment: Quantitative Approaches for Decisions that Matter. 2015. Available online: http://www.lcatextbook.com (accessed on 12 October 2018).
- Curran, M.A. Environmental life-cycle assessment. Int. J. Life Cycle Assess. 1996, 1, 179. [Google Scholar] [CrossRef]
- Finnveden, G.; Hauschild, M.Z.; Ekvall, T.; Guinée, J.; Heijungs, R.; Hellweg, S.; Koehler, A.; Pennington, D.; Suh, S. Recent developments in Life Cycle Assessment. J. Environ. Manag. 2009, 91, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Klöpffer, W.; Grahl, B. Life Cycle Assessment (LCA): A Guide to Best Practice; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ukidwe, N.U.; Hau, J.L.; Bakshi, B.R. Thermodynamic Input-Output Analysis of Economic and Ecological Systems. In Handbook of Input-Output Economics in Industrial Ecology; Suh, S., Ed.; Eco-Efficiency in Industry and Science; Springer: Dordrecht, The Netherlands, 2009; pp. 459–490. ISBN 978-1-4020-5737-3. [Google Scholar]
- Rocco, M.V. Primary Exergy Cost of Goods and Services; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-43655-5. [Google Scholar]
- Othman, M.R.; Repke, J.-U.; Wozny, G.; Huang, Y. A Modular Approach to Sustainability Assessment and Decision Support in Chemical Process Design. Ind. Eng. Chem. Res. 2010, 49, 7870–7881. [Google Scholar] [CrossRef]
- Hugo, A.; Pistikopoulos, E.N. Environmentally conscious long-range planning and design of supply chain networks. J. Clean. Prod. 2005, 13, 1471–1491. [Google Scholar] [CrossRef]
- Suh, S.; Lenzen, M.; Treloar, G.J.; Hondo, H.; Horvath, A.; Huppes, G.; Jolliet, O.; Klann, U.; Krewitt, W.; Moriguchi, Y.; et al. System Boundary Selection in Life-Cycle Inventories Using Hybrid Approaches. Environ. Sci. Technol. 2004, 38, 657–664. [Google Scholar] [CrossRef] [PubMed]
- Lenzen, M. Errors in Conventional and Input-Output—Based Life—Cycle Inventories. J. Ind. Ecol. 2000, 4, 127–148. [Google Scholar] [CrossRef]
- Nease, J.; Adams, T.A., II. Life cycle analyses of bulk-scale solid oxide fuel cell power plants and comparisons to the natural gas combined cycle. Can. J. Chem. Eng. 2015, 93, 1349–1363. [Google Scholar] [CrossRef]
- Singh, B.; Strømman, A.H.; Hertwich, E.G. Comparative life cycle environmental assessment of CCS technologies. Int. J. Greenh. Gas Control 2011, 5, 911–921. [Google Scholar] [CrossRef]
- Available online: http://eplca.jrc.ec.europa.eu/ (accessed on 12 October 2018).
- Hanes, R.J.; Bakshi, B.R. Process to planet: A multiscale modeling framework toward sustainable engineering. AIChE J. 2015, 61, 3332–3352. [Google Scholar] [CrossRef]
- Hanes, R.J.; Bakshi, B.R. Sustainable process design by the process to planet framework. AIChE J. 2015, 61, 3320–3331. [Google Scholar] [CrossRef]
- Cornelissen, R.L.; Hirs, G.G. The value of the exergetic life cycle assessment besides the LCA. Energy Convers. Manag. 2002, 43, 1417–1424. [Google Scholar] [CrossRef]
- Available online: http://www.openlca.org/ (accessed on 13 November 2018).
- Carnegie Mellon University, Green Design Institute. Economic Input-Output Life Cycle Assessment (EIO-LCA) Model; Carnegie Mellon University: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Yang, Y.; Ingwersen, W.W.; Hawkins, T.R.; Srocka, M.; Meyer, D.E. USEEIO: A new and transparent United States environmentally-extended input-output model. J. Clean. Prod. 2017, 158, 308–318. [Google Scholar] [CrossRef] [PubMed]
- Ringkjøb, H.-K.; Haugan, P.M.; Solbrekke, I.M. A review of modelling tools for energy and electricity systems with large shares of variable renewables. Renew. Sustain. Energy Rev. 2018, 96, 440–459. [Google Scholar] [CrossRef]
- Hall, L.M.H.; Buckley, A.R. A review of energy systems models in the UK: Prevalent usage and categorisation. Appl. Energy 2016, 169, 607–628. [Google Scholar] [CrossRef]
- Van Beeck, N. Classification of Energy Models; Tilburg University: Tilburg, The Netherlands, 2000. [Google Scholar]
- Jebaraj, S.; Iniyan, S. A review of energy models. Renew. Sustain. Energy Rev. 2006, 10, 281–311. [Google Scholar] [CrossRef]
- Herbst, A.; Toro, F.; Reitze, F.; Jochem, E. Introduction to Energy Systems Modelling. Swiss J. Econ. Stat. 2012, 148, 111–135. [Google Scholar] [CrossRef]
- Nakata, T. Energy-economic models and the environment. Prog. Energy Combust. Sci. 2004, 30, 417–475. [Google Scholar] [CrossRef]
- Goyal, H.B.; Seal, D.; Saxena, R.C. Bio-fuels from thermochemical conversion of renewable resources: A review. Renew. Sustain. Energy Rev. 2008, 12, 504–517. [Google Scholar] [CrossRef]
- Zaimes, G.G.; Vora, N.; Chopra, S.S.; Landis, A.E.; Khanna, V. Design of Sustainable Biofuel Processes and Supply Chains: Challenges and Opportunities. Processes 2015, 3, 634–663. [Google Scholar] [CrossRef]
- Deshmukh, M.K.; Deshmukh, S.S. Modeling of hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- Shivarama Krishna, K.; Sathish Kumar, K. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
- Floudas, C.A.; Elia, J.A.; Baliban, R.C. Hybrid and single feedstock energy processes for liquid transportation fuels: A critical review. Comput. Chem. Eng. 2012, 41, 24–51. [Google Scholar] [CrossRef]
- Allegrini, J.; Orehounig, K.; Mavromatidis, G.; Ruesch, F.; Dorer, V.; Evins, R. A review of modelling approaches and tools for the simulation of district-scale energy systems. Renew. Sustain. Energy Rev. 2015, 52, 1391–1404. [Google Scholar] [CrossRef]
- Keirstead, J.; Jennings, M.; Sivakumar, A. A review of urban energy system models: Approaches, challenges and opportunities. Renew. Sustain. Energy Rev. 2012, 16, 3847–3866. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.; Huang, G.; Dai, J. A Review on Optimization Modeling of Energy Systems Planning and GHG Emission Mitigation under Uncertainty. Energies 2011, 4, 1624–1656. [Google Scholar] [CrossRef]
- Liu, P.; Georgiadis, M.C.; Pistikopoulos, E.N. Advances in Energy Systems Engineering. Ind. Eng. Chem. Res. 2011, 50, 4915–4926. [Google Scholar] [CrossRef]
- Adams, T.A., II. Future opportunities and challenges in the design of new energy conversion systems. Comput. Chem. Eng. 2015, 81, 94–103. [Google Scholar] [CrossRef]
- Martín, M.; Adams, T.A., II. Future directions in process and product synthesis and design. Comput. Aided Chem. Eng. 2018, 44, 1–10. [Google Scholar]
- Fisher, J.; Henzinger, T.A. Executable cell biology. Nat. Biotechnol. 2007, 25, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Tucker, D.; Shelton, M.; Manivannan, A. The Role of Solid Oxide Fuel Cells in Advanced Hybrid Power Systems of the Future. Electrochem. Soc. Interface 2009, 18, 45. [Google Scholar]
- Tucker, D.; Liese, E.; VanOsdol, J.; Lawson, L.; Gemmen, R.S. Fuel Cell Gas Turbine Hybrid Simulation Facility Design. In ASME 2002 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 183–190. [Google Scholar] [CrossRef]
- Liao, S.H. Expert system methodologies and applications—A decade review from 1995 to 2004. Expert Syst. Appl. 2005, 28, 93–103. [Google Scholar] [CrossRef]
- Stephanopoulos, G.; Han, C. Intelligent systems in process engineering: A review. Comput. Chem. Eng. 1996, 20, 743–791. [Google Scholar] [CrossRef]
- Mele, F.D.; Guillén, G.; Espuña, A.; Puigjaner, L. An agent-based approach for supply chain retrofitting under uncertainty. Comput. Chem. Eng. 2007, 31, 722–735. [Google Scholar] [CrossRef]
- Weidlich, A.; Veit, D. A critical survey of agent-based wholesale electricity market models. Energy Econ. 2008, 30, 1728–1759. [Google Scholar] [CrossRef]
- Ma, T.; Nakamori, Y. Agent-based modeling on technological innovation as an evolutionary process. Eur. J. Oper. Res. 2005, 166, 741–755. [Google Scholar] [CrossRef]
- Ma, T.; Nakamori, Y. Modeling technological change in energy systems–from optimization to agent-based modeling. Energy 2009, 34, 873–879. [Google Scholar] [CrossRef]
- Ma, T.; Grubler, A.; Nakamori, Y. Modeling technology adoptions for sustainable development under increasing returns, uncertainty, and heterogeneous agents. Eur. J. Oper. Res. 2009, 195, 296–306. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Dhaliwal, J.S.; Benbasat, I. The use and effects of knowledge-based system explanations: Theoretical foundations and a framework for empirical evaluation. Inf. Syst. Res. 1996, 7, 342–362. [Google Scholar] [CrossRef]
- Available online: https://www.process-design-center.com/prosyn.html (accessed on 12 October 2018).
- Puig-Arnavat, M.; Hernández, J.A.; Bruno, J.C.; Coronas, A. Artificial neural network models for biomass gasification in fluidized bed gasifiers. Biomass Bioenergy 2013, 49, 279–289. [Google Scholar] [CrossRef]
- Hunt, K.J.; Sbarbaro, D.; Żbikowski, R.; Gawthrop, P.J. Neural networks for control systems—A survey. Automatica 1992, 28, 1083–1112. [Google Scholar] [CrossRef]
- Baughman, D.R.; Liu, Y.A. Neural Networks in Bioprocessing and Chemical Engineering; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. A combined first-principles and data-driven approach to model building. Comput. Chem. Eng. 2015, 73, 116–127. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE: A Matlab Kriging Toolbox; Technical Report; Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- Straus, J.; Skogestad, S. Surrogate model generation using self-optimizing variables. Comput. Chem. Eng. 2018, in press. [Google Scholar] [CrossRef]
- Forrester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Watson, H.A.J. Robust Simulation and Optimization Methods for Natural Gas Liquefaction Processes. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Henzinger, T.A. The theory of hybrid automata. In Verification of Digital and Hybrid Systems; Springer: Berlin, Germany, 2000; pp. 265–292. [Google Scholar]
- Oldenburg, J.; Marquardt, W. Disjunctive modeling for optimal control of hybrid systems. Comput. Chem. Eng. 2008, 32, 2346–2364. [Google Scholar] [CrossRef]
- David, R.; Alla, H. On hybrid Petri nets. Discret. Event Dyn. Syst. 2001, 11, 9–40. [Google Scholar] [CrossRef]
- Barton, P.I.; Khan, K.A.; Stechlinski, P.; Watson, H.A. Computationally relevant generalized derivatives: Theory, evaluation and applications. Optim. Methods Softw. 2017, 1–43. [Google Scholar] [CrossRef]
- Watson, H.A.; Khan, K.A.; Barton, P.I. Multistream heat exchanger modeling and design. AIChE J. 2015, 61, 3390–3403. [Google Scholar] [CrossRef]
- Watson, H.A.; Vikse, M.; Gundersen, T.; Barton, P.I. Optimization of single mixed-refrigerant natural gas liquefaction processes described by nondifferentiable models. Energy 2018, 150, 860–876. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.A.; Gundersen, T.; Barton, P.I. Versatile Simulation Method for Complex Single Mixed Refrigerant Natural Gas Liquefaction Processes. Ind. Eng. Chem. Res. 2017, 57, 5881–5894. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.A.; Barton, P.I.; Gundersen, T. Simulation of a Dual Mixed Refrigerant LNG Process using a Nonsmooth Framework. Comput. Aided Chem. Eng. 2018, 44, 391–396. [Google Scholar]
- Vikse, M.; Watson, H.A.; Gundersen, T.; Barton, P.I. Simulation of Dual Mixed Refrigerant Natural Gas Liquefaction Processes using a Nonsmooth Framework. Processes 2018, 6, 193. [Google Scholar] [CrossRef]
- Straus, J.; Skogestad, S. Variable reduction for surrogate modelling. In Proceedings of the Foundations of Computer-Aided Process Operations, Tucson, AZ, USA, 8–12 January 2017. [Google Scholar]
- Straus, J.; Skogestad, S. Use of Latent Variables to Reduce the Dimension of Surrogate Models. Comput. Aided Chem. Eng. 2017, 40, 445–450. [Google Scholar]
- Guo, B.; Li, D.; Cheng, C.; Lü, Z.; Shen, Y. Simulation of biomass gasification with a hybrid neural network model. Bioresour. Technol. 2001, 76, 77–83. [Google Scholar] [CrossRef]
- Takamatsu, T. The nature and role of process systems engineering. Comput. Chem. Eng. 1983, 7, 203–218. [Google Scholar] [CrossRef]
- Vlachos, D.G. A Review of Multiscale Analysis: Examples from Systems Biology, Materials Engineering, and Other Fluid–Surface Interacting Systems. In Advances in Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume 30, pp. 1–61. ISBN 978-0-12-008530-9. [Google Scholar]
- Grossmann, I.E.; Westerberg, A.W. Research challenges in process systems engineering. AIChE J. 2000, 46, 1700–1703. [Google Scholar] [CrossRef]
- Grossmann, I.E. Challenges in the new millennium: Product discovery and design, enterprise and supply chain optimization, global life cycle assessment. Comput. Chem. Eng. 2004, 29, 29–39. [Google Scholar] [CrossRef]
- Horstemeyer, M.F. Multiscale Modeling: A Review. In Practical Aspects of Computational Chemistry; Springer: Dordrecht, The Netherlands, 2009; pp. 87–135. ISBN 978-90-481-2686-6. [Google Scholar]
- French, C.E. Synthetic biology and biomass conversion: A match made in heaven? J. R. Soc. Interface 2009, 6, S547–S558. [Google Scholar] [CrossRef] [PubMed]
- Mettler, M.S.; Vlachos, D.G.; Dauenhauer, P.J. Top ten fundamental challenges of biomass pyrolysis for biofuels. Energy Environ. Sci. 2012, 5, 7797–7809. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Singh, O.V. Bioconversion of lignocellulosic biomass: Biochemical and molecular perspectives. J. Ind. Microbiol. Biotechnol. 2008, 35, 377–391. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.K.; Chou, H.; Ham, T.S.; Lee, T.S.; Keasling, J.D. Metabolic engineering of microorganisms for biofuels production: From bugs to synthetic biology to fuels. Curr. Opin. Biotechnol. 2008, 19, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Toward Novel Hybrid Biomass, Coal, and Natural Gas Processes for Satisfying Current Transportation Fuel Demands, 1: Process Alternatives, Gasification Modeling, Process Simulation, and Economic Analysis. Ind. Eng. Chem. Res. 2010, 49, 7343–7370. [Google Scholar] [CrossRef]
- Onel, O.; Niziolek, A.M.; Hasan, M.M.F.; Floudas, C.A. Municipal solid waste to liquid transportation fuels—Part I: Mathematical modeling of a municipal solid waste gasifier. Comput. Chem. Eng. 2014, 71, 636–647. [Google Scholar] [CrossRef]
- Field, R.P.; Brasington, R. Baseline flowsheet model for IGCC with carbon capture. Ind. Eng. Chem. Res. 2011, 50, 11306–11312. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. High-efficiency power production from coal with carbon capture. AIChE J. 2010, 56, 3120–3136. [Google Scholar] [CrossRef]
- Kunze, C.; Spliethoff, H. Modelling, comparison and operation experiences of entrained flow gasifier. Energy Convers. Manag. 2011, 52, 2135–2141. [Google Scholar] [CrossRef]
- Singh, R.I.; Brink, A.; Hupa, M. CFD modeling to study fluidized bed combustion and gasification. Appl. Therm. Eng. 2013, 52, 585–614. [Google Scholar] [CrossRef]
- Zitney, S.E.; Syamlal, M. Integrated Process Simulation and CFD for Improved Process Engineering. Comput. Aided Chem. Eng. 2002, 10, 397–402. [Google Scholar]
- Baruah, D.; Baruah, D.C. Modeling of biomass gasification: A review. Renew. Sustain. Energy Rev. 2014, 39, 806–815. [Google Scholar] [CrossRef]
- Sloan, D.A.P.; Fiveland, W.A.P.; Zitney, S.E.; Osawe, M. Plant design: Integrating Plant and Equipment Models. Power Mag. 2007, 151, 8. [Google Scholar]
- Shi, S.-P.; Zitney, S.E.; Shahnam, M.; Syamlal, M.; Rogers, W.A. Modelling coal gasification with CFD and discrete phase method. J. Energy Inst. 2006, 79, 217–221. [Google Scholar] [CrossRef]
- Biegler, L.T.; Lang, Y. Multi-scale optimization for advanced energy processes. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2012; Volume 31, pp. 51–60. [Google Scholar]
- Chen, L.; Yong, S.Z.; Ghoniem, A.F. Oxy-fuel combustion of pulverized coal: Characterization, fundamentals, stabilization and CFD modeling. Prog. Energy Combust. Sci. 2012, 38, 156–214. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. Combining coal gasification, natural gas reforming, and solid oxide fuel cells for efficient polygeneration with CO2 capture and sequestration. Fuel Process. Technol. 2011, 92, 2105–2115. [Google Scholar] [CrossRef]
- Adams, T.A., II; Ghouse, J.H. Polygeneration of fuels and chemicals. Curr. Opin. Chem. Eng. 2015, 10, 87–93. [Google Scholar] [CrossRef]
- Jana, K.; Ray, A.; Majoumerd, M.M.; Assadi, M.; De, S. Polygeneration as a future sustainable energy solution—A comprehensive review. Appl. Energy 2017, 202, 88–111. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. Combining coal gasification and natural gas reforming for efficient polygeneration. Fuel Process. Technol. 2011, 92, 639–655. [Google Scholar] [CrossRef]
- Ghouse, J.H.; Seepersad, D.; Adams, T.A., II. Modelling, simulation and design of an integrated radiant syngas cooler and steam methane reformer for use with coal gasification. Fuel Process. Technol. 2015, 138, 378–389. [Google Scholar] [CrossRef]
- Seepersad, D.; Ghouse, J.H.; Adams, T.A., II. Dynamic simulation and control of an integrated gasifier/reformer system. Part II: Discrete and model predictive control. Chem. Eng. Res. Des. 2015, 100, 497–508. [Google Scholar] [CrossRef]
- Sharma, B.; Ingalls, R.G.; Jones, C.L.; Khanchi, A. Biomass supply chain design and analysis: Basis, overview, modeling, challenges, and future. Renew. Sustain. Energy Rev. 2013, 24, 608–627. [Google Scholar] [CrossRef]
- Yue, D.; You, F.; Snyder, S.W. Biomass-to-bioenergy and biofuel supply chain optimization: Overview, key issues and challenges. Comput. Chem. Eng. 2014, 66, 36–56. [Google Scholar] [CrossRef]
- Iakovou, E.; Karagiannidis, A.; Vlachos, D.; Toka, A.; Malamakis, A. Waste biomass-to-energy supply chain management: A critical synthesis. Waste Manag. 2010, 30, 1860–1870. [Google Scholar] [CrossRef] [PubMed]
- Cafaro, D.C.; Grossmann, I.E. Strategic planning, design, and development of the shale gas supply chain network. AIChE J. 2014, 60, 2122–2142. [Google Scholar] [CrossRef]
- Rezaie, B.; Rosen, M.A. District heating and cooling: Review of technology and potential enhancements. Appl. Energy 2012, 93, 2–10. [Google Scholar] [CrossRef]
- Varma, V.A.; Reklaitis, G.V.; Blau, G.E.; Pekny, J.F. Enterprise-wide modeling & optimization—An overview of emerging research challenges and opportunities. Comput. Chem. Eng. 2007, 31, 692–711. [Google Scholar] [CrossRef]
- Zhang, Q.; Grossmann, I.E. Enterprise-wide optimization for industrial demand side management: Fundamentals, advances, and perspectives. Chem. Eng. Res. Des. 2016, 116, 114–131. [Google Scholar] [CrossRef]
- Lam, H.L.; Klemeš, J.J.; Kravanja, Z. Model-size reduction techniques for large-scale biomass production and supply networks. Energy 2011, 36, 4599–4608. [Google Scholar] [CrossRef]
- Our Common Future, Chapter 2: Towards Sustainable Development-A/42/427 Annex, Chapter 2-UN Documents: Gathering a Body of Global Agreements. Available online: http://www.un-documents.net/ocf-02.htm (accessed on 9 September 2018).
- Elkington, J. Cannibals with Forks: The Triple Bottom Line of 21st Century Business; John Wiley and Sons: Hoboken, NJ, USA, 1999; ISBN 1841120847. [Google Scholar]
- Belgiorno, V.; De Feo, G.; Della Rocca, C.; Napoli, R.M.A. Energy from gasification of solid wastes. Waste Manag. 2003, 23, 1–15. [Google Scholar] [CrossRef]
- Psomopoulos, C.S.; Bourka, A.; Themelis, N.J. Waste-to-energy: A review of the status and benefits in USA. Waste Manag. 2009, 29, 1718–1724. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, H.; Pettersson, F.; Saxén, H. Sustainable development of primary steelmaking under novel blast furnace operation and injection of different reducing agents. Chem. Eng. Sci. 2015, 129, 208–222. [Google Scholar] [CrossRef]
- Deng, L.; Adams, T.A., II. Optimization of coke oven gas desulfurization and combined cycle power plant electricity generation. Ind. Eng. Chem. Res. 2018, in press. [Google Scholar] [CrossRef]
- Klemes, J.J. Handbook of Process Integration (PI): Minimisation of Energy and Water Use, Waste and Emissions; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Fu, C.; Vikse, M.; Gundersen, T. Work and Heat Integration: An emerging research area. Energy 2018, 158, 796–806. [Google Scholar] [CrossRef]
- Karuppiah, R.; Grossmann, I.E. Global optimization for the synthesis of integrated water systems in chemical processes. Comput. Chem. Eng. 2006, 30, 650–673. [Google Scholar] [CrossRef]
- Wang, Y.P.; Smith, R. Wastewater minimisation. Chem. Eng. Sci. 1994, 49, 981–1006. [Google Scholar] [CrossRef]
- Smith, R.L.; Ruiz-Mercado, G.J.; Gonzalez, M.A. Using GREENSCOPE indicators for sustainable computer-aided process evaluation and design. Comput. Chem. Eng. 2015, 81, 272–277. [Google Scholar] [CrossRef]
- Azapagic, A.; Perdan, S. Indicators of Sustainable Development for Industry. Process Saf. Environ. Prot. 2000, 78, 243–261. [Google Scholar] [CrossRef]
- Bamufleh, H.S.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Multi-objective optimization of process cogeneration systems with economic, environmental, and social tradeoffs. Clean Technol. Environ. Policy 2013, 15, 185–197. [Google Scholar] [CrossRef]
- Sinnott, R.K.; Towler, G. Chemical Engineering Design: SI Edition; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Seider, W.D.; Seader, J.D.; Lewin, D.R. Product and Process Design Principles: Synthesis, Analysis and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis and Design of Chemical Processes; Pearson Education: London, UK, 2008. [Google Scholar]
- Larson, E.D.; Jin, H.; Celik, F.E. Large-scale gasification-based coproduction of fuels and electricity from switchgrass. Biofuels Bioprod. Biorefin. 2009, 3, 174–194. [Google Scholar] [CrossRef]
- Hamelinck, C.; Faaij, A.; Denuil, H.; Boerrigter, H. Production of FT transportation fuels from biomass; technical options, process analysis and optimisation, and development potential. Energy 2004, 29, 1743–1771. [Google Scholar] [CrossRef]
- Adams, T.A., II. Learn Aspen Plus in 24 Hours; McGraw-Hill Education: New York, NY, USA, 2018; ISBN 978-1-260-11645-8. [Google Scholar]
- ICIS Pricing. Chemical Industry Trends. Available online: https://www.icis.com (accessed on 10 September 2018).
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Sirdeshpande, A.R.; Ierapetritou, M.G.; Andrecovich, M.J.; Naumovitz, J.P. Process synthesis optimization and flexibility evaluation of air separation cycles. AIChE J. 2005, 51, 1190–1200. [Google Scholar] [CrossRef]
- Wang, H.; Mastragostino, R.; Swartz, C.L. Flexibility analysis of process supply chain networks. Comput. Chem. Eng. 2016, 84, 409–421. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Calfa, B.A.; Garcia-Herreros, P. Evolution of concepts and models for quantifying resiliency and flexibility of chemical processes. Comput. Chem. Eng. 2014, 70, 22–34. [Google Scholar] [CrossRef]
- Horne, R.; Grant, T.; Verghese, K. Life Cycle Assessment: Principles, Practice and Prospects; Csiro Publishing: Clayton, Australia, 2009. [Google Scholar]
- International Organization for Standardization. Environmental Management: Life Cycle Assessment; Principles and Framework; ISO: Geneva, Switzerland, 2006. [Google Scholar]
- Huijbregts, M.A.J.; Steinmann, Z.J.N.; Elshout, P.M.F.; Stam, G.; Verones, F.; Vieira, M.D.M.; Hollander, A.; Zijp, M.; van Zelm, R. ReCiPe 2016: A Harmonized Life Cycle Impact Assessment Method at Midpoint and Endpoint Level. Report I: Characterization; RIVM Report 2016-0104; National Institute for Public Health and the Environment: Bilthofen, The Netherlands, 2016. [Google Scholar]
- Bare, J.C. TRACI: The tool for the reduction and assessment of chemical and other environmental impacts. J. Ind. Ecol. 2002, 6, 49–78. [Google Scholar] [CrossRef]
- Eco-Indicator 99 Methodology Report; Pre Consultants B.V.: Amersfoort, The Netherlands, 22 June 2011.
- Available online: https://uslci.lcacommons.gov/ (accessed on 12 October 2018).
- Available online: https://www.ecoinvent.org/ (accessed on 12 October 2018).
- Azapagic, A.; Howard, A.; Parfitt, A.; Tallis, B.; Duff, C.; Hadfield, C.; Pritchard, C.; Gillett, J.; Hackitt, J.; Seaman, M.; et al. The Sustainability Metrics. Available online: http: //nbis.org/nbisresources/metrics/triple_bottom_line_indicators_process_industries.pdf (accessed on 12 October 2018).
- Jørgensen, A.; Le Bocq, A.; Nazarkina, L.; Hauschild, M. Methodologies for social life cycle assessment. Int. J. Life Cycle Assess. 2008, 13, 96. [Google Scholar] [CrossRef]
- Kober, T.; Panos, E.; Volkart, K. Energy system challenges of deep global CO2 emissions reduction under the World Energy Council’s scenario framework. In Limiting Global Warming to Well Below 2 °C: Energy System Modelling and Policy Development; Springer: Berlin, Germany, 2018; pp. 17–31. [Google Scholar]
- Perloff, J.M. Microeconomics; Pearson Addison Wesley: Boston, MA, USA, 2004. [Google Scholar]
- EIA-The National Energy Modeling System: An Overview. 2009. Available online: https://www.eia.gov/outlooks/aeo/nems/overview/index.html (accessed on 12 October 2018).
- Monteiro, C.; Bessa, R.; Miranda, V.; Botterud, A.; Wang, J.; Conzelmann, G. INESC Porto Wind Power Forecasting: State-of-the-Art 2009; Argonne National Lab.: Lemont, IL, USA, 2009. [Google Scholar]
- E3Mlab of ICCS/NTUA. The PRIMES Model. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/sec_2011_1569_2_prime_model_0.pdf (accessed on 12 October 2018).
- Berndes, G.; Hoogwijk, M.; Van den Broek, R. The contribution of biomass in the future global energy supply: A review of 17 studies. Biomass Bioenergy 2003, 25, 1–28. [Google Scholar] [CrossRef]
- Remme, U.; Goldstein, G.A.; Schellmann, U.; Schlenzig, C. MESAP/TIMES—Advanced Decision Support for Energy and Environmental Planning. In Operations Research Proceedings 2001; Chamoni, P., Leisten, R., Martin, A., Minnemann, J., Stadtler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Loulou, R.; Goldstein, G.; Noble, K. Documentation for the MARKAL Family of Models. Energy Technol. Syst. Anal. Program. 2004, 65–73. Available online: http://iea-etsap.org/MrklDoc-I_StdMARKAL.pdf (accessed on 12 October 2018).
- Schrattenholzer, L. The Energy Supply Model MESSAGE; International Institute for Applied Systems Analysis: Laxenburg, Austria, 1981; Available online: http://pure.iiasa.ac.at/id/eprint/1542/ (accessed on 12 October 2018).
- Krey, V.; Havlik, P.; Fricko, O.; Zilliacus, J.; Gidden, M.; Strubegger, M.; Kartasasmita, I.; Ermolieva, T.; Forsell, N.; Gusti, M. Message-Globiom 1.0 Documentation; International Institute for Applied Systems Analysis: Laxenburg, Austria, 2016; Available online: http://data.ene.iiasa.ac.at/message-globiom (accessed on 12 October 2018).
- Energy PLAN. MARKAL/TIMES. Available online: https://www.energyplan.eu/othertools/national/markaltimes/ (accessed on 12 October 2018).
- Available online: http://www.iiasa.ac.at/web/home/research/researchPrograms/Energy/IAMF.en.html (accessed on 13 November 2018).
- Huppmann, D.; Gidden, M.; Fricko, O.; Kolp, P.; Orthofer, C.; Pimmer, M.; Vinca, A.; Mastrucci, A.; Riahi, K.; Krey, V. The MESSAGEix Integrated Assessment Model and the ix modeling platform (ixmp). Environ. Model. Softw. 2018. Available online: http://pure.iiasa.ac.at/15157 (accessed on 12 October 2018).
- Dowlatabadi, H. Integrated assessment models of climate change: An incomplete overview. Energy Policy 1995, 23, 289–296. [Google Scholar] [CrossRef]
- Parker, P.; Letcher, R.; Jakeman, A.; Beck, M.B.; Harris, G.; Argent, R.M.; Hare, M.; Pahl-Wostl, C.; Voinov, A.; Janssen, M. Progress in integrated assessment and modelling1. Environ. Model. Softw. 2002, 17, 209–217. [Google Scholar] [CrossRef]
- Stanton, E.A.; Ackerman, F.; Kartha, S. Inside the integrated assessment models: Four issues in climate economics. Clim. Dev. 2009, 1, 166–184. [Google Scholar] [CrossRef]
- Rotmans, J. Methods for IA: The challenges and opportunities ahead. Environ. Model. Assess. 1998, 3, 155–179. [Google Scholar] [CrossRef]
- Pfenninger, S. Energy scientists must show their workings. Nat. News 2017, 542, 393. [Google Scholar] [CrossRef] [PubMed]
- Herbst, M.A.; Toro, F.A.; Reitze, F.; Eberhard, J. Bridging Macroeconomic and Bottom up Energy Models-the Case of Efficiency in Industry. Available online: https://www.eceee.org (accessed on 12 October 2018).
- Dannenberg, A.; Mennel, T.; Moslener, U. What does Europe pay for clean energy?—Review of macroeconomic simulation studies. Energy Policy 2008, 36, 1318–1330. [Google Scholar] [CrossRef]
- Miller, R.E.; Blair, P.D. Input-Output Analysis: Foundations and Extensions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- US Bureau of Economic Analysis. Input-Output Accounts Data. Available online: https://www.bea.gov/industry/input-output-accounts-data (accessed on 12 October 2018).
- Bullard, C.W.; Herendeen, R.A. Energy impact of consumption decisions. Proc. IEEE 1975, 63, 484–493. [Google Scholar] [CrossRef]
- Just, J.E. Impacts of new energy technology using generalized input-output analysis. Comput. Oper. Res. 1974, 1, 97–109. [Google Scholar] [CrossRef]
- Matthews, H.S.; Small, M.J. Extending the boundaries of life-cycle assessment through environmental economic input-output models. J. Ind. Ecol. 2000, 4, 7–10. [Google Scholar] [CrossRef]
- Hendrickson, C.; Horvath, A.; Joshi, S.; Lave, L. Peer reviewed: Economic input–output models for environmental life-cycle assessment. Environ. Sci. Technol. 1998, 32, 184A–191A. [Google Scholar] [CrossRef]
- Hendrickson, C.T.; Lave, L.B.; Matthews, H.S. Environmental Life Cycle Assessment of Goods and Services: An Input-Output Approach; Resources for the Future: Washington, DC, USA, 2006. [Google Scholar]
- U.S. Energy Information Administration (EIA). Annual Energy Outlook 2016. Available online: https://www.eia.gov/outlooks/archive/aeo16/appendixe.php (accessed on 8 October 2018).
- Mitra, S.; Pinto, J.M.; Grossmann, I.E. Optimal multi-scale capacity planning for power-intensive continuous processes under time-sensitive electricity prices and demand uncertainty. Part I: Modeling. Comput. Chem. Eng. 2014, 65, 89–101. [Google Scholar] [CrossRef]
- PJM Interconnection, 2011. Daily Day-Ahead Locational Marginal Pricing. Available online: http://www.pjm.com (accessed on 12 October 2018).
- U.S. Energy Information Administration (EIA). Electric Power Annual 2016. Available online: https://www.eia.gov/electricity/annual/ (accessed on 12 October 2018).
- Rolfsman, B. Combined heat-and-power plants and district heating in a deregulated electricity market. Appl. Energy 2004, 78, 37–52. [Google Scholar] [CrossRef]
- Independent Electricity System Operator. Ontario Demand and Market Prices. 2012. Available online: http://www.ieso.ca/imoweb/siteShared/demandprice.asp?sid=ic (accessed on 12 October 2018).
- Nease, J.; Adams, T.A., II. Application of rolling horizon optimization to an integrated solid-oxide fuel cell and compressed air energy storage plant for zero-emissions peaking power under uncertainty. Comput. Chem. Eng. 2014, 68, 203–219. [Google Scholar] [CrossRef]
- Hendrickson, C.T.; Horvath, A.; Joshi, S.; Klausner, M.; Lave, L.B.; McMichael, F.C. Comparing two life cycle assessment approaches: A process model vs. economic input-output-based assessment. In Proceedings of the 1997 IEEE International Symposium on Electronics and the Environment. ISEE-1997, San Francisco, CA, USA, 5–7 May 1997; pp. 176–181. [Google Scholar]
- Joshi, S. Product environmental life-cycle assessment using input-output techniques. J. Ind. Ecol. 1999, 3, 95–120. [Google Scholar] [CrossRef]
- Adriaanse, A.; Bringezu, S.; Hammond, A.; Moriguchi, Y.; Rodenburg, E.; Rogich, D.; Schütz, H. Resource Flows: The Material Basis of Industrial Economies; World Resources Institute: Washington, DC, USA, 1997. [Google Scholar]
- Spreng, D.T. Net-Energy Analysis and the Energy Requirements of Energy Systems; Praeger: Westport, CT, USA, 1988. [Google Scholar]
- Ukidwe, N.U.; Bakshi, B.R. Thermodynamic Accounting of Ecosystem Contribution to Economic Sectors with Application to 1992 U.S. Economy. Environ. Sci. Technol. 2004, 38, 4810–4827. [Google Scholar] [CrossRef] [PubMed]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes; Springer: Berlin, Germany, 1987. [Google Scholar]
- Sciubba, E.; Wall, G. A brief commented history of exergy from the beginnings to 2004. Int. J. Thermodyn. 2007, 10, 1–26. [Google Scholar]
- Szargut, J.; Morris, D.R. Cumulative exergy consumption and cumulative degree of perfection of chemical processes. Int. J. Energy Res. 1987, 11, 245–261. [Google Scholar] [CrossRef]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- Valero, A.; Lozano, M.A.; Serra, L.; Torres, C. Application of the exergetic cost theory to the CGAM problem. Energy 1994, 19, 365–381. [Google Scholar] [CrossRef]
- Valero, A.; Serra, L.; Uche, J. Fundamentals of exergy cost accounting and thermoeconomics. Part I: Theory. Energy Resour. Technol. 2006, 128, 1–8. [Google Scholar] [CrossRef]
- Ayres, R.U.; Ayres, L.W.; Martinás, K. Exergy, waste accounting, and life-cycle analysis. Energy 1998, 23, 355–363. [Google Scholar] [CrossRef]
- Keshavarzian, S.; Rocco, M.V.; Gardumi, F.; Colombo, E. Practical approaches for applying thermoeconomic analysis to energy conversion systems: Benchmarking and comparative application. Energy Convers. Manag. 2017, 150, 532–544. [Google Scholar] [CrossRef]
- Hau, J.L.; Bakshi, B.R. Expanding Exergy Analysis to Account for Ecosystem Products and Services. Environ. Sci. Technol. 2004, 38, 3768–3777. [Google Scholar] [CrossRef] [PubMed]
- Keshavarzian, S.; Gardumi, F.; Rocco, M.V.; Colombo, E. Off-Design Modeling of Natural Gas Combined Cycle Power Plants: An Order Reduction by Means of Thermoeconomic Input–Output Analysis. Entropy 2016, 18, 71. [Google Scholar] [CrossRef]
- Keshavarzian, S.; Rocco, M.V.; Colombo, E. Thermoeconomic diagnosis and malfunction decomposition: Methodology improvement of the Thermoeconomic Input-Output Analysis (TIOA). Energy Convers. Manag. 2018, 157, 644–655. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. High-efficiency power production from natural gas with carbon capture. J. Power Sources 2010, 195, 1971–1983. [Google Scholar] [CrossRef]
- Yue, D.; Pandya, S.; You, F. Integrating Hybrid Life Cycle Assessment with Multiobjective Optimization: A Modeling Framework. Environ. Sci. Technol. 2016, 50, 1501–1509. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Thomas, I.L. Alternative energy technologies. Nature 2001, 414, 332–337. [Google Scholar] [CrossRef] [PubMed]
- Bolat, P.; Thiel, C. Hydrogen supply chain architecture for bottom-up energy systems models. Part 1: Developing pathways. Int. J. Hydrogen Energy 2014, 39, 8881–8897. [Google Scholar] [CrossRef]
- Bolat, P.; Thiel, C. Hydrogen supply chain architecture for bottom-up energy systems models. Part 2: Techno-economic inputs for hydrogen production pathways. Int. J. Hydrogen Energy 2014, 39, 8898–8925. [Google Scholar] [CrossRef]
- Sgobbi, A.; Nijs, W.; De Miglio, R.; Chiodi, A.; Gargiulo, M.; Thiel, C. How far away is hydrogen? Its role in the medium and long-term decarbonisation of the European energy system. Int. J. Hydrogen Energy 2016, 41, 19–35. [Google Scholar] [CrossRef]
- Kahouli-Brahmi, S. Technological learning in energy–environment–economy modelling: A survey. Energy Policy 2008, 36, 138–162. [Google Scholar] [CrossRef]
- Rubin, E.S.; Azevedo, I.M.L.; Jaramillo, P.; Yeh, S. A review of learning rates for electricity supply technologies. Energy Policy 2015, 86, 198–218. [Google Scholar] [CrossRef]
- Van den Broek, M.; Berghout, N.; Rubin, E.S. The potential of renewables versus natural gas with CO2 capture and storage for power generation under CO2 constraints. Renew. Sustain. Energy Rev. 2015, 49, 1296–1322. [Google Scholar] [CrossRef]
- Van den Broek, M.; Hoefnagels, R.; Rubin, E.; Turkenburg, W.; Faaij, A. Effects of technological learning on future cost and performance of power plants with CO2 capture. Prog. Energy Combust. Sci. 2009, 35, 457–480. [Google Scholar] [CrossRef]
- Creutzig, F.; Agoston, P.; Goldschmidt, J.C.; Luderer, G.; Nemet, G.; Pietzcker, R.C. The underestimated potential of solar energy to mitigate climate change. Nat. Energy 2017, 2, 17140. [Google Scholar] [CrossRef]
- Huang, W.; Chen, W.; Anandarajah, G. The role of technology diffusion in a decarbonizing world to limit global warming to well below 2 °C: An assessment with application of Global TIMES model. Appl. Energy 2017, 208, 291–301. [Google Scholar] [CrossRef]
- Patel, S. Duke Hit Hard by Exorbitant O&M Costs at Edwardsport IGCC Facility. Power Magzine. 27 September 2018. Available online: https://www.powermag.com/duke-hit-hard-by-exorbitant-om-costs-at-edwardsport-igcc-facility/?pagenum=3 (accessed on 12 October 2018).
- Wagman, D. Three Factors that Doomed kemper County IGCC. IEEE Spectrum. 30 June 2017. Available online: https://spectrum.ieee.org/energywise/energy/fossil-fuels/the-three-factors-that-doomed-kemper-county-igcc (accessed on 12 October 2018).
- Reiner, D.M. Learning through a portfolio of carbon capture and storage demonstration projects. Nat. Energy 2016, 1, 15011. [Google Scholar] [CrossRef]
- Adams, T.A., II; Hoseinzade, L.; Madabhushi, P.B.; Okeke, I.J. Comparison of CO2 Capture Approaches for Fossil-Based Power Generation: Review and Meta-Study. Processes 2017, 5, 44. [Google Scholar] [CrossRef]
- Voll, A.; Sorda, G.; Optehostert, F.; Madlener, R.; Marquardt, W. Integration of market dynamics into the design of biofuel processes. Comput. Aided Chem. Eng. 2012, 31, 850–854. [Google Scholar]

| Field | Process Systems Engineering (PSE) | Energy Economics (EE) | ||
|---|---|---|---|---|
| Nature of variables | ||||
| Endogenous | Technological (e.g., temperature, pressure, enthalpy, Gibbs free energy, process size) | Economic | ||
| Exogenous | Economic (e.g., raw material prices, equipment prices, product demand, interest rates) Environmental (e.g., Global Warming Potential, Ecotoxity, resource depletion, terrestrial acidification) | Technological, Environmental | ||
| Theoretical underpinnings | Thermodynamics, Fluid mechanics, Kinetics | Economics (producer theory, consumer theory, and market equilibrium) | ||
| Level of aggregation of technologies | Unit operation, Processing plant, Supply chain | Entire energy sector, All economic sectors | ||
| Spatial scale | Local, Regional, National, Global | Regional, National, Global | ||
| Decision making hierarchy | Strategic | Tactical | Operational | Strategic 1 |
| Temporal scale | Several years | Days-Weeks | Seconds-Hours | Several years |
| Classic purposes | Process design & integration: Reviews: [14,15,16,17,18,19,20,21] High Impact/Seminal: [22,23,24,25,26,27,28] Open Models: [29] *, [30] *, [31,32,33] Supply chain design/infrastructure: Reviews: [34,35,36,37,38,39,40] High Impact/Seminal: [9,41,42,43,44,45] | Production Planning and Scheduling: Reviews: [46,47,48,49,50,51,52], High Impact/Seminal: [53,54,55,56,57,58] | Process control: Reviews: [59,60,61,62,63] High Impact: [64,65,66] Flexible operation: Reviews: [67,68,69,70] High Impact: [71,72,73,74,75,76] | Sustainable energy policy planning: Reviews: [10], [77,78,79,80,81] High Impact: [82,83,84,85,86,87,88,89], [90,91,92,93,94], [95] 2 Long term energy forecasting: Reviews: [96,97,98,99,100,101,102] High Impact/Seminal: [103,104,105,106,107,108] |
| Recent trends | Multi-scale systems engineering: Reviews: [38,39,109,110,111,112], High Impact: [9,11,41,113,114,115,116,117,118,119,120] Sustainable process analysis and design: Reviews: [5], [121,122,123,124,125,126,127,128,129,130,131,132], High Impact: [133,134,135,136,137,138,139,140,141,142], Open Models: [143,144,145] | • Outside the scope of this paper | ||
| ECONOMIC SECTORS AS CONSUMERS | Row Sums | |||||||
|---|---|---|---|---|---|---|---|---|
| Energy Production | Mining | Manufacturing | Transportation | Construction | Final Demand | Total Output | ||
| ECONOMIC SECTORS AS PRODUCERS | Energy Production | |||||||
| Mining | ||||||||
| Manufacturing | ||||||||
| Transportation | ||||||||
| Construction | ||||||||
| VALUE ADDED | Labor | GDP | ||||||
| Government services | ||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subramanian, A.S.R.; Gundersen, T.; Adams, T.A., II. Modeling and Simulation of Energy Systems: A Review. Processes 2018, 6, 238. https://doi.org/10.3390/pr6120238
Subramanian ASR, Gundersen T, Adams TA II. Modeling and Simulation of Energy Systems: A Review. Processes. 2018; 6(12):238. https://doi.org/10.3390/pr6120238
Chicago/Turabian StyleSubramanian, Avinash Shankar Rammohan, Truls Gundersen, and Thomas Alan Adams, II. 2018. "Modeling and Simulation of Energy Systems: A Review" Processes 6, no. 12: 238. https://doi.org/10.3390/pr6120238
APA StyleSubramanian, A. S. R., Gundersen, T., & Adams, T. A., II. (2018). Modeling and Simulation of Energy Systems: A Review. Processes, 6(12), 238. https://doi.org/10.3390/pr6120238






