Influence of Thermal Conditions on Particle Properties in Fluidized Bed Layering Granulation
Abstract
1. Introduction
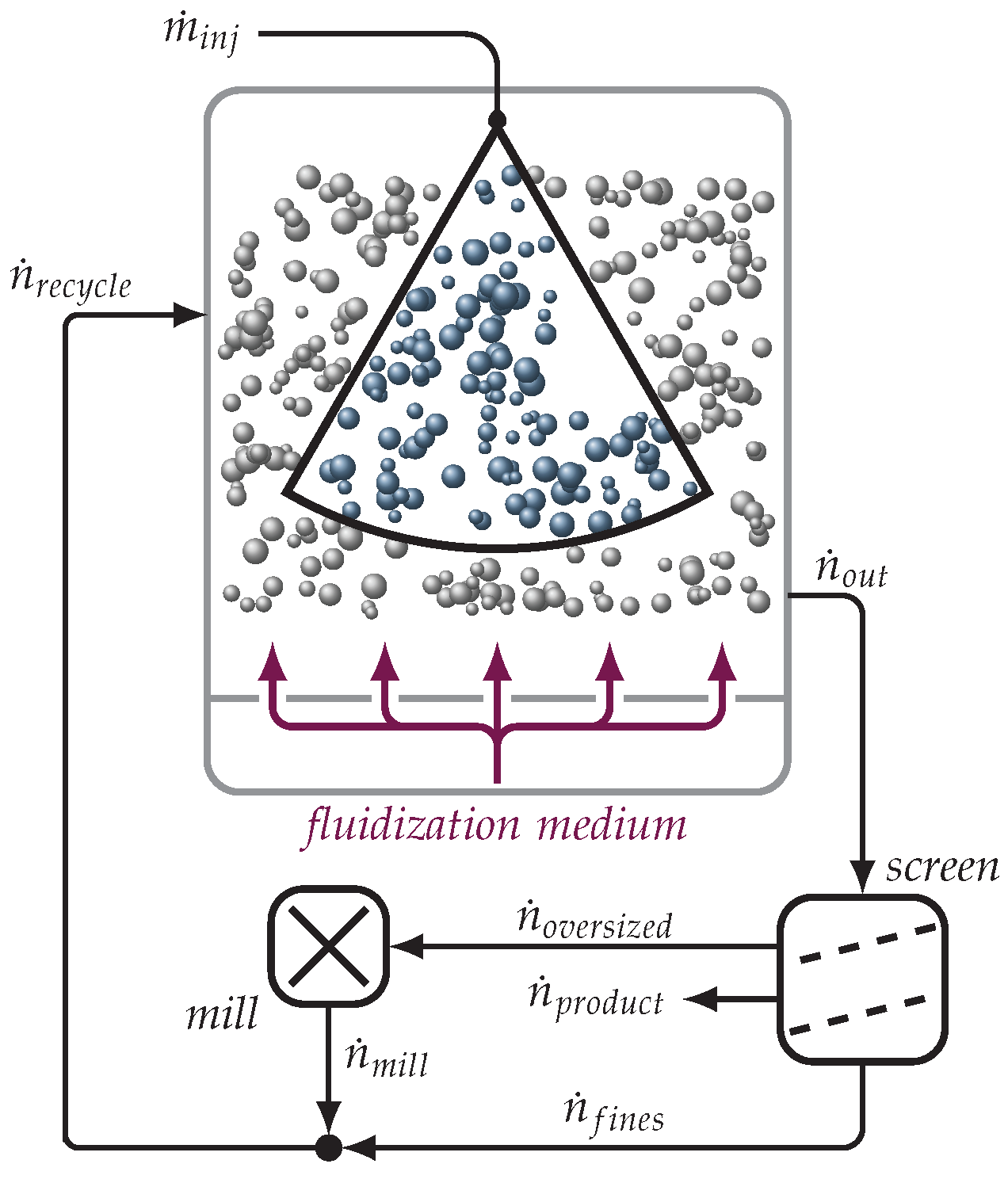
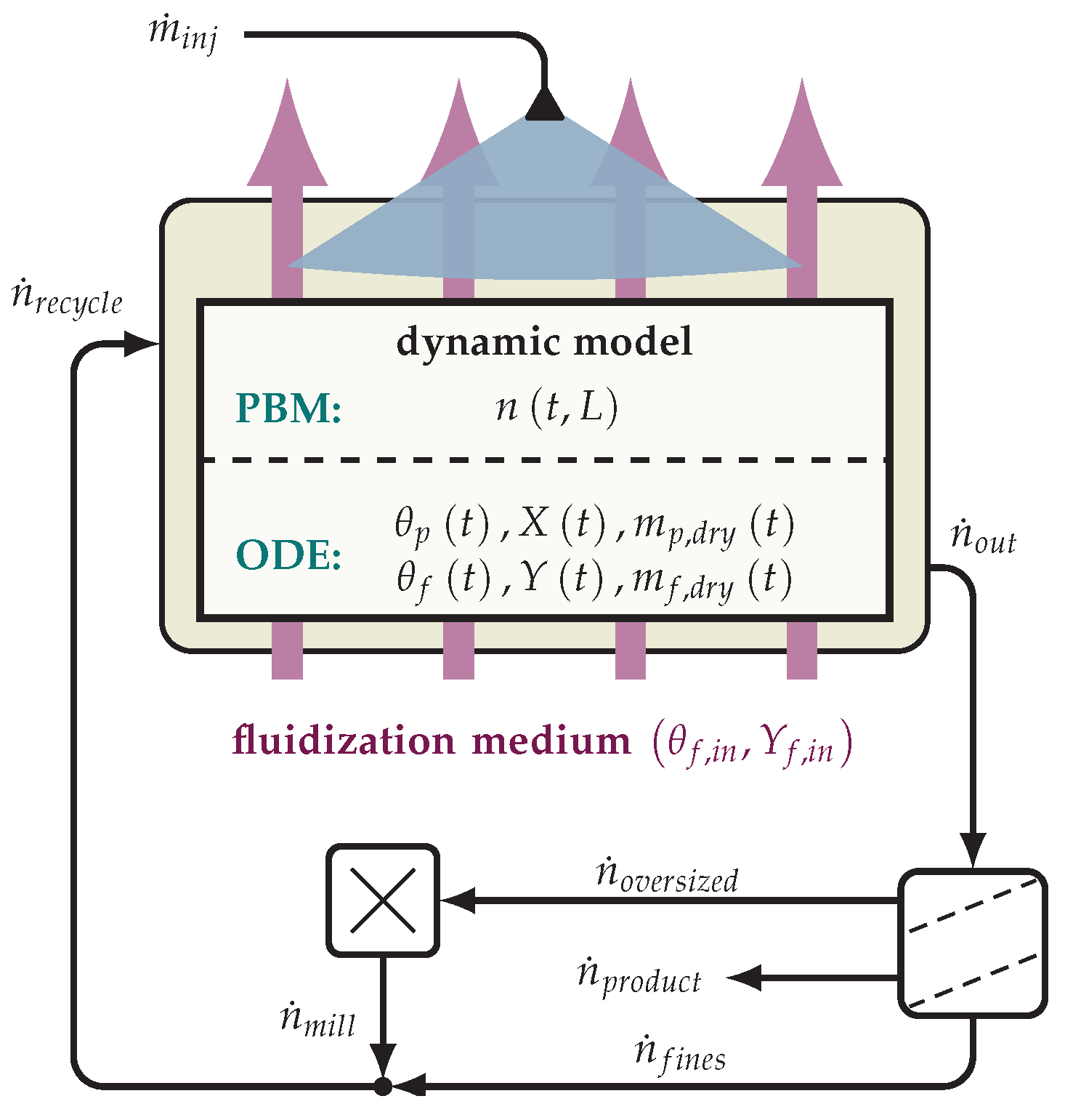
2. Mathematical Model
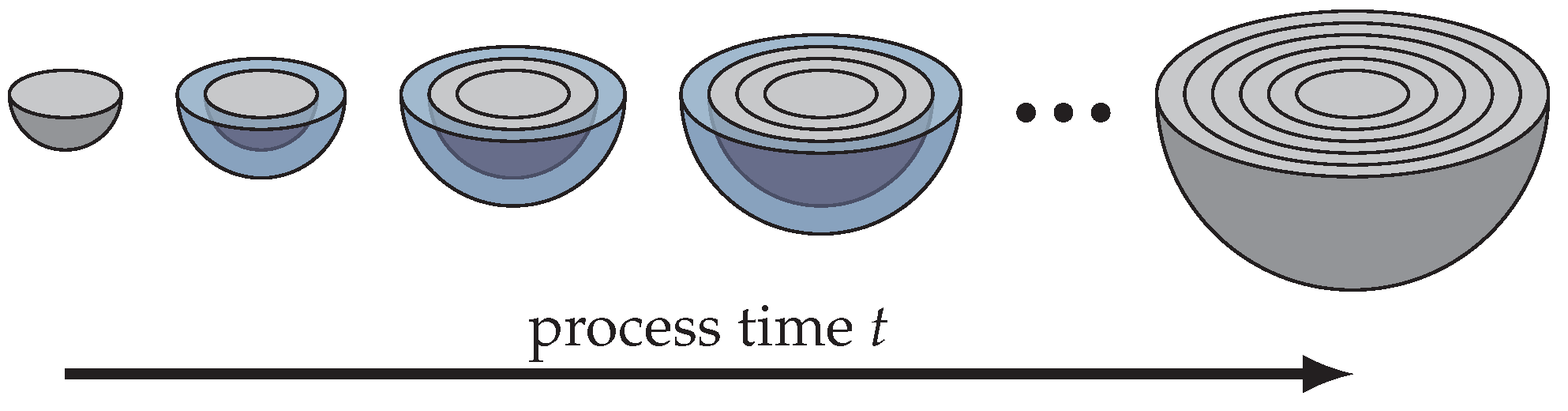
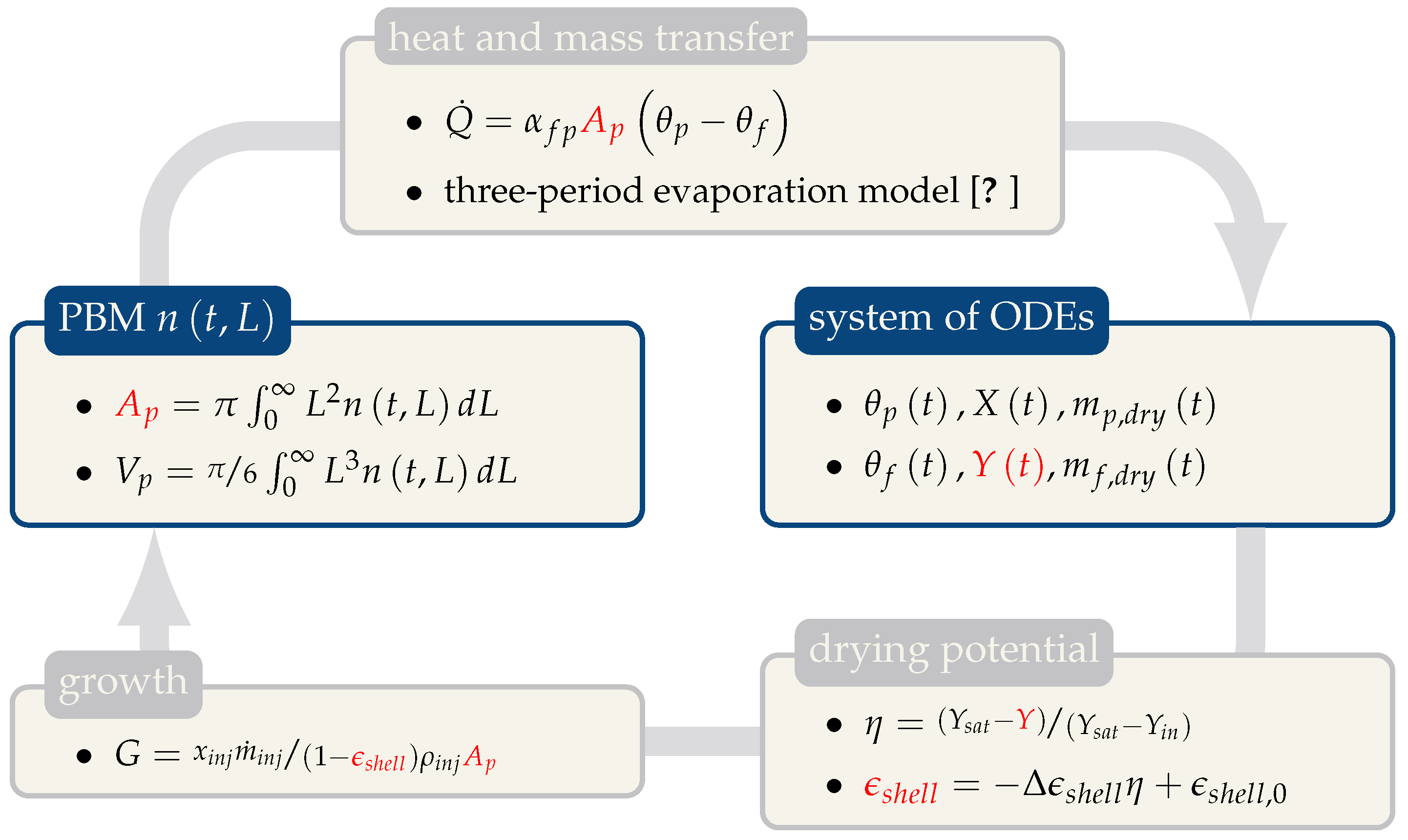
2.1. Population Balance Model
2.2. Heat and Mass Transfer
3. Results and Discussion
3.1. Variations of the Size of Milled Particles
3.2. Variations of Injection Rate
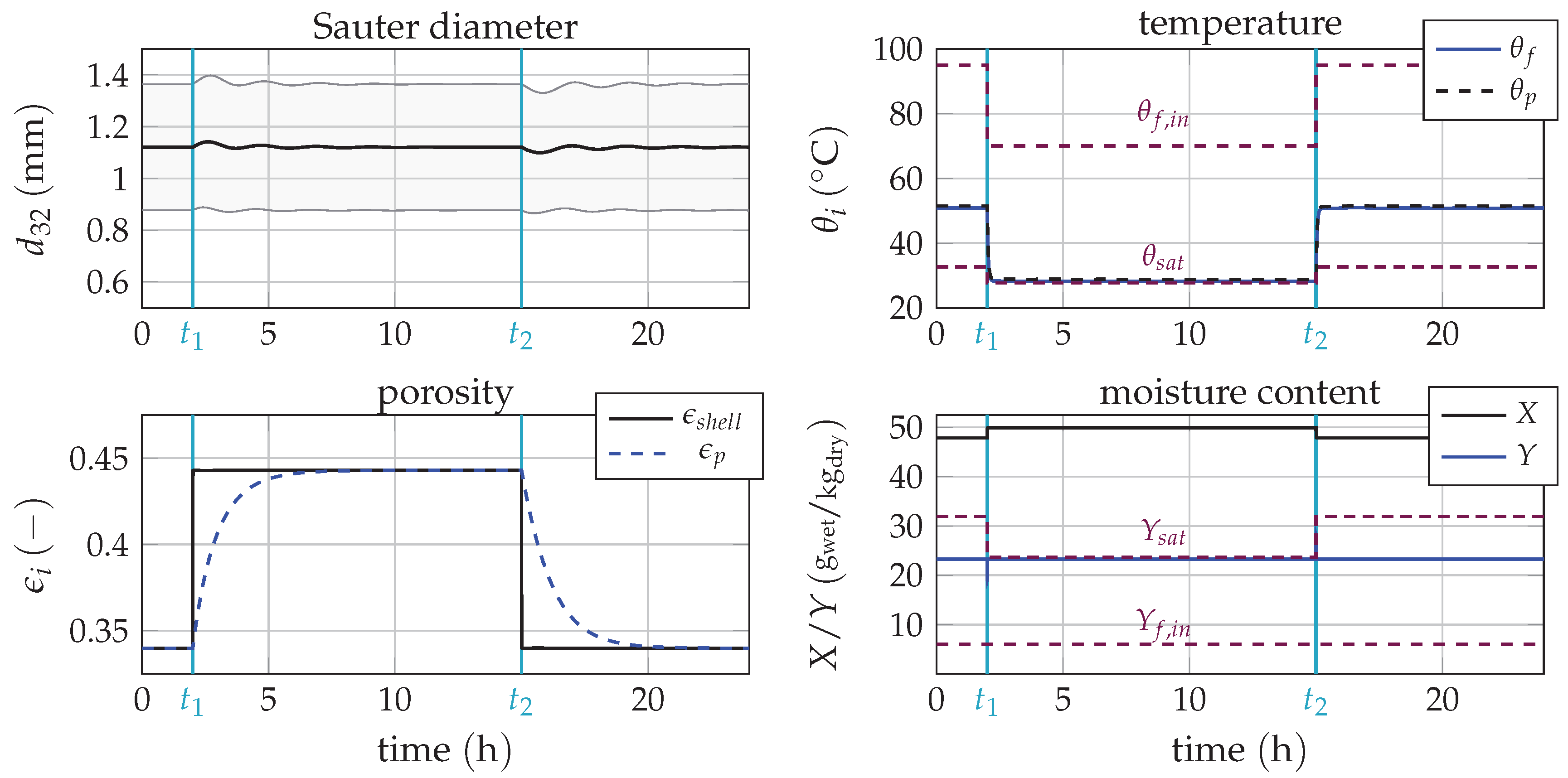
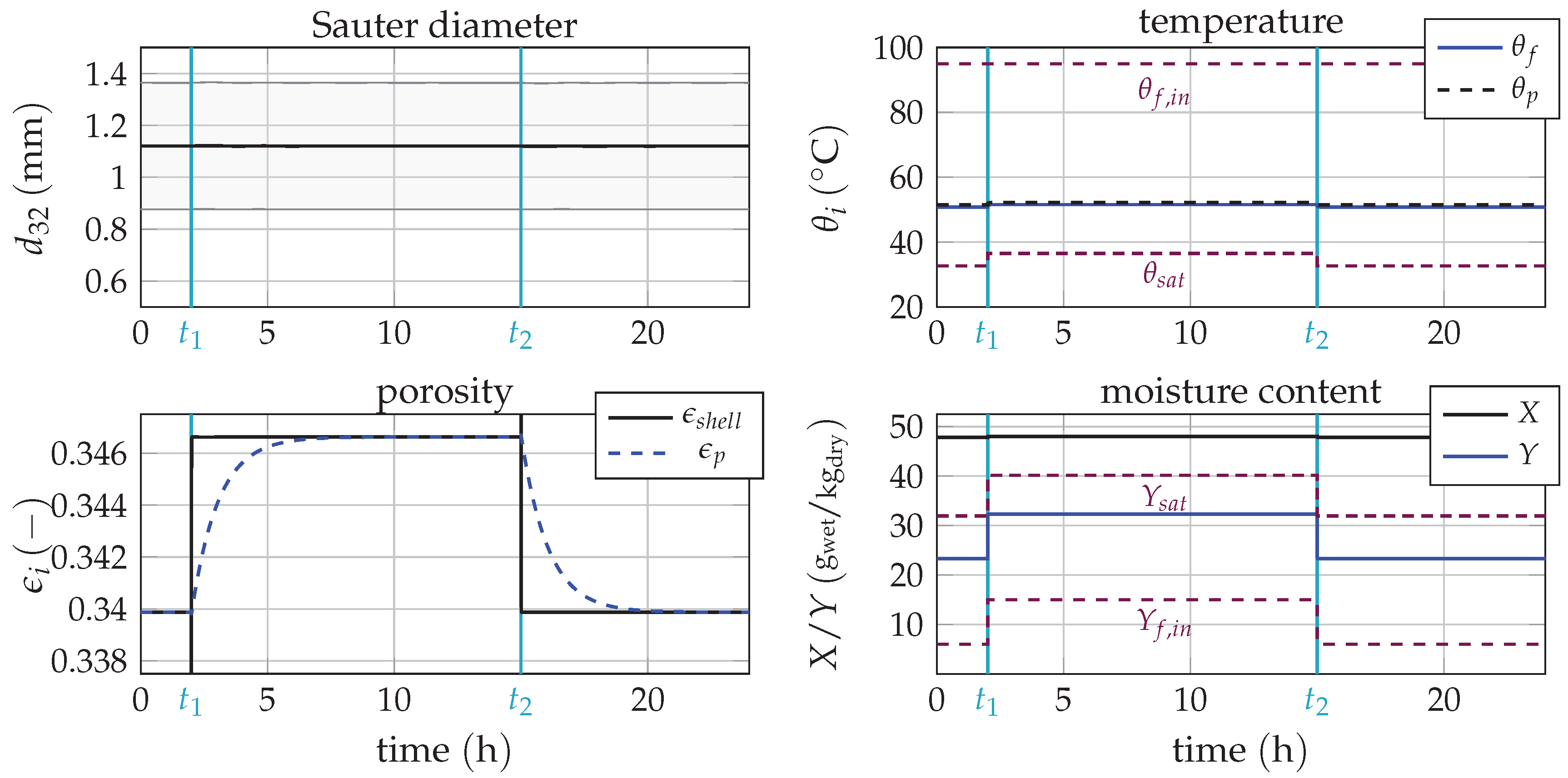
3.3. Variations of the Temperature of the Fluidization Medium
3.4. Disturbance of the Inlet Moisture Content of the Fluidization Medium
4. Conclusions and Outlook
- caloric parameters (e.g., evaporation enthalpy or heat capacities ),
- heat and mass transfer coefficients ( and ),
- parameters related to the drying curve (p, , and ),
- parameters of the relation between shell porosity and drying potential ( and ), and
- parameters of the periphery (mill and screen).
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | surface area (m2) |
| specific heat capacity (J/kg·K)) | |
| d32 | Sauter diameter (m) |
| G | particle growth (m/s) |
| h | mass specific enthalpy (J/kg) |
| H | total enthalpy (J) |
| enthalpy flow (J/ | |
| K | drain (1/s) |
| L | particle size (m) |
| m | mass (kg) |
| mass flow (kg/ | |
| n | number-based particle size distribution (1/ |
| particle flow (1/ | |
| p | material specific drying characteristics (-) |
| q | normalized particle size distribution (1/m) |
| heat flow (J/s) | |
| t | simulation time (h) |
| T | separation function (-) |
| V | volume (m3) |
| x | (mass) fraction of solid (-) |
| X | moisture content of solid (gwet/kgwet) |
| Y | moisture content of fluid (gwet/kgwet) |
| Greek letters | |
| heat transfer coefficient (W/m2·K) | |
| mass transfer coefficient (m/ | |
| normalized moisture content (-) | |
| drying potential (-) | |
| temperature () | |
| mean diameter (m) | |
| normalized drying velocity (-) | |
| parameter set (-) | |
| mass density (kg/m3) | |
| variance (m) | |
| time constant (h) | |
| Subscripts | |
| dry | dry part of particles or fluidization medium |
| evap | evaporation |
| f | fluidization medium |
| fp | fluid phase to particle phase |
| fine | particle fine fraction |
| in | inlet |
| inj | injection |
| l | liquid |
| mill | milled particles |
| out | particle withdrawal or fluid exhaust |
| oversized | particle oversized fraction |
| p | particle phase |
| prod | particle product fraction |
| recycle | particle recycle |
| s | suspension |
| sat | saturation point |
| screen | screen |
| solvent | solvent on particles or in fluidization medium |
| shell | (particle) shell |
| v | vapor |
Appendix A. Default Parameter Set
| particle phase | ||
| 15 | ||
| 4200 | ||
| fluidization medium | ||
| 1 | ||
| 1500 | ||
| 6 | ||
| 95 | ||
| injected suspension | ||
| 40 | ||
| (-) | ||
| 20 | ||
| 1440 | kg/m3 | |
| drying characteristics and porosity | ||
| (-) | ||
| 5 | ||
| 50 | ||
| (-) | ||
| (-) | ||
| screen, mill, and recycle | ||
| 0 | ||
| 20 | ||
References
- Mörl, L.; Heinrich, S.; Peglow, M. Fluidized bed spray granulation. In Granulation; Salman, A.D., Hounslow, M.J., Seville, J.P.K., Eds.; Handbook of Powder Technology; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; Volume 11, pp. 21–188. [Google Scholar]
- Tsotsas, E. Influence of Drying Kinetics on Particle Formation: A Personal Perspective. Dry. Technol. 2012, 30, 1167–1175. [Google Scholar] [CrossRef]
- Antonyuk, S.; Tomas, J.; Heinrich, S.; Mörl, L. Breakage behavior of spherical granulates by compression. Chem. Eng. Sci. 2005, 60, 4031–4044. [Google Scholar] [CrossRef]
- Grünewald, G.; Westhoff, B.; Kind, M. Fluidized Bed Spray Granulation: Nucleation Studies with Steady-State Experiments. Dry. Technol. 2010, 28, 349–360. [Google Scholar] [CrossRef]
- Cotabarren, I.; Schulz, P.G.; Bucalá, V.; Piña, J. Modeling of an industrial double-roll crusher of a urea granulation circuit. Powder Technol. 2008, 183, 224–230. [Google Scholar] [CrossRef]
- Schmidt, M.; Bück, A.; Tsotsas, E. Experimental investigation of process stability of continuous spray fluidized bed layering with internal separation. Chem. Eng. Sci. 2015, 126, 55–66. [Google Scholar] [CrossRef]
- Schmidt, M.; Rieck, C.; Bück, A.; Tsotsas, E. Experimental investigation of process stability of continuous spray fluidized bed layering with external product separation. Chem. Eng. Sci. 2015, 137, 466–475. [Google Scholar] [CrossRef]
- Schmidt, M.; Bück, A.; Tsotsas, E. Experimental investigation of the influence of drying conditions on process stability of continuous spray fluidized bed layering granulation with external product separation. Powder Technol. 2017, 320, 474–482. [Google Scholar] [CrossRef]
- Rieck, C.; Hoffmann, T.; Bück, A.; Peglow, M.; Tsotsas, E. Influence of drying conditions on layer porosity in fluidized bed spray granulation. Powder Technol. 2015, 272, 120–131. [Google Scholar] [CrossRef]
- Hoffmann, T.; Rieck, C.; Schmidt, M.; Bück, A.; Peglow, M.; Tsotsas, E. Prediction of Shell Porosities in Continuous Fluidized Bed Spray Layering. Dry. Technol. 2015, 33, 1662–1670. [Google Scholar] [CrossRef]
- Sondej, F.; Peglow, M.; Bück, A.; Tsotsas, E. Experimental investigation of the morphology of salt deposits from drying sessile droplets by white-light interferometry. AIChE J. 2018, 64, 2002–2016. [Google Scholar] [CrossRef]
- Diez, E.; Meyer, K.; Bück, A.; Tsotsas, E.; Heinrich, S. Influence of process conditions on the product properties in a continuous fluidized bed spray granulation process. Chem. Eng. Res. Des. 2018, 139, 104–115. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Vreman, A.; van Lare, C.; Hounslow, M. A basic population balance model for fluid bed spray granulation. Chem. Eng. Sci. 2009, 64, 4389–4398. [Google Scholar] [CrossRef]
- Heinrich, S.; Peglow, M.; Ihlow, M.; Henneberg, M.; Mörl, L. Analysis of the start-up process in continuous fluidized bed spray granulation by population balance modelling. Chem. Eng. Sci. 2002, 57, 4369–4390. [Google Scholar] [CrossRef]
- Radichkov, R.; Müller, T.; Kienle, A.; Heinrich, S.; Peglow, M.; Mörl, L. A numerical bifurcation analysis of continuous fluidized bed spray granulation with external product classification. Chem. Eng. Process. 2006, 45, 826–837. [Google Scholar] [CrossRef]
- Hampel, N.; Bück, A.; Peglow, M.; Tsotsas, E. Continuous pellet coating in a Wurster fluidized bed process. Chem. Eng. Sci. 2013, 86, 87–98. [Google Scholar] [CrossRef]
- Dreyschultze, C.; Neugebauer, C.; Palis, S.; Bück, A.; Tsotsas, E.; Heinrich, S.; Kienle, A. Influence of zone formation on stability of continuous fluidized bed layering granulation with external product classification. Particuology 2015, 23, 1–7. [Google Scholar] [CrossRef]
- Neugebauer, C.; Palis, S.; Bück, A.; Tsotsas, E.; Heinrich, S.; Kienle, A. A dynamic two-zone model of continuous fluidized bed layering granulation with internal product classification. Particuology 2017, 31, 8–14. [Google Scholar] [CrossRef]
- Bück, A.; Neugebauer, C.; Meyer, K.; Palis, S.; Diez, E.; Kienle, A.; Heinrich, S.; Tsotsas, E. Influence of operation parameters on process stability in continuous fluidised bed layering with external product classification. Powder Technol. 2016, 300, 37–45. [Google Scholar] [CrossRef]
- Drechsler, J.; Peglow, M.; Heinrich, S.; Ihlow, M.; Mörl, L. Investigating the dynamic behavior of fluidized bed spray granulation processes applying numerical simulation tools. Chem. Eng. Sci. 2005, 60, 3817–3833. [Google Scholar] [CrossRef]
- Dosta, M.; Heinrich, S.; Werther, J. Fluidized bed spray granulation: Analysis of the system behavior by means of dynamic flowsheet simulation. Powder Technol. 2010, 204, 71–82. [Google Scholar] [CrossRef]
- Ennis, B.J.; Tardos, G.; Pfeffer, R. A microlevel-based characterization of granulation phenomena. Powder Technol. 1991, 65, 257–272. [Google Scholar] [CrossRef]
- van Meel, D. Adiabatic convection batch drying with recirculation of air. Chem. Eng. Sci. 1958, 9, 36–44. [Google Scholar] [CrossRef]
- Gnielinski, V. G9—Wärmeübertragung Partikel—Fluid in durchströmten Haufwerken. In VDI Wärmeatlas; VDI Verlag: Düsseldorfer, Germany, 2013. [Google Scholar]
- Glück, B. Zustands- und Stoffwerte, 2nd ed.; Verlag für Bauwesen GmbH: Berlin, Germany, 1991. [Google Scholar]
- Kong, Y.X.; Di, Y.Y.; Qi, Y.D.; Yang, W.W.; Tan, Z.C. Low temperature heat capacities and standard molar enthalpy of formation of sodium benzoate C6H5COONa (s). Thermochim. Acta 2009, 488, 27–32. [Google Scholar] [CrossRef]
- Palis, S.; Kienle, A. Stabilization of continuous fluidized bed spray granulation with external product classification. Chem. Eng. Sci. 2012, 70, 200–209. [Google Scholar] [CrossRef]
- Palis, S.; Kienle, A. Discrepancy based control of particulate processes. J. Process Control 2014, 24, 33–46. [Google Scholar] [CrossRef]
- Cotabarren, I.M.; Bertín, D.E.; Bucalá, V.; Piña, J. Feedback control strategies for a continuous industrial fluidized-bed granulation process. Powder Technol. 2015, 283, 415–432. [Google Scholar] [CrossRef]
- Bück, A.; Seidel, C.; Dürr, R.; Neugebauer, C. Robust feedback control of convective drying of particulate solids. J. Process Control 2018, 69, 86–96. [Google Scholar] [CrossRef]


| 1st | - | - | - | |
| 2nd | - | - | - | |
| 3rd | - | - | 65.0 °C | - |
| 4th | - | - | - |
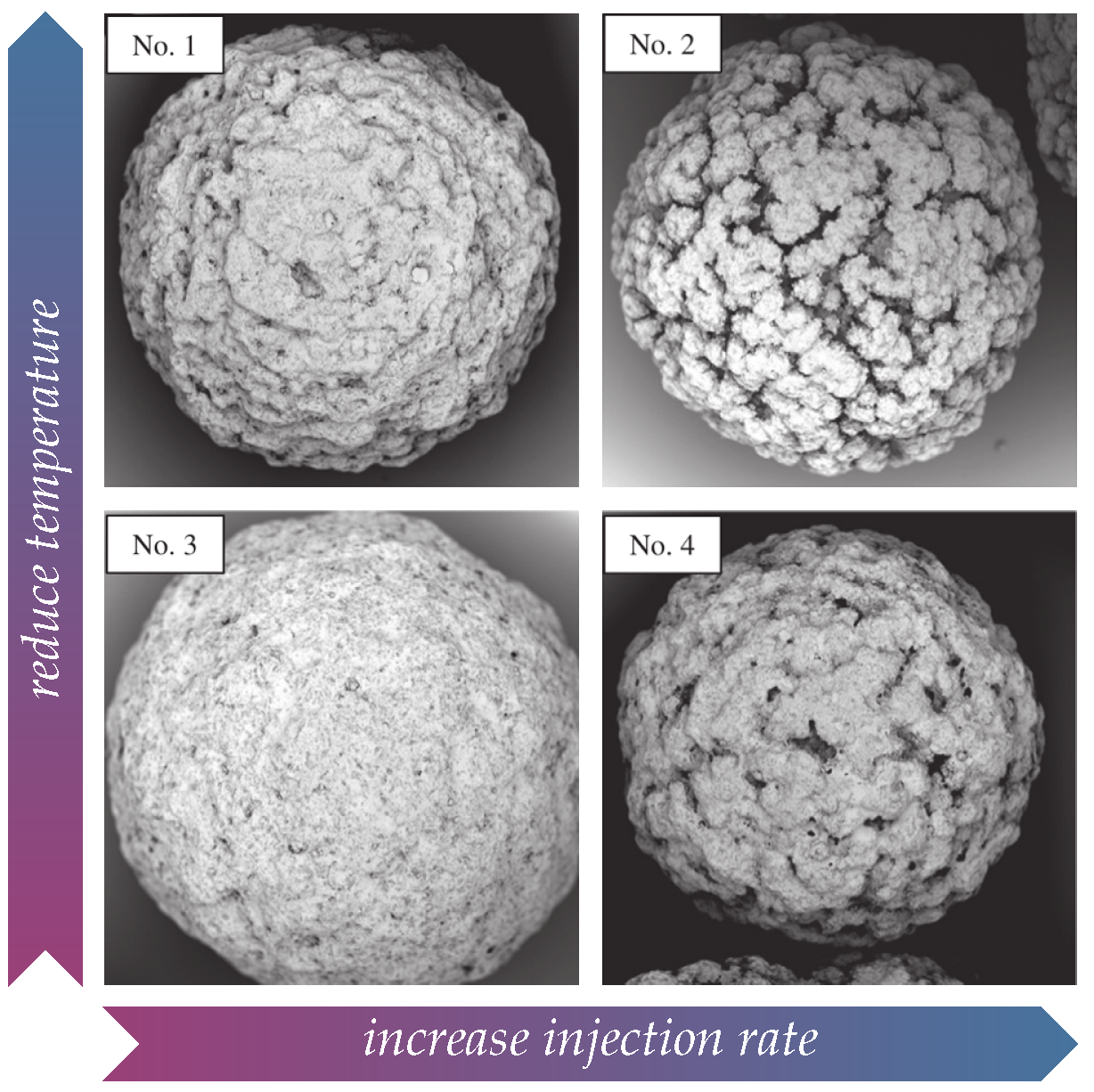
| No. | ||||
|---|---|---|---|---|
| 1 | 50 °C | 0.79 | 0.50 | |
| 2 | 50 °C | 0.56 | 0.64 | |
| 3 | 95 °C | 0.89 | 0.46 | |
| 4 | 95 °C | 0.72 | 0.50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neugebauer, C.; Bück, A.; Palis, S.; Mielke, L.; Tsotsas, E.; Kienle, A. Influence of Thermal Conditions on Particle Properties in Fluidized Bed Layering Granulation. Processes 2018, 6, 235. https://doi.org/10.3390/pr6120235
Neugebauer C, Bück A, Palis S, Mielke L, Tsotsas E, Kienle A. Influence of Thermal Conditions on Particle Properties in Fluidized Bed Layering Granulation. Processes. 2018; 6(12):235. https://doi.org/10.3390/pr6120235
Chicago/Turabian StyleNeugebauer, Christoph, Andreas Bück, Stefan Palis, Lisa Mielke, Evangelos Tsotsas, and Achim Kienle. 2018. "Influence of Thermal Conditions on Particle Properties in Fluidized Bed Layering Granulation" Processes 6, no. 12: 235. https://doi.org/10.3390/pr6120235
APA StyleNeugebauer, C., Bück, A., Palis, S., Mielke, L., Tsotsas, E., & Kienle, A. (2018). Influence of Thermal Conditions on Particle Properties in Fluidized Bed Layering Granulation. Processes, 6(12), 235. https://doi.org/10.3390/pr6120235









