In Silico Identification of Microbial Partners to Form Consortia with Anaerobic Fungi
Abstract
1. Introduction
2. Materials and Methods
2.1. Strains and Culture Conditions
2.2. Growth and Metabolite Measurements
2.3. Evaluation and Selection of Model Organisms
2.4. Dynamic Flux Balance Analysis Formulation
- The flux bounds, Equation (2), are updated. Typically, Michaelis–Menten kinetics are assumed [39]. Since detailed expression for glucose and xylose uptake rates are not known for all the organisms, we assumed, for comparative fairness,where , are the fluxes of glucose and xylose produced by the extracellular enzymes, G, Z are the current concentrations of glucose and xylose, and , are the respective molar masses. The glucose inhibition term ensures that glucose is preferentially metabolized before xylose [32]. The maximum flux constants, and , were taken from literature and are supplied in Section 2.5. See the Supplement for motivation of the derivation of Equation (3).
- A linear program feasibility problem,is solved to ensure that the genome-scale model is feasible for steps 3 and 4. This problem is solved for the “relaxation variables” and (see [36] for justification).
- A standard FBA linear program (LP) is solved to determine the optimal growth rate of the organism given the constraints of step 1. This problem,is solved for the unique optimal growth rate . Given from Equation (5), it is possible to solve for the organism biomass concentration by using for at least one time step into the future.
- A secondary LP,is solved to ensure that the resultant fluxes used to integrate Equation (1) are sufficiently smooth. Here, is the index set of all modeled substrates and products. A full derivation of Equation (6) is given in the Supplement. Briefly, the objective function asserts that is minimized, where the flux derivative at time t, , is approximated to first order.
- Using an integration scheme of choice, e.g., backward Euler, the full dynamic profile of the system may be iteratively simulated. If products are being generated at each time step, Equation (1) needs to include those fluxes as well.
2.5. Simulation Parameters
3. Results and Discussion
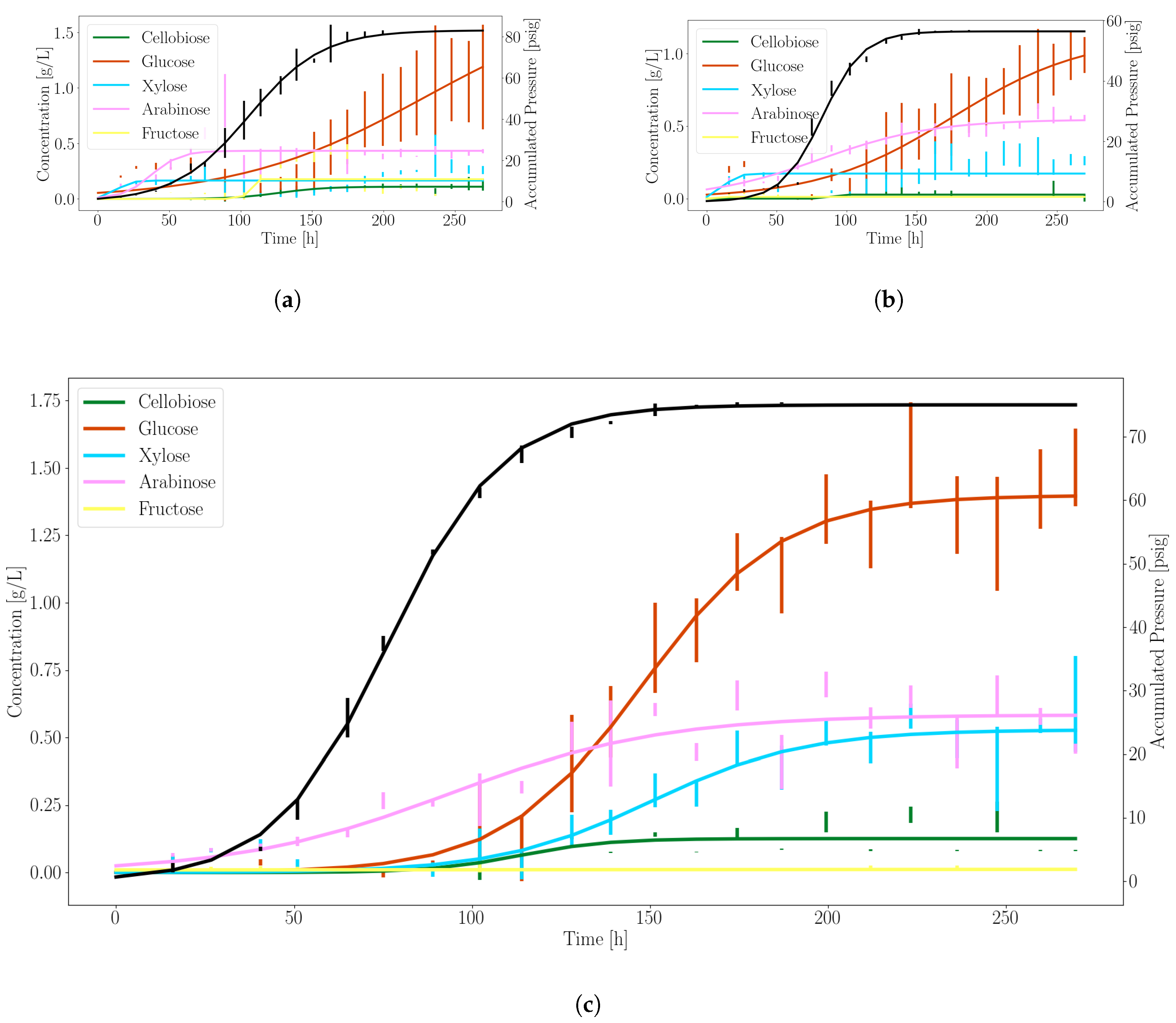
3.1. Anaerobic Fungi Release an Assortment of Products to Enable Consortia Formation
3.2. Dynamic Simulations Predict Consortia Partner Feasibility
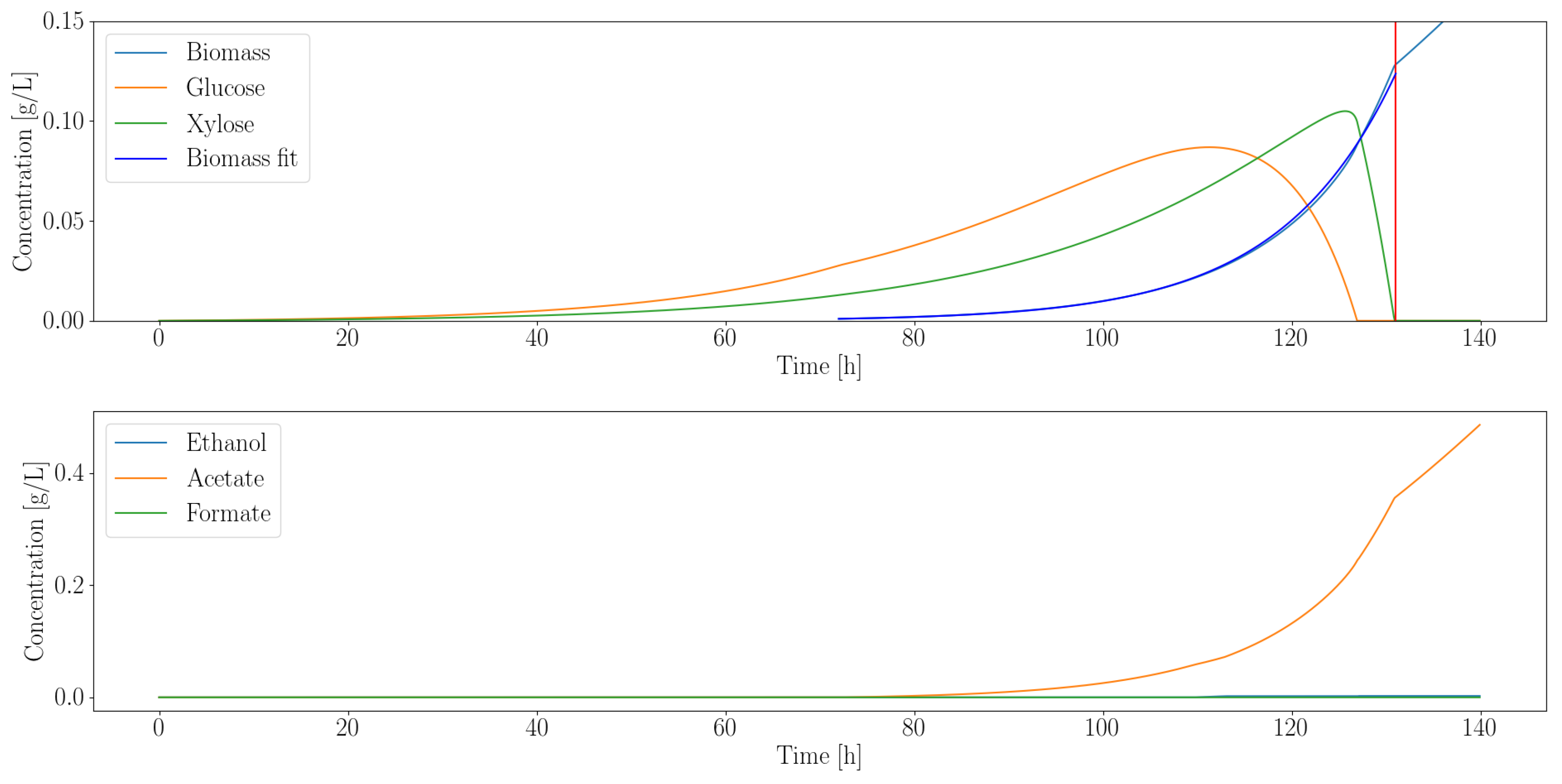
3.2.1. Heterotroph Partnership with Anaerobic Fungi
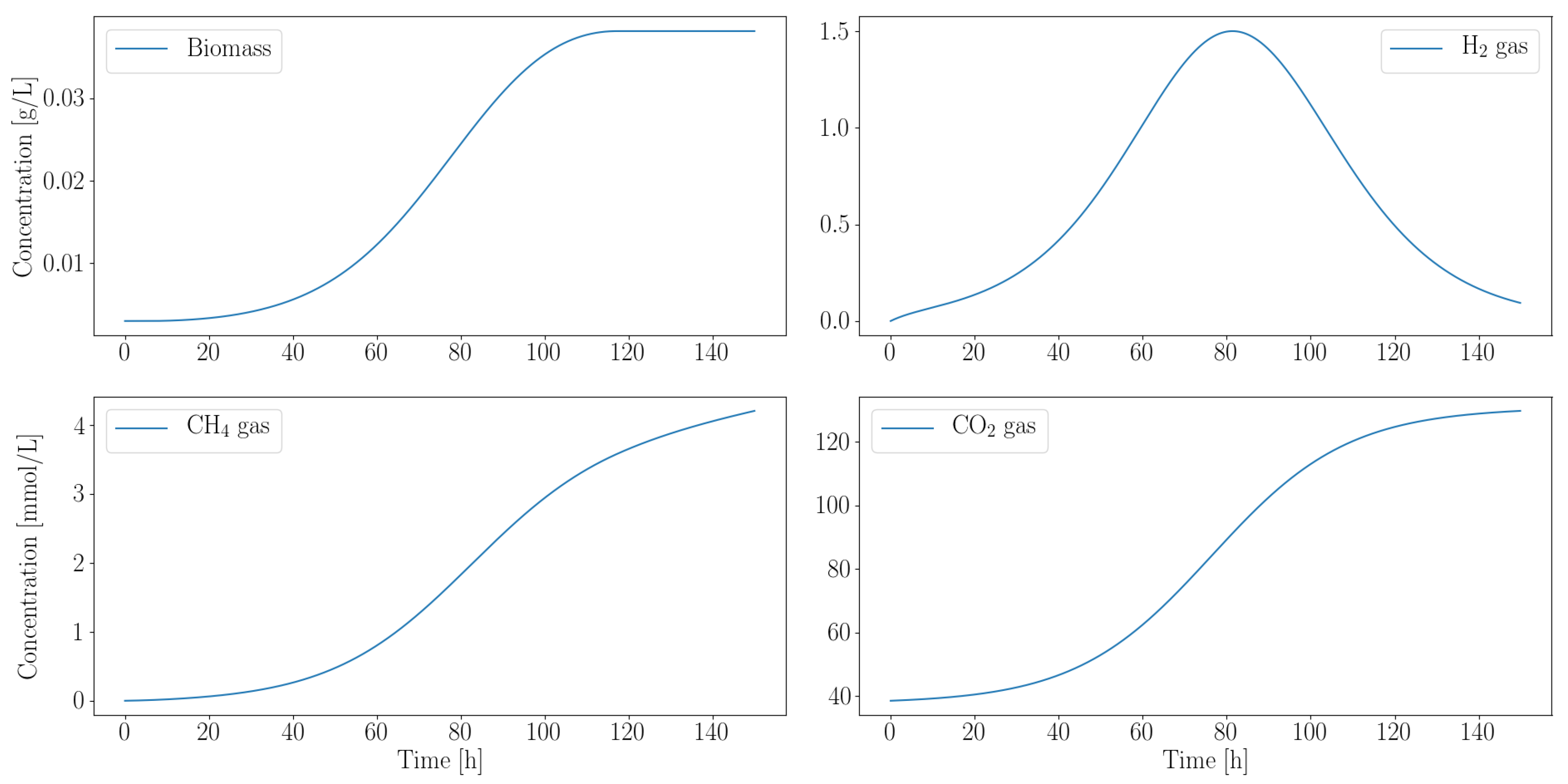
3.2.2. Autotroph Partnership with Anaerobic Fungi
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Otero, J.M.; Nielsen, J. Industrial systems biology. Biotechnol. Bioeng. 2010, 105, 439–460. [Google Scholar] [CrossRef] [PubMed]
- Saini, J.K.; Saini, R.; Tewari, L. Lignocellulosic agriculture wastes as biomass feedstocks for second-generation bioethanol production: Concepts and recent developments. 3 Biotech 2015, 5, 337–353. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.C.; Mi, L.; Pontrelli, S.; Luo, S. Fuelling the future: Microbial engineering for the production of sustainable biofuels. Nat. Rev. Microbiol. 2016, 14, 288–304. [Google Scholar] [CrossRef] [PubMed]
- Sindhu, R.; Binod, P.; Pandey, A. Biological pretreatment of lignocellulosic biomass—An overview. Bioresour. Technol. 2016, 199, 76–82. [Google Scholar] [CrossRef] [PubMed]
- Alper, H.; Stephanopoulos, G. Engineering for biofuels: Exploiting innate microbial capacity or importing biosynthetic potential? Nat. Rev. Microbiol. 2009, 7, 715–723. [Google Scholar] [CrossRef] [PubMed]
- Lynd, L.R.; Van Zyl, W.H.; McBride, J.E.; Laser, M. Consolidated bioprocessing of cellulosic biomass: An update. Curr. Opin. Biotechnol. 2005, 16, 577–583. [Google Scholar] [CrossRef] [PubMed]
- Brenner, K.; You, L.; Arnold, F.H. Engineering microbial consortia: A new frontier in synthetic biology. Trends Biotechnol. 2008, 26, 483–489. [Google Scholar] [CrossRef] [PubMed]
- Paloheimo, M.; Haarmann, T.; Mäkinen, S.; Vehmaanperä, J. Production of Industrial Enzymes in Trichoderma reesei. In Gene Expression Systems in Fungi: Advancements and Applications; Schmoll, M., Dattenböck, C., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 23–57. [Google Scholar]
- Minty, J.J.; Singer, M.E.; Scholz, S.A.; Bae, C.H.; Ahn, J.H.; Foster, C.E.; Liao, J.C.; Lin, X.N. Design and characterization of synthetic fungal-bacterial consortia for direct production of isobutanol from cellulosic biomass. Proc. Natl. Acad. Sci. USA 2013, 110, 14592–14597. [Google Scholar] [CrossRef] [PubMed]
- Martinez, D.; Berka, R.M.; Henrissat, B.; Saloheimo, M.; Arvas, M.; Baker, S.E.; Chapman, J.; Chertkov, O.; Coutinho, P.M.; Cullen, D.; et al. Genome sequencing and analysis of the biomass-degrading fungus Trichoderma reesei (syn. Hypocrea jecorina). Nat. Biotechnol. 2008, 26, 553–560. [Google Scholar] [CrossRef] [PubMed]
- Seppälä, S.; Elmo Wilken, S.; Knop, D.; Solomon, K.V.; O’Malley, M.A. The importance of sourcing enzymes from non-conventional fungi for metabolic engineering & biomass breakdown. Metab. Eng. 2017, 44, 45–59. [Google Scholar] [PubMed]
- Resch, M.G.; Donohoe, B.S.; Baker, J.O.; Decker, S.R.; Bayer, E.A.; Beckham, G.T.; Himmel, M.E. Fungal cellulases and complexed cellulosomal enzymes exhibit synergistic mechanisms in cellulose deconstruction. Energy Environ. Sci. 2013, 6, 1858–1867. [Google Scholar] [CrossRef]
- Solomon, K.V.; Haitjema, C.H.; Henske, J.K.; Gilmore, S.P.; Borges-Rivera, D.; Lipzen, A.; Brewer, H.M.; Purvine, S.O.; Wright, A.T.; Theodorou, M.K.; et al. Early-branching gut fungi possess a large, comprehensive array of biomass-degrading enzymes. Science 2016, 1431, 1192–1195. [Google Scholar] [CrossRef] [PubMed]
- Gruninger, R.J.; Puniya, A.K.; Callaghan, T.M.; Edwards, J.E.; Youssef, N.; Dagar, S.S.; Fliegerova, K.; Griffith, G.W.; Forster, R.; Tsang, A.; et al. Anaerobic fungi (phylum Neocallimastigomycota): Advances in understanding their taxonomy, life cycle, ecology, role and biotechnological potential. FEMS Microbiol. Ecol. 2014, 90, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Henske, J.K.; Wilken, S.E.; Solomon, K.V.; Smallwood, C.R.; Shutthanandan, V.; Evans, J.E.; Theodorou, M.K.; O’Malley, M.A. Metabolic characterization of anaerobic fungi provides a path forward for two-stage bioprocessing of crude lignocellulose. Biotechnol. Bioeng. 2017. [Google Scholar] [CrossRef]
- Senger, R.S.; Yen, J.Y.; Fong, S.S. A review of genome-scale metabolic flux modeling of anaerobiosis in biotechnology. Curr. Opin. Chem. Eng. 2014, 6, 33–42. [Google Scholar] [CrossRef]
- Theodorou, M.K.; Brookman, J.L.; Trinci, A.P. Anaerobic fungi. In Methods in Gut Microbial Ecology for Ruminants, 1st ed.; Makkar, H.P., McSweeney, C.S., Eds.; Springer: Dordrecht, The Netherlands, 2005; Chapter 2.4; pp. 55–67. [Google Scholar]
- Teunissen, M.J.; Op den Camp, H.J.M.; Orpin, C.G.; Huis in ’t Veld, J.H.J.; Vogels, G.D. Comparison of growth characteristics of anaerobic fungi isolated from ruminant and non-ruminant herbivores during cultivation in a defined medium. J. Gen. Microbiol. 1991, 137, 1401–1408. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, M.K.; Davies, D.R.; Nielsen, B.B.; Lawrence, M.I.; Trinci, A.P. Determination of growth of anaerobic fungi on soluble and cellulosic substrates using a pressure transducer. Microbiology 1995, 141, 671–678. [Google Scholar] [CrossRef]
- King, Z.A.; Lu, J.; Dräger, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016, 44, D515–D522. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, H.; Sahin, M.; Nogales, J.; Latif, H.; Lovley, D.R.; Ebrahim, A.; Zengler, K. Characterizing acetogenic metabolism using a genome-scale metabolic reconstruction of Clostridium ljungdahlii. Microb. Cell Fact. 2013, 12, 118. [Google Scholar] [CrossRef] [PubMed]
- Monk, J.M.; Lloyd, C.J.; Brunk, E.; Mih, N.; Sastry, A.; King, Z.; Takeuchi, R.; Nomura, W.; Zhang, Z.; Mori, H.; et al. iML1515, a knowledgebase that computes Escherichia coli traits. Nat. Biotechnol. 2017, 35, 904–908. [Google Scholar] [CrossRef] [PubMed]
- Curtis, S.J.; Epstein, W. Phosphorylation of D-glucose in Escherichia coli mutants defective in glucosephosphotransferase, mannosephosphotransferase, and glucokinase. J. Bacteriol. 1975, 122, 1189–1199. [Google Scholar] [PubMed]
- Flahaut, N.A.; Wiersma, A.; van de Bunt, B.; Martens, D.E.; Schaap, P.J.; Sijtsma, L.; Dos Santos, V.A.; De Vos, W.M. Genome-scale metabolic model for Lactococcus lactis MG1363 and its application to the analysis of flavor formation. Appl. Microbiol. Biotechnol. 2013, 97, 8729–8739. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Scholten, J.C.; Palsson, B.; Brockman, F.J.; Ideker, T. Modeling methanogenesis with a genome-scale metabolic reconstruction of Methanosarcina barkeri. Mol. Syst. Biol. 2006, 2, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mo, M.L.; Palsson, B.Ø.; Herrgård, M.J. Connecting extracellular metabolomic measurements to intracellular flux states in yeast. BMC Syst. Biol. 2009, 3, 37. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Comput. Biol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.; Palsson, B.O.; Varma, A.; Palsson, B.O. Stoichiometric Flux Balance Models Quantitatively Predict Growth and Metabolic By-Product Secretion in Wild-Type Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar] [PubMed]
- Henson, M.A.; Hanly, T.J. Dynamic flux balance analysis for synthetic microbial communities. IET Syst. Biol. 2013, 8, 214–229. [Google Scholar] [CrossRef] [PubMed]
- Henson, J.L.; Hjersted, M.A. Steady-state and dynamic flux balance analysis of ethanol production by Saccharomyces cerevisiae. IET Syst. Biol. 2009, 3, 167–179. [Google Scholar]
- Mahadevan, R.; Edwards, J.S.; Doyle, F.J. Dynamic Flux Balance Analysis of Diauxic Growth in Escherichia coli. Biophys. J. 2002, 83, 1331–1340. [Google Scholar] [CrossRef]
- Hanly, T.J.; Henson, M.A. Dynamic flux balance modeling of microbial co-cultures for efficient batch fermentation of glucose and xylose mixtures. Biotechnol. Bioeng. 2011, 108, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Hanly, T.J.; Urello, M.; Henson, M.A. Dynamic flux balance modeling of S. cerevisiae and E. coli co-cultures for efficient consumption of glucose/xylose mixtures. Appl. Microbiol. Biotechnol. 2012, 93, 2529–2541. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Saa, P.; Nielsen, L.K. ll-ACHRB: A scalable algorithm for sampling the feasible solution space of metabolic networks. Bioinformatics 2016, 32, 2330–2337. [Google Scholar] [CrossRef] [PubMed]
- Hoffner, K.; Harwood, S.M.; Barton, P.I. A Reliable Simulator for Dynamic Flux Balance Analysis. Biotechnol. Bioeng. 2013, 110, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Gomez, J.A.; Höffner, K.; Barton, P.I. DFBAlab: A fast and reliable MATLAB code for dynamic flux balance analysis. BMC Bioinform. 2014, 15, 409. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, B.J.; Pérez-Correa, J.R.; Agosin, E. Construction of robust dynamic genome-scale metabolic model structures of Saccharomyces cerevisiae through iterative re-parameterization. Metab. Eng. 2014, 25, 159–173. [Google Scholar] [CrossRef] [PubMed]
- Hanly, T.J.; Henson, M.A. Unstructured modeling of a synthetic microbial consortium for consolidated production of ethanol. IFAC Proc. Vol. 2013, 12, 157–162. [Google Scholar] [CrossRef]
- Eiteman, M.A.; Lee, S.A.; Altman, E. A co-fermentation strategy to consume sugar mixtures effectively. J. Biol. Eng. 2008, 2, 3. [Google Scholar] [CrossRef] [PubMed]
- Goers, L.; Freemont, P.; Polizzi, K.M. Co-culture systems and technologies: Taking synthetic biology to the next level. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Bokinsky, G.; Peralta-Yahya, P.P.; George, A.; Holmes, B.M.; Steen, E.J.; Dietrich, J.; Soon Lee, T.; Tullman-Ercek, D.; Voigt, C.A.; Simmons, B.A.; et al. Synthesis of three advanced biofuels from ionic liquid-pretreated switchgrass using engineered Escherichia coli. Proc. Natl. Acad. Sci. USA 2011, 108, 19949–19954. [Google Scholar] [CrossRef] [PubMed]
- Haitjema, C.H.; Solomon, K.V.; Henske, J.K.; Theodorou, M.K.; O’Malley, M.A. Anaerobic gut fungi: Advances in isolation, culture, and cellulolytic enzyme discovery for biofuel production. Biotechnol. Bioeng. 2014, 111, 1471–1482. [Google Scholar] [CrossRef] [PubMed]
- Müller, M. Review article: The hydrogenosome. J. Gen. Microbiol. 1993, 139, 2879–2889. [Google Scholar] [CrossRef] [PubMed]
- Marvin-Sikkema, F.D.; Pedro Gomes, T.M.; Grivet, J.P.; Gottsehal, J.C.; Prins, R.A. Characterization of hydrogenosomes and their role in glucose metabolism of Neocallimastix sp. L2. Arch. Microbiol. 1993, 160, 388–396. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.N.; Gilmore, S.P.; O’Malley, M.A. Microbial communities for bioprocessing: Lessons learned from nature. Curr. Opin. Chem. Eng. 2016, 14, 103–109. [Google Scholar] [CrossRef]
- Kohler, P.R.; Metcalf, W.W. Genetic manipulation of Methanosarcina spp. Front. Microbiol. 2012, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Höffner, K.; Barton, P.I. Design of microbial consortia for industrial biotechnology. Comput. Aided Chem. Eng. 2014, 34, 65–74. [Google Scholar]
- Mahadevan, R.; Henson, M.A. Genome-Based Modeling and Design of Metabolic Interactions in Microbial Communities. Comput. Struct. Biotechnol. J. 2012, 3, e201210008. [Google Scholar] [CrossRef] [PubMed]
| Organism | Notes | Reference |
|---|---|---|
| Clostridium ljungdahlii str. 13528 | Bacterium, obligate anaerobe, acetogen | [21] |
| Escherichia coli str. K-12 substr. MG1655 | Bacterium, facultative anaerobe | [22] |
| Escherichia coli str. ZSC113 | Bacterium, facultative anaerobe, glucose deficient | [23] |
| Lactococcus lactis subsp. cremoris MG1363 | Bacterium, facultative anaerobe | [24] |
| Methanosarcina barkeri str. Fusaro | Methanogen, obligate anaerobe | [25] |
| Saccharomyces cerevisiae S288C | Fungus, facultative anaerobe | [26] |
| Organism | ||
|---|---|---|
| Clostridium ljungdahlii str. 13528 | 5 | 5 |
| Escherichia coli str. K-12 substr. MG1655 | 10.5 | 6 |
| Escherichia coli str. ZSC113 | 0 | 6 |
| Lactococcus lactis subsp. cremoris MG1363 | 14.5 | 0 |
| Methanosarcina barkeri str. Fusaro | 0 | 0 |
| Saccharomyces cerevisiae S288C | 6.44 | 0 |
| Product | (g/L/h or psi/h) | (1/h) | (h) |
|---|---|---|---|
| Glucose | 1.39 | 0.05 | 148.17 |
| Xylose | 0.53 | 0.05 | 150.41 |
| Pressure | 75.04 | 0.06 | 76.51 |
| Organism | Growth Rate in M2 (1/h) | Growth rate in MC [15] (1/h) |
|---|---|---|
| N. californiae | 0.029 | 0.046 |
| A. robustus | 0.033 | 0.065 |
| Neocallimastix sp. S1 | 0.027 | No data |
| Organism | Growth Rate (1/h) | Ethanol (g/L) | Acetate (g/L) | Formate (g/L) |
|---|---|---|---|---|
| C. ljungdahlii | 0.08 | 0 | 0.35 | 0 |
| E. coli MG1655 | 0.17 | 0.02 | 0.02 | 0.03 |
| E. coli ZSC113 | 0.04 | 0.01 | 0.02 | 0.03 |
| L. lactis | 0.04 | 0.13 | 0.32 | 0.51 |
| S. cerevisiae | 0.12 | 0.02 | 0 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilken, S.E.; Saxena, M.; Petzold, L.R.; O’Malley, M.A. In Silico Identification of Microbial Partners to Form Consortia with Anaerobic Fungi. Processes 2018, 6, 7. https://doi.org/10.3390/pr6010007
Wilken SE, Saxena M, Petzold LR, O’Malley MA. In Silico Identification of Microbial Partners to Form Consortia with Anaerobic Fungi. Processes. 2018; 6(1):7. https://doi.org/10.3390/pr6010007
Chicago/Turabian StyleWilken, St. Elmo, Mohan Saxena, Linda R. Petzold, and Michelle A. O’Malley. 2018. "In Silico Identification of Microbial Partners to Form Consortia with Anaerobic Fungi" Processes 6, no. 1: 7. https://doi.org/10.3390/pr6010007
APA StyleWilken, S. E., Saxena, M., Petzold, L. R., & O’Malley, M. A. (2018). In Silico Identification of Microbial Partners to Form Consortia with Anaerobic Fungi. Processes, 6(1), 7. https://doi.org/10.3390/pr6010007




