1. Introduction
The use of dynamic optimization for optimizing the performance of transient manufacturing processes has drawn much attention in recent years [
1]. A typical dynamic optimization problem is to find optimal trajectories for process control variables, e.g., flowrates in a chemical process, so that a particular performance index is maximized subject to some process constraints. Numerical solution of dynamic optimization problems poses a number of difficulties. First, optimization over control trajectories gives rise to an infinite-dimensional optimization problem, which must be transformed to an approximate finite-dimensional one by discretizing control trajectories. In so-called indirect methods [
2], control trajectories are discretized automatically along with the state variables as the integration routine solves a two-point boundary value problem. The resolution of the discretization depends on the error-control mechanism of the integrator. A disadvantage of indirect methods is the rather high level of expertise required to formulate the optimality conditions for problems of practical size and complexity. Moreover, it can be very difficult to solve the resulting boundary value problem, especially in the presence of constraints [
2,
3]. Direct methods, on the other hand, rely on a priori discretization of the control trajectories. Two main classes of direct methods are (i) the simultaneous method, where the dynamic model is also discretized, using e.g., collocation techniques and extra optimization variables [
4], to arrive at a fully algebraic model and (ii) the sequential method, where the dynamic model is retained, and instead is resolved using numerical integration [
5]. The focus in this work is on the sequential method that has shown capabilities for handling large-scale, stiff problems with high accuracy [
6], arguably due to keeping the problem dimension relatively small [
7] and the use of adaptive numerical integrators furnished with error control mechanisms.
The quality of the optimal solution is directly related to the quality of the control discretization, with a finer discretization generally offering an improved optimal solution. However, a finer discretization can lead to increased computational cost as a result of increased number of optimization variables, with too fine of a discretization also posing robustness issues [
8]. For the sequential method, it also increases the cost of computing the sensitivity information by introducing extra sensitivity equations to the dynamic model. The integration of sensitivity equations can be a computationally dominant task despite the significant progress made so far regarding their efficient calculation (see [
9,
10,
11]). This is especially true when the number of optimization variables is large, and can be a potentially limiting factor in applying dynamic optimization to large-scale processes.
A second difficulty with dynamic optimization arises from potentially severe nonlinearity caused by the embedded dynamic model. The nonlinearity can result in a highly nonconvex problem exhibiting many suboptimal local solutions. It is known that even small-scale dynamic systems can exhibit multiple suboptimal local solutions [
12,
13,
14]. Unfortunately, a derivative-based optimization method can become trapped in any of these, which can lead to a suboptimal operation and loss of profit.
To deal with the issue of control discretization, nonuniform (i.e., not equally spaced) discretization techniques can be applied to reduce the effective number of discretization points needed. A simple way to do this is by considering the location of the discretization points as extra optimization variables. However, the extra optimization variables can cause additional nonconvexity, and thus suboptimal, local solutions, especially when the number of discretization points is fairly large. In the authors’ experience, this strategy often leads to convergence difficulties, thereby defeating the point of using a coarser discretization for faster convergence. More elegant nonuniform discretization techniques have been proposed, where the discretization points over the time horizon are distributed adaptively based on the behavior of the optimal trajectories. As a result, excessive discretization can be avoided while maintaining the quality of the solution. Srinivasan et al. [
15] proposed a parsimonious discretization method for optimization of batch processes with control-affine dynamics. The method relied on analysis of the information from successive batch runs for approximating the structure of the control trajectory and improving the solution in the face of fixed parametric uncertainty. Binder et al. [
16] presented an adaptive discretization strategy, in which the problem with a coarse discretization of the control trajectory is first solved. Then, using a wavelet analysis of the obtained optimal solution, together with the gradient information, the discretization is refined by eliminating discretization points that are deemed unnecessary and adding new points where necessary. The problem with the refined discretization is then solved to give an improved optimal solution, and the procedure is repeated for further improvements. In a subsequent variant, Schlegel et al. [
17] used a pure wavelet analysis in the refinement step in order to make the strategy better suited for problems with path constraints. In addition, Schlegel and Marquardt [
18] proposed another adaptive discretization strategy that explicitly incorporates the structure of the optimal control trajectory. Specifically, the solution with a coarse discretization is used to deduce the structure based on the active or inactive status of the bound and path constraints, and the deduced structure is used to refine the discretization. A combination of the two strategies is also possible as presented in [
19]. Recently, Liu et al. [
20] proposed an adaptive control discretization method, in which the discretization is refined by a particular slope analysis on the approximate optimal control trajectories. The dynamic optimization problem is solved again with the refined discretization, and the procedure is repeated until a stopping criterion based on the relative improvement of the objective function is met. The foregoing strategies can be applied to a wide class of dynamic optimization problems arising from both batch and continuous processes. Nonetheless, a major drawback of them is the need for repeated solution of the dynamic optimization problem in order to arrive at a satisfactory optimal solution. Depending on the case, this may be even more costly overall than a one-time optimization with a sufficiently fine discretization. In addition, the post-processing of results required for each refinement step would take additional time and expertise.
In this paper, a new approach to control discretization is presented. Similar to the above-mentioned strategies, it aims to create an adaptive discretization based on a deduction of the structure of the optimal trajectories. However, a different philosophy is used for this purpose. Specifically, the proposed approach is based on turnpike theory [
21,
22] in optimal control, which analyzes optimal control problems with respect to the structure of the optimal solution, i.e., optimal trajectories of the control and state variables. Turnpike theory has been used in the context of indirect methods in [
23,
24,
25], where the structure of the optimal trajectories is exploited to approximate the resulting boundary-value problem by two initial-value problems corresponding to the initial and terminal segments of the time horizon. However, the focus in this work is on using turnpike theory for efficient control discretization in direct methods. Of particular interest is the input-state turnpike [
26,
27] structure, where both control and state optimal trajectories are composed of three phases: a transient phase at the beginning, followed by a non-transient phase that is close to the optimal steady state, followed by another transient phase at the end. This type of turnpike is called
steady-state turnpike in this paper. The proposed approach exploits this structure to place the discretization points in an “optimal” way. To do so, an adaptive discretization strategy is built into the dynamic optimization formulation. In this way, the solution structure and locations of the discretization points are adjusted “dynamically” during the optimization iterations so that optimal trajectories with an adapted discretization scheme are obtained at convergence. Therefore, unlike the previous strategies, only one dynamic optimization problem is solved in the proposed approach, and no post-processing of the results is needed. Furthermore, the proposed approach helps deal with the issue of suboptimal solutions by potentially avoiding a number of such solutions whose trajectories do not conform to the turnpike structure. It is noted, however, that this approach is most suitable for optimization of transient continuous processes in which an approximate steady state may occur. It is not meant for optimization of batch or semi-batch processes, in which steady state is not possible.
The remainder of the paper is organized as follows. The problem statement along with some background on turnpike theory is presented in
Section 2. The proposed control discretization approach is described in
Section 3. Numerical case studies are performed in
Section 4, which is followed by some conclusions in
Section 5.
2. Problem Statement and Pertinent Background
The dynamic optimization problem under study can take a quite general form. For simplicity, however, a minimal formulation is considered below:
where
and
are vectors of control and state variables, respectively, with
the state initial conditions;
is the set of admissible controls defined as
with
bounds on
;
and
are vector functions of appropriate sizes representing the dynamic model and process constraints, respectively. Note also that equality constraints or path constraints can be included in the formulation with no impact on the validity of the ensuing developments.
The time-dependent control variables
in Problem (
1)–(
4) give rise to an infinite-dimensional optimization problem. For a numerical solution, the problem dimension must be reduced to a finite one by discretizing
over the time horizon. In this work, the popular piecewise constant discretization approach is used for this purpose. With the time horizon
discretized over
N (not necessarily uniform) epochs
,
,...,
,
is approximated over each epoch by a constant parameter vector as
, with
and
. The discontinuities in
make the dynamic model (
2) a continuous-discrete hybrid dynamic system [
28]. The discrete behavior potentially occurs at times
,
(called event times). The dynamic system is said to switch from one mode to another at these times. The hybrid behavior can have implications regarding the differentiability of the dynamic system, and consequently that of the optimization problem, as discussed later.
The piecewise constant discretization reduces the optimization to one over the finite-dimensional parameter vector
. However, the optimal solution of the approximated problem is generally inferior to that of the original one. To improve the solution, a finer discretization may be used by increasing the number of epochs
N. The effect of increasing
N, and thus the number of optimization variables, on the computational cost of the solution is twofold: (i) it increases the cost of parametric sensitivities that are calculated during solution of the dynamic model, as required by a gradient-based optimization solver; and (ii) it can increase the cost of optimization by requiring more iterations to be performed within the larger search space. In some cases, increasing
N too much can also lead to robustness issues [
8] and failure of the optimization solver.
The above computational concerns become even more important when dealing with large-scale models of real-life manufacturing processes. This motivates efficient control discretization strategies that can maintain the solution quality with a coarser discretization scheme. The new discretization approach presented in this paper relies on turnpike theory, which is reviewed in the following subsection.
Turnpike in Optimal Control
It appears that turnpike theory in optimal control was first discussed in the field of econometrics [
22], and later gained attention in other fields including chemical processes [
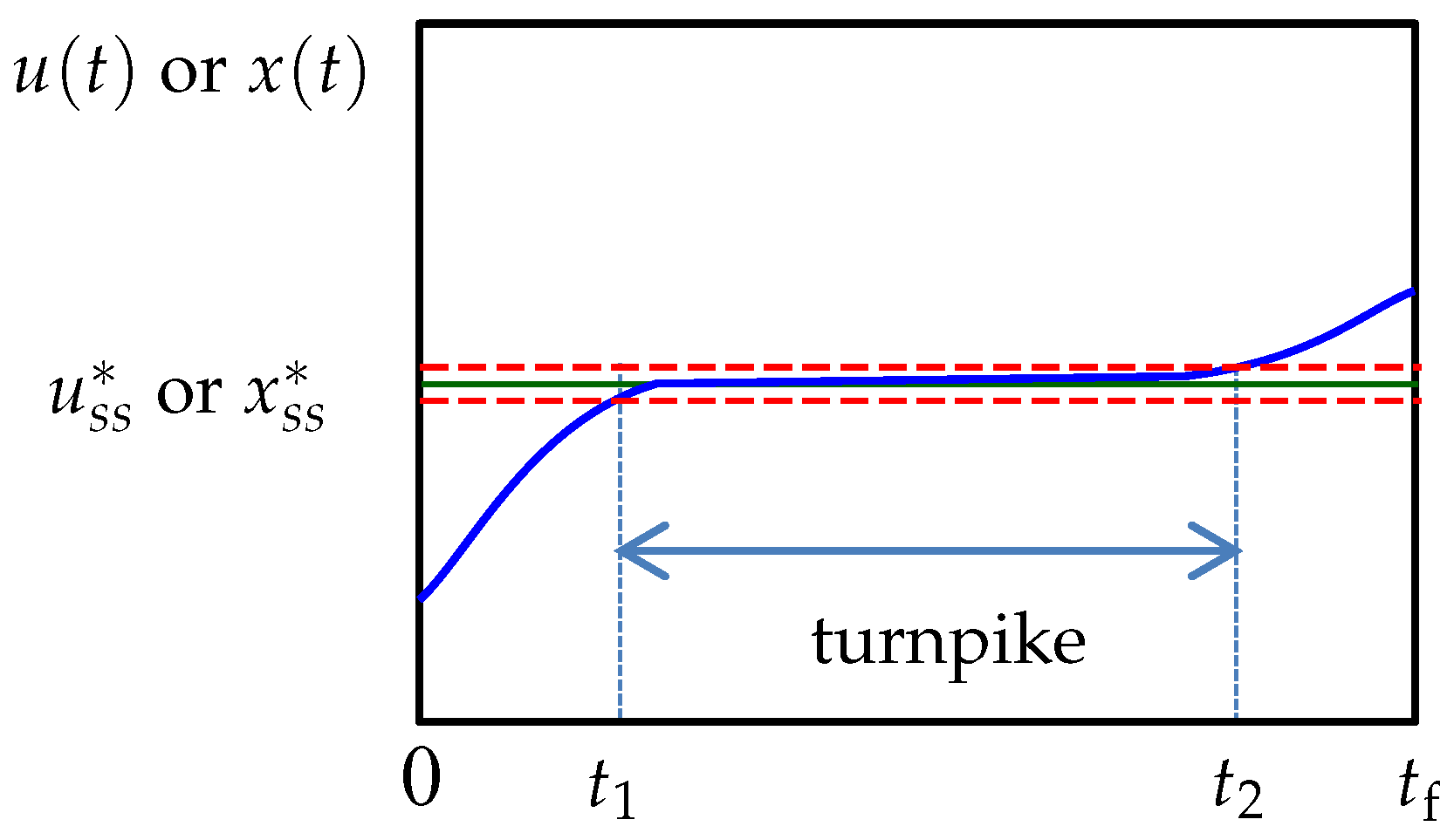
29]. The theory characterizes the structure of the solution of an optimal control problem by describing how the optimal control and state trajectories of a system evolve with time. It was initially investigated for optimal control problems with convex cost functions (in a minimization case). In particular, it was established that, given a time horizon
, the time the optimal trajectories spend outside an
-neighborhood of the optimal steady state is limited to two intervals
and
, where
, with
. The system is said to be in a transient phase in these intervals. The interesting point is that
is independent of
but only dependent on
and the initial and final conditions of the system [
30,
31]. If the time horizon is long enough, i.e.,
, then a turnpike appears between
and
, and the turnpike trajectories lie in the
-neighborhood of the optimal steady state. See
Figure 1 for visualization of the concept. An appealing implication of turnpike theory is that an increase in
will only stretch the duration of the turnpike, and has no effect on the duration and solution of the transient phases [
32]. For relatively large
, the optimal trajectories will traverse close to the optimal steady state for most of the time horizon, and the transient phases will be short in comparison.
The extension of turnpike theory to nonconvex problems has led to generalized definitions of the turnpike, in which it may no longer be a steady state, but a time-dependent trajectory [
31,
33]. Nonetheless, the interest in the present work is in a steady-state turnpike for generally nonconvex problems. Recently, it was shown in [
27,
34] that the steady-state turnpike still occurs if the convexity assumption is replaced by a dissipativity assumption. In particular, they present a notion of strict dissipativity, and prove that, if a dynamic system is strictly dissipative with respect to a reachable optimal steady state, then the optimal trajectories will have a turnpike at that steady state. Such a turnpike emerges in practice if the time horizon is sufficiently long. The equivalence of strict dissipativity and steady-state turnpike is a key result in optimal control and has applications in stability analysis of economic model predictive control [
35,
36].
3. Proposed Adaptive Control Discretization Approach
It is known that the emergence of a steady-state turnpike can be exploited in the numerical solution of optimal control problems, as noted in, e.g., [
32,
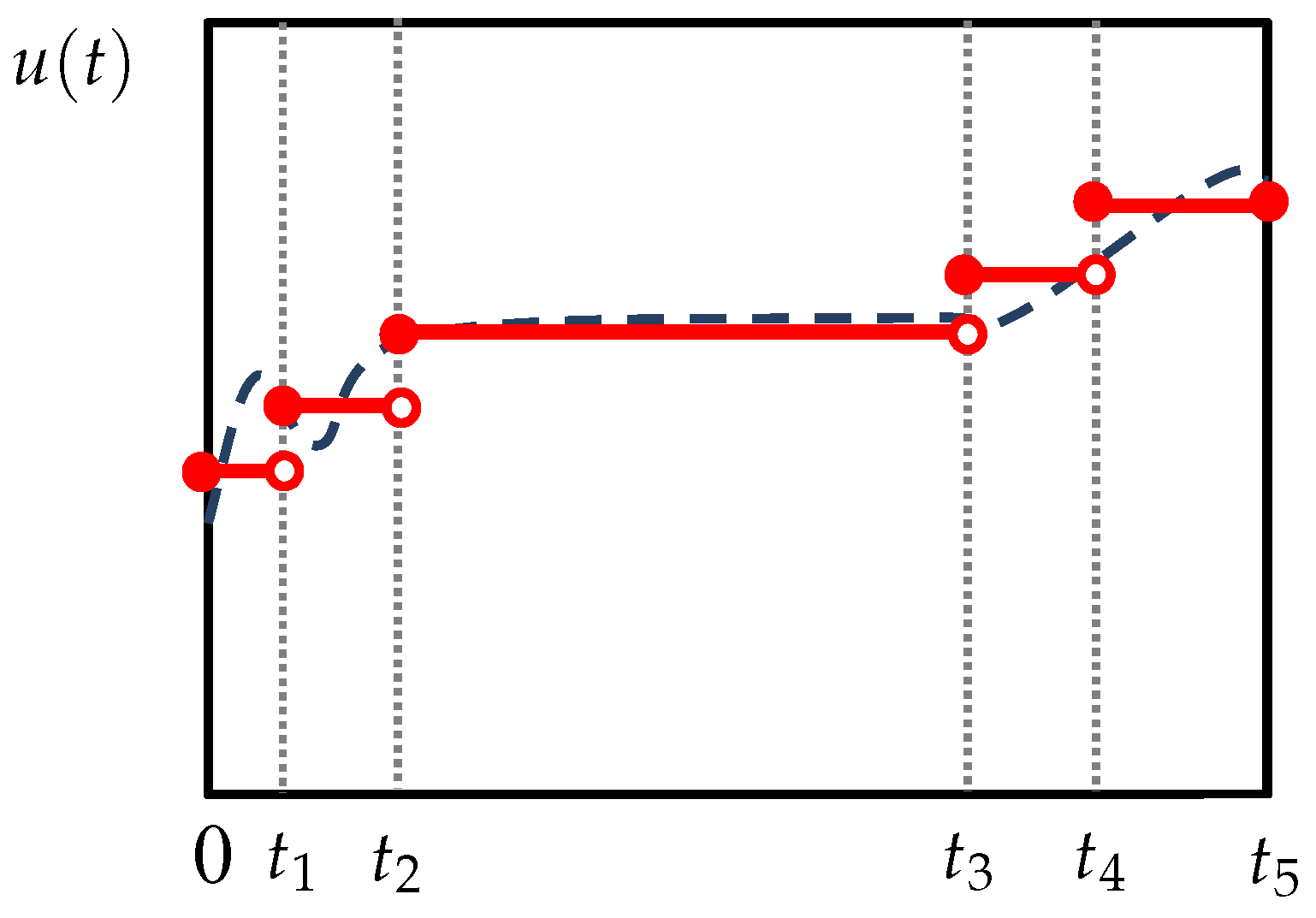
37], especially for problems with sufficiently long time horizons. In particular, the control trajectories need not be discretized over the entire horizon, but only over the intervals before and after the turnpike. If the turnpike interval is considerably long, this results in a coarser discretization and can reduce the computational load, as discussed earlier. However, the difficulty is that the duration of the turnpike and its location in the optimal trajectory are not known a priori. Therefore, it is not possible to adapt the discretization in advance based on the turnpike structure. To resolve this issue, this work considers embedding the tasks of approximating the turnpike structure and adaptive discretization into the dynamic optimization formulation. In this way, no pre- or post-processing for adjusting the discretization is needed. To this end, a first idea involves performing a nonuniform discretization where the duration of the epochs, i.e.,
and
for
are themselves optimization variables. To account for the turnpike, the parametrized controls on one of the intermediate epochs, e.g., the middle one, can be set to their optimal steady-state values. The following optimization problem will then result:
where
gives the smallest integer not less than
a. The optimal steady-state control
is obtained from solving the following static optimization problem:
where
are the bounds on
. Problem (
5)–(
10) will generally prescribe a nonuniform discretization to minimize the objective function. Particularly, the optimizer can adjust
so that only one epoch, here [
,
), is enough to represent the steady-state turnpike. The remaining
epochs are automatically adjusted to cover the transient phases, where a finer discretization is needed. Problem (
5)–(
10) leads to a total of
optimization variables. The nonuniform discretization is shown schematically in
Figure 2, where the middle epoch
is enlarged to cover the steady-state turnpike. In case no turnpike appears in the optimal solution, the
corresponding to the turnpike can be simply pushed to zero by the optimizer. Therefore, the existence of a turnpike is not assumed and need not be verified in advance.
Note that the nonuniform discretization in Problem (
5)–(
10) results in a hybrid dynamic system with variable switching times
. For numerical reasons, a change of variable is usually used to transform Problem (
5)–(
10) to one with fixed switching times [
38,
39]. More details about this transformation are deferred to the next subsection.
With the flexibility in the values of , it is expected that a lower N suffices to achieve the same optimal solution as in a uniform discretization. However, the addition of N optimization variables in the nonuniform discretization strategy can adversely affect the overall computational cost and offset the benefits gained by a coarser discretization. It could contribute to more nonconvexity and thus local suboptimal solutions. The alternative proposed in this work is a semi-uniform adaptive discretization approach, as described in the sequel.
Semi-Uniform Adaptive Control Discretization
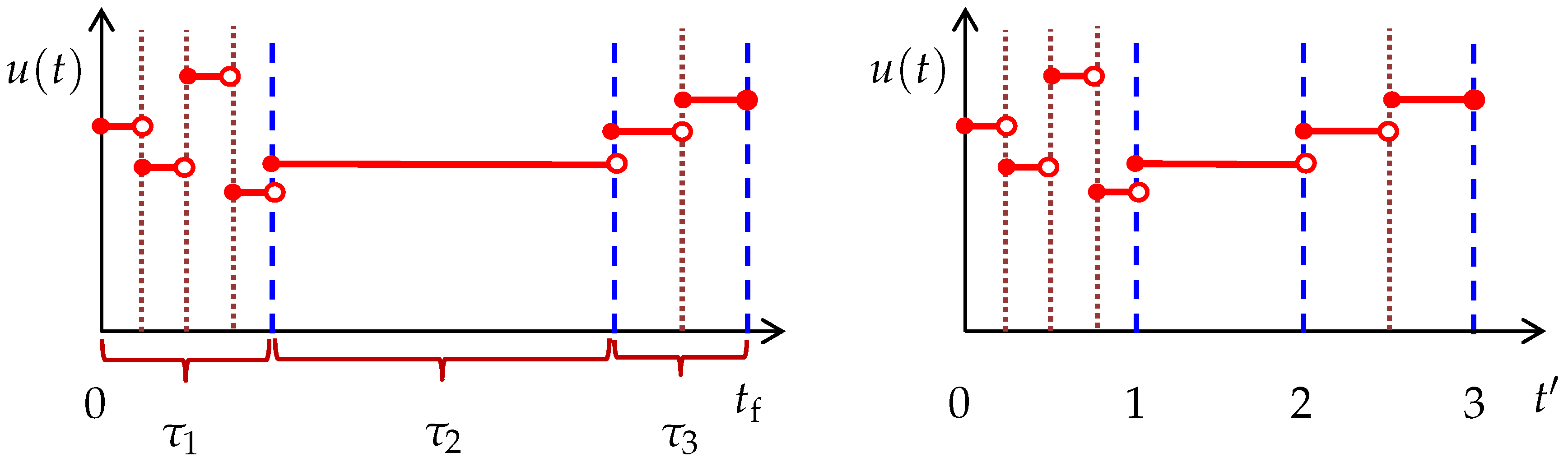
Here, a semi-uniform discretization approach for utilizing turnpike theory is proposed. The idea is to limit the use of nonuniform discretization where possible, while still being able to accommodate the variable durations of the steady-state turnpike and transient phases. To do so, the time horizon is split into the three phases prescribed by turnpike theory: two transient phases and a steady-state turnpike in between (see
Figure 1). A uniform discretization is then applied on the transient phases, which connect to each other by one epoch representing the turnpike. The durations of these three phases are included as extra optimization variables. The approach is depicted in the left plot of
Figure 3, where
,
, and
denote the unknown durations of the first transient, turnpike, and second transient phases, respectively. Observe that the durations of the epochs in each particular phase are equal although they are generally not equal from one phase to another, hence a semi-uniform discretization. In addition, note that each of the transient phases can take a different resolution (i.e., number of epochs). This will allow for a more accurate solution of systems where, based on experience or engineering insights, one transient phase is deemed to be considerably longer or more severe than the other, thereby requiring a finer discretization. The semi-uniform discretization approximates
as follows. Suppose the first transient phase (also called
startup hereafter) is discretized into
uniform epochs. Then, the control vector
over
is approximated as
,
, with
and
. In addition, suppose the second transient (also called
shutdown hereafter) is discretized into
uniform epochs. Then, the control vector
over
is approximated as
,
, with
and
. Notice that
,
represents the one-epoch discretization corresponding to the turnpike. With this discretization scheme, the proposed approach can be formulated through the following dynamic optimization problem:
where
is the total number of epochs. The extra variables
allow for the flexibility required to approximate the transient and turnpike phases well. Unlike the nonuniform formulation, however, the proposed formulation accommodates this flexibility by introducing only three extra optimization variables, regardless of the total number of epochs considered (the total number of optimization variables is
in this formulation). Furthermore, if a steady-state turnpike does not appear for a particular system, the optimizer would push
to zero. Therefore, the emergence of a turnpike need not be known a priori. However, this approach will best serve its purpose of reducing the computational cost if a turnpike exists and appears in the solution trajectories.
Similar to Problem (
5)–(
10), the proposed formulation results in a hybrid dynamic system with variable switching times. This is because the locations of discretization points depend on the variables
. For example, the switch for
from the first epoch to the second occurs at time
according to the following statement:
Similarly, other switching times depend on
and are not fixed. The computation of parametric sensitivities in a hybrid system where the switching times are a function of the parameters is involved and requires some assumptions for the system to ensure existence and uniqueness of the sensitivities [
28]. Moreover, the parametric sensitivities are generally discontinuous over the switches [
38], and additional computations are necessary to transfer the sensitivity values across the switches [
28]. To avoid these numerical complications, the time transformation presented in [
39,
40] is used so that the switching times are fixed in the transformed formulation. In particular, the time horizon
is transformed to a new time horizon
using
in which
is a piecewise constant function on
. With this transformation, Problem (
13)–(
18) is rewritten as:
where
. Interestingly, each of the startup, turnpike, and shutdown phases has a duration of 1 in the
domain, as shown in the right plot of
Figure 3. Moreover, the switch from one phase to another now occurs at fixed times
and
. Accordingly, all the control switches are triggered at fixed times in the new time domain. This ensures existence and uniqueness of the parametric sensitivities and their continuity over the switches [
28].
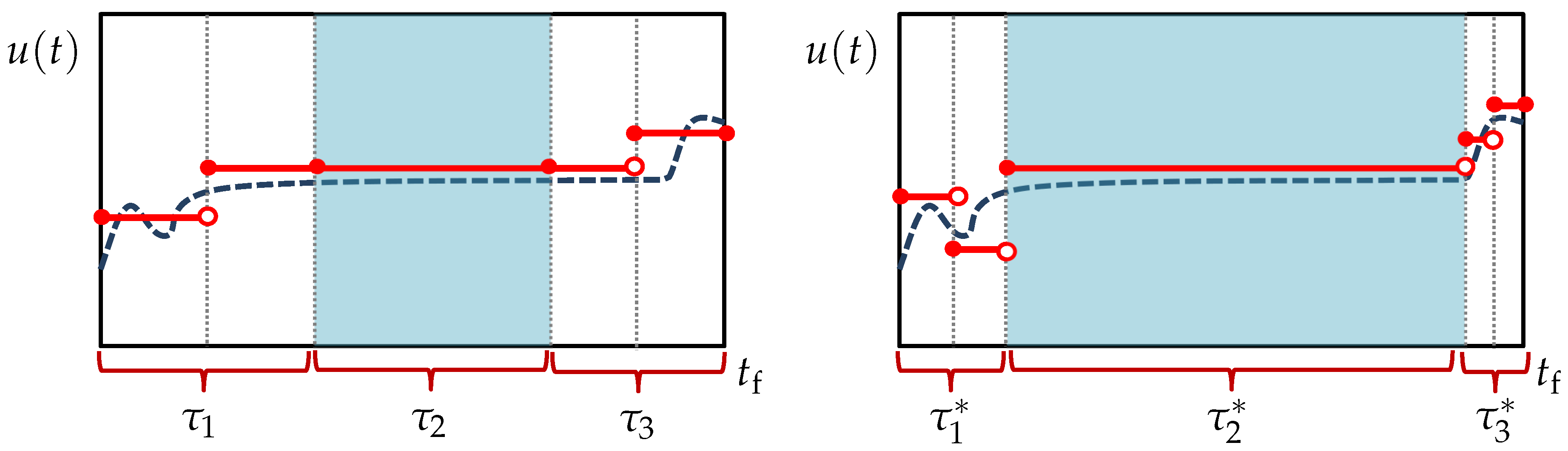
Despite the adaptive discretization strategy incorporated in Problem (
22)–(
27), the quality of the optimal solution can still depend on the resolutions set for the transient phases (
and
). If these resolutions are too coarse, the optimal solution may be compromised because the optimizer may have to adjust the
s away from their true values, e.g., in order to keep the problem feasible. Even with an adequate resolution, it is possible that the
s are under- or over-approximated by the local optimizer, thereby leading to an inferior solution. In some instances, it may be possible to avoid such a suboptimal solution by special modifications to the proposed formulation. In the next subsection, a variant formulation that can avoid a particular suboptimal scenario is presented.
4. Results and Discussion
In this section, three examples are considered to demonstrate the proposed discretization approach, and compare it against conventional uniform discretization and the nonuniform discretization approach, i.e., Problem (
5)–(
10), which was described earlier in this paper. The local gradient-based solver IPOPT [
41] is used to solve the optimization problems. The integration of the hybrid dynamic systems and parametric sensitivity calculations are performed by the software package DAEPACK (RES Group, Needham, MA, USA) [
42,
43]. Note that DAEPACK is best suited for large-scale, sparse problems, and, due to the overhead associated with sparse linear algebra, may not be an optimal choice for the small-scale problems considered here. In addition, the global solver BARON [
44] within the GAMS environment [
45] is used to solve the static Problem (
11)–(
12) to global optimality. The numerical experiments are performed on a 64-bit Ubuntu 14.04 platform with a 3.2 GHz CPU.
4.1. Example 1
Consider the following dynamic optimization problem:
where
. The optimal steady-state values required for the nonuniform discretization and proposed approaches are easily obtained by inspection as
. In addition, the tolerance values used in the variant formulation are set to
and
. The optimal objective values and solver statistics for the uniform discretization with different numbers of epochs, nonuniform discretization, and the proposed approach are provided in
Table 1. With the same number of epochs
, the optimal solution from the proposed approach is significantly better than the one obtained from the uniform discretization. The uniform discretization was able to reach the same optimal solution only when
epochs were applied. In addition, with the same optimal solution
, the proposed approach converges remarkably faster, i.e., about 10 times, compared to the uniform discretization. This speed-up is due to the coarser discretization that has resulted in both fewer iterations and lower cost per iteration. The latter is because, with much fewer optimization variables, the proposed approach has a much smaller parametric sensitivity system to solve during integration. Additionally, fewer epochs mean fewer restarts of the integration at the beginning of each epoch. This can further speed up the integration. Within the proposed approach, it is seen that both the main and variant formulations yield the same solution. The variant formulation requires slightly fewer iterations to converge, which could be due to the smaller search space resulting from Constraint (
33). Nevertheless, its convergence time is slightly higher; this can be attributed to the higher cost per iteration resulting from the auxiliary differential equation representing Constraint (
33) and corresponding sensitivities. Finally, notice that the nonuniform discretization strategy did not converge after 1000 iterations.
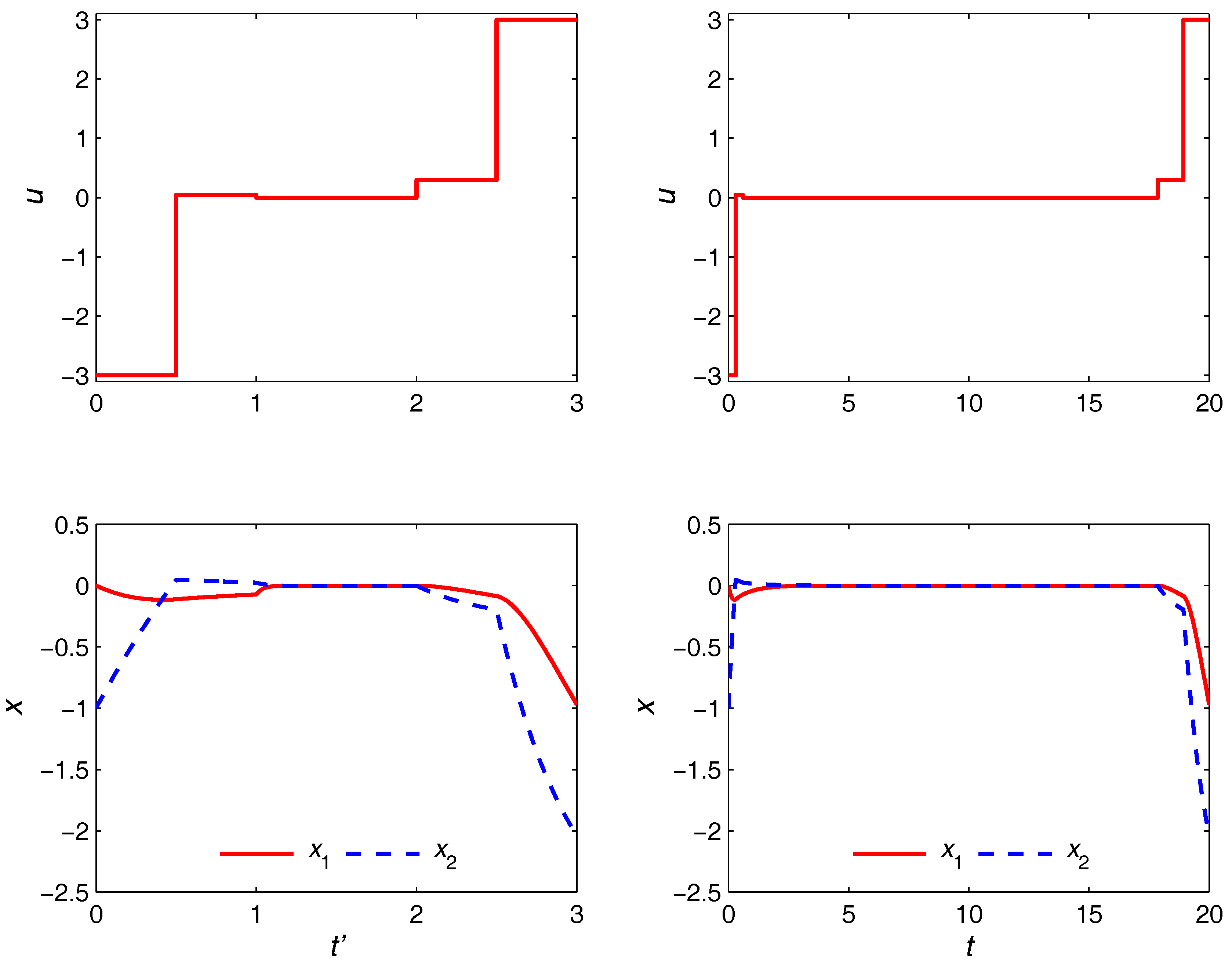
The optimal trajectories obtained from the nonuniform discretization strategy are given in
Figure 5. It is seen that the steady-state turnpike is realized for both
and
cases. However, with the coarser discretization, the turnpike is realized only partially due to the limited number of control moves available and inability to adjust their switching times optimally. Specifically, the control
u must depart from its optimal steady state as early as
in order to use the remaining two epochs to satisfy the terminal equality constraint. On the other hand, with
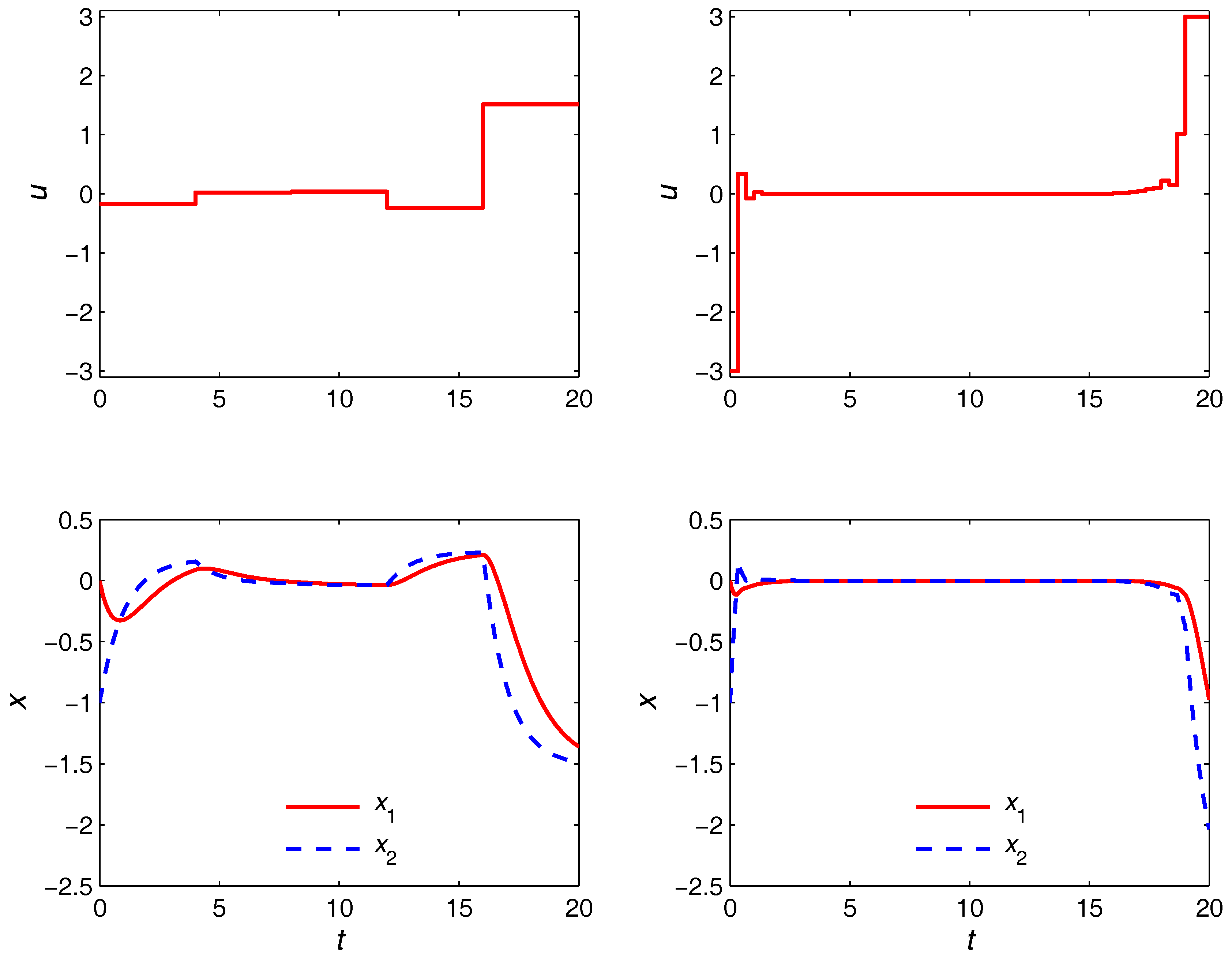
epochs, the turnpike is realized to (possibly) its full extent due to the much higher degree of freedom in the control moves. This is to be compared with the optimal trajectories in the right plot of
Figure 6, where the proposed approach is shown to be able to yield quite the same trajectories with only five control moves. The durations of the transient and turnpike phases in this case are obtained as
. The left plot in
Figure 6 shows the optimal trajectories in the
domain, in which the optimization problem is solved. Observe that the duration of each phase is 1 regardless of the
values.
4.2. Example 2
This example considers a non-isothermal Van de Vusse reactor adapted from [
46], in which the following reactions occur:
with B the desired product. The dynamic model of the reactor is given as:
where
denotes the concentration of i;
T and
are the temperatures of the reactor and cooling jacket, respectively;
V is the reaction volume; and
is the outlet flowrate. Here, the original model in [
46] has been modified to allow a varying volume. It is worth noting that, for the original model, conditions ensuring strict dissipativity, and, thus, potential emergence of turnpike have been verified in [
27]. Nonetheless, such a result is not required in this work since it makes no assumption on the presence of a turnpike. The initial conditions are given as:
In addition, the model constants are provided in
Table 2. For simplicity, the normalized heat transfer coefficients
and
are assumed to be independent of the volume
V [
47]. The operation takes
h. As a safety precaution, the reactor temperature
T must not exceed 110 °C anytime during the operation. Similarly, the concentration of D must not exceed 500
. At the final time, the reactor volume
V must be 0.01 m
3 or less. The optimization variables are the inlet flowrate
and the cooling power
, which are allowed to vary within
m
3 h
−1 and
kJ h
−1, respectively. With the goal of maximizing the production of B, the dynamic optimization problem can be formulated as:
The optimal steady-state values required for the nonuniform discretization and proposed approaches are obtained from
where
is the vector containing all the concentrations, and the steady-state model refers to the dynamic model (
38) with the time derivatives set to zero. Notice that the path constraints on
and
T are included in Problem (
41) as upper bounds for the corresponding variables. Except these and the lower bound of zero on the concentrations, other bounds on the state variables have no process implications and are placed so that the global solver can proceed. Once a global optimum is found, the solution must be checked to make sure these arbitrary bounds are not active.
The global solution of Problem (
41) is obtained in less than
s, with the optimum point
m
3 h
−1,
kJ h
−1,
mol m
−3,
°C, and
m
3.
The optimal solution and solver statistics for the different discretization strategies are given in
Table 3. For the variant formulation of the proposed approach, the settings
and
are used. Similar to the previous example, the proposed approach yields a better optimal solution than the uniform discretization with the same number of epochs. The optimal solution of the latter improves by increasing the number of epochs to
. Nonetheless, it is still inferior to the one obtained from the proposed approach with
. Increasing
N to 70 did not lead to an improved result as the solver failed after 207 iterations. The same problem occurred with
. This shows that a finer discretization is not always beneficial in practice as it can lead to numerical issues. Similarly, the nonuniform discretization with
terminated with a failure message indicating local infeasibility. However, this problem is known to be feasible because a more constrained version of it, i.e., the proposed semi-uniform discretization approach with
, is feasible (see
Table 3). Therefore, the reported local infeasibility is only due to numerical issues that apparently arise from including the duration of epochs as extra optimization variables. In terms of the solution speed, the CPU times show that the proposed approach (main formulation) converges to a
better solution about 10 times faster than the uniform discretization with
. This is in spite of the significantly more iterations that are taken by the proposed approach. The speed-up is even more remarkable for the variant formulation, i.e., about 37-fold.
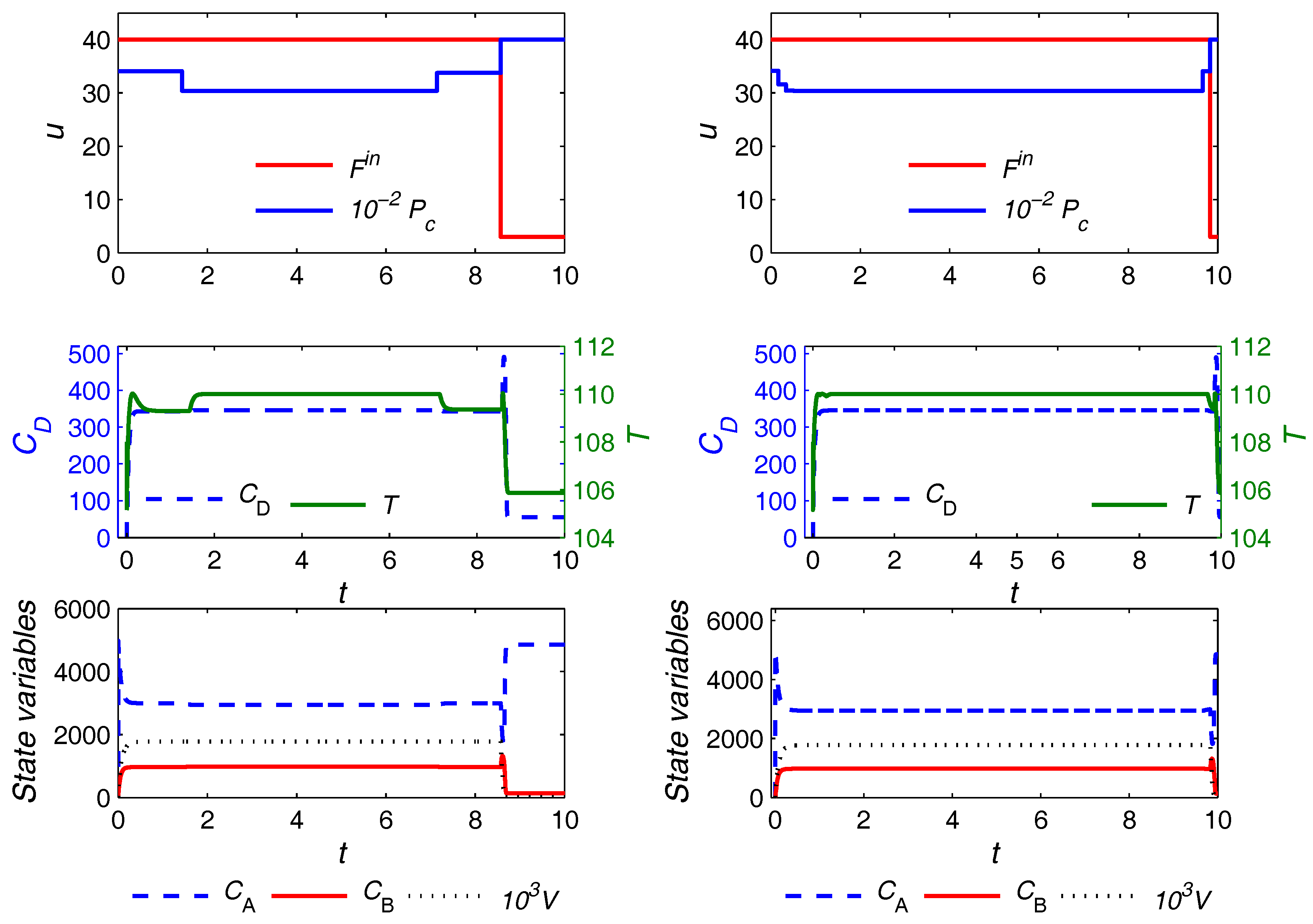
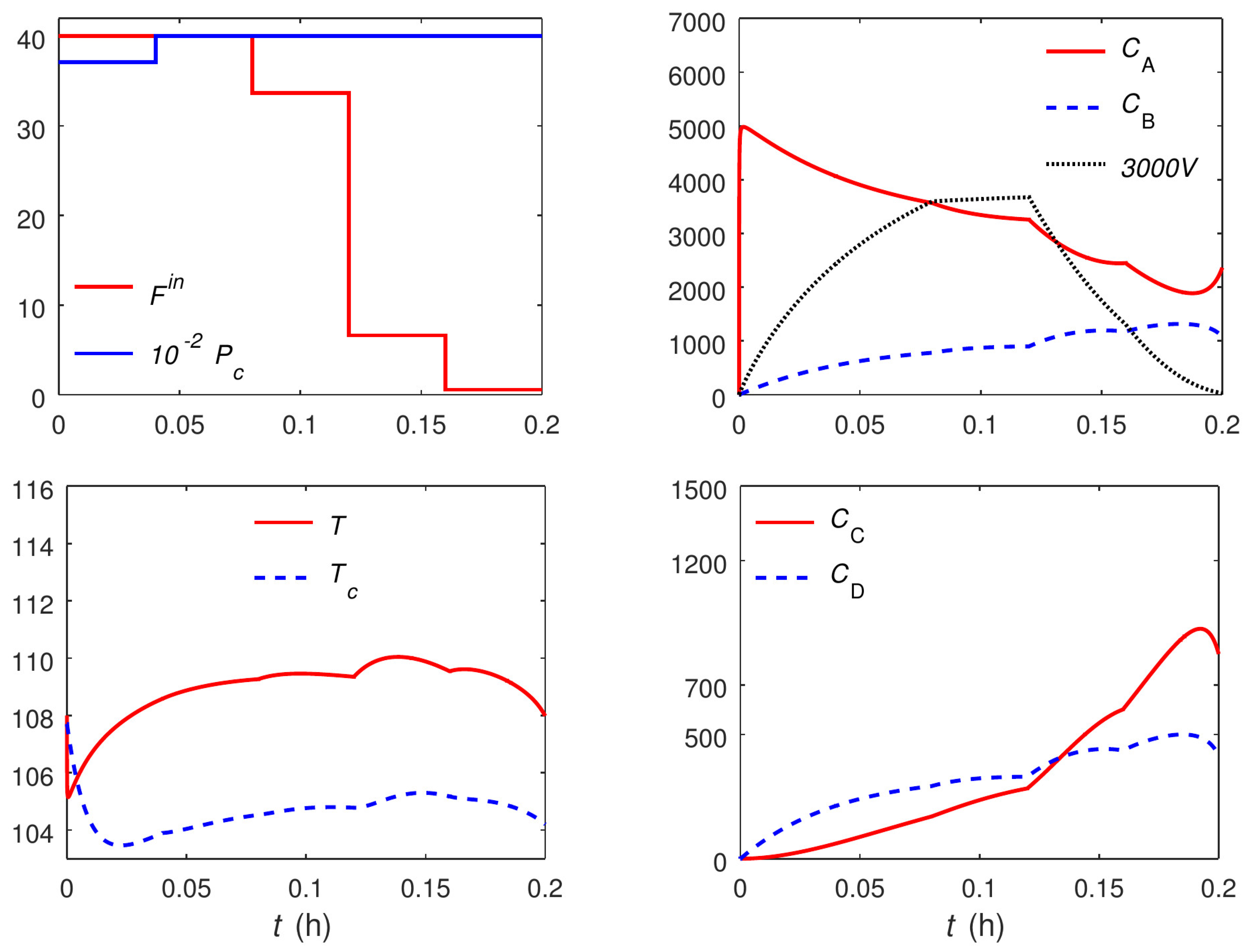
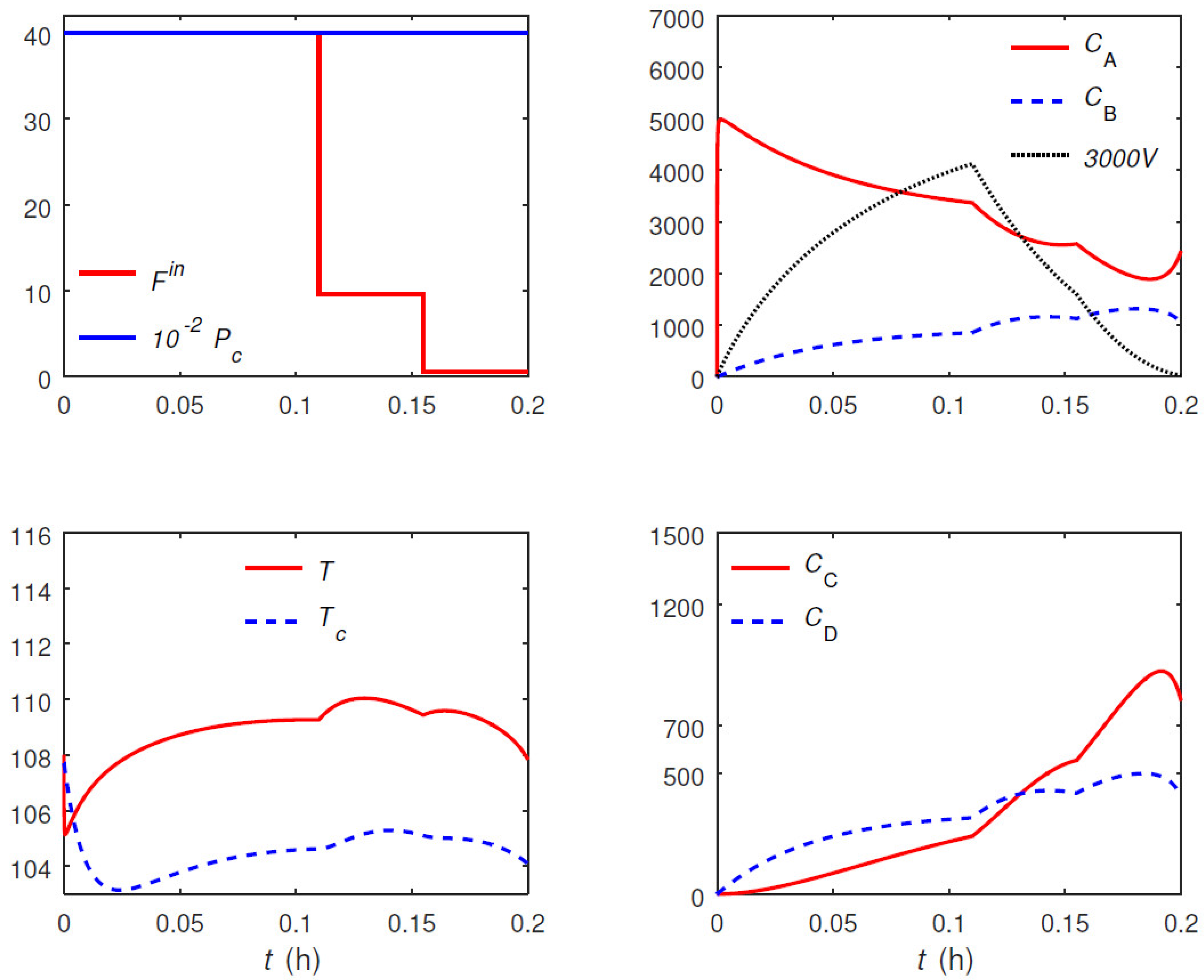
The optimal trajectories for control variables and a selection of the state variables in the case of the uniform discretization with
and the proposed approach (both variants) are plotted in
Figure 7 and
Figure 8, respectively. The units for the quantities are consistent with those reported in
Table 2. Similar observations as in the previous example hold here, and are omitted for brevity. The only notable additional point is that, here, the optimal trajectories from the main and the variant formulations are not exactly the same, although the difference can hardly be noticed. Moreover, the main and the variant formulations converge to slightly different values for the triplet
, i.e.,
and
h for the main and variant formulations, respectively. The optimal objective value from both formulations, however, is almost the same despite the slight difference in the computed optima.
Shorter Time Horizon
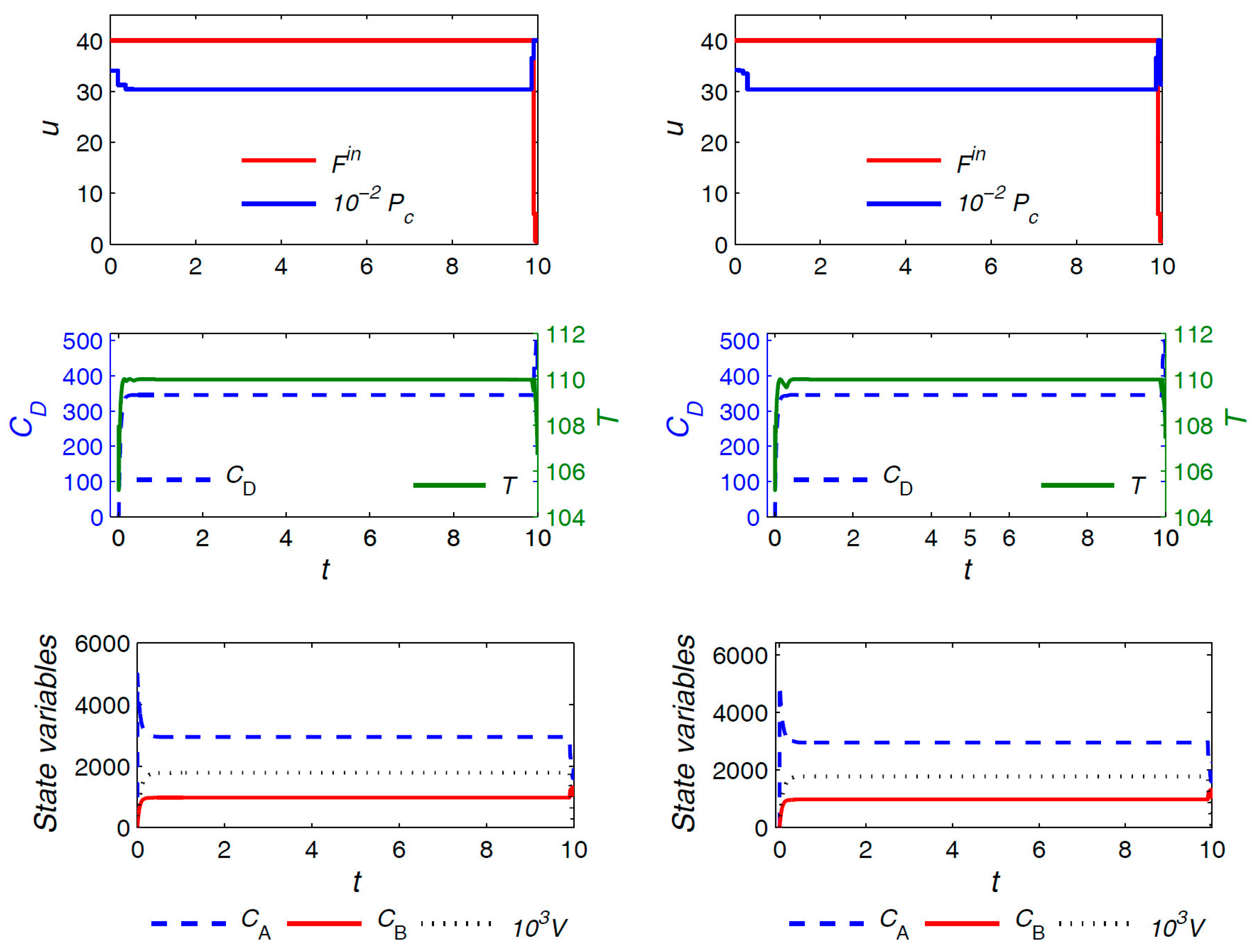
Here, the Van de Vusse reactor is revisited with a time horizon that is too short for the turnpike to appear. The purpose of this case study is to show that the proposed discretization approach still works in such conditions, although it may not be computationally more efficient than conventional discretization. To this end, the final time is reduced to
h, and the problem is solved using the uniform discretization with
and the proposed approach with
(
). The computational results are given in
Table 4, and the optimal trajectories for the case of
are plotted in
Figure 9 and
Figure 10. It is seen that the optimal trajectories do not reach a steady-state turnpike. Despite this, the proposed approach is still able to solve the problem, and even converge to a slightly better solution than the uniform discretization with
. The durations of the transient and turnpike phases are obtained as
h. Interestingly enough, it is seen that the duration of the turnpike is pushed to zero by the optimizer, reducing the effective number of epochs to four. The convergence to a better solution despite the absence of a turnpike and lower number of epochs can be explained by the inherent flexibility of the proposed approach in adjusting the location and duration of epochs. Note, however, that the uniform discretization with
is able to yield yet an improved solution. In both cases, the solution with the uniform discretization converges somewhat faster, than the proposed approach. This suggests that, for very short time horizons, the extra computational overhead introduced by the proposed approach may not be offset by the reduction in the number of epochs.
4.3. Example 3
Finally, dynamic optimization of a continuous stirred-tank reactor adapted from [
47] is presented. The following reactions take place in the reactor:
where P and I are the desired and undesired products, respectively;
and
are the kinetic constants. Two pure streams at the flowrates
and
and concentrations
and
, respectively, enter the reactor. The reactor is modeled as:
with
being the outlet flow rate, where
is a positive constant, and the initial conditions are given by
The model parameters and the initial conditions are found in
Table 5. The operation takes
min, and the objective is to maximize production of P during this period. The inlet flow rates are taken as the optimization variables. The following dynamic optimization problem is formulated:
The optimal steady-state values required for the nonuniform discretization and proposed approaches are obtained from
where
is the vector containing all the concentrations, and the steady-state model refers to Problem (
42) with the time derivatives set to zero. Similar to the previous example, bounds on the volume and the concentrations of A, B, and P have no process implications and are placed so that the global solver can proceed. The obtained global solution is accepted if these arbitrary bounds are not active.
The global solution of Problem (
45) is obtained in 0.016 s, with the optimum point
L min
−1,
mol L
−1, and
L.
Table 6 shows the optimal solution and solver statistics for the uniform, nonuniform, and proposed discretization strategies. The tolerances
and
are used for the variant formulation of the proposed approach. With
epochs, the proposed strategy and its variant yield a considerably improved solution compared to the uniform discretization. The variant formulation outperforms the main one in both number of iterations and CPU time. It also slightly outperforms the uniform discretization with
in the same respects. The durations of the transient and turnpike phases for the proposed approach (both formulations) are obtained as
min.
The uniform strategy converges to the same solution with a much higher number of epochs () and a markedly higher computational time (93% and 200% slower compared to the main and variant formulations, respectively). Here, the nonuniform strategy converges quite closely to the optimal solution of with only two epochs. With only one more epoch, the nonuniform strategy is able to reach this solution (and slightly improves upon it). Nonetheless, the solution takes a much higher CPU time than the one with the proposed strategy, i.e, 1.8 and 2.8 times higher than the main and variant formulations, respectively. The durations of the three epochs used by the nonuniform discretization are obtained as min.
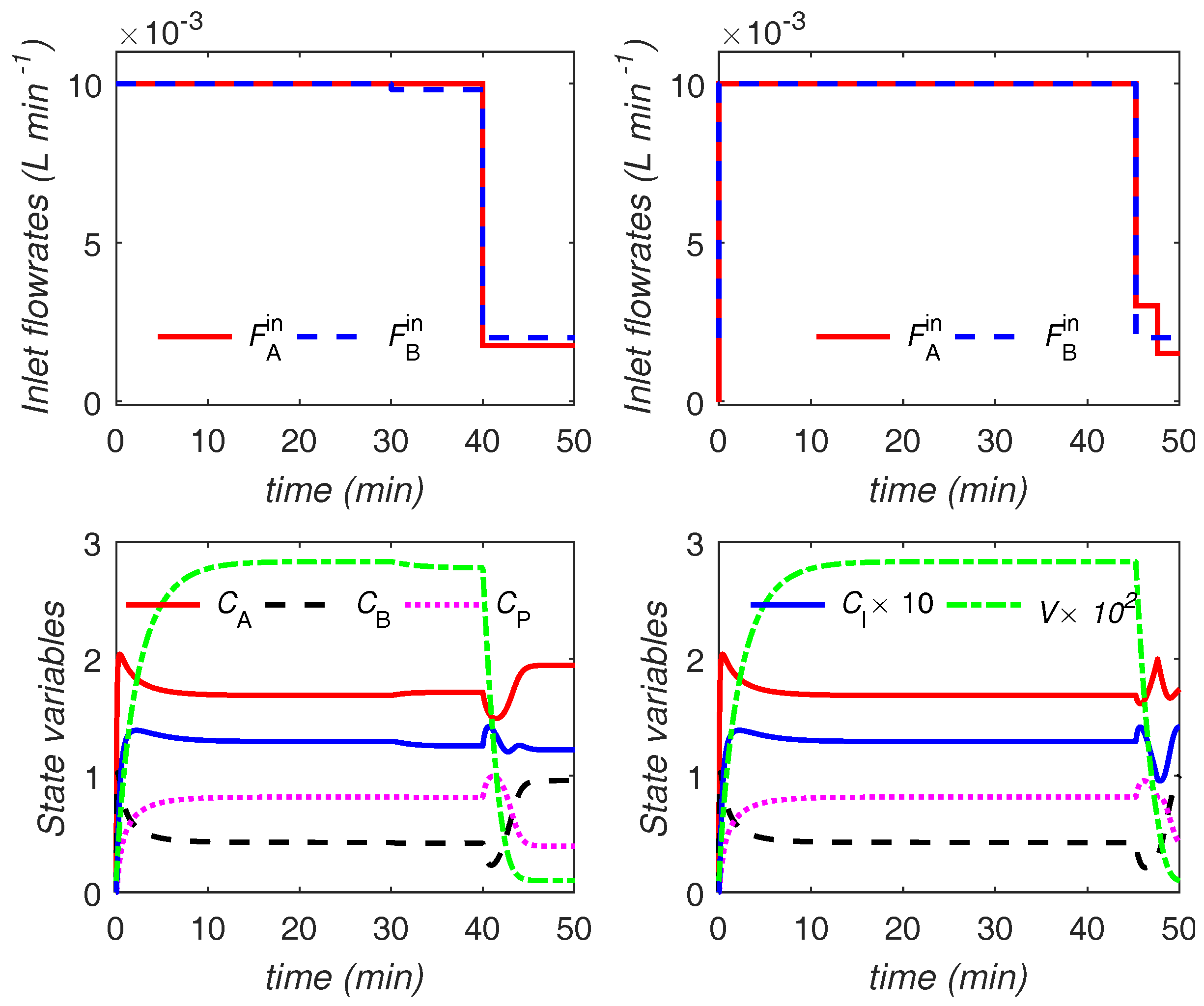
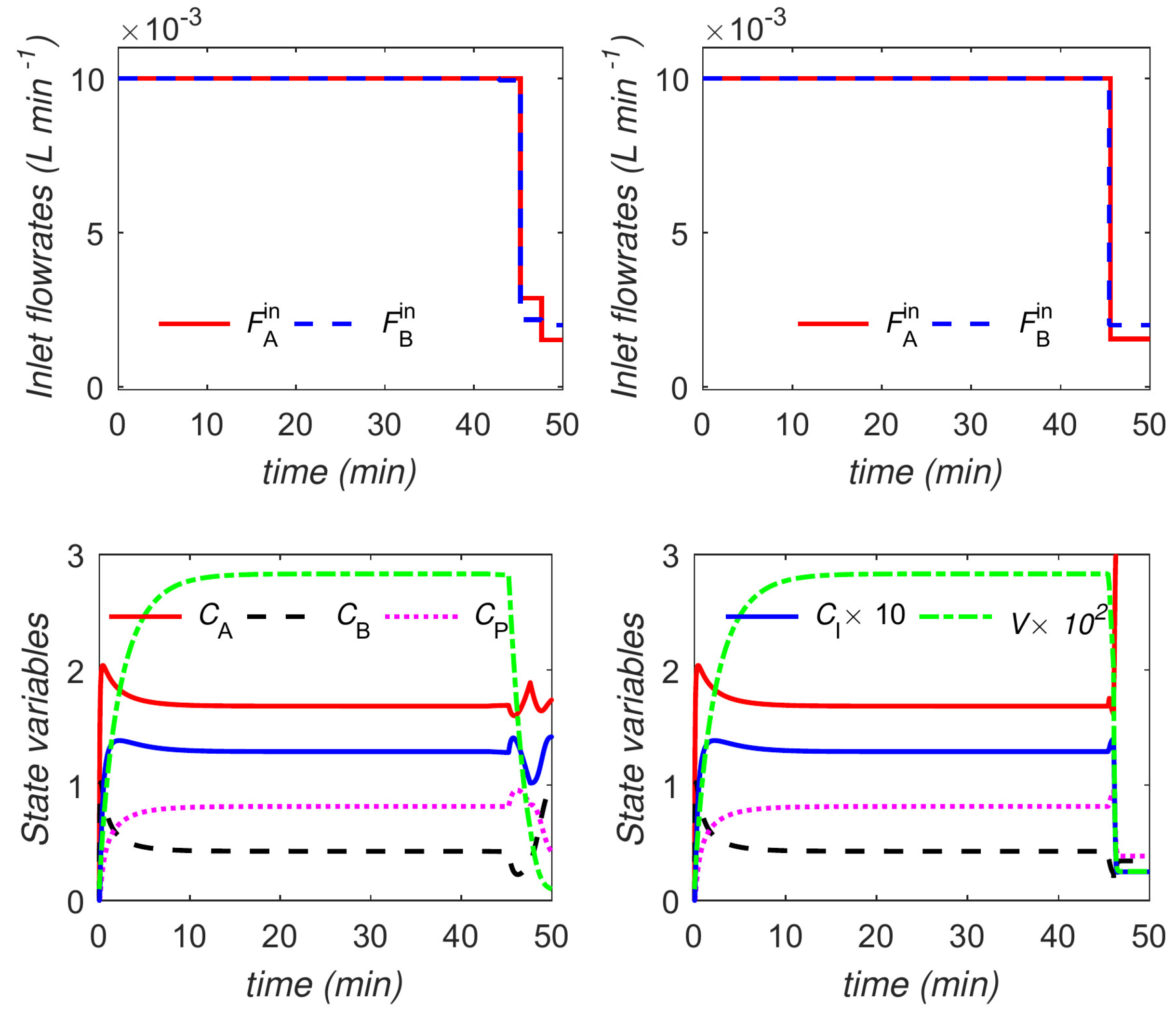
The optimal trajectories are shown in
Figure 11 and
Figure 12. The trajectories for the main and variant formulations of the proposed approach are identical.